Effective Population Size Is Positively Correlated with Levels of Adaptive Divergence among Annual Sunflowers

Abstract

The role of adaptation in the divergence of lineages has long been a central question in evolutionary biology, and as multilocus sequence data sets have become available for a wide range of taxa, empirical estimates of levels of adaptive molecular evolution are increasingly common. Estimates vary widely among taxa, with high levels of adaptive evolution in Drosophila, bacteria, and viruses but very little evidence of widespread adaptive evolution in hominids. Although estimates in plants are more limited, some recent work has suggested that rates of adaptive evolution in a range of plant taxa are surprisingly low and that there is little association between adaptive evolution and effective population size in contrast to patterns seen in other taxa. Here, we analyze data from 35 loci for six sunflower species that vary dramatically in effective population size. We find that rates of adaptive evolution are positively correlated with effective population size in these species, with a significant fraction of amino acid substitutions driven by positive selection in the species with the largest effective population sizes but little or no evidence of adaptive evolution in species with smaller effective population sizes. Although other factors likely contribute as well, in sunflowers effective population size appears to be an important determinant of rates of adaptive evolution.

Introduction

The relative contributions of adaptive and nonadaptive evolution in the divergence of lineages have been much debated by evolutionary biologists (Kimura 1968, 1983; King and Jukes 1969; Gillespie 1994a; Fay and Wu 2001). Various tests have been developed to identify the signature of adaptive divergence based on patterns of polymorphism within species compared with patterns of divergence between them at one or more loci (Hudson et al. 1987; Templeton 1987; McDonald and Kreitman 1991), and a number of methods have been developed specifically to measure the proportion of amino acid differences driven by positive selection, α, based on polymorphism and divergence data (Charlesworth 1994; Fay et al. 2001; Smith and Eyre-Walker 2002; Boyko et al. 2008; Eyre-Walker and Keightley 2009). Results vary widely among taxa, with evidence of limited adaptive divergence in hominids (Bustamante et al. 2005; Boyko et al. 2008), yeast (Doniger et al. 2008; Liti et al. 2009), and Arabidopsis (Bustamante et al. 2002; Barrier et al. 2003; Foxe et al. 2008) but substantially higher levels of adaptive divergence in Drosophila (Bachtrog 2008; Sella et al. 2009), bacteria (Charlesworth and Eyre-Walker 2006; Lefebure and Stanhope 2009), viruses (Nielsen and Yang 2003), rodents (Halligan et al. 2010), sunflowers (Strasburg et al. 2009), aspens (Ingvarsson 2010), and the brassicaceous species Capsella grandiflora (Slotte et al. 2010).

The causes of variation among taxa in rates of adaptive divergence are not clear, although a number of hypotheses have been suggested. Most commonly, variation in effective population size has been invoked, as effective population size is positively correlated with both the frequency with which adaptive mutations occur and the efficiency of selection acting on weakly adaptive mutations. Results for the taxa listed above are largely, although not completely, consistent with the expectation that species with larger effective population sizes will show stronger evidence of adaptive divergence—that is, a higher proportion of amino acid differences that appear to have been driven by positive selection. However, both theoretical (Ohta 1972, 1973, 1992; Gillespie 1994b) and empirical (Eyre-Walker et al. 2002; Woolfit and Bromham 2003, 2005) work indicates that weakly deleterious substitutions are more commonly fixed in small populations, potentially resulting in an increased rate of amino acid divergence between species with small effective population sizes that does not reflect adaptive evolution. The degree and manner in which effective population size influences nonsynonymous divergence is expected to be dependent on a number of factors, including the distribution of fitness effects of new mutations, models of selection, and patterns of linkage (Ohta 1992; Gillespie 1999).

Some recent work has suggested that effective population size may not be a significant determinant of rates of adaptive divergence. Bachtrog (2008) found that two Drosophila species whose effective population sizes differ by a factor of five had comparable proportions of adaptive amino acid fixations (α ≈ 0.5). Gossmann et al. (2010) studied nine plant species pairs and found little evidence of adaptive amino acid divergence in any pair except two sunflower species. Their set of species pairs spanned a wide range of effective population sizes, and although the sunflower species had the largest effective population sizes and were the only species to show evidence of adaptive divergence, other species with effective population sizes on the order of Drosophila and rodents showed patterns similar to animal species with very small effective population sizes. Gossmann et al. (2010) interpreted these results to suggest that other factors may be more important than effective population size in determining the rate of adaptive divergence among plant species.

To further evaluate the role of effective population size in determining rates of adaptive divergence, we have collected data from six sunflower species (five annual species and a single perennial species, Helianthus tuberosus) for 35 loci. The species vary dramatically in geographic range and effective population size. The two most widespread species, H. annuus and H. petiolaris (the two species included in the analyses of Gossmann et al. 2010), are found throughout much of the central and western United States and have estimated effective population sizes in the millions (Strasburg and Rieseberg 2008). The other three annual species have much more restricted ranges—H. argophyllus occurs on the southeastern Texas coastal plain, H. exilis occurs in a small area of the Inner Coastal Mountain Range in central California, and H. paradoxus is restricted to fragmented salt marsh habitat in western Texas and New Mexico. All three species harbor considerably less genetic variation than H. annuus and H. petiolaris, and the effective population sizes of H. argophyllus and H. paradoxus have been estimated using the computer program IM (Hey and Nielsen 2004) to be in the range of 250,000–300,000 and 50,000–100,000, respectively (Strasburg JL, unpublished data). We examine levels of adaptive evolution in these species using a number of tests, focusing on two recently developed methods. Eyre-Walker and Keightley (2009) described an approach for simultaneously estimating the distribution of fitness effects of new mutations and the rate of adaptive evolution. This method attempts to account for the effects of weakly deleterious mutations, which can bias estimates of adaptive evolution upward or downward depending on the demographic history of the species. Weakly deleterious mutations are expected to cause an upward bias in α in species that have recently undergone population growth because deleterious alleles that were more likely to drift to fixation in the past and contribute to divergence are now more efficiently removed by selection and contribute less to polymorphism (McDonald and Kreitman 1991; Eyre-Walker 2002). Conversely, weakly deleterious mutations may bias α estimates downward in stable or shrinking populations because they contribute disproportionately to polymorphism versus divergence. We also use the Gossmann et al. (2010) reparameterization of α, ω_a, to estimate adaptive divergence independent of number of effectively neutral substitutions, which may be negatively correlated with effective population size (Popadin et al. 2007; Piganeau and Eyre-Walker 2009).

We examine patterns of divergence in the annual sunflowers using H. tuberosus as outgroup. In addition, in order to account for the possibility that limited divergence between annual and perennial sunflowers may bias estimates of adaptive divergence, we estimate adaptive divergence in all six sunflower species using the lettuce species Lactuca sativa as outgroup. Lettuce and sunflower diverged 32–35 Ma (Kim et al. 2005), whereas annual and perennial sunflowers diverged fewer than 8 Ma (Schilling 1997). We also collected population-level sequence data from five loci for four lettuce species, allowing us to estimate rates of adaptive divergence in those species as well using H. tuberosus as outgroup.

We find that, regardless of which species (H. tuberosus or L. sativa) is used as outgroup, estimates of adaptive divergence are significantly positive for the two annual sunflower species with the largest effective population sizes, negative for the species with the smallest effective population size and intermediate for the other two species. This general pattern holds regardless of analytical method, although confidence intervals are broad and estimates are not significantly different from zero for some methods. In addition, regardless of which outgroup is used point estimates of α and ω_a are significantly correlated with effective population size. When L. sativa is used as outgroup, estimates of α are still significantly positive for the largest sunflower species, and most methods still result in a significant correlation between α and effective population size. Thus, in contrast to the recent results of Gossmann et al. (2010), we find that in annual sunflowers, there is a significant association between effective population size and rates of adaptive divergence.

Materials and Methods

Collections and DNA Isolation

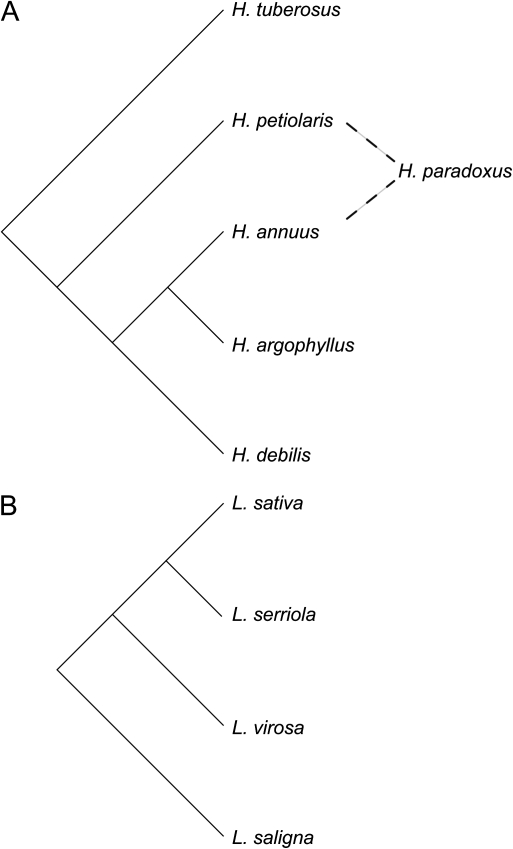
A total of 59 samples were collected from six Helianthus species and 95 samples from four Lactuca species (locality and accession information are given in supplementary file S1, Supplementary Material online). The full sunflower panel includes 6 individuals each from H. petiolaris, H. paradoxus, H. exilis, and H. argophyllus; 12 individuals from H. tuberosus; and 23 individuals from H. annuus. H. tuberosus is perennial; the other five species belong to a clade of annual species. The lettuce panel includes 34 individuals from L. sativa, 22 from L. serriola, 27 from L. saligna, and 12 from L. virosa. Species relationships are shown in figure 1. Leaves and/or achenes were collected from natural populations or obtained from the United States Department of Agriculture Germplasm Resources Information Network. Achenes were germinated in greenhouses at University of British Columbia, University of California—Davis, or Indiana University, and leaf tissue was sampled for genetic analysis. DNA was extracted using a DNeasy Plant Mini Kit or DNeasy 96 Plant Kit (Qiagen, Valencia, CA).

FIG. 1.

Relationships among the (A) Helianthus and (B) Lactuca species analyzed here. Helianthus paradoxus is a homoploid hybrid species derived from H. annuus and H. petiolaris. Relationships are from Rieseberg (1991) and Koopman et al. (1998).

Polymerase Chain Reaction Amplification and Sequencing

For each of the 35 loci, expressed sequence tag (EST) databases for a number of sunflower and lettuce species (collected as part of the Compositae Genome Project—http://compgenomics.ucdavis.edu/) were searched using Arabidopsis thaliana coding sequence, and primers were designed based on alignments of all available EST sequences and A. thaliana coding and genomic sequence, if alignable. Where possible, primers were designed to anneal in conserved exon regions flanking one or more introns. Primer sequences and amplification conditions are described in supplementary file S2, Supplementary Material online. All sunflower data and population-level lettuce data were collected via Sanger sequencing of polymerase chain reaction (PCR) products amplified from genomic DNA. Unincorporated primers and dNTPs were removed using ExoSAP-IT (USB, Cleveland, OH), and sequencing reactions using both forward and reverse primers were carried out on PCR products using ABI Big Dye Terminator version 3.1 and resolved using an ABI 3730 capillary sequencer (Applied Biosystems, Foster City, CA). For individuals heterozygous for a single indel haplotypes were phased by comparing forward and reverse sequences at variable sites. For individuals heterozygous for multiple indels or for phasing haplotypes in individuals with no length heterozygosity, in some cases, PCR products were cloned using a TOPO-TA cloning kit (Invitrogen, Carlsbad, CA). Clone sequences were compared with sequences obtained through direct sequencing and to other clone sequences for the same individual to help identify polymerase errors and PCR-mediated recombination (Meyerhans et al. 1990). In other cases, individuals with multiple variable sites were phased arbitrarily and treated as genotypic data. Both haplotypic and genotypic data are included here, and analyses are restricted to those that are not affected by single nucleotide polymorphism phase. Sequences were aligned using Sequencher version 4.7 (Gene Codes Corporation, Ann Arbor, MI), with minor adjustments made by eye. Ambiguous alignments, generally involving short regions of repetitive DNA, were removed prior to all analyses. Data sets are complete and fully phased for 11 loci; sample sizes vary for the other 24 loci, and in some cases, one or more species is not represented (sample sizes and summary genetic data for each locus are given in supplementary file S3, Supplementary Material online). L. sativa outgroup data were obtained by sequencing normalized mRNA-Seq libraries using Illumina Genome Analyzers (Illumina Inc., San Diego, CA). Initial assemblies were made using CLC Workbench and Velvet (Zerbino and Birney 2008), with subsequent assembly using CAP3 (Huang and Madan 1999). Full details of the L. sativa transcriptome assembly will be presented elsewhere (Matvienko M, Kozik A, Michelmore R, in preparation). Homologous lettuce EST sequences were identified for 34 of the 35 loci; for one of these loci, no coding region could be identified, leaving 33 loci for sunflower analyses with lettuce outgroup. All sequences have been deposited in GenBank, and accession numbers are given in supplementary file S4, Supplementary Material online.

Data Analyses

Coding regions and reading frames were determined by comparing genomic sequences to EST sequences, and protein sequences were Blasted against the National Center for Biotechnology Information (NCBI) protein database to help verify gene identity. For one locus (no. 60 in supplementary file S3, Supplementary Material online), no coding regions could be reliably identified; in this case, all sequence was considered noncoding. For analyses involving sunflowers with H. tuberosus as outgroup, both coding and noncoding sequences were retained; for analyses involving both sunflower and lettuce sequences, noncoding sequence alignments were largely ambiguous when sequences were available in both groups, so analyses were limited to coding sequences. Coding alignments between sunflower and lettuce were made based on amino acid sequences using an online version of ClustalW (Larkin et al. 2007). For 11 loci, one or more coding regions were removed because we considered the alignment between sunflower and lettuce to be ambiguous; we expect this to result in more conservative estimates of adaptive divergence, as some regions that were truly homologous but highly divergent in amino acid sequence may have been removed.

Sequence diversity, π, and Watterson’s (1975) θ were calculated for entire sequences as well as noncoding, synonymous, and nonsynonymous partitions using DnaSP version 5.10.00 (Librado and Rozas 2009). Effective population sizes were estimated from average synonymous diversity weighted by the number of synonymous sites for loci with at least six sampled alleles, and a synonymous substitution rate of 1 × 10⁻⁸ per site per year based on EST libraries and fossil calibrations from a number of Helianthus species and other closely related species (Barker MS and Rieseberg LH, unpublished data). DnaSP was also used to calculate synonymous and nonsynonymous divergence between ingroup and outgroup species using the methods of Nei and Gojobori (1986). Interspecific gross and net sequence divergence were calculated using the program Sites (Hey and Wakeley 1997). Folded site frequency spectra for nonsynonymous, synonymous, and noncoding mutations were also calculated in Sites.

McDonald–Kreitman (MK) tests (McDonald and Kreitman 1991) between various species pairs were performed in DnaSP. In addition, four modifications of the MK test (Fay et al. 2001; Bierne and Eyre-Walker 2004; method II of Eyre-Walker and Keightley 2009; Gossmann et al. 2010) were performed using Adam Eyre-Walker’s program DoFE (available at http://www.lifesci.susx.ac.uk/home/Adam_Eyre-Walker/Website/Software.html). For sunflower analyses with H. tuberosus outgroup, both noncoding and synonymous sites were counted; only synonymous sites were counted for tests involving both sunflowers and lettuce. The implementation of method II of Eyre-Walker and Keightley (2009) and the reparameterization presented in Gossmann et al. (2010) require that an equal number of alleles be sampled for all loci. Because our sampling varies substantially among loci (see table 1), we chose a number of alleles for each species that represents a tradeoff between sampling as many loci as possible and being able to accurately reflect the site frequency spectrum of each locus; we sampled eight alleles each for H. petiolaris, H. paradoxus, H. exilis, and H. argophyllus, 18 alleles for H. tuberosus, and 22 alleles for H. annuus. For loci with population-level sampling in lettuce species, we sampled 18 alleles for L. serriola, 25 alleles for L. saligna, and ten alleles for L. virosa. Data sets were complete for all five loci for L. sativa, so no random sampling was required. For loci with more than these numbers of alleles, we randomly sampled the appropriate number of polymorphisms at each site without replacement. Analyses in DoFE were performed with 1 million steps in the Markov chain Monte Carlo chain following a burn-in of 100,000 steps; and at least two independent analyses were run for each data set to verify convergence.

Table 1.

Summary Information for Each Species.

Species	Average Number of Alleles	Total Segregating Sites	Average πsyn	Average θsyn	Ne
Helianthus petiolaris	8.7	874	0.034	0.037	843,407
H. paradoxus	9.0	152	0.005	0.004	119,305
H. exilis	9.2	685	0.022	0.023	545,530
H. tuberosus	13.2	913	0.027	0.023	676,810
H. argophyllus	9.1	288	0.014	0.015	361,402
H. annuus	35.4	1493	0.027	0.024	673,968
L. sativa	34.0	5	0.001	0.001	31,563
L. serriola	21.2	15	0.004	0.007	103,074
L. saligna	26.6	9	0.003	0.003	78,111
L. virosa	12.0	41	0.012	0.020	303,647

Note.—Average synonymous π and θ values are based on loci for which at least six alleles were available and are weighted by the number of synonymous sites at each locus. effective population size (N_e) values are based on weighted average synonymous diversity values and a synonymous substitution rate of 1 × 10⁻⁸ per site per year. Information for Lactuca sativa only includes the five loci for which there is population-level sampling.

Results

Sequence Diversity and Divergence

Within sunflowers, aligned sequences ranged in length from 471 to 1,955 bp, with an average length of 825 bp and a cumulative length of 28.9 kb. The total data set is roughly 60% coding (17.6 and 11.3 kb coding and noncoding, respectively). For alignments involving both sunflower and lettuce, the total aligned length is 16.5 kb or an average of 499 bp per locus (all coding). Sampling and summary genetic diversity information is provided in table 1 (more detailed locus-by-locus data are provided in supplementary file S3, Supplementary Material online), and data on sequence divergence between ingroup and outgroup species are given in table 2. Synonymous nucleotide diversity varies substantially among sunflower species, from an average of 0.5% in H. paradoxus to 3.4% in H. petiolaris. Synonymous sequence divergence between the perennial H. tuberosus and the other five sunflower species, all of which are part of a clade of annual species nested within the perennial species (Schilling et al. 1998), averages roughly 5%. Estimates of effective population size based on the average synonymous diversity range from roughly 120,000 for H. paradoxus to over 800,000 for H. petiolaris (table 1). H. annuus and H. tuberosus have effective population sizes close to 700,000 followed by H. exilis and finally H. argophyllus, at roughly 350,000. Although the estimates for H. paradoxus and H. argophyllus are fairly consistent with our previous estimates made using the computer program IM, those for H. annuus and H. petiolaris are substantially lower; this is likely due to the different methodologies behind these estimates and reflects the fact that the latter two species may have undergone significant population size expansion (Strasburg and Rieseberg 2008). However, the relative ranking among species with respect to effective population size is consistent across analyses. Synonymous sequence divergence between sunflowers and lettuce is far higher than divergence within sunflowers, generally in the range of 55–60%. Effective population sizes in lettuce species are also generally smaller than in sunflowers but vary by an order of magnitude, from roughly 32,000 in L. sativa to 300,000 in L. virosa.

Table 2.

Uncorrected Synonymous and Nonsynonymous Divergence Between Ingroup and Outgroup Species.

Ingroup	Outgroup	Ka	Ks
Helianthus petiolaris	H. tuberosus	0.008	0.053
H. paradoxus	H. tuberosus	0.009	0.047
H. exilis	H. tuberosus	0.009	0.055
H. tuberosus	H. annuus	0.007	0.046
H. argophyllus	H. tuberosus	0.008	0.053
H. annuus	H. tuberosus	0.007	0.046
H. petiolaris	H. annuus	0.006	0.049
H. annuus	H. petiolaris	0.006	0.049
H. petiolaris	L. sativa	0.082	0.540
H. paradoxus	L. sativa	0.078	0.521
H. exilis	L. sativa	0.084	0.530
H. tuberosus	L. sativa	0.086	0.530
H. argophyllus	L. sativa	0.087	0.527
H. annuus	L. sativa	0.084	0.525
Lactuca sativa	H. tuberosus	0.067	0.609
L. serriola	H. tuberosus	0.067	0.609
L. saligna	H. tuberosus	0.067	0.601
L. virosa	H. tuberosus	0.067	0.593

NOTE.—Values are averages across all loci.

Patterns of Adaptive Divergence

We performed several tests to investigate the possibility of nonneutral evolution. We performed these tests for all five annual species using H. tuberosus as outgroup, as it is the most genetically divergent, with polymorphic and fixed site counts summed across loci. We also analyzed H. tuberosus using the annual species H. annuus as outgroup and analyzed H. annuus and H. petiolaris using each other as outgroup for a more direct comparison to previous work involving these two species (Strasburg et al. 2009; Gossmann et al. 2010). In addition, as mentioned above, we examined rates of adaptive divergence in all six sunflower species using the more divergent L. sativa as outgroup to account for possible bias caused by recent divergence between ingroup and outgroup, and we analyzed L. sativa and three other lettuce species using H. tuberosus as outgroup. Results for the original MK test and four modifications are shown in table 3, but we focus here on two methods that explicitly deal with segregating slightly deleterious mutations, the methods of Eyre-Walker and Keightley (2009) and Gossmann et al. (2010), as these are expected to be the most informative with regard to the effect of population size and rates of adaptive divergence. Detailed input data for implementing these tests in DoFE are provided in supplementary file S5, Supplementary Material online, and results are given in table 3 and figure 2.

Table 3.

Standard and Modified MK Test Results.

Species (outgroup)	McDonald and Kreitman (1991)		Fay et al. (2001)		Bierne and Eyre-Walker (2004)		Eyre-Walker and Keightley (2009)		Gossmann et al. (2010)
	α	P value	α	95% CI	α	95% CI	α	95% CI	ωa	95% CI
Helianthus petiolaris(H. tuberosus)	0.142	P = 0.607	0.318	(−0.889, 0.694)	0.656	(0.206, 0.850)	0.620	(0.293, 0.817)	0.271	(0.087, 0.554)
H. paradoxus(H. tuberosus)	−1.162	P < 0.0001	−0.828	(−3.057, 0.034)	−0.460	(−1.560, 0.165)	−1.001	(−2.685, 0.074)	−0.095	(−0.265, 0.042)
H. exilis(H. tuberosus)	−1.146	P = 0.0002	−0.442	(−2.503, 0.260)	0.141	(−0.509, 0.504)	−0.124	(−0.809, 0.358)	0.011	(−0.079, 0.115)
H. tuberosus(H. annuus)	0.155	P = 0.466	0.315	(−2.542, 0.749)	0.339	(−0.411, 0.676)	−0.064	(−2.184, 0.808)	0.459	(0.009, 1.496)
H. argophyllus(H. tuberosus)	−1.128	P = 0.0002	−0.448	(−2.777, 0.275)	−0.452	(−1.652, 0.199)	−0.043	(−0.755, 0.432)	0.020	(−0.070, 0.114)
H. annuus(H. tuberosus)	0.155	P = 0.466	0.242	(−3.822, 0.739)	0.410	(−0.290, 0.710)	0.592	(0.336, 0.760)	0.263	(0.109, 0.474)
H. petiolaris(H. annuus)	0.259	P = 0.400	0.540	(−0.281, 0.779)	0.750	(0.300, 0.913)	0.508	(0.053, 0.780)	0.206	(0.040, 0.458)
H. annuus (H. petiolaris)	0.259	P = 0.400	0.495	(−0.353, 0.766)	0.751	(0.301, 0.910)	0.578	(0.173, 0.811)	0.384	(0.102, 0.836)
H. petiolaris(L. sativa)	0.327	P = 0.004	0.235	(−0.174, 0.512)	0.361	(0.123, 0.517)	0.558	(0.392, 0.711)	0.080	(0.054, 0.103)
H. paradoxus(Lactuca sativa)	−1.170	P = 0.003	−1.397	(−3.097, −0.587)	−1.171	(−3.071, −0.271)	−1.004	(−2.735, 0.033)	−0.098	(−0.294, 0.019)
H. exilis(L. sativa)	−0.011	P = 0.935	−0.290	(−0.815, 0.259)	−0.084	(−0.484, 0.191)	0.227	(−0.044, 0.476)	0.032	(−0.006, 0.061)
H. tuberosus(L. sativa)	−0.364	P = 0.008	−0.539	(−1.306, 0.051)	−0.453	(−0.928, −0.115)	0.210	(−0.552, 0.523)	0.030	(−0.016, 0.061)
H. argophyllus(L. sativa)	0.311	P = 0.052	0.275	(−0.153, 0.591)	0.228	(−0.247, 0.491)	0.474	(0.167, 0.697)	0.070	(0.026, 0.103)
H. annuus(L. sativa)	0.204	P = 0.027	0.211	(−0.185, 0.501)	0.284	(0.084, 0.421)	0.605	(0.446, 0.783)	0.087	(0.060, 0.117)
L. sativa(H. tuberosus)	−0.204	P = 0.509	−0.501	(−1.351, 0.154)	0.030	(−0.770, 0.480)	−0.126	(−3.258, 0.928)	0.056	(−0.122, 0.122)
L. serriola(H. tuberosus)	−0.166	P = 0.573	−0.385	(−1.075, 0.269)	0.062	(−0.688, 0.487)	0.640	(−0.302, 0.961)	0.083	(0.019, 0.128)
L. saligna(H. tuberosus)	−0.304	P = 0.329	−0.679	(−1.482, 0.184)	0.013	(−0.687, 0.463)	−0.646	(−4.252, 0.701)	−0.020	(−0.326, 0.106)
L. virosa(H. tuberosus)	−0.098	P = 0.725	−0.378	(−0.932, 0.353)	0.174	(−0.476, 0.549)	0.486	(−0.196, 0.844)	0.070	(0.008, 0.122)

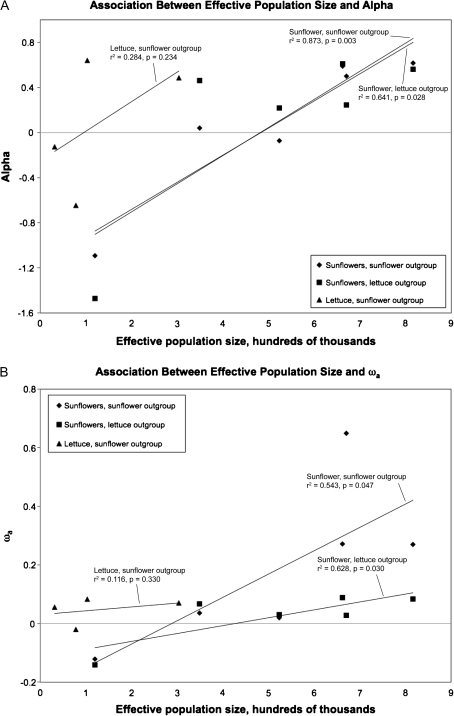
FIG. 2.

Association between effective size and two measures of adaptive divergence. (A) Eyre-Walker and Keightley’s (2009) α. (B) ω_a, the reparameterization of α from Gossmann et al. (2010).

The estimates of α and ω_a are qualitatively similar for each comparison involving a sunflower species as ingroup—in only three cases is one estimate positive and the other negative, and in two these three cases both estimates are near zero and nonsignificant (table 3). The exception is H. tuberosus with H. annuus outgroup, in which the ω_a estimate is significantly positive while the α estimate is just slightly (nonsignificantly) below zero. Two of the largest species, H. annuus and H. petiolaris, consistently show evidence of significant adaptive protein evolution regardless of outgroup or method. The other large species, H. tuberosus, also has generally positive estimates of α and ω_a, although it is only significant for ω_a with H. annuus outgroup. In contrast, the smallest species, H. paradoxus, consistently has negative estimates of α and ω_a. The two species of intermediate size, H. argophyllus and H. exilis, generally have intermediate estimates of α and ω_a. When H. tuberosus is used as outgroup, both parameter estimates for both species are very near zero; when L. sativa is used, estimates are somewhat higher (and significantly positive for H. argophyllus for both α and ω_a), although they are still below those of H. annuus and H. petiolaris. Estimates on average tend to be somewhat lower when L. sativa is used as outgroup, although there are a number of exceptions—most notably, the H. argophyllus estimates just mentioned. But regardless of which outgroup is used, there is a significant positive correlation between effective population size and α (r² = 0.79, one-tailed P = 0.009 for H. tuberosus outgroup; r² = 0.63, one-tailed P = 0.030 for L. sativa outgroup) or ω_a (r² = 0.65, one-tailed P = 0.026 for H. tuberosus outgroup; r² = 0.60, one-tailed P = 0.034 for L. sativa outgroup). We also note that there is a positive correlation between effective population size and the other three measures of adaptive divergence shown in table 3; this correlation is significant for all methods with H. tuberosus outgroup, and nearly significant (P values range from 0.061 to 0.068) for all methods with L. sativa outgroup. However, for the reasons discussed, above the Eyre-Walker and Keightley (2009) and Gossmann et al. (2010) are likely to be more informative with regard to the relationship between effective population size and adaptive evolution.

We also analyzed the sunflower ingroup/H. tubersosus outgroup data considering only coding sequence to see if there was an effect of possible nonneutral evolution at noncoding sites. Compared with analyses using both coding and noncoding sequence, estimates of adaptive divergence are generally somewhat higher, although in most cases the difference is relatively small (data not shown). The correlation with effective population size remains significant for both α (r² = 0.65, one-tailed P = 0.027) and ω_a (r² = 0.55, one-tailed P = 0.046).

Finally, we estimated levels of adaptive divergence in the four lettuce species for which we have polymorphism data. With the exception of L. virosa, these species have less genetic variability than any of the sunflower species considered here (see table 1). With limited data available, confidence intervals on α estimates are very broad and always encompass 0. The two species with the largest effective population sizes, L. virosa and L. serriola, have significantly positive ω_a estimates, whereas the other two species have nonsignificant estimates. Both estimates of adaptive divergence are positively correlated with effective population size, although the correlation is not significant for either method. The inferences that can be drawn from these results are obviously very limited, and data from more loci would be required to better understand patterns of adaptive evolution in these taxa.

Distribution of Effects of New Mutations

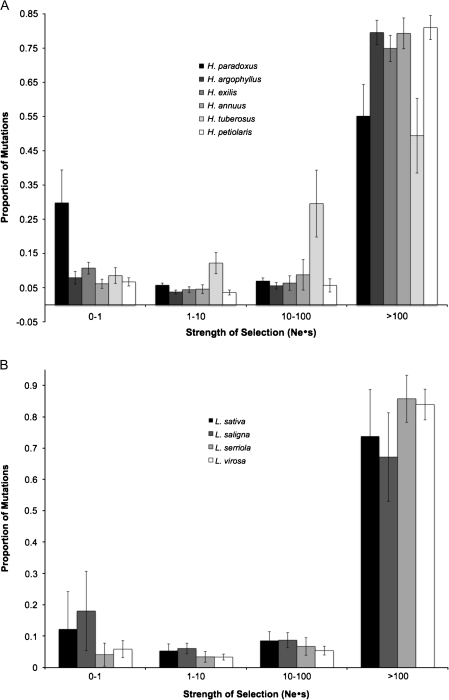
The method of Eyre-Walker and Keightley (2009) also allows for the estimation of the distribution of fitness effects of new nonsynonymous mutations, assuming neutrality of synonymous mutations. Results are shown in figure 3. For all sunflower and lettuce species, the majority of new nonsynonymous mutations are strongly deleterious (N_es > 100). There is a general trend in both sunflowers and lettuce of species with smaller effective population size having a lower proportion of strongly deleterious mutations and a higher proportion of weakly deleterious mutations that behave as effectively neutral (N_es < 1). These results are broadly consistent with the expectation that the frequency of effectively neutral mutations will be inversely related to effective population size (Woolfit and Bromham 2003; Eyre-Walker and Keightley 2007; Popadin et al. 2007) and are also consistent with the results of Gossmann et al. (2010).

FIG. 3.

Distribution of fitness effects of new mutations. (A) Sunflower species, Lactuca sativa outgroup (results for Helianthus tuberosus outgroup are given in supplementary file S6, Supplementary Material online). (B) Lettuce species, H. tuberosus outgroup. Species are ordered from smallest to largest effective population size.

Discussion

Our results indicate that adaptive divergence is occurring in annual sunflower species, but it is mostly limited to the species with larger effective population sizes. H. petiolaris, the species with the largest effective population size, has significantly positive estimates of α and ω_a regardless of outgroup. The other widespread annual, H. annuus, shows a similar pattern, as does H. tuberosus, which has an effective population size comparable with H. annuus (although only one H. tuberosus estimate is significantly positive). H. exilis and H. argophyllus, with intermediate effective population size estimates, also have intermediate α estimates; and the species with the smallest effective population sizes, H. paradoxus, has consistently negative estimates of α. Our estimates for H. annuus and H. petiolaris are somewhat lower than, but broadly consistent with, our estimates of α = 0.75 made using a different data set and the standard MK test (Strasburg et al. 2009). Gossmann et al. (2010) reanalyzed these data using the method of Eyre-Walker and Keightley (2009) and also obtained estimates somewhat lower than that of Strasburg et al. (2009), but still qualitatively similar to that result and to the results, we report here although their estimates of α and ω_a for H. annuus were nonsignificant.

Although correlations between effective population size and measures of adaptive divergence are slightly lower with lettuce outgroup, they remain statistically significant or nearly so for all five methods presented in table 3. This suggests that there is likely some upward bias in the strength of the association between effective population size and adaptive divergence due to limited overall divergence with H. tuberosus when it is used as outgroup. This bias may be expected if neutral mutations have not had time to drift to fixation, whereas advantageous mutations fix rapidly, creating a bias toward more adaptive mutations among those that have fixed that is more pronounced at larger effective population sizes. It is useful to note that choice of outgroup is constrained in both directions—limited divergence may result in the bias discussed above and too much divergence may result in multiple fixations at the same site or with regions of ambiguous alignment (which we encountered in 11 genes here).

Our results, taken with those of Gossmann et al. (2010) and Slotte et al. (2010), suggest that there may be an effect of effective population size on levels of adaptive divergence in plants as well as animals but that statistically detectable adaptive divergence requires quite large effective population sizes. Almost all the animal, bacterial, and viral species for which adaptive divergence has been documented have estimated effective population sizes of ∼550,000 or more, with Drosophila miranda (Bachtrog 2008) and Mus musculus castaneus (Halligan et al. 2010) on the low end of that range up to 1–2 million for D. melanogaster and many millions for some bacteria and viruses. Slotte et al. (2010) documented adaptive divergence in the brassicaceous species C. grandiflora, with an effective population size of roughly 500,000. Gossmann et al. (2010) found evidence for adaptive divergence in sunflowers but not in Zea mays, with an estimated effective population size of 590,000; but all other species in their study had effective population sizes of <150,000. Thus, in all these studies, the only evidence for adaptive divergence is in species with effective population sizes of at least 350,000 (H. argophyllus in which we found some evidence of adaptive divergence) and more consistently in species with effective population sizes of roughly 700,000 or more. One possible outlier is the European aspen Populus tremula, with an α estimate of 0.30 (Ingvarsson 2010). Ingvarsson (2008) estimated its effective population size to be at least 118,000; but Ingvarsson (2010) considered this to be a lower bound and suggested that 500,000 may not be unrealistic.

Population structure is another factor sometimes mentioned as a possible determinant of rates of adaptive evolution, as it can decrease local effective population sizes, increase the risk of local extinction, and prevent the spread of adaptive mutations among subpopulations (Barton 1993; Whitlock 2003; Aguilee et al. 2009). For example, it has been suggested that the high levels of population structure in A. thaliana (Nordborg et al. 2005; Bakker et al. 2006; Beck et al. 2008) may contribute to low levels of adaptive divergence in this species (Gossmann et al. 2010; Slotte et al. 2010). In contrast, European aspen has very little population structure (Ingvarsson 2010) as does C. grandiflora (Slotte et al. 2010). However, to our knowledge, a more comprehensive comparison of levels of population structure and estimates of adaptive divergence has not been performed. There appears to be very little population structure within the annual sunflowers showing the highest levels of adaptive divergence, H. annuus and H. petiolaris (Yatabe et al. 2007; Strasburg and Rieseberg 2008; Raduski et al. 2010). There also appear to be high levels of gene flow among H. exilis populations (Sambatti and Rice 2006). Less information is available for the other three species examined here. H. argophyllus has a narrow distribution with relatively limited geographic or habitat barriers to gene flow, whereas H. paradoxus occurs in naturally fragmented salt marsh habitat and may be expected to show more geographic population structure; indeed, analyses of microsatellite variation indicate that somewhat more genetic variation is distributed among H. paradoxus populations than is the case for H. annuus or H. petiolaris (Welch and Rieseberg 2002). However, population structure here is completely confounded with species effective population size, and no firm conclusions can be drawn about any role of structure itself.

Population growth may potentially upwardly bias estimates of α. Although the method of Eyre-Walker and Keightley (2009) attempts to control for recent changes in effective population size, long-term differences between historical and current effective population sizes may still be problematic. There is evidence that increases in effective population size have occurred in both H. annuus and H. petiolaris since their divergence (Strasburg and Rieseberg 2008), so this is potentially a factor in our significant α estimates. Eyre-Walker and Keightley (2009) describe the expected bias in α estimates due to population size change in their model in which the fitness effects of new deleterious mutations follows a gamma distribution. The amount of bias depends on both the degree of population size change and the shape parameter of the gamma distribution, b (see eq. 10 of Eyre-Walker and Keightley 2009). In table 4, we give the “true” value of α based on our estimated values of α and b for a range of population growth scenarios. For most comparisons, the estimate of b is quite low, meaning a relatively lower proportion of mutations are nearly neutral; as a result population growth has a limited impact on α estimates for most species (the most notable exception being H. tuberosus with L. sativa outgroup, where the estimate of b is more than twice almost all the other estimates). Even under a scenario of 10-fold increase in effective population size, both H. annuus and H. petiolaris still have strongly positive α estimates regardless of which outgroup is used. In two cases, nonsignificantly positive α estimates become negative with increasing population growth, but in no cases does a significantly positive α estimate become negative over the range of growth values we consider here. The degree to which the correlation between effective population size and adaptive divergence is affected will depend on the relative growth rates of the different species; at present, we do not have enough demographic information to fully address this question. We did apply the main method presented in Eyre-Walker and Keightley (2009) as implemented using the DFE-alpha server (http://liberty.cap.ed.ac.uk/∼eang33/upload.html) to explicitly estimate population size change along with α and the distribution of fitness effects of new mutations; however, the population growth results were not biologically realistic. For example, substantial population growth was inferred in H. argophyllus, H. exilis, and H. paradoxus, three species with very restricted ecological and geographical ranges. The greatest population growth was inferred for H. exilis, a species with an extremely limited distribution in central California that could not realistically have undergone such growth. Likewise, for H. annuus, the most widespread species and the one that has perhaps experienced the greatest population growth, the estimate of growth was quite low, roughly one-third that of H. exilis (based on L. sativa outgroup). Nonetheless, for completeness, we include these population growth estimates as well as estimates of α and b made using DFE-alpha in supplementary file S7, Supplementary Material online. Using the true values of α derived from this method, adaptive divergence is still significantly correlated with effective population size regardless of outgroup (r² = 0.67, P = 0.023 for H. tuberosus outgroup; r² = 0.63, P = 0.030 for L. sativa outgroup).

Table 4.

Effect of Population Size Change on α Estimates.

Species (outgroup)	αest	b	αtrue
			N2/N1 = 2	N2/N1 = 4	N2/N1 = 6	N2/N1 = 8	N2/N1 = 10
Helianthus petiolaris (H. tuberosus)	0.620	0.148	0.579	0.534	0.505	0.483	0.466
H. paradoxus (H. tuberosus)	−1.001	0.082	−1.118	−1.242	−1.318	−1.373	−1.417
H. exilis (H. tuberosus)	−0.124	0.110	−0.213	−0.310	−0.370	−0.414	−0.449
H. tuberosus (H. annuus)	−0.064	0.133	−0.166	−0.278	−0.349	−0.401	−0.443
H. argophyllus (H. tuberosus)	−0.043	0.123	−0.136	−0.237	−0.300	−0.347	−0.384
H. annuus (H. tuberosus)	0.592	0.126	0.555	0.514	0.489	0.470	0.455
H. petiolaris (H. annuus)	0.508	0.145	0.456	0.398	0.362	0.335	0.313
H. annuus (H. petiolaris)	0.578	0.124	0.541	0.499	0.474	0.454	0.439
H. petiolaris (Lactuca sativa)	0.558	0.188	0.496	0.426	0.381	0.346	0.318
H. paradoxus (L. sativa)	−1.004	0.096	−1.142	−1.289	−1.380	−1.447	−1.500
H. exilis (L. sativa)	0.227	0.151	0.142	0.048	−0.012	−0.057	−0.093
H. tuberosus (L. sativa)	0.210	0.402	−0.043	−0.378	−0.622	−0.821	−0.991
H. argophyllus (L. sativa)	0.474	0.174	0.407	0.331	0.282	0.245	0.215
H. annuus (L. sativa)	0.605	0.232	0.536	0.455	0.401	0.360	0.326

NOTE.—Estimated values of α and b, the shape parameter of the gamma distribution of the fitness effects of deleterious mutations, are from the method of Eyre-Walker and Keightley (2009). “True” values of α for different ratios of current (N₂) to ancestral (N₁) population size were calculated using equation (10) of Eyre-Walker and Keightley (2009).

A few additional issues should be considered in interpreting our results. H. tuberosus is a hexaploid, and it is possible that genome duplication in H. tuberosus has affected patterns of divergence among paralogs within that species (Han et al. 2009) and consequently between it and the annual sunflowers. Gossmann et al. (2010) point out that the absence of evidence for adaptive divergence in most of the species they analyzed may be due to the fact that it is occurring among paralogs. However, we see similar patterns of adaptive divergence whether H. tuberosus or L. sativa is used as outgroup, so we do not expect the polyploidy of H. tuberosus to have a major effect on our results. To our knowledge, the genes are all single copy in the other sunflower species and the lettuce species. Another factor to consider is that H. annuus hybridizes with all the other annual species with the exception of H. paradoxus. In particular, H. annuus and H. petiolaris appear to have genomes that are very porous to gene flow (Yatabe et al. 2007; Kane et al. 2009; Strasburg et al. 2009). This might affect the results of MK tests between these two species, as neutral variants may pass freely between the two species while variants contributing to adaptive divergence are prevented from introgressing. However, the annual species do not hybridize with H. tuberosus, and estimates of adaptive divergence in H. annuus and H. petiolaris are similar regardless of whether one of them or H. tuberosus is used as the outgroup (see table 3). Further examination of the effects of introgression on measures of adaptive divergence would be valuable. Finally, H. paradoxus is a homoploid hybrid species between H. annuus and H. petiolaris (Rieseberg et al. 1990). It underwent a severe bottleneck associated with its formation, 0.5–1.0 Ma (Buerkle and Rieseberg 2008; Ungerer et al. 2009), followed by a moderate increase in population size. Based on museum collections, there is some evidence that its population size has declined in the past 100–200 years (Heiser 1958). It is not immediately obvious to what degree its formation through mixing and reassortment of the H. annuus and H. petiolaris gene pools and its subsequent demographic changes may have affected patterns of divergence.

We have compared levels of adaptive divergence among six sunflower species that differ significantly in effective population size but for which a number of other factors are shared. All six species are obligate outcrossers; five of the six are annuals, and they have similar life histories. There is relatively little variation in levels of population structure at least for the species for which information is available; more specifically, the species with low population structure include both species with large effective population sizes and high levels of adaptive divergence (H. annuus and H. petiolaris) and species with smaller effective population sizes and limited or no evidence of adaptive divergence (H. exilis and possibly H. argophyllus). Thus, a number of factors considered to potentially be associated with levels of adaptive divergence, which are confounded with effective population size in comparisons of highly divergent taxa, are more easily separated here. Although the comparisons here are not entirely independent because the annual species share a common history through the divergence of the annual clade, we still see dramatically different estimates of adaptive divergence that correlate with estimates of effective population size. Some caution is warranted due to the fact that only six species are included. H. paradoxus appears to be the species that contributes most strongly to the association we see (see fig. 2); when it is removed from the analysis the correlation between effective population size and adaptive divergence remains positive but becomes nonsignificant for α and ω_a. The same is true for most other species as well. Sampling of more of the 12 annual sunflower species or roughly 50 total North American sunflower species would be helpful in this regard. Nonetheless, although other factors are certainly involved as well, these results provide evidence that effective population size can be a significant determinant of rates of adaptive evolution.

Supplementary Material

Supplementary files S1–S7 are available at Molecular Biology and Evolutiononline (http://www.mbe.oxfordjournals.org/).