Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Apr 1.
Published in final edited form as: Circ Cardiovasc Genet. 2011 Feb 3;4(2):188–196. doi: 10.1161/CIRCGENETICS.110.957928

The Effect of Survival Bias on Case-Control Genetic Association Studies of Highly Lethal Diseases

Christopher D Anderson 1,2,3,*, Michael A Nalls 4,*, Alessandro Biffi 1,2,3,*, Natalia S Rost 1,2,3, Steven M Greenberg 2, Andrew B Singleton 4, James F Meschia 5, Jonathan Rosand 1,2,3
PMCID: PMC3080449  NIHMSID: NIHMS278582  PMID: 21292865

Abstract

Background

Survival bias is the phenomenon by which individuals are excluded from analysis of a trait because of mortality related to the expression of that trait. In genetic association studies, variants increasing risk for disease onset as well as risk of disease-related mortality (lethality) could be difficult to detect in genetic association case-control designs, possibly leading to underestimation of a variant's effect on disease risk.

Methods and Results

We modeled cohorts for three diseases of high lethality (intracerebral hemorrhage, ischemic stroke, and myocardial infarction) using existing longitudinal data. Based on these models, we simulated case-control genetic association studies for genetic risk factors of varying effect sizes, lethality, and minor allele frequencies (MAF). For each disease, erosion of detected effect size was larger for case-control studies of individuals of advanced age (age > 75 years) and/or variants with very high event-associated lethality (Genotype Relative Risk for event-related death > 2.0). We found that survival bias results in no more than 20% effect size erosion for cohorts with mean age < 75 years, even for variants that double lethality risk. Furthermore, we found that increasing effect size erosion was accompanied by depletion of MAF in the case population, yielding a “signature” of the presence of survival bias.

Conclusions

Our simulation provides formulas to allow estimation of effect size erosion given a variant's odds-ratio (OR) of disease, OR of lethality, and MAF. These formulas will add precision to power calculation and replication efforts for case-control genetic studies. Our approach requires validation using prospective data.

Keywords: Stroke, hemorrhage, myocardial infarction, genetics, epidemiology

INTRODUCTION

Genetic association tests employing a case-control design depend on comprehensive ascertainment of cases in order to ensure an accurate representation of causal factors for analysis [1,2]. Survival bias, a form of ascertainment bias due to selective exclusion of individuals who suffer mortality related to the disease being studied, is difficult to predict, estimate, or control [3-5]. Myocardial infarction (MI), acute ischemic stroke (AIS), and intracerebral hemorrhage (ICH) are prototypical diseases with high event-related mortality (lethality) that are affected by this phenomenon. For these conditions, prospective longitudinal studies of incident disease may offer advantages over cross-sectional studies capturing both prevalent and incident disease for the identification not only of those genetic variants that increase fatal outcome from disease, but also those variants that influence both risk of disease as well as risk of disease-associated lethality. Cross-sectional studies are nonetheless commonly employed because of their advantages in efficiency of disease ascertainment.

The presence of survival bias risks under-ascertainment of genotypes associated with high lethality, with consequent underestimation of disease risk effect sizes for those genotypes associated with both increased disease risk and disease-associated lethality [6]. Although no variants have yet been identified which simultaneously confer modest risk of disease and substantial risk of lethality from such disease, such a scenario remains possible, and could impact any comparison of longitudinal and case-control genetic association studies. For example, a recent genome-wide association study (GWAS) of ischemic stroke, based on a meta-analysis of longitudinal cohort data, demonstrated an association at the chromosome 12p13 locus [7]. An independent attempt at replication using a meta-analysis of case-control data failed to support this association [8]. One potential explanation for failed replication could be that variants at 12p13 increase risk of stroke as well as stroke-related lethality, thereby limiting their detection in patients enrolled using cross-sectional designs. Replication efforts using such a study design would therefore have limited power to detect a true association with disease. Tools that allow calculation of effect size erosion due to survival bias are necessary to determine if this explanation is plausible.

We hypothesized that by modeling diseases of high lethality based on data available from large population-based cohorts, we could simulate the effect of survival bias on genome-wide association studies (GWAS) of variants associated with both disease and lethality. Using AIS, ICH, and MI, we simulated case-control studies across a continuum of population ages, assuming a variety of minor allele frequencies (MAF), Genotype Relative Risk (GRR) of disease (GRR-D), GRR of lethality (GRR-L), and recruitment rates of lethal cases. We then created formulas for estimating the erosion of effect size for case-control studies of each of these diseases, as well as a formula for extrapolation of estimates to other diseases not modeled.

METHODS

Literature search for data from Longitudinal Cohorts

A PubMed (http://www.pubmed.org) search was performed independently by C.D.A. and A.B. in order to identify articles reporting prevalence, incidence and mortality of AIS, ICH, and MI. Search terms are shown in the Appendix. In order to be considered eligible for modeling, reported data had to refer to studies conducted after 1990 (to account for recent trends in incidence and mortality from vascular disease), with incidence and event-associated mortality detailed separately by age category. We also included only data from high-income industrialized countries, in order to model scenarios consistent with populations currently enrolled in most genetic association studies [9-27]. Data from stroke longitudinal cohorts that did not distinguish ischemic from hemorrhagic stroke were not considered eligible. We found only one article reporting data separately for ischemic stroke subtypes by Trial of Org 10172 in Acute Stroke Treatment (TOAST) criteria [14].

Model Building for Disease Impact on the General Population

All simulations were performed using the R statistical package v2.10.0 (http://www.r-project.org). We modeled disease incidence rate within each age category by computing weighted (based on sample size) medians for incidence data from published longitudinal cohorts. Disease-associated mortality rate was computed similarly, while all-cause mortality was modeled on the basis of summary WHO data for industrialized countries (http://www.who.int/whosis/mort/download/en/index.html). We generated year-by-year disease incidence and mortality rates using the approx interpolation function in the R stats library.

We then proceeded to model the impact of each disease over time on longitudinal cohorts of 100,000 healthy individuals. At cohort inception, individuals were assumed to be aged 45 years (mean), with a normal distribution and standard deviation (SD) of 7 years. Additional modeling using different SDs (range: 4 – 10 years) did not alter results significantly. This simulated longitudinal cohort was followed prospectively for 35 years. Each year, new disease cases (MI, ICH, or AIS) were registered based on incidence data from our literature search. Among these cases, a portion resulted in disease-associated death. Finally, a proportion of both survivors from the disease event and normal controls experienced disease-unrelated death as appropriate for their age category based on WHO epidemiologic data. Mortality unrelated to vascular disease was adjusted for cases surviving the disease-event according to published data [9-27] to reflect the excess all-cause mortality in individuals expressing vascular disease phenotypes [Supplemental Tables S1-S2]. Cumulative disease incidence and disease-free survival are plotted in Supplemental Figure S1.

Genetic risk modeling

We simulated a single marker conferring increased risk for disease expression, assumed to be a common genetic variant in the population being studied. For the purposes of our simulation, only the minor allele was chosen for association with disease and lethality. Simulations were run for MAF of 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40 and 0.45. The effect of this marker was expressed in terms of GRR-D, with different simulations accounting for values of 1.05, 1.10, 1.15, 1.20, 1.25, 1.30, 1.35, 1.40, 1.45 and 1.50. These values were selected to reflect effect sizes usually associated with common variants in genetic association studies [28]. We also modeled GRR-L, expressed as the relative risk of death due to disease: simulated GRR-L included 1.05, 1.10, 1.15, 1.20, 1.25, 1.30, 1.35, 1.40, 1.50, 1.60, 1.70, 1.80, 1.90, 2.0, 2.5, 3.0, 3.5 and 4.0. GRR-D was assessed after each year of longitudinal follow-up using a Cox proportional hazards model.

Simulation of case-control genetic association studies

In order to quantify the impact of survival bias on case ascertainment, we simulated a case-control study conducted within the modeled population each year (for MI, ICH, and AIS). Samples ranged in mean age from 45 to 80 years (SD = 7 years). For each year of cohort follow-up, 1000 cases and 1000 controls were enrolled via simple random sampling with replacement from survivors, and effect size (expressed as odds ratio (OR) for each copy of the risk allele) was computed using logistic regression analysis. All combinations of pre-specified genetic parameters (MAF, GRR and GRR-L) were simulated independently. Results were expressed in terms of erosion of effect size due to survival bias, computed as the ratio between the observed OR and the underlying “true” GRR. Observed MAFs for cases and controls were also recorded for each simulation and stored. In order to model the effect of lethal case recruitment, we performed separate simulations assuming 0% through 40% ascertainment of lethal cases in our case-control studies (0% and 40% lethal case ascertainment results reported).

Effect size erosion estimation formulas

To provide a disease-specific formula to estimate the impact of survival bias on observed OR in case-control studies for MI, ICH, and AIS, we used results from all simulated scenarios (9 MAF values X 10 GRR values X 18 GRR-L values = 1620 simulations) to regress the erosion of effect size due to survival bias (dependent variable, expressed as OR/GRR and log-transformed for normality). Predictors included mean age of enrolled subjects, MAF of the genetic marker in the study population, risk for phenotype expression (GRR-D) and risk of phenotype-associated mortality (GRR-L).

Furthermore, we computed a general (non-disease specific) formula based on user-specified disease incidence and mortality rates for the age range of interest. Specified annual incidence rates for formula computation ranged from 0.0001 to 0.03, and specified disease-associated mortality ranged from 0.01 to 0.40. All genetic parameter (MAF, GRR-D and GRR-L) ranges were identical to those simulated for AIS, ICH and MI. The resulting formula (based again on linear regression) allows for quantification of effect size erosion due to survival bias in diseases other than MI, AIS and ICH, provided that age-specific incidence and mortality data are available to investigators.

Sensitivity analyses

In order to verify the consistency of our simulation approach we conducted several sensitivity analyses. (1) We performed separate simulations of disease incidence and mortality in men and women based on literature data to assess sex specific effects. (2) We modeled earlier ages of disease onset (range of simulation values: 2 – 10 years earlier than published data) associated with the causal genetic marker of interest. This was done to simulate the effect of several known genetic risk variants acting on both disease risk and age of onset [29] (3) We simulated a genetic-conferred risk of non-disease-related increase in mortality (range of simulated values: 1.05 – 2.0) to our model(s). This analysis allowed us to evaluate the impact of survival bias on discovery efforts for variants acting on both disease risk and accelerated aging / biological frailty (e.g. APOE in Alzheimer's disease). (4) We performed additional modeling of vascular disease recurrence and recurrence-associated mortality (based on literature data). This analysis aimed at assessing whether the concomitant effect of the variant of interest on first-ever disease manifestation, disease recurrence and risk of disease-related death (at all time points, independent of all-cause mortality) modified the impact of survival bias. (5) We compared results obtained from interpolating incidence and mortality data on a year-by-year basis against the direct use of published data by age-category. (6) We performed separate analyses using both the lowest and highest published incidence and mortality figures for each age category in each disease in order to account for the variability in the published estimates for these figures. (7) In simulation of longitudinal cohort studies we varied the number of healthy individuals at enrollment to values of 50,000, 200,000, 500,000 and 1,000,000. (8) In simulation of case-control studies for each disease state, we varied the number of cases and controls sampled from the survivor population for each year at values of 500/500, 1000/1000, 2500/2500and 5000/5000.

Results for all sensitivity analyses (1-8) listed above (assessed as the percent of GRR lost due to survival bias) never differed from reported results by more than 5% (data not shown).

RESULTS

Literature Search and Construction of Disease Models

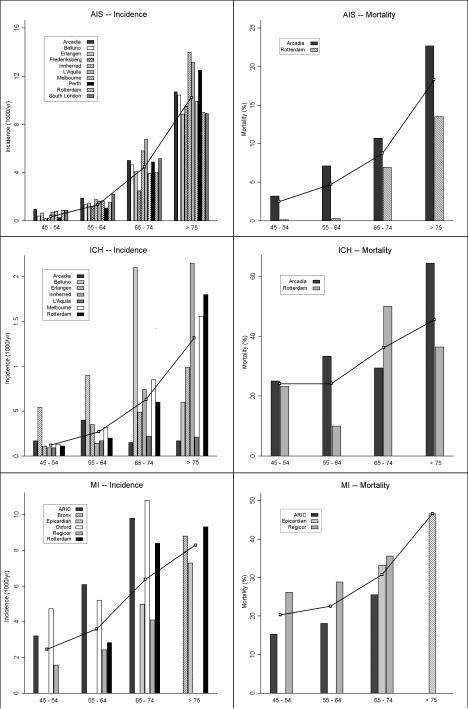
A PubMed (http://www.ncbi.nlm.nih.gov/pubmed) search identified 10 articles for AIS, 7 articles for ICH, and 6 articles for MI providing incidence and mortality data by age category, presenting data obtained since 1990 [9-27]. Based on this search, we constructed models for each disease and used an interpolation algorithm to simulate data for each year [Figure 1]. We then constructed longitudinal and cross-sectional studies of genetic variants influencing both disease incidence and lethality, across a range of MAF, GRR-D, and GRR-L [Figure 2]. Hazard ratios for disease (HR-D) in the simulated longitudinal study were compared to the odds ratio for disease (OR-D) from the simulated case-control study for each year of follow-up in the inception cohort of 100,000 individuals.

Figure 1.

Figure 1

Open in a new tab

AIS = Acute Ischemic Stroke. ICH = Intracerebral Hemorrhage. MI = Myocardial Infarction. Bars represent the incidence and mortality estimates for each disease for the age ranges specified, according to the published reports for each cohort. Lines represent the interpolated incidence and mortality curves used to create the disease models for simulation of longitudinal and case-control study designs.

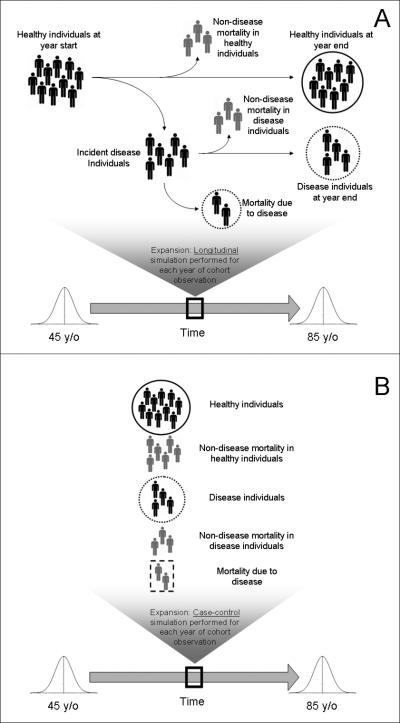
Figure 2.

Figure 2

Open in a new tab

Simulation design for longitudinal study model (A) and simulation design for case-control study model (B). For each panel, solid circles represent the non-diseased population from which controls are recruited, and dashed circles represent the diseased population from which cases are recruited. In Panel B, the dashed square represents the individuals who experienced disease-related mortality, and are therefore not present in the pool of diseased individuals for case recruitment.

Measurement of the effects of survival bias

We tabulated the output of the longitudinal (HR-D) and case-control (OR-D) genetic simulations, and reported results as the erosion of apparent effect size obtained using a case-control design (i.e. the percentage of HR-D that was lost to detection due to survival bias in calculation of an OR-D using a case-control study design) [Figure 3-5]. For all diseases, effect size erosion increased with increasing mean ages of enrolled individuals and increasing variant-conferred GRR-L. These findings reflect the close association between baseline disease lethality and extent of ascertainment lost due to survival bias. Case-control studies with higher rates of mortality among carriers of the causal variant, whether because of lethal effects of the variant itself or because of the higher disease mortality among older individuals, suffered from larger effect size erosions [Figure 3-5].

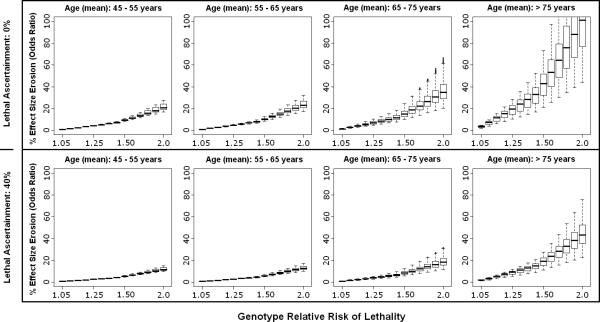
Figure 3.

Figure 3

Open in a new tab

Effect size erosion in case-control design is plotted according to varying cohort ages and genetic relative risk of lethality (GRR-L) for acute ischemic stroke. The median (thick line) and range (box-plot with whiskers) for each GRR-L simulation reflects the ranges of minor allele frequency and genetic relative risk of disease. The top panel assumes 0% ascertainment of lethal cases, while the bottom panel assumes 40% ascertainment of lethal cases.

Figure 5.

Figure 5

Open in a new tab

Effect size erosion in case-control design is plotted according to varying cohort ages and genetic relative risk of lethality (GRR-L) for myocardial infarction. The median (thick line) and range (box-plot with whiskers) for each GRR-L simulation reflects the ranges of minor allele frequency and genetic relative risk of disease. The top panel assumes 0% ascertainment of lethal cases, while the bottom panel assumes 40% ascertainment of lethal cases.

As an illustration of this phenomenon, for a genetic variant that simultaneously increased the risk for ischemic stroke (GRR-D range 1.05 – 2.0) and doubled the risk of death from that stroke (GRR-L = 2.0), the effect size erosion was substantially less than 20%, assuming a cohort of 65-75 years-old and no enrollment whatsoever of lethal cases [Figure 3]. By comparison, a variant increasing risk for ICH in a similar fashion would be subject to an average erosion in observed effect size of approximately 40%, with the possibility of reversal of observed effect in some situations as cases possessing the risk allele become selectively excluded to such a degree that the risk allele begins to achieve a higher frequency in controls compared with cases. This can be seen in situations where the effect size erosion surpasses 100% [Figure 4].

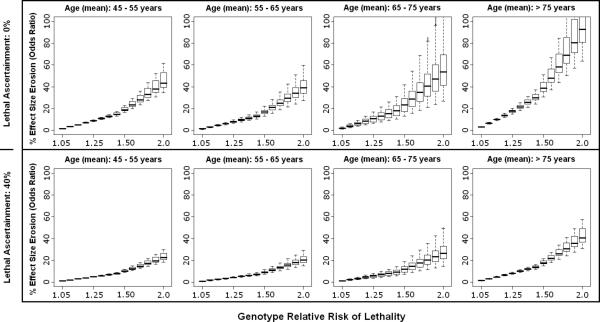
Figure 4.

Figure 4

Open in a new tab

Effect size erosion in case-control design is plotted according to varying cohort ages and genetic relative risk of lethality (GRR-L) for intracerebral hemorrhage. The median (thick line) and range (box-plot with whiskers) for each GRR-L simulation reflects the ranges of minor allele frequency and genetic relative risk of disease. The top panel assumes 0% ascertainment of lethal cases, while the bottom panel assumes 40% ascertainment of lethal cases.

Erosion in effect size estimates decreased substantially for all diseases with just 40% enrollment of lethal cases, and decreased even further for more conservative estimates of GRR-L. In ICH, the condition with the highest lethality, enrollment of 40% of lethal cases reduced the erosion in effect size estimate (on average) to < 20%, and prevented reversal of effect from being observed up to GRR-L of 2.0 [Figure 4].

Simulation of Observed Minor Allele Frequencies

Using the genetic case-control study simulations by year for each disease, we calculated the observed MAF for the simulated variant in cases, and compared this with the specified population MAF at simulation outset, for MAF 0.10 - 0.30 assuming no population stratification. For this analysis, GRR-D of 1.05 – 1.5 and 0% – 40% ascertainment of lethal cases were modeled (results shown GRR-D of 1.3 with lethal-case ascertainment of 0% and 40%). For all population MAFs tested, we observed a GRR-L and age-dependent decrease in observed case MAF. This MAF depletion was predictably less severe for 40% lethal case ascertainment than for 0% ascertainment [Supplementary Figure S2-S4]. The severity of depletion of MAF was strongly dependent on GRR-L for all simulated values of GRR-D and lethal-case ascertainment (all p < 0.05). As a result, depletion in observed MAF in cases compared to the population MAF could be suggestive of the presence of survival bias.

Formulas for Estimation of Effect Size Erosion in Case-Control Genetic Studies

Based on these simulations, we used linear regression to identify a formula for each disease that approximates the percent erosion of effect size estimate for a genetic variant, with a priori assumptions of cohort mean age (range 40 – 80), and the variant's MAF (range 0.05 – 0.45), GRR-D (range 1.05 – 1.50), and GRR-L (range 1.05 – 4.0). Note that because ICH has a lower annual incidence than AIS or MI, the MAF exerts a proportionally larger influence on effect size erosion than in the other two diseases states.

graphic file with name nihms-278582-f0001.jpg

To allow extension of our simulation results to other highly-lethal phenotypes, we again used a linear regression to create a general case formula to estimate effect size erosion. This formula requires the variant's MAF, GRR-D and GRR-L (same ranges as above) as input, in addition to disease annual incidence (Φ, range 0.0001 - 0.03) and disease-related mortality (Θ, range 0.01 - 0.40) estimates for the age range of included subjects.

graphic file with name nihms-278582-f0002.jpg

Application of the general formula to AIS, ICH and MI using incidence and mortality data from the published literature returned estimates of effect size erosion due to survival bias within 5% of those provided by disease-specific formulas presented above.

We offer the following as a theoretical application of our formulas. We can construct a scenario of 2 genetic studies of ICH, one in a population-based longitudinal cohort and another in a hospital-based case-control cohort with a mean age of 67 years. Let us suppose that the longitudinal study identified a novel variant with an HR = 1.7 for risk of ICH, and an OR = 2.0 for ICH-related mortality, with a MAF = 0.15 in the general population. Turning to the hospital-based case-control study, let us assume that researchers were unable to consent and enroll any lethal ICH cases. Using these data, we can apply our formula for effect size erosion in ICH to show that the case-control researchers should expect a 33% erosion in their effect size estimate for the same variant, yielding an expected OR = 1.14. If the case-control study is underpowered to detect an OR of this size, it may fail to confirm the ICH risk association for the variant identified in the population-based study. Of note, if the case-control researchers were able to enroll 40% of lethal cases from the population, the variant's observed OR for ICH risk would rise to 1.46, and power to detect the variant would increase.

DISCUSSION

Our results demonstrate that failure to enroll lethal cases can distort the measured effect sizes for genetic variants affecting both disease incidence and lethality. However, the effect size erosion is less than 20% in ischemic stroke, and while more substantial in extremely high mortality diseases like ICH and MI, it can be reduced to less than 20% if ascertainment of at least a proportion (40%) of lethal cases can be assured. Variants that increase disease risk while more than doubling the risk for disease-related mortality (lethality), and case-control genetic association studies performed on cohorts > 75 years of age do result in more substantial erosion in effect size estimates for disease risk, but these situations are unlikely to be encountered in the real-world of complex disease genetics.

Incomplete ascertainment of individuals possessing a variant increasing risk of both disease and lethality leads to an observed MAF in cases that is lower than the true value. With increasing lethality risk and cohort age, we have shown that this observed case MAF can drop below the MAF of the population from which the cohort is drawn. In such a situation, the variant would spuriously appear to be protective, rather than harmful, since it is seen less often in cases than controls. This apparent reversal of effect would appear in the presence of an imbalance between alleles, as homozygotes would not been seen as often as expected due to their dramatically increased risk of lethality. As a result, the variant would not be in Hardy-Weinberg equilibrium, which would provide a warning that this apparent reversal of effect was not a true result. We have shown a significant correlation between the GRR-L and the degree of observed MAF deviation from the population value. When comparing results obtained from case-control studies to those obtained from prospective longitudinal cohort studies, this signature of depleted MAF in cases may prove useful for detecting the presence of survival bias. MAF depletion can disappear with improved lethal case enrollment. 40% enrollment of lethal cases results in no MAF depletion below the population MAF, even for cohorts of advanced age and diseases of high mortality such as ICH and MI, as long as the GRR-L is relatively low (1.3). For higher GRR-L values, MAF depletion can remain substantial even with 40% lethal case ascertainment.

The ascertainment rate of individuals with event-related lethality is of critical import in the estimation of power erosion due to survival bias. For our simulations, we first estimated a 0% ascertainment rate for lethal cases, which is quite conservative for at least some highly lethal phenotypes [30]. We have shown in our analysis that increasing the ascertainment rate for lethal cases to 40% substantially reduces the effect size erosion due to survival bias. Researchers wishing to apply our formulas to their populations should substitute the non-ascertainment rate due to disease lethality (if known) for the absolute lethality rate whenever possible, in order to avoid over-estimation of effect size erosion for their cohort.

Using our simulation results, we have constructed disease-specific formulas for the estimation of effect size erosion, as well as a general case formula that can be used for other highly lethal diseases of known incidence and mortality. These formulas will allow designers of future case-control genetic analyses of diseases of high lethality to predict the erosion of true effect size for their study, allowing for more accurate ad hoc power calculations. These formulas will also be of utility to investigators seeking to replicate the findings of prior genetic studies, as the modeling of survival bias in addition to Winner's Curse [31] should allow for very precise power calculations. Thus, in the case of attempted validation of genetic association with chromosome 12p13 in ischemic stroke [7,8], the original longitudinal study identified an association at rs12425791 with OR = 1.39. After correction for Winner's Curse using WINNER v1.1 (http://csg.sph.umich.edu/boehnke/winner), this association decreases to OR = 1.25. Applying our model for ischemic stroke, using the known population MAF of the variant in both the longitudinal discovery and case-control replication cohorts (0.20), and assuming that the variant doubles the risk of stroke lethality (GRR-L = 2.0), we find that the expected OR in the case-control replication effort is 1.14. This case-control study had 0.999 power to detect this effect size. The lack of replication at rs12425791 in populations ascertained using a case-control design is therefore unlikely to have arisen due to failure to ascertain sufficient numbers of fatal cases of stroke. Of note, no evidence exists that the 12p13 locus is associated with such a dramatically increased risk of disease-associated lethality, but the use of such a substantial estimate of lethality provides a conservative estimate of effect size erosion in replication.

Our study has limitations. Even longitudinal studies are not exempt from the possibility of survival bias, as individuals are often not enrolled and genotyped until later in life, when some potentially lethal variants could have already been depleted from the population. However, this is likely to increase the similarity of results between longitudinal and case-control studies, and therefore our simulation, by assuming perfect ascertainment in longitudinal cohorts, represents the most conservative comparison between the two. Our simulations only apply to common genetic variants; therefore, additional methods will be required to model survival bias in experiments identifying rare variants, or analyses employing other functional units (i.e. exon or gene-based units instead of SNPs). In such analyses, deviations from population MAFs would be unreliable due to the inherent imprecision in MAF estimates for rare variants. This issue is unlikely to have affected recent replication efforts, as most genetic association studies to date have not been designed to detect rare or private variants. An additional limitation is that the models for MI, ICH, and AIS used for our simulations were built using incidence and mortality data for these diseases from longitudinal studies performed in 1990 - present [9-27]. If disease incidence and overall mortality decrease, these formulas will need to be updated. Similarly, our formulas were constructed from incidence and mortality data from high-income industrialized societies, limiting their generalizability. Experiments performed in under-developed countries or following groups with restricted access to healthcare could under-estimate the effects of survival bias due to increased overall mortality and event-related lethality [32,33,21]. Likewise, our formulae were constructed using a priori ranges for MAF, GRR-D, and GRR-L. Values falling outside of these ranges would necessitate reconstruction of the formulae. Another potential limitation is that specific variants could predominantly exert a lethal effect on specific age groups (i.e. increasing the lethality of late-onset stroke). This effect has not been modeled in our simulation, and thus could lead to incorrect estimates of effect size erosion for certain age groups. Finally, our study has been performed entirely by simulation. Validation of our estimates of effect size erosion in comparison with real-world longitudinal and case-control cohorts is needed if our results are to be considered wholly accurate.

Survival bias represents a substantial concern in the design of case-control genetic association studies of disease with high fatality rates. Our simulation shows that the impact of survival bias is relatively small for most cohort ages and variant lethalities, and is further minimized by proactive enrollment of lethal cases. The tools provided by this study will be useful in calculation of power for future genetic association studies of common variants. Future studies are needed in order to validate and extend our findings to other diseases, and to adapt our approach to other functional units of genetic analysis.

Supplementary Material

1

Acknowledgments

Funding Sources: The authors’ work on this study was supported by funding from the American Heart Association/Bugher Foundation Centers for Stroke Prevention Research (0775011N, 0755984T), Deane Institute for Integrative Study of Atrial Fibrillation and Stroke, National Institute for Neurologic Disorders and Stroke (R01 NS063925, R01 NS059727, P50 NS051343, K23NS064052-01A1). This research was also supported in part by the Intramural Research Program of the NIH, National Institute on Aging under Annual Report number Z01-AG000954-06:2007.

Footnotes

Journal Subject Codes: [4] Acute myocardial infarction; [8] Epidemiology; [43] Acute Cerebral Hemorrhage; [44] Acute Cerebral Infarction; [55] Genetics of Stroke; [89] Genetics of cardiovascular disease

Conflict of Interest Disclosures: None

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Applebaum KM, Malloy EJ, Eisen EA. Reducing healthy worker survivor bias by restricting date of hire in a cohort study of Vermont granite workers. Occup Environ Med. 2007;64:681–687. doi: 10.1136/oem.2006.031369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Jensen H, Benn CS, Lisse IM, Rodrigues A, Andersen PK, Aaby P. Survival bias in observational studies of the impact of routine immunizations on childhood survival. Trop Med Int Health. 2007;12:5–14. doi: 10.1111/j.1365-3156.2006.01773.x. [DOI] [PubMed] [Google Scholar]
  • 3.Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. Third Edition Lippincott-Williams-Wilkins Publishers; Philadelphia, PA: 2008. [Google Scholar]
  • 4.Woodward M. Epidemiology: Study Design and Data Analysis. Second Edition CRC Press; Boca Raton, FL: 2004. [Google Scholar]
  • 5.Szklo M, Nieto FJ. Epidemiology: Beyond the Basics. Second Edition Aspen Publishing; Gaithersburg, MD: 2004. [Google Scholar]
  • 6.Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
  • 7.Ikram MA, Seshadri S, Bis JC, Fornage M, DeStefano AL, Aulchenko YS, Debette S, Lumley T, Folsom AR, van den Herik EG, Bos MJ, Beiser A, Cushman M, Launer LJ, Shahar E, Struchalin M, Du Y, Glazer NL, Rosamond WD, Rivadeneira F, Kelly-Hayes M, Lopez OL, Coresh J, Hofman A, DeCarli C, Heckbert SR, Koudstaal PJ, Yang Q, Smith NL, Kase CS, Rice K, Haritunians T, Roks G, de Kort PL, Taylor KD, de Lau LM, Oostra BA, Uitterlinden AG, Rotter JI, Boerwinkle E, Psaty BM, Mosley TH, van Duijn CM, Breteler MM, Longstreth WT, Jr, Wolf PA. Genomewide association studies of stroke. N Engl J Med. 2009;360:1718–28. doi: 10.1056/NEJMoa0900094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.International Stroke Genetics Consortium, Wellcome Trust Case-Control Consortium 2 Failure to Validate Association between Variants on 12p13 and Ischemic Stroke. N Engl J Med. 2010;362:1547–1550. doi: 10.1056/NEJMc0910050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Feigin VL, Lawes CM, Bennett DA, Anderson CS. Stroke epidemiology: a review of population-based studies of incidence, prevalence, and case-fatality in the late 20th century. Lancet Neurol. 2003;2:43–53. doi: 10.1016/s1474-4422(03)00266-7. [DOI] [PubMed] [Google Scholar]
  • 10.Feigin VL, Lawes CM, Bennett DA, Barker-Collo SL, Parag V. Worldwide stroke incidence and early case fatality reported in 56 population-based studies: a systematic review. Lancet Neurol. 2009;8:355–369. doi: 10.1016/S1474-4422(09)70025-0. [DOI] [PubMed] [Google Scholar]
  • 11.Vemmos KN, Bots ML, Tsibouris PK, Zis VP, Grobbee DE, Stranjalis GS, Stamatelopoulos S. Stroke incidence and case fatality in southern Greece: the Arcadia stroke registry. Stroke. 1999;30:363–370. doi: 10.1161/01.str.30.2.363. [DOI] [PubMed] [Google Scholar]
  • 12.Lauria G, Gentile M, Fassetta G, Casetta I, Agnoli F, Andreotta G, Barp C, Caneve G, Cavallaro A, Cielo R, Mingillo D, Massimiliano M, PierGiorgio O. Incidence and prognosis of stroke in the Belluno province, Italy. First-year results of a community-based study. Stroke. 1995;26:1787–1793. doi: 10.1161/01.str.26.10.1787. [DOI] [PubMed] [Google Scholar]
  • 13.Kolominsky-Rabas PL, Sarti C, Heuschmann PU, Graf C, Siemonsen S, Neundoerfer B, Katalinic A, Lang E, Gassmann KG, von Stockert TR. A prospective community-based study of stroke in Germany--the Erlangen Stroke Project (ESPro): incidence and case fatality at 1, 3, and 12 months. Stroke. 1998;29:2501–2506. doi: 10.1161/01.str.29.12.2501. [DOI] [PubMed] [Google Scholar]
  • 14.Kolominsky-Rabas PL, Weber M, Gefeller O, Neundoerfer B, Heuschmann PU. Epidemiology of ischemic stroke subtypes according to TOAST criteria: incidence, recurrence, and long-term survival in ischemic stroke subtypes: a population-based study. Stroke. 2001;32:2735–2740. doi: 10.1161/hs1201.100209. [DOI] [PubMed] [Google Scholar]
  • 15.Jørgensen HS, Plesner AM, Hübbe P, Larsen K. Marked increase of stroke incidence in men between 1972 and 1990 in Frederiksberg, Denmark. Stroke. 1992;23:1701–1704. doi: 10.1161/01.str.23.12.1701. [DOI] [PubMed] [Google Scholar]
  • 16.Ellekjaer H, Holmen J, Indredavik B, Terent A. Epidemiology of stroke in Innherred, Norway, 1994 to 1996. Incidence and 30-day case-fatality rate. Stroke. 1997;28:2180–2184. doi: 10.1161/01.str.28.11.2180. [DOI] [PubMed] [Google Scholar]
  • 17.Carolei A, Marini C, Di Napoli M, Di Gianfilippo G, Santalucia P, Baldassarre M, De Matteis G, di Orio F. High stroke incidence in the prospective community-based L'Aquila registry (1994-1998). First year's results. Stroke. 1997;28:2500–2506. doi: 10.1161/01.str.28.12.2500. [DOI] [PubMed] [Google Scholar]
  • 18.Thrift AG, Dewey HM, Macdonell RA, McNeil JJ, Donnan GA. Incidence of the major stroke subtypes: initial findings from the North East Melbourne stroke incidence study (NEMESIS). Stroke. 2001;32:1732–1738. doi: 10.1161/01.str.32.8.1732. [DOI] [PubMed] [Google Scholar]
  • 19.Islam MS, Anderson CS, Hankey GJ, Hardie K, Carter K, Broadhurst R, Jamrozik K. Trends in incidence and outcome of stroke in Perth, Western Australia during 1989 to 2001: the Perth Community Stroke Study. Stroke. 2008;39:776–782. doi: 10.1161/STROKEAHA.107.493643. [DOI] [PubMed] [Google Scholar]
  • 20.Hollander M, Koudstaal PJ, Bots ML, Grobbee DE, Hofman A, Breteler MM. Incidence, risk, and case fatality of first ever stroke in the elderly population. The Rotterdam Study. J Neurol Neurosurg Psychiatry. 2003;74:317–321. doi: 10.1136/jnnp.74.3.317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Stewart JA, Dundas R, Howard RS, Rudd AG, Wolfe CD. Ethnic differences in incidence of stroke: prospective study with stroke register. BMJ. 1999;318:967–971. doi: 10.1136/bmj.318.7189.967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Pérez G, Pena A, Sala J, Roset P, Masiá R, Marrugat J. Acute myocardial infarction case fatality, incidence and mortality rates in a population registry in Gerona, Spain, 1990-1992. REGICOR Investigators. Int J Epidemiol. 1998;27:599–604. doi: 10.1093/ije/27.4.599. [DOI] [PubMed] [Google Scholar]
  • 23.Nadelmann J, Frishman WH, Ooi WL, Tepper D, Greenberg S, Guzik H, Lazar EJ, Heiman M, Aronson M. Prevalence, incidence and prognosis of recognized and unrecognized myocardial infarction in persons aged 75 years or older: The Bronx Aging Study. Am J Cardiol. 1990;66:533–537. doi: 10.1016/0002-9149(90)90477-i. [DOI] [PubMed] [Google Scholar]
  • 24.Gabriel R, Alonso M, Reviriego B, Muñiz J, Vega S, López I, Novella B, Suárez C, Rodríguez-Salvanés F. Ten-year fatal and non-fatal myocardial infarction incidence in elderly populations in Spain: the EPICARDIAN cohort study. BMC Public Health. 2009;9:360. doi: 10.1186/1471-2458-9-360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Volmink JA, Newton JN, Hicks NR, Sleight P, Fowler GH, Neil HA. Coronary event and case fatality rates in an English population: results of the Oxford myocardial infarction incidence study. The Oxford Myocardial Infarction Incidence Study Group. Heart. 1998;80:40–44. doi: 10.1136/hrt.80.1.40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.de Torbal A, Boersma E, Kors JA, van Herpen G, Deckers JW, van der Kuip DA, Stricker BH, Hofman A, Witteman JC. Incidence of recognized and unrecognized myocardial infarction in men and women aged 55 and older: the Rotterdam Study. Eur Heart J. 2006;27:729–736. doi: 10.1093/eurheartj/ehi707. [DOI] [PubMed] [Google Scholar]
  • 27.Lee CD, Folsom AR, Pankow JS, Brancati FL, Atherosclerosis Risk in Communities (ARIC) Study Investigators Cardiovascular events in diabetic and nondiabetic adults with or without history of myocardial infarction. Circulation. 2004;109:855–860. doi: 10.1161/01.CIR.0000116389.61864.DE. [DOI] [PubMed] [Google Scholar]
  • 28.Johnson AD, O'Donnell CJ. An open access database of genome-wide association results. BMC Med Genet. 2009;10:6. doi: 10.1186/1471-2350-10-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Abdullah KG, Li L, Shen GQ, Hu Y, Yang Y, MacKinlay KG, Topol EJ, Wang QK. Four SNPS on chromosome 9p21 confer risk to premature, familial CAD and MI in an American Caucasian population (GeneQuest). Ann Hum Genet. 2008;72:654–657. doi: 10.1111/j.1469-1809.2008.00454.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Asplund K, Bonita R, Kuulasmaa K, Rajakangas AM, Schaedlich H, Suzuki K, Thorvaldsen P, Tuomilehto J. Multinational comparisons of stroke epidemiology. Evaluation of case ascertainment in the WHO MONICA Stroke Study. World Health Organization Monitoring Trends and Determinants in Cardiovascular Disease. Stroke. 1995;26:355–360. doi: 10.1161/01.str.26.3.355. [DOI] [PubMed] [Google Scholar]
  • 31.Zhong H, Prentice RL. Correcting “winner's curse” in odds ratios from genomewide association findings for major complex human diseases. Genet Epidemiol. 2010;34:78–91. doi: 10.1002/gepi.20437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Sridharan SE, Unnikrishnan JP, Sukumaran S, Sylaja PN, Nayak SD, Sarma PS, Radhakrishnan K. Incidence, types, risk factors, and outcome of stroke in a developing country: the Trivandrum Stroke Registry. Stroke. 2009;40:1212–1218. doi: 10.1161/STROKEAHA.108.531293. [DOI] [PubMed] [Google Scholar]
  • 33.Cooper R, Cutler J, Desvigne-Nickens P, Fortmann SP, Friedman L, Havlik R, Hogelin G, Marler J, McGovern P, Morosco G, Mosca L, Pearson T, Stamler J, Stryer D, Thom T. Trends and disparities in coronary heart disease, stroke, and other cardiovascular diseases in the United States: findings of the national conference on cardiovascular disease prevention. Circulation. 2000;102:3137–3147. doi: 10.1161/01.cir.102.25.3137. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS278582-supplement-1.pdf (196.5KB, pdf)

RESOURCES