Abstract
Reconstruction of the anatomy of the proximal humerus is a prerequisite to achieving good long-term clinical results after shoulder arthroplasty. Modern, adjustable prostheses have greater flexibility of inclination, retroversion, and medial and dorsal offset in comparison with older prostheses. Such improvements should allow for better reconstruction of the centre of rotation compared to older prostheses. Reconstruction of the humeral head centre was assessed in 106 modern adjustable (Affinis) and 47 second-generation prostheses. All reconstructions were compared both to the preoperative state and the unoperated shoulder. To describe the pre- and postoperative states, the geometry and position of the humeral head in relation to the glenoid were analysed on patient radiographs. Applying the defined parameters, modern adjustable prostheses showed better reconstruction than second generation prostheses. Parameter values measured in reconstructions using fourth generation prostheses were comparable to those of the unoperated shoulder, but differed significantly from the preoperative state. Second generation prostheses, in contrast, only show non-specific differences in parameter values. This suggests that an approximate reconstruction of normal anatomy can be achieved using a modern fourth generation prosthesis. Reconstruction of the complex anatomy of the proximal humerus is significantly better with modern adjustable prostheses compared to second generation prostheses. Improved clinical outcome can therefore be predicted in a functional and intact rotator cuff. The advantage of using modern prostheses systems over older models is clearly demonstrated in this study.
Introduction
The anatomy of the proximal humerus can vary with respect to inclination, retrotorsion and the medial and dorsal offsets (the offset of the centre of rotation in relation to the humeral axis) [1, 6, 9, 14, 17, 20, 21]. Due to this, many groups call for this anatomy to be repaired as precisely as possible when implanting a humeral prosthesis in order to achieve optimal postoperative joint function [1, 4, 5, 7, 8, 10, 13, 15, 16, 18, 20, 22, 23]. Others go further and insist on reconstruction of the centre of rotation specifically [17].
In many cases of osteoarthritis, flattening of the humeral head can be identified (Fig. 1a, b), resulting in conditional lateral displacement of the centre of rotation in relation to shaft axis but causing a medial shift of the of the rotational centre in relation to the glenoid. Other patients show a primary osteoarthritis with no significant deformation of the humeral head (Fig. 1c). The technical demands for reconstruction of the rotational centre differ considerably in both cases.
Fig. 1.
a Deformation of the right shoulder in primary osteoarthritis and the healthy side of the same patient. b The flattened humeral head within the intact glenoid causes a lateral shift of the humeral head centre in relation to the shaft axis, but causing a medial displacement of the centre of rotation in relation to the glenoid. The inclination of the osteotomy plane is difficult to define but this is of no influence on the rotational centre if it is performed in the demonstrated way. If the lateral aiming point of the osteotomy (exactly at the anatomical neck) is the same in all cases a lower osteotomy angle would provoke an additional lateral displacement of the rotational centre. c Primary osteoarthritis of the shoulder with no substantial deformity of the humeral head or shoulder socket
Modern prostheses allow adaptation to both the primary and also pathologically altered secondary anatomy. These prostheses generally allow eccentric adjustment of the prosthesis head in relation to the shaft. Some also feature variable, adjustable inclination.
In order to reconstruct a shoulder as closely as possible to the contralateral side, there are two possible approaches. One possibility is to measure the contralateral side and apply those on the prosthesis (if a prosthesis with variable inclination is used). A second option is to perform the osteotomy using a resection guide with a defined inclination. Assuming that, in the majority of cases, the angle of inclination in any given patient conforms to the statistical means derived from anatomical studies, a good approximation to normal anatomical conditions can be achieved. The aim of our study was to investigate how to approximate the anatomical parameters to the healthy side after shoulder replacement.
Therefore the hypotheses of our study are:
With prosthesis with fixed inclination (or using a resection guide in case of prosthesis with variable inclination) and a double eccentric head we anticipate that the pre- and postoperative centre of rotation will differ significantly. Whereas the postoperative centre of rotation will not differ significantly from the contra lateral shoulder.
In contrast, first- and second-generation conventional prostheses may not show a clear tendency.
To test our hypotheses, we have compared reconstruction of the centre of rotation in patients implanted with adjustable prostheses versus those implanted with second-generation prostheses.
Materials and methods
The retrospective investigation was reviewed and approved by the review board of the Marienstift Arnstadt/Germany.
Radiographs from 154 patients with hemi-prosthesis were evaluated. Of those, 106 consecutive patients received a modern adjustable prosthesis (Affinis, Mathys Ltd. Bettlach, Switzerland; Fig. 2a–c) in 2006 and 2007. Surgical indications were primary osteoarthritis (n = 52), post traumatic osteoarthritis (n = 18), fracture sequelae (n = 14), rheumatoid arthritis (n = 12), avascular humeral head necrosis (n = 4) and other reasons (n = 6). In addition, 48 consecutive patients received second-generation prostheses between 1994 and 2001. Indications were primary osteoarthritis (n = 11), post traumatic osteoarthritis (n = 10), fracture sequelae (n = 16), rheumatoid arthritis (n = 9) and avascular humeral head necrosis (n = 2). In these 48 patients, 44 Neer II (Kirschner), two Bio-Modular (Biomet) and two Cofield (Smith and Nephew) prostheses had been implanted. Exclusion criteria in both groups were pathological deformities in the contralateral shoulder.
Fig. 2.
Double eccentric adjustability of the Affinis prosthesis (Mathys Ltd., Bettlach, Switzerland). a, b Lateral and medial positions of the prosthesis head after maximal displacement of the taper and maximally eccentric head position. c Eccentric humeral head with taper
Radiographs were taken preoperatively in the anteroposterior plane of the damaged and healthy shoulder in order to plan the surgery. In the past the axial view of the contra lateral side has not been performed as a standard (operations between 1994 and 2001). Therefore the rotational centre could only be determined from the frontal plane. All prostheses were implanted by the same surgeon. Evaluations were performed by two assessors not involved in the surgical procedure.
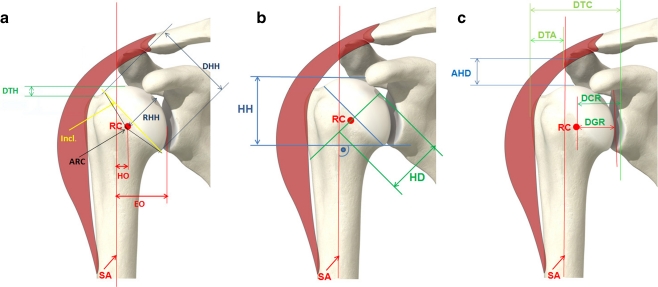
Figure 3a–c shows parameters describing humeral anatomy as defined by various groups [3, 6, 11, 12, 14, 18, 20, 25]. The humeral head centre was defined by a transparent template on which circles of different diameters were drawn.
Fig. 3.
Radiograph parameters. a, b Parameters used to define the bony geometry of the humeral head. c Parameters used to define the characteristics (centralisation) of the humeral head centre. AHD acromio-humeral distance, ARC articular surface arc, DCR distance coracoid/ rotational centre, DGR distance glenoid/ rotational centre, DHH diameter of humerus head, DTA distance greater tuberosity/acromion, DTC distance greater tuberosity/coracoid, DTH distance greater tuberosity/top of humerus head, EO effective offset, HD depth of humerus head, HH height of humerus head, HO humerus offset, Incl inclination angle, RC rotational centre, RHH radius of humerus head, SA shaft axis
Statistical methods
In this study all parameters were measured in metric units. An alpha-error rate of 5% was applied throughout. Possible cumulative errors were not adjusted. Pre- versus postoperative value and opposite shoulder versus postoperative shoulder were compared with either a one- or two-sided paired t-test, respectively. The Affinis prosthesis model was used as the point of reference to which the second-generation models were individually compared.
Results
Parameters which describe the reconstruction of humeral geometry showed a significant difference between pre- and postoperative value (Table 1, upper panel) for the adjustable prosthesis. In addition, parameter values for the postoperative state approached those of the contralateral shoulder and there was no significant difference between the two.
Table 1.
Radiological parameters for specification of humeral geometry
| Parameters | Preoperative, mean ± SD (mm) | Postoperative, mean ± SD (mm) | Opposite side, mean ± SD (mm) | P value, pre-/postoperative | P value, postoperative/ opposite side |
|---|---|---|---|---|---|
| Modern adjustable prosthesis / Affinis; n = 106 | |||||
| EO | 37.42 ± 7.78 | 40.05 ± 6.65 | 41.26 ± 6.67 | 0.0001 | 0.4300 |
| HO | -0.31 ± 5.41 | 3.90 ± 2.69 | 4.48 ±1.47 | 0.0001 | 0.1720 |
| DHH | 53.48 ± 7.46 | 51.90 ± 4.28 | 51.57 ± 4.92 | 0.0030 | 0.8830 |
| RHH | 29.43 ± 4.10 | 28.26 ± 2.65 | 27.04 ± 2.74 | 0.0010 | 0.4100 |
| ARC | 128.43 ± 21.09 | 137.45 ± 5.06 | 142.09 ± 13.26 | 0.0001 | 0.4100 |
| DTH | 19.20 ± 4.74 | 19.81 ± 4.63 | 20.39 ± 4.45 | 0.2150 | 0.4700 |
| HH | 40.45 ± 5.02 | 40.02 ± 5.93 | 38.74 ± 5.03 | 0.3620 | 0.0950 |
| HD | 28.72 ± 8.09 | 33.23 ± 6.29 | 32.48 ± 4.08 | 0.0001 | 0.2080 |
| Second generation prostheses; n = 47 | |||||
| EO | 34.83 ± 12.71 | 36.68 ± 10.91 | 38.14 ± 8.63 | 0.5050 | 0.2210 |
| HO | 1.62 ± 4.24 | 3.53 ± 3.43 | 4.14 ± 2.62 | 0.0001 | 0.2800 |
| DHH | 50.38 ± 6.29 | 48.51 ± 5.80 | 49.64 ± 8.36 | 0.2000 | 0.1780 |
| RHH | 27.28 ± 3.49 | 28.81 ± 5.29 | 27.25 ± 3.51 | 0.0380 | 0.3550 |
| ARC | 137.55 ± 18.17 | 127.04 ± 16.36 | 147.64 ± 14.00 | 0.1360 | 0.0001 |
| DTH | 20.93 ± 3.81 | 24.74 ± 6.98 | 20.67 ± 6.06 | 0.0001 | 0.0360 |
| HH | 35.24 ± 5.02 | 33.19 ± 5.93 | 36.68 ± 5.03 | 0.1300 | <0.0001 |
| HD | 29.00 ± 6.18 | 33.02 ± 6.47 | 33.14 ± 6.27 | <0.0001 | 0.2170 |
EO effective offset, HO humerus offset, DHH diameter of humerus head, RHH radius of humerus head, ARC articular surface arc, DTH I distance greater tuberosity/top of humerus head, HH height of humerus head, HD depth of humerus head
With second-generation prostheses the results were different. All implants used had a modular head, but one which could not be eccentrically adjusted. Postoperative parameter measurements differed from preoperative values in some cases only. The comparison to the contralateral shoulder showed high inconsistency (Table 1, lower panel).
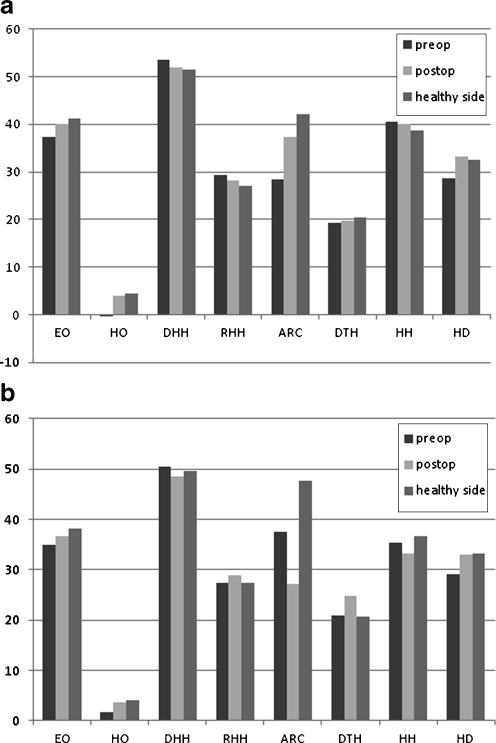
The results mentioned above are especially clear in the graphic presentations of the head geometry (Fig. 4). Most parameters demonstrate an approximation to the values of the healthy side for the adjustable prosthesis (Fig. 4a), but no clear tendency in second-generation prostheses (Fig. 4b).
Fig. 4.
a Results of radiological parameters to define the bony geometry of the humeral head (adjustable prostheses (Affinis), n = 106). b Results of radiological parameters to define the bony geometry of the humeral head (second generation prostheses, n = 47; legends see Fig. 3)
The relationship between the humeral head centre and the glenoid showed the same tendency (Table 2). With the adjustable prosthesis, there were significant differences between all pre- and postoperative parameter values, whereas no significant difference between postoperative and the contralateral shoulder was observed (Table 2, upper panel). Also, with these measurements the second-generation prostheses results were different. No consistency was observed between pre- and postoperative, and between postoperative and contralateral shoulder (Table 2, lower panel). The graphs would show the same relations demonstrated in Fig. 4, but for reasons of space are not demonstrated here.
Table 2.
Radiological parameters for specification of the centring of humeral head
| Parameters | Preoperative, mean ± SD (mm) | Postoperative, mean ± SD (mm) | Opposite side, mean ± SD (mm) | P value, pre-/postoperative | P value, postoperative/ opposite side |
|---|---|---|---|---|---|
| Modern adjustable prosthesis / Affinis; n = 106 | |||||
| AHD | 10.08 ± 4.37 | 11.46 ± 4.85 | 10.14 ± 2.85 | 0.0010 | 0.4810 |
| DTA | 9.07 ± 8.31 | 13.44 ± 7.70 | 14.57 ± 5.03 | 0.0001 | 0.9650 |
| DTC | 56.81 ± 9.23 | 60.01 ± 7.28 | 61.76 ± 8.89 | 0.0001 | 0.1680 |
| DCR | 37.45 ± 7.08 | 36.01 ± 5.93 | 36.22 ± 5.65 | 0.0100 | 0.0940 |
| DGR | 25.49 ± 5.33 | 24.44 ± 3.47 | 23.66 ± 5.33 | 0.0120 | 0.4850 |
| Second generation prostheses; n = 47 | |||||
| AHD | 10.20 ± 5.36 | 8.49 ± 5.58 | 9.18 ± 2.76 | 0.013 | 0.956 |
| DTA | 9.07 ± 10.60 | 11.46 ± 10.74 | 9.71 ± 6.36 | 0.037 | 0.316 |
| DTC | 59.00 ± 11.91 | 59.00 ± 11.55 | 62.93 ± 8.80 | 0.467 | 0.064 |
| DCR | 35.17 ± 9.49 | 33.91 ± 8.93 | 35.50 ± 5.24 | 0.289 | 0.314 |
| DGR | 21.53 ± 6.36 | 21.57 ± 5.52 | 20.64 ± 4.75 | 0.978 | 0.422 |
AHD acriomio-humeral distance, DTA distance greater tuberosity/acromion, DTC distance greater tuberosity/coracoid, DCR distance coracoid/rotational centre, DGR distance glenoid/rotational centre
Discussion
The results strongly confirm our hypothesis that with modern adjustable prosthesis an adaptation to the anatomical parameters of the healthy contralateral shoulder can be achieved. Significant differences were found between pre- and postoperative values of the operated shoulder showing the displacement of the rotational centre. This was demonstrated in almost all measured parameters.
It is interesting to note that the difference in postoperative values compared to the contralateral shoulder values of parameters EO and HO is only 1.21 mm and 0.58 mm in the Affinis prosthesis (Table 1, upper panel). Therefore the centre of rotation is within 4 mm; the maximum range of tolerance defined by other groups [17, 24]. When comparing postoperative centre of rotation to the original position, Pearl et al. reported values of 14.7 mm and 2.1 mm for second- and third-generation prostheses, respectively [17, 19, 20]. However, it was not clear whether they compared the postoperative state with the preoperative state or with the non-operated shoulder. In comparing our preoperative data with the postoperative parameter values, we observed differences of 2.63 mm for parameter EO and 4.21 mm for parameter HO giving values within or just over the 4 mm limit, respectively.
Second generation prostheses (Table 1, lower panel) show no characteristic tendency and lesser significant differences between the pre- and postoperative values or between the postoperative values and the contralateral side, supporting the original hypothesis which predicted no particular trend.
The difference between second- and modern-adjustable-prostheses is especially marked with regard to parameter ARC (Table 1). Pearl et al. suggested the deviation should be no more than 30° of the original value [17]. For both prosthesis types the results fall within this limit, although the 4.64° deviation of the adjustable prosthesis is clearly less than the 20.6° deviation of the second-generation prosthesis. The significant difference between pre- and postoperative values along with postoperative parameter values approaching those of the contra lateral shoulder are clearly seen using the modern adjustable prosthesis. In contrast, the ARC measurement in second-generation prostheses shows a significant difference between postoperative state and contralateral shoulder, but no significant difference between pre- and postoperative state. These different results are astonishing because this parameter largely depends on the size of the head component.
Remarkably, the changes predicted in the initial hypotheses are observed not only in the data describing humeral head geometry, but also in the parameter values describing the relationship of the humeral head to the glenoid (Table 2). This was not necessarily expected; aside from the reconstruction of the anatomy of the humeral head there are other factors influencing the position of the head of the humerus in relation to the glenoid, e.g. the condition of the rotator cuff or contracture of the joint capsule. With this modern adjustable prosthesis (Table 2, upper panel), all parameters showed a significant difference pre- and postoperatively, with postoperative values approaching those of the contralateral shoulder.
Overall, the results support our hypothesis; the use of a prosthesis with fixed inclination and adjustable double eccentric head almost completely approaches the anatomy of the contralateral shoulder. Second-generation prostheses did not show these results in our study.
Our observations are consistent with the findings of other groups, who observed improved adaptive capabilities with modern adjustable prostheses compared with conventional first- or second-generation models. It is not yet clear if better adaptation leads to longer prosthesis survival [17, 18]. It has however been shown that range of movement can be improved and the danger of subacromial impingement is reduced [15, 24, 25]. Exact reconstruction of the centre of rotation is also important for normal function of the rotator cuff muscles [15, 16]. This leads to a reduction in the eccentric load of the glenoid [4]. Early clinical results and experimental analysis support the advantage of modern adjustable prosthesis designs in subsequent function [2]. Ianotti et al. showed that second-generation prostheses required specific modifications of the surgical technique to replicate normal anatomical parameters approximately using a three-dimensional computer surgical simulator (modified varus or valgus humeral osteotomy and additional application of smaller and flattened humeral head components) [12].
The results support our hypothesis that clear improvements in the fit of the prosthesis to the anatomical conditions can be seen using a modern adjustable model compared to conventional prostheses. This effects a correction of the parameters representing the deformed anatomy and at the same time an approximation to the normal anatomy of the healthy side, especially of the rotational centre of the humeral head.
The influence of these findings on survival and functional outcome cannot be shown with this study and requires further investigation.
Acknowledgements
We would like to thank D. Pfluger and P. Münger for statistical analysis.
Conflict of interest The independent statistical analysis was supported by Mathys Ltd., Bettlach, Switzerland. UI received consultant payments from Mathys.
Ethics standard The institutional review board of the Marienstift Arnstadt/Germany has approved the study proposal, and all of the patients agreed by informed consent.
References
- 1.Boileau P, Walch G. Anatomical study of the proximal humerus: surgical technique considerations and prosthetic design rationale. In: Walch G, Boileau P, editors. Shoulder arthroplasty. Springer Berlin: Heidelberg; 1999. pp. 69–82. [Google Scholar]
- 2.Buchler P, Farron A. Benefits of an anatomical reconstruction of the humeral head during shoulder arthroplasty: a finite element analysis. Clin Biomech. 2004;19:16–23. doi: 10.1016/j.clinbiomech.2003.09.009. [DOI] [PubMed] [Google Scholar]
- 3.Duparc F, Duparc J. Shoulder endoprosthetics. Common principles and important characteristics. In: Duparc F, editor. Techniques in orthopaedics and traumatology [in German] München, Jena: Urban und Fischer; 2005. pp. 65–73. [Google Scholar]
- 4.Favre P, Moor B, Snedeker JG, Gerber C. Influence of component positioning on impingement in conventional total shoulder arthroplasty. Clin Biomech. 2008;23:175–183. doi: 10.1016/j.clinbiomech.2007.09.009. [DOI] [PubMed] [Google Scholar]
- 5.Harryman DT, Sidles JA, Harris SL, Lippitt SB, Matsen FA. The effect of articular conformity and the size of the humeral component on laxity and motion after glenohumeral arthroplasty. J Bone Joint Surg Am. 1995;77:555–563. doi: 10.2106/00004623-199504000-00008. [DOI] [PubMed] [Google Scholar]
- 6.Hertel R, Knothe U, Ballmer FT. Geometry of the proximal humerus and implications for prosthetic design. J Shoulder Elbow Surg. 2002;11:331–338. doi: 10.1067/mse.2002.124429. [DOI] [PubMed] [Google Scholar]
- 7.Hopkins AR, Hansen UN, Amis AA, Taylor M, Emery RJ. Glenohumeral kinematics following total shoulder arthroplasty: a finite element investigation. J Orthop Res. 2007;25:108–115. doi: 10.1002/jor.20290. [DOI] [PubMed] [Google Scholar]
- 8.Iannotti JP, Norris TR. Influence of preoperative factors on outcome of shoulder arthroplasty for glenohumeral osteoarthritis. J Bone Jt Surg Am. 2003;85:251–258. doi: 10.2106/00004623-200302000-00011. [DOI] [PubMed] [Google Scholar]
- 9.Irlenbusch U, Gebhardt K, Rott O, Werner A. Reconstruction of the rotational centre of the humeral head depending on the prosthetic design [in German] Z Orthop. 2008;146:211–217. doi: 10.1055/s-2007-989448. [DOI] [PubMed] [Google Scholar]
- 10.Irlenbusch U, Irlenbusch L. Update in shoulder endoprosthetics [in German] Z Orthop Unfallchir. 2007;4:289–309. doi: 10.1055/s-2007-966867. [DOI] [Google Scholar]
- 11.Jeong J, Bryan J, Ianotti JP. Effect of a variable prosthetic neck-shaft angle and the surgical technique on replication of normal humeral anatomy. J Bone Joint Surg Am. 2009;91:1932–1941. doi: 10.2106/JBJS.H.00729. [DOI] [PubMed] [Google Scholar]
- 12.Jerosch J, Moursi MG, Schunck J. Shoulder resurfacing in patients with degenerative joint disease [in German] Orthop Prax. 2007;43:635–641. [Google Scholar]
- 13.Kasten P, Maier M, Rettig O, Raiss P, Wolf S, Loew M. Proprioception in total, hemi and reverse shoulder arthroplasty in 3D motion analyses: a prospective study. Int Orthop. 2009;33:1641–1647. doi: 10.1007/s00264-008-0666-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.McPherson EJ, Friedman RJ, An YH, Chokesi R, Dooley RL. Anthropometric study of normal glenohumeral relationships. J Shoulder Elbow Surg. 1997;6:105–112. doi: 10.1016/S1058-2746(97)90030-6. [DOI] [PubMed] [Google Scholar]
- 15.Nyffeler RW, Sheikh R, Jacob HA, Gerber C. Influence of humeral prosthesis height on biomechanics of glenohumeral abduction. J Bone Joint Surg Am. 2004;86:575–580. doi: 10.1302/0301-620X.86B8.15228. [DOI] [PubMed] [Google Scholar]
- 16.Nyffeler RW, Gerber C. The relevance of anatomical reconstruction. Nice shoulder course: shoulder arthroscopy and arthroplasty. Current concepts. Montpellier: Sauramps Medical; 2004. pp. 315–316. [Google Scholar]
- 17.Pearl ML, Kurutz S, Postachini R. Geometric variables in anatomic replacement of the proximal humerus: how much prosthetic geometry is necessary? J Shoulder Elbow Surg. 2009;18:366–370. doi: 10.1016/j.jse.2009.01.011. [DOI] [PubMed] [Google Scholar]
- 18.Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14:99S–104S. doi: 10.1016/j.jse.2004.09.025. [DOI] [PubMed] [Google Scholar]
- 19.Pearl ML, Kurutz S, Robertson DD, Yamaguchi K. Geometric analysis of selected press fit prosthetic systems for proximal humeral replacement. J Orthop Res. 2002;20:192–197. doi: 10.1016/S0736-0266(01)00111-5. [DOI] [PubMed] [Google Scholar]
- 20.Pearl ML, Kurutz S. Geometric analysis of commonly used prosthetic systems for proximal humeral replacement. J Bone Joint Surg Am. 1999;81:660–671. doi: 10.1302/0301-620X.81B4.9380. [DOI] [PubMed] [Google Scholar]
- 21.Roberts SNJ, Foley APJ, Swallow HM, Wallace WA, Coughlan DP. The geometry of the humeral head and the design of the prosthesis. J Bone Joint Surg Br. 1991;73:647–650. doi: 10.1302/0301-620X.73B4.2071652. [DOI] [PubMed] [Google Scholar]
- 22.Thomas SR, Sforza G, Levy O, Copeland SA. Geometrical analysis of Copeland surface replacement shoulder arthroplasty in relation to normal anatomy. J Shoulder Elbow Surg. 2005;14:186–192. doi: 10.1016/j.jse.2004.06.013. [DOI] [PubMed] [Google Scholar]
- 23.Walch G, Boileau P. Prosthetic adaptability: a new concept for shoulder arthroplasty. J Shoulder Elbow Surg. 1999;8:443–451. doi: 10.1016/S1058-2746(99)90074-5. [DOI] [PubMed] [Google Scholar]
- 24.Williams GR, Wong KL, Pepe MD, Tan V, Silverberg D, Ramsey ML, et al. The effect of articular malposition after total shoulder arthroplasty on glenohumeral translations, range of motion and subacromial impingement. J Shoulder Elbow Surg. 2001;10:399–409. doi: 10.1067/mse.2001.116871. [DOI] [PubMed] [Google Scholar]
- 25.Wirth MA, Ondrla J, Southworth C, Kaar K, Anderson BC, Rockwood CA., 3rd Replicating proximal humeral articular geometry with a third-generation implant: a radiographic study in cadaveric shoulders. J Shoulder Elbow Surg. 2007;16:S111–S116. doi: 10.1016/j.jse.2006.09.008. [DOI] [PubMed] [Google Scholar]