Small Subitizing Range in People with Williams syndrome

Abstract

Recent evidence suggests that the rapid apprehension of small numbers of objects-- often called subitizing-- engages a system which allows representation of up to 4 objects but is distinct from other aspects of numerical processing. We examined subitizing by studying people with Williams syndrome (WS), a genetic deficit characterized by severe visuospatial impairments, and normally developing children (4–6.5 years old). In Experiment 1, participants first explicitly counted displays of 1 to 8 squares that appeared for 5 s and reported “how many”. They then reported “how many” for the same displays shown for 250 ms, a duration too brief to allow explicit counting, but sufficient for subitizing. All groups were highly accurate up to 8 objects when they explicitly counted. With the brief duration, people with WS showed almost perfect accuracy up to a limit of 3 objects, comparable to 4 year-olds but fewer than either 5 or 6.5 year-old children. In Experiment 2, participants were asked to report “how many” for displays that were presented for an unlimited duration, as rapidly as they could while remaining accurate. Individuals with WS responded as rapidly as 6.5 year-olds, and more rapidly than 4 year-olds. However, their accuracy was as in Experiment 1, comparable to 4 year-olds, and lower than older children. These results are consistent with previous results indicating that people with WS can simultaneously represent multiple objects, but that they have a smaller capacity than older children, on par with 4 year-olds. This pattern is discussed in the context of normal and abnormal development of visuospatial skills, in particular those linked to the representation of numerosity.

When adults observe brief presentations of displays containing 1-4 objects, they can say “how many” with very high accuracy, a phenomenon known as subitizing (Kaufman, Lord, Reese, & Volkmann, 1949). Such accuracy holds only for small sets of objects, with errors sharply increasing for numbers larger than 4 (Mandler & Shebo, 1982; Revkin, Piazza, Izard, Cohen, & Dehaene, 2008). With longer exposure durations, accuracy is also high for larger numbers, but the time to respond increases systematically, starting around 4 objects (Mandler et al., 1982; Svenson & Sjöberg, 1978).¹ These profiles suggest that there are two separate mechanisms at work for tasks in which people judge “how many”. Indeed, recent arguments and evidence make a strong case for the separation of subitizing from other numerical processes, with subitizing being a mechanism in which attention is divided among objects (i.e. individuation), but without any representation of numerosity (Hyde & Spelke, 2009; Xu & Chun, 2009). By contrast, counting clearly requires representation of number, and also requires the association of exact numerosities with number names. In this paper, we examine the effects of impaired visuospatial processing on subitizing and counting by studying the ability of people with Williams syndrome (WS) to subitize displays, as well as to count them. The results are compared to those in normally developing children, shedding light on the emergence of these capacities under both normal and abnormal conditions of development.

Several lines of evidence suggest that subitizing may be a mechanism in which a small set of individual objects are represented in their spatial locations, without explicit representation of number. First, human observers appear to be constrained to visually perceiving up to about four individual objects at a time; this limit appears in tasks ranging from those requiring storage of information in visual working memory (Luck & Vogel, 1997) to tracking multiple moving objects (Pylyshyn & Storm, 1988; see Cowan, 2001 for a review). Developmental work suggests that infants can keep track of a maximum of about three objects. If infants are shown objects being placed sequentially into an opaque box, they can keep track of 1, 2, or 3 individual objects but they cannot represent 4 or more objects (Feigenson, Dehaene, & Spelke, 2004; Feigenson & Carey, 2005; Starkey & Cooper, 1995). Building on such phenomena, Xu and Chun (2009) have summarized evidence that object individuation-- with its ceiling of 4 in adulthood-- engages the inferior intraparietal sulcus (IPS) of the brain, supporting a representation of the individual objects themselves, without any specific features. They also provide evidence that object complexity, which varies with specific object features, engages different areas of the brain (superior IPS and higher visual areas).

The idea that mechanisms representing small sets of objects are separate from those representing numerosity per se is supported by a variety of studies (for review, see Piazza & Izard, 2009). For example, both infants and adults can apprehend and compare displays of dots with numerosities too large to count; their estimates of the numerosities in such displays conform to Weber's law, with the ratio of the compared numerosities determining whether the sets are discriminable (Halberda, Mazzocco, & Feigenson, 2008; Xu & Spelke, 2000). Even though infants can discriminate large numerosities, their representation of small sets of objects is strikingly limited to 3, but not 4, objects (Feigenson et al., 2005). Moreover, different variables modulate infants' responses of small vs. large arrays (Feigenson, Carey, & Spelke, 2002; Xu et al., 2000), with clear sensitivity to non-numerical variables in small arrays, but not large arrays. The small and large number systems have also been shown to have different ERP signatures and may display distinct patterns of fMRI activation (Ansari, Lyons, van Eimeren, & Xu, 2007; Hyde et al., 2009). Finally, whereas the inferior IPS is implicated in apprehension of small object arrays, other parietal regions show sensitivity to numerosity itself. For example, in posterior parietal lobe, activation increases over ranges from 1-7, but there is a sudden and sharp increase with each additional object from 4 to 7 (Piazza, Giacomini, Le Bihan, & Dehaene, 2003; see also Sathian et al., 1999). Some have suggested that this increase is linked to the attentional shifts required as the observer moves from item to item, marking and counting each one on a mental number line (Hubbard, Piazza, Pinel, & Dehaene, 2005).

The idea that subitizing engages a mechanism that allows the deployment of attention across multiple objects without explicitly tapping into a representation of the number of objects in the display suggests that it might be possible to damage subitizing without comparable associated damage to explicit representations of number. In this paper, we examine this idea by studying subitizing and explicit counting of the same arrays by people with Williams syndrome-- a genetic deficit resulting from a hemizygous micro-deletion on chromosome 7q11.23 (Ewart et al., 1993; Meyer-Lindenberg, Mervis, & Berman, 2006). People with WS have mild to moderate retardation, with severe impairments in a range of visuospatial functions, but relatively spared language.

There are several reasons that people with WS might provide unique insight into the mechanisms underlying subitizing, and their relationship with numerical representations. First, evidence suggests that the severe visual-spatial impairment in this population is linked to structural and functional abnormalities in the parietal lobe, especially the IPS (Eckert et al., 2005; Kippenhan et al., 2005; Meyer-Lindenberg et al., 2004; Reiss et al., 2000). Given conjectures that the system of apprehending multiple small objects engages the inferior IPS (Xu et al., 2009), people with WS may be susceptible to impairment in subitizing, although parietal lobe abnormalities might also lead to difficulties in shifting attention that are needed to count accurately. Second, people with WS show spatial impairment that is quite uneven, with severe compromise on copying and visual-spatial construction tasks (Bellugi, Lichtenberger, Jones, Lai, & George, 2001; Mervis et al., 2000), but relative strength in other tasks that require computing spatial relationships such as biological motion perception (Jordan, Reiss, Hoffman, & Landau, 2002; Reiss, Hoffman, & Landau, 2005), object recognition (Landau, Hoffman, & Kurz, 2006), and face recognition (Paul, Stiles, Passarotti, Bavar, & Bellugi, 2002; Tager-Flusberg, Plesa-Skwerer, Faja, & Joseph, 2003).

Third, previous evidence shows that people with WS have severe impairments in a visual-spatial task that-- like subitizing-- requires simultaneous attention to more than one object. In Multiple Object Tracking (MOT), people must track multiple objects as they move along independent trajectories (Pylyshyn & Storm, 1988). In such tasks, normal adults can usually accurately track about 4 objects and, under some circumstances, can track more (Alvarez & Franconeri, 2007). Pylyshyn (2000) proposed that this is accomplished by a visual mechanism that deploys a small number of “indexes” (maximum of 4) which serve as pointers to individual objects, but provide no information about their identity or numerosity; he explicitly linked this mechanism to subitizing (Pylshyn, 2000). The mechanism is also closely related to the individuation mechanism proposed by Xu and Chun (2009). In the MOT task, adolescents and adults with WS can only accurately track up to 2 objects (O'Hearn, Landau, & Hoffman, 2005; O'Hearn, Hoffman, & Landau, 2009). This performance indicates severe impairment, as it is equal to the performance shown by normally developing 4 year-old children, but worse than that for 5 or 6 year-old children, who can track 3 or 4 objects at a time. This raises the possibility that -- like MOT-- the subitizing range in people with WS will be like that of normal 4 year-olds, and smaller than that of 5 or 6 year-olds.

In the first experiment presented below, we examined accuracy for naming the number of objects in an array. We included a Counting and a Subitizing task, and accuracy was measured. In the Counting task, participants saw displays of squares for 5 s and were asked to explicitly count them. This task was included to ensure that the participants with WS knew all number names and could accurately count and name set sizes of 1 through 8. In the Subitizing task, participants saw the same displays for only 250 ms, and were asked to report, “how many squares” they saw. If subitizing engages the same mechanisms as MOT, then we would expect the WS participants to be able to report up to 2 or possibly 3 squares; moreover, this limit should be similar to normal 4 year-olds, and lower than 5 or 6 year-olds.

Experiment 1

Methods

Participants

The WS group included 8 males and 7 females (M age 20 years, 8 months; range 11;3 to 48;8; 8 children and 7 adults, all but 2 in their twenties), positively diagnosed by a geneticist and the FISH test (fluorescence in situ hybridization; Ewart et al., 1993). Thirteen typically developing children participated in each of 3 age groups: 4-year-olds (7 M: M = 4;6: range 4;0 to 4;11), 5-year-olds (5 M : M = 5;7: range 5;0 to 6;0), and 6.5-year-olds (8 M: M = 7;4: range 6;6 to 7;8). The WS overall cognitive profile was typical for this syndrome: The group had a mean IQ of 60 ± 12 (KBIT; Kaufman & Kaufman, 1990), and participants were severely impaired on a standardized test of block construction (Elliot, 1990; 11 of 15 participants fell at the 1^st percentile for age, 3 fell at the 4^th, 5^th, and 7^th percentile, respectively, and 1 was untested). People with WS were recruited through the Williams Syndrome Association, and typically developing children through preschools.

Design, Stimuli, & Procedure

Participants performed in a Counting task and a Subitizing task, in that order. Stimuli in both tasks consisted of 1 to 8 dark squares on a light background, randomly placed with their centers at least 1.35″ apart (Figure 1). Each square was randomly assigned 1 of 3 sizes (.37″; .57″; .78″).² People viewed these displays on an LCD monitor from a distance of 18 to 25 inches. The screen (resolution 1024 × 768 × 32) subtended approximately 28 × 21 degrees-of-visual-angle. Before the Counting task, individuals practiced counting squares on a piece of paper one by one, using their fingers to point to each square when there were more than 3 or 4 squares. Before the Subitizing task, individuals practiced guessing the number of items on the screen, doing at least 6 practice trials until they were skilled at responding to rapidly presented displays.

Figure 1.

Illustration of task on Experiment 1. Experiment 2 used the same displays but the items remained on the screen until the microphone sensed a response, and the mask did not appear.

The Counting task was carried out primarily to ensure that the individuals with WS knew all of the number names and could apply these accurately in counting the set sizes to be tested in the Subitizing task. Previous studies suggested that they could do this, given enough time (O'Hearn & Landau, 2007). In the Counting task, each of the eight possible numerosities (targets 1-8) was presented 3 times in random order, for a total of 24 trials. Participants were told to count the squares carefully, and were encouraged to count out loud. The trial started with a fixation cross on the screen. When the participant was ready, the experimenter started the trial. The fixation then stayed on for .5 s, followed by the display. Each display was presented for 5 s, followed by a mask consisting of a random dark and light gray texture. With the mask on, participants reported how many squares there were, and the experimenter typed their responses into a window in the corner of the display. After entering this information, the window disappeared and a fixation cross appeared on the screen. The experimenter then checked to make sure the participant was ready to continue (by asking “Ready?”), and then started the next trial.

In the Subitizing task, each of the targets (1-8) was presented 6 times in a random order, for a total of 48 trials. Participants were instructed to look carefully at the display and report the number of squares. Each trial type was identical to its counterpart in the Counting task except that displays were presented for 250 ms instead of 5 s. Displays were followed by the same mask that was used in the Counting task. The exposure duration provided enough time for participants to see the displays and should have been sufficient for subitizing (Mandler et al., 1982; Starkey et al., 1995), but it did not provide enough time to verbally count the squares one by one while the display was still on. Each trial was preceded by the same check on the participants' readiness (“Ready?”) as in the Counting task.

Results

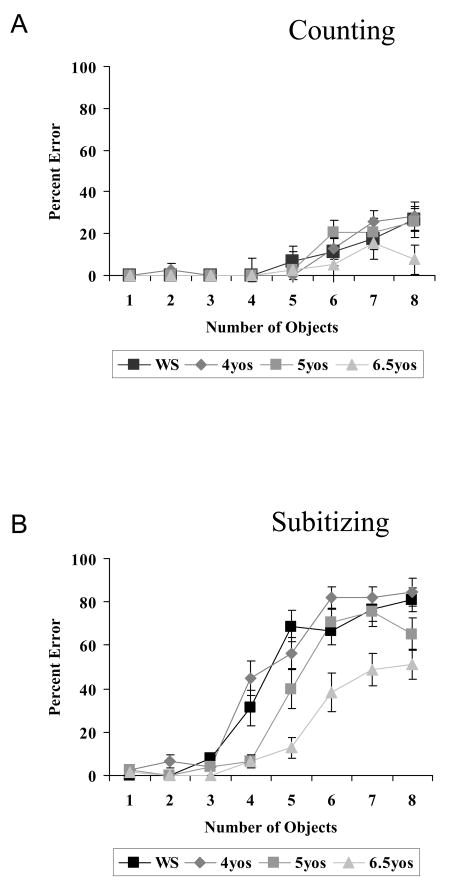
Data from the Counting task are shown in Figure 2A, as the percent of errors as a function of target type for the WS group and the three typically developing groups. Results indicate that all groups were relatively skilled at this task, with near perfect performance for set sizes up to about 5, and modest increases in error rates for larger sizes. A mixed model analysis of variance with factors of group (WS, 4, 5, 6 year-olds) and target (1-8) showed a main effect of Target Number [F(7,350) = 17.08, p < .001], but no effect of Group [F(3,50) = 1.07, p = ns] nor interaction between Target Number and Group [F(21,350) = .80, p = ns]. In addition to the extremely high accuracy of all groups, 80% of the errors (total= 63) among normally developing children and 100% of the errors (total= 28) among people with WS were numbers that were 1-2 more or less than the target number, and this pattern did not vary as the numbers increased. This type of error likely stems from occasionally re-marking already counted objects, or missing uncounted ones. The results of this task indicate that the WS participants, like the normally developing controls, had adequate control over the number names, and that these were mapped correctly onto the actual numerosities shown in the displays.

Figure 2.

Percent errors on Experiment 1 by target number in the three groups of typically developing children (4-year-olds, 5-year-olds and 6.5-year-olds), along with the individuals with WS. A. Counting. B. Subitizing.

The results of the Subitizing task, shown in Figure 2B, present quite a different picture, with the groups differing a great deal in their accuracy over target number. A mixed model analysis of variance resulted in significant main effects of Group (F(3, 50) =21.57, p< .001) and Target Number (F(7,350) = 150.70, p< .001) and, importantly, a significant interaction between Group and Target Number (F(21, 350) = 4.14, p< .001). This interaction was explored further with planned comparisons that examined performance at each target among the individuals with WS compared to each age group separately.

People with WS did not perform differently from 4-year-olds; an ANOVA indicated there was no effect of Group [F(1,26) = 1.15, p = ns] nor a Target Number × Group interaction [F(7,182) = 1.57, p = ns]. In contrast, the WS group performed more poorly than 5-year-olds, especially at higher target numbers. There was a main effect of Group [F(1,26) = 6.56, p < .02]) and a Target Number × Group interaction [F(7,182) = 3.12, p < .01], reflecting poorer performance for sets of 4 and 5 objects [4 objects: t(26) = -2.74, p < .02, 5 objects: t(26) = -2.55, p < .02]. The WS group also performed more poorly than 6.5-year-olds, with a main effect of Group [F(1,26) = 48.43, p < .001] and an interaction between Target Number and Group [F(7,182) = 6.74, p < .001], reflecting poorer performance at targets 3 through 8 (3 targets [t(26) = -2.63, p < .02], 4 targets [t(26) = -2.69, p < .02], 5 targets [t(26) = -6.16, p < .001], 6 targets [t(26) = -2.60, p < .02], 7 targets [t(26) = -3.06, p < .01], and 8 targets [t(26) = -3.46, p < .01].³

In order to estimate the number of objects that each group could subitize, we carried out a non-parametric analysis of the number of targets that were reported with 100% accuracy. Our reasoning was that, if participants could subitize at a particular target number and were fully cooperating, one would expect them to get all 6 trials correct (100%). Using the highest target number with 100% accuracy, we examined how many people in each group could subitize up to 3 targets vs. 4 or more. In the WS group, 10 of 15 participants were fully accurate up to 3 items, with the remaining 5 fully accurate for 4 or more. All of the normally developing 4 year-olds (N=13) were fully accurate at up to 3 targets, but none were for 4 or more targets. The WS distribution was reliably different from that of the 4 year-olds (Fisher's exact test, p=.04). Normally developing 5 year-olds were split, with 6 children fully accurate up to 3 targets, and 7 at 4 or more, not reliably different from the WS group (Fisher's exact p = .45). All of the normally developing 6.5 year-olds (N=13) were fully accurate at 4 or more objects, again reliably different from the WS group (Fisher's exact test, p<.001).⁴ In sum, the majority of the WS participants and all of the 4-year-olds could subitize up to 3 items (but not 4) at 100% accuracy, and the 6.5 year-olds could all subitize 4 or more. Five year-olds fell in between the 4's and 6.5's, split between subitizing up to 3 items, and subitizing 4 or more. Comparisons of the distributions of the normally developing groups showed that the 4 year-olds were reliably different from both 5 year-olds and 6.5 year-olds (Fisher's exact, p=.005, p<.001) and that the 5 and 6.5 year-olds were also different from each other (Fisher's exact, p =.02).

Given the very different pattern of performance in the Subitizing task compared to the Counting task, we also asked whether the error patterns were different. Recall that the errors in the Counting task were almost exclusively errors of providing a number that was different from the target by 1-2, and that this held for all target numbers for which there were errors (largely for targets 5-8). In contrast, the error matrix for the Subitizing task showed many more errors, and a greater spread of errors around the target as target numbers increased. If strict limits on the number of objects that can be subitized preclude knowing “how many” for targets outside this range, people might estimate numerosity by using the approximate number system for these larger target displays (see Revkin et al., 2008). One of the signatures of this system is the systematic increase in variability of response with increasing target set size, but with a constant ratio between the two, called the coefficient of variation (see Dehaene, 1997; Halberda et al., 2008). We computed the coefficient of variation at each target number (i.e. the standard deviation divided by the mean for the answers produced by participants). The results (shown in Figure 3) suggest that, at least for several of the groups, the coefficient of variation is flat above the estimated subitizing range. This pattern of errors looks quite different from the one generated in the Counting task, which showed exclusively errors adjacent to the target, without variation over target size.

Figure 3.

Mean coefficient of variation on Experiment 1 across target numbers 1 to 8 for the three groups of typically developing children and individuals with WS.

Experiment 1: Summary

Our analyses suggest that the subitizing range for most people with WS is remarkably similar to that of normally developing 4 year-olds, consistent with our findings for multiple object tracking (MOT; O'Hearn et al., 2009). In that study, we found that people with WS (some of whom participated in the present study) could track a maximum of approximately 2 objects. This estimate of capacity was not reliably different from those for 4 year-old normally developing children but was lower than that for 5 or 6.5 year-old children. Although the subitizing task we used in the present study is quite different from the multiple object tracking task used to generate these estimates of capacity, it is striking that, in both studies, the people with WS-- adolescents and adults-- did not differ from normally developing 4 year-old children in their estimated capacity limit.

We had decided to use brief presentations in the subitizing task of Experiment 1 because we were concerned about the possibility that the WS group would either be very slow and/or show large variability in their reaction time compared to the normally developing child groups. However, since all groups performed relatively well on Experiment 1 with a brief presentation, we carried out a modified replication of Experiment 1, in which we left the displays visible until there was a response, and measured both accuracy and reaction time. This allowed us to examine both measures together, to determine whether differences in reaction time might explain the patterns of accuracy across the groups. It is possible that other factors associated with the higher numbers, such as crowding or the area utilized, affected the WS group disproportionately at the short delay because they are slower at extracting visual information from the display. Our modified task controlled for this possibility by giving participants as much time as they needed to view the display, while encouraging them to be very accurate.

Experiment 2

Methods

Participants

The WS group included 5 males and 7 females (M age 18 years, 6 months; SD 4 years, 11 months; 5 participated in the previous study), positively diagnosed by a geneticist and the FISH test (Ewart, 1993). As in Experiment 1, there were 3 age groups: 12 4-year-olds (5 M, 7 F: M = 4:6 range 4;0 to 4;11), 12 5-year-olds (4 M, 8 F: M = 5;5: range 5;0 to 5;10), and 11 6.5-year-olds (6 M, 5 F: M = 6;6: range 6;2 to 7;10). The WS group had a mean composite IQ of 69 ± 13 (KBIT), slightly higher then the previous sample, but again displayed the typical profile found in WS. Participants were recruited in the same manner as Experiment 1. None of the normally developing children had participated in Experiment 1.

Design, Stimuli, & Procedure

The stimuli were identical to Experiment 1 but without the mask. Reaction time was measured via a microphone (Abrams & Jenning, 2004), with the answer box appearing as soon as the microphone detected a response. Each number of items (1 through 8) was presented 6 times, for a total of 48 trials, in a random order. Several practice trials were given prior to testing. Participants were encouraged to be as accurate as possible to minimize any speed accuracy trade-offs that might differ between groups. The instructions were: “When I hit the button, some squares are going to appear on the screen. Your job is to tell the computer how many there were. The computer will be listening for you and it only wants to hear numbers so be careful and don't say things like “um”. Sometimes you will just know how many squares there are really fast and if that happens, I want you to tell the computer the answer as fast as you can! Sometimes you won't know the answer so quick and then I want you to count in your head and tell me the answer when you know it. I want you to do your best and try to tell me the exact number each time. Ready to try?” If participants made a mistake, they were told again that, while they should try to be fast, accuracy was most important so they should take the time they needed in order to be accurate. The procedure was subject-paced, as in Experiment 1, with the same check by the experimenter on the participants' readiness prior to each trial.

Statistical Analyses

We examined two dependent measures: accuracy as analyzed in Experiment 1 and RT on correct trials. Studies using brief displays (200 ms) indicate that children as young as 2 years old can subitize up to 3 objects, and that this limit increases with age (Starkey & Cooper, 1995). Studies of older children using RT as a measure indicate that a discontinuity in RT is evident between the subitizing and counting ranges, though the slope in the subitizing range can be substantial (5 year-olds, 195 ms/dot; Chi & Klahr, 1975: 7-8 year-olds, 110 ms/dot; Svenson & Sjoberg, 1978: see also Trick et al., 1996 for a number discrimination task). Thus, evidence indicates that there is development during the preschool and early school age years in both the limit of the subitizing range, and the slope of the function in the subitizing (and counting) range. Hence we examined both of these functions in the WS group and in the groups of normally developing children.

Accuracy was analyzed as in Experiment 1. Reaction time patterns were examined for overall differences across groups. One 4 year-old had no correct trials with 5 to 8 items, thus the RT data from this participant was not included in analyses of these numbers nor the repeated measures analyses. One participant with WS had no correct trials with 8 items, so was excluded from repeated measures analyses that included all target numbers. However, none of the results changed in a repeated measures analysis on 1 to 7 items, which included this participant with WS. In addition to the repeated measures ANOVA and planned comparisons, we also examined the slopes of the RT curves by fitting a bilinear model to each individual's RT data from 1 to 7 (8 was excluded because of potential group differences in the ‘guessing end effect’; Sathian, et al., 1999; Piazza et al., 2003). The 1^st slope presumably reflects the relatively shallow increases in the subitizing range and the 2^nd slope reflects the steeper slope found in the counting range (Mandler & Shebo, 1982; Tuholski, Engle & Baylis, 2001; Riggs et al., 2006). For each individual, we found the intercept between these two lines that minimized the sum of squares and this number of items was considered the limit or ‘breakpoint’ (i.e., end of the subitizing range), with the constraint that the slope of the 1^st line was no more than 250 ms/item (on the basis of the previous developmental literature mentioned above).

Results

Accuracy

Even though accuracy was stressed for all groups, there were differences between groups in the percent of trials that were errors (Figure 4A). The mixed model ANOVA on these data revealed a main effect of Target Number [F(3.01, 132.21) = 20.72, p < .001], with trends for a main effect of Group [F(3,44) = 2.54, p < .06] and a Target Number by Group interaction [F(9.01, 132.21) = 1.69, p <.10]. There was no Group effect or interaction between Group and Target Number when the WS group was compared to 4 year-olds (p's > .59) or 5 year-olds (p's >.15). When compared to 6.5 year-olds, there was a significant main effect of Group [F(1,21)=8.17, p< .01] and an interaction between Group and Target Number [F(3.38,71.03)=4.72, p< .01]. This reflected more errors for the WS group with 5 or more objects (5 objects, t(12.11)=-2.59, p<.03, 6 objects, t(17.95)=-2.02, p<.06, 7 objects, t(16.52)=-2.83, p<.02, 8 objects, t(13.61)=-3.21, p<.01). Comparison of the normally developing groups showed no significant differences between age groups (4, 5, 6.5 year-olds), though there were trends for differences between the 4 and 6.5 year-olds, shown by a main effect of Group [F(1,22)=3.94, p< .07] and an interaction between Group and Target Number [F(2.47,54.29)=2.68, p< .07], reflecting differences at 7 and 8 objects only (p's <.05).

Figure 4.

Performance on Experiment 2 by target number in the three groups of typically developing children (4-year-olds, 5-year-olds and 6.5-year-olds), along with the individuals with WS. A. Accuracy. B. Reaction Time on correct trials.

These parametric analyses indicated the WS group made more errors than 6.5 year-olds but were similar to 4 and 5 year-olds. Non-parametric measures confirmed this result. We examined the highest numerosities for which individuals scored 100% correct. We compared these data for numerosities of 4 and fewer vs. 5 and more. (This higher split reflected that mistakes were less frequent in Experiment 2 than on the Subitizing Task in Experiment 1, as would be expected by the unlimited duration.) Participants scoring 100% for numerosities of 4 and fewer included 9 people with WS, 4 4 year-olds, 3 5 year-olds, and 1 6.5 year-old. Participants scoring 100% for numerosities of 5 and greater included 3 people with WS, 8 4-year olds, 9 5 year-olds, and 10 6.5 year-olds. The pattern across groups was reliably different (Chi-square (3)=12.02, p =.007). The WS distribution was not reliably different from that of the 4 year-olds (Fisher's exact test, p=.10), but was different from normally developing 5 year-olds and 6.5 year-olds (Fisher's exact p = .04; p<.01).⁵ Comparisons of the distributions of the normally developing groups showed that the 4 year-olds were not reliably different from either 5 year-olds or 6.5 year-olds (Fisher's exact, p=.10, p=.31) and that the 5 and 6.5 year-olds were also not different from each other (Fisher's exact, p =.59).

Reaction time

While accuracy in the WS group aligned most closely with the 4 year-olds, the pattern for reaction time was quite different: individuals with WS were faster at responding than 4 and 5 year-olds, but were not different from 6.5 year-olds (Figure 4B). A mixed model repeated measures ANOVA with Group (WS, 4 year-olds, 5 year-olds, 6.5 year-olds) as a between subject factor and Number (1 to 8) as a within subject factor resulted in significant main effects of Group (F(3, 42) =7.62 p< .001) and Target Number (F(2.92,122.81) = 220.97, p< .001) and a significant interaction between Group and Target Number (F(8.77, 122.81) = 2.97, p< .01). We then examined this interaction further with planned comparisons that examined performance across target number in the individuals with WS compared to each age group separately. People with WS responded faster than 4-year-olds. There was a main effect of Group [F(1,21) = 19.54, p < .001] and a Target Number × Group interaction [F(2.58,54.15) = 6.56, p = .001]. T-tests indicated that the WS group was faster than 4 year-olds at every target number (1 target [t(23) = -2.58, p < .02], 2 targets [t(23) = -2.06, p < .06], 3 targets [t(23) = -2.10, p < .05], 4 targets [t(23) = -3.13, p < .01], 5 targets [t(23) = -3.28, p < . 01], 6 targets [t(23) = -4.49, p < .001], 7 targets [t(23) = -4.44, p < .001], 8 targets [t(23) = -3.35, p < .01]). The WS group also responded faster overall than 5-year-olds, shown in a main effect of Group [F(1,21) = 4.51, p < .05]) but no Target Number × Group interaction [F(2.86, 60.10) = 2.08, p = .12]. The WS group did not perform differently than 6.5-year-olds (Group [F(1,20) = .04, p = ns]; Target Number × Group interaction [F(1.72,34.34) = .56, p = ns]).⁶ When the typical groups were compared to each other using a Repeated measures ANOVA, there was a main effect of group (F(2,32)=7.45, p=.002) but no interaction between Group and Target Number. Post-hoc comparisons using Tamhane's t indicated that 4 year-olds were slower than 6.5 year-olds (p< .002) but that the 5 year-olds did not differ from either typically developing group (p's >.15).

In order to examine potential group differences in the “breakpoint” between the subitizing and counting ranges, and the slopes of each, we then examined the bilinear function for the RT curves, as described in the statistical analyses section.⁷ Six WS individuals, 2 4 year-olds, 5 5 year-olds, and 6 6.5 year-olds had breakpoints at 4 items, with the rest showing breakpoints below 4. A chi-square on these numbers failed to reveal a significant difference between groups (Chi-square (3)=3.35, p=.34). However, when the 4 year-olds were compared directly to the 6.5 years, there was a trend for difference (Chi-square(2) =4.96, p=.08), hinting that there were developmental changes that we were underpowered to detect, consistent with the accuracy data from Experiment 1. The failure to find breakpoint differences between the WS group and the normally developing groups may also reflect a lack of power or sensitivity of the RT measure.

We next analyzed the slopes for each part of the bilinear model (before and after the breakpoint for each participant), using oneway ANOVAs across all 4 groups. The slopes in the subitizing range showed no difference across groups (F 3, 40= 1.22, p=.32), and the values for the slopes were similar to findings in previous studies of children (WS, 102 ms/item: 4 year-olds, 111 ms/item: 5 year-olds, 119 ms/item; see Svenson & Sjoberg, 1978), except for 6.5 year-olds who displayed more adult-like RTs (66 ms/item). The slopes for the “counting” range did reveal a difference between groups (F(3,40)=3.7p=.02). This difference reflected that the WS group had a flatter slope in the “counting range” than 4 year-olds (p<.05). There were no other differences between groups (all other p's > .2). Importantly, the slopes in the counting range were substantially higher than those in the subitizing range in all groups (WS, 484 ms/ item; 4 year-olds; 800 ms/ item: 5 year-olds 606 ms/item: 6.5 year-olds, 585 ms/item).

Summary Experiment 2

Even though accuracy was stressed in this study, individuals with WS started to make mistakes at lower numerosities than 5 and 6.5 year-olds, similar to the pattern evident in 4 year-olds. In contrast, for reaction time, the WS group was as fast as the 6.5 year-olds across all numbers, and faster than 4 and 5 year-olds. This was not due to a lack of developmental improvement in RT during this period, since RT improved with age from 4 to 6.5 years of age. The RT data indicate that individuals with WS are not just generally slow at visually processing the displays, a potential confound in Experiment 1. The WS group is older, and may have learned how to respond ‘quickly’. However, responding quickly apparently carried a penalty with it for this group, resulting in more errorful performance at numerosities beyond the range of rapid enumeration, i.e. the subitizing range.

Discussion and Conclusions

On the basis of our behavioral results from the MOT task, we hypothesized that individuals with WS would be able to rapidly enumerate a few objects, but would have a smaller capacity than older children, and be more similar to 4 year-olds. Our accuracy measures support this conclusion. In the Subitizing task of Experiment 1, using briefly presented displays, we found that the adolescents and adults with WS showed a strikingly impaired profile with performance on par with 4 year-olds. The WS group was no different in accuracy from any of the normally developing child groups for the smallest numerosities, but they performed worse than 5 year-olds for 4 or 5 objects, and worse than 6 year-olds for 3 through 8 objects. Accuracy measures from Experiment 2 exhibited a similar pattern, despite the fact that participants could look at the display until they responded, and were given as much time as they wanted to make their response. In that case, the WS group performed no differently from 4 or 5 year-olds, and performed worse than 6 year-olds, reliably so for 5 or more objects. In both experiments, the accuracy data for all groups showed a clear difference between smaller set sizes and larger ones, suggesting that we were tapping into different mechanisms, consistent with suggestions from a range of theorists (Feigenson & Carey, 2005; Hyde & Spelke, 2009; Piazza & Izard, 2009; Revkin, et al., 2008; Xu & Chun, 2009).

Any differences in accuracy across groups could not be attributed to differences in explicit counting, or to the ability to map number names onto the displays, because all groups were close to ceiling when asked to explicitly count displays of the same range of numerosities. Although there are similarities in the explicit counting task and the subitizing task (both require that people report “how many”, drawing on knowledge of the number names and their mapping to numerosities), the patterns of performance were quite different. Accuracy for people with WS and normally developing 4 to 6.5 year-olds was almost perfect for all set sizes (1-8), indicating that they knew how to count objects and accurately name the cardinal number of the set they observed. There was some increase in errors as set size increased, but these error rates were quite low, and there were no differences across groups. Moreover, the pattern of errors also differed between the explicit Counting task and the Subitizing task in Experiment 1. In the Counting task, errors were largely one or two fewer or larger than the actual set size. This pattern did not vary over set size, suggesting that the errors were probably produced by errors in the explicit counting process, for example re-counting already counted objects, or missing an object to be counted. The Subitizing task, by contrast, showed a different error profile. Above the number at which participants reached 100% accuracy, the coefficient of variation-- the ratio between the mean and standard deviation for a target number-- was essentially flat, suggesting that in the larger set range, people may have switched to using the approximate number system (Dehaene, 1997; Halberda et al., 2008).

The reaction time measures from Experiment 2 further fill out the picture for the Subitizing task. First, the results showed that, although the WS group's accuracy was comparable to 4 year-olds, their reaction times were faster than the 4 year-olds, similar to 6.5 year-olds. The relatively speedy reaction times in the WS group apparently carried a penalty, however, with poorer accuracy than the equally speedy 6.5 year-olds, for numerosities starting around 4 objects. Importantly, a striking finding was that all groups – including 4 year-olds and individuals with WS – showed a relatively flat RT function for numerosities 1-3 (along with very accurate performance), with higher slopes for numerosities and more errors starting at 4 items. Together, these RT data suggest that the rapid enumeration task engaged two separate mechanisms, one for small numbers (up to 3 or 4) and a separate one(s) for larger numbers.

In the small number range, individuals with WS were able to extract the appropriate visual information and respond very rapidly, and almost completely accurately, despite their visuospatial impairments. The finding for WS is consistent with another study reporting 100% accuracy for set sizes of 1, 2, and 3 presented at 250 ms (Ansari, Donlan, & Karmiloff-Smith, 2007). Normally developing 5 year-olds achieved 100% accuracy for set sizes of 3 or 4, and 6.5 year-olds all achieved 100% accuracy for set sizes of 4 or more-- the number usually cited as the upper limit for adults (see Cowan, 2001 for a review). While typically developing children did become faster responders with age, and capacity appeared to increase slightly, the shape of this function did not change substantially with age or group status. That the bilinear function was evident in all groups suggests that this dissociation between small and large numbers is relatively robust across development. The limit of approximately 3 items is consistent with the numerical capacity reported in infancy and 2 year-olds (Feigenson, et al., 2004; Starkey & Cooper, 1995) and thus it may be relatively impervious to developmental changes or atypical development, even disorders with severe visuospatial deficits such as WS.

What do these results tell us about the architecture of visuospatial representation of multiple objects and how it develops both typically and in WS? First, the results strongly suggest a clear distinction in all groups between apprehension of small numerosities (roughly up to 3 or 4) and apprehension of numerosities past this range. These data are consistent with theories suggesting that separate, possibly non-numerical processes apply when we report “how many” for small displays (Kaufman et al., 1949; Mandler & Shebo, 1982; Xu & Chun, 2009). Second, we found clear evidence of a relatively low limit for this range among people with WS, compared to normally developing children who are much younger. For people with WS, limits in accuracy on the subitizing task are roughly equivalent to that of normally developing 4 year-olds. The same pattern has been found using a multiple object tracking task (O'Hearn et al., 2005; O'Hearn et al., 2010). Although the subitizing task and the MOT task appear quite distinct (following multiple targets as they move around a screen vs. guessing how many objects are in a single, static display), the results suggest some common source of difficulty for people with WS. Moreover, they suggest that these individuals have reached a point-- as adolescents and young adults, on average 18 to 20 years old-- that appears quite similar to young children.

These facts accord well with the idea that both tasks involve indexing, or individuating multiple objects, and that there are strict limits on this capacity in people with WS-- a limit that is not resolved over development. We should note that our absolute estimate of the WS capacity in the MOT task (using the K statistic) was about 2, whereas our estimate of the subitizing range in the present study is about 3. We are not surprised that the absolute estimates are somewhat different; this would be expected based on differences in task requirements alone, as well as differences in how the estimates are produced. There were also some differences between the 4 year-olds and the WS group: there was more variability in the WS group (nonparametric analysis, Experiment 1) and they were faster (Experiment 2), as we would expect for this older, more heterogeneous group. What is more important, we think, is the similar profile between WS adults and normally developing 4 year-olds in their accuracy in both studies, suggesting strict limits on the number of objects in small sets that can be simultaneously represented.

Our proposal that our subitizing and MOT results are linked is strengthened by Piazza and Izard's (2009) interpretation of subitizing. They suggest that the phenomenon of subitizing may not reflect a special system dedicated to small numerosities per se, but rather, a basic architectural aspect of the visual-spatial system that represents small sets of individual objects, but not the number of their set. Piazza and Izard hypothesize that the posterior parietal areas of the brain may set up a map with “peaks” of activation for up to about 4 salient locations in the visual field (Gottlieb, 2007). In normal adults, these peaks can be read out for a variety of different purposes, which might include subitizing, multiple object tracking, or visual-spatial short-term memory tasks. Both multiple object tracking and visual-spatial short-term memory have been shown to engage posterior parietal areas (Culham, Cavanagh, & Kanwisher, 2001; Todd & Marois, 2004; Xu & Chun, 2006), suggesting that an impairment in these regions could lead to reduced limits on the number of peak activations possible. Consistent with this possibility, people with WS have been shown to have structural and functional abnormalities in the parietal areas, especially the intraparietal sulcus (Kippenhan et al., 2005; Meyer-Lindenberg et al., 2004; Van Essen et al., 2006). Parietal lobe abnormalities have also been identified in other genetic disorders, such as Turner syndrome (Brown et al., 2004) and 22q11.2 deletion (Bearden et al., 2007) that also exhibit visuospatial deficits, as well as some reports of a small “subitizing range” (Bruandet, Molko, Cohen, & Dehaene, 2004; Simon, Bearden, Mc-Ginn, & Zackai, 2005). Given the proposal by Piazza and Izard (2009), at least some of the visual-spatial disorders in these groups might be attributed to limits in representing small sets of multiple objects.

We should note that not all investigators agree that subitizing reflects a non-numerical mechanism. Some have proposed that a single system of magnitude representation underlies judgments of numerosity for both small and large sets (Cordes, Gelman, Gallistel, & Whalen, 2001; Gallistel & Gelman, 1992). In this view, our results would be explained as the result of an approximate number system that has very low variability for small sets of objects; the low variability would result in very high accuracy for small sets (but see Revkin et al., 2008 for evidence against this prediction in normal adults). Although we cannot conclusively rule out this explanation, the growing evidence for the “special” treatment of small object sets (reviewed in the introduction) leads us to favor the idea that people with WS have impairments to this system, and that this is what leads to their low limit in the subitizing task. Moreover, the link to our MOT findings, as well as other findings on visual short-term memory in this population (Hoffman, Reiss, & Landau, in preparation), suggest similar set-size limits across tasks that are unlikely to involve numerical representation (See also evidence from Green & Bavelier, 2005 of a link between enumeration and MOT that may reflect common VSTM involvement).

Finally, this smaller capacity may actually be related to other processes that operate on small numbers of objects. Recent studies have indicated that subitizing may not actually be preattentive, as Pylyshyn proposed; attentional load affects performance in the subitizing range (Xu & Lui, 2008; Railo et al., 2008; Vetter et al., 2008; Burr et al., 2010). Ongoing work is attempting to identify the exact mechanism underlying the limited capacity of MOT and subitizing in adults, and this work challenges the indexing theory (e.g., spacing; Franconeri et al., 2010: interference, Shim et al., 2008). These crucial studies should provide additional insights into the mechanism(s) responsible for the limitations evident in WS.

Although our report focuses on subitizing as a reflection of limited capacity in representing small sets of objects, the deficits we report raise obvious questions about possibly related deficits in number processing. The brain areas that are damaged in people with WS are not exclusively linked to the individuation of multiple objects. Indeed, they are also engaged in tasks that clearly require representation of number, for example, comparison of two numbers, calculation, and number approximation (see Hubbard et al., 2005 for a review). Although research so far is quite limited, there is some evidence that magnitude representation may be impaired in WS, both in tasks using reasoning along a symbolic number line (Krajcsi, Lukacs, Igacs, Racsmany, & Pleh, 2008; O'Hearn et al., 2007; Paterson, Girelli, Butterworth, & Karmiloff-Smith, 2006) and magnitude estimation (Ansari et al., 2007; Van Herwegen, Ansari, Xu, & Karmiloff-Smith, 2008; Halberda et al., in progress). Deficits in the approximate number system would be expected to have severe impact on a variety of later math learning (Halberda et al., 2008), and discovering the relationship between operations on small sets and large sets will be important in understanding the variety of impairments linked to parietal lobe damage.