Maximum-likelihood methods in cryo-EM. Part II: application to experimental data

Abstract

With the advent of computationally feasible approaches to maximum likelihood image processing for cryo-electron microscopy, these methods have proven particularly useful in the classification of structurally heterogeneous single-particle data. A growing number of experimental studies have applied these algorithms to study macromolecular complexes with a wide range of structural variability, including non-stoichiometric complex formation, large conformational changes and combinations of both. This chapter aims to share the practical experience that has been gained from the application of these novel approaches. Current insights on how to prepare the data and how to perform two- or three-dimensional classifications are discussed together with aspects related to high-performance computing. Thereby, this chapter will hopefully be of practical use for those microscopists wanting to apply maximum likelihood methods in their own investigations.

Introduction

An increasing number of maximum likelihood (ML) methods for image processing have recently become available to the electron microscopist. These methods hold great potential for the data analysis in a variety of different cryo-electron microscopy (cryo-EM) modalities. However, a literature search for applications of ML approaches in experimental studies shows that these almost exclusively concern classification tasks in (asymmetric) single-particle analysis.

If one excludes the methodological papers themselves, no reports on the application of ML approaches to two-dimensional (2D) alignment (Sigworth, 1998) or icosahedral virus reconstruction (Doerschuk & Johnson, 2000; Yin et al., 2001, 2003) are available. ML processing of 2D crystals (Zeng et al., 2007) has so far only been applied to cyclic nucleotide-modulated potassium channel, MloK1 (Chiu et al., 2007), and ML classification of sub-tomograms by the kerdenSOM algorithm (Pascual-Montano et al., 2002) has only been reported for cadherins (Al-Amoudi et al., 2007). In contrast, multiple reports are available that describe applications of ML classification approaches to single-particle analysis. Both the kerdenSOM (Pascual-Montano et al., 2001) and the ML2D algorithm (Scheres et al., 2005) have been applied to multiple two-dimensional studies (Table 1), and various reports describing three-dimensional analysis of macro-molecular complexes with different types of structural heterogeneity by ML3D classification (Scheres et al., 2007a) are available (Table 2).

Table 1.

ML applications in single particle 2D analysis

Reference	Sample	ML approach
(Gomez-Lorenzo et al., 2003)a	SV40 large T antigen	kerdenSOM
(Dang et al., 2005)b	cytolysin	kerdenSOM
(Gomez-Llorente et al., 2005)c	MCM	kerdenSOM
(Gubellini et al., 2006)d	photosynthetic core complex	ML2D+kerdenSOM
(Nunez-Ramirez et al., 2006)e	G40P	kerdenSOM
(Stirling et al., 2006)f	CCT:PhLP3:tubulin	ML2D
(Valle et al., 2006)g	SV40 large T antigen	kerdenSOM
(Martin-Benito et al., 2007a)h	CCT:Fab	ML2D
(Martin-Benito et al., 2007b)i	thermosome:prefoldin	ML2D
(Arechaga et al., 2008)j	TrwK	ML2D
(Cuellar et al., 2008)	CCT:Hsc70NBD	ML2D
(Radjainia et al., 2008)k	Adiponectin	ML2D
(Rehmann et al., 2008)l	EPAC2:cAMP:RAP1B	ML2D
(Tato et al., 2007)m	TrwA:trwB	ML2D+kerdenSOM
(Boer et al., 2009)n	repB	ML2D
(Greig et al., 2009)o	Colicin Ia	ML2D
(Klinge et al., 2009)p	DNA polymerase α	ML2D
(Landsberg et al., 2009)q	AAA ATPase Vps4	ML2D
(Recuero-Checa et al., 2009)r	DNA ligase IV-Xrcc4	ML2D
(Reiriz et al., 2009)s	α, γ-peptide nanotubes	ML2D
(Albert et al., 2010)t	groEL:AGXT	ML2D+kerdenSOM

^aEMBO J. 22, 6205–6213.

^bJ. Struct. Biol. 150, 100–108.

^cJ. Biol. Chem. 280, 40909–40915.

^dBiochemistry 45, 10512–10520.

^eJ. Mol. Biol. 357, 1063–1076.

^fJ. Biol. Chem. 281, 7012–7021.

^gJ. Mol. Biol. 357, 1295–1305.

^hStructure 15, 101–110.

ⁱEMBO Rep. 8, 252–257.

^jJ. Bacteriol. 190, 4572–5479.

^kJ. Mol. Biol. 381, 419–430.

^lNature 455, 124–127.

^mJ. Biol. Chem. 281, 7012–7021.

ⁿEMBO J. 28, 1666–1678.

^oJ. Biol. Chem. 284, 16126–16134.

^pEMBO J. 28, 1978–1987.

^qStructure 17, 427–437.

^rDNA Repair 8, 1380–1389.

^sJ. Am. Chem. Soc. 131, 11335–11337.

^tJ. Biol. Chem. 285, 6371–6376.

Table 2.

ML applications in single particle 3D analysis

Reference	Sample	Heterogeneity type
(Recuero-Checa et al., 2009)a	DNA ligase IV-Xrcc4	data cleaning
(Wang et al., 2009)b	RISC loading complex	substoichiometric complex
(Nickell et al., 2009)c	26S proteasome	substoichiometric complex
(Klinge et al., 2009)d	DNA polymerase α	flexible arm
(Greig et al., 2009)e	Colicin Ia	unclear
(Julian et al., 2008)	Hybrid state 70S Ribosome	ratcheting and ligand occupation
(Rehmann et al., 2008)f	EPAC2:cAMP:RAP1B	data cleaning
(Cuellar et al., 2008)	CCT:Hsc70NBD	substoichiometric complex
(Cheng et al., 2010)	Stalled 70S Ribosome	ligand occupation

^aDNA Repair 8, 1380–1389.

^bNat. Struct. Mol. Biol. 16, 1148–1153.

^cProc. Natl. Acad. Sci. U.S.A. 106, 11943–11947.

^dEMBO J. 28, 1978–1987.

^eJ. Biol. Chem. 284, 16126–16134.

^fNature 455, 124–127.

Perhaps an important reason for the relatively wide spread use of the ML algorithms for single-particle classification lies in their implementation in the Xmipp package (Sorzano et al., 2004b). This open-source software package has a graphical interface that guides the user through the image processing workflow and eases the task of parallel execution on a variety of hardware architectures (Scheres et al., 2008). This facilitates the testing of new computer programs by the inexperienced experimentalist and enhances the visibility of novel algorithms.

Still, it is often hard to deduce how to use new methods from the technical papers that describe them. Moreover, it is typically not until a new method has been applied to a variety of experimental data sets that a more profound understanding of its optimal processing strategies is obtained. This chapter aims to facilitate the use of ML methods by sharing the experience obtained thus far with single-particle classification. It first describes how one typically prepares the data for ML refinement, and then discusses how to perform 2D and 3D classification. In addition, as ML approaches may require large amounts of computing time, relevant aspects of high-performace computing are highlighted.

This chapter focuses on a range of issues that have arisen in different experimental studies. Some of these issues are not restricted to ML classification alone, but also play a role in other refinement approaches. Many of these issues were never published, either because they concerned negative results or because they were not deemed relevant for the biologically oriented publications. Taken together, I hope that this contribution will be of practical help to others who want to apply ML image processing approaches in their investigations.

Data preprocessing

In general terms, data preprocessing aims to provide a set of images that is as closely as possible in accordance with the statistical model that underlies the ML approach. All currently available ML approaches in single-particle analysis assume that each experimental image is a noisy projection of one or more 3D objects in unknown orientations. In most approaches the noise is assumed to be independent, additive and Gaussian. Only in two of the currently available ML approaches (Scheres et al., 2007b; Doerschuk & Johnson, 2000) the effects of the contrast transfer function (CTF) are included in the data model. In these approaches the data model is expressed in Fourier space. All other approaches use a real-space data model.

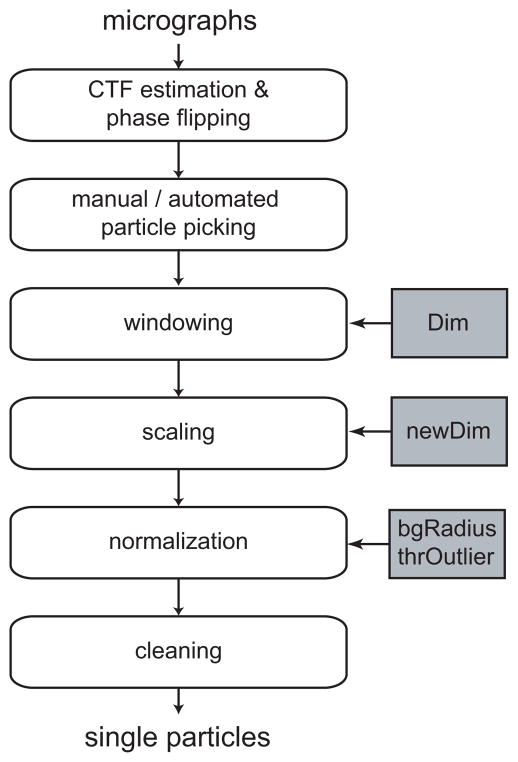
This section gives a step-wise description of the operations that are typically performed to convert a collection of experimental micrographs into a data set of single particle images that is suitable for ML refinement. A schematic overview of these steps is given in Figure 1.

Figure 1.

Schematic view of a typical image preprocessing workflow. Important parameters that are discussed in the main text are highlighted in grey. These are the dimension of the boxed particles (Dim), the dimension of the downscaled particles (newDim), the radius of the circle that determines the particle noise area (bgRadius) and the threshold in standard deviations of the image that is used to discard outlier pixel values (thrOutlier).

Micrograph preprocessing

The first preprocessing step is to estimate the CTF effects by fitting a theoretical model to the power spectra of the experimental micrographs. This is a common step in many cryo-EM image processing strategies and a variety of programs are available for this task (Frank, 2006). The reciprocal-space variant of single-particle ML refinement (MLF, Scheres et al., 2007b) is capable of handling theoretical CTF models provided they are rotationally symmetric. Therefore, micrographs with strong drift or astigmatism should be discarded at this stage, and non-astigmatic CTF models should be calculated for the remaining micrographs. Currently available real-space ML approaches do not model CTF effects. Still, it is also useful for these approaches to discard micrographs with strong astigmatism or drift as they lead to inconsistencies in the data. In addition, to partially make up for the absence of a CTF model, real-space ML approaches often benefit from a phase-flipping correction in the micrographs.

Particle selection

One then needs to identify individual particles of interest in the micrographs. One can perform this task manually or use (semi-)automated procedures. This choice will often depend on the amount and quality of the data, and on the size and shape of the particles under study. Automated procedures are typically a much faster and less tedious option, but one should be aware that human experts still outperform automated approaches in most cases (Zhu et al., 2004). Data sets obtained from (semi-) automated particle selection procedures often contain more false positives than those selected manually. False positives may comprise a wide range of artifacts, such as irreproducibly damaged or aggregated particles, contaminations or spurious background features. The number of false positives should be minimized because they violate the most basic assumption of the data model: that every image contains a reproducible signal.

Particle extraction

Once the particles of interest have been selected, they are to be extracted (boxed) from the micrographs as individual images. The only parameter to be adjusted at this step is the size of the squared images. Several considerations play a role in deciding on the image size. One one hand, the extracted images should obviously be large enough to accomodate the particles in all directions and should include sufficient space to account for residual origin offsets. On the other hand, smaller images will reduce the computational load and have the advantage that fewer neighbouring particles are present in the images. Neighbouring particles are artifacts that are not accounted for in the data model and should thereby be avoided. In conventional refinement approaches one often deals with neighbouring particles by masking the experimental images. However, masks also fall outside the scope of the data model of currently available ML approaches. Masking the experimental images would lead to a systematic under-estimation of the standard deviation in the experimental noise, since this estimation is performed using all pixels of the image. By extracting the particles in smaller images one reduces the amount of neighbouring particles without violating the data model, which is the main reason why one often performs ML refinements with relatively tightly boxed particles.

Scaling

Often cryo-EM micrographs are sampled at higher frequencies than needed. According to information theory, the highest resolution that can be obtained from the images is two times the pixel size, while limits of at least three times are more common in practice. That means that a pixel size of say 2 Å allows estimating the underlying signal up to a resolution of approximately 6 Å. However, while 2 Å pixels are relatively common in cryo-EM, very few reconstructions up to 6 Å resolution have been reported. In many cases other factors like CTF envelope functions or structural heterogeneity put stronger limitations on the resolution than the sampling frequency. In those cases, the images may be resampled onto larger pixels, i.e. one may use smaller images, without compromising the attainable resolution.

Other problems may be separated into subtasks that may be solved at distinct resolutions. A typical example is 3D refinement of structurally heterogeneous projection data. Often the structural variability can be described at low-intermediate resolutions so that ML3D classification (see below) may be performed with downscaled images. Then, after the structural heterogeneity has been dealt with, the resulting classes may be refined separately to higher resolutions using the original images.

Downscaling has the obvious advantage that subsequent image processing will be computationally cheaper, which is especially relevant for ML approaches that require large amounts of computing time and memory. However, using small images has yet another, perhaps less obvious, advantage. Since signal to noise ratios in cryo-EM data tend to fall off with resolution, downscaling typically results in an increase of the overall signal to noise ratio. Consequently, refinements with smaller images tend to be more robust to overfitting and model bias. Similar effects could be achieved by low-pass filtering of the data. But low-pass filtering introduces correlations among the pixels, which conflicts with the data model and is therefore not recommended in combination with ML approaches.

Normalization

All images in the data set are assumed to have equal powers in the noise and in the signal. Since this may not be necessarily true for a cryo-EM data set, one typically normalizes the images. Image normalization aims to bring the entire data set to a common greyscale by applying additive and multiplicative factors to each of the individual images. Perhaps the most straightforward approach to image normalization would be to subtract the image means and to divide by the standard deviations, resulting in zero mean and unity standard deviation for all images in the data set. Although this is a resonable approximation for more or less spherically shaped particles, it will yield suboptimal results for strongly elongated particles (Sorzano et al., 2004a). For the latter, projections along the long axis of the particle will be significantly more intense than projections perpendicular to that axis, which will give rise to systematic differences in the image means and standard deviations. Therefore, it is better to calculate the mean and standard deviation values for a defined area of the images that only contains noise. One often uses the area outside a circle with a diameter that is typically several pixels smaller than the image size (see Figure 2). Additional advantages of this procedure are that the signal will be positive, the expected value for the solvent will be zero and the standard deviation in the noise will be one. Based on the latter, one may start the likelihood optimization with an initial estimate for the standard deviation in the noise of unity.

Figure 2.

An illustration of image normalization. All pixels outside the white circle in the upper right image are assumed to contain only noise. These pixels are used to fit a least-squares background plane and to calculate the standard deviation of the noise. The upper row shows original images as they were extracted from the micrographs. The two images on the left show ramping backgrounds, the two images on the right show pixels with extremely low (i.e. black) intensity values. The lower row shows the same four images after normalization.

Several modifications of the normalization procedure may yield better results in specific cases (see Figure 2). Often, locally ramp-shaped gradients in background intensity are visible in the micrographs. In those cases, rather than subtracting a constant value one may fit a least squares plane through the pixels in the noise area of each image and subtract the resulting plane. Alternatively, one could apply high-pass filters to deal with these low-resolution effects. However, high-pass filters fail to describe the physics of the underlying problem and introduce correlations among the pixels in the filtered image, thereby again violating the assumption of independency in real-space ML approaches.

Other micrographs contain exceptionally white or black pixel values, which may result from broken pixels in the digital camera, from X-rays that hit the film or camera, or from dust particles or other artifacts in the process of scanning photographic film. These extremely high or low pixel values correspond to outliers in the assumedly Gaussian distributions of the experimental noise and should be removed from the data. One possibility to do so is to replace pixels with values larger than a given number (e.g. four or five) times the standard deviation in the image by a random instance from a Gaussian with zero mean and unity standard deviation. Typically, one does not perform this correction if there are no visual indications of these artifacts in the data, since statistically a small fraction of the pixels is always expected to have such large or small values.

Data cleaning

Finally, it is often useful to check (once more) for remaining outliers in the data. In particular automated particle selection procedures tend to yield data sets with large amounts of artifacts, but also manually selected data may still contain features that are not described by the statistical data model. One could again propose completely automated procedures for the detection of atypical features, but one should keep in mind that human experts are typically much better at this task than computer algorithms. Therefore, visual inspection of the selected particles is often the best way to remove remaining artifacts from the data.

Still, computer algorithms may alleviate the tedious task of looking at all particles. One example is an ad hoc sorting procedure that was implemented in the xmipp_sort_by_statistics program and that has resulted useful on multiple occasions. This simple algorithm sorts all particles on a continuous scale from typical to atypical particles. To this purpose the program calculates a large number of features for every individual particle. These features include mean, standard deviation, minimum and maximum values, but also features like the number of pixels with values above or below one standard deviation and features related to differences between image quadrants. The current implementation contains a total of 14 features and this list could in principle be expanded or reduced to better reflect specific cases. For every feature f, the program calculates a mean (μ_f) and a standard deviation (σ_f) value over all particles in the data set. (Alternatively, in some cases improved results may be obtained by calculating μ_f and σ_f over a subset of the particles that one is confident about.) For each ith image, one then calculates the average Z-score over all F features:

$${\overline{Z}}_i=\frac{1}{F}\sum _{f=1}^F\frac{\mid f_i-{\mu }_f\mid }{{\sigma }_f},$$ (1)

where f_i is the feature value for the ith image. Subsequently, one sorts the images on Z̄_i and visualizes them in typical matrix views where images with low average Z-scores are at the top and images with high values are at the bottom. It is still up to the human expert to decide which particles to discard, but often this process is much easier as nice particles tend to be at the top and many more artifacts are present near the bottom of the sorted particle list (see Figure 3).

Figure 3.

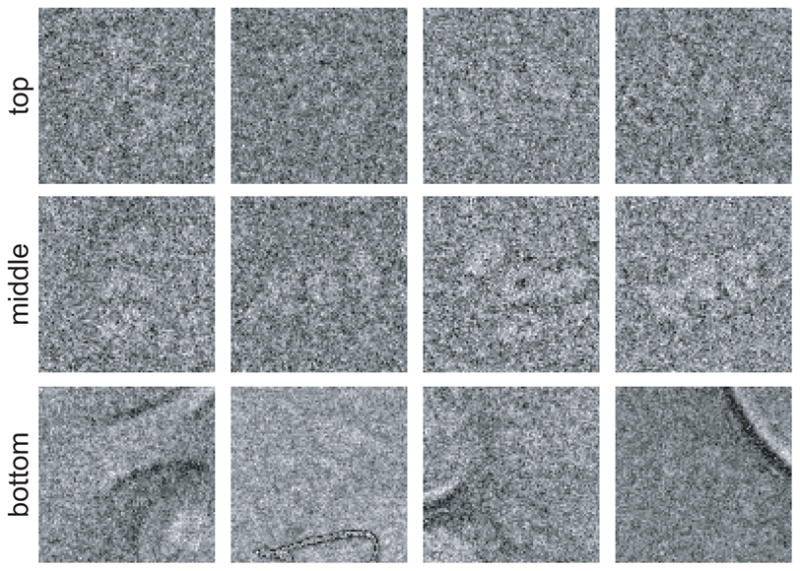
The results of automated image sorting based on average Z-scores. The top row shows images with relatively low Z-scores, the middle row images with average Z-scores and the bottom row shows images with relatively high Z-scores. The number of bad particles typically increases with higher Z-scores, which may facilitate the interactive removal of outliers by the user.

2D classification

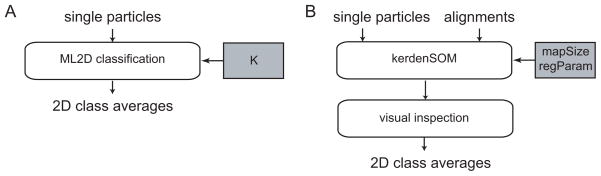
2D analysis of cryo-EM data may be a useful tool to answer a wide range of biological questions. Most often however, it is used as a means of data quality assessment or as a preprocessing step prior to 3D reconstruction. In general, 2D averaging procedures are much faster and more robust than their 3D counterparts. The lower complexity of the problem often allows retrieving 2D signals (class averages) from the noisy data in a reference-free manner, i.e. without a prior estimate of the signal. This greatly reduces the pitfalls of model bias as encountered in 3D procedures. Still, images cannot be aligned well without separating distinct classes and it is hard to separate classes when the images are not aligned well. Conventionally, this chicken and egg problem has been addressed by iterative schemes of alignment, classification and re-alignment of the resulting classes, see (Frank, 2006) for a comprehensive overview. Two ML approaches have recently emerged as powerful add-ons to existing approaches: a multi-reference alignment scheme called ML2D (Scheres et al., 2005) and a neural network called kerdenSOM (Pascual-Montano et al., 2001). A schematic overview of how these approaches are used is shown in Figure 4 and both approaches are described in more detail below.

Figure 4.

Schematic view of the use of the ML2D (A) and kerdenSOM (B) algorithms. Important parameters that are discussed in the main text are highlighted in grey. These are the number of classes to be used in ML2D classification (K) and the size of the map (mapSize) and its regularization parameters (regParam) for the kerdenSOM algorithm.

ML2D

The ML2D algorithm may be used to simultaneously align and classify single-particle images (Scheres et al., 2005). Reference-free class averages are obtained in a completely unsupervised manner by starting multi-reference alignments from average images of random subsets of the unaligned data. The only parameter that is is adjusted by the user is the number of references (K). This number should ideally reflect the number of different 2D structures that are present in the data, but that number is typically not known. In practice, one afronts this problem by running the algorithm multiple times with different values for K. Higher values for K are accepted if interpretation of the resulting class averages leads to new information. However, a maximum number of classes does exist. The more classes, the fewer particles participate in each class (or more strictly, the lower the weighted sums of particle contributions to each class). Averaging over a low number of particles leads to noisy averages, which result in suboptimal alignments and classifications. Therefore, in practice one often limits K so that on average there are at least 200–300 cryo-EM particles per class, while these numbers are typically much lower for negative stain data.

An intrinsic characteristic of the ML approach is that it does not assign images to one particular class or orientation. Instead, images are compared to all references in all possible orientations and probability weights are calculated for each possibility. Class averages are then calculated as weighted averages over all possible assignments and used for the next iteration. Still, in practice the probability distributions often converge to approximate delta-functions. In this situation, each image effectively contributes to only a single class and orientation, and division of the data into separate classes or the assignment of optimal orientations is justified. The sharpness of the probability distributions may be monitored by their maximum value. Since the distributions integrate to unity, maximum values close to one indicate near-delta functions and values close to zero indicate broad distributions. This value may also serve to identify outliers as those particles that still have relatively broad distributions upon convergence.

Two theoretical drawbacks of the real-space ML2D approach are that it does not take the CTF into account and that it assumes white noise in the pixels. Although this does not withhold ML2D from obtaining useful results in many cases, more precise descriptions of the CTF-affected signal and non-white noise are employed by the MLF2D algorithm (Scheres et al., 2007b). An additional advantage of this algorithm is its intrinsic multi-resolution approach where higher frequencies are only included in the optimization process if the class averages extend to such resolutions. For some cases the MLF approach has been observed to yield much improved results compared to its real-space counterpart. Often, these cases concern data with a large spread in defocus values or with relatively low-resolution signals. For other cases however, the MLF algorithm has been observed to converge to suboptimal solutions with a few highly populated and many empty classes. Sometimes, these problems are alleviated by running the MLF algorithm without CTF correction. In general, it is difficult to predict whether the real-space or the reciprocal space approach will be better for a given data set and one typically performs tests with both algorithms. The approach that works best in 2D is often also the optimal choice in 3D. Thereby, the relatively cheap tests in 2D may save computing time in subsequent 3D refinements.

An additional advantage of the unsupervised character of ML(F)2D is that it is easily incorporated into high-throughput data processing pipelines. One example is the implementation of the ML2D approach inside the Appion pipeline (Lander et al., 2009). This interface aims to streamline cryo-EM data processing by facilitating the use of flexible image processing workflows that use multiple programs from various software packages, for more information see the chapter by Carragher in this issue. Typical applications of ML2D inside this pipeline include the generation of templates for automated particle picking, data cleaning (by discarding images that give rise to bad class averages or with relatively flat probability distributions), and the generation of class averages for subsequent random conical tilt or common lines reconstructions (Voss et al., 2010).

kerdenSOM

The kerdenSOM algorithm, which stands for kernel density self-organizing map, is a neural network based on ML principles (Pascual-Montano et al., 2001). The kerdenSOM algorithm may be used to classify images that have been pre-aligned. However, rather than classifying the particles in a predefined number of classes, the algorithm outputs a two-dimensional map of average images called code vectors. A regularized likelihood target function results in an output map that is organized. This means that the differences between neighbouring code vectors are relatively small and that structural differences vary smoothly across the map. Then it is up to the user to decide how many structural classes are present in the map.

Although the user does not have to choose a fixed number of classes, he does have to decide on the size of the output map and on the parameters that determine its regularization. Larger output maps can accomodate more different structures, but too large maps may have very few particles contributing to each code vector. Too strong regularization results in very smooth output maps that cannot describe the structural variability in the data, while too weak regularization leads to unorganized maps where it is difficult to identify continuous structural variations among the data. Therefore, the kerdenSOM algorithm is often run multiple times with different sizes of the output map and different regularization parameters. This is facilitated by the reduced computational costs compared to ML2D classification, but interpretation of the corresponding results does make the kerdenSOM algorithm relatively user-intensive.

An important advantage of using prealigned particles is that the classification may be focused on a particular region of interest in the images. In this scenario only pixels inside a binary mask are included in the likelihood optimization. This speeds up the calculations and prevents structural variations in other regions of the images to interfere with the classification. This strategy has proven particularly useful in combination with the ML2D algorithm (e.g. see ML2D+kerdenSOM entries in Table 1). Here one first uses ML2D to align the images and separate classes corresponding to relatively large structural differences. Then, one focuses the kerdenSOM on a particular area of a given class. For example, ML2D may be used to separate top and side views of a complex and the kerdenSOM may be focused on the non-stoichiometrical binding of a factor that is only visible in the side view. Apart from its implementation in the Xmipp package, this workflow is also accessible through the Appion pipeline.

3D classification

Because molecules are 3D objects, 3D reconstructions from cryo-EM single-particle projections typically provide much more information than 2D class averages. However, 3D reconstruction is a much more complex mathematical problem than 2D averaging. One consequence of this increased complexity is that 3D reconstructions often depend on the availablity of an initial estimate of the underlying signal. Suitable initial models may be derived from known structures of similar complexes or they may be determined de novo by angular reconstitution or random conical or orthogonal tilt experiments, see (Frank, 2006) and the chapter by Leschziner in this issue for more details. Still, even for structurally homogeneous data sets obtaining a reliable model is often far from straightforward, and bias towards incorrect models may introduce important artifacts in the results.

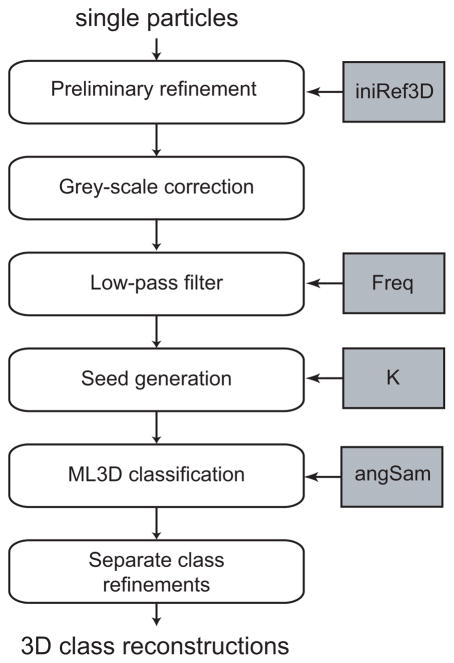
The situation is even more complex if multiple 3D structures are present in the data. The combination of distinct conformations in a single reconstruction leads at best to a general loss of resolution or to the loss of electron density in specific areas for partially flexible or non-stoichiometric complexes. Larger conformational changes may cause much more prominent artifacts, even up to the point where the refined structure no longer reflects any of the conformations in the sample. Nevertheless, structural heterogeneity also offers a unique opportunity to obtain information about multiple functional states, provided that projections from different structures can be classified. ML methods have recently emerged as powerful tools for this complicated task. 3D multi-reference refinement by ML (ML3D, Scheres et al., 2007a) has provided the first unsupervised classification tool that is applicable to a wide range of structurally heterogeneous data sets (e.g. see Table 2). An overview of the image processing workflow for ML3D classification is shown in Figure 5 and the separate steps are discussed in detail below.

Figure 5.

Schematic view of the ML3D classification workflow. Important parameters that are discussed in the main text are highlighted in grey. These are the initial 3D model (iniRef3D), the frequency of the low-pass filter (Freq), and the number of classes (K) and the angular sampling (angSam) to be used in the ML3D refinement.

Preparing the starting model

ML3D refinement depends on an initial 3D reference structure and the selection of a suitable model has been found to be a pivotal step for successful classification. The expectation maximization algorithm that underlies the ML3D approach is a local optimizer, i.e. it converges to the nearest local minimum. Despite the marginalization over the orientations and class assignments, model bias has still been observed to play an important role in ML3D classification. Therefore, it is recommended to start ML3D classifications from a consensus model that ideally reflects to some extent all the different structures in the heterogeneous data set. This is almost a contradiction in terms. Perhaps a hypothetical example illustrates the role of the consensus model: if the data were already separated into K structurally homogeneous subsets, separate refinements of the consensus model against each of the subsets should be able to converge to the K different structures that are present in the data.

In many cases a suitable starting model may be obtained by refinement of the complete data set against a single 3D reference, followed by a strong low-pass filter. The effective resolution of the low-pass filter plays a crucial role here, as high frequencies in the starting model are prone to induce local minima and too restrictive filters result in featureless blobs that cannot be refined. One typically filters the consensus model “as much as possible”. That is, one filters the consensus model to the lowest possible resolution for which refinement against the heterogeneous data still converges to a solution that is similar to the unfiltered model. For many cases useful low-pass filters have been observed to lie in the range of 0.05–0.07 pixel⁻¹ (using downscaled images as described above).

The direct use of low-pass filtered PDB models, negative stain reconstructions or geometrical phantoms as starting models in ML3D classification has been observed to yield suboptimal results. It is often better to first refine such a model against the complete, structurally heterogeneous data set. In principle, any program could be used for this task. Rather than aiming at high-resolution information (the resulting model will be low-pass filtered anyway), this refinement should aim at removing false low-resolution features from the model. For example, negative stain models may be flattened, the dimensions of geometrical phantoms may be off, atomic models may be incomplete or have an unrealistically high contrast, etc. Another common pitfall is a small difference in pixel size between the starting model and the actual data set, which may arise from suboptimal calibrations of the microscope magnification. The latter may also be checked by comparing projections of the starting model with reference-free class averages of the structurally heterogeneous data, as for example obtained using ML2D.

Although any refinement program could be used to generate the starting model, one should keep in mind that some software packages provide reconstructions for which the absolute intensity (or grey scale) is not consistent with the intensity of the experimental images. This may be because the reconstruction algorithm itself is not implemented in a consistent way, or because the reconstruction is normalized internally. Re-projections of such maps are on a different grey scale than the signal in the experimental images. This is typically harmless in conventional refinements where maximum cross-correlation searches are insensitive to additive or multiplicative factors. However, the squared difference terms inside the Gaussian distributions are highly sensitive to these factors and ML refinements of models with inconsistent grey scales may give rise to extreme artifacts. A typical observation in such cases is that all experimental images contribute to only a single projection direction and the corresponding reconstruction is severely artifactual.

All algorithms from the Xmipp package yield reconstructions with consistent grey scales. Consequently, in case of doubt one may correct the grey scale by performing a reconstruction inside the Xmipp package. To this purpose, one could transfer the orientations from the other software package to Xmipp, but this may involve cumbersome conversion issues. Often it is easier to subject the refined model from the other package to a single, additional iteration of conventional projection matching refinement inside the Xmipp package. As the resulting model will be low-pass filtered anyway, this step may be performed in a quick manner using a coarse angular sampling and a fast reconstruction algorithm.

Multi-reference refinement

ML3D classification is a multi-reference refinement scheme and thus requires multiple starting models. A key achievement of the ML3D approach is that distinct structures can be separated in an unsupervised manner, i.e. without prior knowledge about the structural variability in the data. In particular, multi-reference ML refinements were observed to converge to useful solutions when starting from initial models (seeds) that are random variations of a single consensus model. To generate randomly different seeds one typically divides the structurally heterogeneous data set into random subsets and performs a single iteration of ML3D refinement of the consensus model against each of the subsets separately. Perhaps, alternative ways like adding different instances of random noise to the consensus model would also work. However, the division of the data in random subsets is more closely related to traditional k-means and does not introduce any additional parameters (e.g. how much noise to add).

Apart from the starting model itself, the most important parameter in ML3D classification is K, the number of 3D models that are refined simultaneously. As in ML2D classification, K should ideally reflect the number of different structures in the data, but because that number is unknown K is typically varied over multiple runs. Again, the maximum number of references is ultimately determined by the amount of experimental data available. Often, (asymmetric) reconstructions from less than 5,000–10,000 cryo-EM particles become too noisy to allow reliable alignment and classification. In practice, K may also be limited by available computing resources. In general, 3D ML refinement is computationally demanding and the current implementation was optimized for speed by storing the reference projections of all models in memory. Thereby, memory requirements scale linearly with K so that high numbers may require more computer memory than physically available.

Hardware limitations also put stringent limitations on the angular sampling rate. Because memory requirements scale quadratically with the angular sampling rate, and computing times scale even cubically, high angular sampling rates quickly become computationally prohibitive. Therefore, ML3D classification is typically performed with relatively coarse angular sampling rates. In most applications reported thus far an angular sampling rate of approximately 10 degrees was used. This intrinsically limits the resolution that can be obtained by ML3D, but fortunately in many cases the structural variability can be resolved at medium-low resolutions. An additional effect of the coarse sampling is that otherwise similar reference structures may rotate several degrees with respect to each other during the optimization process. These rotated references may better accomodate particles with orientations that fall in between the coarse angular sampling used in the refinement (Scheres et al., 2007a). The latter should also be taken into account when choosing K, because the presence of different rotated versions of the same conformation reduces the number of different conformations that can be separated for a given number of K.

ML3D multi-reference refinement is typically performed for a user-defined number of iterations, often around 25. Convergence may be monitored by analysis of the log-likelihood value during the iterations and the number of particles that change their optimal orientations or class from one iteration to the next. Typically, one stops the calculations when the log-likelihood increase has leveled off and when the number of the particles that still change their optimal orientation or class has stabilized to a small fraction of the data set. As in the ML2D case, the width of the probability distributions may be monitored by their maximum values, and these distributions tend to converge to approximate delta functions. The latter again allows one to divide the data set into separate classes, which ideally should be structurally homogeneous. These classes may then be refined separately to higher resolution using conventional refinement algorithms and the original images without downscaling.

Interpretation of the classification results

As mentioned above, one of the main advantages of ML3D classification is its unsupervised character. This circumvents the main pitfall of biasing the classification towards a false assumption about the classes in supervised approaches. Still, the starting model may lead to bias in the alignment of the particles, which will in turn affect classification (e.g. see Figure 6). The problem of model bias is not unique to ML3D classification. It plays an important role in many 3D refinement programs for cryo-EM single particle data. A typical sign that the refinement process is affected by model bias is that the references do not gain new structural details. Often, the refined structures remain similar to the initial seeds at intermediate-low resolution and only seem to accumulate noise at higher frequencies. In other cases, the references may even disintegrate during the refinement process. A good indication that the refinement is not affected by model bias is that various, different starting models all converge to a similar solution. Still, especially for relatively small particles with no or low symmetry, the absence of a good starting model may be an important obstacle for successful 3D alignment and classification.

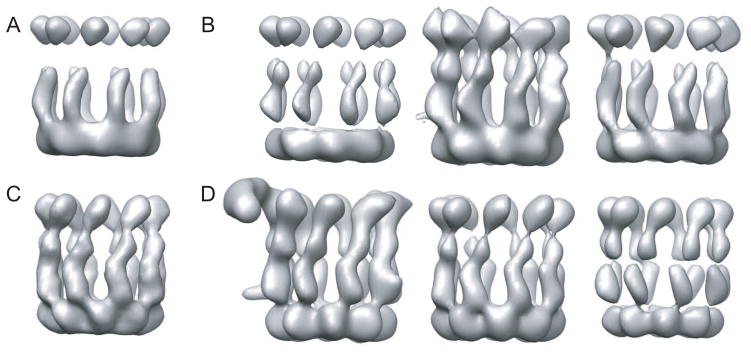
Figure 6.

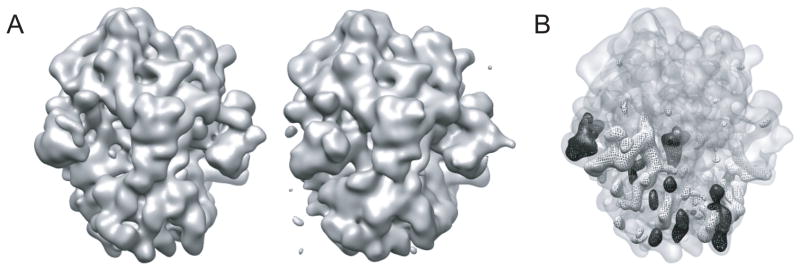
An example of model bias affecting ML3D classification. Using a suboptimal initial reference (A), ML3D classification yielded suboptimal results (B). Using an improved initial model (C), ML3D classification separated uncomplexed CCT from CCT:Hsc70NBD complexes. See (Cuellar et al., 2008) for more details.

Even if a good starting model is available, the results of 3D classifications of cryo-EM data should be interpreted with care. Many hypothetical divisions of the data may give rise to 3D reconstructions with plausible structural differences. However, due to the high noise levels in the data, these differences are not necessarily related to actual structural variability in the data. Although interpretation of the classes in the light of prior biochemical and structural knowledge may be an extremely powerful criterion to decide on the plausibility of a classification, it is often also a highly subjective endeavour with a considerable risk of overinterpretation. Fortunately, there are several, more objective tests that one can (and perhaps should) perform.

Firstly, the differences between the refined structures could have arisen from the random variations among the initial starting seeds. Although the initial variations are typically small, they may be amplified during the refinement of the noisy data. However, in that case a second classification starting from different random seeds will not likely result in the same classes. Therefore, it is often useful to check the reproducibility of the classification by comparing classes from multiple classification runs that were started from different random seeds. Significant class overlaps (e.g. of more than 75%) are usually an indication of reliable classification.

Secondly, structurally homogeneous data sets should behave better in refinement than structurally heterogeneous data sets. Therefore, to test whether classes obtained by ML3D are more homogeneous than the original structurally heterogeneous data set, one could compare conventional refinement statistics. However, this comparison is complicated by the fact that the classes obtained by ML3D classification are per definition smaller than the original data set. A solution to this problem is to randomly divide the original data set into subsets of identical size as those obtained by ML3D classification. The random division is not expected to resolve any of the structural heterogeneity. Therefore, refinements of the subsets obtained by ML3D classification should then yield better statistics, e.g. Fourier Shell Correlations, than refinements of the random subsets of identical size. Similarly, the refined ML3D classes should give rise to less intense 3D variance maps (Penczek et al., 2006) than the refined random subsets.

Indications for remaining structural heterogeneity in the classes are the same ones as those that were used to identify the heterogeneity in the first place. Low density values for factors that bind non-stoichiometrically, fuzzy density or relatively low resolution for flexible domains, or overall too low resolutions may indicate that the classes are still heterogeneous. In that case one could opt to repeat the original classification with a higher number of classes, but this may not be feasible because of limited computing resources. Alternatively, one may also divide one or more of the classes separately into multiple subclasses. In this way, the structural heterogeneity may be removed in a hierarchical manner, focusing on ever smaller details in subsequent steps (e.g. see Figure 7).

Figure 7.

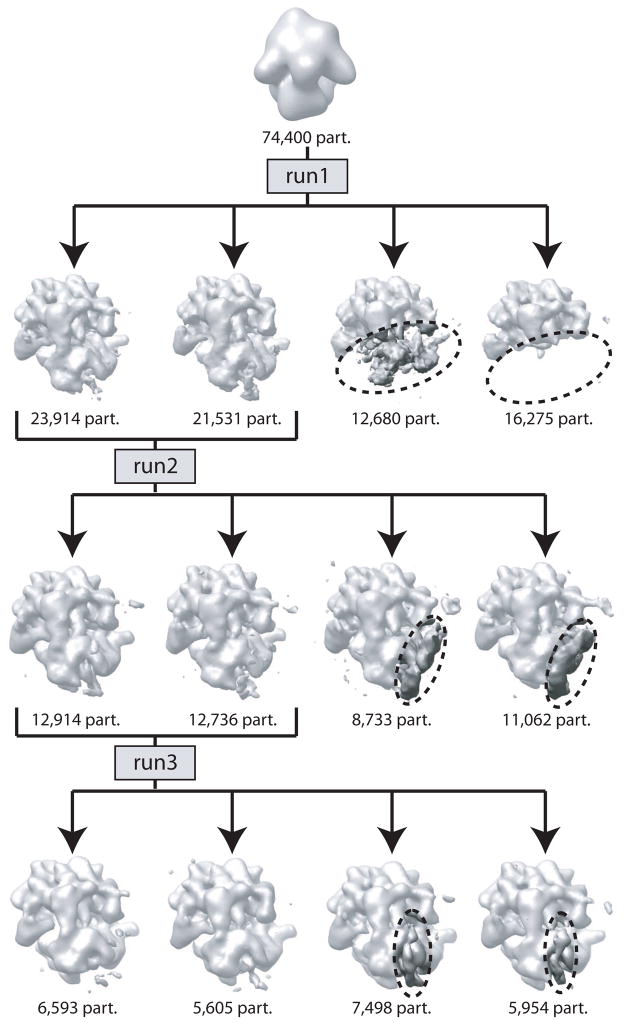
An example of hierarchical classification by ML3D. In three consecutive runs (run 1–3) ML3D classification is used to separate a dataset of 74,400 ribosome particles into multiple classes. Run1 separates intact ribosomes from disintegrated, 50S particles; run2 separates particles with strong density for tmRNA and run3 classifies the remaining intact ribosomes into particles without apparent tmRNA density and particles with weak tmRNA density in an alternative conformation. See (Cheng et al., 2010) for more details.

A final comment on the analysis of structural differences between classes concerns the use of normalized difference maps. Rather than comparing two maps that are rendered at a given threshold side by side in a 3D visualization program, it is often much more informative to visualize the positive and negative differences between both. If ones assumes that the differences between two independent reconstructions of identical structures is zero-mean and Gaussian distributed, one may interpret the difference map in a statistical manner. In such an interpretation, areas of positive or negative difference density above a certain threshold (e.g. three times the standard deviation) may be considered as significant. In the difference maps, presence or absence of factors typically show up as isolated peaks, domain movements are characterized by positive density on one side of the domain and negative density on the other, and the solvent region should not contain strong difference density (e.g. see Figure 8).

Figure 8.

An illustration of the use of difference maps in the analysis of distinct structural classes. Side-by-side visualization of maps rendered at the same threshold does not readily reveal the structural differences between them (A). Positive (black) and negative (white) difference maps rendered at five standard deviations better reveal compositional and conformational differences (B).

However, in order to subtract one map from the other several issues need to be taken into consideration. Firstly, it is important that both maps are aligned. As maps may rotate with respect to each other during ML3D refinement, realignment of the output maps is often necessary. Secondly, both maps should be on the same resolution. Typically, subsets of different sizes yield reconstructions at different resolutions, and both maps should be filtered to the lowest common resolution. Finally, both maps should be on the same intensity scale and have similar power spectra, or B-factor decays. This will generally be true for maps that were reconstructed from subsets of a single data set, but special care should be taken when subtracting maps obtained from other microscopy experiments or atomic structures.

High-performance computing

Because of their elevated computational costs, 3D ML approaches rely heavily on high-performance computing approaches. For example, classification of 91,000 ribosome particles into four classes was reported to take more than six months of computing time (Scheres et al., 2007a), while these calculations were actually performed within a few days using 64 processors in parallel. In order to make efficient use of available computing resources it may be necessary to have some understanding of the available hardware and the parallelization strategies employed.

The most expensive part of the expectation maximization algorithm is the E-step, where for every particle an integration over all possible orientations and classes is evaluated. This step is similar to the alignment step in conventional refinement approaches. Fortunately, each of the typically thousands of individual particles can be processed independently within each E-step. In parallel computing such problems are called embarrassingly parallel, as very little effort is typically required to split them into a number of parallel tasks. Only when reaching the M-step (i.e. the reconstruction step) the information from all particles is to be combined, but this step is typically much less expensive.

Parallelization strategies may be divided into two categories depending on the computer hardware that is used. Shared-memory parallelization employs multi-core processors that share a single centralized memory¹, while distributed parallelization is used for computing nodes with their own local memory that are connected via a network. As parallel processes in a multi-core processor have access to the same memory, the implementation of shared-memory parallelization is often relatively easy. Single processes may be programmed to launch multiple threads to perform separate tasks simultaneously. Apart from the relative ease of software development (which may be of little concern to the experimentalist) multi-threaded programs are also relatively easy to use. Executing these programs in parallel does not involve additional complications and they can be run on commonly available multi-core desktop computers.

In distributed parallelization, parallel tasks are executed on different nodes that cannot see each other’s memory, and information exchange between nodes is typically performed by message passing. Thereby, the efficiency of distributed parallelization schemes is often a trade-off between the costs of computation and communication. The main advantage of distributed parallelization is scalability. Many thousands of nodes may be used simultaneously in large computing clusters, whereas shared-memory parallelization is limited by the number of cores on a single processor (currently up to eight). However, even when using common standards like MPI (Gropp et al., 2009), the installation of message passing programs is often more complicated than for sequential programs. Moreover, not all electron microscopy labs have access to a computing cluster, and jobs are often executed through specific queueing systems that may present an additional stumbling block for the experimentalist.

The ML2D and ML3D programs in the XMIPP package have been implemented using a hybrid parallelization approach using both threads and MPI². Thereby, one can take full advantage of modern, multi-core computer clusters. In this scenario MPI takes care of passing messages between a possibly high number of multi-core nodes, each of which runs multiple threads in parallel. The shared-memory parallelization is particularly useful in 3D classification where memory resources pose important limitations on the angular sampling and the number of classes. By sharing the memory inside a multi-core node one prevents the duplication of part of the memory as would be the case in distributed parallelization. Thereby, within a single node much more memory is available so that a higher number of classes may be refined and with finer angular samplings.

In most cases, parallelization of the E-step can be done with excellent efficiency, but this is not the case for the M-step. The M-step of ML2D is very quick, basically the calculation of K 2D average images, and thus does not play an important role. The M-step in ML3D comprises K 3D reconstructions which are performed using a modified weighted least-squares (wls) ART algorithm (Scheres et al., 2007a). These reconstructions are relatively fast compared to the E-step, but a distributed parallelization scheme is not straightforward for this type of algorithm (Bilbao-Castro et al., 2009). Therefore, the current wlsART implementation only uses threads, although the K independent reconstructions may each be performed by a different MPI process. The M-step may thereby become a bottle neck if the number of MPI processes is much larger than K. Therefore it is important to realize that if the M-step starts taking similar amounts of time as the E-step, using more MPI processes will no longer lead to important gains in speed.

Outlook

Image classification plays an increasingly important role in single-particle cryo-EM as it offers the unique opportunity to characterize multiple structural states from a single sample. While these potentials are being illustrated for a growing number of macromolecular complexes, it is becoming clear that these complexes are even more flexible than anticipated. For example, using biophysical single-molecule techniques and single-particle cryo-EM it was shown that even at room temperature thermal energy alone appears to be sufficient to induce major conformational changes in the 70S ribosome (Cornish et al., 2008; Julian et al., 2008; Agirrezabala et al., 2008). These observations are changing our view of molecular machines in a profound way and will eventually lead to even bigger challenges in image classification. In response to these insights, many different 3D classification tools have recently emerged, see (Spahn & Penczek, 2009) for a recent review. Compared to existing alternatives, ML classification may be an attractive choice in many experimental studies because of its unsupervised character, its robustness to high noise levels, and its simultaneous assignment of orientations and classes.

As mentioned in the introduction, their implementation in the Xmipp package (Sorzano et al., 2004b) may have played an important role in the relatively wide spread use of ML single-particle classification approaches. Therefore, it is promising that similar programming efforts are being made for ML approaches in other cryo-EM modalities as well. Recently, a dedicated program has been written for ML refinement of icosahedral viruses (Prust et al., 2009), while the ML approach for 2D crystals has been implemented in the 2dx software package (Gipson et al., 2007) that provides a user-friendly interface to the MRC package (Crowther et al., 1996).

New results with ML methods in other cryo-EM modalities are other promising indicators that ML approaches may eventually become of general use in many aspects of cryo-EM data processing. Recently, the ML approach for icosahedral virus refinement by Doerschuk & Johnson (2000) and Yin et al. (2001, 2003) was successfully applied to classify an assembly mutant of CCMV (Lee, 2009), and ML sub-tomogram averaging (Scheres et al., 2009) provided reference-free alignment and classification of 100S ribosome particles (submitted, in collaboration with Julio Ortiz). Together with the continuing increase in available computing power, ML methods and related statistical approaches are thereby expected to play progressively central roles in a wide range of experimental cryo-EM studies.