Accurate Temperature Imaging Based on Intermolecular Coherences in Magnetic Resonance

Abstract

Conventional magnetic resonance methods that provide interior temperature profiles, which find use in clinical applications such as hyperthermic therapy, can develop inaccuracies caused by the inherently inhomogeneous magnetic field within tissues or by probe dynamics, and work poorly in important applications such as fatty tissues. We present a magnetic resonance method that is suitable for imaging temperature in a wide range of environments. It uses the inherently sharp resonances of intermolecular zero-quantum coherences, in this case flipping up a water spin while flipping down a nearby fat spin. We show that this method can rapidly and accurately assign temperatures in vivo on an absolute scale.

Temperature, one of the most fundamental intrinsic quantities of matter, is very difficult to measure noninvasively beneath the surface of an object. A general method to image interior temperatures in soft matter could find a wide range of experimental applications in fields ranging from bulk catalysis and process chemistry to clinical treatment. In medicine alone, temperature distributions in the body have been linked to the critical regulation of metabolism, immune function, and longevity. (1) Hyperthermic cancer treatments and radiation therapy are used to kill cancer cells at different stages of growth (2–7), and numerous groups have developed thermally sensitive formulations (e.g., liposomes) that release drugs selectively within a heated region (8–11). In practice, however, the utility of all of this work is compromised by the difficulty of accurate temperature imaging in vivo. (12) In general, current methods break down in the very systems that are of greatest interest, those that are inhomogeneous and that change with time.

Here, we present a magnetic resonance imaging approach for rapid, high-resolution in vivo temperature imaging. It involves selective detection of intermolecular multiple quantum coherences (iMQCs), (13–21) which in this case correspond to exciting water spin resonances while simultaneously de-exciting lipid resonances from molecules that are separated by the “correlation distance,” typically tens of micrometers. The method is not restricted to biological tissues; in essence, it uses a temperature-insensitive resonance to clean up the response of a temperature-sensitive resonance, with the critical advantage that the two types of spins need not be in the same molecule or even in exactly the same position. It required the development of a new generation of pulse sequences that enable efficient and rapid iMQC detection to reduce the effects of physiological noise. In contrast to existing methods, it is intrinsically insensitive to static and transient inhomogeneity, does not require exogenous contrast, and can rapidly provide accurate temperature measurement on an absolute scale.

Image-compatible methods of obtaining absolute temperatures are an intense area of research, but most techniques require injection of exogenous contrast agents, such as paramagnetic species. The best current approach to clinical MR thermometry (22–24) uses the change in resonance frequency of water protons with temperature (0.01 parts per million/°C, or 3 Hz/°C in a 7 tesla magnet). The water frequency has been used as a thermometer for decades in traditional nuclear magnetic resonance (NMR) (25), where line shapes are narrow and shifts are unambiguous, and in that case absolute temperatures can be measured by the frequency difference between water and a reference peak (26–28). However, line shapes in vivo are broad and shifting, because the topography of the local magnetic field changes dramatically with motion, heating, drift, and susceptibility gradients; this field is heterogeneous over the sampling volume, thus generating a range of resonance frequencies that leads to an inhomogeneous line shape. These macroscopic effects easily overshadow the thermal coefficient and, even with elaborate approximations and correction factors (29), can lead to large inaccuracies.

Chemical shift imaging (CSI) methods, such as two-dimensional (2D) CSI or computational techniques that decompose the fat and water images, are also promising, but these compare fat spins (S) and water spins (I) distributed across the entire voxel, typically of much larger dimensions (1 to 10 mm) than the correlation distance (30). As a result, the proton frequency shift method is the one commonly used, and only to image relative temperatures, for example, during a heating therapy. In that case, the temperature gradients themselves give rise to complicated, nonlinear gradients in the local magnetic field. (31) Furthermore, the heating probe itself induces large magnetic susceptibility gradients that amplify the consequences of motion, so that a 1- to 5-mm displacement of the probe falsifies the temperature measured 1.5 cm away by 10°C or more (32). Finally, current methods are unsuitable for fatty tissue such as breast, although breast cancer treatment is anticipated to be one of the most promising targets of hyperthermic therapies.

One approach to detection that is insensitive to the problem of inhomogeneity in the macroscopic field is to use so-called zero-quantum transitions, which conventionally involve flipping two spins on the same molecule in opposite directions. The frequency shifts that arise from microscopic phenomena (including those related to temperature, if the two resonances have a different temperature dependence) are retained. However, water's magnetically equivalent spins cannot be used, and other molecules with multiple peaks found in vivo (such as in fat or lipid) have no appreciable temperature dependence (33).

Flipping two separated spins in different directions [intermolecular zero-quantum coherences (iZQCs)] removes most of the inhomogeneous broadening (34), as demonstrated, for example, in the HOMOGENIZED sequence (16). In addition, water-fat iZQCs maintain the frequency difference between the spins (and hence the temperature dependence of the water chemical shift) because the chemical shift of lipids does not change with temperature over a biologically relevant range. Flipping both spins in the same direction [intermolecular double-quantum coherences (iDQCs)] could do this as well if the iDQCs are ultimately detected by echoing them into conventional coherences (which inherently evolve at the water or fat frequency, but not both). However, iZQCs and iDQCs are normally indirectly detected by incrementing an internal delay in a repeated pulse sequence. Imaging using only the iMQCs between two inequivalent spins is not easily accomplished; signal intensity from like-spin iZQCs, such as the water-water iZQCs in vivo, is often simultaneously detected and is often much larger than the desired mixed-spin or crosspeak signal. Resolving the temperature-dependent crosspeak frequency from the water-water signal would generally require a full 4D (two spatial, two spectral) Nyquist-sampled experiment. Any such sequence is both relatively slow and highly sensitive to physiological noise.

Ultrafast imaging methods have previously been applied to speed up iZQC data acquisition; these methods allow coherences to evolve along the same pathways for slightly different times and acquire signal by partial transfer into observable magnetization (19). We now introduce a new generation of pulse sequences (Fig. 1) that simultaneously excite coherences along multiple different paths without signal loss, which permits acquisition of two independent points in a single shot to measure a temperature change. Data acquired with this sequence demonstrates that temperature maps can rapidly and accurately monitor temperature, both in vitro and in vivo.

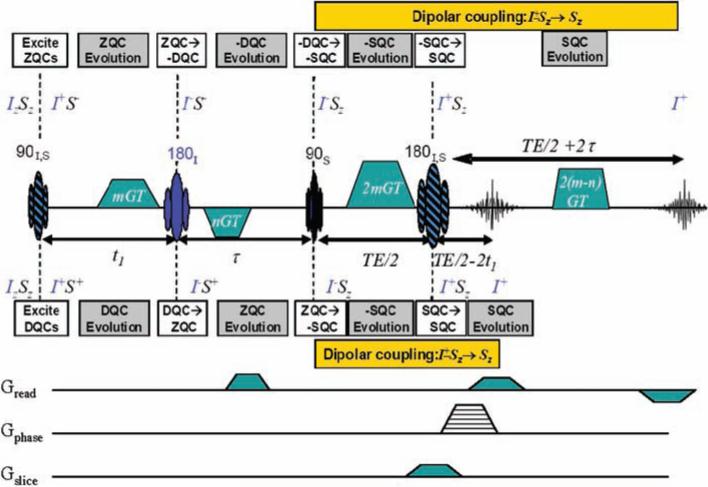
Fig. 1.

HOT pulse sequences for iZQC thermometry. The HOT sequence excites inhomogeneity-free transitions at the difference frequency between water (spin I, in blue) and fat (spin S, in black). It acquires two separate echoes, which evolve for ±(t₁ + τ)at the difference frequency ω_I – ω_S, so the phase difference gives an absolute measure of temperature. Single-line image acquisition (using the gradients on the bottom three lines) gives a full image in a few minutes; EPI could be even faster.

By modern magnetic resonance standards, the sequence is very simple: two broadband radio frequency (rf) pulses (shown as striped ovals), two selective rf pulses (solid color ovals), and several gradient pulses (trapezoids). Conventional MR experiments start from I_z or S_z in the equilibrium density matrix, and it is straightforward to show that this sequence then produces no signal, because no combination of the gradient areas provides any possible echo for arbitrary values of m and n in the gradient pulses. However, iMQCs result from two-spin (or higher) terms in the equilibrium density matrix, which in this sequence produce two echoes at two different times via two completely separate coherence pathways. After the first pulse, the two-spin term in the equilibrium density matrix I_zS_z is transformed into I_xS_x, which contains ZQ, –DQ, and +DQ contributions. All of these terms are transformed in the usual way by subsequent pulses, as illustrated in Fig. 1, and the evolution follows the standard “spin physics” well known in the NMR community. Simple algebra (adding up the expected effect of inhomogeneous broadening or a gradient on the listed operators during the different time periods) predicts all of the observed properties, including the insensitivity to local field variations. All four gradient pulses are needed to rephase the pathway at the top, which echoes 2 τ late because of the −DQ evolution in τ; at the echo, the coherence has a net evolution at the water-fat difference frequency for a total of t₁ + τ. Only the first three gradient pulses are needed to rephase the pathway at the bottom, which echoes 2 t₁ early because of the +DQ evolution in t₁; at the echo, it evolved at the negative of this frequency for t₁ + τ. Using the same evolution rules, it can be shown that the water-water or fat-fat two-spin terms (I_z1 I_z2 or S_z1 S_z2) never refocus. This sequence selectively transfers coherences that evolve off-resonance in the indirectly detected dimension, prompting its acronym to be HOMOGENIZED with Off-resonance Transfer, or the HOT sequence.

As with all intermolecular multiple-quantum experiments, the two-spin operators are ultimately made observable by dipolar interactions in solution (35). During the period indicated in gold in Fig. 1, n dipolar couplings of the form D_1n I_z1S_zn all interact with terms such as I_x1S_zn (which would be called antiphase coherences in 2D NMR) to create observable magnetization such as I_y1. Because of the gradients, the sign in front of the term I_xiS_zn depends on the relative orientation and separation of spins 1 and n (as does the sign of the dipolar coupling D_1n itself). At a specific distance dictated by these areas (which we call the correlation distance), spherical symmetry is completely broken, the effects of the many couplings constructively interfere, and observable signals are produced (iMQC signals in vivo are typically 5 to 10% of the equilibrium magnetization). In imaging applications, we add conventional imaging gradients [single-line, as shown in the bottom panel of Fig. 1, or echo planar imaging (EPI)] to acquire two images at once, and the phase difference is a direct measure of local temperature, with dramatically reduced contributions from physiological noise compared to single-echo acquisitions.

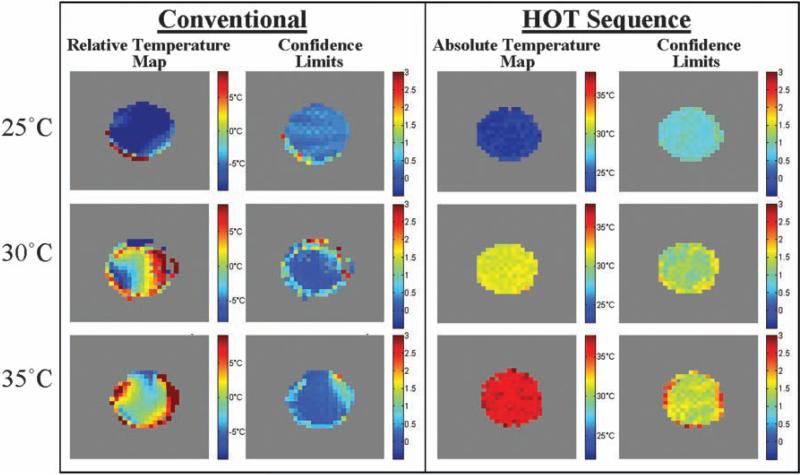
As a calibration of the accuracy of HOT thermometry, we used a single-window version of Fig. 1 to acquire temperature images of a fat-water phantom that was allowed to equilibrate to a uniform temperature (Fig. 2) (TE = 60 ms; pulse sequence repetition time TR = 5 s; τ = 2.67 ms; t₁ = 3 to 11 ms). Alongside each image at each temperature, we also show 90% confidence intervals based on the quality of the fit in each voxel to a single evolution frequency. In each case, what is shown here is not the absolute signal intensity but the measured resonance frequency of the voxel (and its associated error bars). Whereas the conventional data report large temperature gradients in these uniformly heated samples (an error caused by susceptibility-induced frequency shifts), HOT signals only change with temperature. In other words, the conventional method is precise but not accurate; HOT is less precise (because it has less signal) but far more accurate.

Fig. 2.

Temperature maps of a phantom at three uniform temperatures. Conventional thermometry (color bar shows relative temperature inferred by water frequency) and iZQC thermometry (color bar shows absolute temperature from iZQC frequency) of an equilibrated fat-water phantom. The conventional method is precise but inaccurate, reporting a wide range of temperatures that are actually variations in local B₀. In contrast, HOT thermometry gives more uncertainty in the observed slope because of the lower signal-to-noise ratio, but these images accurately reflect the uniform temperature of the phantom.

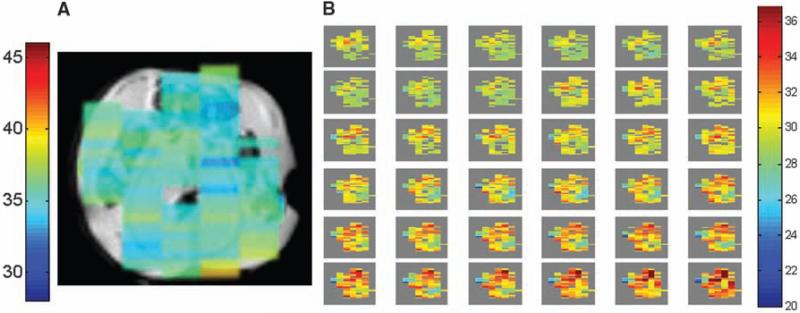
Figure 3 demonstrates HOT thermography in vivo using the two-window protocol in Fig. 1, which acquires images in just 2 min (ungated images of hindquarters of a live mouse, with TE = 40 ms; TR = 2 s; mGT = 1 ms*8.4 G/cm; nGT = 1 ms*21 G/cm; t₁ = 3 ms; τ = 10.66 ms; voxel size 0.25 cm³). In Fig. 3A, an in vivo image is shown of an obese mouse (OBM), superimposed on a structural image of a thinner slice, which is an excellent model for the fatty tissue in breast. The temperature image shows considerable uniformity, as would be expected at the natural body temperature of the mouse. This data was acquired using single-line acquisition; EPI could provide still greater acceleration factors. The 2-min protocol was sufficiently fast, however, to allow us to dynamically image a heating procedure in vivo. A series of temperature images is shown in Fig. 3B of a different OBM that is being heated by contact with an external warm water tube (same imaging parameters as previously described and using no spatial smoothing or image coregistration between temperature images). These images further establish that the phases of iZQC images reflect temperatures in vivo in a clinically accessible scan time.

Fig. 3.

(A) A 2-min HOT temperature image of OBM superimposed on an anatomical image of a thinner slice shows a relatively uniform distribution, as would be expected. These ungated images were acquired from the hindquarters of alive mouse at 7 T. (B) A series of HOT images on a different OBM heated by contact with a warm water tube. Images were taken every 2 min, and rectal temperature increased from 28.6°C to 39°C during the course of the experiment.

Further extensions of the HOT pulse-sequence are possible. For example, this scan used a separately acquired reference image to correct the phases for sequence imperfections, but we have shown that adding an additional module consisting of [(n – m)GT gradient pulse, delay T′, 180 pulse] at the end of this sequence gives yet another echo after T′-t₁-τ that is purely I spin conventional magnetization and hence can be used for phase correction or coregistration. Phase-shift effects of heterogeneity in the fat composition can be minimized by judicious choice of pulse delays. This technique can be used to generate accurate temperature maps on almost any sample with at least two abundant components (assuming their electronic screenings do not have identical thermal shifts) on an absolute scale. However, it is notable that the signal from a HOTexperiment scales as the product of the two magnetizations, M_IM_S, so optimal signal is attained when both spins are in high abundance. At lower fields, such as those found in clinical settings, temperature shifts are smaller, but in general T₂ is longer. Thus, the iZQC coherences can evolve for longer periods, giving an adequate separation of phase. Furthermore, because iZQC signal intensity grows in during TE, a longer T₂ can offset the lower magnetization available at higher field. Thus, the method can easily be adapted to a wide range of applications that would benefit from real-time imaging of this fundamental physical property.