Shape selection of twist-nematic-elastomer ribbons

Abstract

How microscopic chirality is reflected in macroscopic scale to form various chiral shapes, such as straight helicoids and spiral ribbons, and how the degree of macroscopic chirality can be controlled are a focus of studies on the shape formation of many biomaterials and supramolecular systems. This article investigates both experimentally and theoretically how the chiral arrangement of liquid crystal mesogens in twist-nematic-elastomer films induces the formation of helicoids and spiral ribbons because of the coupling between the liquid crystalline order and the elasticity. It is also shown that the pitch of the formed ribbons can be tuned by temperature variation. The results of this study will facilitate the understanding of physics for the shape formation of chiral materials and the designing of new structures on basis of microscopic chirality.

Recent researches have revealed that chirality plays a critical role in controlling the shape of self-assembled supramolecular aggregates. A range of chiral shapes, including tubes with “barber-pole” markings, spiral ribbons (with cylindrical curvature and helical central line), and helicoids (with Gaussian saddle-like curvature and straight central line), have been observed in a rich variety of biological materials and their synthetic analogues. These materials include several amphiphiles (1–3), peptides (4–7), diacetylenic lipids (8, 9), gemini surfactants (10, 11), and multicomponent mixtures in bile (12, 13). Such aggregates often become bilayers, and the bilayer membranes form tubules, spiral ribbons, or helicoids in contrast to the normal expectation that the minimum energy state of the bilayers would be flat, or be large spherical vesicles with the minimum curvature. In addition, the correlation between material characteristics and the macroscopic shape of chiral aggregates is markedly complicated. For example, mixed bilayers of saturated and diacetylenic phospholipids change their shape between micron-scale cylindrical tubules, spiral ribbons, or nanometer-scale tubules, in response to temperature variation (14). Charged gemini surfactants with chiral counterions show a transition between spiral ribbons and helicoids as a function of molecular chain length (10). Many theoretical studies have been reported to explain what determines the size and shape of tubules, helicoids, and spiral ribbons (10, 15–18).

In this article, we will show, both experimentally and theoretically, how a flat twist-nematic-elastomer (TNE) film when subjected to temperature change can easily achieve the goal of shape selection between helicoids and spiral ribbons. Nematic elastomers (NEs) are a unique class of materials (19–23). Formed by cross-linking liquid crystalline polymers, NEs possess both the elastic properties of rubbers and the orientational properties of liquid crystals. The combination of these two properties makes the shape of NEs very sensitive to external stimuli. In this article, we will focus on NE films in which the nematic order orientation changes smoothly by 90° from the bottom surface to the top surface with the director at the midplane parallel to the long or short axis of the film as shown in Fig. 1. The director’s change in orientation through the film’s thickness leads to gradients in the induced strain when the film is heated or cooled, giving rise to complex changes in the sample’s overall shape. Broer and coworkers (24, 25) reported that temperature variation or light irradiation can turn a flat ribbon of densely cross-linked stiff liquid crystal networks with a similar twist orientation into a ribbon of saddle-like shape or spiral ribbon. Godinho et al. (26) showed that the self-winding of helices in jets and electrospun fibers obtained from cellulosic mesophases results from an off-axis core line defect disclination. The NEs (i.e., loosely cross-linked elastomeric liquid crystal networks) possess considerably stronger coupling between mesogen orientation and network deformation than the materials in these studies (24–26). We will demonstrate that the NE films with the twist configuration mentioned above form helicoids or spiral ribbons in response to temperature variation. We will also show that these TNE films select the shape according to the value of their width-to-thickness ratio: the narrow TNE films twist around their central lines upon temperature change, forming helicoids; however, when the width-to-thickness ratio of the films becomes larger than a certain critical value, the central lines of the films curve into helices and the films themselves form spiral ribbons. In addition, we will also show how the helical/twist pitch and handedness change with temperature and the width-to-thickness ratio of the films.

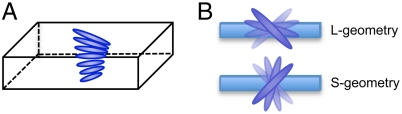
Fig. 1.

Schematics of the director configuration of TNE ribbons: (A) side view, (B) top view of the L- and S-geometry. Nematic director twists left-handedly by 90° between the top and bottom surfaces with the director at the midplane parallel to the long or short axis of the ribbon.

In contrast to the chiral supramolecular aggregates of the order of nano- or micrometer scale, the shape selection and variation of the TNE films occur in the macroscopic scale of the order of milli- or centimeter, and the dimensional parameters of the TNE films can be experimentally varied as desired and the pitch of formed ribbons can thus be well controlled. These features facilitate to characterize the geometrical parameters of the shapes and to elucidate the dimensional effect on the shape selection. The results of the present study will provide an important basis of the understanding of the physics for the shape formation of chiral materials, and the designing of new structures on basis of microscopic chirality.

Results

Experiment.

Here we focus on the shape variation of TNE films with various widths driven by temperature change. The director in the TNE films left-handedly rotates by 90 ° between the upper and bottom surfaces. The twist nematic configuration was imprinted in the elastomer matrix by the cross-linking reaction in the presence of a nonreactive chiral dopant. This chiral imprinting was demonstrated in the preparations of cholesteric liquid crystal elastomers.(27–29) The side-chain-type TNEs were prepared by photopolymerization of the achiral mesogenic monoacrylate (A-6OCB in Fig. 2) and 1,6-hexanediol diacylate (cross linker) dissolved in a miscible nematic solvent with a controlled amount of the nonreactive chiral dopant (S-811 in Fig. 2) that induces a 90° left-handed rotation of director between the two glass substrates. The surfaces of the glass substrates were coated with uniaxially rubbed polyimide layer, and they were placed in such a manner that the rubbing direction could cross with each other. The polarized optical microscopy confirmed that the dried elastomeric films with a thickness of 35.2 μm possessed a 90° twist director configuration even after the removal of the chiral dopant and nematic solvent. The long ribbon specimens were cut out from the film sheet so that the director at the midplane is either along the long axis or along the short axis of the ribbons (designated as L- and S-geometry, respectively, see Fig. 1). The ribbons with various widths (ca. 0.2 ∼ 0.8 mm) were prepared, and the length of the ribbons (5 ∼ 10 mm) was considerably longer than the widths. We observed the shape of the ribbons immersed in a temperature-controllable silicone oil bath by optical microscopy. The silicone oil is a nonsolvent for the TNEs, and the ribbons have no mechanical constraint in the oil bath.

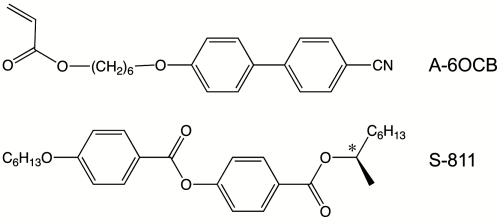
Fig. 2.

Monoacrylate mesogenic monomer A-6OCB and chial dopant S-811.

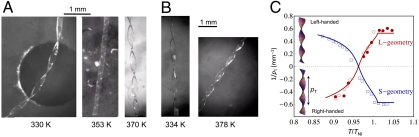
We find that the TNE ribbons select a helicoid or spiral ribbon depending on the width. In the narrow case, the shape is a helicoid with Gaussian saddle-like curvature (Fig. 3), while the shape in the wide case is a spiral ribbon with cylindrical curvature (Fig. 4). In both cases, the temperature (T) variation greatly changes the structural parameters of the ribbons such as twist pitch (p_T) (of helicoids), helical pitch (p_H), and diameter (d) (of spiral ribbons), involving a reversal of handedness (Figs. 3 and 4). This shape change is thermally reversible (Fig. 3C). The strong T effect on the ribbon shape originates from a large change in local nematic order induced by T variation. In fact, in the nematic phase of T < T_NI(T_NI = 367 K is the nematic-isotropic transition temperature) with T-dependent nematic order, the structural parameters strongly depend on T, while they are independent of T in the isotropic phase of T > T_NI with no nematic order (Figs. 3C and 4C). The ribbons become almost flat at a certain temperature (T_flat) around 353 K, as shown in Fig. 3A. It should be noted that T_flat is different from the preparation temperature of the films (T₀ = 313 K). The preparation state involving ca. 50wt% solvent at T₀ corresponds to the initial flat state with twist alignment, but the subsequent volume reduction to the dry state causes a twist distortion due to a finite strain gradient driven by anisotropic shrinking. In general, a finite volume change in nematic gels results in a considerably anisotropic shape variation (30, 31). In fact, the ribbons at the temperatures slightly above T₀ show a considerable twist (Figs. 3C and 4C), although no structural data in the dry state at T₀ was obtained due to the glassy state: The glass transition temperature of the dry film was ca. 50 °C.

Fig. 3.

Helicoids formed by the narrow TNE films with the thickness 35.2 μm. (A) Shape of the L-geometry ribbons: left-handed at 370 K; almost flat at 353 K; right-handed at 330 K. The ribbon width is 0.23 mm. (B) Shape of the S-geometry ribbons: right-handed at 378 K; left-handed at 334 K. The ribbon width is 0.22 mm. (C) Temperature dependence of the inverse of the twist pitch (p_T). The pitches of the left- and right-handed twist are defined to be positive and negative, respectively. The open and filled symbols represent the data obtained in the cooling and heating processes, respectively; and the (red) circles and the (blue) squares represent the data of the L-geometry and those of the S-geometry, respectively. The lines represent the theoretical predictions.

Fig. 4.

Spiral ribbons formed by the wide TNE films with the thickness 35.2 μm. (A) Shape of the L-geometry ribbons: left-handed at 374 K; right-handed at 336 K. The ribbon width is 0.76 mm. (B) Shape of the S-geometry ribbons: right-handed at 374 K; left-handed at 330 K. The ribbon width is 0.83 mm. (C) Temperature dependence of the inverses of the helical pitch (p_H) and the diameter (d), where the lines represent the theoretical predictions. The pitches of the left- and right-handed twist are defined to be positive and negative, respectively. The inverse of the pitches is represented by the open symbols and the inverse of the diameters by the filled symbols. The (red) circles and (blue) squares represent, respectively, the data of the L-geometry and the data of the S-geometry. The thick (solid or dashed) lines represent the theoretical predictions for the structural parameters of spiral ribbons, and the thin dashed lines are the theoretic prediction of the pitch inverse of helicoids.

The direction of the director at the midplane relative to the long axis of the ribbons change the handedness of the helicoids and spiral ribbons: At the temperatures below T_flat, the helicoids and spiral ribbons with L-geometry are right-handed, while those with S-geometry are left-handed (Figs. 3 and 4). In other words, the cooling (that is, an increase in local nematic order) induces the right- and left-handed winding in L- and S-geometries, respectively.

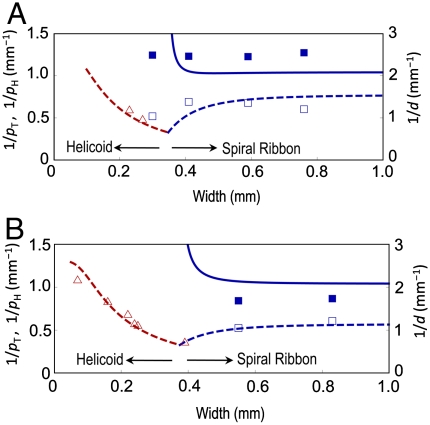
The shape transition between helicoids and spiral ribbons driven by width variation is clearly observed in the high-temperature isotropic state where the structural parameters are substantially independent of T (Fig. 5). For both L- and S-geometries, the shape transition occurs, but the critical width of the transition for L-geometry (w_c ≈ 0.3 mm) is smaller than that for S-geometry (w_c ≈ 0.4 mm). We also notice that the spiral ribbons with L- and S-geometries are not symmetric, and the spiral ribbon with L-geometry is wound a little more tightly than that with S-geometry: The values of p_H and d with L-geometry are slightly smaller than those with S-geometry. This trend is also observed in Fig. 4. In contrast, the helicoids with L- and S-geometries are almost symmetric, which can be seen in Fig. 3.

Fig. 5.

Width effect on the shape selection of the TNE ribbons with (A) L-geometry and (B) S-geometry. The ribbon thickness is 35.2 μm. The shape is observed at 378 K in the isotropic state. The shape transition occurs at ca. 0.3 mm and ca. 0.5 mm for L- and S-geometries, respectively. The (red) triangles represent the pitch inverse of the helicoids, and the open and filled (blue) squares represent the pitch inverse and diameter inverse of the spiral ribbons, respectively. The lines are the theoretical predictions.

Theory.

We develop a theoretic model to explain the experimental results. The two physical quantities we need are liquid crystal order tensor Q_ij and nonlinear strain tensor 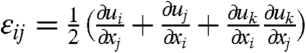, where the Einstein summation convention on repeated indices has been assumed. x and u represent, respectively, the position of a mass point before deformation and the corresponding displacement vector induced by the deformation. The elastic energy is assumed to take a simple form,

[1]

where μ is the shear modulus, α the coupling constant, and δQ_ij the change of liquid crystal order tensor induced by external stimuli. Given the incompressibility constraint ϵ_ii = 0 for small deformations, this simple energy form is then good enough to capture the main feature of the problem we study here. Note that δQ_ij is now defined in the body frame to ensure rotational invariance (32). We further assume that when subjected to external stimuli the change of the body-frame order tensor is mainly caused by the order parameter change δS and that the principle axes of the order tensor keep fixed in the body frame although they do rotate with the film in the laboratory frame, namely, we assume 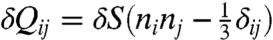, where n is the orientation of the nematic director at T_flat, twisting from the bottom surface to the top surface of the film. Integrating the above energy density along the direction perpendicular to the film plane and along the short axis of the film yields an effective 1D energy density (17) as a function of the curvature tensor C_ij,

[2]

where d and w are respectively the thickness and width of the film, 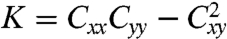is the Gaussian curvature, and x and y represent, respectively, the directions parallel to the long and short axis of the film. The curvature tensor equals C_ij = ∂²h/∂x_i∂x_j, where h is the out-of-plane normal displacement. The linear term in C_xy is a chiral symmetry-breaking term, inducing the film to twist; the first term represents the in-plane stretch energy cost (33); and the other terms are the bending energy cost. The coefficients, which will be given in the Methods section, are determined by three parameters: the ratio between w and d, the product of the coupling constant α and the order parameter change δS, and the twist angle span θ_S.

The theoretical results can be obtained by minimizing f_1D with respect to C_ij: for a given temperature change, narrow films form helicoids with the curvature of their central line C_xx being zero and the torsion of their central line C_xy determined by the equation 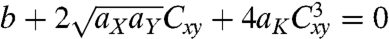; wide films form spiral ribbons with 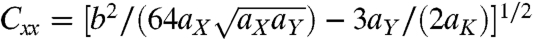and 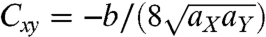. The Gaussian curvature is 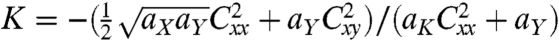. Note that K is always negative; only in the limit w/d → ∞, K tends to zero and the films form perfect spiral ribbons. (Ribbons of various curvatures are shown in Fig. S1). The critical width w_c that determines what type of ribbon to form is given by the condition a_kb² = 96(a_Xa_Y)^3/2. In the case of θ_S = π/2, this condition simplifies to

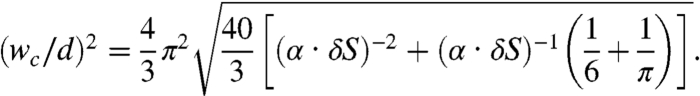[3]

To compare the theoretical predictions with the experimental observations, we proceed to connect the product of the coupling constant and the order parameter (αS) to temperature T. For this purpose, we examine how much a corresponding nematic elastomer with planar orientation extends as temperature is lowered. It is easy to deduce from Eq. 1 that the extension along the nematic director in this case is 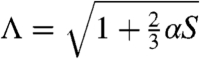. By fitting the experimentally measured curve of Λ(T) (see Fig. S2), we obtain αS = 3.3(1.01 - T/T_NI)^2/3 as the T dependence of αS.

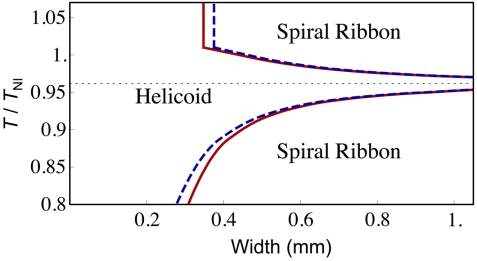
Given the relation between T and αS, we can then determine how C_xx, C_xy, and the critical width w_c vary with temperature T. The pitch and the diameter of the helicoids and spiral ribbons can thus be determined accordingly. The theoretical predictions of their change with temperature are plotted in Fig. 3C and Fig. 4C. In Fig. 4C, the thin dashed lines represent the pitch of helicoids; outside the thin-dashed-line region, the helicoids become spiral ribbons whose diameter first increases rapidly and then decreases slowly with temperature change (see Fig. S1 for an illustration of the shape change). Fig. 5 shows how the pitch and diameter of the ribbons vary with the width. From these figures we can find that the theoretical results agree well with the experimental observations. Shown in Fig. 6 is the phase diagram in the temperature-width space. This figure and Eq. 3 show clearly that w_c goes to infinity as T approaches T_flat. Alternatively speaking, a sample with the width larger than the minimum of w_c always first forms a helicoid and then becomes a spiral ribbon as the temperature is further tuned away from T_flat, as shown in Fig. 4C.

Fig. 6.

Theoretical Phase diagram of TNE ribbons in the width-temperature space. The ribbon thickness is 35.2 μm. The phase boundary of the L-geometry and the S-geometry is represented, respectively, by the red solid line and the blue dashed line. The handedness of the formed ribbons changes as the dotted line at T_flat/T_NI = 0.962 is crossed.

Discussion

In summary, TNE films can form helicoids or spiral ribbons upon temperature change. The optimal shape and curvature (34, 35) of the films depend on the competition between the bending energy cost and the in-plane elastic energy cost. Films with a small width-to-thickness ratio are easier to be stretched than to be bended and thus form helicoids, which have a large Gaussian curvature but no bending; while, on the contrary, those with a large width-to-thickness ratio are easier to be bended than to be stretched and thus form spiral ribbons, with a small Gaussian curvature but a large bending. The pitch and handedness of the formed ribbons are completely determined by only two parameters: the temperature and the width-to-thickness ratio.

To obtain helicoids/spiral ribbons, a chiral symmetry-breaking driving force is a must (otherwise temperature change would cause only a uniform stretch or shrink of the whole sample). In the systems we consider, the twist (chiral) arrangement of the achiral nematogens from the bottom to the top surface of the film was initially induced by the chiral dopants. After the removal of these dopants, this twist (chiral) arrangement is memorized by the polymer network; and it yields the required chiral driving force, when temperature change occurs and induces a tendency of local shape change (stretch or shrink along the nematic director). Therefore, the chiral symmetry breaking in TNE films is induced by the chiral arrangement of achiral molecules rather than by the chiral molecular-structure as in the case of supramolecular aggregates.

On the whole, the experimental results agree well with the theoretical results. However, in the experiments, the precise characterization of the shape at the temperatures near T_flat was difficult due to the saddle-like shape having no definite winding. Therefore, the data of the structural parameters near T_flat are lacking in Figs. 3C and 4C. This difficulty precluded the experimental assessment of the theoretical prediction of the transition from spiral ribbons to helicoids occurring at T close to T_flat for wide TNE films. The reasons causing the relatively large difference between the experimental results and the theoretical results for the low temperature part of the L-geometry in Fig. 4C are not clear to us.

We also investigated samples in which the nematic director on the midplane of the films does not align along the long or short ribbon axis. In this case, straight helicoids are not allowed because of the absence of the antisymmetry about the midplane. The dependence of the shape of the formed spiral ribbons on the width and temperature is similar to those of the L-geometry and S-geometry described above. Although the span angle θ_s is fixed to be 90° in the experiments, our theory is also able to predict how θ_s affects the ribbon shape: approximately speaking, for fixed width and temperature, when θ_s increases from zero, the pitch and diameter of the formed ribbons first decrease, reaching a minimum at somewhere between π/2 and π, and then show a decaying oscillation behavior afterwards. A detailed analysis of how the twist configuration along the normal direction of films changes the ribbon shape will be presented elsewhere.

Methods

Materials.

The monoacrylate mesogenic monomer A-6OCB (Fig. 1) was synthesized by the method described in literature (36). 4-n-Hexyloxy-4′-cyanobiphenyl 6OCB (Sigma-Aldrich) and 1,6-hexanediol diacrylate (Sigma-Aldrich) were employed as miscible nematic solvent and cross linker, respectively, and they were used as received. The chiral dopant S-811 (Fig. 2) and photoinitiator bis(cyclopentadienyl)bis[2, 6-difluoro-3-(1-pyrryl)phenyl]titanium (Irgacure 784®) were kindly supplied from Merck KGaA and Chiba Specialty Chemicals Co., respectively. The mixing of A-6OCB with the nematic solvent was required to broaden the temperature range of the nematic phase, because the nematic phase of A-6OCB is very narrow (only ca. 2 °C) due to the high crystallizability. The mixing ratio of A-6OCB and nematic solvent was 5∶4 by weight. The cross-linker concentration was 7 mol%.

Sample Preparation.

The chiral properties of the mixtures of A-6OCB, 6OCB, and S-811 were characterized by the pitch of the resultant helicoidal structure corresponding to the distance of a 2π screw rotation of the molecular packing. The pitch was evaluated by the Cano wedge method (37, 38). The inverse pitch almost linearly varies with the concentration of S-811, which is similar to the behaviors of conventional liquid crystal mixtures with chiral dopants. The total twist angle of the mesogens was defined as the angle between the bounding mesogenic molecules at the bottom and top glass substrates whose surfaces were coated with a uniaxially rubbed polyimide layer. S-811 induced a left-handed twist configuration of the mesogens. For the sample preparation, the top and bottom glass substrates were placed in such a manner that the rubbing direction could cross with each other. The concentration of S-811 (0.06 wt%) was adjusted such that the total twist angle could become 90°, the distance between the two substrates being 40 μm.

For cross-linking reaction, the glass cell was irradiated using a xenon lamp with emission at a wavelength 526 nm for 30 min. The cross-linking temperature was 40 °C which is ca. 8 °C lower than the transition temperature of the mixture. The cell was immersed in dichloromethane for several days until the resultant gel film detached from the glass substrates due to the swelling pressure. The films were allowed to swell fully in dichloromethane in order to wash out the unreacted materials and chiral dopants. The swollen gel films were gradually deswollen by stepwise addition of methanol to dichloromethane. The ribbon specimens with L- and S-geometries (Fig. 1B) were cut out from the dried film at a temperature where the film became flat (T_flat ≈ 353 K), because the dried film at room temperature was considerably curled and twisted. We confirmed that the dried film possessed a 90° twist rotation of director by polarized optical microscopy.

Measurements.

The length and width of the ribbon specimens were measured by optical microscope. The thickness of the ribbon was evaluated to be 35.2 μm using a laser displacement sensor LT-9500 and LT-9010M (Keyence) at T_flat.

The shape of the ribbons immersed in a custom-made temperature-controllable bath of a silicone oil was observed with an optical microscope with CCD camera. The silicone oil was a nonsolvent for the specimen. The ribbons in the oil bath were subjected to no mechanical constraint. The twist pitch, helical pitch, and diameter at each temperature were evaluated by video analysis. The temperature was varied stepwise after confirming the equilibration of the shape of the specimen at each temperature.

Derivation of the 1D Effective Energy.

We use the energy given in Eq. 1. The nematic director n remains parallel to the film plane (or the xy-plane), and therefore, δQ_xz = δQ_yz = 0. The angle θ between the director n and the long axis of the film (or the x-axis) changes linearly with the depth to the film surfaces: for the L-geometry, we have θ = -θ_Sz/d, where z is the distance to the midplane of the film, and θ_S is the twist angle span, namely, the difference between the angle on the top surface (z = d/2) and the angle on the bottom surface (z = -d/2); for the S-geometry, θ = -θ_Sz/d + π/2. The Frank energy has been ignored here because the typical length scale, i.e., the pitch of the ribbons, in these experiments is of the order millimeters. Given the traceless constraint and the condition that ϵ_xz = ϵ_yz = 0, the strain tensor has only three independent components, ϵ_xx, ϵ_yy, and ϵ_xy. To reduce the full 3D energy density to an effective 2D one, we then express the displacement vector u of points away from the midplane in terms of the displacement vector u^m of points on the midplane (33). To the linear order of z, we have 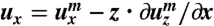, , 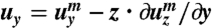and . Substituting the expressions for u and expressions for θ into Eq. 1 and then integrating along the z-direction yield a 2D energy density including terms linear in ϵ_xx and ϵ_yy, whose reference space is the equilibrium state of T_flat. 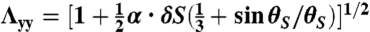To eliminate these linear terms, we change the reference space of the strain tensor to a new state, the equilibrium state of the case that the out-of-plane normal displacement is suppressed, which is acquired by a deformation from the flat geometry with the stretch along the long ribbon axis to be and the stretch along the short axis to be for the L-geometry and and for the S-geometry. We then express the in-plane elastic energy as a function of the Gaussian curvature (33). Assuming the curvature is nearly constant on the ribbon surface (17) and integrating the 2D energy density along the short ribbon axis, we thus obtain Eq. 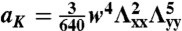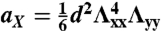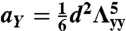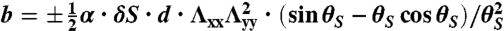2, in which the coefficients are , , , and (+ for the L-geometry and − for the S-geometry). The L-geometry and S-geometry are not exactly symmetric to each other because the Λxx and Λ_yy of the L-geometry are different from those of the S-geometry.