MEASUREMENT OF TEMPERATURE DEPENDENT CHANGES IN BONE MARROW USING A RAPID CHEMICAL SHIFT IMAGING TECHNIQUE

Abstract

PURPOSE

To provide quantitative temperature monitoring for thermal therapies in bone marrow by measuring temperature-dependent signal changes in the bone marrow of ex vivo canine femurs heated with a 980-nm laser at 1.5T and 3.0T.

MATERIALS AND METHODS

Using a multi-gradient echo (≤ 16) acquisition and signal modeling with the Stieglitz-McBride algorithm, the temperature sensitivity coefficients (TSC, ppm/°C) of water and multiple lipid components’ proton resonance frequency (PRF) values are measured at high spatiotemporal resolutions (1.6 × 1.6 × 4mm³, ≤ 5sec). Responses in R₂* and amplitudes of each peak were also measured as a function of temperature simultaneously.

RESULTS

Calibrations demonstrate that lipid signal may be used to compensate for B₀ errors to provide accurate temperature readings (<1.0°C). Over a temperature range of 17.2 to 57.2 °C, the TSC’s after correction to a bulk methylene reference are −0.87 × 10⁻²±4.7 × 10⁻⁴ ppm/°C and −0.87 × 10⁻²±4.0x10⁻⁴ ppm/°C for 1.5T and 3.0T, respectively.

CONCLUSION

Overall, we demonstrate that accurate and precise temperature measurements can be made in bone marrow. In addition, the relationship of R₂* and signal amplitudes with respect to temperature are shown to differ significantly where conformal changes are predicted by Arrhenius rate model analysis.

INTRODUCTION

Primary bone neoplasms, such as osteosarcoma and Ewing’s sarcoma, and metastatic lesions in bone are often associated with high morbidity. Although primary bone cancers account for only 0.001% of all cancer diagnoses (1), approximately two-thirds to three-quarters of patients with advanced breast or prostate carcinoma have bony metastases. In addition, thyroid, lung, and renal carcinomas metastasize to bone in 30–40% of cases (2). In all, approximately 30% of cancer patients will develop bony metastases (3) and these lesions are the most common sources of cancer-related pain (4).

Treatment for these lesions include systemic therapies such as chemotherapy, hormonal therapy, and the use of biphosphonates, as well as local therapies such as radiation therapy and surgery (5). Recent studies on the use of minimally-invasive techniques such as laser-induced thermal therapy (LITT) treatments (6), radiofrequency (RF) ablations (7), and focused ultrasound (FUS) treatments (8–11) have shown effectiveness while reducing morbidity. In addition, magnetic resonance (MR) has been shown to be very valuable asset to localize, plan, monitor and verify these interventional procedures (8–11).

In MR, measuring changes in the proton resonant frequency (PRF) (12,13) is the most commonly used method to quantitatively monitor temperature during these minimally-invasive treatments. The PRF is typically measured indirectly by taking the complex phase difference (CPD) from subsequent gradient echo acquisitions (14). However, CPD is difficult to implement in bone marrow because of the general tendency for reduced or highly variable SNR and the insensitivity of the lipid chemical shift to temperature (15). Field drifts, susceptibility, and motion can also confound the accuracy of temperature measurements in this area (16). Because of these limitations, use of CPD during ablation of bone lesions is challenging and frequently suboptimal (8–11).

In this work, we investigate the response of bone marrow tissue to laser-induced heating by monitoring the temperature dependent changes in MR measurements of the water and lipid components. We measure the noise performance and accuracy of the temperature measurements in ex vivo canine bone marrow at 1.5T and 3.0T, as well as the PRF, R₂*, and amplitude changes as functions of temperature. The overall goal of this work is to demonstrate accurate and precise temperature imaging as well as determine the R₂* and T₁-W amplitude’s response to temperature to aid in monitoring thermal therapies and verifying treatment response in bone marrow. Novel measurements of multiple lipid components’ TSC values as well as simultaneous R₂* and T₁-W imaging at high spatiotemporal resolutions are also investigated for their potential utility in MR temperature imaging.

MATERIALS AND METHODS

Spectral Parameter Estimation from a Rapid Multi-Gradient Echo Acquisition

When a limited number of echoes are used to sample the FID, Fourier-based spectral characterization suffers from a tradeoff of truncation errors versus loss of spectral resolution from heavy signal filtration (17). In these cases, an expansion into a more natural basis set for the FID, such as damped complex exponentials, often aids in spectral parameter identification (18). The MR signal, x(n), at each echo from a multi-gradient echo acquisition can be modeled in the time domain discretely as a sum of damped complex exponentials, that is,

$$x(n)=\sum _{k=1}^N\left(\sum _{t={TE}_0}^{{TE}_0+(n-1)·\mathit{ESP}}{C}_k{e}^{-\left(2\pi i{f}_k+1/T_{2k}^{\ast }\right)t}\right)+w(n)$$ [1]

where N is the number of MR-detectable chemical species (i.e. water, methylene, methyl, etc.), TE₀ is the minimum echo time, n is the echo train length, ESP is the spacing between echoes, C, f, and R₂* are the complex amplitude, PRF, and apparent spin-spin relaxation rate of each chemical specimen, respectively, and w(n) is white noise with zero mean. As seen in previously published work (19,20), this is effectively an auto-regressive moving average (ARMA) model of the FID and an iterative Stieglitz-McBride (SM) algorithm has been investigated and validated for accurate and precise determination of the PRF, R₂* and amplitude of one and two-peak systems (assuming water or water with bulk methylene) by representing the signal as a rational polynomial in the z-domain in the case for reduced number of echoes (≤ 16). A fast 2D, rf-spoiled multi-gradient echo (MGE) acquisition was used along with the SM algorithm to calculate the PRF, R₂* and amplitude of each detectable chemical species for each MR-guided experiment outlined in this study.

Proton Resonant Frequency Shift Calibration and Noise Analysis at 1.5T and 3.0T

Canine femurs (n=5) used in this study were obtained during necropsy from animals being utilized in a separate study. All experiments involving animals were performed in accordance with an Animal Care and Use Protocol approved by our Institutional Animal Care and Use Committee. These femurs were use for calibration measurements using clinical MR scanners at 1.5T (Excite HD, GE Healthcare, Waukesha, WI) and 3.0T (TwinSpeed Excite HD, GE Healthcare, Waukesha, WI). The medial portion of each bone was cut axially to expose the yellow marrow and to insert a water-cooled applicator housing a 980-nm laser fiber with a 1-cm diffusing tip powered by a 15 W diode laser source (BioTex Inc., Houston, TX). In one ablation on the 3.0T system, an external laser (China Daheng Group, Inc. Beijing, China) was used to heat the marrow through the cortical bone. A fluoroptic temperature probe (M3300, Luxtron, Santa Clara, CA) was inserted in order to provide an absolute measurement of temperature for calibration experiments. In each calibration experiment, the MGE acquisition (1.5T: ETL=16 echoes; minimum TE (TE₀)=2.0 ms; ESP=3.2 ms; TR=69 ms; FA=40°; rBW=244 Hz/pixel, acquisition matrix=128x128; voxel volume=1.6x1.6x4.0 mm³; 5 sec/image; parallel imaging acceleration factor=2. 3.0T: ETL=16; TE₀=2.1 ms; ESP=1.8 ms; TR=69 ms; FA=40°;rBW=325 Hz/pixel, acquisition matrix=128x128; voxel volume=1.6x1.6x4.0 mm³; 5 sec/image; parallel imaging acceleration factor=2) was used. Acquisitions used flyback gradients as opposed to bipolar gradients to maximize signal fidelity. Note that the ESP chosen resulted in aliasing of the lipid within the spectral window. ESP values in each experiment were carefully chosen such that observable lipid peaks would not wrap into the water peak and thus enable us to dynamically monitor changes in spectral parameters (19). Use of a higher ESP facilitated use of a lower receiver bandwidth to increase SNR. Relaxing the aliasing restriction also improved spatiotemporal resolution by negating the need for interleaved echo acquisitions.

Modeling and spectral identification using the SM algorithm, as well as all data analysis, was performed using algorithms developed in-house with MATLAB (MathWorks, Natick, MA). A 2 x 2-voxel ROI adjacent to the sensitive region of the fluoroptic probe was chosen and the PRFs were measured as a function of temperature to calculate the temperature sensitivity coefficient (TSC). For calibration purposes, water and bulk methylene PRFs were measured at 1.5T while terminal methylene and methyl peaks were included in studies at 3.0T. Slope, intercept, and correlation coefficient were calculated for each temperature sensitivity calibration using linear least-squares regression analysis. The temperature estimates using the calculated TSC were correlated to the fluoroptic probe measurements. Estimates were also compared to CPD-measured water PRF calibration using a paired two-tailed Student’s t-test. Estimated uncertainties (noise) from each calculated parameter were measured as the standard deviation and compared with the calculated Cramer-Rao Lower Bound (CRLB) for the acquisition, which represents the theoretical lower bound of the uncertainty (20,21). Temperature uncertainties calculated from the measured TSC and PRF uncertainties were compared to temperature uncertainties from the complex-phase difference using the echo with the least uncertainty from the MGE acquisition.

R₂* and Amplitude Response as a Function of Temperature

ROIs (2 x 2 voxels) were chosen in areas that reached ablative temperatures (≥54 °C) with each pixel processed individually. Using the calculated temperature sensitivity coefficients from water and bulk methylene PRF, the changes in the PRFs were converted to temperature changes and added to the baseline temperature provided by the fluoroptic temperature probe; thereby providing absolute temperature readings. The R₂* and signal amplitude (with and without R₂* correction) values for water, bulk methylene, terminal methylene and methyl protons were measured as a function of absolute temperature. The slopes of lines were measured at different temperature ranges and compared using a two-tailed Student’s t-test with equal variances (as determined by an F-Test).

The R₂* values and T₁-W amplitudes (with and without R₂* correction) as a function of temperature were compared with the Arrhenius rate model for thermal damage where

$$\mathrm{\Omega }=\underset{0}{\overset{t}{\int }}{Ae}^{\frac{-E_a}{RT(\tau )}}d\tau$$ [2]

A is the frequency factor, E_a is the activation energy, R is the universal gas constant (8.315 JK⁻¹mol⁻¹) and T(τ) is the absolute temperature as a function of time, τ (22). A and E_a values were chosen to predict protein denaturation (A: 3.1 x 10⁹⁸ s⁻¹, E_a: 6.3 x 10⁵ J mol⁻¹) (23). In this study, Ω ≥ 1 signified tissue damage and this threshold has been used in previous studies (24,25).

RESULTS

Water, bulk methylene, terminal methylene and methyl peaks were resolvable at 1.5T and 3.0T. Figure 1 demonstrates representative modeled spectra from ex vivo yellow bone marrow in the medial femur observed using the spectral parameters derived from the SM algorithm at 1.5T (Fig. 1a) versus the unfiltered FFT spectrum (with 1024 zero padded interpolation) and the modeled spectrum at 3.0T (Fig. 1b). Each spectrum was from one voxel (1.6 x 1.6 x 4.0 mm³). Also note that the lipid peaks were aliased due to the low spectral bandwidth from the large ESP. In (Fig. 1b), as temperature rises, the water peak shows a notable shift in the PRF compared to the three lipid peaks. A spectrum obtained from a PRESS (TE/TR: 144/2000) acquisition at 1.5T show the unaliased lipid peaks and the water peak (Fig. 1c).

Figure 1.

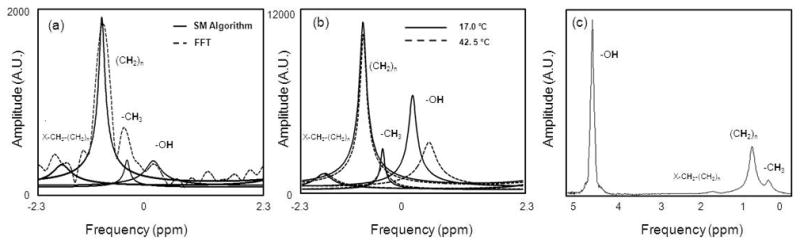
Representative measured bone marrow spectra from 16-echo MGE acquisitions. At 1.5T (Fig. 1a) a 4-peak ARMA modeling (solid) versus unfiltered FFT (1024 point interpolation) (dashed). As previously confirmed (19), ARMA peak locations do not suffer from truncation artifacts. At 3.0T (Fig. 1b) four-peak model at 17.0°C (solid) and 42.5°C (dashed) demonstrates temperature dependent water PRF and temperature independence of lipid peak PRFs. For comparison, a spectrum from a PRESS acquisition at 1.5T is shown in (Fig. 1c).

As expected, excellent correlation with fluoroptic temperature measurements were observed in the water PRF but much less correlation in the lipid PRF. Table 1 (19,26) quantifies temperature relationships observed during calibrations at 1.5T over the temperature range of 37.4 to 57.0 °C. Figure 2 demonstrates the change in the water (squares) and bulk methylene (diamonds) PRF as a function of fluoroptic temperature measurement at 1.5T. The TSC of the difference between the water and lipid PRF values in the three calibrations were found to be statistically the same (−0.87x10⁻² ± 2.7x10⁻⁶ ppm/°C (R²=0.942), −0.87x10⁻² ± 4.6x10⁻⁴ ppm/°C (R²=0.961) and −0.85x10⁻² ± 3.2x10⁻⁴ (R²=0.920), 0.17 < p < 0.99). Using these TSC values, the root mean squared error (RMSE) between the temperature estimates and the fluoroptic probe was 0.39 °C (Range: −0.29–0.90 °C) for calibration 1, 0.96 °C (Range: −0.54–1.13 °C) for calibration 2 and 0.54 °C (Range: −0.84–0.93 °C) for calibration 3. If the temperature measurements were made using water PRF without lipid correction along with the TSC of the water PRF only, the RMSEs were 1.0 °C (Range: −1.36–1.69 °C), 2.11 °C (Range: −1.41–2.69 °C) and 1.31 °C (Range: −1.22–2.91 °C) for calibrations 1, 2 and 3, respectively.

Table 1.

Measured PRF temperature sensitivity coefficients from three calibrations at 1.5T

Chemical Shift	TSC [ppm/°C] (R2)
Water	−1.07 × 10−2 ± 1.0 × 10−4 (0.981)	−1.11 × 10−2 ± 2.4 × 10−4 (0.974)	−0.98 × 10−2 ± 1.3 × 10−4 (0.969)
Bulk Methylene	−0.20 × 10−2 ± 1.0 × 10−4 (0.438)	−0.24 × 10−2 ± 1.5 × 10−4 (0.738)	−0.12 × 10−2 ± 1.1 × 10−4 (0.440)
Difference	−0.87 × 10−2 ± 2.7 × 10−4 (0.942)	−0.87 × 10−2 ± 4.0 × 10−4 (0.961)	−0.85 × 10−2 ± 3.2 × 10−4 (0.920)

Figure 2.

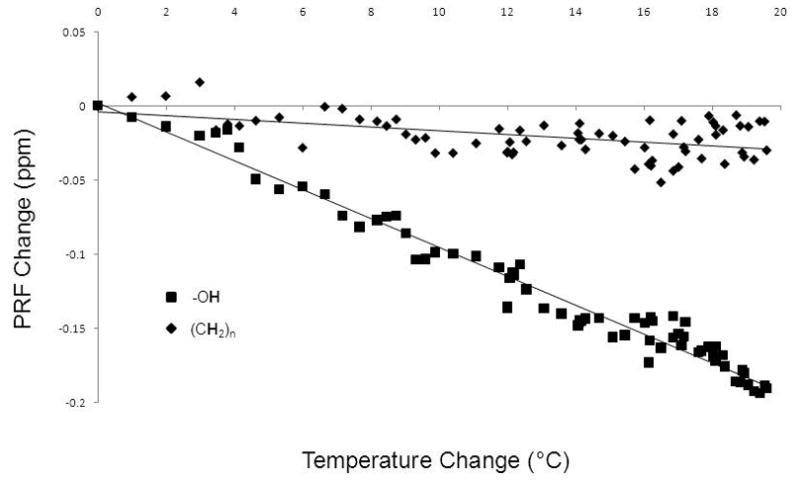
Temperature calibration curves for one calibration at 1.5T (Temperature Range (37.4–57.0 °C). The temperature sensitivity coefficients (TSCs) of the water (squares) and lipid (diamonds) PRFs were -0.98x10⁻² ± 1.3x10⁻⁴ ppm/°C (R²=0.969) and −0.12x10⁻² ± 1.1x10⁻⁴ ppm/°C (R²=0.440), respectively. By taking the difference of the two PRFs as a function of temperature, the TSC was −0.85x10⁻² ± 3.2x10⁻⁴ ppm/°C (R²=0.920).

The temperature measurements from the CSI technique compared to the temperature calculated by the fluoroptic probe in calibration 1 are shown in figure 3. The slopes of the regression lines for the water-bulk methylene temperature readings and the water PRF were 1.00 ± 0.02 ppm/°C (R²=0.987) and 0.99 ± 0.07 ppm/°C (R²=0.942) with intercepts at 0.03°C and 1.01°C, respectively. For comparison, the solid line shown has a slope of unity. If the difference in the water PRF alone was used for temperature monitoring, it would tend to overestimate the temperature when compared to the fluoroptic probe (p<0.001).

Figure 3.

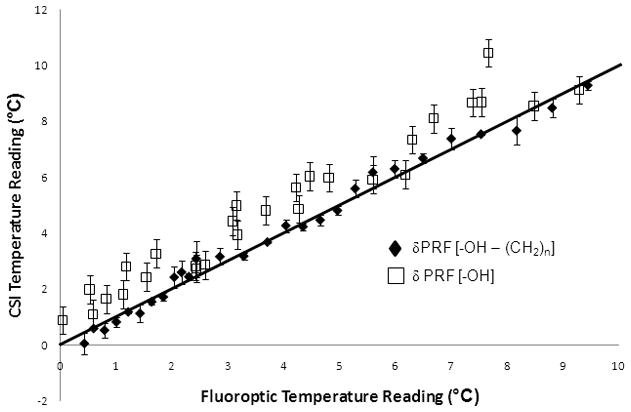
The temperature measurements from the CSI technique compared to the true temperature calculated by the fluoroptic probe. The RMSE for the susceptibility-corrected temperature readings and the water PRF readings were 0.393 °C and 1.031 °C. The slopes of the regression lines for the water-lipid temperature readings and the water PRF 0.999 (R²=0.987) and 0.988 (R²=0.942) with intercepts at 0.030°C and 1.014°C, respectively. For comparison, the line shown in the figure has a slope of unity.

The measured uncertainties in the spectral parameter estimations made using the 2-peak model at 1.5T are summarized in Table 2. Values in parentheses are the calculated theoretical uncertainty for the acquisition provided by the CRLB. The measured uncertainties agree with the CRLB at the 95% confidence interval. Using the calculated TSC values, the temperature uncertainty was calculated as 0.58 ± 0.09 °C when the difference of the water and lipid PRF values was used for temperature measurements. Comparably, the uncertainty in the CPD was measured as 1.46 ± 0.19°C using the echo from the acquisition with the least uncertainty (TE=14.8 ms).

Table 2.

Measured uncertainties in the estimated spectral parameters at 1.5T

Parameter	Water (CRLB)	Bulk Methylene (CRLB)
PRF (ppm)	0.00355 ± 0.00054 (0.004)	0.00191±0.00035 (0.0021)
T2* (ms)	2.27 ± 0.51 (2.22)	0.48 ± 0.14 (0.57)
Amplitude (CoV)	0.023 ± 0.009 (0.018)	0.017 ± 0.004 (0.015)

The mean spectral parameter estimations measured at 3.0T resulting from application of a 4-peak model are also summarized in Table 3 (27,28). The TSCs of these peaks are shown in Table 4 (19,26) over a temperature range of 18.4 to 57.2 °C. As with the 1.5T calibrations, the water-bulk methylene TSC was statistically the same (p=0.11). Using the TSC of the difference in the water and bulk methylene PRF, the RMSE compared to the fluoroptic probe were 0.19 °C and 0.59 °C for the two calibrations. Using CPD with a TE of 9.1 ms, the RMSE was 1.89 °C. The noise in the temperature estimates using bulk methylene as an internal reference is measured at 0.78 ± 0.08 °C. The noise in the temperature estimates were higher (2.87 ± 0.05 °C and 3.21 ± 1.12 °C) when using the lower SNR terminal methylene and methyl protons, respectively, as internal references. Using the mean of all three lipid peaks as a reference, the uncertainty was lower at 1.00 ± 0.02 °C. Using the water peak only with its measured TSC, uncertainty was 0.91 ± 0.38 °C. Uncertainty in the CPD was measured as 1.93 ± 0.70°C using the echo with the least uncertainty (TE=9.1 ms).

Table 3.

Measured PRF, T2* and amplitude values using a four-peak model

Chemical Shift	PRF (ppm)	T2* (ms)	Amplitude (Normalized)
Water	4.686 ± 0.009	56.2 ± 8.9	0.575 ± 0.054
Bulk Methylene	1.186 ± 0.007	9.5 ± 0.2	1.000 ± 0.014
Terminal Methylene	2.029 ± 0.004	3.6 ± 0.4	0.297 ± 0.014
Methyl	0.863 ± 0.015	18.1 ± 0.7	0.369 ± 0.062

Table 4.

Measured PRF temperature sensitivity coefficients from the multiple protons at 3.0T

Chemical Shift	TSC [ppm/°C] (R2)
Water	−1.03 × 10−2 ± 1.4 × 10−4 (0.978)	−1.28 × 10−2 ± 2.3 × 10−4 (0.981)
Bulk Methylene	−0.15 × 10−2 ± 0.9 × 10−4 (0.904)	−0.42 × 10−2 ± 3.1 × 10−4 (0.972)
Terminal Methylene	−0.19 × 10−2 ± 2.7 × 10−4 (0.211)	−0.44 × 10−2 ± 4.4 × 10−4 (0.487)
Methyl	−0.70 × 10−2 ± 3.1 × 10−4 (0.618)	−0.84 × 10−2 ± 4.7 × 10−4 (0.816)
Difference	−0.88 × 10−2 ± 3.0 × 10−4 (0.917)	−0.86 × 10−2 ± 2.3 × 10−4 (0.964)

Maps of the estimated spectral values at 3.0T during heating with an external laser through cortical bone are shown in Figure 4. The temperature changes during the ablation using the bulk methylene as the internal reference are shown (Fig. 4a) as are the differences in water T₂* (Fig. 4b) and water amplitude (Fig. 4c). For better visualization, images for the T₂* and amplitude changes were inverted to show positive contrast in areas of decreasing signal. The T₁-W image at the same time point (110 seconds into treatment) is shown in (Fig. 4d) for reference.

Figure 4.

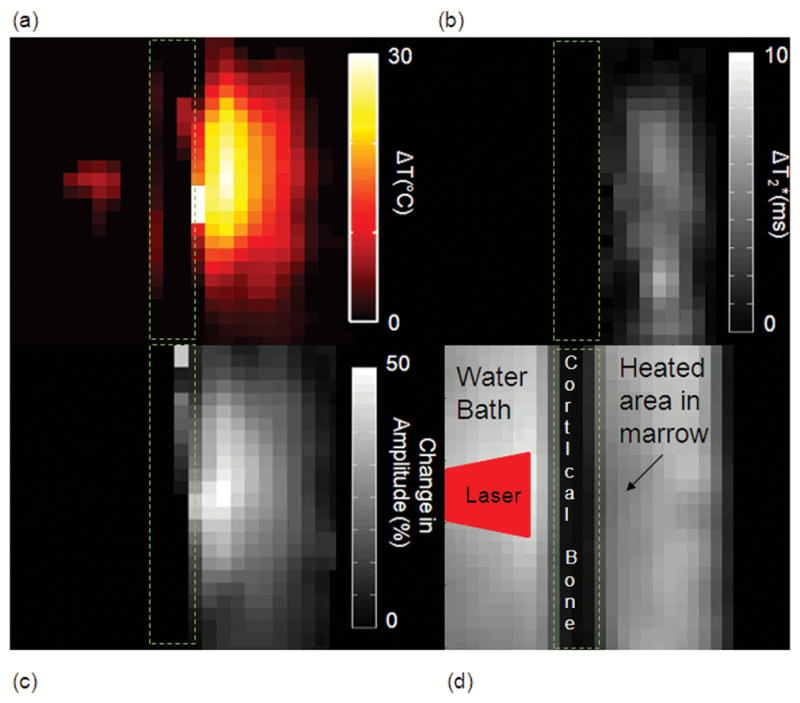
(Fig. 4a) Temperature map of the external laser ablation at 3.0T using the bulk methylene as the internal reference. This map is at 110 seconds into treatment. Cumulative difference in the water T2* (Fig. 4b) and amplitude (Fig. 4c) at the same time point. These two images were inverted to show positive contrast to decreasing signal (Fig. 4d) The T1-W image at the same time point shows a signal hypointensity at the site of heating. The location of the laser beam is also illustrated.

The R₂* and signal amplitude of water and each lipid in bone marrow were plotted along with the Arrhenius rate estimate for irreversible tissue damage as a function of temperature in figure 5. The slopes of these plots are shown in table 5. The water and lipid R₂* and amplitude plots show regions of linearity, but there were points where a marked shift in linearity was observed and a slope polarity shift at approximately 54 °C where Ω ≥ 1.0.

Figure 5.

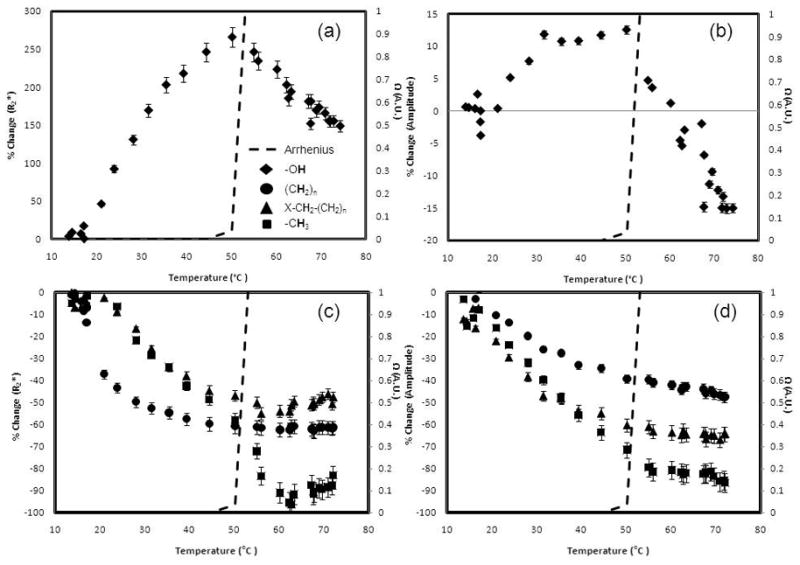
The water R₂* (Fig. 5a) and amplitude (Fig. 5b) as well as the lipid R₂* (Fig. 5c) and amplitude (Fig. 5d) at 3.0T. The dashed line in each plot represents the Arrhenius dose model calculation (A: 3.1 x 10⁹⁸ s^−1, E_a: 6.3 x 10⁵ J mol⁻¹) (23). Changes in the slope can be seen when the Arrhenius dose, Ω, approaches 1.0, which signifies damage to the tissue.

Table 5.

Linear regression slopes at a temperature range of 17.2to 72.0 °C

	R2* (%/°C) (R2) Ω<1.0	Ω ≥ 1.0	Amplitude (%/°C) (R2) Ω<1.0	Ω ≥ 1.0
Water	6.7 ± 0.4 (0.956)	−4.3 ± 0.2 (0.907)**	0.4 ± 0.1 (0.773)	−1.1 ± 0.2 (0.830) **
Bulk Methylene	−1.4 ± 0.1 (0.741)	8.0e-5 ± 0.1 (0.080)**	−0.6 ± 0.2 (0.943)	−0.4 ± 0.1 (0.932)
Terminal Methylene	−1.6 ± 0.2 (0.940)	0.5 ± 0.3 (0.789)**	−0.7 ± 0.1 (0.934)	−0.2 ± 0.2 (0.609)
Methyl	−1.9 ± 0.1 (0.972)	−0.5 ± 0.2 (0.088)**	−1.7 ± 0.2 (0.993)	−0.4 ± 0.2 (0.709) *

^*p<0.05,

^**p<0.001 compared to slope at Ω<1.0

Similarly, the T₁-W signal measurements of water provided by the MGE acquisition was measured as a function of temperature. The overall slope was −0.8 ± 7.4e–3 %/°C (R²=0.987). However, as seen in the R₂* measurements, there are shifts in the slope at approximately 54 °C. During heating, the slope between 17 °C and 54 °C was −0.7 ± 2.9e–2 %/°C (R²=0.977). At 54 °C and above, the slope was −1.0 ± 3.4e–2 %/°C (R²=0.964). The slopes were statistically different (p<0.001). A hysteresis effect was observed during cooling of the marrow. During cooling, the temperature response at temperatures above 54 °C was −5.8 ± 3.6e-2 %/°C (R²=0.978). Below 54 °C the slope was −5.0 ± 1.6e–1 %/°C (R²=0.924). These slopes were statistically different (p<0.001) when heating and cooling curves were compared in the temperature ranges.

DISCUSSION

We investigated changes in spectral parameters acquired during the heating of bone marrow with the use of a fast chemical shift imaging technique. Temperature dependent changes in the chemical shift, R₂* relaxation and signal amplitudes of water, bulk methylene, terminal methylene and methyl groups were measured in real-time during heating with a 980-nm laser source in ex vivo canine tissue. While thermal therapies were performed only in tissues containing yellow marrow in this study, our work could be extended to tissues which contain predominantly red marrow such as vertebral bodies.

In calibration experiments at 1.5T and 3.0T, PRF TSC values consistent with previous studies (19,26,29) were observed when the difference between the water and bulk methylene PRFs are used for temperature estimation. Pure water has a measured TSC of -0.01 ppm/°C (12). In fatty tissue, De Poorter et al (29) measured an overall TSC of −0.0097 ppm/°C with a susceptibility constant of −0.0013 ppm/°C giving a corrected field shift of −0.0088 ppm/°C, which is consistent with results reported here. McDannold et al (26) and Taylor et al (19) measured similar TSC values in a mayonnaise-lemon juice phantom. As expected, using water PRF shift alone did not result in consistent temperature sensitivities due to varying degrees of susceptibility and drift between experiments. For example, at 3.0T the water PRF was highly linear with temperature (R²=0.981). However, its TSC was approximately 15–19% higher in one calibration than what was seen at 1.5T. When the difference between the water and bulk methylene is taken to effect to correct for susceptibility, the TSC is −0.0086 ± 0.0002 ppm/°C, within the 95% confidence interval of the measurements taken at 1.5T. Using the measured TSC by taking the difference between water and bulk methylene protons, we measured accurate temperature readings in each experiment (0.96 °C, 0.39 °C, and 0.54 °C at 1.5T; 0.19 °C and 0.59 °C at 3.0T). It is important to note that this susceptibility effect on the temperature sensitivity of lipid containing tissue is independent of whether or not lipids are suppressed. In addition, although the RMSE and uncertainty were lower compared to single-echo CPD, one could reduce the acquisition time and/or bandwidth (to increase SNR) to improve accuracy and precision with CPD techniques. This would not, however, account for susceptibility or field drift effects which were seen in the water PRF measurements in this study.

To the authors’ knowledge, no MR thermometry study has investigated the temperature sensitivity of multiple lipid peaks simultaneously with this level of spatiotemporal resolution. It was found that although the terminal methylene peaks and methyl peaks could be resolved at 1.5T, the uncertainty was on the order of 0.03–0.08 ppm making calibrations difficult to ascertain with confidence. At 3.0T, each of the four peaks had sufficient SNR and spectral resolution for precise measurements so that the temperature dependence of each component of the lipid peak could be analyzed. For the use of lipid for an internal, temperature independent, reference, highest accuracy and precision was demonstrated with bulk methylene for PRF-based reference thermometry. This was primarily due to a smaller uncertainty in the measurement and is likely due to the higher SNR of bulk methylene compared to the other lipid protons. This technique and PRESS both showed the chemical shifts that are expected in bone marrow in vivo but some degradation is possible in the time between necropsy and imaging. Therefore, more validation studies in vivo are needed to investigate temperature dependencies of these chemical species in order to apply them to monitoring and verification of treatment effects.

In many bone lesions, the primary component will be water, especially in the center of the lesion. If no lipid is present, we expect high precision with temperature measurements as seen in previous studies in non-lipid tissue (19,20). However, toward the borders of the lesion voxels will contain lipid from the marrow. It is important that lipid is taken account for in order to accurately measure the temperature, identify the borders of the ablative region, and verify if the entire lesion received an adequate thermal dose. Also, extrapolating the lipid field map into the lesion, much like what has been done with referenceless thermometry (30), could possibly be performed to improve temperature estimates in bone lesions and warrants investigation.

With this fast CSI technique, other parameters (peak-specific R₂* and T1-weighted amplitude) can also be measured to provide an important opportunity to look at changes as a function of temperature. It is important to note that we did not see changes in linearity in the PRF at high temperatures (see figure 2), which is consistent to previous studies where high linearity was found up to 80 °C (16). In this analysis, we did see changes in linearity of the R₂* and amplitude signal during heating and a hysteresis effect during cooling, similar to what has been observed in other tissues (31,32). We’ve noted significant changes in the temperature dependence of these parameters in the range where the Arrhenius rate model predicts damage (22,23) thereby demonstrating that it could be a useful dosimetry tool for bone ablations. For example, when the temperature history results in Ω ≥ 1, there was a consistent, sharp, measureable change in the slope of the R₂* versus temperature. Differential scanning calorimetry (DSC) studies have shown that bone marrow proteins like thrombopoietin undergoes denaturation at approximately these same temperatures (33). The molecular mechanisms for these changes are not exactly clear and understanding the relationship between the dynamics and structure of proteins and the surrounding water is a current challenge (34). Possible theories to these changes due to the protein denaturation include the change in the dipolar coupling between water molecules and denatured proteins (35). Additionally, release of water in the hydration layers of the denaturing proteins may explain the decrease in R₂* (34).

Water and lipid R₂*-corrected amplitudes also exhibited similar non-linearities in the same temperature ranges as seen in Fig.5(c) and (d). These changes were more evident than measuring changes in the overall T₁-W signal (from the first echo of the acquisition), which has also been shown here and previously to be non-linear with temperature in this range, presumably due to irreversible protein conformation changes (31). It is important to note that these changes in slopes were seen with and without R₂* correction over physiologically relevant temperatures (37 °C and above).

Therefore, it appears that using the multiparametric spectral estimates may return information on physical tissue changes taking place, such as conformational phase transitions of proteins, which directly influence the proton chemical macroenvironment and, thereby, relaxation as observed in R₂* mapping and T₁-W signal changes. This work is currently being extended to other ex vivo tissue samples, such as brain, liver, prostate and kidney, with similar results and in vivo studies planned. These observations warrant further investigation in vivo and in other tissue, particularly in the presence of heat sensitization agents which might be used to lower the therapeutic window as direct validation of protein denaturation and it may be extremely useful in the investigation of thermal approaches to ablation as well as drug delivery or enzyme activation.

In conclusion, high spatiotemporal resolution measurements of PRF shifts, R₂* and T1-W amplitudes of multiple chemical species were made during real-time during heating of bone marrow. Calibration experiments demonstrated that the temperature insensitive lipid PRFs, such as the bulk methylene peak, can be used to reliably correct for changes induced by B₀ shifts during heating and provide more accurate temperature imaging. Using bulk methylene as an internal reference, the TSC values were −0.87 × 10⁻²±4.7 × 10⁻⁴ ppm/°C and −0.87 × 10⁻²±4.0 ×10⁻⁴ ppm/°C for 1.5T and 3.0T, respectively, and are consistent to published values (19,26,29). Multiple lipid peaks can be resolved, and measurements indicate that the higher SNR peaks provide the least uncertainty for temperature estimation. R₂* and amplitudes, which were simultaneously measured, were non-linear with temperature, and their response to temperature changed significantly (p<0.001) when protein denaturation was predicted using Arrhenius rate model analysis.