Study of Biomechanics of Porous Coated Root Form Implant Using Overdenture Attachment: A 3D FEA

Abstract

The purpose of this article is to do a three-dimensional finite element stress analysis, in relation to root form implant supported by overdenture attachment, during axial and non-axial loading. Two porous coated Titanium–aluminum–vanadium (Ti–6Al–4V) implants with overdenture abutment were embedded in both simple and 3D model of interforaminal region of mandible. The material properties of tissue ingrowth bonded interface were calculated considering Iso-Strain condition. The masticatory forces: axial load of 35 N, a horizontal load of 10 N, and an oblique load of 120 N, was applied for the two qualities of cancellous bone. It implied that porous topography of the implant led to optimal stress transfer at the tissue ingrowth bonded interface and insignificant punching stress at the apex than a smooth surface implant. The inferior bone quality was deformed even under physiologic loads and showed wider stress pattern. Simulated implant abutment to implant bone interface stress may be significantly affected by the quality of the bone and the surface topography of the implant. The interface is affected to a lesser extent by the prosthetic material properties. Threedimensional anatomical model was more close to reality than the geometry of much simpler altered models.

Introduction

Edentulousness is more prevalent in people with advancing age. Different treatment options recommended for increasing retention of mandibular denture include ridge augmentation, vestibuloplasty or placement of dental implants [1] for anchorage. Fewer implants with a removable prosthesis offer a less complex, less expensive and thus readily acceptable option for an edentulous patient. Consequently, Implant supported removable prosthesis has gained significant psychologic acceptance [2–9].

The masticatory forces induce axial forces and bending moments, which could result in stress on the implant as well as on the bone. Stresses beyond the optimum range will compromise the longevity of the implant. Also the changes that occur in the trabecular pattern [10, 11] of aged bone make bone quality [12] the major factor to be considered for the long-term success of implant.

Conventional analytical techniques for solving stress take longer time in modifications of the model and evaluation of the internal structure of the bone. Hence, a more recently developed technique called Finite Element Method [13–15] has been used. It is a high experimental dispersion that suggests a numerical approach for mechanical analysis of the biological system, which can be applied with a suitable degree of reliability and accuracy, but without the risk and expense of implantation in vivo.

The interface material [16] properties may lead to better homogenization of stress in the peri-implant compact and cancellous bones. A porous coated implant surface [17–20] was taken to study the biomechanical aspects compared to smooth surface. A three dimensional anatomical model of the mandible probably gives a closer representation of stress behaviour and may act as theoretically superior tool when compared to simpler two or three dimensional models.

Therefore, the objectives of this study were to study the biomechanical aspects of porous coated implants under different masticatory loads, by varying the cancellous bone quality. This was performed on a three-dimensional anatomical model of mandible, which was evaluated with respect to simpler two-dimensional and three-dimensional models.

Materials and Methods

A three-dimensional model of the interforaminal region of edentulous mandible was constructed from Computerized tomographic images of a human skull. It was converted into three-dimensional solid model (Fig. 1a, b) using CAD/CAM software [14, 21, 22]. The other simplified 3-D model was also designed for comparative analysis.

Fig. 1.

a Super imposing of cortical bone over the cancellous bone. b Three-Dimensional Solid Model of the interforaminal region of edentulous mandible

Implants and abutments with superstructure (the Dalla Bona attachment) were modeled on a computer (Software Pentium IV, Best Engineering Solutions, Bangalore) within the limitations of this study (Fig. 2) using a finite element program (ANSYS Version 8.0, Bangalore).

Fig. 2.

FEM model of Dalla Bona attachment along with implant

Two solitary Titanium–aluminum–vanadium (Ti–6Al–4V) [23–25] implants [3] were embedded at a distance of 13 mm from the midline [26]. These were commercially available as Endopore implants (EndoPore^TM) [17, 27, 28]. They were of 12 mm in length [29] and 4.1 mm in diameter with 5º taper [18, 28] and the root portion was 10 mm long. The surface of the implant was designed with a porous coating [23, 24] consisting of two to three layers of micro spheres. These spherical particles have an average diameter of 100 μm and a porous coating of 300 μm thickness [17, 30] amenable to bone tissue-ingrowth [23]. A row of thin interface elements was placed between the porous root and the bone to model the tissue-ingrowth bonded interface (Fig. 3). The interface element was assumed to be a rectangular cantilever beam of uniform dimension in the model [16, 19, 20].

Fig. 3.

Tissue ingrowth bonded interface placed between the porous root and the bone

The mucosa of uniform thickness of 2 mm over the cortical bone and the mandibular overdenture [5, 31] (acrylic) was designed to fit the model on a simplified three-dimensional model (Fig. 4) to abridge the analysis.

Fig. 4.

Simplified three-dimensional model showing mucosa and mandibular overdenture

Elements and Nodes

The three-dimensional finite element model corresponding to the geometric model was generated using Ansys’s Pre-Processor.

Default element size with SOLID 187 element [32, 33] was selected. It was a higher order three-dimensional 10-node element with a quadratic displacement behavior (Fig. 5). The element was defined as 10 nodes having three degrees of freedom at each node: translations in the nodal x, y, and z directions. The elements were constructed so that their size aspect ratio would yield reasonable solution accuracy. The completed anatomical model consisted of total a number of 130,956 nodes and 93,444 elements (Fig. 6) with 391,903 degree of freedoms.

Fig. 5.

Three-dimensional 10-node element with a quadratic displacement behavior (SOLID 187 element)

Fig. 6.

Anatomical three dimensional finite element model with meshing

Material Properties

All the vital tissues (cortical bone, cancellous bone and mucosa), implant with superstructure and acrylic resin were presumed to be linearly elastic, homogenous and isotropic [25, 34, 35].

The mechanical properties of the interface material (bone tissue ingrown into porous implant surface) were mathematically calculated, assuming it to be a composite of Young’s modulus of different materials such as the titanium alloy and bone. The Young’s modulus of the whole system as composite is calculated considering an Iso-Strain condition [36] to be 56,450 MPa for Type I and 54,450 MPa for Type II cancellous bone. The Young’s modulus of the composite is derived in terms of the elastic modulus and the volume fraction of the implant and bone. The load on the composite is equal to the sum of the load on the implant and the load on the bone.

Therefore,

where, P_C = load on the composite, P_I = load on the implant, P_B = load on bone

We have,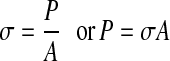

where, σ = stress, P = load, A = area.

Finally, we get the following equation…

where, E_c = Young’s Modulus of composite, E_b = Young’s Modulus of bone, E_i = Young’s Modulus of implant.

The corresponding elastic properties such as Young’s Modulus (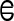) and Poisson’s ratio (δ) of cortical bone, cancellous bone and implant were determined (according to literature survey [11, 37, 38] as shown in Table 1).

Table 1.

Material properties

Material	Young’s Modulus (MPa)	Poisson’s ratio
Cortical bone [11]	26600	0.30
Cancellous bone [38]
Type I	9500	0.30
Type II	5500	0.30
Implant (titanium alloy) [37]	110000	0.35
Interface [16, 19]
Model I (cancellous bone Type I)	56450	0.35
Model II (cancellous bone Type II)	54450	0.35
Acrylic [37]	3000	0.35
Mucosa [37]	1	0.37

Boundary Conditions

Symmetrical boundary conditions were imposed at the mid symphyseal region since only half of the mandible was modeled. On the distal side, all the three translations were fixed [15] (Fig. 7) indicated by light blue colour.

Fig. 7.

Boundary conditions indicated in light blue colour and applied loading conditions shown in red colour

Loading Conditions

In the present study, the magnitude and the directions of the bite forces were derived from the studies [25] and grouping of models was done as shown in Table 2.

• Vertical load of 35 N applied over the abutment.

• Horizontal load of 10 N applied at 0° over the abutment in labiolingual direction indicated by red colour.

• Oblique load of 70 N applied at 120° to the occlusal plane on the abutment from linguo-labial direction (Fig. 7) indicated by red colour to imitate the same forces as applied by the muscles of mastication [39].

Table 2.

Grouping of models based on quality of cancellous bone

	Model (A)	Model (B)	Model (C)
Directions	Vertical (90°)	Horizontal (0°)	Oblique (120°)
Forces	35 N	10 N	70 N
Bone quality	Type I	Type I	Type I
	Type II	Type II	Type II

Analysis of Stress Pattern

A total of three models were made and grouped into three for the ease of analysis.

These different models were analysed by Processor and displayed by Post-Processor of the Finite Element Software (Ansys, version 8.0) using Von Mises Stress Analysis [25, 34, 40].

Results

The results of the tracing of Von Mises stress field were in the form of color-coded bands. Each color band represents a particular range of stress value, which was given in Mega Pascals and the strain values of cancellous bone in microns.

The stress distribution was virtually identical in both bone models except the magnitude and extent was more dominant in type II bone model. A slight difference in the stress concentration was seen under horizontal (mesiobuccal and buccal aspect of the implant) and oblique (buccal plate) loading. The maximum stress was mainly concentrated in the upper half of the implant (mainly at the neck of the attachment) and minimum or no stress was found at the apex (from Tables 3, 4, 5, 6, 7, 8).

Table 3.

Overall, Von Mises stress in the anatomical model with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	12.272	12.292
Horizontal forces 10 N (Model B)	25.888	28.401
Oblique forces 70 N (Model C)	130.54	131.731

Table 4.

Von Mises stress in the cortical bone with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	4.496	5.371
Horizontal forces 10 N (Model B)	16.343	14.46
Oblique forces 70 N (Model C)	82.639	83.505

Table 5.

Von Mises stress in the cancellous bone with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	0.725284	0.5955
Horizontal forces 10 N (Model B)	0.624	0.4400
Oblique forces 70 N (Model C)	3.358	2.374

Table 6.

Maximum strain in the cancellous bone with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	7.7 × 10−5	1.11 × 10−4
Horizontal forces 10 N (Model B)	6.5 × 10−5	8.01 × 10−5
Oblique forces 70 N (Model C)	3.5 × 10−4	4.32 × 10−4

Table 7.

Von Mises stress on interface (bone-implant) with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	2.106	2.741
Horizontal forces 10 N (Model B)	2.615	2.453
Oblique forces 70 N (Model C)	11.78	11.73

Table 8.

Von Mises stress in the implant with different masticatory forces

Forces	Type I	Type II
Vertical forces 35 N (Model A)	12.272	12.292
Horizontal forces 10 N (Model B)	22.629	23.909
Oblique forces 70 N (Model C)	121.44	121.5

Irrespective of the direction of loading, strain in the cancellous bone was maximum in the poor bone quality model i.e. Type II bone quality. The strain in the cancellous bone was found to be maximum during oblique loading and minimum during horizontal loading (Table 6).

Maximum stress was developed at the interface corresponded to the area where maximum strain was developed in the cancellous bone irrespective of the bone quality. The magnitude of the stress is shown in the Table 7.

Discussion

Many implant designs have been introduced to overcome biomechanical deficits [14, 41, 42]. A new implant design with rough surface topography has been introduced and is considered to maximize the stress transfer homogenization along the bone–implant interface. Therefore, surface roughness of the implant has been taken as a parameter for the study. Also the quality of cancellous bone is supposed to play a major role in success of osseointegration. For that reason the stress and strain in the bone of different quality were investigated.

In 2-D FEA [43] method it was not possible to study, horizontal or oblique bite forces. Therefore, for valid representation of clinical situation [15], a 3-D FEA method was used. Also, some assumptions were made in geometric considerations, material properties, boundary conditions and the bone–implant interface to make the modeling and solving process possible [13]. Henceforth, some parameters were evaluated on a comparatively simpler 3D model. The stress on mucosa and overdenture was found to be insignificant, hence were not considered. The male and female parts of the attachment were one solid structure. Therefore, the loads were directly transferred from superstructure to the implant and did not influence the results of study [44]. The ramus and the condyles of the mandible were also substructured as done in many other studies Meijer et al. [15, 30].

The accuracy of the results decreased with the increase in element size. However, for this study, the gradual increase in element size protected the area of interest from being affected by the inaccuracies of the stresses in large elements. The acceptable percentage of error for FEA model should be less than 3% and here it was 0.3%. The results of this analysis concur with findings of other studies that have used different investigation methods. Therefore, the model employed in this study was considered to satisfactorily simulate reality. It was advisable to focus on qualitative comparison rather than quantitative data.

Material Properties

Material properties and their structural basis help us to understand the bone quality type and influence the stress and strain distribution. The cortical bone was modeled isotropically [40, 45] due to difficulty in establishing the principal axis of anisotropy. Schwartz et al. [44] reported that the cortical bone density following edentulousness was maintained. Therefore, in all the models, modulus of elasticity for cortical bone was not varied and was assumed to be 26.6 GPa.

The elastic modulus of a bone sturdily depends on the apparent density or porosity of the tissue. Many authors [10, 12, 46] have shown that with edentulism the inner trabecular pattern changes from the well-oriented course to a thin, randomly arranged trabecular form having little calcified matrix and many large marrow vascular spaces. The quality of the cancellous bone strongly influences implant displacement, which increases as bone rigidity decreases. Thus, Young’s modulus of cancellous bone was changed to evaluate its influence on the stress/strain in bone and implant. Two types of the cancellous bone quality have been taken into account, that is, Type I and Type II (as per classification by Lekholm and Zarb) [5, 25] Young’s moduli of cancellous bone were selected from the study of Rho and associates [38] as follows: the values for bone Type I and bone Type II are 9.5 and 5.5 GPa, respectively. The mean trabecular Young’s modulus was significantly less than that of cortical bone.

The Bone–Implant Interface

The surface topography of an implant influences the bone–implant interface sequentially osseointegration. The porous topography forms the three dimensional mechanical interlock resulting from bone ingrowth, provides for optimal stress transfer at the bone–biomaterial interface, predictable and minimal crestal bone loss and superior resistance to torsional forces. According to studies conducted by Cook et al. [16], implant with tissue ingrowth-bonded interface shows a better stress distribution Cochran [41] demonstrated that a rough implant surface have increased bone-to-implant contact and require greater forces to break bone-to-implant interface and were more successful as compared to smooth surface.

The thin shell of cortical bone that surrounds the natural tooth root withstands the functional load and the periodontal membrane distributes it uniformly. Weinstein [20] reported that the assumption of a direct bone-to-implant interface (i.e., an ankylosed implant) might not be a good representation for a porous rooted implant retained by bone ingrowth. In this study, the Ti–6Al–4V porous coated implant has been modelled, with a tissue ingrowth-bonded interface between the bone and implant, to simulate the function of periodontal membrane and to achieve osseointegration.

Loading Conditions

In this study, three different masticatory forces were applied that simulated situation found in vivo to which an overdenture wearer had been subjected [15, 30, 39]. The muscle forces were static in lieu of dynamic forces in the models that is unlikely to happen in reality. Nevertheless, the clinician must extrapolate these results to clinical situations.

Cortical Bone Stress

The cortical bone was the load-carrying member for both bone models (Fig. 8). This could be the probable reason for the highest stress concentration around the implant neck, which was also found in many 3D-Finite element analyses [25, 37].

Fig. 8.

Von Mises stresses in complete model

The highest magnitude of the stress was seen in relation to horizontal forces that could be related to the larger magnitude of oblique loads. The lowest amount of stress was with axial loads, as the load was applied parallel to the long axis of the implant.

Cancellous Bone Stress and Strain

Young’s modulus was set constant for cortical bone in all the models and differed for cancellous bone. Therefore, if the same load is applied, cancellous bone will show the same stress pattern, but the value of strain will vary. The probable reason is that as the density of bone decreases, the overall micro strain increases for the same load. To have better understanding of biomechanical behaviour, equivalent strains were considered for cancellous bone.

Higher the Young’s modulus more is the stiffness; more will be the stress in the bone, which is found in Type I .The probable reason for lower stress and greater strains in Type II could be attributed to its lower elastic modulus.

Correlation between Bone–Implant Interface Equivalent Stress and Bone Quality

The softer cancellous bone withstood the axial load less efficiently and was remarkably displaced downwards. Thus, high or moderate stress was found over the bone–implant interface during axial loading .While during non-axial loading, higher strain and lesser stress in the bone were developed which could be because of lower Young’s modulus of Type II model, compared to Type I model.

Implant-Abutment Stress

The implant and attachment had highest elastic modulus so most of the stress was located at the junction of the ball with the rest of the abutment as it is the narrowest portion in cross-sectional diameter. It varied with the direction and magnitude of loads. When non-axial loads were applied, implant bending occurred; probable reason could be that a reduced portion of the supporting bone is involved in counteracting that load, leading to maximum stress levels in the implant [47]. Under axial loads minimum stress was found, similar to the stress pattern in cortical bone.

The stress concentration at the apex of the implant (Fig. 9) was insignificant, and showed gradual distribution of the load from the top to the mid-region of the implant and minimal to the apex. The reason for this could be the presence of tissue ingrowth bonded interface that contributed for more stress transfer homogenization unlikely to smooth surface implant where the interface is rigid. It found to produce high levels of punching stress, concentrated mainly in the neck and the apex of implant.

Fig. 9.

Von Mises stress in implant

Finite Element Analysis [48] is based on mathematical calculations; and the living tissues are beyond the confines of set parameters and values. As a matter of fact, actual experimental techniques and clinical trials should follow to establish the true nature of the biologic system and therefore further investigations are required [49].

Conclusion

Based on the limitations of this study the non-axial loads are detrimental irrespective of implant surface topography and should be avoided by careful designing of prostheses or by providing freedom for contact movements between the teeth in the horizontal plane.

The cortical bone plays a major role in the dissipation of the stress. Type-II or inferior bone quality underwent more deformation. Thus, even loading within physiologic limits can lead to slippage of the bond at the interface thereby causing micro-fractures.

Tissue ingrowth bonded interface showed better stress transfer homogenization. The results showed negligible stress at the apex of the implant during axial loading, which concur with the proposed hypotheses. Maximum amount of stress was generated at the site of load application i.e. implant abutment.

Three-dimensional model of the interforaminal region was in better agreement than the geometry of much simpler models. The modeling methodology, conditions of the support and load system, and the anatomic variations played important roles.