A BEHAVIORAL ANALYSIS OF ALTRUISM

Abstract

Altruistic acts have been defined, in economic terms, as “...costly acts that confer economic benefits on other individuals”. In multi-player, one-shot prisoner's dilemma games, a significant number of players behave altruistically; their behavior benefits each of the other players but is costly to them. We consider three potential explanations for such altruism. The first explanation, following a suggestion by the philosopher Derek Parfit, assumes that players devise a strategy to avoid being free-loaders – and that in the present case this strategy dictates cooperation. The second explanation says that cooperators reject the one-shot aspect of the game and behave so as to maximize reward over a series of choices extending beyond the present situation (even though reward is not maximized in the present case). This explanation assumes that people may learn to extend the boundaries of their selves socially (beyond their own skin) as well as temporally (beyond the present moment). We propose a learning mechanism for such behavior analogous to the biological, evolutionary mechanism of group selection. The third explanation assumes that people's altruism is based on a straightforward balancing of undiscounted costs to themselves against discounted benefits to others (social discounting). The three proposed explanations of altruism complement each other.

The object of behavioral analysis is to identify reinforcers of acts. But an individual altruistic act apparently has no reinforcer; if it did, it would not be altruistic. Altruism thus seems to defy behavioral analysis. Altruistic acts have been defined, in economic terms, as “...costly acts that confer economic benefits on other individuals” (Fehr & Fischbacher, 2003). This definition does not say that the cost to the actor and the benefit to others must be equally valued. And, it does not say whether the “other individuals” are relatives of, friends of, or complete strangers to the actor. If you put a dollar in a machine and someone else gets (and eats) the candy bar, your act is altruistic according to the definition above. It may be that few of us would pay a dollar to give a perfect stranger a candy bar but we might very well pay a penny. Or, if the benefit to the stranger were very high (say, he was starving) we might pay a dollar – or even more than a dollar – to give him a candy bar. Or, if the beneficiary were not a stranger but our own child (and we were not at the moment worrying about cavities or obesity), many of us would pay the dollar. Such acts, fitting within Fehr and Fischbacher's (quite reasonable) definition of altruism, are extremely common in everyday life; behavioral analysis cannot just ignore them.

To illustrate how common altruistic behavior is, consider the multi-person prisoner's dilemma game that Rachlin has played with audiences over the last 15 years at public lectures. Let us call it, “the lecture game.” At the start of the lecture game, blank index cards are handed out to 10 random members of the audience and the others are asked (as we ask the reader) to imagine that they had gotten a card. The task of the 10 players is to choose X or Y subject to the following rules (displayed on a slide):

1. If you choose Y you will receive $100 times Z.

2. If you choose X you will receive $100 times Z plus a bonus of $300.

3. Z equals the number (of the 10 players) who choose Y.

The audience is told, regretfully, that the money is purely hypothetical; then several properties of the game are pointed out. First, for any particular player, it is always better to choose X. By choosing X a player subtracts 1 from Z and thereby loses $100 but more than makes up for that loss by the $300 bonus. The net gain for choosing X is therefore $200 regardless of what anyone else chooses. The point is then emphasized further by saying that any lawyer would advise choosing X.

It is noted that if everyone obeyed their lawyers and chose X, Z would equal zero and each person would earn just $300 while if everyone disobeyed their lawyers and chose Y, Z would equal 10 and each person would earn $1,000. Hence the dilemma. It is then pointed out, that there is no right or wrong answer and that all choices will be forever anonymous. The 10 audience members with cards are then asked to mark them with X or Y as they would if the money were real, and the cards are collected.

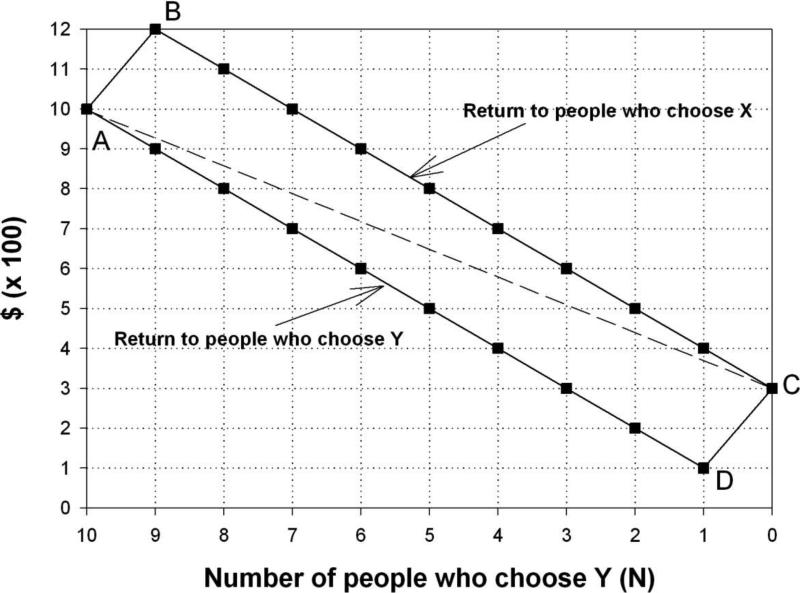
Over the years this game has been played dozens of times: with college students, with philosophers, with economists (American-capitalist and Italian-socialist), and with psychologists (American, Japanese and Polish). The median response is 5 Y's to 5 X's. If there is any bias it is usually in the direction of more Y's than X's. The chart in Figure 1 is then shown to the audience and used to look up the earnings of the X and Y choosers. For example, if 5 of the 10 participants chose Y, Z = 5 and each Y-chooser would get $500 while each X-chooser would get $800. In keeping with standard prisoner's dilemma terminology, an X-choice is called a “defection” and a Y-choice is called a “cooperation.” Although the money earned in the lecture game is hypothetical, laboratory experiments with real money (albeit in lesser amounts) have found significant numbers of cooperations in one-shot, multi-person prisoner's dilemma games such as this one (Camerer, 2003).

Figure 1.

Diagram of multi-person prisoner's dilemma game (lecture game). Lines A-D and B-C show returns to players who choose Y (cooperate) or choose X (defect) as a function of the decreasing number of players (out of 10) who choose Y (note reversed x-axis). The dashed line shows average earnings across the 10 players.

Because a Y-choice always earns $200 less than an X-choice, choosing Y is a “costly act.” Because a Y-choice increases Z by 1, and each of the 9 other players earns $100 more than she would have otherwise, choosing Y “confers economic benefits on other individuals.” Because the choices are completely anonymous, it cannot be claimed that a player's reputation would be enhanced by choosing Y. Thus, according to Fehr and Fischbacher's definition, Y-choices in the lecture game are altruistic. Altruism towards one's family members may be explained in terms of genetic selection, but it is unlikely that any lecture-game players were related. Although there is indeed a bias in altruistic behavior toward relatives over non-relatives (Jones & Rachlin, 2008) numerous instances of altruism in everyday life are directed toward friends, acquaintances and even complete strangers.

The philosopher, Derek Parfit (1984, pp. 61-62) listed a sample of situations from everyday life modeled by multi-person prisoner's dilemma games such as the lecture game:

• Commuters: Each goes faster if he drives, but if all drive each goes slower than if all take busses;

• Soldiers: Each will be safer if he turns and runs, but if all do more will be killed than if none do;

• Fishermen: When the sea is overfished, it can be better for each if he tries to catch more, worse for each if all do;

• Peasants: When the land is overcrowded, it can be better for each if he or she has more children, worse for each if all do....

• There are countless other cases. It can be better for each if he adds to pollution, uses more energy, jumps queues, and breaks agreements; but if all do these things, that can be worse for each than if none do.... In most of these cases the following is true. If each rather than none does what will be better for himself, or his family, or those he loves, this will be worse for everyone.¹

Some of the situations Parfit cites (fishermen, peasants) may be described in terms of Hardin's (1968) “tragedy of the commons” – overuse by individuals of a common resource; all are multi-person prisoner's dilemma games.

Sometimes, depending on circumstances, the lecture game is followed by a discussion (without revealing what anyone actually chose) of why a person should choose Y in this anonymous game. One reason people often give for choosing Y is that they believe that many or most of the other players will choose Y. This rationale is common but not strictly rational. Since the cost of a Y-choice is constant at $200, regardless of what anyone else chooses, what anyone else chooses should, in theory, not influence any person's individual choice. What others choose in this game will indeed have a strong effect on a player's earnings. But, within this one-shot, anonymous game, no player can have any direct influence on another player's choice. It is true that if a person chooses Y she will be better off if all other players chose Y, and she earns $1,000, than if any other player or players had chosen X. But, given that all other players chose Y, she would be still better off if she alone had chosen X and earned $1,200.

Parfit (1984, pp. 100-101) considers choosing Y because you believe that others will choose Y as a rationale for cooperating and makes an appealing suggestion for quantifying this rationale. First, he suggests, determine how much you would earn if all players, including you, defected (chose X); in the lecture game, that would be $300. Then make your best guess of how many other players will probably cooperate (how many would choose Y). Then determine how much you would earn if you also cooperated. If the amount you earned by cooperating is at least as great as the amount you would earn if all players including you defected then, according to Parfit, you should cooperate. In order to earn $300 or more by cooperating in the lecture game, at least 2 other players would also have to cooperate. If you were a player in the lecture game, knowing that about half of the 10 players usually cooperate, and you wanted to follow Parfit's suggestion, you would cooperate. However, as Parfit admits, his suggestion does not resolve the dilemma. If two other lecture-game players chose Y and you also chose Y, you would earn $300 whereas, if you had chosen X, you would have earned $500. Why should you not have chosen X? Although Parfit's suggestion has intuitive appeal, and corresponds to people's verbal rationalizations, it is not a good explanation, in itself, of why people behave altruistically.

A second reason that people may give for choosing Y is simply that choosing Y is altruistic (or good or generous or public-spirited) and they see themselves as altruistic (or good or generous or public-spirited) people. Choosing X would not fit in with their self-image and would make them feel bad about themselves. We believe that this seemingly vacuous reason for cooperating is actually a good reason and worth discussing in some detail. But it is first necessary to outline a behavioral concept of the self – to answer the question: Where does one person end and another begin? Skinner (1969) claimed that the skin is not important as a boundary. We agree with this claim, but for reasons different from Skinner's. Skinner meant that events within the skin are subject to behavioral investigation (Zuriff, 1979). We take Skinner's earlier position that the proper sphere of behavior analysis is the organism as a whole (Skinner, 1938). But we see the organism as extending beyond the skin.

The Extended Self

Parfit (1984) argues for what he calls reductionism (p. 211): “Each person's existence just involves the existence of a brain and body, the doing of certain deeds, the thinking of certain thoughts, the occurrence of certain experiences, and so on.” According to Parfit, individual actions take time and overlap with each other giving us the illusion of a continuous self. But, aside from that overlap, there is no “further thing” – either spiritual or physical – to a person's self. You may have as few interests in common with yourself twenty years from now as you do currently with a distant cousin. A person's continuous character is, according to Parfit, no more (or less) real than the character we ascribe to groups of people such as families, clubs, firms, or nations. He says (p. 211): “Most of us are reductionists about nations....Nations exist. Though nations exist, a nation is not an entity that exists separately, apart from its citizens and its territory.”

If your future self is in principle no closer to your present self than is another person, it follows that there is no essential difference between your relations to your future self and your relations to other people. Since your concern or lack of concern for other people involves moral issues, Parfit says, so does your concern or lack of concern for your future self. Therefore, issues of social cooperation and altruism on the one hand and self-control on the other are treated in the same way. A motorcyclist's refusal to wear a helmet would be, for Parfit, a moral issue, not just because other people may have to pay a price for her brain injury, but also because her future self may have to pay a price.

Parfit's reductionist view of the self would be behavioristic as well, were it not for his supernatural view of the mind. For him, “the thinking of certain thoughts” is akin to William James's “stream of consciousness” (James, 1890). From our teleological-behavioral viewpoint however both “the thinking of certain thoughts” and “the occurrence of certain experiences” are nothing but “the doing of certain deeds.” Thought and experience both may be understood in terms of temporally extended patterns of overt behavior (the doing of deeds). For us, a person's self consists of the temporal extension and overlap of that person's various overt behavioral patterns (Rachlin, 1994, 2010a). In human as well as nonhuman existence, many of those patterns are coordinated with those of others (other brains and bodies). Their overlap – their common interest – extends our selves nearer or further into our society. Just as delay discount functions (value as a function of reward delay) may be said to measure the extension of our selves into the past and future, so social discount functions may be said to measure the extension of our selves into social space (Rachlin & Jones, 2009).

The economist Julian Simon (1995) makes a similar reductionistic claim in economics. According to Simon, people allocate available resources on 3 dimensions:

1. Current consumption by the person;

2. Consumption by the same person at later times (delay discounting);

3. Consumption by other people (social discounting).

According to Simon, “Instead of a one-dimensional maximizing entity, or even the two-dimensional individual who allocates intertemporally, this model envisages a three-dimensional surface with an interpersonal ‘distance’ dimension replacing the concept of altruism” (p. 367, italics ours).

Delay discounting enters normally into economic utility functions and is not considered to be in itself irrational. But the third of Simon's dimensions, consumption by other people, may seem fundamentally different from delay. Economists typically consider the sacrifice of your own well being for that of someone else to be irrational; they consider altruism to be an exception to utility maximization. But such views ignore the dimension of social distance. From Parfit's and Simon's and our own viewpoint, a person who values a benefit to another person at some fraction of a benefit to himself is not acting any less rationally (or more altruistically for that matter) than a person who values a delayed reward at some fraction of a current reward.

We do not know if social and temporal extension (beyond the skin or beyond the present moment) are independently learned or whether one is primary and the other derived. We are aware of no evidence whether social or temporal extensions of the self are primarily learned or primarily innate. The next section will attempt to present a plausible account of how they might be learned based on an inherited tendency to pattern behavior.

Altruism and Evolution

We view the self as extended beyond the present moment into past and future time as well as into social space. Because altruistic behavior is so common and so useful in human society, it seems to us likely that three evolutionary mechanisms (biological, behavioral, and cultural) work together to produce it. Several mechanisms for biological evolution of altruism have been proposed. One relies on the selection of groups of altruistic organisms as units even under conditions where individuals are selected for selfishness (Sober & Wilson, 1998). A group of individuals (say a tribe), within which there is little individual altruism, may be forced to move out of a fertile area and be replaced by another group within which there is a high level of altruism, even though the former tribe may have stronger or more skillful individual members. By analogy, basketball teams where individuals sacrifice their own scoring opportunities for the good of the team may survive and prosper in their leagues even though individuals who score more points are more highly rewarded (in terms of money and glory) than those who score fewer. Mathematical models of group selection show that the crucial factor for group selection is the rate of replacement of groups within the larger population relative to the rate of replacement of individuals within the groups; when groups with a preponderance of selfish individuals die out and are replaced within the population relatively faster than altruistic individuals die out and are replaced within groups, altruism may increase in the population as a whole (Boyd, Gintis, Bowles, & Richerson, 2005).

Evolutionary theorists (for instance, Dawkins, 1989) typically focus on biological and cultural levels of evolution – innate mechanisms and cultural rules. They generally ignore changes of behavior within an organism's lifetime in response to environmental contingencies (behavioral evolution). Where such changes are not ignored they are attributed to inherited developmental processes or simply to rational thought. But learning within an organism's lifetime is as much an evolutionary process as biological and cultural evolution. The analogy between behavioral and biological evolution was pointed out not long after biological evolution was proposed (Thorndike, 1911) and has since been repeated and refined (Staddon & Simmelhag, 1971; Baum, 2005).

Of course, altruistic behavior like all learned behavior depends strongly on biological inheritance. The crucial question is: What is inherited and what may be learned over an organism's lifetime? Some theorists believe that altruistic tendencies may be directly inherited by individuals in successful groups (Sober & Wilson, 1998); others believe that altruistic behavior results from the inheritance of a sense of fairness in allocation of resources (“strong reciprocity”) (Fehr & Fischbacher, 2003). But we believe that organisms may learn to be altruistic with neither an altruistic tendency itself nor an innate sense of fairness. The crucial inherited tendency necessary for the learning of altruism may be a direct sensitivity to the consequences of temporally extended patterns of acts.

Consider some primitive inherited acts. Infants vary their rate of sucking not by altering pauses between individual sucks but by altering pauses between bursts of sucks (Wolff, 1968). That is, we have a natural tendency to group acts into patterns; rats vary their rate of licking at a drinking spout and pigeons vary rates of pecking in a corresponding way (Teitelbaum, 1977). Ethologists have discovered and studied more elaborate “fixed action patterns” in consumption and mating. Such patterns are more or less modifiable over the organism's lifetime by environmental contingencies that select patterns or sequences of acts, not individual movements (Hinde, 1966). Over the lifetime of the organism some patterns are reinforced and may be modified by reinforcement.

As Neuringer and colleagues have shown (Neuringer, 2004), behavioral patterns may be directly shaped by environmental contingencies. For example, Grunow and Neuringer (2002) rewarded rats for different levels of variability in 3-lever sequences of presses. Rats rewarded for high variability emitted highly variable patterns; rats rewarded for low variability emitted more tightly clustered patterns. The rats were then rewarded in addition for a particular, ordinarily rare, sequence. Those rats initially rewarded for very high variability (therefore regularly emitting the initially rare sequence), differentially increased its rate. It was as if the initially rare pattern emerged as a unit from a population of other patterns by a process of differential reinforcement. The environment created by Grunow and Neuringer selected the rewarded sequence just as the natural environment selects the fittest organisms. Over the course of the experiment individual presses on each of the 3 levers were equally reinforced. It is highly unlikely that any sequence could have been learned as a chain of individual presses. This significant experiment and others like it (Neuringer, 2004) show that patterns of responses may be reinforced as whole units.

It is a common finding with humans and nonhumans that although a particular larger-later reward may be preferred to a particular smaller-sooner reward when both are relatively distant, this preference may reverse as time passes and the delay to both rewards decreases; the smaller reward is obtained and the larger is lost. Such reversals are paradigm cases of lack of self-control. Ainslie (2001) calls them “failures of will.” However, if a commitment to the larger reward is made prior to the point of reversal, the larger reward will be obtained (Rachlin & Green, 1972). Siegel and Rachlin (1996) found that commitment need not be absolute. Pigeons that began a sequence of 30 pecks on a key leading to the larger reward kept pecking that key (and obtained the larger reward they originally preferred); they did not switch over to the key leading to the smaller reward at the point in time where its value rose above that of the larger reward. The response pattern, once begun, was continued past the point where preference would have reversed. Siegel and Rachlin call this kind of persistence, “soft-commitment.” In general, in experiments with humans as well as with non-humans, when the contingencies are such that patterning would increase overall reinforcement rate, patterning tends to increase (Rachlin, 1995).

Just as genetic replication creates the variation in structure upon which biological evolution acts, so biological evolution creates the variation in innate behavior patterns upon which behavioral evolution acts. However (just as variation in the structure and nervous systems of organisms is sensitive to environmental conditions and evolves over generations), behavioral variability is itself highly sensitive to environmental contingencies (as Grunow and Neuringer showed).

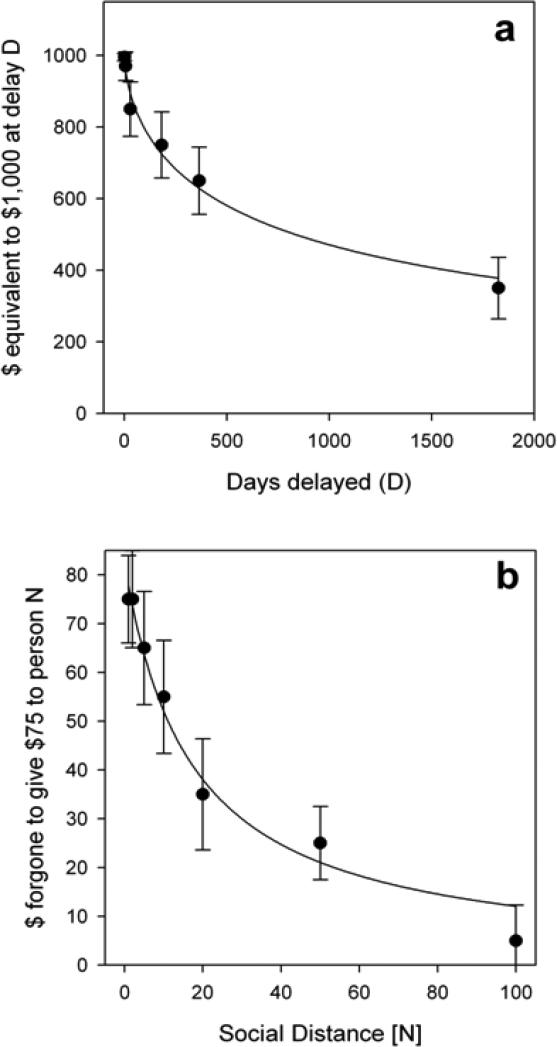
Figure 2a shows a human delay discount function. Such functions are typically obtained by determining an amount of money, to be received immediately, equivalent in value to a larger amount to be received after various delays typically ranging from a day to several years. The functions thus obtained are hyperbolic in form and people differ in the steepness of their individual functions; those who have better self-control have shallower delay discount functions than those who have worse self-control (Madden & Bickel, 2010). But the question arises: What do delay discount functions actually measure? A molecular theory might say that a person's delay discount function reflects some property of that person's nervous system. Of course every act of every organism is ultimately explicable in terms of neural events – just as any motion of any physical object is ultimately explicable in terms of atomic physics. The question for the behaviorist is whether the act may be explained in terms of contingencies between behavior and environment acting over the long term (Rachlin, 2010b). In this regard we point to the fact that the steepness of individuals’ delay discount functions is not fixed; they vary not only between individuals but also within an individual over time (Green et al. 2004), over differing commodities, and over different magnitudes of a single commodity (Raineri & Rachlin, 1993). The underlying attribute of a given act consistent with such variability in steepness of delay discounting is the temporal extent of the pattern or patterns of which the act is a part. When a pattern of consumption is wide, extending over many weeks or months, the delay discount function obtained will be shallow; when a pattern is narrow, delay discounting will be steep.

Figure 2.

a. Delay discount function. Median value of a $1000 reward as a function of delay to the reward's receipt. b. Social discount function. Median value to Person-A of $75 given to Person-B as a function of the social distance between them (B's rank in a list of the 100 socially closest people to A).The error bars are standard errors of the mean.

Older people tend to discount delayed rewards less than do younger people (Green et al., 1994). We believe that as people age they learn to pattern their behavior over a wider and wider temporal extent. The reason they learn this is because the value of wider patterns is generally greater than the value of narrower patterns. This may be the case even when the value of every single narrow component of the wider pattern is less than that of its alternative (Herrnstein & Prelec, 1992). For example, an alcoholic may value a year of sobriety higher than a year of drunkenness but that same alcoholic, drunk or sober, may value having a drink more than refusing it at every instant during the year. The problem is that organizing behavior over a pattern of abstinence that lasts a year is difficult (and organizing behavior into a year-long pattern of social drinking is still more difficult) (Rachlin, 2000). Let us say that the alcoholic has been abstinent for 6 months and is now at a party where drinks are freely available. She then has to put aside her current preference, her current set of values, and behave consistently with the pattern begun 6 months ago. To put it another way, she must learn to respect and cooperate with her past and future selves – and to behave so as to maximize their interests, as a group, even when they conflict with those of her present self. It is in the best interests of her present self to have a drink. In the short run the drink will give her pleasure and in the long run this individual drink will not harm her health or cause her to lose her job or alienate her family. But over her life she may have learned that a pattern of drinking is harmful while a pattern of abstaining (or social drinking) is valuable. She must learn to ignore the rewards and punishers (distant as well as present) of her individual acts and behave so as to maximize the rewards of extended patterns.

Altruism as a Form of Self-Control

Returning to the lecture game, it is important to note that, although it is nominally “one-shot,” there is actually no such thing as a true one-shot game. The concept, “one-shot” implies that an act of choice may occur without a context. It is true that in the lecture game no context is explicitly stated. But no act occurs in a vacuum. All players must have had experience with similar games (see Parfit's list quoted previously). Although choices in the lecture game are anonymous, most such games are not anonymous in real life. Cooperation may be reinforced in the long run by social approval and inclusion as well as by explicit reciprocation. Symmetrically, defection may be punished. A fisherman who consistently overfishes for example is likely to be shunned or otherwise punished by his fellow fishermen if not by society. A person may learn over time to identify games of this type and to cooperate in those games. Why? Because a pattern of cooperation is often reinforced even though individual cooperative acts are not reinforced or may even lead to aversive consequences.

It may not be beneficial in the long run for an individual to attempt fine discriminations between such situations, to divide them into those where cooperation is ultimately reinforced and those where it is not. First, such discriminations may be difficult or time consuming. At every red light you could look around to see if a car is coming on the cross street or whether a police car is present; or you could just stop at all red lights. Most of us just stop – even in the middle of the night at a lonely intersection. It is easier to obey the general rule than to discriminate among such situations.

A second reason to cooperate in any particular case is that even when, in some prisoner's dilemma situations, we have spent time and effort to discriminate, we may have learned to question our best and most considered judgments in the midst of those situations. Because the value of the immediate particular reward for defection is at its maximum at the point of decision, it is likely to blind us to the ultimately higher value of the more abstract and temporally extended reward for cooperation. The alcoholic may have learned that her decisions in the evening at a party or at a local bar often differ, in the direction of having a drink, from her decisions in the morning, at home in the midst of her family, or at work. If she is wise, when she gets to the party, she will disregard her best present judgment of the relative values of the outcomes, especially if it implies choices that break a pattern she has adopted and conformed to in the past. Rachlin (2000) has argued that such attention to “sunk costs,” considered by economists to be an error, is actually the basis, perhaps the main basis, for self-control in everyday human life.²

The lecture-game players who choose Y know that their choices are anonymous but may not discriminate between this game and many other similar games where choices are not anonymous. Just as always stopping at red lights (except in dire emergencies) is the best policy in the long run, always cooperating in real-life prisoner's dilemma games may also be the best policy in the long run. In other words, the long-term benefits of cooperation as a general rule may outweigh its long-term costs even in particular situations where cooperation is clearly not reinforced.

Pure Altruism

It does not follow from the above argument that every altruistic act derives from self-control. Just as we learn over our lives to extend our effective selves beyond the present moment, so we may learn to extend our effective selves beyond our skins to others whose interests overlap with our own. Just as delay discount functions measure a person's temporal extent, so social discount functions measure a person's extent in social space. Although, as we have just claimed, altruistic behavior may emerge from self-control, and although there is a significant positive correlation across individuals between steepness of delay discounting and steepness of social discounting (Rachlin & Jones, 2008), there are many exceptions. Some people are Scrooge-like – selfish but highly self-controlled; others show the opposite pattern – unselfish with respect to others but highly impulsive with respect to their own future benefit. Even within the realm of self-control, people may be self-controlled in some areas but not in others. A person may be a compulsive gambler but a moderate drinker.

Social discounting may be primary; if self-control is analogous to the resolution of a conflict between our own present selves and our selves extended over time, it is conceivable that we learn self-control only by analogy to a primary process of social cooperation – as the sacrifice of our own present interests in favor of the group of our long-term interests. This idea would be consistent with Parfit's reductionism. If a person is like a nation, patterning of behavior over time would be derivable from patterning of behavior over social space.³

It is unclear whether one or the other type is primary or whether social and delay discounting are independent processes. Simon (1995) implies the latter when he posits orthogonal dimensions of temporal and social extent. In the previous section we showed how altruistic behavior may arise from a balance of short and long-term interests of the individual.

We do not know if social and temporal extension (beyond the skin or beyond the present moment) are independently learned or whether one is primary and the other derived. We are aware of no evidence whether social or temporal extensions of the self are primarily learned or primarily innate. But we have attempted to present a plausible account of how they might be learned based on an inherited tendency to pattern behavior. Now we will show how altruistic behavior may arise from a balance of the interests of the individual with those of the group.

Costs Versus Benefits

Corresponding to a view of the self as extended in time (the outcome of a conflict between narrower and wider temporal interests) is a view of the self as extended in social space (the outcome of a conflict between narrower and wider social interests). Just as delay discount functions measure the extent of a person's temporal interests, so social discount functions measure the extent of a person's social interests. This section will describe how social discount functions may be obtained and how they may explain choices such as the choice of Y in the lecture game. As indicated previously, the cost of choosing Y in the lecture game is $200 regardless of what other players choose; by choosing Y, increasing Z by 1, a player gains $100 but loses the $300 bonus that would have been obtained by choosing X, for a net loss of $200. What are the benefits of choosing Y? By choosing Y and increasing Z by 1 a player increases the amount of each of the 9 other players’ rewards by $100 regardless of whether they chose X or Y. But how does giving $100 to each of 9 other people benefit oneself?

The introduction to this article claimed that a person, not willing to put a dollar into a candy machine in order to give someone else a candy bar, might be willing to put in a penny. Assuming that holds, there must be some amount of money ($X, between $0.01 and $1.00) above which he would keep the money and below which he would insert it. That amount is how much it is worth to him to give a candy bar to a stranger. Transposing this illustration to the question at hand, we ask, How much would it be worth to a participant in the lecture game to give $100 to each of the 9 other participants?

An important determinant of such balancing is the social distance between a player and each of the other 9 players. The closer one person feels to the others, the more likely she will be to choose Y. Moreover, different people may have wider or narrower extended selves. The sociopath may have an extended self circumscribed closely by his own skin while the saint may have a self extended to all of nature. Jones and Rachlin (2006) and Rachlin and Jones (2008) attempted to measure such differences by means of social discount functions using a method akin to the usual procedure for obtaining delay discount functions (Raineri & Rachlin, 1993). Rachlin and Jones (2008) gave participants a booklet with these paper and pencil instructions:

The following experiment asks you to imagine that you have made a list of the 100 people closest to you in the world ranging from your dearest friend or relative at position #1 to a mere acquaintance at #100. The person at number one would be someone you know well and is your closest friend or relative. The person at #100 might be someone you recognize and encounter but perhaps you may not even know their name. You do not have to physically create the list – just imagine that you have done so.

The next seven pages each summarized the above instructions and then presented a list of questions as follows, with a different N-value on each page:

Now imagine the following choices between an amount of money for you and an amount for the #[N] person on the list. Circle A or B to indicate which you would choose in EACH line.

A. $85 for you alone.	B. $75 for the #[N] person on the list.
A. $75 for you alone.	B. $75 for the #[N] person on the list.
A. $65 for you alone.	B. $75 for the #[N] person on the list.
.........................(continued down to)..................................
A. $0 for you alone.	B. $75 for the #[N] person on the list.

Column-A listed 9 amounts decrementing by $10 on each line between $85 and $5. For half of the participants the money amounts decreased from $85 to $0 as above; for the other half the order was reversed. In Column-B, social distance [N] differed from page to page. The social distances were: 1, 2, 5, 10, 20, 50, and 100 in random order. On each line, participants (P₀'s) were asked to choose between an amount of money for themselves and $75 for the person at social distance N (P_N).

Figure 2b shows the group results. As with delay discounting, the medians (of 198 participants) were well described by a hyperbolic discount function (R² = .997):

$$v=\frac{V}{1+kN}$$ (1)

where V is the undiscounted value of the reward ($75) given to P_N, v is the value to the participant of the reward, N is the social distance between P₀ and P_N and k is a constant. The median k for the data of Figure 2b is 0.055. Equation 1 was fit to the data of individual participants (Stony Brook undergraduates) assuming V = A = $75 and a k-value was obtained for each of them. The bigger k, for a given undergraduate, the steeper her discount function, the less she values the receipt of $75 by a classmate. All participants had positive k-values; that is, they would be more generous to people socially close to them than to people far away.

Let us assume now that the players in the lecture game are Stony Brook undergraduates in an introductory psychology class. If we knew the social distance between a member of the class and a random other member (one of the 9 other players) we could rescale the discount function of Figure 2 from $75 to $100 on the y-axis and determine how much it is worth for a player to give $100 to another player at that social distance. A separate experiment with a group of 44 undergraduates from the same population was performed to make that determination.

After reading instructions (as in social discounting experiments) to imagine a list of 100 of their closest friends or relatives, each participant read the following:

Now try to imagine yourself standing on a vast field with those 100 people. The actual closeness between you and each other person is proportional to how close you feel to that person. For example, if a given person were 10 feet away from you then another person to whom you felt twice as close would be 5 feet away from you and one to whom you felt half as close would be 20 feet away. We are going to ask you for distances corresponding to some selected individuals of the 100 on your hypothetical list.

Remember that there are no limits to distance – either close or far; even a billionth of an inch is infinitely divisible and even a million miles can be infinitely exceeded. Therefore, do not say that a person is zero distance away (no matter how close) but instead put that person at a very small fraction of the distance of one who is further away; and do not say that a person is infinitely far away (no matter how far) but instead put that person at a very great distance compared to one who is closer.

Of course there are no right or wrong answers. We just want you to express your closeness to and distance from these other people in terms of actual distance; the closer you feel to a person, the closer you should put them on the field; the further you feel from a person, the further they should be from you on the field. Just judge your own feelings of closeness and distance.

Each of the following 7 pages differed in N-value, randomly ordered, and stated the following question:

How far away from you on the field is the [Nth] person on your list? Feel free to use any units you wish (inches, feet, miles, football fields, etc. Just indicate what the unit is). Please write a number and units of measurement for the [Nth] person on your list:

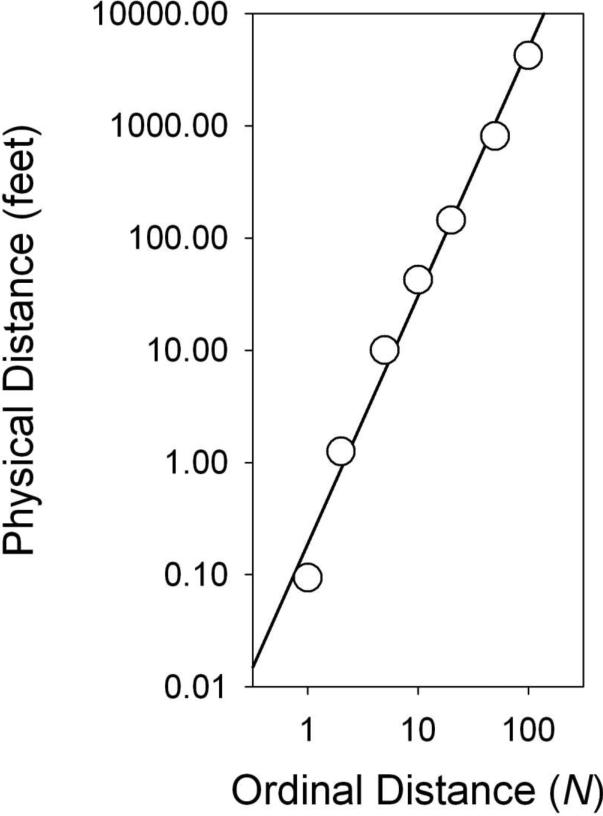
Participants found no difficulty in responding consistently to the rather odd instructions of this experiment. The judgments were converted to feet from whatever units the participants used and then averaged. Medians across participants are plotted in Figure 3 on a log-log scale. The best-fitting straight line (r² = .988) is:

$$\begin{array}{cc}\hfill \text{log}d& =2.2\left(\text{log}N\right)-0.72\hfill \\ \hfill d& =0.19N^{2.2}\hfill \\ \hfill N& =2.1d^{0.45}\hfill \end{array}$$ (2)

where d = distance in feet. As in psychophysical magnitude estimation experiments, a power function describes the median data well.

Figure 3.

Median judged physical distance to another person as a function of that person's social distance (rank in a list of 100 socially closest people).

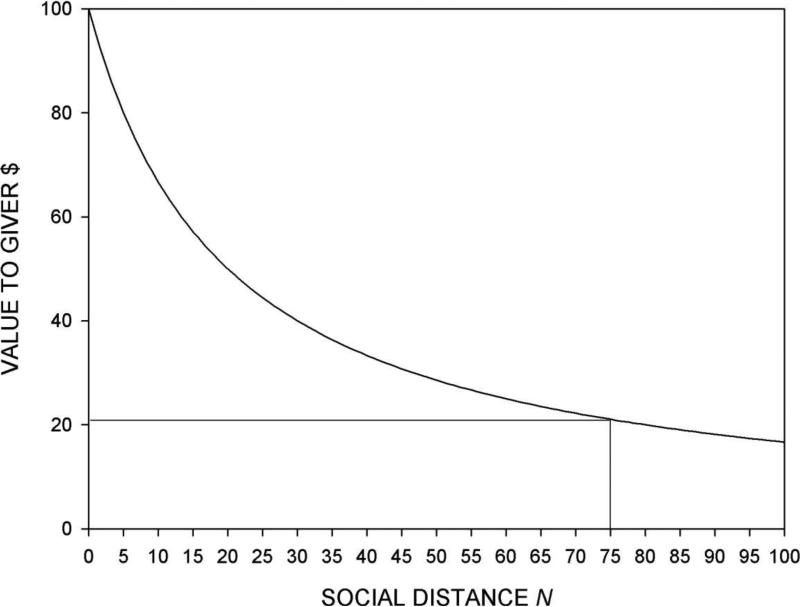
Still a third group of 50 Stony Brook introductory psychology students was given the instructions above but, instead of placing a series of people at various social distances (N's) on the field, they were asked to place on the field only a single random member of the class. The median distance from a participant of a random classmate was 2,300 feet! From the above equation, at d = 2300, N ≈ 75. Figure 4 normalizes the y-axis of Figure 3 at $100. At N = 75, the crossover point is about $21. That is, a typical Stony Brook introductory psychology student would be indifferent between $21 for herself and $100 for a random member of the class.⁴

Figure 4.

The social discount function of Figure 2b rescaled from $75 to $100. Receipt of $100 by the 75^th person on a list of 100 closest people is worth about $21 to the participant.

In the lecture game a player's Y-choice gives $100 to 9 other players. Assuming (very roughly) that the value of giving 9 other players $100 each is 9 times the value of giving one other player $100, the total benefit obtained by a Y-choice is $189 (9 × $21). This is a ballpark approximation to the cost of a Y-choice ($200). Of course the many assumptions and approximations that went into this calculation call this particular equivalence into question. Nevertheless the basic idea, that direct costs to a lecture-game player may be balanced by benefits to others, remains valid.

Cooperation in prisoner's dilemma games, and games in general, tends to be greater with greater social closeness of the players (Jones & Rachlin, 2009; Camerer, 2003). Among groups with closer bonding (say among members of the same family or the same athletic team or even people who have just had a conversation together or who are engaged in a mutual project) we would expect smaller social distances hence more Y-choices in the lecture game.

Charity begins at home

We have been assuming, in the social discounting equation (Equation 1), that value (V) was equal to the amount of money being discounted (A). This assumption was reasonable as long as the amounts in question were small additions to a presumably much larger total wealth and where total wealth of the giver (G) in an altruistic exchange was not widely different from that of the receiver (R). We now briefly consider the situation where the wealth of the giver significantly exceeds that of the receiver – i.e., charity.

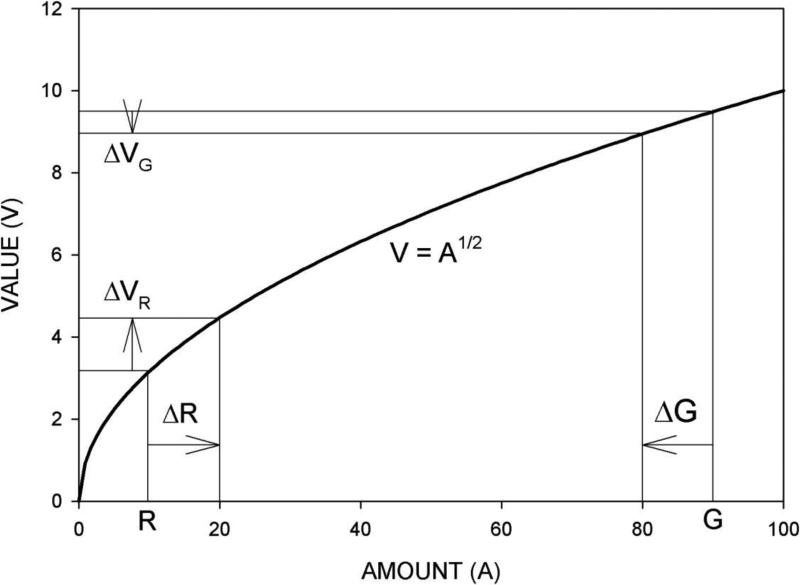
If a more-wealthy giver gives a certain amount (ΔG) to a less-wealthy receiver the giver's wealth is reduced and the receiver's wealth increased by that same amount (ΔR = ΔG). If, as the most fundamental law of economics asserts, marginal value decreases as amount increases, the value received by the receiver will be greater than the value given by the giver (ΔV_R > ΔV_G). Figure 5 illustrates this relationship with Bernoulli's square-root value function (V = A^1/2). Thus, a giver, by giving part of his wealth to a poorer person, increases total value (V_R + V_G); the gain in value (ΔV_R) is greater than the loss (ΔV_G).

Figure 5.

Value as a square-root function of wealth. The loss of value of a fixed amount of money given by a richer to a poorer person is less than the gain in value to the poorer person.

One problem with this explanation for why richer people should give money to poorer people is that there is no intrinsic place to stop, except at the point where everyone's wealth is equal. In Figure 5 that would be where A_R = A_G = 50 units. It may be claimed that there are transaction costs that limit giving to somewhere above the point of universal wealth equality, but this fails to account for the amount people actually give to charity; almost all of us stop giving well before realistic transaction costs could possibly be meaningful.

The problem of course is that a given gain in a receiver's wealth is less valuable to the giver than it is to the receiver. That is, we do not fully value other people's gains; they are discounted. As Equation 1 indicates, G discounts R's gain in value by the social distance between them. Although ΔV_R for a given wealth transfer may be greater than ΔV_G, the crucial factor in G's willingness to part with his money is how much ΔV_R is worth to him, not to R. This is not to say that marginal decrease in value has no effect on charitable giving. The value of a fixed amount of money does indeed increase as it is transferred from a richer to a poorer person. But then that value is decreased again as it is discounted by social distance – as determined by Equation 1. Wealth difference acts in one direction but social distance acts in the other. And, as we often observe, the latter may cancel out the former.

Why Be Altruistic?

We have offered three reasons. The first was to follow Parfit's suggestion and cooperate as long as, in your estimation, enough others cooperate so that your gain equals or exceeds what it would have been if all had defected. This strategy avoids the “sucker” option – being the only cooperator or being among a very few cooperators – but, as Parfit notes, does not avoid the basic dilemma. People often give some approximation to this reason as the answer, in the lecture game, to “Why would you choose Y?” For example, they might say, “I would choose Y if I felt that everyone else (or almost everyone else) was choosing Y.” But this answer does not specify what reinforces a Y-choice. It is like a person on a variable-time schedule (i.e., free reinforcement) saying, “I pressed the button rapidly in order to get the reward.” She would have gotten the same reward (or, if effort counts, a bigger one) for not pressing the button.

Perhaps it is not the behavior of others that determines our choices in this situation but our own behavior in other situations. This is the second reason we offered for altruism. A person may have a history of reinforcement of altruistic behavior and, even though she believes that altruism will not be rewarded here and now, she does not want to break the pattern. Why not? Because in the past, in such situations, her best considered choices have been proven wrong. That is, her altruism here and now is an act of self-control, part of a soft-commitment pattern. Although, by choosing Y in this situation, she maximizes reinforcement overall, this reason is difficult to verbalize; it involves admitting that her choice takes account of her own limitations. Verbalization of such a reason may involve social costs.⁵ Instead she may point to the pattern itself (she may say, “I am a good person.”) and leave it at that.

The third reason we offered for altruism was a balancing of costs and benefits (punishments and rewards) determined by a social discount function. Such balancing would not be deliberate; it is the observer's calculation not the player's. To verbalize this reason for choosing Y in the lecture game, a person would have to say, “I just felt like it.” Like admitting your limitations, verbalizing this apparently trivial reason may involve social costs.

Although these three reasons have been presented as distinct explanations, they are not mutually exclusive. Each of the first two reasons (Parfit's suggestion and soft commitment) is consistent with the third (a balancing of costs and benefits through social discounting). Let us consider the first reason (Parfit's suggestion). Social distance is not perfectly reflexive but we would expect the social distance from Person-X to Person-Y to correlate strongly with that from Y to X. Given such correlation, a behavioral pattern that conforms to Parfit's rule might easily arise. The social discount function suggests that a person should cooperate in the lecture game if the ratio of players to social distance is sufficiently large. Parfit's rule says that a person should cooperate if the ratio of players to defectors is sufficiently large. Given the reflexive nature of social distance, the more socially distant the other players are, the more of them would be expected to defect. The more of them expected to defect, the more likely Parfit's suggestion will lead to defection.

Similarly, the second and third reasons (soft commitment and social discounting) might easily coincide. Perhaps a pattern of cooperation has been reinforced in situations in which the ratio of beneficiaries (other players) to social distance (of those beneficiaries) is sufficiently large. Even though the particular lecture game might be anonymous and without direct reinforcement for cooperating, deviating from that reinforced pattern of cooperation may just not be worth the $200 gain.

Alternatively, it could be that social distance is itself largely a product of cooperative interactions. A pattern of cooperation between Person-A and Person-B may well result in a decrease in social distance between them. If that were the case, a pattern of cooperation through soft commitment (the second reason) could increase the ratio of players to social distance in the particular lecture game (the third reason). A cooperation choice in a particular game might then be attributed to either of these two reasons.

Thus, differences among the three reasons to cooperate are more a matter of style and social reinforcement of differing verbalizations than of substance. From a behavioral viewpoint, the difficulty of explaining altruistic behavior is not intrinsically greater (or lesser) than the difficulty in explaining self-control in everyday life instances of complex ambivalence. It is not contradictory for a behaviorist to say that altruism is reinforced provided the reinforcer is understood as acting not on that act alone but on the pattern that the act is part of. This is just as true for the social-discounting reason as it is for the soft-commitment reason. A social discount function is after all a measure of the extent of a behavioral pattern.