Folding Kinetics of the Cooperatively Folded Subdomain of the IκBα Ankyrin Repeat Domain

Abstract

The ankyrin repeat domain of IκBα consists of a cooperative folding unit of roughly four ankyrin repeats (AR1-4) and of two weakly-folded repeats (ARs5-6). The kinetic folding mechanism of the cooperative subdomain, IκBα_67-206, was analyzed using rapid mixing techniques. Despite its apparent architectural simplicity, IκBα_67-206 displays complex folding kinetics, with two sequential on-pathway high-energy intermediates. The effect of mutations to or away from the consensus sequences of ARs on folding behavior was analyzed, particularly the GXTPLHLA motif, which have not been examined in detail previously. Mutations toward the consensus generally resulted in an increase in folding stability, whereas mutation away from the consensus resulted in decreased overall stability. We determined the free energy change upon mutation for three sequential transition state ensembles along the folding route for 16 mutants. We show that folding initiates with the formation of the interface of the outer helices of AR3 and AR4, and then proceeds to consolidate structure in these repeats. Subsequently, AR1 and AR2 fold in a concerted way in a single kinetic step. We show that this mechanism is robust to the presence of AR5-6 as they do not strongly affect the folding kinetics. Overall, the protein appears to fold on a rather smooth energy landscape, where the folding mechanism conforms a one-dimensional approximation. However, we note that the ankyrin repeat does not necessarily act as a single folding element.

Introduction

IκBα, an inhibitor of the transcription factor, NFκB, contains an ankyrin repeat domain (ARD) with six ankyrin repeats (ARs). IκBα is bound to NFκB in the cytoplasm, until extracellular signals trigger ubiquitin-mediated proteosome-dependant degradation of the IκBα ¹, allowing NFκB to enter the nucleus and up-regulate transcription of a variety of target genes, among which is the gene for IκBα ¹. Newly synthesized IκBα then enters the nucleus and interferes with the NFκB-DNA interaction, eventually returning the NFκB to the cytoplasm and the cell to the resting state. It has been shown that IκBα is only fully folded when bound to NFκB; AR5 and AR6 of IκBα are weakly folded in free IκBα ^2,3. Upon urea challenge, AR1 through AR4 unfold cooperatively, whereas AR5 and AR6 undergo a non-cooperative transition ⁴.

The folding behavior of AR proteins is interesting because there are no long-range contacts and stabilization is only through local interactions ⁵. ARs are composed of a β-hairpin, two anti-parallel α-helices (distinguished as “inner” or “helix 1” and “outer” or “helix 2”), and a variable loop. Each repeat makes contacts only within the repeat and with residues of adjacently stacked repeats. With contacts only a short sequence distance away, it has been proposed that the folding of ARDs is “one-dimensional” ⁶.

The folding of several ARDs has been studied in detail. D34 ⁷ and the Notch ⁸ ankyrin domain, with twelve and seven ARs each, were analyzed making a single mutation in an analogous position on each repeat. This type of analysis assumes the single position can represent the whole AR unit and, thus, allows direct comparison of the effect of each AR on folding of the ARD. In each Notch AR, the Ala at the start of helix 1 was mutated to Gly, and comparison of the folding kinetics of these mutants showed that Notch folds through an on-pathway intermediate in which the three central ARs were structured ⁹. In each D34 AR, the valine and/or one of the two leucine residues in helix 2 were mutated and comparison of these mutants showed that folding involved a polarized intermediate, in which the C-terminal half of the protein were structured. However, mutation in the C-terminal ARs altered the intermediate, and shifted the folding pathway ¹⁰.

The folding kinetics of mutant ARDs were studied in p16^INK4A and myotrophin. In these studies, conservative mutations, generally removing a single methyl group from the side chain of the residue, were examined across the protein sequence to determine how interactions throughout the protein are formed along the folding pathway, allowing a classic phi-value analysis to be performed. The four AR-containing protein, p16^INK4A, was found to unfold sequentially, via a polarized transition state in which the two C-terminal ARs were structured but the two N-terminal ARs were not ¹¹. Similarly, myotrophin folds sequentially, with the C-terminal ARs initiating the folding reaction ¹². In each of these studies, mutations in a particular AR were considered as a group, with the goal of identifying which ARs were folded at the transition state of the folding pathway.

Additionally, the folding p19^{INK4d 13,14} and tANK ¹⁵ were studied with NMR complementing equilibrium and kinetics experiments to obtain residue-specific folding information. Both of these five AR-containing proteins were found to have populated intermediates at equilibrium with the three C-terminal ARs folded.

Several groups have published consensus sequences of the AR motif based on bioinformatic analysis of the hundreds of available AR sequences ^{16,17,18,19,20,21}. These sequences differ in the details, but share a core “minimum” consensus with two main regions: one region encompasses the hairpin and the beginning of helix one, the second region covers the end of helix two and part of the variable loop (Figure 1a) ²². In adddition, the folding of full-consensus designed ARDs (DARPins) have been studied ^{18,19,20,23,24,25}. Natural ARDs are generally marginally stable, but designed ARD proteins based on the consensus sequence have much higher thermal and chemical stability. Consensus ARDs also fold much faster and unfold much more slowly than naturally occurring ARDs of similar size ²⁴. Naturally occurring ARDs deviate substantially from the consensus: IκBα matches the minimum consensus for just over 50% of residues. IκBα and other large ARDs, such as the Notch ARD, conform more to the consensus in residues 4-12, while smaller ARD-containing proteins, such as p16 and myotrophin, conform better in residues 20-30. Guo, et al recently showed that the TPLH motif in the first region of the AR consensus is a major stabilizing factor in central repeats of AR proteins ²⁶. However, how the consensus residues confer stability on ARDs, and why naturally occurring ARDs deviate so much from the consensus is still not well understood.

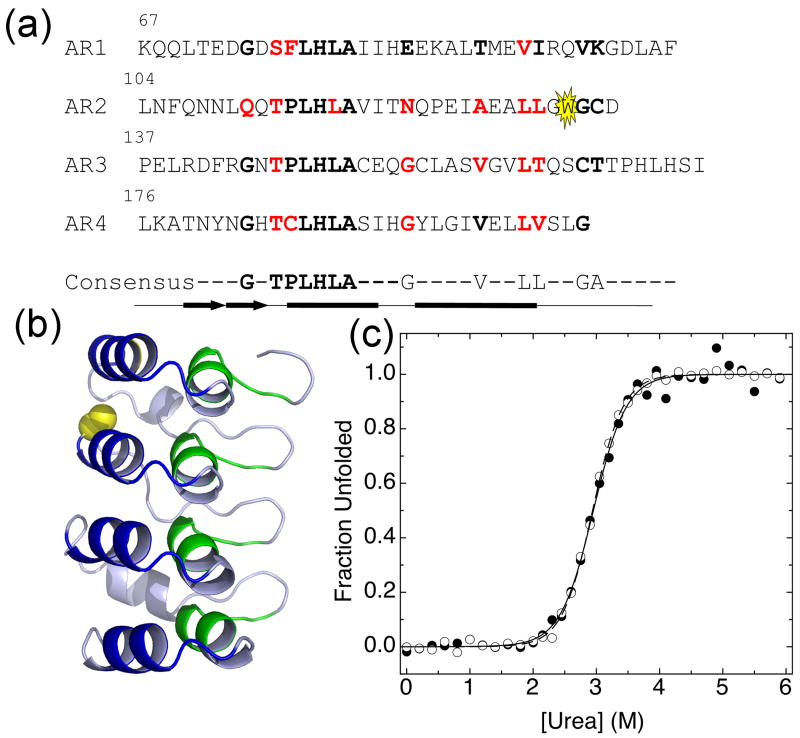
Figure 1.

(a) The IκBα_67-206W sequence with consensus positions in bold. Tryptophan reporter is highlighted in yellow. Mutated residues are shown in red. Secondary structure is shown below the sequence: the thick arrows represent a β-hairpin and the thick lines represent α-helices. The minimum consensus is represented below the sequence, with highly conserved residues shown and less conserved residues represented by dashes. (b) IκBα_67-206W structure, from NF-κB/IκBα_70-287 structure (PDB: 1NF1) ²⁸. The backbone of the first consensus region encompassing the hairpin and the beginning of helix one is colored green and the backbone of the second consensus region encompassing helix two and the first part of the variable loop is colored blue. A133 is highlighted in yellow. Modifications were performed in PyMol ⁴⁴. (c) Fraction unfolded from equilibrium urea denaturation of IκBα_67-206W (3 μM), monitored by the CD signal at 225, closed circles, or fluorescence, open circles. Lines are from global fits of equilibrium denaturation curves at several temperatures to a two-state model with shared m-values (CD m-value is 2.06 kcal mol^-1 M^-1, fluorescence m-value is 2.12 kcal mol^-1 M^-1).

Here, we examined the folding kinetics of the first four repeats of IκBα, IκBα_67-206, the cooperative folding unit in the IκBα ARD. IκBα_67-206 displays complex folding behavior, indicative of the presence of on-pathway high-energy intermediates. We also performed mutational analysis, using the AR consensus as a guide to determine the effect of individual consensus positions on folding behavior. Our studies particularly focus on the consensus residues GXTPLHLA, which have not been examined in detail previously. Restoration of a consensus residue resulted in an increase in mutant stability, whereas mutation away from the consensus resulted in decreased stability. Additionally, we found that the majority of mutations affected the unfolding rate, while the only mutations found to affect the folding rate were located in the second helices of AR3 and AR4. By scanning the consensus, we were able to identify parts of a single AR that influence the folding and unfolding rates. We suggest that folding initiates by the formation of the interface of the outer helices of AR3 and AR4, which appears to be folded in the first transition state, while the remainder of the protein folds later. We also show that these conclusions carry over to the full six repeats of IκBα as the presence of ARs 5 and 6 do not appear to affect the folding pathway.

Results

Introduction of a tryptophan probe in the cooperatively folding part of IκBα: IκBα_67-206 A133W

We previously showed that IκBα_67-206 has similar stability to IκBα_67-287, but lacks the steep pre-transition baseline characteristic of the non-cooperative transition attributed to AR5-6 in IκBα_67-287 ⁴. In order to probe just the cooperative folding transition, a deletion mutant of IκBα was used, containing only the first four ARs: IκBα_67-206. A tryptophan residue was engineered into AR2 (A133W) as a fluorescent reporter, as the only natural tryptophan in IκBα is in AR6 (Figure 1a, b). The four-AR fragment of the ARD of IκBα recapitulates the entire cooperatively folding unit of the full-length ARD. The A133W mutant, hereafter referred to as IκBα_67-206W (Table 1), had the same stability as wild type IκBα_67-206 ⁴, and allowed unfolding to be monitored by both fluorescence and circular dichroism. For IκBα_67-206W, both fluorescence and CD equilibrium unfolding curves overlaid well and gave similar stabilities, demonstrating that both the local reporter (W133 in AR2) and the global reporter (CD monitoring helical structure) follow the same two-state cooperative transition (Figure 1c).

Table 1. Folding properties of wild type IκBα_67-206W at different temperatures.

Experiment:	Equilibriuma		Kineticsb
Temperature	CD ΔGeq	Fluorescence ΔGeq	k12	k21	k32	k43	ΔGeqc
5°C	6.3±0.2	6.5±0.1	1.5	1.7 × 104	48	0.41	5.9
10°C	6.1±0.2	6.2±0.1	2.2	1.9 × 104	63	0.74	5.7
15°C	5.8±0.2	6.0±0.1	2.9	0.80 × 104	37	1.6	6.3
20°C	5.7±0.2	5.9±0.1	3.5	0.56 × 104	42	3.2	6.3
25°C	5.9±0.2	6.3±0.1	6.2	0.68 × 104	61	5.9	6.0

Folding stabilities (ΔG_eq) are reported in kcal mol^-1 and rates in s^-1.

^aEquilibrium denaturation experiments were measured by circular dichroism or total fluorescence. All temperatures were globally fit to a two-state model with baseline drift with shared m-values of 2.06 kcal mol^-1 M^-1 for CD and 2.12 kcal mol^-1 M^-1 for fluorescence. Reported errors are fit errors from the global fit of all temperatures.

^bKinetics experiments were measured by stop-flow fluorescence. All temperatures were globally fit to a four-state model with shared m-values (in kcal mol^-1 M^-1): m₁₂ = -0.15; m₂₁ = 0.96; m₃₂ = 0.87; m₄₃ = 0.11; m₂₃ and m₃₄ were set to 0 kcal mol^-1 M^-1 and k₂₃ and k₃₄ were set to 1 × 10⁵ s^-1. The equilibrium m-value calculated from the m-values for all rate constants is m_eq = -m₁₂ + m₂₁ + m₃₂ + m₄₃ = 2.09 kcal mol^-1 M^-1, in agreement with the equilibrium measurement. To determine experimental error, three independent data sets for wild type IκBα_67-206W at 10°C were globally fit with shared m-values. Individual rates were determined for each data set; from these, the standard deviation in each rate was calculated as 14% for k₁₂, 22% for k₂₁, 22% for k₃₂, and 2.6% for k₄₃.

^cΔG_eq was calculated from the individual rates: ΔG_eq = R T ln (k₄₃ * k₃₂ * k₂₁ / (k₁₂ * k₂₃ * k₃₄)). Standard deviation in ΔG_eq was calculated to be 5.7%, based on propagation of the standard deviations of the rates.

IκBα_67-206W folding kinetics

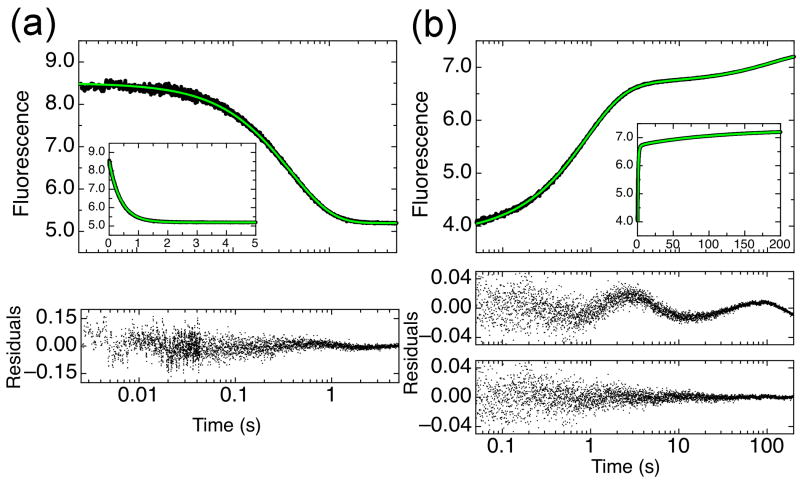
The folding kinetics of IκBα_67-206W were measured by stopped-flow fluorescence at 10°C. The decrease in fluorescence induced by unfolding of IκBα_67-206W by urea was fit to a single exponential because additional phases did not significantly improve the fit (Figure 2a). Refolding experiments showed an increase in fluorescence induced by rapid mixing of denatured IκBα_67-206W with low concentrations of urea. Two to three exponential terms were required to fit the refolding curves (Figure 2b), depending on the final denaturant concentration (see below). Importantly, the fluorescence change for both refolding and unfolding experiments has been fully accounted for, indicating that there are no additional kinetic phases taking place within the dead-time of the instrument (Figure 3a).

Figure 2.

Refolding and unfolding traces for IκBα_67-206W at 10°C, monitored by total fluorescence. Insets show the same data with linear time scale. (a) Folded IκBα_67-206W was rapidly mixed to a final urea concentration of 6.5M and the change in fluorescence (of W133) was monitored (●). The unfolding trace was fit with a single exponential function (green line) with residuals shown below the plot. (b) IκBα_67-206W, unfolded in 4M urea, was rapidly mixed to a final urea concentration of 0.7M (●). The refolding trace was fit with triple exponential function (green line), with residuals for a double or triple exponential function with residuals shown below for comparison.

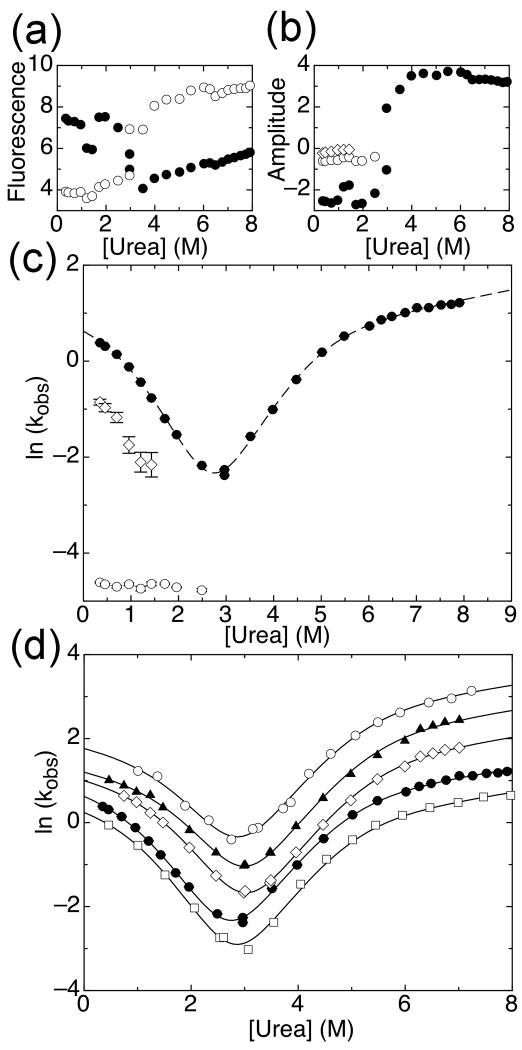
Figure 3.

Folding kinetics of IκBα_67-206W. (a) Starting (open circles) and ending (closed circles) fluorescence signals for refolding and unfolding traces. (b) Amplitudes of refolding and unfolding phases: unfolding and main refolding phase (closed circles), slow refolding phase (open circles), intermediate refolding phase (open diamonds). (c) Effect of urea concentration on the observed folding or unfolding rate of IκBα_67-206W at 10°C: unfolding and main refolding phase (closed circles), slow refolding phase (open circles), intermediate refolding phase (open diamonds). Line shows the fit of the data collected at 10°C from the global fit of several temperatures to a four-state model with shared m-values (m₁₂ = -0.15 kcal mol^-1 M^-1, m₂₁ = 0.96 kcal mol^-1 M^-1, m₃₂ = 0.87 kcal mol^-1 M^-1, m₄₃ = 0.11 kcal mol^-1 M^-1; m₂₃ and m₃₄ were set to 0 kcal mol^-1 M^-1). (d) Main refolding and unfolding phases for IκBα_67-206W at 5°C (open squares), 10°C (closed circles, same as in (b) but shown for comparison), 15°C (open diamonds), 20°C (closed triangles), and 25°C (open circles). Lines shown are from the global fit described in (c).

The observed unfolding and refolding rates from single mixing stopped flow experiments were plotted against urea concentration to yield a chevron plot (Figure 3c). The plot reveals two distinct regions of unfolding distinguished by a significant change in slope near 5.5M urea. The unfolding phase connects well with one of the refolding phases; this main refolding phase had the largest amplitude of the three refolding phases, accounting for 68-85% of the total amplitude (Figure 3b). The main refolding phase showed a strong denaturant dependence. At low urea concentrations, a small downward curvature was observed in the chevron curve.

The slowest refolding phase had the second largest amplitude, accounting for approximately 18% of the total amplitude (Figure 3b). This phase was relatively insensitive to denaturant concentration, with a rate of 9.3 × 10^-3 s^-1, up to urea concentrations of 2.5M, beyond which the phase was not observed. Interrupted unfolding experiments show that this phase is due to a slow isomerization in the unfolded state (Supplementary Figure 1). The rate constant for this refolding phase becomes faster in the presence of cyclophilin-A, directly showing that folding of these molecules is limited by Xaa-Pro peptide bond isomerization (Supplementary Figure 2). IκBα_67-206W has five proline residues, all of which are in the trans conformation in the crystal structures ^27,28. We conclude that the slowest refolding phase corresponds to isomerization-limited folding of unfolded IκBα_67-206W molecules with one or more non-native Xaa-Pro peptide bonds ²⁹.

A third phase, intermediate in rate, had the smallest amplitude (Figure 3b). This phase accounted for approximately 15% of the total amplitude at low urea concentrations, and its amplitude decreased gradually with increasing urea concentration until 2M urea, where it was no longer observed. This phase showed denaturant sensitivity similar to the main phase. It should be noted that the uncertainty in the rates of this phase are high, due to the small separation in rate from the main phase. Cyclophilin A shows little effect on the rate of this phase, suggesting that the reaction is not limited by proline isomerization, however we were unable to obtain any further information on this phase due to its small amplitude. We speculate that this phase may be related to partial folding of IκBα_67-206W molecules with non-native Xaa-Pro peptide bonds ²⁹ or to isomerization of Xaa-NonPro peptide bonds in the unfolded state ³⁰.

Models to describe the folding kinetics of IκBα

The chevron plot formed by the single IκBα_67-206W unfolding phase and the main refolding phase (Figure 3c) likely represents the main folding and unfolding event. Since there is a single relaxation, IκBα_67-206W folding is a two-state process without populated intermediates. However, the slight curvature at low urea concentrations and the significant change in slope at high urea concentrations suggests that the transition state region for IκBα_67-206W is complex.

Curved chevron plots can be explained by a broad transition state region ³¹. In this case, the curvature is described by a quadratic dependence of the free energies of activation on urea concentrations ^32,33. This model could not describe the varying degrees of curvature in the chevron plot for IκBα_67-206W. A three-state folding model with an on-pathway high-energy intermediate ³⁴, which was used to describe the folding of the Notch ARD ³² and myotrophin mutants ¹², predicts a chevron with a kink only in the unfolding arm ³⁵. This model described the data well at high urea concentrations, but did not account for the curvature in the refolding arm of the chevron. A linear four-state model (Equation 1) with two on-pathway, high-energy intermediates was required to fit the data^34,36.

$$\text{D}\underset{{\text{k}}_{21}}{\overset{{\text{k}}_{12}}{\rightleftarrows }}{\text{I}}_1\underset{{\text{k}}_{32}}{\overset{{\text{k}}_{23}}{\rightleftarrows }}{\text{I}}_2\underset{{\text{k}}_{43}}{\overset{{\text{k}}_{34}}{\rightleftarrows }}\text{N}$$ Equation 1

In this model, the two intermediates are of higher free energy than both the unfolded and the folded state, and do not populate to a detectable amount. Fitting such a model to the data provides information about the relative free energies of the transition state ensembles (TSEs) flanking the intermediates but not on the free energy of the intermediates themselves. To account for this, for data fitting, k₂₃ and k₃₄ were fixed to 1 × 10⁵ s^-1 and m₂₃ and m₃₄ were fixed at 0 kcal mol^-1 M^-1. The linear four-state model describes the main folding reaction of IκBα_67-206W at 10°C well (Figure 3c, Table 1).

Effect of temperature

The folding kinetics of IκBα_67-206W were examined at several temperatures. The observed refolding and unfolding rates increased across urea concentrations with temperatures from 5°C to 25°C while retaining similar slopes (Figure 3d). As the temperature increased, the curvature observed in the refolding rates increased. The chevron plots at each temperature were globally fit using the four-state model with shared m-values (Figure 3d). At all temperatures, the folding ΔGs calculated from the folding and unfolding rates agreed with stabilities obtained from equilibrium experiments which were separately globally fit to a two-state model (Table 1). Thus, the four-state model can describe the folding kinetics of IκBα_67-206W at different conditions. This result shows that the apparent changes of slope in the chevron plot are due to change in the microscopic rate constants for an otherwise robust mechanism of IκBα_67-206W folding.

Consensus mutations

To probe the effect of sequence on the folding behavior of IκBα_67-206W, single mutations were made to consensus positions in the protein (Figure 1a). Where the IκBα_67-206W sequence diverged from the consensus, the consensus was restored (e.g., Q111G); where the IκBα_67-206W sequence agreed with the consensus, conservative mutations were made (e.g., T113S). All mutants were expressed and purified, except L130V, G155A, and L202V, which could not be purified in monomeric form; the stabilities and folding kinetics were then measured and compared to IκBα_67-206W. In total, 19 mutations were introduced, and of these, 16 yielded soluble protein that could be analyzed for folding kinetics and stability.

Initially, the stability of each mutant was determined by equilibrium urea denaturation, measured by CD or fluorescence (Table 2). As with IκBα_67-206W, there was good agreement between the two probes. This shows that the two-state mechanism for IκBα_67-206W equilibrium denaturation is robust to changes in sequence. Some mutants had considerable change in stability compared to IκBα_67-206W. V93L, Q111G, N122G, A127V, T164L, C186P, and V203L all had significantly higher stabilities than IκBα_67-206W, while T113S, L117V, L131V, T146S, L163V, T185S, and G194A had lower stabilities.

Table 2. Folding properties of IκBα mutants.

A. Folding properties of IκBα67-206W mutants
Experiment:	Equilibriuma		Kineticsb
Mutant	CD ΔGeq	Fluorescence ΔGeq	k12	k21	k32	k43	ΔGeqc	Figure
IκBα67-206W	6.5±0.2	6.9±0.1	2.4	2.4 × 104	57	0.71	5.7	dashed line
S76T/F77P	6.9±0.2	7.5±0.1	3.0	2.1 × 104	51	0.55	6.1	4a
V93L	8.6±0.2	9.1±0.1	2.0	0.91 × 104	13	0.25	7.5	4b
Q111G	8.4±0.2	9.2±0.1	3.7	2.0 × 104	4.7	0.30	7.9	4c
T113S	5.6±0.2	6.1±0.1	2.1	1.3 × 104	68	1.3	5.5	4d
L117V	5.5±0.2	5.8±0.1	2.2	1.4 × 104	89	1.7	5.2	4e
N122G	7.5±0.2	8.2±0.1	2.7	1.5 × 104	20	0.78	6.6	4f
A127V	6.8±0.2	7.3±0.1	1.8	0.79 × 104	12	1.5	6.6	4g
L131V	4.7±0.2	5.0±0.1	2.6	2.0 × 104	186	1.1	4.9	4h
T146S	4.9±0.2	5.3±0.1	2.3	1.6 × 104	123	0.93	5.3	4i
V160A	6.7±0.2	7.2±0.1	2.7	1.8 × 104	39	0.75	6.1	4j
L163V	5.2±0.2	5.6±0.1	0.65	1.7 × 104	114	0.55	4.9	4k
T164L	7.3±0.2	7.8±0.1	9.7	0.76 × 104	75	0.61	7.1	4l
T185S	5.7±0.2	6.1±0.1	4.0	4.3 × 104	42	1.0	5.6	4m
C186P	7.2±0.2	7.7±0.1	2.1	1.6 × 104	28	0.67	6.3	4n
G194A	5.4±0.2	5.8±0.1	1.0	3.1 × 104	38	0.98	5.1	4o
V203L	7.3±0.2	7.8±0.1	4.0	0.50 × 104	33	0.72	7.2	4p

B. Folding properties of IκBα67-287W mutants
Experiment:	Equilibriuma		Kineticsb
Mutant	CD ΔGeq	Fluorescence ΔGeq	k12	k21	k32	k43	ΔGeqc	Figure
IκBα67-287W	7.1±0.2	7.4±0.3	0.48	1.3 × 103	25	0.37	7.1	5b
W258F	7.2±0.3	7.4±0.3	0.97	4.0 × 103	30	0.36	6.8	5a
Q111G	8.7±0.3	9.2±0.3	0.55	0.94 × 103	2.4	0.18	9.1	6b
T164L	7.5±0.3	7.5±0.3	1.8	0.47 × 103	139	28	7.6	6d
V203L	7.4±0.3	7.4±0.3	0.70	0.88 × 103	38	0.35	7.3	6f

Folding stabilities (ΔG_eq) are reported in kcal mol^-1 and rates in s^-1.

^aEquilibrium denaturation experiments measured by circular dichroism or total fluorescence. All IκBα_67-206W mutants were globally fit to a two-state model with baseline drift with shared m-values of 2.19 kcal mol^-1 M^-1 for CD and 2.35 kcal mol^-1 M^-1 for fluorescence. IκBα_67-287W mutants were also globally fit with shared m-values of 2.13 kcal mol^-1 M^-1 for CD and 2.20 kcal mol^-1 M^-1 for fluorescence. Reported errors are fit errors from the global fit of all mutants.

^bKinetics experiments were measured by stop-flow fluorescence. All IκBα_67-206W mutants were globally fit to a four-state model with shared m-values (in kcal mol^-1 M^-1): m₁₂ = -0.11; m₂₁ = 0.98; m₃₂ = 0.89; m₄₃ = 0.11; IκBα_67-287W mutants were similarly globally fit to a four-state model with shared m-values (in kcal mol^-1 M^-1): m₁₂ = -0.15; m₂₁ = 0.96; m₃₂ = 0.87; m₄₃ = 0.11. For both, m₂₃ and m₃₄ were set to 0 kcal mol^-1 M^-1 and k₂₃ and k₃₄ were set to 1 × 10⁵ s^-1. The equilibrium m-value calculated from the m-values for all rate constants is m_eq = -m₁₂ + m₂₁ + m₃₂ + m₄₃ = 2.10 kcal mol^-1 M^-1 for IκBα_67-206W mutants and 2.09 kcal mol^-1 M^-1 for IκBα_67-287W mutants, both in agreement with the equilibrium measurement. To determine experimental error, three independent data sets for wild type IκBα_67-206W at 10°C were globally fit with shared m-values. Individual rates were determined for each data set; from these, the standard deviation in each rate was calculated as 14% for k₁₂, 22% for k₂₁, 22% for k₃₂, and 2.6% for k₄₃.

^cΔG_eq was calculated from the individual rates: ΔG_eq = R T ln (k₄₃ * k₃₂ * k₂₁ / (k₁₂ * k₂₃ * k₃₄)). Standard deviation in ΔG_eq was calculated to be 5.7%, based on propagation of the standard deviations of the rates.

To investigate the mutants further, we performed stop-flow refolding and unfolding kinetics experiments to obtain chevron plots. It was possible to categorize the chevron plots into three different types (Figure 4). Two mutants, both mutations towards the consensus, (S76T/F77P double mutant and V160A) did not differ significantly from wild type (Figure 4a, j). The main phase of each chevron plot was globally fit with the four-state model using shared m-values (Figure 4, Table 2). In the following sections, we compare the results with IκBα_67-206W (hereafter referred to as WT) according to how each mutation affected the folding kinetics.

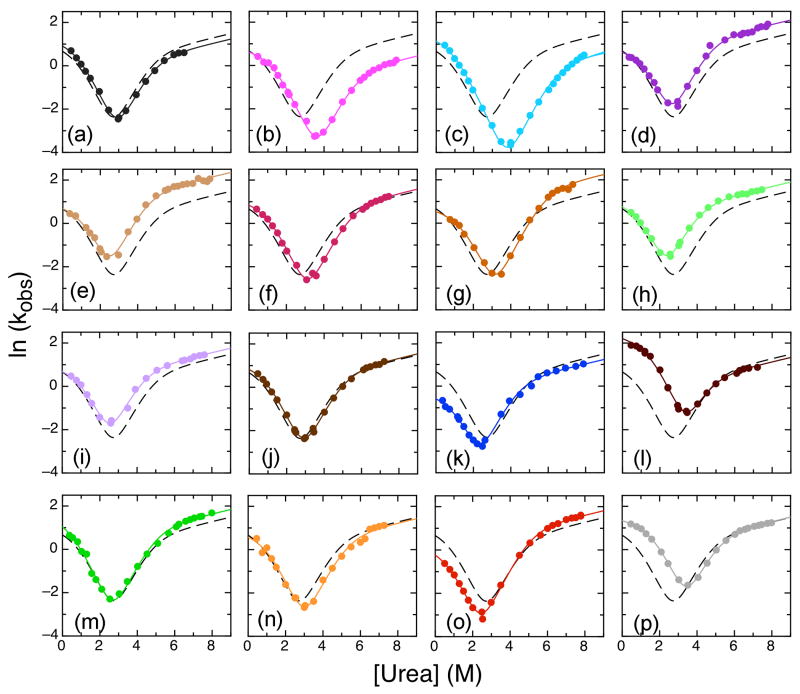
Figure 4.

Chevron plots for IκBα_67-206W mutants showing observed unfolding and major refolding rates at 10°C. Lines shown are from the global fit of WT IκBα_67-206W and all mutants to four-state model with shared m-values (m₁₂ = -0.11 kcal mol^-1 M^-1, m₂₁ = 0.98 kcal mol^-1 M^-1, m₃₂ = 0.89 kcal mol^-1 M^-1, m₄₃ = 0.11 kcal mol^-1 M^-1; m₂₃ and m₃₄ were set to 0 kcal mol^-1 M^-1). The WT IκBα_67-206W fit is shown in all plots for comparison (black dashed line). Mutants shown are: (a) S76T/F77P (dark grey); (b) V93L (pink); (c) Q111G (cyan); (d) T113S (dark purple); (e) L117V (tan); (f) N122G (magenta); (g) A127V (brown); (h) L131V (light green); (i) T146S (light purple); (j) V160A (brown); (k) L163V (blue); (l) T164L (dark red); (m) T185S (green); (n) C186P (orange); (o) G194A (red); (p) V203L (light grey).

Only AR3 and AR4 mutations affected refolding kinetics

Of 16 mutants analyzed, only five showed more than a two-fold change in the k₁₂: L163V, T164L, T185S, G194A, and V203L (Table 2). L163V, a mutation away from the consensus in helix 2 of AR3, decreased k₁₂ from 2.4 s^-1 for the WT protein to 0.65 s^-1, and was destabilized by 0.78 kcal mol^-1 (Figure 4k). Restoring the consensus, T164L also showed a strong effect by increasing k₁₂ to 9.7 s^-1. This mutation stabilized the protein by 1.4 kcal mol^-1 (Figure 4l).

In AR4, the T185S mutation away from the consensus increased k₁₂ to 4.0 s^-1 but also increased the unfolding rates and did not show an overall affect on ΔG. The G194A mutation, between helices 1 and 2, slowed refolding, decreasing k₁₂ to 1.0 s^-1, and destabilized the protein by 0.6 kcal mol^-1 (Figure 4o). Finally, the V203L mutation, restoring the consensus in helix 2 of AR4, increased k₁₂ to 4.0 s^-1 without affecting the overall unfolding rate, resulting in a stabilization of 1.5 kcal mol^-1 (Figure 4p).

Most mutations had altered unfolding kinetics

The majority of mutations mainly caused changes in the unfolding rates (Figure 4, Table 2). Three mutations, V93L (Figure 4b), Q111G (Figure 4c), and C186P (Figure 4n), all towards the consensus, unfolded more slowly than WT; fits of the chevron plots also showed slower unfolding rates (k₂₁, k₃₂, and k₄₃) than WT, resulting in stabilization of the proteins by 1.8, 2.2 and 0.6 kcal mol^-1 respectively. Two additional mutations, N122G (Figure 4f), and A127V (Figure 4g), slowed k₂₁ and k₃₂ but not k₄₃. Both these mutants were also stabilized by 0.9 kcal mol^-1.

Faster unfolding rates were observed for five mutants: T113S (Figure 4d), L117V (Figure 4e), L131V (Figure 4h), T146S (Figure 4i), and T185S (Figure 4m), all mutations away from the consensus. Of these mutations, all but T185S increased k₄₃ and k₃₂ and they destabilized the protein by 0.2, 0.5, 0.4, and 0.8, respectively. The T185S mutation increased k₄₃ but decreased k₃₂ and also increased the refolding rate resulting in no overall change in stability.

Folding of the 6AR protein and mutants

We showed previously that the naturally occurring W258 in AR6 does not follow the cooperative unfolding transition and we speculated that AR5-AR6 do not contribute to the cooperative folding of IκBα_67-287 (the full 6ARs) ⁴. To directly test this speculation, we introduced the A133W mutation into IκBα_67-287 and silenced the W258: IκBα_67-287 A133W/W258F. This construct allowed direct comparison of the behavior of A133W fluorescence within the four- and six-AR constructs. Since IκBα_67-287 is more aggregation prone than its four-AR counterpart, we choose to perform these experiments at a lowered temperature of 5°C. Experiments were performed at several concentrations from 1-3 μM IκBα_67-287 and no concentration dependence of the folding kinetics was observed. Unfolding experiments with IκBα_67-287 A133W, which still contains W258, and the single tryptophan-containing IκBα_67-287 A133W/W258F revealed one or two folding phases while refolding experiments showed two to four phases, similar to the four-AR protein. Despite the difference in rates, the chevron plots for both six-AR-containing proteins were remarkably similar to the four-AR IκBα_67-206 A133W (Figure 5, Table 2). We introduced three mutations studied in the 4AR protein to determine if the mutations would have the same effect in the 6AR protein (Table 2). We chose mutants with a large stabilizing effect on the 4AR protein: Q111G, which decreased the unfolding rate (Figure 6a, b), T164L, which increased the refolding rate (Figure 6c, d) and V203L, which also increased the refolding rate (Figure 6e, f). These mutations in the 6AR context showed similar affects as had been seen in the 4AR context again suggesting that the presence of AR5-6 does not strongly affect the main folding route of the full-length ARD. The effects of the Q111G and T164L mutations were quantitatively similar in the four-AR and six-AR context, but the effect of the V203L mutation was less in the six-AR context. This result is most likely due to the proximity of the V203L mutation to the additional repeats.

Figure 5.

Chevron plots for IκBα_67-287 A133W/W258F (red circles) and A133W (black triangles) showing main unfolding and refolding rates at 5°C. Solid lines show global fits of all six-AR mutants to a four-state model with shared m-values (m₁₂ = -0.15 kcal mol^-1 M^-1, m₂₁ = 0.96 kcal mol^-1 M^-1, m₃₂ = 0.87 kcal mol^-1 M^-1, m₄₃ = 0.11 kcal mol^-1 M^-1; m₂₃ and m₃₄ were set to 0 kcal mol^-1 M^-1). For comparison, the fit of four-AR IκBα_67-206W (main phase at 5°C) to four-state model is shown as a dashed line.

Figure 6.

Chevron plots for IκBα A133W mutants showing observed unfolding and refolding rates at 5°C (six-AR) and 10°C (four-AR). (a) Four-AR IκBα_67-206 A133W Q111G, (b) six-AR IκBα_67-287 A133W Q111G, (c) four-AR IκBα_67-206 A133W T164L, (d) six-AR IκBα_67-287 A133W T164L, (e) four-AR IκBα_67-206 A133W V203L, (f) six-AR IκBα_67-287 A133W V203L. Lines show global fits of all four-AR or six-AR mutants to a four-state model with shared m-values (as described in Figure 4 and Figure 5) of WT (dashed line) and mutants (solid lines). The color scheme for the individual mutations is the same as was used in Figure 4.

Discussion

IκBα_67-206W shows a simple, two-state mechanism for equilibrium denaturation that yet has complex folding kinetics; the chevron plot was non-linear at both low and high urea concentrations, inconsistent with a simple two-state folding model. Simple folding models that may account for non-linearity including a two-state model with broad transition state ensemble and a three-state model with a metastable intermediate proved insufficient. On the other hand, a four-state model with two high-energy intermediates fully accounted for the chevron plots of the wild type IκBα_67-206W at all tested temperatures and the chevron plots for all mutants. In addition, folding ΔG values obtained from globally fitting all of the mutant equilibrium unfolding curves to a two-state model and those obtained from globally fitting all of the kinetic data agreed well.

Consensus stabilization

The folding kinetics of 16 mutants of IκBα_67-206W were analyzed and compared; of these, eight conservative mutations were made at positions conforming to the consensus (T113S, L117V, L131V, T146S, V160A, L163V, T185S, and G194A), and all except V160A and T185S destabilized IκBα_67-206W. Eight mutations (S75T/F77P, V93L, Q111G, N122G, A127V, T164L, C186P, and V203L) restored the consensus at positions not in agreement with the consensus; all of these stabilized IκBα_67-206W. Previous studies on IκBα_67-287, a longer construct containing all six ARs of IκBα, also reported that Q111G and C186P stabilized ⁴. These results suggest a strong correlation between the ankyrin consensus and the folding stability of IκBα_67-206W. For every mutation that changed the folding stability of IκBα_67-206W, the construct with the consensus residue was always more stable. This result is consistent with the observation that full consensus AR proteins have very high stabilities ^18,23,24. Although it was known that full consensus proteins are more stable, a comprehensive analysis of every consensus position has not been studied. The stability of the full consensus protein could have been because one or two of the consensus amino acids were responsible for stability while the others had some other function. Here, we specifically probed the consensus positions and our results show that each and every consensus position, one at a time, imparts stability. Furthermore, the results show that the consensus residues have differential effects on folding kinetics depending on their location within a single repeat.

Effect of mutations on folding

The effect of mutations on the folding and unfolding rates of IκBα_67-206W can be used to develop a picture of the folding pathway. Phi-value analysis is a useful tool for analyzing the change in folding rate upon mutation as compared with the change in stability ³⁷:

$$\Delta \Delta G_{\mathit{\text{TSE}}}=\frac{\mathit{\text{RT}}ln{k}_f^{\mathit{\text{WT}}}}{\mathit{\text{RT}}ln{k}_f^{\mathit{\text{mut}}}},\Phi =\frac{\Delta \Delta G_{\mathit{\text{TSE}}}}{\Delta \Delta G_{\mathit{\text{eq}}}}$$ Equation 2

Mutants that change the stability of the protein but do not affect the folding rate have a Φ_F value of 0, suggesting that the contacts to this residue are not formed yet in the transition state. Conversely, mutants that change the stability of the protein solely because of a change in folding rate have Φ_F value of 1. Applying phi-value analysis to a set of mutations throughout a protein can give structural information about the transition state for folding, and can show which regions or structural features fold first.

Phi-value analysis on a more complex folding pathway such as the one we observed for IκBα_67-206W can also be performed on the individual transition state ensembles (TSEs) in the folding reaction. The folding rate to each TSE was calculated and used to determine the ΔΔG for each TSE. To determine the average degree of folding in each TSE, we performed a Leffler analysis on the ΔΔGs of each TSE (Figure 7, Table 3) ^37,38. We found it useful to plot the ΔΔG values for residues in AR 3 and 4 separately from those in AR 1 and 2 and to fit each separately. The results revealed that the slope of the Leffler plot for AR 1 and 2 was near zero for TSEs 1 and 2, corresponding to an average phi-value close to zero. On the other hand, the slope for AR 3 and 4 was 0.45 for TSE1 and 0.79 for TSE2, indicating a progressive folding of this region along the reaction coordinate. This differentiation between N- and C-terminal repeats is made more apparent by plotting the average phi-value for each group against the degree of compaction along the reaction coordinate, α (Figure 7d). AR 3 and 4 again show folded character much earlier than AR 1 and 2, which are not folded until the folding reaction is nearly complete. This result recapitulates previous phi-value analyses on other four AR-containing proteins, p16 ¹¹ and myotrophin ¹². For p16, the majority of mutants have high phi-values; only a few mutants, clustered on ARs 1 and 2, have phi-values near 0. Myotrophin showed a similarly C-terminal-polarized transition state.

Figure 7.

Leffler plots of ΔΔG_TSE compared to ΔΔG_equilibrium for IκBα_67-206W mutants for (a) TSE 1, (b) TSE 2, and (c) TSE 3. AR 1 and 2 mutants (open squares) are shown with linear fits of these mutants (long-dashed lines), with slopes of 0.03, 0.07, and 0.70, corresponding to the average phi-values for AR 1 and 2 mutants in the three TSEs. AR 3 and 4 mutants (closed diamonds) are shown with linear fits of these mutants (short-dashed lines), with slopes of 0.45, 0.79, and 0.95, corresponding to average phi-values for AR 3 and 4 mutants in the three TSEs. For reference, solid lines of slope 0 and 1 are shown, corresponding to average phi-values of 0 and 1. (d) Average phi-value versus α, the location of each TSE along the reaction coordinate, for AR 1 and 2 mutants (closed circles) and AR 3 and 4 mutants (open circles). α was calculated globally as 0.05, 0.52, 0.95 for IκBα_67-206W and 0.07, 0.35, 0.95 for IκBα_67-287W from the kinetic m-values using the following equations:

$$\begin{array}{l}{\alpha }_{\text{TSE}1}={-\text{m}}_{12}/{\text{m}}_{\text{eq}}\\ {\alpha }_{\text{TSE}2}=({-\text{m}}_{12}+{\text{m}}_{21})/{\text{m}}_{\text{eq}}\\ {\alpha }_{\text{TSE}3}=({-\text{m}}_{12}+{\text{m}}_{21}+{\text{m}}_{34})/{\text{m}}_{\text{eq}}\end{array}$$

Table 3. Folding landscape of IκBα_67-206W mutants.

A. IκBα67-206W mutants
Mutant	ΔΔGeqa	ΔΔGTSE 1	ΔΔGTSE 2	ΔΔGTSE 3	ΦTSE 1	ΦTSE 1	ΦTSE 1
S76T/F77P	-0.4	-0.13	-0.19	-0.25	n/ab
V93L	-1.8	0.10	-0.45	-1.27	-0.05	0.24	0.69
Q111G	-2.2	-0.24	-0.36	-1.76	0.11	0.16	0.79
T113S	0.2	0.08	-0.27	-0.17	n/a
L117V	0.5	0.04	-0.28	-0.03	n/a
N122G	-0.9	-0.05	-0.33	-0.92	0.06	0.38	1.06
A127V	-0.9	0.15	-0.48	-1.35	-0.16	0.52	1.47
L131V	0.8	-0.03	-0.14	0.53	-0.04	-0.18	0.69
T146S	0.4	0.03	-0.21	0.23	n/a
V160A	-0.4	-0.06	-0.22	-0.42	n/a
L163V	0.8	0.73	0.53	0.93	0.93	0.68	1.18
T164L	-1.4	-0.79	-1.43	-1.27	0.58	1.05	0.94
T185S	0.1	-0.29	0.03	-0.13	n/a
C186P	-0.6	0.09	-0.15	-0.55	-0.15	0.25	0.94
G194A	0.6	0.48	0.62	0.39	0.84	1.08	0.68
V203L	-1.5	-0.29	-1.17	-1.48	0.20	0.80	1.01

B. IκBα67-287W mutants
Mutant	ΔΔGeqa	ΔΔGTSE 1	ΔΔGTSE 2	ΔΔGTSE 3	ΦTSE 1	ΦTSE 1	ΦTSE 1
Q111G	-2.0	-0.08	-0.25	-1.56	0.04	0.13	0.80
T164L	-0.5	-0.73	-1.29	-0.34	1.46	2.57	0.69
V203L	-0.2	-0.21	-0.42	-0.19	n/ab

^aΔΔG's were calculated in comparison to WT IκBα_67-206W or IκBα_67-287W for using data from kinetics experiments. Φ-values were calculated from ΔΔG_TSE/ΔΔG_eq.

^bPhi-values were not calculated for mutants with ΔΔG_eq less than 0.5.

To uncover more detail, residue-specific phi-value analysis was performed on each of the TSEs for the IκBα_67-206W mutants that had an overall ΔΔG_eq > 0.5 kcal mol^-1 (Table 3). The phi-values revealed that residues L163, T164, and G194 had high phi-values in TSE1 (Figure 8a). These residues are all located in helix 2 (L163 and T164 in AR3 and G194 in helix 4). Thus, folding appears to initiate with only the interaction between the outer helices of AR3 and AR4. Although myotrophin, p16, and IκBα_67-206W all have similar transition states with parts or all of the two C-terminal repeats folded, IκBα_67-206W appears to have a much smaller folded region, at least in the first TSE, with only the outer helices of ARs 3 and 4 folded.

Figure 8.

Phi-values for (a) TSE 1, (b) TSE 2, and (c) TSE 3 are plotted on the structure of IκBα_67-206W. The backbone of the protein is colored as in Figure 1. Mutated residues are shown in spheres and colored by Φ-value, with yellow for below 0.3, orange for 0.3 to 0.6, and red above 0.6, modifications performed in PyMol ⁴⁴.

Moderate phi-values for N122 and A127 indicate that helix 2 in AR2 of IκBα_67-206W folds in TSE2 (Figure 8b). Consistent with the Leffler analysis, it isn't until TSE3, which is 95% as compact as the native state, that residues within helix 1 and the β-hairpins (Q111 and C186) appear to fold (Figure 8c). In fact, the C186P mutation in AR4 only has a phi-value near one in TSE3 indicating that all of AR4 is not folded at once. Indeed, the results presented here suggest that the two parts of the consensus represent different folding/stacking nuclei and that the outer helices (helix 2 of each repeat) fold/stack early in the folding pathway whereas the inner helices (helix 1) and β-hairpins fold/stack later. It is possible, then, that as was suggested in our earlier theoretical work ⁶, a single AR does not represent a single foldon and that further refinements of a general ARD folding mechanism will be required, in which other elements are treated as foldons rather than whole ARs.

Comparison of the 4AR and 6AR proteins

We had previously shown via equilibrium experiments that AR5-6 did not appear to contribute to the equilibrium stability of IκBα. Here we showed for three separate cases that mutations in the cooperative folding 4AR unit had the same effect in the full 6AR context. These results strongly suggest that the not only do AR5-6 not contribute to equilibrium stability, they also do not affect to the folding pathway of the cooperatively folding part of the IκBα ARD. This is in contrast to many other studies in which adding ARs to a cooperatively folding ARD enhances stability and sometimes alters the folding pathway ^14,21,39. These results again highlight that the AR5-6 region of IκBα is weakly folded and will perhaps have unique characteristics as compared to repeats in other well-studied ankyrin repeat domain-containing proteins.

Materials and Methods

Expression/Purification

IκBα mutations were introduced using QuikChange mutagenesis ⁴⁰. Human IκBα constructs were expressed and purified as described previously ⁴¹. The final purification step was on a Superdex-75 gel filtration column (GE Healthcare). The proteins were stored at 4°C and used within 1 week of gel filtration. Protein concentrations were determined by spectrophotometry, using extinction coefficients of 2980 M^-1 cm^-1 for IκBα_67-206, 8480 M^-1 cm^-1 for IκBα_67-206W and mutants; 12950 M^-1 cm^-1 for IκBα_67-287 with a single tryptophan and 18450 M^-1 cm^-1 for IκBα_67-287 with two tryptophans.

Urea preparation

Urea (Fisher Scientific, Pittsburg, PA, USA) was dissolved in water, and then treated with AG 501-X8 (D) resin (BioRad Laboratories, Hercules, CA, USA) for 1 hour to remove cyanate contaminants ⁴². Resin was filtered out with a 0.2μm filter and buffer salts were added to the purified urea. Urea concentrations were checked using refractometry ⁴³. Urea was used within 2 days of resin treatment to prevent re-accumulation to cyanate.

Equilibrium folding experiments

Equilibrium folding experiments were performed with an Aviv 202 spectropolarimeter (Aviv Biomedical, Lakewood, NJ, USA) with a Hamilton Microlab 500 titrator (Hamilton, Reno, NV, USA). A 1 cm fluorescence quartz cuvette containing 2.0 ml of 1–4 μM of the native protein in buffer (10 mM NaHPO₄, 50 mM NaCl, 1 mM DTT, 0.5 mM EDTA, pH 7.5) and was titrated with denatured protein (7.3 – 8.4 M urea in buffer), in 30 to 40 injection steps. After each injection, samples were equilibrated with constant stirring at 70-80 rpm for 180s prior to data collection. The CD signal was collected at 225 nm, averaged over 5 to 10 seconds, and the fluorescence signal was collected through a 320 cut-off filter with an excitation wavelength of 280nm, averaged over 2 to 5 seconds. Experiments were performed at 10°C unless otherwise stated.

Equilibrium folding curves were fit to a two state folding model, assuming a linear dependence of the folding free energy on denaturant concentration ⁴³. The pre (native) and post (unfolded) transition baselines were treated as linearly dependent on denaturant concentration. The data were globally fit to:

$$S_{\mathit{\text{obs}}}=(a_1+p_1[\mathit{\text{Urea}}])+a_2+p_2[\mathit{\text{Urea}}])\text{exp}(-(\Delta G-m[\mathit{\text{Urea}}]/RT))/(1+\text{exp}(-(\Delta G-m[\mathit{\text{Urea}}]/RT)))$$

where S_obs is the observed signal, p₁ and p₂ are the pre and post transition baselines, a₁ and a₂ their corresponding y-intercepts; ΔG is the folding free energy in water and m is the cooperativity parameter (m-value). The data were fit using a non-linear least square fitting algorithm in Kaleidagraph (Synergy Software, Reading, PA, USA) or Profit (QuantumSoft, Uetikon am See, Switzerland).

Folding kinetics

Kinetic folding experiments were performed on an Applied Photophysics Pi*-180 stopped flow instrument (Applied Photophysics, Leatherhead, UK). For unfolding experiments, 3 to 10 μM protein in buffer (25 mM Tris-HCl, 150 mM NaCl, 1 mM DTT, 0.5 mM EDTA, pH 7.5) was rapidly diluted 1:10 with buffered 2.8 to 8.8 M Urea. For refolding experiments, 3 to 10 μM IκBα_67-206 or 1-3 μM IκBα_67-287 was unfolded in buffered 4 to 5 M Urea for at least 30 minutes, and then was rapidly diluted 1:10 with buffered 0 to 3 M Urea. Fluorescence was collected perpendicular to the 280 nm emission with a 320 nm cutoff filter over 2 to 200 seconds. At each urea concentration, at 5 to 9 traces averaged and fit to a sum of exponential decays:

$$\mathit{\text{Signal}}=c+\sum _i{A}_i\text{exp}(-k_{i}t)$$

where c is the final fluorescence value, A_i is the amplitudes of the change in fluorescence of each phase, and k_i the observed rate of folding of each phase.

Observed rates were plotted versus final urea concentration to yield chevron plots. Plots were fit to a four-state model ^34,36:

$$\text{D}\underset{{\text{k}}_{21}}{\overset{{\text{k}}_{12}}{\rightleftarrows }}{\text{I}}_1\underset{{\text{k}}_{32}}{\overset{{\text{k}}_{23}}{\rightleftarrows }}{\text{I}}_2\underset{{\text{k}}_{43}}{\overset{{\text{k}}_{34}}{\rightleftarrows }}\text{N}$$ Equation 1

The function and equation are included in the Supplementary Material. Since we have no direct evidence for population of the intermediates, k₂₃ and k₃₄ were set to 1×10⁵ and m₂₃ and m₃₄ to 0. The data collected at different temperatures were globally fit with shared m-values. All of the data for the different mutants were also globally fit with shared m-values. Fitting of unfolding and refolding traces as well as chevron plots was performed with Profit (QuantumSoft, Uetikon am See, Switzerland).

Abbreviations

NFκB

nuclear factor kappa B

IκBα

inhibitor of NFκB

AR

ankyrin repeat

ARD

ankyrin repeat domain

CD

circular dichroism

TSE

transition state ensemble

DTT

dithiothreitol

EDTA

ethylenediamine tetraacetic acid