A Comprehensive Statistical Model for Cell Signaling and Protein Activity Inference

Abstract

Protein signaling networks play a central role in transcriptional regulation and the etiology of many diseases. Statistical methods, particularly Bayesian networks, have been widely used to model cell signaling, mostly for model organisms and with focus on uncovering connectivity rather than inferring aberrations. Extensions to mammalian systems have not yielded compelling results, due likely to greatly increased complexity and limited proteomic measurements in vivo. In this study, we propose a comprehensive statistical model that is anchored to a predefined core topology, has a limited complexity due to parameter sharing and uses micorarray data of mRNA transcripts as the only observable components of signaling. Specifically, we account for cell heterogeneity and a multi-level process, representing signaling as a Bayesian network at the cell level, modeling measurements as ensemble averages at the tissue level and incorporating patient-to-patient differences at the population level. Motivated by the goal of identifying individual protein abnormalities as potential therapeutical targets, we applied our method to the RAS-RAF network using a breast cancer study with 118 patients. We demonstrated rigorous statistical inference, established reproducibility through simulations and the ability to recover receptor status from available microarray data.

I. Introduction

Cells are complex molecular machines contained within phospholipid membranes that isolate a unique chemical environment. A key component of the cellular machinery is the set of protein signaling networks, which permit a cell to sense the internal and external environments and respond by altering metabolism and gene expression. Signaling networks comprise interacting signaling pathways, with each pathway containing a number of individual signaling proteins.

Signaling proteins can modify their behavior based on conformational changes induced by other signaling proteins. In the typical case, a kinase (a protein capable of adding a phosphate group to a protein) modifies its target protein by adding phosphate groups at serine or threonine amino acid residues. The modified protein undergoes a conformational change, activating its own kinase activity, leading to modification of a new target protein. This chain of phosphorylation causes a signal to be transduced through the cytosol of the cell, resulting in changes in enzymatic activity or activation or suppression of a transcriptional regulator (i.e., a transcription factor or co-factor). In addition to kinases, there are phosphatases that remove phosphate groups, thus reversing the signal from a kinase. Also, for certain signaling proteins, activity is generated by cleavage of a parent protein or dimerization, which is especially common for receptor tyrosine kinases that reside on the cell membrane and respond to external environmental cues, such as hormones or growth factors.

A. Statistical Network Modeling

Biological data are inherently probabilistic and generally display hierarchical relationships. Statistical analysis is then a logical approach for modeling large-scale molecular networks and for identifying specific nodes within a signaling network that are optimal therapeutic targets. In particular, graphical Markov models, such as Bayesian networks, have gained considerable interest lately in biomedical research because they naturally accommodate hierarchical network structure and reduce model identification to estimating low-dimensional conditional distributions.

However, despite their early promise, few major insights have emerged from such modeling efforts, at least for mammalian data. It is likely many of the problems that have arisen in applying Bayesian networks to these data arise from the high dimensionality of the data and, in the case of reverse engineering regulatory networks, from the necessity of learning both the underlying topology and estimating the corresponding statistical parameters. As a result, methods designed to reduce what needs to be learned from data by incorporating prior knowledge have come into use. They are even more required when, like in the present study, small sample sizes come in combination with a large proportion of unobservable components in the process of interest.

In particular, in the work described here, in order to apply graphical Markov models to learning signaling networks, we utilize existing knowledge about biological wiring diagrams as well as sharply reduce dimensionality by parameter-sharing. In addition, we account for cell heterogeneity by modeling the observed expression data as cell averages. Recent evidence on TRAIL induced cell death suggests that variability in protein concentrations between even clonal cells can lead to phenotypic variation that homogeneous models cannot address [7]. Our approach yields a stable model which can be identified with current sample sizes.

B. Wiring Diagram

Unlike standard Bayesian network approaches, which attempt to learn a wiring diagram in addition to statistical parameter estimates, we begin with a defined core signaling network, thus eliminating the combined problem of insufficient sample size and of hidden components for determining parameters for our statistical models.

A number of the core pathways of protein-protein interactions have been detailed, especially those affecting disease, for example in cancer studies [19], [23]. Since these pathways play critical roles in embryogenesis across many organisms, there is a substantial knowledge base [10]. For any given system, the core pathways need to be modified in terms of specific cell types, which is presently best done through review of the literature [14]. In this way a core signaling network can be created for a system of interest, with the pathways considered critically linked to transcriptional regulators.

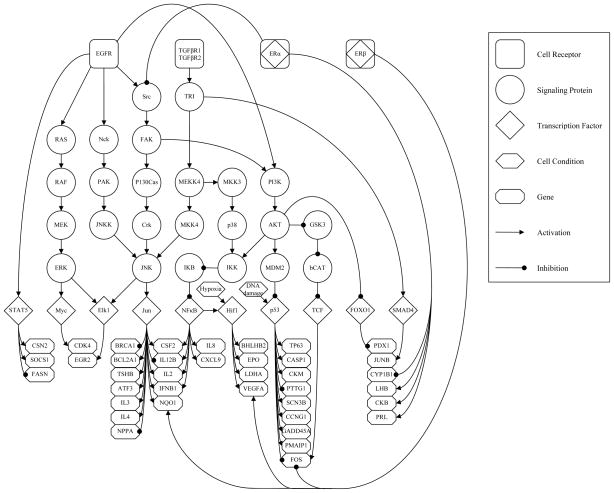
More specifically, studies on mutation in breast cancers have verified driver mutations of key signaling components in multiple pathways that lead to breast cancer development [13]. Both the RAS-RAF proliferation pathway and the PI3K cell fate pathways have multiple driver mutations, suggesting these are excellent targets for studies aimed at developing a method suitable for identifying targets for therapeutic intervention. With such applications in mind, we constructed a network based on the core signaling processes in breast cancer. This network is shown in Figure 1. We then identified a public domain microarray data set from a breast cancer study that included phenotypic information on receptor status [3]. This data set was collected using the Affymetrix U133A GeneChip and deposited in ArrayExpress (TABM158) [17]. We annotated the network in Figure 1 for the targets of the transcription factors from TRANSFAC Professional v11.4 [15] using our annotation pipeline, associating Affymetrix probes with Unigene clusters for gene identification [11]. These data will be used to learn the parameters of our Bayesian network and to validate the learned model by deducing the status of upstream signaling proteins in the form of probabilities of activation, comparing the estimated activation levels with ground-truth obtained from the clinical status measurements provided in [17].

Fig. 1.

Graphical representation of the signaling network of interest. Cell receptors (rounded squares) are roots along with cellular conditions (hexagons) and sit on top of the network as initiators of downstream signaling. Signaling proteins (circles) followed by transcription factors (diamonds) are given in the middle of the hierarchy. Genes (octagons) are leaves of the network and given at the bottom as final targets of transcription. Types of causal interaction between components are given with arcs directed from parent to child, arrow and round heads are used to indicate activation and inhibition, respectively.

C. A Multi-Level Model

Applying Bayesian networks directly to the graph in Figure 1 is not straightforward for several reasons. First, this ignores an important component of the data acquisition process, which is that the measured transcript levels are averaged over large ensembles of cells. Taking this into account in the model induces notable differences compared to what would correspond to a single cell model. In a proper tissue-level model, each observation arises from a large group of networks, each representing a cell. Second, the status of the signaling proteins is not observed. The only observed variables are tissue-level (hence cell-averaged) gene expression levels. Despite the averaging and hidden variables, we are still able to predict the receptor status given the observed transcript levels.

Our model is organized on two levels, the first one incorporating cell-dependent variables, and the second one including factors that are common to large cell assemblies (tissues), but are subject-dependent. An overview is presented in Figure 2.

Fig. 2.

Illustration of a microarray experiment. Tissue sample obtained from a test subject is assumed to contain a large ensemble of cells. Signaling in each cell is modeled by the same Bayesian network that generates gene specific mRNA independent from other cells given patient’s phenotypic receptor activation probabilities. mRNA accumulated from all cells is processed through hybridization, scanning etc. to yield final gene expression readouts, which constitute the only observable variables. Thus, the overall process motivates our multi-level approach and the assumption that measured gene expression levels are proportional to their single cell conditional expectations given patient dependent root activation probabilities.

At the cell level, we model signaling pathways as Bayesian networks in which the information is flowing from receptors (which constitute the roots of the networks to which are added certain cellular conditions, such as hypoxia) to genes. This process is assumed to be working within each cell, independently of the others. With an additive noise component, a gene expression measurement is modeled as the logarithm of a linearly increasing function of total gene-specific RNA abundance summed over a large population of cells. Final transcript readouts constitute the only observable components in our model.

The parameters of the Bayesian network at the cell level are assumed to be identical within each subject. This implies that the measurements stem from sums of independent and identically distributed random variables. Most of these parameters are also assumed to be identical across subjects, with the exception of the cell receptor activation probabilities. These probabilities are subject-dependent and assumed to be randomly generated. Putting things in a generative order, we model the process leading to a micro-array measurement as the following sequence of operations, performed independently for each subject:

1. Specify the receptor activation probabilities. These are shared by all cells in the analyzed tissue.

2. For each cell, let the gene expression be obtained from the state of the terminal nodes in a Bayesian network that models the signaling pathway.

3. For each gene, define the total expression to be the sum of the gene expressions over a large population of cells.

4. The final expression measurement is modeled as the logarithm of a linearly increasing function of this total expression with some additive observation noise.

D. Organization of the Paper

Our paper is organized as follows: In section II, we review previous related work on cell signaling networks. In section III, we lay out our statistical model in detail, elaborating the cell, tissue, population and measurement levels. Then, in section IV, we present the learning algorithm for model identification, with applications and experiments discussed in section V. Finally, some conclusions are drawn in section VI.

II. Related Work

Bayesian network models have been used in a wide variety of ways. For example, the relationships between nodes do not need to represent actual physical connections; consequently, Bayesian networks can model the effects of clinical variables on outcome, even relying on molecular data as well [4]. This can be viewed as a phenomenological perspective, where we abstract away the direct molecular causative agents, but retain predictive relationships between measured variables [5]. Bayesian networks have also been used to model traditional genetic networks, such as with time series data, where the up-regulation of a gene is identified as a causative agent for expression of other genes [6].

Other approaches to creating robust models might be attempted. Ordinary differential equation (ODE) models, such as modeling of ERBB signaling response [1], can capture great complexity, but they rely on large numbers of poorly determined parameters. This can limit their provability, since large ranges of parameter values on many components must be explored to guarantee uniqueness. Alternatively, networks can be reconstructed from limited measurements of protein state and abundance, such as from flow cytometry [20], or from prior data on beliefs of connectivity [16]. In these cases, the goal is to construct the connectivity and flow of the network for a small number of proteins from proteomic measurements. In contrast to these methods, we wish to estimate changes in signaling on a larger network. However, we are able to abstract away some of this complexity in favor of simplifying the model by assigning the same parameters to all similar nodes and assuming we know the network connectivity. This leads to a provable network capable of determining the state of individual network components.

Bayesian networks have been used to explore high-throughput biological data and to reconstruct biological networks. In a seminal paper in the field, Friedman and colleagues reconstructed transcriptional regulatory networks for yeast based on microarray data [6]. However, attempts to extend this work to mammalian systems did not lead to compelling results, perhaps due to the greatly increased complexity of transcriptional regulation. More recently Djebbari and Quackenbush [5] and Ulitsky and Shamir [22] have used Bayesian networks to integrate protein-protein interaction data and microarray data to improve inference. However, these recent approaches are not focused on capturing physical molecular interactions, as we propose here.

III. A Comprehensive Model

A. Individual Cell Model

Interacting signaling pathways of an individual cell are modeled as a Bayesian network over a pre-determined directed acyclic graph = (V, E), where V is the set of nodes (or vertices) and E is the set of oriented edges. The graph used in this paper is depicted in Figure 1. Some nodes v ∈ V represent a protein which participates in signal transduction, namely a cell receptor, intermediate signaling protein or transcription factor (TF). Other nodes stand for a cellular condition, such as DNA damage and Hypoxia, and the terminal nodes (those with no children) represent genes, the final targets of signal transduction.

A directed edge (u, v) ∈ E, from u towards v (u, v ∈ V), represents a potential functional interaction between u and v. Each such edge is labeled with the type of regulation, either activating (up-regulating) or inhibitory (down-regulating). Let pa(v) = {u: (u, v) ∈ E} denote the set of v’s parents, i.e. nodes that have an edge towards v. Accordingly, let A_v and I_v denote the disjoint subsets of pa(v) consisting of the parents that activate and inhibit v, respectively.

We denote by R ⊂ V the set of roots of the network, i.e., the nodes with no parents, which can be either cell receptors or certain cellular conditions which initiate downstream signaling. Also, let G ⊂ V stand for the terminal nodes of 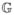; clearly G ∩ R = ∅ (since there are no isolated nodes). While v will usually denote a generic node, we will use whenever possible r to denote a receptor node and g to represent a gene.

Each node v ∈ V carries a random variable X_v, which quantifies the signaling activity of node v in network. We will use small case letters (e.g. x_v) for realizations of random variables, and we will write X_B to indicate the set of random variables {X_v, v ∈ B}. For example, X_G is the set of variables associated with genes. These random variables are interpreted as follows. For each gene g ∈ G, X_g stands for the expression level of gene g in the cell, i.e., the amount of transcribed mRNA. All other variables X_v, v ∈ V\G are binary, and represent the state of signaling at node v, where X_v = 0 means “off” and X_v = 1 means “on,” interpreted as the presence of signal at site v, ready to propagate down. The stochastic process X_V = {X_v: v ∈ V} is our representation of signaling activity in a single cell, and we assume the joint distribution is a Bayesian network. Therefore, the probability that the whole system is in state x_V = {x_v, v ∈ V} is

$$P(X_V=x_V)=\prod _{r\in R}{p}_r(x_r)\prod _{v\in V\backslash R}{p}_v(x_v\mid x_{\text{pa}(v)}).$$

Turning to the parametrization of the model, consider first the root nodes r ∈ R; since X_r is binary, there is one parameter per node, denoted φ_r = p_r(1) = P(X_r = 1). For transitions, for each v ∈ V, we attribute a function φ_v: {0, 1}^|pa(v)| → [0,1] which quantifies the net effect of the collection of signals x_pa(v) from the parents of v. The extreme values, 0 and 1, correspond to pure inhibition and pure activation, respectively. More precisely,

• If v is neither a root nor a terminal node,

  $$\begin{array}{l}{\phi }_v(x_{\text{pa}(v)})=E[X_v\mid X_{\text{pa}(v)}=x_{\text{pa}(v)}]\\ =P(X_v=1\mid X_{\text{pa}(v)}=x_{\text{pa}(v)})\end{array}$$

  which completely specifies the transition probability at v. They are “hard wired” in our model.

• If g ∈ G, the only property of the distribution of mRNA abundance X_g that will be needed is the conditional expectation given the parent TFs. We then introduce a scaling coefficient a_g > 0 and take

  $$E[X_g\mid X_{\text{pa}(g)}=x_{\text{pa}(g)}]=a_g{\phi }_g(x_{\text{pa}(g)}).$$ (1)

  We can interpret this as follows: transcription is either “on” or “off” with probability φ_g(x_pa(g)). When it is “on”, the mean is a_g and when it is “off” the abundance is zero.

A possible choice, if v is not a root, is to take

$${\phi }_v(x_{\text{pa}(v)})=\frac{{\sum }_{u\in \text{pa}(v)}{x}_u{\mathbf{1}}_{\{u\in A_v\}}+(1-x_u){\mathbf{1}}_{\{u\in I_v\}}}{\mid \text{pa}(v)\mid }.$$ (2)

It is easy to see that φ_v is linearly increasing in the difference between the number of active up-regulating and down-regulating parents of v, which is clearly an over-simplified model of “transcriptional synergy”, at least in the case of “competing” parents. More complex forms could be considered which are more faithful to the chemical interactions, perhaps even accounting for TF binding energies. However, in our particular network, only a relatively small portion of nodes have competing parents and our choice like (2) has the major advantage of being parameter-free, allowing one to pre-compute certain quantities which appear repeatedly during parameter identification. Moreover, simulating the Bayesian network is significantly more efficient under the assumption of linearity in equation (2) (see 3.5).

B. Tissue Model

At the patient level, the measured abundance of mRNA for each gene on the microarray originates from a very large ensemble of cells contained in the sample tissue. Let 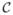denote this ensemble of cells, with size C = |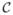|, and let 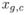be amount of transcribed mRNA for gene g ∈ G in cell 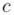∈ 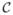. The total abundance is denoted by 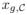= 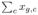. By the law of large numbers, assuming the the Bayesian networks for the cells are independent, we have

$$x_{g,\mathcal{C}}\approx CE[X_g\mid a_g,{\phi }_R]$$

where a_g and φ_R = {φ_r: r ∈ R} are the model parameters that affect X_g. In addition, due to the Markov property of the network,

$$\begin{array}{l}E[X_g\mid a_g,{\phi }_R]=E[E[X_g\mid a_g,X_{\text{pa}(g)}]\mid {\phi }_R]\\ =E[a_g{\phi }_g(X_{\text{pa}(g)})\mid {\phi }_R].\end{array}$$

Writing

$${\xi }_g({\phi }_R)=E[{\phi }_g(X_{\text{pa}(g)})\mid {\phi }_R],$$ (3)

for the expected transcription rate of gene g given the root activation probabilities φ_R, and dropping the approximation above, the transcript abundance in the tissue is

$$x_{g,\mathcal{C}}=a_{g}C{\xi }_g({\phi }_R).$$ (4)

C. Population Level

It is not realistic to assume that the activation rates of the receptors and cellular conditions at the roots of the network are the same for every subject. Consequently, the final component of the model is to consider these rates to be subject-dependent, in fact random variables at the population level. That is, there is a random variable ${\mathrm{\Phi }}_R^{(n)}=\{{\phi }_r^{(n)},r\in R\}$ for each patient n = 1, …, N. These variables are assumed independent and identically distributed across patients, for a given tissue type. Each component φ_r, r ∈ R, independently follows a Beta prior

$${\phi }_r\sim \beta (a_r,b_r).$$

with parameters a_r and b_r.

D. Measurement Model

It is well known that the actual measurement process, i.e., the steps leading up to what is actually recorded for each gene and patient, is complex, and should take into account the various stages of a microarray experiment including hybridization, scanning, background correction and normalization. As reported by numerous authors [7], [8], [9], we assume a linear relationship between scanned intensities of expression and actual RNA abundances. In particular, after undergoing all these steps, we consider the final log-expression reading $y_g^{(n)}$, obtained for gene g ∈ G and subject n = 1, …, N, to be the logarithm of a linearly increasing function of the corresponding tissue mRNA abundance $x_{g,\mathcal{C}}^{(n)}$, say

$$y_g^{(n)}=log(b_g^{(n)}+c_g^{(n)}{x}_{g,\mathcal{C}}^{(n)}).$$ (5)

The gain parameter $c_g^{(n)}$ represents the net factor, that comes between patient n’s actual molecule count for gene g and its processed probe intensity, before being transformed to log-scale. It involves the multiplicative measurement noise and accounts for experimental effects like hybridization efficiency, scanner gain and normalization. On the other hand, the additive term $b_g^{(n)}$ stands for the part of the intensity, that does not stem from the experimented mRNA, but rather effects like unspecific hybridization, detector offset etc.

Analyzing this representation in further detail with individual roles of the aforementioned steps and taking noise into account (see Appendix A), (5) can be approximated by

$$y_g^{(n)}={\lambda }_g+log{\xi }_g({\phi }_R^{(n)})+{\eta }^{(g,n)}$$ (6)

where λ_g is an offset parameter specific to gene g; and η^(g,n) is an i.i.d. realization of the measurement noise which, in log-scale is assumed to be an additive and zero mean Gaussian random variable with subject and gene independent variance σ².

In summary, our overall model, as illustrated in Figure 2, incorporates the entire process from the Bayesian network modeling of individual cell signaling, to patient-to-patient differences in receptor activation, to log-expression readouts at the population level. As a result, the final observation made for gene g for a given patient is modeled as a Gaussian random variable Y_g with conditional mean λ_g + log ξ_g (φ_R), parametrized by the gene-dependent offset λ_g and subject-dependent root activation rates φ_R = {φ_r: r ∈ R}, and each φ_r has a Beta distribution with node-specific parameters a_r and b_r. The level of transcriptional regulation ξ_g(φ_R) for target g is evaluated using the single-cell Bayesian network model. Finally, the variance σ² accounts for the variation in measurement error, which is the same for all genes.

E. Expected Transcription Rate Function

Recall from equation (3) that for each gene g ∈ G, ξ_g(φ_R) represents the cell-level average transcription rate of g, where we interpret this equation as a conditional expectation given the root activation rates are fixed to be φ_R. Let R_g denote the set of roots which are ancestors of g, so that ξ_g(φ_R) only depends on φ_Rg. Since these root variables are binary and independent,

$$P(X_{R_g}=x_{R_g})=\prod _{r\in R_g}{\phi }_r^{x_r}{(1-{\phi }_r)}^{1-x_r}.$$

Consequently,

$${\xi }_g({\phi }_R)=\sum _{x_{R_g}\in {\{0,1\}}^{\mid R_g\mid }}\left(E[{\phi }_g(X_{\text{pa}(g)})\mid X_{R_g}=x_{R_g}]\times \prod _{r\in R_g}{\phi }_r^{x_r}{(1-{\phi }_r)}^{1-x_r}\right).$$ (7)

It will be important in the following to have a quick access to the value of ξ_g(φ_R) for any given choice of the root activation rates. One possibility is to pre-compute all the coefficients of the above polynomial expression (i.e., all the E[φ_g(X_pa(g))|X_Rg = x_Rg]), which are parameter-free, and evaluate the polynomial when needed. This is tractable as long as 2^|R_g| remains manageable, which is the case with our network where |R_g| does not exceed 5. The pre-computation of the conditional expectations has to be done only once. It can be done exactly for small networks (including, again, our case), or for specific topologies. In the general case, approximate (and often good) values can be computed using belief propagation methods, or Monte-Carlo sampling. When |R_g| is too large for this strategy to be tractable, it is still possible to compute or approximate ξ_g(φ_R) for a given φ_R using belief propagation each time its value is needed (without pre-computation).

Finally, we notice that the computation of ξ_g can be done very efficiently when, for each v ∈ V, the function φ_v depends linearly on the states x_pa(v) of the parents. This property is true in particular in the model proposed in (2). In that case, ξ_g can be evaluated using dynamic programming along the network’s top-down hierarchy, thanks to the following proposition, proved in Appendix B.

Proposition III.1

Suppose that for all v ∈ V,

$$E[X_v\mid X_{\text{pa}(v)}]=c_v+\sum _{u\in \text{pa}(v)}{c}_{uv}{X}_u$$

for some coefficients c_v and c_uv. Then for all v ∈ V,

$$E[X_v\mid {\phi }_R]=d_v+\sum _{r\in R}{d}_{rv}{\phi }_r$$

for the coefficients d_v and d_rv determined by the recursions d_v = c_v + Σ_u∈pa(v) c_uvd_u and d_rv = Σ_u∈pa(v) c_uvd_ru.

Thus, in the case of proposition III.1, it suffices to pre-compute coefficients d_rg for r ∈ R and g ∈ G to ensure a computation of ξ_g(φ_R) in a time which is linear in the number of roots.

IV. Learning Algorithm

Our model has both observed and hidden variables. The observed ones are the gene expression levels ${\mathbf{y}}_G=\{y_g^{(n)}:g\in G,n=1,\dots ,N\}$ over N subjects. All other variables are unobserved. Among these, we are particularly interested in the root activation rates ${\mathrm{\Phi }}_R=\{{\phi }_r^{(n)}:r\in R,n=1,\dots ,N\}$, which constitute the hidden phenotypic information about the individuals in the population. The joint density of gene expression values and activation rates is given by

$$\begin{array}{l}{f}_{GR}(y_G,{\phi }_R\mid \theta )=f_{G\mid R}(y_G\mid {\phi }_R;\theta )f_R({\phi }_R\mid \theta )\\ =\prod _{g\in G}{f}_{g\mid R}(y_g\mid {\phi }_R;\theta )\prod _{r\in R}{f}_r({\phi }_r\mid \theta )\end{array}$$

where θ = {λ_g, a_r, b_r, σ²: g ∈ G, r ∈ R} is the set of parameters. The conditional densities on genes are Gaussian,

$$f_{g\mid R}(y_g\mid {\phi }_R;\theta )=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp\left\{-\frac{{(y_g-{\lambda }_g-log{\xi }_g({\phi }_R))}^2}{2{\sigma }^2}\right\},$$

and the activation rates have standard beta distributions

$$f_r({\phi }_r\mid \theta )=\frac{{\phi }_r^{a_r-1}{(1-{\phi }_r)}^{b_r-1}}{B(a_r,b_r)},$$

where, for each root node r ∈ R, $B(a,b)={\int }_0^1{x}^{(a-1)}{(1-x)}^{(b-1)}dx$ is the beta function. The objective of learning, i.e., model identification, is to infer θ based on y_G, where we assume each Y_g to be conditionally independent of the other expression values Y_G\{g} given activation rates φ_R. The other hidden variables, namely the signaling proteins and transcription factors, as well as their wiring, appear implicitly in functions ξ_g(g ∈ G).

The standard method for learning such a latent variable model is the expectation maximization (EM) algorithm. Briefly, EM provides an improving sequence (θ̂^(t))_t≥1 of parameter estimates by iteratively maximizing the conditional expectation of the complete data log-likelihood, given i.i.d. incomplete observations. In particular, each iteration t of EM involves (i) an E-step which requires computing of the missing data posterior, f_R|G(Φ_R|y_G;θ̂^(t)), in order to evaluate the current objective function

$$Q(\theta \mid {\widehat{\theta }}^{(t)})=E[log{f}_{GR}({\mathbf{Y}}_G,{\mathrm{\Phi }}_R\mid \theta )\mid {\mathbf{y}}_G;{\widehat{\theta }}^{(t)}]$$ (8)

and (ii) an M-step, in which one solves for the new parameter estimates

$${\widehat{\theta }}^{(t+1)}=arg\underset{\theta }{max}Q(\theta \mid {\widehat{\theta }}^{(t)})$$

by maximizing the objective function. This procedure is repeated until convergence is evident.

Evaluating (8) is usually simplified when the likelihood of the complete model (including both hidden and observed variables) belongs to an exponential family, which is the case here, since we can write

$$log{f}_{GR}({\mathbf{y}}_G,{\mathrm{\Phi }}_R\mid \theta )=-\mathrm{\Lambda }(\theta )+\langle \mathrm{\Pi }(\theta ),\mathbf{S}({\mathbf{y}}_G,{\mathrm{\Phi }}_R)\rangle$$

where 〈·, ·〉 denotes the vector scalar product; Λ and Π are scalar and vector valued functions of θ; and S(y_G, Φ_R) is a vector-valued complete data sufficient statistic. Explicit formulae for Λ, Π and S are provided in Appendix D. The maximum likelihood estimator can be expressed as a function of the sufficient statistic, in the form

$$\mathbf{S}\mapsto {\widehat{\theta }}_{\text{ML}}(\mathbf{S}).$$

The computation of θ̂_ML(S) with our model is described in Appendix E. Since (8) can be rewritten as

$$Q(\theta \mid {\widehat{\theta }}^{(t)})=-\mathrm{\Lambda }(\theta )+\langle \mathrm{\Pi }(\theta ),E[\mathbf{S}\mid {\mathbf{y}}_G;{\widehat{\theta }}^{(t)}]\rangle$$

it follows that the E-step can be reduced to computing the conditional expectation of the sufficient statistic, namely

$${\mathbf{S}}^{(t+1)}=E[\mathbf{S}\mid {\mathbf{y}}_G;{\widehat{\theta }}^{(t)}]$$ (9)

while the M-step is simply given by

$${\widehat{\theta }}^{(t+1)}={\widehat{\theta }}_{\text{ML}}({\mathbf{S}}^{(t+1)}).$$ (10)

However, due to the marginal beta distribution of Φ_R, there is no simple closed form for the the computation of (9) in the E-step and straightforward EM is intractable here. Instead, we will consider a stochastic variant, the Stochastic Approximation EM (SAEM) algorithm, wherein the E-step is approximated with Monte Carlo integration. Under mild conditions [4], [12], SAEM converges to (local) maxima of the objective function if the complete data log-likelihood belongs to a curved exponential family, which is the case in our model. Basically, SAEM replaces the E-step of conventional EM with a stochastic approximation running in parallel, involving the simulation of missing data Φ_R. In its simple form, the SAEM algorithm makes an iterative approximation of S^(t+1) by defining

$${\widehat{\mathbf{S}}}^{(t+1)}={\widehat{\mathbf{S}}}^{(t)}+{\gamma }^{(t)}(\mathbf{S}({\mathrm{\Phi }}_R^{(t)},{\mathbf{y}}_G)-{\widehat{\mathbf{S}}}^{(t)})$$ (11)

where (γ^(t))_t≥1 ∈ [0,1] is a decreasing sequence of positive step sizes starting with γ⁽¹⁾ = 1, and ${\mathrm{\Phi }}_R^{(t)}$ is a simulated sample of Φ_R, drawn conditionally to y_G for the current parameter θ^(t). The M-step is then given by

$${\widehat{\theta }}^{(t+1)}={\widehat{\theta }}_{\text{ML}}({\widehat{\mathbf{S}}}^{(t+1)}).$$ (12)

In principle, in order to ensure the convergence of the SAEM algorithm, one should take ${\sum }_{t=1}^{\infty }{\gamma }^{(t)}=\infty$ and ${\sum }_{t=1}^{\infty }{({\gamma }^{(t)})}^2<\infty$.

So the SAEM algorithm replaces computing conditional expectations by sampling from the conditional distribution which is most of the time much more feasible. Moreover, variants of this algorithm allow for coupling the iterations with Markov chain Monte-Carlo sampling, when direct sampling is not feasible or not efficient (which is the case for our model). One can also use more than one sample ${\mathrm{\Phi }}_R^{(t)}$ at each step, using a sample average in (11). The explicit implementation of the variant we have used is described in the next sections, for a single iteration t.

A. Simulation

Given the current parameter values θ̂^(t) and observed expression data y_G, we generate M^(t) ≥ 1 realizations ${\mathrm{\Phi }}_R^{(t,m)}=\{{\phi }_r^{(n,t,m)}:r\in R,n=1,\dots ,N\}$, (m = 1, …, M^(t)) of missing data under their joint posterior f_R|G(·|y_G; θ̂^(t)). For this, we use Gibbs sampling algorithm, which sequentially produces an instance for each φ_r, from its univariate conditional given the observations and already sampled current states of other root variables φ_R\{r}. The resulting sequence ${({\phi }_R^{(n,t,m)})}_{m\ge 1}$ of realizations will then constitute a Markov chain, whose stationary distribution is the sought-after posterior f_R|G.

For each r ∈ R, let G_r be the set of genes which are descendants of r and let R_r be the set of root nodes other than r which have a descendant in G_r. It is not hard to show (see Appendix C) that the conditional density of φ_r given the rest of the variables (Y_G, φ_R\{r}) only involves quantities indexed from G_r ∪ R_r. Hence, letting f_r|GrRr denote this univariate conditional, the m^th realization ${\phi }_R^{(n,t,m)}$ of missing root variables for subject n and iteration t of SAEM, is produced by Gibbs sampling as follows:

1. Set

   $${\phi }_R^{(n,t,m)}\leftarrow \{\begin{array}{ll}{\phi }_R^{\prime }\sim U({[0,1]}^{\mid R\mid }),\hfill & \text{if}t=1\text{and}m=1;\hfill \\ {\phi }_R^{(n,t-1,m)},\hfill & \text{if}t>1\text{and}m=1;\hfill \\ {\phi }_R^{(n,t,m-1)},\hfill & \text{otherwise}.\hfill \end{array}$$
2. Visit the root nodes in some fixed order and, for each r ∈ R, set

   $${\phi }_r^{(n,t,m)}\leftarrow {\phi }_r^{\prime }\sim f_{r\mid G_r{R}_r}(·\mid y_{G_r}^{(n)},{\phi }_{R_r}^{(n,t,m)};{\widehat{\theta }}^{(t)})$$

   This step is made explicit in Appendix C.

B. Stochastic Approximation

We update the sufficient statistic according to

$${\widehat{\mathbf{S}}}^{(t+1)}={\widehat{\mathbf{S}}}^{(t)}+{\gamma }^{(t)}\left(\frac{{\sum }_{m=1}^{M^{(t)}}\mathbf{S}({\mathrm{\Phi }}_R^{t,m},{\mathbf{y}}_G)}{M^{(t)}}-{\widehat{\mathbf{S}}}^{(t)}\right)$$ (13)

C. Maximization

We compute θ̂^(t+1) = θ̂_ML (Ŝ^(t+1)), the latter function being described in Appendix E. In summary, the model parameters are efficiently learned by keeping track of complete data sufficient statistics, which are improved with new realizations of missing data.

D. Root Activation Probabilities

The sequences ${({\phi }_R^{(t,m)})}_{t\ge 1,m\ge 1}$ that are generated by the SAEM algorithm can also be used to estimate, subject dependent, expected root activation probabilities given corresponding gene expression levels. That is, the conditional expectation $E[{\phi }_R\mid y_G^{(n)};{\widehat{\theta }}^{(t)}]$ can be recursively approximated by

$${\widehat{\phi }}_R^{(n,t)}={\widehat{\phi }}_R^{(n,t-1)}+{\gamma }^{(t)}\left(\frac{{\sum }_{m=1}^{M^{(t)}}{\phi }_R^{(n,t,m)}}{M^{(t)}}-{\widehat{\phi }}_R^{(n,t-1)}\right)$$ (14)

which, at SAEM’s convergence is returned as patient n’s phenotype estimate ${\widehat{\phi }}_R^{(n)}$.

V. Experiments with the RAS-RAF Network

In this section we present experiments in learning the network, measuring the stability of model identification, and estimating the states of the hidden variables, especially the activation states of the receptors. Our data consist gene expression levels measured for 38 genes and collected from 118 breast cancer patients. The observed genes are listed in Table I, with their known transcription factors and associated type of regulation. The data set also contains complete measurements for the ERα status of patients.

TABLE I.

Observed genes and their parent transcription factors; the type of regulation (activating or inhibiting) is indicated by the arrows

Gene	Parent Transcription Factor(s)
CSF2	NFkB↑ JUN↑
TP63	p53↑
EGR2	Elk1↑
CYP1B1	ERα↓
LHB	ERα↑
BHLHB2	Hif1↑
CKB	ERα↑
PRL	ERα↑
BRCA1	JUN↓
CSN2	STAT5↑
BCL2A1	JUN↑
EPO	Hif1↑
CASP1	p53↑
JUNB	SMAD4↑
FOS	ERβ↓, p53↓, TCF↑
LDHA	Hif1↑
PDX1	FOXO1↓
CKM	p53↑
PTTG1	p53↓
NQO1	ERβ↑, JUN↑
TSHB	JUN↑
ATF3	JUN↑
SCN3B	p53↑
SOCS1	STAT5↑
IL8	NFkB↑
IL12B	JUN↓, NFkB↑
IL3	JUN↑
VEGFA	Hif1↑, ERβ↑
IL4	JUN↑
NPPA	JUN↓
CXCL9	NFkB↑
CCNG1	p53↑
GADD45A	p53↑
FASN	STAT5↓
IL2	JUN↑, NFkB↑
IFNB1	JUN↑, NFkB↑
CDK4	Myc↑
PMAIP1	p53↑

A. Validating Identifiability of Model

Before discussion experiments with real patient data, we first check if the model can be accurately identified from artificial gene expressions simulated with known parameters. Given θ, we can generate subject dependent receptor activation rates ${\mathrm{\Phi }}_R=\{{\phi }_r^{(n)}:r\in R,n=1,\dots ,N\}$ according to their beta priors f_R(·|θ); and conditioned on them, we can sample gene expressions ${\mathbf{y}}_G=\{y_g^{(n)}:g\in G,n=1,\dots ,N\}$ from f_G|R(·|Φ_R; θ). Then, we can evaluate the fit between true parameters θ and their estimates θ̂ that are learned by applying the algorithm on simulated observations y_G. In particular, since the SAEM algorithm also returns predictions Φ̂_R of receptor activation rates, we can compare those subject specific estimates with their simulated true counterparts Φ_R that are kept hidden during learning.

For a better analysis, we can conduct the above procedure at different noise levels. Note that, with simulated phenotypes Φ_R, our model assumes the log of expected transcription rates $log{\xi }_g({\mathrm{\Phi }}_R)=\{log{\xi }_g({\phi }_R^{(n)}):n=1,\dots ,N\}$ as the noise-free signal that determines the subject dependent variation for each gene g ∈ G. Letting $\overline{log{\xi }_g}={\sum }_{n}log{\xi }_g({\phi }_R^{(n)})/N$ denote the corresponding sample average, and given the variance σ² of measurement noise, the signal to noise ratio (SNR) measured in dB, is found by

$$\text{SNR}=10{log}_{10}\frac{{\sum }_g{\sum }_n{(log{\xi }_g({\phi }_R^{(n)})-\overline{log{\xi }_g})}^2}{\mid G\mid N{\sigma }^2}.$$

Table II lists a summary of model identification accuracies at different SNR levels. For each r ∈ R, correlation coefficients between the simulated true vector ${[{\phi }_r^{(n)}]}_{n=1}^N$ and its learned estimate ${[{\widehat{\phi }}_r^{(n)}]}_{n=1}^N$, are given as an average score over 10 independent experiments per each choice of SNR, where experiments differ in random selections of true parameters used to simulate data of sample size N = 100. Clearly the model is accurately identified with moderately sized learning samples and even with SNR = 0, where the standard deviation in log ξ_g (φ_R) averaged across all genes g ∈ G, i.e. the root mean squared amplitude of the subject dependent signal is the same as that of noise. In particular, the estimations for the receptors ERα and EGFR inferred from simulated data are more precise, since they affect the majority of the genes observed.

TABLE II.

Model Identification from simulated data. Correlation coefficients between true (simulated) activation rates ${[{\phi }_R^{(n)}]}_{n=1}^N$ and their learned estimations ${[{\widehat{\phi }}_R^{(n)}]}_{n=1}^N$ at different SNR levels. Scores averaged over 10 experiments with randomly selected parameters for simulation. Sample size N = 100.

SNR (dB)	ERα	ERβ	EGFR	TGFβR	DNA d.	Hypoxia
−10	0.72	0.26	0.76	0.53	0.51	0.33
−5	0.87	0.45	0.89	0.77	0.67	0.54
0	0.94	0.69	0.95	0.89	0.86	0.74
5	0.97	0.88	0.98	0.93	0.92	0.88
10	0.98	0.94	0.99	0.97	0.97	0.94

B. Estimating Receptor Activity from Real Data

One important way to measure the utility of the model is to estimate the states of the receptor proteins from the gene expression data. In our model, these states are binary variables, each sampled independently from a patient-dependent activation rate. Consequently, it is these rates which are the more natural targets of estimation. For each of the 118 patients, we are provided with a binary label for the measured phenotypes, either “ERα-positive” or “ERα-negative”. Our activation rate estimates ${\{{\widehat{\phi }}_{\text{ER}\alpha }^{(n)}\}}_{n=1}^N$ are scalars. The rank-sum test, also known as Mann-Whitney-Wilcoxon test, offers a natural and robust way to compare predictions, especially by averaging over different parameter initializations. It is a nonparametric procedure for testing the hypothesis that two independent samples are identically distributed.

Let ER⁺, ER⁻ ⊂ {1,2, …, N} be the sub-populations of patients who are ERα-positive and ERα-negative, respectively. In our case, the null hypothesis H₀ is that the activation rates from these two sub-populations are identically distributed. Our data are the estimated rates ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{+}=\{{\widehat{\phi }}_{\text{ER}\alpha }^{(n)}:n\in {ER}^{+}\}$ and ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{-}=\{{\widehat{\phi }}_{\text{ER}\alpha }^{(n)}:n\in {ER}^{-}\}$, where |ER⁺| = N⁺ = 75 and |ER⁻| = N⁻ =43.

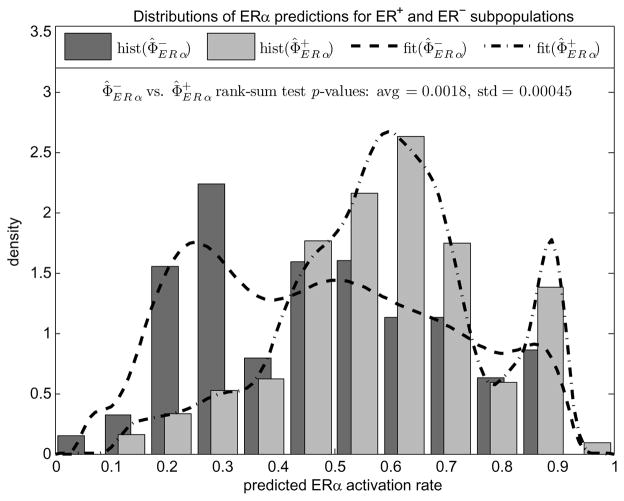
Figure 3 compares the histograms of estimates ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{+}$ and ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{-}$ (superposed with their non-parametric density fits for better visualization) obtained with 20 repeated experiments where each run of the algorithm differs in random parameter initializations. The rank-sum test p-value (see Appendix F for a description of rank-sum test) averaged over these 20 experiments is found 0.0018 with standard deviation 0.00045. As can be seen in the separation of histogram modes, the estimates are reproducible and consistent with phenotypes.

Fig. 3.

Normalized histograms and nonparametric density fits of patient dependent predictions for ERα activation rates corresponding to ER⁺ and ER⁻ sub-populations. Histograms are generated and rank sum test p-values are averaged over 20 independent runs.

The data set also reproduces the EGFR status for 79 of the 118 patients, again recorded as EGFR-positive or EGFR-negative, but with only 8 positives. The same rank-sum test approach to correlate this information and the EGFR rate predicted by the model, failed to provide a significant p-value, but this would have been very hard to achieve due to limited power of rank-sum test with such a small number of available EGFR-positive patients.

C. Estimating the States of Other Signaling Proteins

We can also infer the states of the non-receptor hidden components, i.e. signaling proteins and transcription factors. Having estimated ${\widehat{\phi }}_R^{(n)}$ for each patient n, the subject-specific expected status ${\widehat{\overline{x}}}_v^{(n)}=E[X_v\mid {\widehat{\phi }}_R^{(n)}]$ of each network component v ∈ V\G can be directly evaluated similar to the way in which we computed the ξ_g’s in equation (7). Letting R_v denote the root ancestors of v, we get

$${\widehat{\overline{x}}}_v^{(n)}=\sum _{x_{R_v}\in {\{0,1\}}^{\mid R_v\mid }}\left(E[X_v\mid X_{R_v}=x_{R_v}]\times \prod _{r\in R_v}{({\widehat{\phi }}_r^{(n)})}^{x_r}{(1-{\widehat{\phi }}_r^{(n)})}^{1-x_r}\right).$$ (15)

where, again, the expectations involved in the sum are parameter-free and can be pre-computed using proposition III.1. Note that, with that notation, subject n’s expected status ${\widehat{\overline{x}}}_r^{(n)}$ at a root r ∈ R is the same as the prediction of the corresponding activation rate ${\widehat{\phi }}_r^{(n)}$.

For a node v with only one parent, say u, the above computation simplifies to ${\widehat{\overline{x}}}_v={\widehat{\overline{x}}}_u$ (resp. $1-{\widehat{\overline{x}}}_u$), since while evaluating the expectation E[X_v|X_Rv = x_Rv], (2) will give φ_v(x_u) = P(X_v = 1|X_u = x_u) = E[X_v|X_u = x_u] = x_u (resp. 1 − x_u), if u activates (resp. inhibits) v. In other words, along linear sequences, signaling is assumed to propagate deterministically, where each node either copies or reverses the status of its single parent. Thus, our model is invariant to adding/removing components at such pathways, that is, topologies that reduce to the same collapsed structure, yield the same data likelihood as well as the same predictions for common nodes.

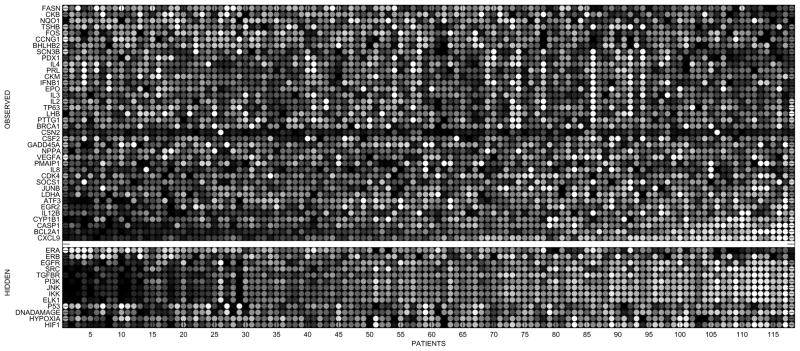
Figure 4 shows a gray scale heat map (black: low, white: high) of estimates for hidden components appended to the observed gene expressions, where to avoid redundancy, hidden nodes with only one parent are excluded, since, as mentioned above, they can be directly deduced from the ones already shown. Spot (v, n) gives the estimated or observed status of signaling component v, for patient n. Each row is scaled to a common dynamic range by subtracting the mean and normalizing with standard deviation. Columns (i.e. patients) are arranged according to the projection rank of the corresponding gene profile on to the direction of largest variation in gene space, namely the first eigenvector of covariance matrix of observations. Besides demonstrating our ability to estimate subject dependent status of cell signaling, analysis of this picture is limited since ground truths for hidden nodes are missing. However it is noteworthy that our inference of hidden nodes aligns with the first order variation amongst genes.

Fig. 4.

Grayscale heat map of patient-specific networks. Each row corresponds to a network component and each column to a patient. The rows are scaled to a common dynamic range. The columns are arranged according to the projection rank of the corresponding gene profile on to the direction of largest variation in gene space. The white stripe separates the observed log gene expression levels on top from the estimates of the hidden components. Hidden nodes that have only one parent (the ones that are intermediate proteins along linear cascades) are excluded to avoid repetition, since their predictions are the same or inverse of their parent, directly deducible from the ones already shown.

D. Validating Reproducibility and Sensitivity to Sample Size

In order to assess the method’s generalization power and sensitivity to sample size we used a ”repeated random sub-sampling validation” procedure, where we repeatedly partitioned the available gene expression data into two random halves, and checked the fit between models learned from these two disjoint subsets.

In order to describe this validation study, let B ⊂ {1,…, N} be a sub-population of patients and let θ̂^(B) denote the model parameters learned from the corresponding expression data ${\mathbf{y}}_G^{(B)}=\{y_g^{(n)}:g\in G,n\in B\}$. Then, based on the model with estimated parameters θ̂^(B), let ${\widehat{\phi }}_R^{(k\mid B)}=E[{\phi }_R\mid y_G^{(k)};{\widehat{\theta }}^{(B)}]$ denote the predicted receptor activation rates for patient k, who may or may not be in B.

The expectation involved in ${\widehat{\phi }}_R^{(k\mid B)}$ can be evaluated by Monte Carlo integration as discussed in the simulation step of SAEM, i.e. by Gibbs sampling the model, with parameters θ̂^(B) and conditional to corresponding observations $y_G^{(k)}$. Note that, if k ∈ B, in other words if the queried patient is in the training set, then, as we reported so far, ${\widehat{\phi }}_R^{(k\mid B)}$ is already an output of our learning algorithm, and it is found in the same way by equation (14).

Now, let A and 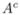be two disjoint halves of the experimented population {1,…,N}. To validate our method, we want to compare, for each n, the estimations ${\widehat{\phi }}_R^{(n\mid A)}$ against ${\widehat{\phi }}_R^{(n\mid A^c)}$, that are predicted for the same person, but with respective model parameters θ̂^(A) and 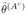, learned from two disjoint sets of subjects.

Table III shows the reproducibility results, where for each r ∈ R, we give the corresponding scatter plot of ${\widehat{\phi }}_r^{(n\mid A)}$ vs. ${\widehat{\phi }}_r^{(n\mid A^c)}$, for n = 1,…,N, and accumulated over 20 random selections of A. Averaged over these repeated random sub-sampling experiments, the resulting correlation coefficient between predicted vectors ${[{\widehat{\phi }}_r^{(n\mid A)}]}_{n=1}^N$ and ${[{\widehat{\phi }}_r^{(n\mid A^c)}]}_{n=1}^N$ is used as a measure of fit between models learned on disjoint patient populations, showing how well the method generalizes, with even smaller learning samples.

TABLE III.

Repeated random sub-sampling validation of the method: Estimated receptor activation rates are compared after training on disjoint sub-populations. Results are superposed/averaged with 20 random selections of sub-sample $A\subset \{1,\dots ,N\}(\mid A\mid =\frac{N}{2})$.

Root r ∈ R	ERα	ERβ	EGFR	TGFβR1-2	DNA damage	Hypoxia
${\widehat{\phi }}_r^{(n\mid A)}$ vs. ${\widehat{\phi }}_r^{(n\mid A^c)}$ (n = 1,…, N)
$\mathit{corr}\left\{{[{\widehat{\phi }}_r^{(n\mid A)}]}_{n=1}^N,{[{\widehat{\phi }}_r^{(n\mid A^c)}]}_{n=1}^N\right\}$	0.98	0.99	0.98	0.98	0.96	0.91

E. Validating Robustness with respect to Realistic Modifications in Network Topology

In Section V.C, we discussed the invariance of statistical inference under structural perturbations like collapsing or elongating linear pathways. Denoting the original core topology of Figure 1 by 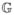, we now want to examine the robustness of our model with respect to biologically realistic revisions 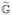, which are similar to 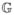but not equivalent in the previous sense.

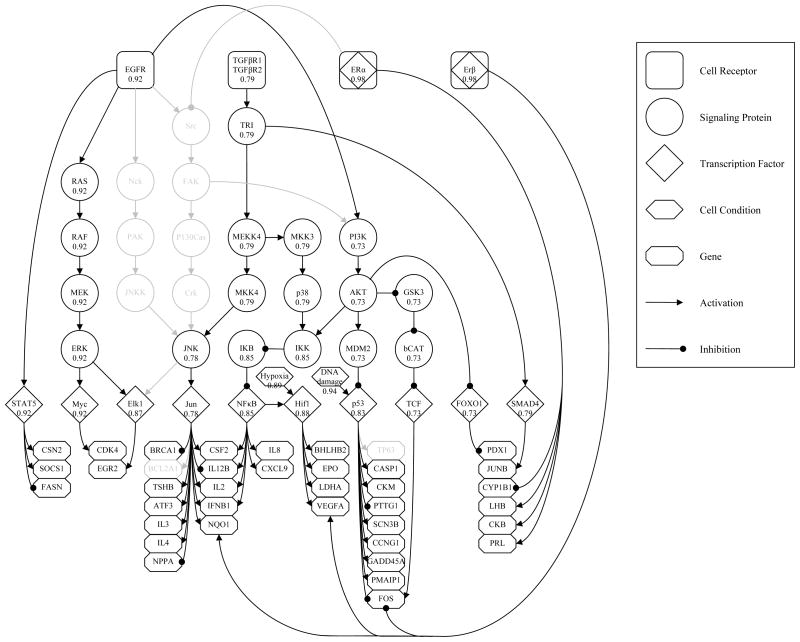
As another expert interpretation of the original graph 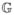, we consider the modified wiring diagram of Figure 5. Note that, compared to , lacks few genes that were originally observed, and several other proteins and connections. Absent components and their discarded pathways are also shown in light gray for better visualizing the difference.

Fig. 5.

A simpler expert interpretation of the original core topology of Figure 1. Discarded components and edges are shown in light gray for comparison. Scores at each node indicate the correlation coefficient between the corresponding status estimates under the original and modified wirings.

On the same gene expression data, we ran our algorithm using the revised topology and compared the new estimations to their counterparts found with . Figure 5 also quantifies the resulting agreement of inference for nodes that are common under both models. Attached to each v and averaged over 20 independent experiments, we give the correlation coefficient between subject dependent status estimations ${[{\widehat{\overline{x}}}_v^{(n\mid \mathbb{G})}]}_{n=1}^N$ and ${[{\widehat{\overline{x}}}_v^{(n\mid \stackrel{\sim }{\mathbb{G}})}]}_{n=1}^N$ based on respective structures and , and evaluated according to (15). The significance of correlations demonstrate the robustness of the model with respect to different wiring assumptions that agree with biological reality.

VI. Discussion and Conclusion

Cell signaling processes play a central role in the etiology of many diseases, and signaling proteins provide a logical target for therapeutic intervention with numerous therapeutics under development [19]. The success of imatinib mesylate (IM, Gleevec) in treating chronic myelogenous leukemia has greatly increased the hope for targeted therapy, however these new targeted therapeutics are designed to disrupt a single signaling protein. As studies in glioblastoma multiforme have demonstrated, each individual tumor has a different specific set of aberrant signaling proteins [18], [21], making it essential to identify in each individual which proteins need to be targeted for treatment.

The logical method to identify an aberrant signaling protein is to look for changes in protein post-translational modifications (PTMs), since most signal propagation takes the form of phosphorylation changes in proteins or cleavage events changing protein localization and structure. However, these measurements are presently very limited in vivo. An alternative approach is to use the mature microarray technology targeted at mRNA transcripts, since transcriptional changes resulting from activation or suppression of transcriptional regulators are primary endpoints for many signaling processes. Microarray data coupled to models of signaling networks provide a potential avenue for identification of individual signaling protein abnormalities.

We have designed a statistical model for cell signaling, which accounts for cell heterogeneity, can be robustly learned from available microarray data and supports rigorous statistical inference. Our effort was mainly invested in laying out a comprehensive framework to identify and quantify aberrations in signaling. Consequently, we used prior knowledge and considered a documented core topology (Figure 1) that is particular to our breast cancer study and available expression data. We followed a multi-level approach to elaborate the overall generative process starting from hidden phenotypes to final log-expressions with different statistical interpretations in cell, tissue, population and measurement levels.

It is worth noting here that, for computational purposes, we constructed our Bayesian network formulation at the cell level, with parameter-free, linear and generic transition probabilities as given in equation (2), which, it may be argued, oversimplify the underlying chemical processes. However, the overall model allows the user to incorporate his/her expert knowledge and to explain signaling dynamics with more complex, nonlinear choices, which in turn may enhance the predictive accuracy of the method. In fact, without sacrificing efficiency, one can assume alternative formulations to (2) that are still linear but favor the known dominance of one or more competing parents at crossing pathways; or, for instance, one can differentiate interactions at the signaling level from those at the level of transcription. To further enrich the model, one can even introduce extra parameters that can be validated as more protein data becomes available.

Note also that, due to lack of measurements on all hidden variables but ERα, the biological validation of our model remains currently very limited. On the other hand, ERα ground truth usually correlates with the majority of the genes. Thus, if the task were to predict ERα statuses only, one would argue for simpler Bayesian approaches with performances comparable to ours. However, this argument should not lessen the utility of our model which lays out a comprehensive framework to infer on each hidden component. In that regard, our ERα predictions we report here, should not be interpreted as an achievement, which otherwise could not be made, but rather a consistency check.

Finally, we have demonstrated model’s identifiability, reproducibility through simulations and robustness under biologically meaningful revisions of topology. Using real patient data, we validated its ability to recover receptor status in a breast cancer study. As signaling plays a central role in the etiology of many diseases, identification of the aberrant proteins driving signaling errors will provide information for personalized therapeutic intervention. It is expected that this will improve patient prognosis and reduce undesirable side-effects during treatment.

Appendix

A. Measurement Process

As argued in [2], we first assume the additive part $b_g^{(n)}$ of equation (5) is negligibly small due to background correction applied by scanner’s imaging software. Secondly, again proposed by the same authors, we consider a multiplicative decomposition for the gain factor $c_g^{(n)}$

$$c_g^{(n)}=\frac{d_g}{D^{(n)}}exp\{{\eta }^{(g,n)}\}.$$ (16)

We interpret each component as follows: Combined with the scanner gain, d_g represents the background corrected hybridization efficiency of the probe set assigned to gene g. The quantity D⁽ⁿ⁾, on the other hand, stands for the normalization constant applied across all probes of patient n. We take d_g to be gene specific and fixed for all subjects, whereas D⁽ⁿ⁾ to be subject dependent and the same for all genes. We further assume that D⁽ⁿ⁾ is proportional to the number C⁽ⁿ⁾ of cells contained in subject n’s experimented tissue, since it is usually set to the total intensity captured from the corresponding array. Finally, the remaining variation in $c_g^{(n)}$ is attributed to a multiplicative error term given as an exponential, whose argument is modeled i.i.d. for all genes and subjects, and realized as η^(g,n) for gene g and patient n.

Combining equations (4), (5) and (16), we obtain equation (6), i.e. our measurement model for log expression of gene g and patient n

$$y_g^{(n)}={\lambda }_g+log{\xi }_g({\phi }_R^{(n)})+{\eta }^{(g,n)}$$

where, probe specific parameters and the ratio C⁽ⁿ⁾/D⁽ⁿ⁾, which is constant by assumption, are absorbed by the final readout offset ${\lambda }_g=log\frac{a_g{d}_g{C}^{(n)}}{D^{(n)}}$, that is specific to gene g and independent of patients. In log scale, measurement noise η becomes additive and described as a zero mean Gaussian random variable with variance σ², which is the same for all genes and subjects.

B. Proof of Proposition 3.1

The result follows from the Markov property of the process and the linearity of the expectation. If v ∈ R, the claim holds by definition, with d_v = 0 and d_rv = δ(r,v). Otherwise, suppose the claim holds for all parents of v; then by induction we have

$$\begin{array}{l}E[X_v\mid {\phi }_R]=E[E[X_v\mid X_{\text{pa}(v)}]\mid {\phi }_R]=E\left[c_v+\sum _{u\in \text{pa}(v)}{c}_{uv}{X}_v\mid {\phi }_R\right]\\ =c_v+\sum _{u\in \text{pa}(v)}{c}_{uv}E[X_u\mid {\phi }_R]\\ =c_v+\sum _{u\in \text{pa}(v)}{c}_{uv}\left(d_u+\sum _{r\in R}{d}_{ru}{\phi }_r\right)\\ =\underset{d_v}{\underbrace{\left(c_v+\sum _{u\in \text{pa}(v)}{c}_{uv}{d}_u\right)}}+\sum _{r\in R}\underset{d_{rv}}{\underbrace{\left(\sum _{u\in \text{pa}(v)}{c}_{uv}{d}_{ru}\right)}}{\phi }_r\\ =d_v+\sum _{r\in R}{d}_{ru}{\phi }_r\end{array}$$

C. Gibbs Sampling

Gibbs sampling in the simulation step of SAEM, visits each root node r ∈ R, repeatedly in a fixed order, and produces a realization of the corresponding activation rate φ_r from its conditional density, given the current instantiations of other root variables and already observed gene expression levels. Then, it can be shown that, the sequence of simulated root activation rates, that are consecutively drawn from their univariate conditionals, constitutes a Markov chain, whose stationary distribution is the joint posterior f_R|G of interest.

Using Bayes rule and the Markov property, the conditional density of the activation rate φ_r of root r ∈ R, given the realizations (y_G, φ_R\{r}) of remaining variables, can be written as

$$\begin{array}{l}\frac{f_{GR}(y_G,{\phi }_r,{\phi }_{R\backslash \{r\}}\mid \theta )}{{\int }_0^1{f}_{GR}(y_G,{\stackrel{\sim }{\phi }}_r,{\phi }_{R\backslash \{r\}}\mid \theta )d{\stackrel{\sim }{\phi }}_r}=\frac{f_R({\phi }_r,{\phi }_{R\backslash \{r\}}\mid \theta )f_{G\mid R}(y_G\mid {\phi }_r,{\phi }_{R\backslash \{r\}};\theta )}{{\int }_0^1{f}_R({\stackrel{\sim }{\phi }}_r,{\phi }_{R\backslash \{r\}}\mid \theta )f_{G\mid R}(y_G\mid {\stackrel{\sim }{\phi }}_r,{\phi }_{R\backslash \{r\}};\theta )d{\stackrel{\sim }{\phi }}_r}\\ =\frac{f_r({\phi }_r\mid \theta ){\prod }_{g\in G_r}{f}_{g\mid R}(y_g\mid {\phi }_r,{\phi }_{R_r};\theta )}{{\int }_0^1{f}_r({\stackrel{\sim }{\phi }}_r\mid \theta ){\prod }_{g\in G_r}{f}_{g\mid R}(y_g\mid {\stackrel{\sim }{\phi }}_r,{\phi }_{R_r};\theta )d{\stackrel{\sim }{\phi }}_r}\end{array}$$

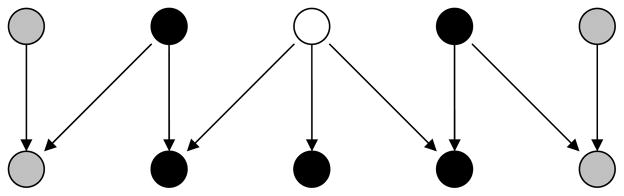
where G_r is the set of gene descendants of r, and R_r contains the roots other than r that have descendants in G_r. Terms ∏_r′∈R\{r} f_r′(φ_r′|θ) ∏_g∈G\Grf_g|R(y_g|φ_R\{r}; θ) that do not involve anything indexed with r, cancel each other in the second line, yielding the final expression, which only depends on realizations at nodes G_r ∪ R_r, i.e. the “Markov blanket” of r in G ∪ R (see Figure 6). Thus, we denote φ_r’s univariate conditional by f_r|GrRr(·|y_Gr, φ_Rr;θ).

Fig. 6.

A simple DAG with 5 roots and 5 leaves. Markov Blanket of the white node is the set of black nodes.

Sampling from f_r|GrRr is still not straightforward. Among different ways of doing this, we used factored sampling due to its simple formulation in our case. Since

$$f_{r\mid G_r{R}_r}(·\mid y_{G_r},{\phi }_{R_r};\theta )\propto f_r(·\mid \theta )\prod _{g\in G_r}{f}_{g\mid R}(y_g\mid ·,{\phi }_{R_r};\theta ),$$

generating K samples {s⁽¹⁾,…, s(^K)} from prior beta density f_r(·|θ) and choosing s⁽ⁱ⁾ (i = 1,…, K), with probability

$${\pi }_i=\frac{{\prod }_{g\in G_r}{f}_{g\mid R}(y_g\mid {\phi }_{R_r},s^{(i)};\theta )}{{\sum }_{j=1}^K{\prod }_{g\in G_r}{f}_{g\mid R}(y_g\mid {\phi }_{R_r},s^{(j)};\theta )},$$

as the new realization for φ_r, will approximate a variate from f_r|GrRr, as K tends to be large.

Notice that, drawing samples from standard beta priors is straightforward with available statistical packages, and so is evaluating weights π_i. Also, with a reasonable K, one does not have to wait for Gibbs sampling to mix within every single execution of the simulation step, since last samples returned from a given iteration of SAEM, are already used to initialize the chain for the next iteration.

D. Complete Data Log-likelihood

The complete data log-likelihood is

$$log{f}_{GR}({\mathbf{y}}_G,{\mathrm{\Phi }}_R\mid \theta )=-\mathrm{\Lambda }(\theta )+\langle \mathrm{\Pi }(\theta ),\mathbf{S}({\mathbf{y}}_G,{\mathrm{\Phi }}_R)\rangle .$$

In our case, functions Λ and Π are given by

$$\begin{array}{l}\mathrm{\Lambda }(\theta )=N\left(\sum _{r\in R}logB(a_r,b_r)+log\sqrt{2\pi }\sigma +\frac{1}{2{\sigma }^2}\sum _{g\in G}{\lambda }_g^2\right),\\ \mathrm{\Pi }(\theta )=N\left(\begin{array}{c}{\left(\begin{array}{c}{a}_r-1\\ b_r-1\end{array}\right)}_{r\in R}\\ \frac{1}{2{\sigma }^2}{\left(\begin{array}{c}2{\lambda }_g\\ -1\\ -2{\lambda }_g\\ -1\\ 2\end{array}\right)}_{g\in G}\end{array}\right)\end{array}$$

with sufficient statistic

$$\mathbf{S}({\mathbf{y}}_G,{\mathrm{\Phi }}_R)=\frac{1}{N}\sum _{n=1}^N\left(\begin{array}{c}{\left(\begin{array}{c}log{\phi }_r^{(n)}\\ log(1-{\phi }_r^{(n)})\end{array}\right)}_{r\in R}\\ {\left(\begin{array}{c}{y}_g^{(n)}\\ {[y_g^{(n)}]}^2\\ log{\xi }_g({\phi }_R^{(n)})\\ {[log{\xi }_g({\phi }_R^{(n)})]}^2\\ y_g^{(n)}log{\xi }_g({\phi }_R^{(n)})\end{array}\right)}_{g\in G}\end{array}\right).$$ (17)

E. Complete Data Maximum Likelihood

We here give the expression of the maximum likelihood estimator θ̂_ML in function of the sufficient statistic S described in (17). First, let ${\mathbf{s}}_r={[s_r^{(i)}]}_{i=1}^2$ and ${\mathbf{s}}_g={[s_g^{(i)}]}_{i=1}^5$ denote the two- and five-dimensional sub-vectors of the sufficient statistic in (17), corresponding to root r ∈ R and gene g ∈ G, respectively. The corresponding maximum likelihood estimator θ̂_ML is given as follows:

• For each root r ∈ R, â_r and b̂_r of the beta prior f_r will satisfy

  $$\begin{array}{l}\psi ({\widehat{a}}_r)-\psi ({\widehat{a}}_r+{\widehat{b}}_r)=s_r^{(1)}\\ \psi ({\widehat{b}}_r)-\psi ({\widehat{a}}_r+{\widehat{b}}_r)=s_r^{(2)}\end{array}$$

  where ψ(x) = Γ′(x)/Γ(x) is the digamma function. A closed-form solution to that system does not exist, but, similar to standard maximum likelihood parameter estimation of a beta density, â_r and b̂_r are found numerically.

• For each gene g ∈ G, the corresponding updated offset parameter is given by

  $${\widehat{\lambda }}_g=s_g^{(1)}-s_g^{(3)}$$
• Finally, the noise variance is obtained by

  $${\widehat{\sigma }}^2=\frac{1}{\mid G\mid }\sum _{g\in G}{s}_g^{(2)}-2s_g^{(5)}+s_g^{(4)}-{\widehat{\lambda }}_g^2.$$

F. The Rank-sum Test for Estimating Receptor Status

The rank-sum test is performed by first ranking each sample ${\widehat{\phi }}_{\text{ER}\alpha }^{(n)}$ in ascending order within the union of both populations. The test statistic U is the sum of the ranks coming from the “negative” population ${\mathrm{\Phi }}_{\text{ER}\alpha }^{-}$. (The choice of which rank sum is immaterial and leads to the same p-value.) Since both N⁺ and N⁻ are sufficiently large, U is approximately normal under H₀ with mean

$${\mu }_U=\frac{N^{-}(N^{+}+N^{-}+1)}{2}$$

and standard deviation

$${\sigma }_U=\sqrt{\frac{N^{+}{N}^{-}(N^{+}+N^{-}+1)}{12}}.$$

We expect that the population ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{-}$ to generate smaller activation rates than the population ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{+}$. Consequently, the alternative hypothesis H₁ states that U has a smaller mean than μ_U and the corresponding p-value is the left tail area of normal density $\mathcal{N}({\mu }_U,{\sigma }_U^2)$ determined by the observation U = u; that is, the probability P_H0(U ≤ u) of observing a test statistic U as small or smaller than the actual rank sum u found for ${\widehat{\mathrm{\Phi }}}_{\text{ER}\alpha }^{-}$ under the null hypothesis.