Decoding the activity of neuronal populations in macaque primary visual cortex

Abstract

Visual function depends on the accuracy of signals carried by visual cortical neurons. Combining information across neurons should improve this accuracy because single neuron activity is variable. We examined the reliability of information inferred from populations of simultaneously recorded neurons in macaque primary visual cortex. We considered a decoding framework that computes the likelihood of visual stimuli from a pattern of population activity by linearly combining neuronal responses, and tested this framework for orientation estimation and discrimination. We derived a simple parametric decoder assuming neuronal independence, and a more sophisticated empirical decoder that learned the structure of the measured neuronal response distributions, including their correlated variability. The empirical decoder used the structure of these response distributions to perform better than its parametric variant, showing that their structure contains critical information for sensory decoding. Our work shows how neuronal responses can best be used to inform perceptual decision-making.

A central question in computational and systems neuroscience is how signals carried by sensory neurons support perceptual judgments. To put these signals to use in behavioral tasks, the brain must accurately decode the responses of neurons encoding a sensory signal ^1-6. There are many reasons to think that the brain performs this decoding by combining signals from populations of neurons. First, the variability of a neuron’s response to repeated presentations of the same stimulus is considerable, and limits what can be inferred from individual neurons ^7-10. Second, the synaptic architecture of visual cortex ¹¹ makes it virtually impossible for a signal from any one neuron to lead directly to a behavioral outcome. Third, perceptual judgments are only weakly correlated with variations in the response of single neurons in sensory cortex ^12,13.

Many studies have focused on how much information about a stimulus is encoded in population activity ^2,14-18. Specifying how that information could be extracted from the population code is a challenge ^19,20. This latter issue is the problem of population decoding, a computational question that investigates how, and with what accuracy, a sensory stimulus can be inferred from the responses of neuronal populations, for example by a downstream neuron. Previous decoding studies have examined how a single stimulus estimate could be directly inferred from population responses, for instance by calculating the population vector ²¹ or the least-squares error estimator ²². Sensory decoding is, however, more general than reading out sensory responses for a particular psychophysical task such as estimation. A decoding framework should provide a rigorous account of the reliability of information embedded in population responses for a wide range of psychophysical tasks, including estimation and discrimination. We formulate the problem of sensory decoding as inference – computing stimuli given an observed population response ^1,4-6,23-29. The relevant information for inference can be rigorously represented by the likelihood function: the conditional probability of observing a neuronal response given a stimulus, evaluated across stimuli. The likelihood function is a rich representation for decoding. It has three features that make it a more attractive candidate for modeling decoding then ad hoc strategies ^21,22. First, it provides a rigorous explanation for many behavioral data ^30,31, especially cue combination ^26,32-34. Second, it is a parsimonious representation of the underlying neuronal responses because it can be used across a wide range of tasks such as deriving a single stimulus estimate (for example, the maximum of the likelihood), or discriminating between stimuli (by comparing their likelihoods). Third, it is an accurate yet simple representation because it can often be approximated by simple linear neuronal pooling rules ^5,25,26,35. Computing likelihoods with neurons has, however, proven to be challenging ⁶. In earlier work, approximations to the likelihood function were computed using parametric ^8,25,35-38 or mechanistic ³⁹ assumptions about the structure of the neuronal data. Furthermore, the response variability between neurons is correlated ^{2,16,18,39,40}. This property was ignored in many decoding models ^25,35,37, but not all ^20,36,41,42. The impact of these interneuronal correlations on decoding accuracy remains an open question.

We begin with a framework explored in previous theoretical work, in which the logarithm of the likelihood function is computed by a simple feedforward network that combines neuronal responses using weights derived from their response properties ^26,43. Using neuronal populations recorded from the primary visual cortex of anesthetized monkeys, we quantified the decoding accuracy from this likelihood-based framework in two example tasks: orientation estimation and discrimination. We first evaluated the predictions of a parametric decoder that weighted neurons using a fixed rule derived from assumptions about the structure of the neuronal data. We then extended this model and developed an empirical decoding framework, which learned the parameters of the log-likelihood function from the measured neuronal response distributions. This empirical decoder, unlike the parametric one, adapted itself to the actual response distributions, including their correlated variability, using an assumption-free data-driven pooling rule that learned how to combine neuronal signals from the population activity. We found that the structure of the neuronal response distributions carries sensory information that a data-driven decoder can extract to improve its performance.

Results

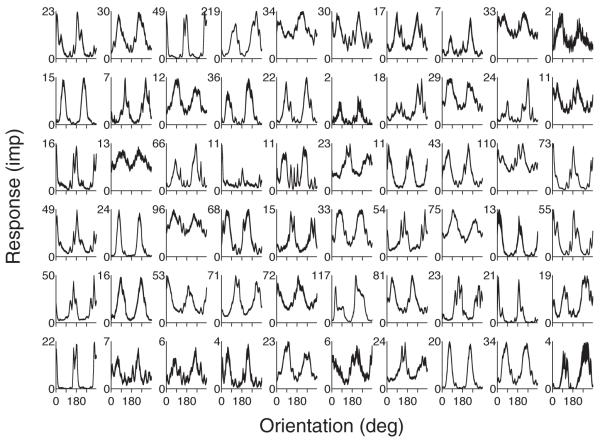
To study population decoding, we recorded ensembles of single units in the superficial layers of macaque primary visual cortex (V1) using an array of fixed microelectrodes ¹⁶. We analyzed the responses of 5 populations recorded from 3 monkeys. We presented sinusoidal gratings that covered the receptive fields of all recorded neurons; the gratings drifted in 72 different equally spaced directions (36 orientations). We chose spatial frequency and drift rate to maximize the ensemble response. Each grating was presented for 1280 ms, and was followed by blank screen for 1280 ms. The response of each neuron was taken as the number of spikes evoked during the stimulus period. Following spike sorting, we obtained populations of between 40 and 74 neurons. The orientation tuning curves from one array (Fig. 1) reveal the typical heterogeneity of the neuronal response properties of our population. Most neurons were responsive (response: 17.1 ± 1.0 impulses, mean ± s.e.m.), and orientation selective (full-width at half height: 51.2 ± 0.9 deg).

Figure 1.

Orientation tuning curves (spike count, mean ± s.e.m.) for a population of 60 neurons (data set 3).

Deriving the likelihood function from neuronal responses

Uncertainty about a visual stimulus in the face of variable neuronal responses can be resolved using the response of a population of neurons to compute the likelihoods of possible stimuli ^{1,2,4,6,23,26-28,36,37}. The computation of likelihood is often based on assumptions about the structure of the neuronal response distributions, in particular their variability. Our neuronal responses could be considered as belonging to the exponential family with linear sufficient statistics (Supplementary Fig. 1), and therefore the logarithm of the likelihood function is a linear function of the neuronal responses ^26,43. The log-likelihood of an orientation θ given a measured set of neuronal responses r_i is represented by a weighted sum of the responses from the N neurons using a vector of pooling weights W and an offset B:

$$\log L\left(\theta \right)=\sum _{i=1}^N{W}_i\left(\theta \right)r_i+B\left(\theta \right)$$ (1)

The pooling weights represent how strongly each neuron contributes to the computation of the log-likelihood function for a given orientation, and the offset is an adjustment to the log-likelihood function. We used the simplest member of the exponential family as our first approximation of a likelihood-based decoder: we assumed the neuronal spike counts to be Poisson distributed and statistically independent from neuron to neuron. For this Poisson Independent Decoder (PID), the pooling weights are derived from the logarithm of the neuronal tuning functions ^5,25,35, and the offset incorporates the overall bias in the coverage of orientations that inevitably results from considering neuronal samples of limited size.

The PID assumes the statistics of the neuronal response in V1, which naturally raises the question of how its performance is affected by those assumptions. We therefore developed a variant decoder – the Empirical Linear Decoder (ELD) – for which the pooling weights and offset are learned from the data. For this, we considered the Support Vector Machine (SVM), an empirical discriminator from statistical learning theory ^44,45. The SVM does not make particular distributional assumptions, but rather learns the structure of the neuronal response distributions. To derive the ELD, we considered the linear variant of the SVM to discriminate pairs of neighboring orientations, and used the corresponding SVM parameters to construct an empirically derived log-likelihood function that is linear in the neuronal responses (eq. 1). The ELD allowed us to ask whether considering the empirically observed neuronal response distributions improved the decoding accuracy compared to working with parametric assumptions.

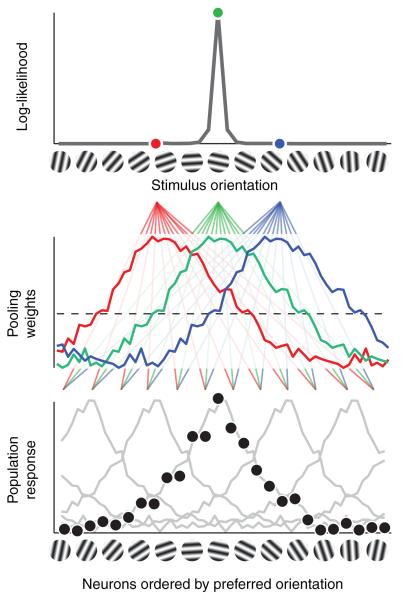
The computations associated with deriving the log-likelihood function for the ELD are illustrated in Figure 2. The average population activity for an ensemble of neurons ordered by preferred orientations exhibits a narrow bell-shaped curve. A stimulus elicits a population response centered on the neuron with the closest preferred orientation (black dots). The log-likelihood function evaluated at any given orientation is the product of the population activity and the pooling weight for this orientation. Examination of the average pooling weights reveals that neurons with preferred orientations closest to the stimulus orientation are pooled using the largest positive weights, and their activity therefore contributes the most to the resulting log-likelihood. Neurons with preferred orientations farther away from this orientation (closer to orthogonal) have negative weights, and their activity reduces the log-likelihood. The log-likelihood function had a peak at the estimated stimulus and fell off for more different orientations. Despite the broad neuronal pooling, the log-likelihood function was sharply tuned, thus being an efficient re-encoding of the underlying population response. To quantify the accuracy of decoding from populations of sensory responses, we tested our likelihood-based decoders in two example psychophysical tasks: orientation estimation and discrimination.

Figure 2.

Scheme of the linear log-likelihood decoding framework with parameters of the Empirical Linear Decoder derived from data set 3. To emphasize how the log-likelihood function is constructed, we ordered neurons by preferred orientations, and averaged the neuronal response across trials and stimulus orientations to avoid distractions due to the different orientation responses. The average population activity was replicated for five stimulus orientations (lower panel). A given stimulus elicited the population response represented by the black dots, each dot corresponding to the response of one neuron. We computed the average neuronal pooling weight across orientations and replicated it for three orientations, one of which coinciding with the stimulus (middle panel). The population response corresponding to a stimulus (dots in lower panel) is combined with the pooling weights for each orientation (three colored curves in middle panel) to yield the log-likelihood function evaluated at these orientations (three colored dots in upper panel). The pooling weights can be seen as the coefficients of filters that determine how a neuron’s response contributes to the log-likelihood: a neuron’s contribution is positive when the stimulus is close to this neuron’s preferred orientation, and is negative for remote stimuli.

Estimating orientation

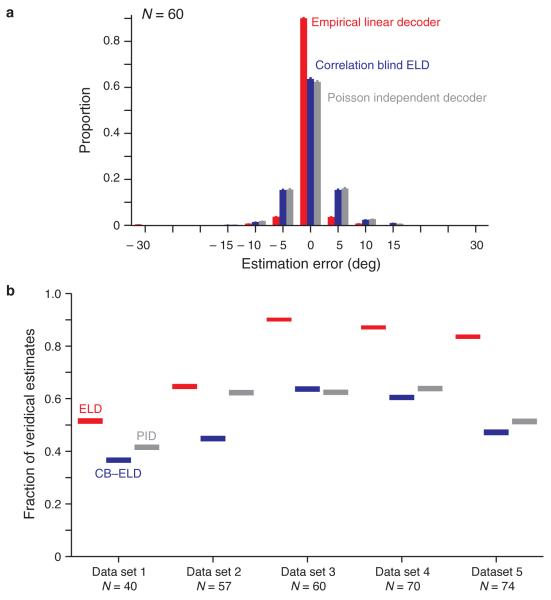
We examined the orientation estimation accuracy of the PID by asking how closely the maximum of the log-likelihood function matched the stimulus. We computed the distribution of estimation errors across all orientations and trials for a population of 60 neurons. The PID orientation estimates were correct in approximately 60% of cases. The accuracy was significantly better for the ELD (Fig. 3a). This suggests that the assumptions inherent in the PID yield a neuronal read-out that is less accurate than empirically deriving the log-likelihood from the data. To verify these findings for the 4 other sets of V1 population responses, we evaluated the estimation accuracy by measuring the proportion of veridical orientation estimates (Fig. 3b). The PID yielded an estimation accuracy that was on average 24 ± 6 % (mean ± s.e.m.) lower than the ELD, with differences among data sets mainly due to variations in the population sizes and tuning of individual neurons (see Discussion).

Figure 3.

Orientation estimation accuracy for the Empirical Linear Decoder (ELD), the correlation-blind ELD (CB-ELD), and the Poisson Independent Decoder (PID). (a) The orientation estimate corresponding to a given neuronal population response was the orientation maximizing the log-likelihood function computed from this response. The estimation error is the difference between the estimated and true orientations. The absolute value of the overall estimation error (mean ± s.e.m.) for data set 3 was 0.77 ± 0.05 deg, 2.21 ± 0.06 deg and 2.27 ± 0.06 deg for the ELD, CB-ELD and PID respectively. To describe estimation in more detail, we represented the distribution of estimation errors (mean ± s.e.m. estimated by bootstrap). The proportion of orientation estimates at the veridical stimulus orientation was 0.90 ± 0.00, 0.64 ± 0.01 and 0.62 ± 0.01 for the ELD, CB-ELD and PID respectively. (b) We compared data sets using the proportion of veridical estimates (mean ± s.e.m. estimated by bootstrap).

Two factors could make the ELD superior to the PID: it does not assume any particular response distribution, and it does not assume that responses are independent. It is quite straightforward to explore the influence of the covariance of neuronal responses. Most of our pairs of neurons showed correlated trial-to-trial variability with an average correlation of 0.17 across all pairs and data sets (distribution of coefficients in Supplementary Fig. 2), in agreement with most ^16,40 but not all ⁴⁶ other studies. To remove these correlations without changing the response statistics of individual neurons, we randomly shuffled the responses of each neuron to each orientation across trials. We then trained the ELD on this shuffled (and therefore correlation-free) data, and tested its performance on the raw (unshuffled) data. Comparing the performance of this correlation blind (CB) decoder with the full ELD tells us how much interneuronal correlations affect the computations for decoding by quantifying the information that is lost when (raw) neuronal responses are read-out using a decoder that is “correlation-blind” ^2,41. The CB-ELD yielded less accurate orientation estimates than the ELD (Fig. 3a), and across data sets the estimation accuracy of the CB-ELD was lower by 33 ± 3 % (mean ± s.e.m.) compared to the ELD (Fig. 3b). These results show that a log-likelihood function empirically derived from measured neuronal responses is able to reflect changes in their correlated variability, and that ignoring these correlations hurts the decoding accuracy. In contrast, the PID used a fixed rule, and was not affected by trial shuffling of the responses because it is correlation blind by assumption. Because the PID and the CB-ELD had comparable accuracy (Fig. 3a,b), we wondered whether the ELD reduces to the PID in the absence of correlations. It emerges that even though their performance is similar, the decoders differ internally in their pooling weights; a quantitative measure of this difference is described in Supplementary Figure 3.

Discriminating orientations

We modeled estimation from a population of neurons by using the peak of the log-likelihood function to extract a single stimulus estimate. We now turn to orientation discrimination, which will depend on shape of the log-likelihood function. To discriminate two orientations given a population response, the decoder has to compare the likelihoods associated with the alternatives, for example by computing the logarithm of the ratio of the likelihoods. This log-likelihood ratio is a linear decision function defined by its discrimination weight vector w and discrimination offset b:

$$\begin{array}{cc}\hfill & \log LR({\theta }_1,{\theta }_2)=\log \left(\frac{L\left({\theta }_1\right)}{L\left({\theta }_2\right)}\right)=\log L\left({\theta }_1\right)-\log L\left({\theta }_2\right)\hfill \\ \hfill & =\sum _{i=1}^N[W_i\left({\theta }_1\right)-W_i\left({\theta }_2\right)]r_i+[B\left({\theta }_1\right)-B\left({\theta }_2\right)]=\hfill \\ \hfill & =\sum _{i=1}^N{w}_i({\theta }_1,{\theta }_2)r_i+b({\theta }_1,{\theta }_2)\hfill \end{array}$$ (2)

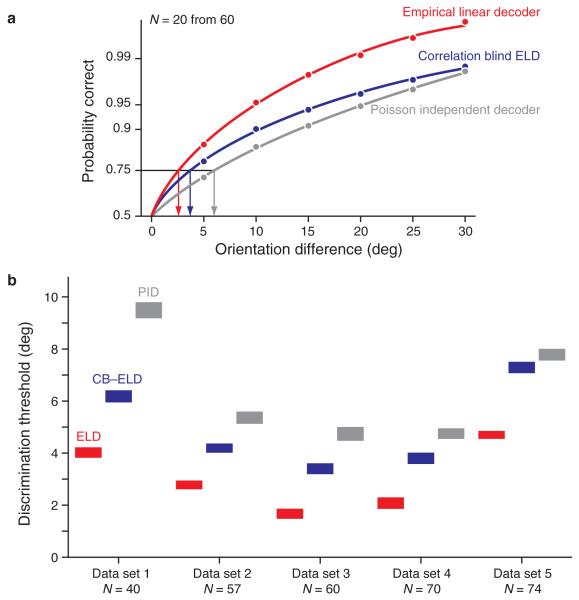
The parameters of the log-likelihood ratio (eq. 2) are the difference between the parameters of the log-likelihood representation (eq. 1) evaluated at the two orientations θ₁ and θ₂. The sign of the log-likelihood ratio indicates which of θ₁ or θ₂ is more likely to have elicited the observed population response. We quantified discrimination performance with a population neurometric function that measures the discrimination accuracy as a function of the angular difference Δθ between the two orientations. Each point of the neurometric function gives the discrimination accuracy between θ and θ+Δθ, averaged across all 72 values of θ. The population neurometric function of the ELD in Figure 4a shows that the discrimination accuracy increased monotonically with Δθ, as is typical of a psychometric function that represents behavioral performance in a discrimination task. The PID and CB-ELD yielded less accurate discrimination than the ELD, just as they were less accurate for orientation estimation (Fig. 4a). The same was true for the other 4 sets of V1 population responses (Fig. 4b). These results generalized across neuronal population subsamples of different sizes from our 5 data sets (Supplementary Fig. 4). In summary, orientation discrimination is more accurate when the empirical structure of the neuronal response distributions is taken into account, especially when including interneuronal correlations.

Figure 4.

Orientation discrimination accuracy for the Empirical Linear Decoder (ELD), the correlation-blind ELD (CB-ELD), and the Poisson Independent Decoder (PID). (a) The population neurometric functions represent the discrimination accuracy (mean ± s.e.m. across orientations) as function of the orientation difference. The interpolations were done using a cumulative Weibull distribution fitted using maximum likelihood. To avoid showing a neurometric function that mainly covers the asymptotic regime (accuracies close to 1), the discrimination accuracies were averaged across random subsets of 20 neurons from data set 3. The orientation discrimination threshold yielding an accuracy of 0.75 (mean ± s.e.m. estimated by bootstrap) was 2.58 ± 0.16 deg, 3.70 ± 0.17 deg and 5.99 ± 0.20 deg for the ELD, CB-ELD and PID respectively. (b) We evaluated the discrimination accuracy across data sets by comparing their orientation discrimination thresholds (mean ± s.e.m. estimated by bootstrap) computed using entire populations.

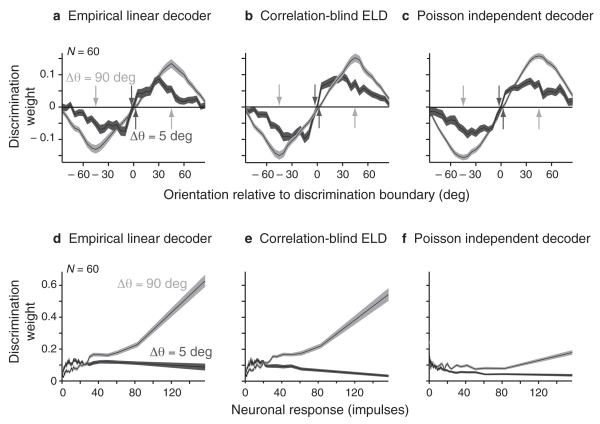
The function of both the PID and ELD derives from how they linearly pool sensory responses to approximate the log-likelihood function. To understand how these decoders assign weights to neurons with different response characteristics, we examined the weighting profile of each decoder in a series of discrimination tasks covering a range of values of Δθ. We averaged the discrimination weights (w in eq. 2) across neurons with respect to the discrimination boundary, which we varied in steps of 5 deg around the clock to sample all possible discriminations. For coarse discriminations (Δθ = 90 deg), the most positive and negative average weights matched the target orientations (Fig. 5a,b,c light, the arrows indicating the discriminanda). Therefore, when discriminating between very different orientations, neurons whose preferred orientations are aligned with the discriminanda are most strongly recruited: discrimination is facilitated because the responses of these neurons differ strongly. However, for fine discriminations (Δθ = 5 deg), this mechanism is ineffective because neurons tuned for one of the discriminated orientations respond almost as well to the other. To overcome this, the decoders emphasize neurons with preferred orientations further apart from the discriminanda (Fig. 5a,b,c dark), effectively assigning the highest weights to neurons for which the stimuli are located at the flanks, rather than the peaks, of the tuning curve (also illustrated in Supplementary Fig. 5). Thus when decoding sensory responses according to a linear representation of the log-likelihood function, the neuronal pooling mechanisms change automatically and adaptively with the perceptual task. The importance of off-optimal neurons in fine discriminations is an automatic consequence of likelihood-based decision-making and does not require ad hoc computations to create a particular decision rule.

Figure 5.

Dependency of the discrimination weighting functions with respect to stimulus orientation and neuronal response magnitude for data set 3. (a) The discrimination weights were averaged across neurons after being aligned to each of the 72 possible discrimination boundaries. Neuronal preferred orientations were estimated from a fit to a von Mises function. The weights (mean ± s.e.m.) of the Empirical Linear Decoder (ELD) are shown for fine (dark) and coarse (light) discriminations. (b,c) Same as a, but for the correlation blind ELD (CB-ELD) and the Poisson Independent Decoder (PID). (d) The absolute value of the discrimination weights of the ELD (mean ± s.e.m.) is plotted against the neuronal response strength (spike counts) across all orientations by ordering for each neuron the discrimination weights by increasing neuronal response to one of the two discriminated orientations. We plotted their running average using a window over the 100 nearest neighbors for fine (dark) and coarse (light) discriminations. (e,f) Same as d, but for the CB-ELD and the PID.

The average discrimination weights empirically derived from the data (ELD and CB-ELD) were qualitatively similar to weights based on parametric assumptions on the neuronal response distributions (PID). However, the superiority of the ELD over the PID in orientation discrimination tasks (Fig. 4a,b) must be a consequence of the different discrimination weights the two decoders assign to individual neurons, as reflected in Supplementary Figure 3 by the differences between their pooling weights (W in eq. 1, from which the discrimination weights are derived in eq. 2). The ELD made adjustments to the PID weights, and we suppose that the difference in their discrimination weights varies from neuron to neuron in a way that may be obscured when considering only the average across neurons as in Figure 5a,b,c.

To study the differences in neuronal pooling mechanisms for orientation discrimination on the level of single neurons, we asked how the discrimination weights (w in eq. 2) depended on the responsiveness of individual neurons. For fine discriminations, the weights associated with the ELD, CB-ELD and PID were largely independent of the responsiveness of the neurons, yielding a uniformly distributed population read-out (Fig. 5d,e,f dark). This suggests that for fine perceptual discriminations, neuronal pooling mechanisms are determined mostly by the neurons’ preferred orientations (off-optimal neurons, see above) and much less by their responsiveness. However, for coarse discriminations the ELD and CB-ELD, and to a lesser degree the PID, relied more strongly on the neurons responding most (Fig. 5d,e,f light), approaching a winner-takes-all population code ^1,23. In other words, a subset of very responsive neurons tuned to the target orientations contributed particularly strongly to discriminating between remote orientations. These results suggest that an empirical neuronal pooling mechanism may recruit neurons with different response strengths differently depending on the perceptual task. Our results also show that the impact of correlations on the neuronal pooling mechanisms (as visualized by comparing the ELD and CB-ELD) depended little on neuronal responsiveness. The difference between the weights of the ELD and PID for the more responsive neurons may therefore reflect a deviation from the Poisson hypothesis – stronger responses may be less variable than Poisson statistics predict, perhaps because of the regularizing influence of the neuronal refractory period. The ELD, but not the PID, can take this deviation into account to optimize neuronal pooling, exemplifying the advantage of an empirical read-out rule (ELD) over a fixed rule (PID).

Discussion

We investigated how the identity of sensory stimuli can be inferred from the responses of populations of neurons in primary visual cortex, and how the neuronal pooling mechanisms associated with a simple linear decoding framework vary with perceptual tasks and neuronal response characteristics. This framework allowed us to probe the impact of interneuronal correlations on population coding, a topic that is extensively debated. Some argue that in homogenous populations of neurons correlations impair decoding ^13,18. Others note that under some conditions, correlations can increase the information available for decoding ^4,14,41, especially for heterogeneous neuronal populations ²⁰. Experimental findings reported in the retina ^39,42, in V1 of anesthetized monkeys ¹⁷, and in small populations of somatosensory ³⁸ and motor ³⁶ neurons suggest that correlations can modestly increase the information available for decoding. Our findings extend these studies by showing how accurately stimulus information can be extracted from the responses of large ensembles of sensory cortical neurons when the structure of the data, in particular interneuronal correlations, is taken into account. We showed that ignoring the correlations contained in the data decreases the decoding accuracy. We also asked whether correlations affect the total amount of information available in population codes (Supplementary Fig. 6), and found that discriminating neuronal data containing correlations is more accurate than discriminating data without them. This finding suggests that correlations can help decoding when using a read-out rule empirically derived from the data. Because neuronal response are correlated (Supplementary Fig. 2), biological decoders must be capable of learning this structure if they are to perform most accurately.

Three main characteristics set apart a likelihood-based decoding strategy from other ad hoc approaches to decoding. First, the importance of likelihood-based computations is well known in psychophysical examinations of human behavior where subjects were shown to rely on likelihood-based strategies to combine cues across features ³³, modalities ³² and time ³⁴. Second, likelihood function provides a unified currency for how the responses of sensory neurons can contribute to a variety of perceptual task using the same representation. We illustrated this point by investigated likelihood-based decoding from neuronal populations for two tasks: orientation estimation and discrimination. Third, provided the neuronal responses can be considered as belonging to the exponential family with linear sufficient statistics, the linear representation of the log-likelihood function is simple, yet accurate. We verified in Supplementary Figure 7 that decoding based on the linear log-likelihood function is more accurate than reading out a single stimulus estimate from the neuronal response using the population vector ²¹ or the least-squares error estimator ²². These point estimators also poorly generalize across tasks: they are estimators, and thus need ad hoc rules to deal with discriminations. Furthermore, likelihood-based decoding strategies that linearly weight neuronal responses automatically solve the problem of finding the most informative neurons, thus avoiding ad hoc pooling rules ^1,7,8,10,15. This allows us also to see a neuronal correlate of the orientation repulsion effect, a phenomenon known in general for psychophysical fine discriminations for some time ³⁰, and more recently the mechanisms of a perceptual illusion ³¹.

An important test for the linear log-likelihood framework is contrast invariance: how well does a decoder that learned its parameters at a given stimulus contrast generalize to decoding neuronal responses elicited by a different stimulus contrast? We examine this question in Supplementary Figure 8 using neuronal responses recorded from the same population at high and low contrast. While the linear log-likelihood framework (eq. 1) is not contrast invariant per se, the pooling weights W are close to contrast invariant if the offset term B is learned for each contrast condition. The contrast-dependent offset term thus allows the linear log-likelihood framework to function differently at each contrast, without having to re-compute the neuronal pooling weights. One might wonder whether it is plausible to require the offset parameter to have a contrast-dependent value, given that the contrast of any particular scene is not known a priori. This seems less unreasonable when one considers that contrast can be captured by the total local population activity, which could be pooled to set the gain or offset in a neural decoding circuit using commonly-accepted mechanisms ⁴⁷.

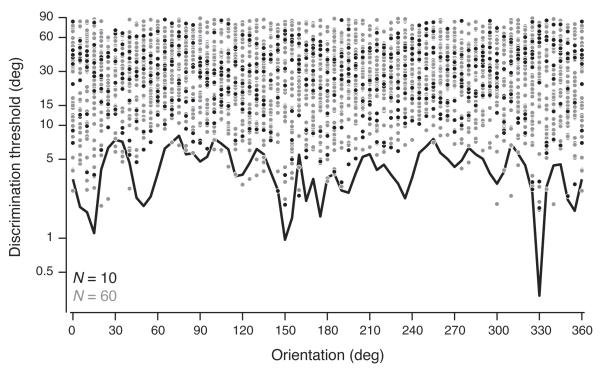
A natural question is how well our decoding accuracies compare to behavioral findings. The discrimination thresholds that we obtained from full populations (40 to 74 neurons) were between 2 and 5 deg (see Fig. 4b), thus reasonably close to previously reported behavioral thresholds and also to the thresholds of the most sensitive neurons for a given orientation discrimination ^7,10. However, it is unreasonable to make direct comparisons to behavior from our population recording because such comparisons hinge on knowing the time window over which sensory activity contributes to the behavioral decision, and on the particulars of the contributing neuronal population. We addressed the latter point indirectly by asking whether the size of the neuronal population is a good indicator of decoding accuracy. For a given neuronal population, a larger pool size yields better decoding (each curve in Supplementary Fig. 4 is monotonically decreasing). However these studies mask an important aspect: the heterogeneous properties of the neuronal populations that we happened to capture in our experiments, in particular the neuronal tuning properties (amplitude, bandwidth, preferred orientation, baseline) and response variability. This heterogeneity accounts for the wide range in orientation discrimination thresholds across data sets for a given neuronal pool size (the curves in Supplementary Fig. 4 are all significantly distinct). We studied this heterogeneity in more detail by comparing the orientation discrimination thresholds of individual neurons to those of an entire population of 60 neurons using the empirical decoder (Fig. 6, all dots and gray line). The population discrimination threshold at any given orientation was slightly lower than the threshold of the most selective neuron at that orientation, showing the distributed nature of the information useful for discrimination. We then randomly chose a subset of 10 neurons (Fig. 6, black dots and line), and found that on average the population discrimination threshold increased from 2.26 ± 0.13 deg to 4.26 ± 0.22 deg (mean ± s.e.m.). The population threshold was also more uneven across orientations for the smaller population size, suggesting that the poorer decoding accuracy is mainly due to a decrease in orientation coverage from individual neurons induced by the smaller population sample. Furthermore, for some orientations the single neurons thresholds were better than the population thresholds (dots below line), and the smaller population yielded more accurate decoding than the larger one (black line below gray line), because adding “noisy” neurons can degrade performance in our decoders. This reveals that the decoders fall short of optimality, which is to be expected because any linear decoder can only approximate, but never match, the full information content of the population response. We conclude that the response heterogeneity within a neuronal sample, especially the coverage of orientation by individual neurons, is a stronger indicator of decoding performance than the population size.

Figure 6.

Orientation discrimination thresholds of the Empirical Linear Decoder corresponding to an accuracy of 75% using data set 3. The discrimination thresholds were derived from the neurometric functions evaluated at each stimulus orientation. We computed the discrimination thresholds of the entire population of 60 neurons (gray line) and for each neuron individually (all dots, each corresponding to the threshold of one neuron). We then chose a random subset of 10 neurons, and computed the corresponding population threshold (black line, the black dots indicating the corresponding individual thresholds).

The likelihood function captures the accuracy with which a neuronal population can represent a sensory input. Our work shows how the nervous system could use a simple linear pooling strategy to compute log-likelihood functions from populations of correlated neurons. The linear log-likelihood model could be implemented in a feedforward circuit using synaptic weights ^1,25, and has thus a strong kinship to feedforward models of cortico-cortical connections. In this interpretation, the log-likelihood function is not a decoder per se; it rather sets the stage for decoding by re-encoding the sensory input. Regardless of how these computations might be implemented, the access to the linear log-likelihood would enable the central nervous system to evaluate sensory information in the context of prior information, using Bayesian principles ^23,27, through summation of neuronal response vectors rather than through awkward multiplications of re-encoded probability distributions ^26,29,43.

Our work shows that the accuracy with which linear pooling mechanisms approximate the log-likelihood function depends on whether they take into account the neuronal response distributions, including their correlated variability. We showed that a decoder based on parametric descriptions of neuronal responses could infer stimuli from evoked responses reasonably well. Our empirical decoder serves as an example for how simple modifications of a parametric decoder can result in more accurate sensory decoding. The refinements in the neuronal pooling evident in empirical decoding might underlie changes in behavioral sensitivity that are learned from experience, and recent work on perceptual learning falls comfortably within this framework ⁴⁸. An empirical decoder could then reflect these changes in the value and significance of sensory evidence. Whether – and how – the nervous system learns more efficient decoding strategies by incorporating knowledge about the statistics of its sensory responses remains to be discovered.

Appendix

Methods

Visual stimulation

We presented stimuli on a gamma-corrected CRT monitor (Eizo T966, mean luminance 33 cd/m²) at a resolution of 1280 by 960 pixels and a refresh rate of 100 Hz. Stimuli were generated using EXPO software on an Apple Macintosh computer (http://corevision.cns.nyu.edu). We used drifting sinusoidal gratings at full contrast presented through a large circular aperture and surrounded by a gray field of mean luminance. The monkey viewed the stimuli binocularly. The orientation of the grating was varied around the clock in steps of 5 deg, yielding a total of 72 orientations. The spatial frequency of the grating was chosen to elicit a robust response on average from the whole population of neurons, and was then kept fixed during the experiment. In practice, in different experiments we used spatial frequencies between 1.1 and 1.3 c/deg. The gratings all drifted smoothly at 6.25 Hz. Because the visual axes were relatively close together for the first two experiments, we used single large apertures (8.7 and 9.9 deg) to cover all the receptive fields in both eyes. Because the direction of gaze of the two eyes was particularly divergent in the third monkey (data set 5), we presented two identical stimuli, one covering the receptive fields of each eye, using two smaller 2.6 deg apertures. We made no attempt to adjust the retinal disparity of the stimuli. For the purpose of this study, all data sets were analyzed similarly. The stimuli were presented for 1280 ms, and were followed by a blank screen of mean luminance for another 1280 ms. We recorded 50 trials for each stimulus condition. The presentation order of the stimuli was randomized.

Recording methods

We recorded from three hemispheres of two pig-tailed (M. nemestrina) and two hemispheres of one cynomolgus (M. fascicularis) opiate anesthetized, paralyzed adult male macaque monkeys. The procedures for acute electrophysiology used in our laboratory have been described in detail elsewhere ⁴⁹. Briefly, we maintained anesthesia with an intravenous infusion of 4-30 μg/kg/h of sufentanil citrate in lactate dextrose-saline (4-10 ml/kg/h). The monkey was paralyzed to prevent eye movements by an infusion of vercuronium bromide (100 μg/kg/h). We continuously monitored vital signs: heart rate, lung pressure, electroencephalogram, body temperature, urine volume and specific gravity, and end-tidal partial pressure in CO₂. Gas-permeable contact lenses protected the corneas, and supplementary lenses chosen by direct ophtalmoscopy provided refraction. At the end of the experiment, the animal was sacrificed with an overdose of sodium pentobarbitol. All experimental procedures were conducted in compliance with the US National Institutes of Health Guide for the Care and Use of Laboratory Animals and with the approval of the New York University Animal Welfare Committee.

We collected data from populations of simultaneously recorded neurons in the primary visual cortex (area V1) using methods described elsewhere ¹⁶. The extracellular recordings were obtained from an array of 10 by 10 fixed silicon microelectrodes of length 1 mm spaced by 400 μm. The array was inserted using a high-velocity pneumatic gun to minimize bleeding and tissue damage. The electrodes were inserted about 0.6 mm into cortex, yielding recordings from the superficial layers of V1. The neuronal signal on each channel was amplified (gain of 5000) and bandpass filtered between 250 Hz and 7.5 kHz. It was then digitized at a sampling rate of 30 kHz. Single-unit activity was first obtained from a PCA-based offline spike sorting algorithm. This stage was followed by a careful manual inspection and refinement of the neuron’s isolation based on the shape of the waveforms (multiple window discrimination).

Evoked activity was estimated over the full stimulus presentation. We neglected the contamination by the blank preceding each grating because 1. This period of the response (the first ~ 60 ms corresponding to typical V1 response latencies ⁵⁰) was of negligible duration compared to the 1280 ms stimulus presentation time and 2. This contamination was the same for each grating. Spontaneous activity was assessed on the last 500 ms of each blank presentation to avoid contamination induced by the preceding grating. To get visually driven neurons, we only accepted neurons of which the peak or trough of their tuning curve fell outside of the window defined by the mean and one standard deviation of their spontaneous activity. Furthermore, we obtained meaningful sample of V1 neurons by only considering neurons with tuning curves that could be well approximated (r² ≥ 0.75) by bimodal circular Gaussian functions (the sum of two von Mises functions with different preferred orientations, amplitudes and bandwidths), allowing us to accommodate for direction (mono-modal) or orientation (bi-modal) tuning. We obtained populations of simultaneously recorded neurons of sizes 40, 57, 60, 70, and 74. Each data set was obtained in a ~ 3 hour-long recording session.

Poisson Independent Decoder

For the Poisson Independent Decoder (PID), we approximated the distribution of spike counts with a Poisson probability distribution, and pooled the likelihood functions across neurons assuming statistical independence. This allowed us to retrieve a representation of the log-likelihood function of a stimulus orientation θ that linearly combines the population response r_i of the N neurons:

$$\begin{array}{cc}\hfill & \log L\left(\theta \right)=\log \left(\prod _{i=1}^{N}p(r_i\mid \theta )\right)=\sum _{i=1}^N\log \left(\frac{f_i{\left(\theta \right)}^{r_i}}{r_i!}\text{exp}(-f_i\left(\theta \right))\right)\hfill \\ \hfill & =\sum _{i=1}^N\log \left(f_i\left(\theta \right)\right)r_i-\sum _{i=1}^N{f}_i\left(\theta \right)-\sum _{i=1}^N\log (r_i!)=\sum _{i=1}^N{W}_i\left(\theta \right)r_i+B\left(\theta \right)\hfill \end{array}$$

The pooling weight W is the logarithm of the individual tuning curves f_i(θ) defined by the average response of each neuron to a given orientation ⁵,²⁵,³⁵. Due to the steep nonlinearity of the logarithm close to 0, we put a floor ε on f_i(θ). We chose to set ε as the inverse of the number of trials, effectively asserting that there should be at least one spike across all trials for each stimulus orientation. The orientation-dependent component of the offset term B represents the sum across individual tuning curves. This offset term is a measure of the heterogeneity of the neuronal population sample. For a finite population of neurons with regularly spaced preferred orientations and similar tuning parameters (amplitude, bandwidth, and baseline), the offset will be very close to constant. In this case the offset just shifts the log-likelihood function up or down independently of the stimulus, and does therefore not influence decoding. However, for a finite population with heterogeneous neurons, especially with non-uniform distribution of preferred orientations, the offset term is stimulus dependent. In this case, the log-likelihood function will be affected by the offset term: the neuronal responses are combined with the poling weights, and the offset is added to this combination.

Empirical Linear Decoder

The discrimination between neuronal population responses corresponding to two stimulus orientations is a pattern classification problem. A classifier divides the space spanned by the neuronal response population vector into two classes, each of which is more strongly associated with one of the two stimulus orientations. A good classifier makes few errors on the training data, while generalizing well to novel data. We chose to use a simple, yet accurate and robust classifier from statistical learning theory: the Support Vector Machine SVM ⁴⁵. The SVM has been shown to exhibit the best generalization ability and least overfitting for a wide range of applications, including sparse and noisy data ⁴⁴. The SVM is a non-parametric classifier that empirically derives its parameters from the structure embedded in the data. The linear variant of the SVM is ideally suited as a model for the Empirical Linear Decoder (ELD) in orientation discrimination tasks because 1. It discriminates between neuronal responses corresponding to two different orientations using a linear decision function and 2. It computes its parameters from the neuronal response distributions without making assumptions on the shape of the spike count distributions, or on the structure of the interneuronal interactions.

The linear SVM estimates a separating hyperplane by maximizing the normalized margin between the two classes of responses, while minimizing the classification errors (responses on the wrong side of the hyperplane) and the responses within the margin stripe. For a data set of spike counts from a population of N neurons recorded on P trials, we denote the response vector by r_p ∈ R^N where p = 1,K ,P and the class labels by t_p = ±1 corresponding to the two stimulus orientations. The SVM algorithm is a minimization problem that finds the normal vector w ∈ R^N and offset b ∈ R of the separating hyperplane as follows:

$$\underset{w,b,\xi }{\text{min}}\left({\parallel w\parallel }^2+C\sum _{p=1}^P{\xi }_p\right)$$

subject to the constraints for each p = 1,K ,P:

$$t_p(w\cdot r_p+b)\ge 1-{\xi }_p\text{and}{\xi }_p\ge 0$$

where ξ_p are “slack” variables allowing for class overlap (responses correctly classified although being closer to the hyperplane that the margins for 0 < ξ_p ≤ 1) or misclassified responses (responses on the wrong side of the hyperplane for ξ_p > 1). The regularization parameter C is set by cross-validation. Discrimination between two stimulus orientations θ₁ and θ₂ is finally done using the sign of the SVM decision function:

$$y({\theta }_1,{\theta }_2)=\sum _{i=1}^N{w}_i({\theta }_1,{\theta }_2)r_i+b({\theta }_1,{\theta }_2)\equiv \log LR({\theta }_1,{\theta }_2)$$

We then equated the SVM decision function with the log-likelihood ratio log LR(θ₁,θ₂) of the ELD. The SVM decision function was used as a local linear approximation of the difference between the log-likelihood evaluated at two stimulus orientations. The entire log-likelihood function was then reconstructed by computing the cummulative sum of the ELD log-likelihood ratios between adjacent orientations, akin to reconstructing a function given its finite differences:

$$\log L\left({\theta }_i\right)=\sum _{k=2}^i\log LR({\theta }_k,{\theta }_{k-1})=\sum _{j=1}^N{W}_j\left({\theta }_i\right)r_j+B\left({\theta }_i\right)$$

with log L(θ₁) = 0. Because the length of the weight vector w is arbitrary, we independently renormalized the SVM weights corresponding to each discrimination (or equivalently scaled the log-likelihood ratios) in order to minimize the orientation estimation bias computed from the reconstructed log-likelihood functions. By construction, the log-likelihood function of the ELD is linear in the neuronal responses, and its parameters are empirically derived from the neuronal data using the SVM algorithm.

Evaluating linear decoding

For the estimation and discrimination weights studies, we obtained directional data (mono-modal tuning curves) by considering each neuron twice: its tuning was separated in the range from 0–180 deg and in the range from 180–360 deg, yielding two tuning curves each spanning 180 deg. When computing the discrimination errors and thresholds, we considered the data in the full 360 deg range. To ensure good generalization ability, the discrimination errors and weights were averaged across 10-fold cross-validation sets. To compute the discrimination accuracies for neuronal subsets, we used random sampling without replacements. The number of these samples depended on the population size, and was governed by the following heuristic: for a subset of N neurons from a neuronal population of size N_tot, we chose $n_c\frac{N_{tot}}{N}$ random samplings where n_c is the covering number (n_c = 10 in Fig. 4a).