A Geometry-Based Particle Filtering Approach to White Matter Tractography

Abstract

We introduce a fibre tractography framework based on a particle filter which estimates a local geometrical model of the underlying white matter tract, formulated as a `streamline flow' using generalized helicoids. The method is not dependent on the diffusion model, and is applicable to diffusion tensor (DT) data as well as to high angular resolution reconstructions. The geometrical model allows for a robust inference of local tract geometry, which, in the context of the causal filter estimation, guides tractography through regions with partial volume effects. We validate the method on synthetic data and present results on two types in vivo data: diffusion tensors and a spherical harmonic reconstruction of the fibre orientation distribution function (fODF).

1 Introduction

Tractography is the process of reconstructing possible white matter fibre pathways from diffusion MRI data. An increasing variety of algorithms dedicated to this problem are available, as reviewed recently in [1,2]. Many such methods are developed with a focus on the specific model used to represent the diffusion process, e.g. [3,4] for diffusion tensors, or e.g. [5,6] for more complex parametric and non-parametric models of diffusion. Additionally, directional information from the diffusion MRI signal is often integrated without a geometrical model of the pathways to be reconstructed. This is the case for existing methods based on the unscented Kalman filter, e.g. [2], or particle filters, e.g. [1,7].

In this paper, we propose a novel tractography approach which models the trajectories of white matter pathways as 3D curves, and infers these curves independently of the underlying model of the diffusion process. The method incorporates a geometrical model for co-varying 3D curve sets, called `streamline flows' (SF) [8,9], which is infered at each position along the fibre with a particle filter, so that the estimation at each step builds upon previous estimates. With a small parameter set, the SF model captures within a 3D neighborhood $\mathcal{N}$ the full 3D geometry of a collection of curves that may vary within $\mathcal{N}$ in the tangential direction, as well as in the normal and bi-normal directions. Modeling fibre tracts as a collection of curves that `flow' together in 3D space, and infering a local geometrical model for such structures allows for increased robustness in tractography to partial volume effects in areas where different fibre populations with distinct orientations co-exist. This is particularly useful when working with DT data, as tractography may then proceed to areas not reachable with standard methods. We demonstrate our method with synthetic and in vivo data, with diffusion tensors as well as a spherical harmonic reconstruction of the fODF.

2 3D Streamline Flows and the Generalized Helicoid

The work in [8,9] argues for the representation of white matter fibres as sets of dense, locally parallel 3D curves called `streamline flows', and derives their differential geometry, which is characterized by three curvature functions: the tangential, normal and bi-normal curvatures. A local model for such flows is then proposed in [8,9] which consists of two orientation functions θ(x, y, z) and ϕ(x, y, z), which define the local orientation of the flow (its tangent vector) at every point (x, y, z) in E³ (three-dimensional Euclidean space):

$$\begin{array}{cc}\hfill \theta (x,y,z)& ={\tan }^{-1}\left(\frac{K_{T}x+K_{N}y}{1+K_{N}x-K_{T}y}\right)+K_{B}z,\hfill \\ \hfill \varphi (x,y,z)& =\alpha \theta (x,y,z).\hfill \end{array}$$ (1)

Here α is a constant, and K_T, K_N and K_B are scalar parameters that specify the values of the tangential, normal and bi-normal curvatures of the flow. This formulation is justified in [8,9] via minimal surface theory as a smooth local model for 3D streamline flows with a small parameter set that describes the flow geometry. In fact, the formulation for θ (and ϕ) given in (1) is that of a generalized helicoid. Generalized helicoids are minimal hypersurfaces in n-dimensional Euclidean space Eⁿ, whose geometry has been studied in e.g. [10].

3 Particle Filter Based Tractography

3.1 Theory

This section reviews the particle filter method, described in full elsewhere [11,12]. Details specific to our implementation are given in Section 3.2.

Let S_t ∈ Rⁿ be a state vector at time t evolving at discrete time steps according to S_t+1 = f_t(S_t) + n_t, where n_t is i.i.d. random noise with known probability distribution function (pdf). At time t, observations Y_t ∈ R^p become available. These measurements relate to the state vector via the observation equation Y_t = h_t(S_t) + ν_t, where ν_t is measurement noise with known pdf. It is assumed that the initial state distribution p(S₀), the state transition function denoted by f_t and the observation likelihood given the state, denoted by p(Y_t|S_t), are known. The particle filter is a sequential Monte Carlo method which produces at each time t a cloud of K particles, ${\left\{S_t^{\left(i\right)}\right\}}_{i=1}^K$, whose empirical measure follows closely p(S_t|Y_1:t), the posterior distribution of the state given past observations.

The algorithm starts by drawing K samples (particles) from the initial state distribution p(S₀) in order to approximate it by $p_0^K\left(S\right)=\frac{1}{K}{\sum }_{i=1}^K\delta (S_0-S_0^{\left(i\right)})$, and then implements Bayes' recursion at each time step. Assuming that one can sample from the posterior distribution p(S_t|Y_1:t), an empirical estimate of this distribution is given by $p_t^K(S_t\mid Y_{1:t})={\sum }_{i=1}^K{\omega }_t^{\left(i\right)}\delta (S_t-S_t^{\left(i\right)})$, where ${\omega }_t^{\left(i\right)}$ is the weight associated with the i-th particle. In this paper, the state process is assumed to be Markovian, i.e., the likelihood can be expressed as p(Y_t|S_0:t) = p(Y_t|S_t). This leads to the following recursion relation for the weights [12]:

$${\omega }_t^{\left(i\right)}\propto {\omega }_{t-1}^{\left(i\right)}\frac{p(Y_t\mid S_t^{\left(i\right)})p(S_t^{\left(i\right)}\mid S_{t-1}^{\left(i\right)})}{q(S_t^{\left(i\right)}\mid S_{t-1}^{\left(i\right)},Y_t)},$$ (2)

where q(·) is the importance sampling density, and $p(S_t^{\left(i\right)}\mid S_{t-1}^{\left(i\right)})$ is the prior distribution that ensures smoothness. The empirical distribution for the posterior is then given by $p_t^K(S_t\mid Y_t)={\sum }_{i=1}^K{\tilde{\omega }}_t^{\left(i\right)}\delta (S_t-S_t^{\left(i\right)})$, where ${\tilde{\omega }}_t^{\left(i\right)}$ are normalized weights. Finally, resampling is performed so that particles with low weights are eliminated [12]. At each time step, the maximum a posteriori (MAP) estimate $S_t^{MAP}$ given by the particle with the largest normalized weight ${\tilde{\omega }}_t^{MAP}$ is stored and used for tractography as described in Section 3.3.

3.2 Implementation

Our implementation uses a state vector S = {K_T, K_N, K_B, α, m_x, m_y, m_z, β}, where the first four components parametrize a local SF model for the underlying tracts, as defined by (1). The last four determine the orientation of the SF model in E³, with vector m = [m_x, m_y, m_z] and a rotation angle β around m. Two SF examples generated using (1) are visualized in Fig. 1.

Fig. 1.

Two views of a set of two streamline flow examples (one in green and one in red) generated using (1), each sampled with nine streamlines. Left: An orthographic projection from above. Right: A 3D view. The flow parameters are as follows: Green: K_T = −0.3, K_N = 0, K_B = 0, α = 0. Red: K_T = 0.2, K_N = 0.3, K_B = 0.1, α = 0.3.

The initial state distribution p(S₀) is obtained by setting the m_x, m_y and m_z components of each particle to the principal eigenvector of a DT reconstruction in each seed voxel. The other five state components are set to 0. The state transition function f_t is then used to propagate the particles with normally distributed noise n_t ~ N(0, Σ), where Σ is user-defined.

The observation likelihood $p_t(Y_t\mid S_t^{\left(i\right)})$ is computed by instantiating the streamline flow defined by $S_t^{\left(i\right)}$ in a voxel neighborhood $\mathcal{N}$ of size n × n × n. At each voxel with position vector x = (x, y, z) in $\mathcal{N}$, the ODF ψ_x is then evaluated in the direction of the streamline flow at x, as given by (1). The observation likelihood is then defined as the average of these values:

$$pt(Y_t\mid S_t^{\left(i\right)})\equiv \frac{1}{\mid \mathcal{N}\mid }\sum _{\mathbf{x}\in \mathcal{N}}{\Psi }_{\mathbf{x}}(\theta \left(\mathbf{x}\right),\varphi \left(\mathbf{x}\right)).$$ (3)

Note that no restrictions are placed on ψ, as it may be a diffusion tensor, or any other diffusion or fibre ODF.

To ensure smoothness of the tractography, we define a prior based on $S_{t-1}^{MAP}$ rather than on $S_{t-1}^{\left(i\right)}$, i.e., $p(S_t^{\left(i\right)}\mid S_{t-1}^{\left(i\right)})\propto \exp (-\parallel S_t^{\left(i\right)}-S_{t-1}^{MAP}\parallel ∕\sigma )$. Finally, we q(·) to q(·) ~ N (0, Σ). Both σ and Σ are user-defined.

3.3 Tractography Algorithm

Given the MAP estimate $S_t^{MAP}$ obtained at each time step, our method consists in performing streamline tractography over a short distance following the SF field defined by $S_t^{MAP}$. Given a neighborhood $\mathcal{N}$ of size n × n × n voxels, we follow the streamline flow over a distance of n/3 voxels starting from the center of $\mathcal{N}$. Performing tractography by following the infered streamline flow model allows for a regularization of the path and for robustness to partial volume effects.

4 Experiments and Results

4.1 Synthetic Data Validation

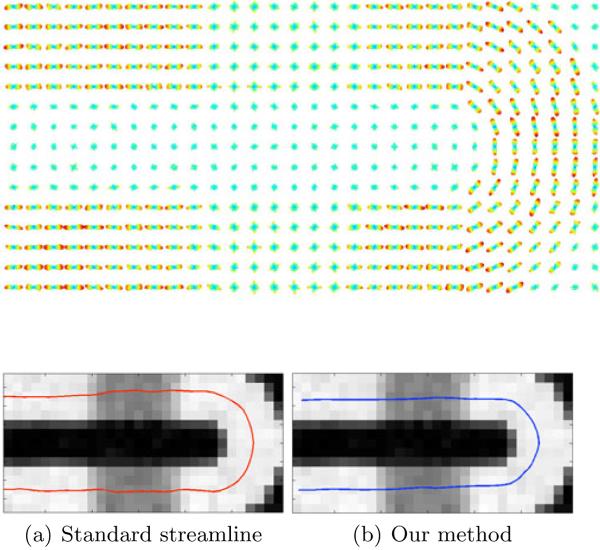
A synthetic fODF volume that simulates a U-fibre with two 90° crossing regions was generated using the methodology described in [13]. First, a diffusion-weighted MR signal was simulated over a 15×30×5 voxel grid using a single tensor model for each fibre population, with eigenvalues [1200, 100, 100] * 10⁻⁶ s/mm², and background tensors with eigenvalues [1500, 1500, 1500] * 10⁻⁶ s/mm². The signal from both fibre populations was then added in the crossing regions, followed by the addition of Riccian noise over the entire volume to achieve a signal-to-noise ratio of 7. In a second step, an icosahedral sampling of the unit hemisphere was used to generate a set of 81 gradient directions. Together with the synthetic diffusion-weighted signal, they were incorporated in the reconstruction scheme of [13] to produce an fODF volume, illustrated in Fig. 2. We compared our particle filter tractography method with a standard streamline method [3] on this dataset, with results shown in Fig. 2. Our method was run with K = 1000 particles, and a neighborhood $\mathcal{N}$ size of 5 × 5 × 5 voxels. Both methods were seeded with a single seed. No major difference between the methods is observed, although our method gives a somewhat smoother path.

Fig. 2.

Top: a slice though the synthetic fODF volume. Bottom: tractography result using standard streamline tractography [3] (a) and using our method (b). The tractography is overlaid on an image displaying generalized FA. Both tracts were seeded in the bottom left corner of the path.

4.2 In vivo Data Validation

Diffusion-weighted images of a human brain were acquired on a GE Signa HDxt 3.0T scanner using an echo planar imaging sequence with a double echo option, an 8 Channel coil and ASSET with a SENSE-factor of 2. The acquisition consisted in 51 directions with b = 900 s/mm², and 8 images with b = 0 s/mm², with scan parameters TR=17000 ms, TE=78 ms, FOV=24 cm, 144 × 144 encoding steps, 1.7 mm slice thickness, 85 axial slices covering the whole brain.

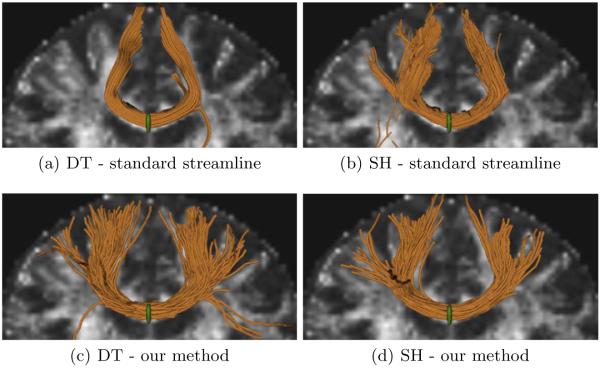
We demonstrate our tractography method both on DT data as well as on a spherical harmonic (SH) reconstruction of the fODF obtained with the method of [13], with order 8 spherical harmonics and a regularization parameter λ = 0.006. Tractography was initiated in a small region of interest (ROI) located in the midsagittal slice of the corpus callosum, with 10 streamline seeds per voxel. We ran our particle filter method using K = 1000 particles for the DT example, and K = 100 particles for the SH data. A smaller number of particles for SH data is sufficient possibly because more directional information is available as compared to DT. The size of neighborhood $\mathcal{N}$ was 5 × 5 × 5. Tractography was stopped when the fractional anisotropy (FA) (or the generalized FA for the case of SH data) was below a threshold, or when tractography reached the border of the brain mask. For comparison purposes, we repeated the experiments with the same seeds on the same datasets using a standard streamline tractography method [3], with the same stopping criteria. In the case of SH data, a `branching' scheme was added to the standard method, so that when more than one peak is detected in the ODF, another streamline is seeded at that location. It can be noted from the results in Fig. 3 that our method substantially outperforms the standard method by recovering the transcallosal projections, with both types of datasets. False positive fibres obtained on the SH data by the standard method were removed using exclusion ROIs.

Fig. 3.

Tractography originating from a small seed region (green) in the midsagittal slice of the corpus callosum. Top row: standard streamline tractography [3] with DT data (a) and SH data (b). Bottom row: Our particle filter tractography method applied to DT data (c) and SH data (d). The FA image is shown in the background for gross anatomic reference. Note the tracts are not exactly in the plane of the FA image and are located more anteriorly.

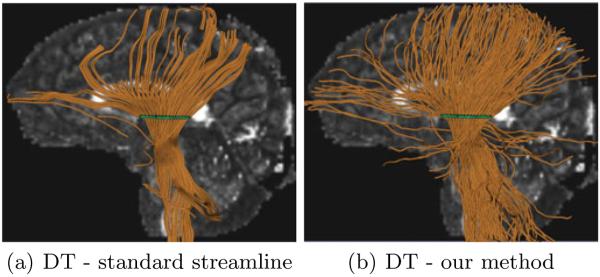
The methods were also compared on DT data with a seed ROI located in the cortico-spinal tract (CST) of the left hemisphere, with 2 streamline seeds per voxel and K = 1000 particles for our method. The results are shown in Fig. 4. Again, our method substantially outperforms standard streamline tractography. Although the in vivo evaluation presented here is only qualitative, it does demonstrate the recovery of tracts that are anatomically known to be present (e.g. [14]), but that the standard method fails to recover.

Fig. 4.

Tractography on DT data originating from a seed region (green) in the cortico-spinal tract. (a): Standard streamline tractography [3]. (b): Our particle filter tractography method The FA image is shown in the background for gross anatomic reference. Note the tracts are not in the plane of the FA image and are located more laterally.

5 Discussion and Conclusion

This paper introduced a novel method for performing fibre tractography, formulated in a manner independent of the underlying diffusion model. The method makes use of a particle filter which estimates, at each position along the fibre, the best streamline flow model for the local fibre tract geometry. Tractography is then performed in the space of this locally estimated model, which results in the regularization of the fibre path and the ability to proceed through regions of partial volume effects, both with with diffusion tensor and high angular resolution diffusion data. This aspect of the algorithm is important, since it can result in significantly improved tractography in contexts when only low angular resolution acquisitions are available, e.g. in clinical settings. A current limitation of the method is that it propagates a single path and does not fully utilize all the information inherent in the local SF field. In future work, we will augment the algorithm with branching capabilities in locations where the estimated SF model indicates a fanning fibre configuration. The main drawback of our method with respect to traditional streamline tractography is the computational cost, proportional to the number of particles and associated mostly with computing (3). However, our results indicate that even a relatively small number of particles can produce improved tractography. Our in vivo results are not as smooth as those obtained with the standard method, but a more efficient implementation should allow for a larger number of particles and thus smoother tracts.

Algorithm 1.

The particle filter based tractography algorithm.

foreach Seed Point do

Compute p(So) as described in §3.2;

t ← 1;

while (G)FA > threshold and current tract position is inside brain mask do

for i = 1 to K do

$S_t^{\left(i\right)}\leftarrow S_{t-1}^{\left(i\right)}+n_t$;

Compute ${\omega }_t^{\left(i\right)}$ using (2), as described in §3.2;

${\tilde{\omega }}_t^{\left(i\right)}\leftarrow {\omega }_t^{\left(i\right)}∕{\sum }_i^K{\omega }_t^{\left(i\right)}$;

${\tilde{\omega }}_t^{MAP}\leftarrow {\max }_i\left({\tilde{\omega }}_t^{\left(i\right)}\right)$;

Perform local tractography using $S_t^{MAP}$, as described in §3.3;

Perform particle resampling [12];

t ← t + 1;