From the first intention movement to the last joiner: macaques combine mimetic rules to optimize their collective decisions

Abstract

Mechanisms related to collective decision making have recently been found in almost all animal reigns from amoebae to worms, insects and vertebrates, including human beings. Decision-making mechanisms related to collective movements—including pre-departure and joining—have already been studied at different steps of the movement process, but these studies were always carried out separately. We therefore have no understanding of how these different processes are related when they underlie the same collective decision-making event. Here, we consider the whole departure process of two groups of Tonkean macaques (Macaca tonkeana), using a stochastic model. When several exclusive choices are proposed, macaques vote and choose the majority. Individuals then join the movement according to a mimetism based on affiliative relationships. The pre-departure quorum and the joining mimetic mechanism are probably linked, but we have not yet identified which transition mechanism is used. This study shows that decision-making related to macaque group movements is governed by a quorum rule combined with a selective mimetism at departure. This is the first time that transition mechanisms have been described in mammals, which consequently helps understand how a voting process leads to social amplification. Our study also provides the first complete proof that there is continuity in the decision-making processes underlying collective movements in mammals from the first intention movement right through to the last joiner.

1. Introduction

Animal groups use complex decision-making processes to synchronize their activities and movements [1–3]. Studies on collective decision-making have increased sharply over the last 15 years, and have described mechanisms such as social amplification in almost all animal reigns from amoebae to worms, insects and vertebrae, including human beings [2,4–8]. Authors reported the occurrence of pre-departure processes such as social amplification (increasing probability to display behaviour according to the number of individuals performing this behaviour; [9,10]) in wolves [11] and gorillas [12] or voting (choice between exclusive alternatives according to the majority) in African buffalos [13] and hamadryas baboons [14]. In other species, the initiation process appears to suffice in order to propose and to start a movement [15]. Repeated initiations allowing group movements could either be carried out by one specific individual alone—defined as a personal leadership—or by several group members—defined as a distributed leadership [16]. After initiation of the movement—preceded or not by a pre-departure process—other group members join the movement and hence become followers [17]. This joining of individuals may follow a specific organization based on individual characteristics or social relationships [18]. In some species, authors reported that males are more often located at the front and the back of the movement, whereas females and juveniles occupy more central positions [19–21]. Authors suggest that this organization may be a strategy for juveniles to decrease predation risk and for males to increase their access to food sources. In other species, individuals join the movement according to their kinship or to their affiliative relationships because being associated to specific related or dominant individuals may increase individual fitness [18–21].

There is a growing body of evidence that pre-departure and joining processes are ruled by amplification. In ants (Temnothorax sp. [22]) or in honeybees (Apis mellifera [23]), the probability of an individual immigrating to a specific nest depends on a threshold number of individuals having already chosen this nest. A quorum response could also explain group movement decisions in three-spine sticklebacks (Gasterosteus aculeatus) when two directions are proposed: animals choose the direction taken by the majority of individuals [24]. Thus, in fishes, ants or bees, individuals respond to a quorum threshold when several exclusive choices are possible. In other species, the individual probability to join a movement depends on mimetic rules without any threshold [15,25]. This mimetic process is anonymous [15,25] or selective [26] and follows a linear law (absence of threshold). In white-faced capuchin monkeys, the probability of any individual joining the movement and the probability of the first departed individual cancelling its initiation both follow linear rules and lead to a threshold function: until at least three individuals have joined the movement, the departure can be cancelled at any time [15]. After the joining of three individuals, all group members join the movement as an acceptance of a sub-majority.

Decision-making mechanisms related to collective movements—including pre-departure and joining—have been studied at different steps of the movement process. These studies showed similarities between species and these similarities illustrate a parsimony and an optimality of collective decision-making then illustrated a parsimony and optimality of collective decision-making [1,22–24,26]. However, these different steps were always studied separately. Therefore, we have no real knowledge of how these different processes are related when they underlie the same collective decision-making event. In fact, no study has yet been carried out to elucidate exactly which transition mechanism links the pre-departure and departure processes. Here, we consider the whole departure process—pre-departure, initiation and joining—of two groups of Tonkean macaques (Macaca tonkeana; 10 and 22 individuals, respectively), using a stochastic model.

In a series of previous studies conducted on this species, we showed that macaques may have to vote between several exclusive choices [27]. Wild Tonkean macaques typically live in primary and secondary forests in Sulawesi (Indonesia) and are frugivorous. As fruit trees are scattered throughout the forest, this dispersion may lead animals to choose between different food patches and vote. Individuals displayed preliminary behaviours in the direction they favoured, irrelevant of their hierarchical rank, age or sex [17,26,27]. The decision to start and move was then ruled by a sequence of quorums: the group went in the direction for which a majority of individuals had displayed preliminary behaviours. When a direction was chosen and the initiation completed, individuals joined the movement according to a selective mimetism based on affiliative relationships [26]. We also found that the number of notifying individuals influences the probability of group members to join the movement [17]. When a pre-departure period is present, the quorum response seems to apply on top of the selective mimetism. This means that mechanisms allowing the collective movement are not different, whether only one direction is proposed or two. This suggests that the pre-departure quorum and the joining mimetic mechanism are probably linked, but the exact transition mechanism responsible is still unknown.

Moreover, we have yet to establish exactly how far such combinations of mechanisms could contribute to optimizing the collective decision, and how the decision-making process changes from one to two proposed directions. In order to answer these questions, we analysed each step of the process—pre-departure, initiation and joining—and implemented them in a model. Modelling helps gain a better insight into processes underlying collective decisions (e.g. [15,28,29]). In this model, individuals within a resting area have to choose and move together to one of two possible foraging areas. By using an agent-based model, we can recapture all data relating to mechanisms of collective decision-making and implement them in the chronology they happened. Observed phenomena are then compared with simulated ones.

2. Methods

(a). Subjects and environment

The two study groups of Tonkean macaques were bred in semi-natural conditions at the Strasbourg University Primatology Center. They ranged in a 0.5 ha park (fenced field), containing different patches of vegetation between which individuals could collectively switch. The first Tonkean macaque group studied (November 2005 to March 2006), consisted of 10 individuals. The second group (study carried out from December 2003 to April 2004) consisted of 22 individuals. The composition of both groups was similar to that found in wild groups [30,31]. Animals had free access to an inside shelter with commercial pellets and water ad libitum. Fruit and vegetables were distributed once a week, outside observation sessions.

(b). Observational protocol

The beginning of a group movement was defined by the first departure of an individual who walked more than 10 m in less than 40 s, according to criteria used by Leca et al. [16] and Sueur & Petit [17,18]. The departure of the first individual over a distance of more than 10 m was an obvious signal for other group members. A ‘joiner’ was defined as any individual walking more than 5 m in a direction that formed an angle of less than 45° with the direction of the first departing individual. The following behaviours were recorded and named as ‘preliminary behaviours’ when exhibited before departure [17,27]: back glance and intention movement. A back glance is defined as an individual turning its head and looking towards other group members. If the eyes of animals could not be observed, we used the direction of the head—with an angle greater than 135° from the direction of the movement—to determine a back glance (see [32] for more details). An intention movement is considered to have occurred when an individual walks between 1 and 5 m, in a specific direction. A stop of more than 2 s after an advance was considered to show the end of the behaviour. Direction of the body axis of individuals indicated the direction of the future group movement [13]. We considered the back glances as preliminary behaviours when an individual had previously made at least one intention movement and had moved away from the group. These preliminary behaviours are formal indications of a choice between two candidates and could be considered as a vote [13,14,27]. We called individuals displaying preliminary behaviours notifying individuals. We considered a direction to exist when there were at least two preliminary behaviours for that direction. If the directions of at least two individuals displaying preliminary behaviours formed an angle greater than 45°, we considered these directions to be different. The enclosure where each group lived was marked with reference points, and the position (±1 m) of each animal as well as the distance it walked was recorded. Group movements occurring in agonistic or sexual contexts were discarded from the analysis. Previous studies showed that the different possible activities of individuals, before or after moving, did not influence the decision-making process in any way [17]. Events were only taken into account if more than two-thirds of group members were present in or around the area ≤10 m from the starting point of the first departed individual. Using video scoring, C.S. recorded the type as well as the frequency of any behaviour displayed by each group member. Measurements were taken using the all occurrence sampling method, both during the 20 minutes prior to a group movement, and after the start of the group movement [33].

(c). Modelling

We implemented the model in Netlogo v. 3.1.4 [34]. At the start of a simulation, all agents (N) are in an area called the resting area and have to move to another area qualified as a foraging area. Two foraging areas are present in order to induce the voting process. At each time step (one second) in the model, a number between 0 and 1 is randomly attributed for each resting agent (i.e. at the resting area); when this number is smaller than the theoretical probability of each equation (from 1 to 6), the individual changes its state (i.e. decides to move, chooses a direction and so on); if this number is higher than the theoretical departure probability, the agent stays in the same state. We include individual identities and the network of affiliative relationships for the observed group in the model. Affiliative relationships are taken from previous studies [18,26,27,32]. We set the number of simulations to 10 000 for each group.

(d). Statistical analysis

Even though many routes were available and taken by the group in the enclosure, no event was recorded in which more than two directions were displayed before the departure of a group. We used analysis of probability distribution (survival analysis) to analyse the probability of displaying a preliminary behaviour [15]. Relations between variables were analysed using curve estimation tests [26,27,35]. Only the values of the model fitting best with the observed data are indicated in the results. Tests were performed using SPSS v. 10 (SPSS Inc., Chicago, USA). α was set at 0.05. Means were ±s.e.m.

3. Results

(a). Probability to display a first preliminary behaviour

We first analysed the process(es) used to display first preliminary behaviours in one or two directions and thus assessed how two different directions of movement appear.

Analyses of observed data show that the probability 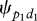to display a first preliminary behaviour p₁ in one direction d₁ is constant per time unit: the distribution of the durations between the end of the previous collective movement and the first preliminary behaviour of a new collective movement follows an exponential curve (curve test estimation: F_1,30 = 470; R² = 0.94; s.e.m. = 0.168; p < 0.00001 for group 1; F_1,27 = 918; R² = 0.97; s.e.m. = 0.146; p < 0.00001 for group 2). This probability 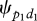equals 0.0013 for group 1 and 0.0015 for group 2. The probability 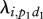per individual therefore equals 0.00013 for group 1 and 0.00007 for group 2:

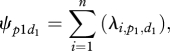3.1

where n is the number of resting individuals. For equation (3.1), n = N, the number of individuals in the group. N = 10 for group 1, and 22 for group 2.

Comparisons between observed and simulated data show that the simulated durations between the end of a previous collective movement and a first preliminary behaviour of a new collective movement are similar to the observed ones (Mann–Whitney test; group 1: N_obs = 37, N_sim = 10.000, mean_obs = 893.81 ± 1253.73, mean_sim = 891.37 ± 900.34; Z = −1.707, p = 0.074; group 2: N_obs = 30, N_sim = 10.000, mean_obs = 616.56 ± 578.87, mean_sim = 548.39 ± 521.20; Z = −0.679, p = 0.497).

This suggests that macaques proposed either one or two different directions prior to their collective movements. In this study, the simulations show that if the two first preliminary behaviours are not connected, the number of collective movements with two proposed directions should not exceed 1/10 of the collective movements performed when only one direction is proposed. This ratio of 1/10 can be obtained analytically by dividing the probability to independently display a first preliminary behaviour in the second direction (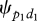 = 0.0013 for group 1) by the mean probability to depart in only one proposed direction (Ψ_01,t ≈ 0.0126 for group 1). However, the observed ratio is about one-third in both groups (respectively, 29.5% for group 1 and 38% for group 2). This means that the probability Ψ_p1d2 to display a first preliminary behaviour p₁ in the second direction d₂ is not independent of the first preliminary behaviour emitted in the first direction d₁. This last analysis shows that the first individual notifying in the second direction seemed to mimic (for the time dimension but not for the spatial dimension) the behaviour of the first individual notifying in the first direction. These two individuals shared the same time decision (consensus on time) but not the same direction decision.

(b). Probability to take part in the voting process

After the first preliminary behaviour is displayed, other individuals participate in the voting process and display preliminary behaviours in turn [17,27]. The time elapsed between the notifying of two different individuals involved in the voting process in one direction (d₁ or d₂) is 26.56 ± 39.64 s for group 1 and 17.89 ± 23.85 s for group 2. For both groups, these durations are about 34 times lower than the mean duration between the end of a previous collective movement and a first preliminary behaviour for a new collective movement. Moreover, the time elapsed between the first preliminary behaviour in one direction and the first one in the second direction is 28.14 ± 33.58 for group 1 and 18.54 ± 22.44 for group 2. This suggests an influence of the behaviour in the first direction on the second one rather than an independent probability to notify in the second direction. These results show that displaying preliminary behaviour involves a mimetic process following notifying behaviour by some group members.

However, the probability of an individual to display a preliminary behaviour in one direction may be dependent either on the number of notifying individuals in this direction or on the number of notifying individuals in both directions, as suggested by the results of the previous section concerning probability to display a first preliminary behaviour in direction 2.

We tested both hypotheses in our model. The influence of the number of notifying individuals in both directions seems to be confirmed by the shape of the duration distribution between the joining of two notifying individuals. The duration distribution for both directions followed a parabolic curve for group 1 (curve estimation test: F_1,6 = 9.44; R² = 0.61; s.e.m. = 6.446; p = 0.02) and group 2 (curve estimation test: F_1,5 = 11.24; R² = 0.70; s.e.m. = 4.535; p = 0.02). However, if we only consider the direction in which the behaviour is displayed, the duration distribution is a parabolic curve for group 1 (curve estimation test: F_1,6 = 8.01; R² = 0.56; s.e.m. = 6.544; p = 0.03) but not for group 2 (curve estimation test: F_1,5 = 0.64; R² = 0.1; s.e.m. = 6.346; p = 0.457). The probability that an individual will take part in the voting process is influenced by the number of notifying individuals in both directions and not simply by the number of individuals notifying the direction in which the individual displayed its preliminary behaviour.

After the display of a first preliminary behaviour, the probability Ψ_p,d to display a preliminary behaviour p, whatever the direction, therefore, depends on a mimetic process:

3.2

with C_p, the mimetic coefficient, equalling approximately 0.002 for both groups. 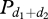is the number of notifying individuals in direction 1 and in direction 2.

Following this rule, the simulated ratio, ‘number of collective movements with two proposed directions divided by the number of collective movements with only one proposed direction’ (see §2), equals 28.6 per cent for group 1 and 38.8 per cent for group 2 and is similar to that observed for group 1 (χ²-test: χ² > 0.60; d.f. = 1; p = 0.806) and for group 2 (χ² > 0.27; d.f. = 1; p = 0.870). This result confirms that the first individual notifying in the second direction is influenced by the first individual notifying in the first direction. The third notifying individual, whatever the direction, is influenced by the two first notifying individuals, and so on.

(c). Probability to depart in a given direction

The voting process described above allows the group to choose one direction among two alternatives. This decision is observed through the departure of one individual—the initiator—who moves in the direction of the majority, i.e. the direction for which the most individuals have notified. A previous study showed that this probability to depart in the direction taken by the majority depended on two decisions: (i) the departure time decision and (ii) the departure direction decision [27].

This previous study also showed that the departure time decision is ruled by a quorum. The probability Ψ_01,t to initiate the group movement is

3.3

This function is a sigmoid where λ_i,t is the intrinsic probability per individual to initiate a movement [27]. While individuals of each group may have different intrinsic probabilities λ_i,t, these differences are not influenced by dominance, age or sex of group members. 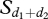represents a threshold, namely the sum of the notifying individuals in direction 1 and direction 2. This threshold—for which the probability that individuals initiate a movement equals 0.5—equals 9 for group 1 and 5 for group 2. q₁ represents the degree of sensitivity of individuals to the system and equals 5 for both groups. This degree of sensitivity affects the slope of the sigmoid curve that has been fitted to the data. Higher values of λ correspond to the fitted curves having a steeper slope, particularly around the threshold value. In essence, a higher degree results in a quicker transition between resting and departing as the difference between notifying individuals for both directions increases and then a higher discrimination from animals [36,37]. For instance, fishes or ants only show a degree of sensitivity of 2 [24,38].

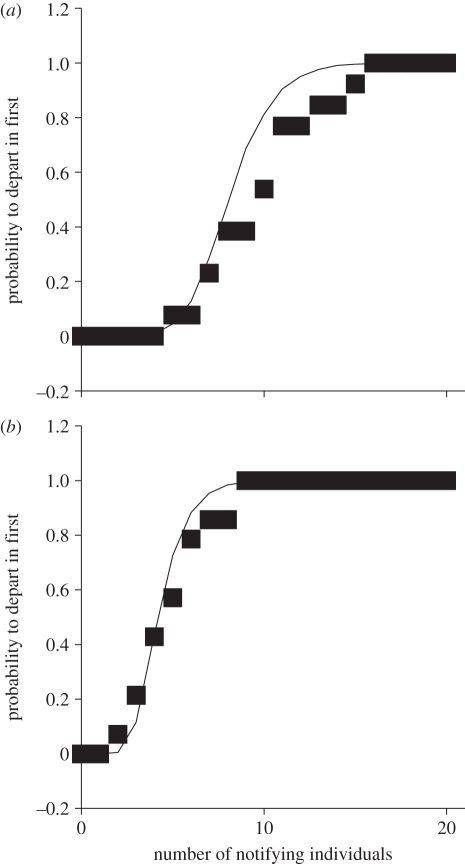
Results show that the simulated probability to initiate a movement, following the above rule, is similar to those observed in group 1 (curve estimation test: F_1,19 = 404; R² = 0.95; s.e.m. = 0.091; p < 0.00001; figure 1a) and in group 2 (curve estimation test: F_1,19 = 859; R² = 0.97; s.e.m. = 0.056; p < 0.00001; figure 1b). In figure 1, the number of notifying individuals may be higher than the number of group members, as shown for group 1, because notifying individuals may change their mind and switch direction during the voting process. In these cases, they are counted twice, once for each direction.

Figure 1.

Probability to depart first, i.e. to initiate a collective movement, according to the number of notifying individuals (a) for group 1 and (b) for group 2. Black squares represent the observed data. Lines represent the simulated data.

Sueur et al. [27] also showed that, after deciding about the departure time, the initiator chooses the direction of movement, and the probability Ψ_01,d to choose the direction is

3.4

This function is also sigmoid. 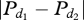is the absolute difference between the number of notifying individuals in direction 1 and the number of notifying individuals in direction 2. The threshold is 0 for both groups. This means that the absolute difference in the notifying individuals between direction 1 and direction 2 only needs to equal 1 or more for the initiator to choose the direction with the majority of notifying individuals. q₂ represents the degree of sensitivity of the system, and equals 17 in both groups. Indeed, group 2 always chose the direction with the highest number of notifying individuals (in all 14 cases), whereas group 1 only chose the direction with the lowest number of notifying individuals once in 13 cases.

Results show that the simulated probability to choose the direction with the most notifying individuals, following equation (3.4), is similar to those observed in group 1 (curve estimation test: F_1,24 = 60.5; R² = 0.72; s.e.m. = 0.135; p < 0.00001) and in group 2 (curve estimation test: F_1,26 = 3.45e⁺³⁰⁸; R² = 1; s.e.m. < 0.0001; p < 0.00001). This confirms that Tonkean macaques choose the direction to move using a quorum response with a very sensitive threshold in comparison with that observed in examples such as ants or fishes.

(d). Probability to join the movement

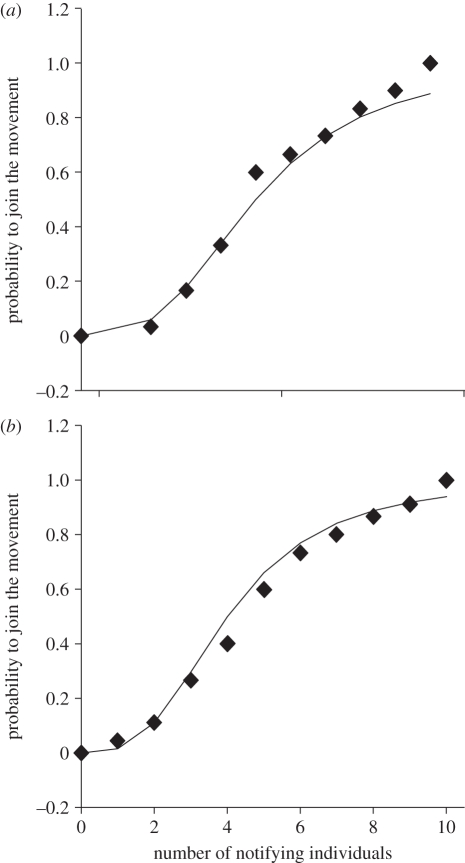
After the initiator has chosen the direction and started the group movement, other group members join the movement [17,26]. A previous study [26] showed that the probability Ψ_i,d that an individual i will join the movement and become the joiner j in the direction d depends on its intrinsic probability to join λ_i,d and on a mimetic process based on the affiliative relationships he had with the already moving individuals. However, the number of notifying individuals also influences the probability that individuals will join the movement as shown by Sueur & Petit [17]. Such influence is made by a quorum similar to the one in equation (3.3). The probability that an individual will be the first joiner (curve estimation test; group 1: F_1,8 = 820; R² = 0.99; p < 0.00001, figure 2a; group 2: F_1,6 = 393; R² = 0.98; s.e.m. = 0.045; p < 0.00001, figure 2b) or be the last joiner (curve estimation test; group 1: F_1,9 = 1797; R² = 0.99; s.e.m. = 0.046; p < 0.00001; group 2: no data available for which all group members join the movement) depends on a threshold of the number of notifying individuals. So, as far as joining a movement is concerned, an individual is first influenced by the quorum of notifying individuals, then by the individuals who have already joined the movement and those with whom he is highly affiliated. The probability Ψ_i,d for an individual i to join the movement is therefore

3.5

where C_j is the mimetic coefficient and equals 0.002. r(i, k)_d represents the affiliative relationships between the individual i and the already moving individual k (if k is not moving but resting, then r(i, k) = 0). q₁ is the sensitivity of the process and equals 3 for group 1 and 2 for group 2. 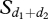is the threshold number of notifying individuals in directions d₁ and d₂ and equals 4 for group 1 and 2 for group 2.

Figure 2.

Probability to join the movement and to become the first joiner according to the number of notifying individuals (a) for group 1 and (b) for group 2. Black lozenges represent the observed data. The unbroken line represents the theoretical sigmoid curve fitting with the observed data.

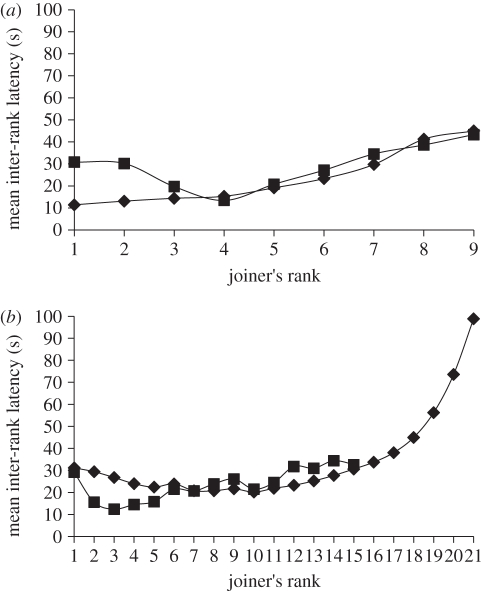
This rule allows us to recreate the distribution of inter-rank latencies for joiners (time elapsed between the joining of the joiner j − 1 and the joiner j) in both groups of Tonkean macaques (Kolmogorv–Smirnov test; group 1: N_obs = N_sim = 9, Z = 0.953, p = 0.352, figure 3a; group 2: N_obs = 15; N_sim = 21, Z = 0.958, p = 0.259, figure 3b, N_obs = 15 joiners, as no movements with more than 15 joiners were observed in this group). After the joining of the last individual, the collective decision to move is over.

Figure 3.

Distribution of the mean inter-rank latencies according to the joiner's rank (a) for group 1 and (b) for group 2. Rank 1 represents the first joiner, i.e. the second participant of a movement, and so on. Black squares represent the observed data. Black lozenges represent the simulated data. For group 2, the observed distribution stops at 15 joiners because no movements with more than 15 joiners were observed.

4. Discussion

An increasing number of studies on collective decision-making are illustrating that the pre-departure process seems to facilitate the departure of a collective movement [27,38–41]. This pre-departure process may make consensus between individuals easier when conflicts of interest arise about time decision and direction decision [27,42]. This study shows that decision-making related to macaque group movements are primarily governed by mimetism for notifying behaviours during the pre-departure period, and then by a quorum rule combined with selective mimetism at departure. These two processes implement the decisions about timing and the direction in which individuals will move. Transition mechanisms linking these two phases of collective decisions—namely pre-departure and departure—show for the first time in mammals how a voting process leads to social amplification. Our study also provides the first complete proof in mammals that there is continuity in the decision-making processes underlying collective movements, lasting from the first intention movement to the last joiner.

We found the same mechanisms of decision in both groups of Tonkean macaques. The groups showed a same quorum answer—with a similar proportion of movements with two directions proposed and a similar probability to show a first behaviour before departure—and a same selective mimetism. Only the threshold of the number of notifying individuals to depart first in a given direction is different between two groups. This threshold equals 9 for the small group and 5 for the large one. We might expect that the large group should show a higher threshold than the small one: more individuals need to show their preferences. However, similar results were found in a previous study [28]: the larger the group, the smaller the proportion of individuals needed to guide the group with a given accuracy. Our study reinforces assumptions and results of Couzin et al. [28].

Different mechanisms underlie the whole decision-making process in macaques. Some mechanisms are linear [15,25] such as the one found in the joining process in macaques [26]. Other examples are highly nonlinear, such as the quorum response showed by each individual for following the direction of the majority [22–24,27]. We actually show here that joining a movement depends on two mechanisms, namely a quorum response and selective mimetism acting in synergy. In Tonkean macaques, quorum response and selective mimetism regulate together the transitions of individuals from one state (resting) to another one (moving). One could believe that voting process and selective mimetism act independently and at different times, one during the pre-departure process and the other one during the joining process. In fact, we found that individuals combined the two processes in a single decision when deciding to join. They consider both the number of notifying individuals and their affiliative relationships with already moving individuals when choosing. The synergy of these two mechanisms allows macaques to consider the growing number of departed individuals and therefore the ineluctability of a collective movement, since groups remain cohesive. This is a modulation between being coordinated with the majority of the group and being coordinated with individuals with whom one has alliances or shares similar motivations. Note that these findings are very useful to help us identify the clues that animals may use for making their decisions. In this perspective, one can wonder whether specific mechanisms could have evolved in response to specific needs the animals have to cope with, i.e. keeping group cohesion, staying with preferred individuals, etc. [29,43].

The combination of these different mechanisms is reminiscent of collective decision in capuchins monkeys where two mechanisms—a mimetic one and a cancellation one—allow the synchronization of the individuals and prevent group fission [15]. Cancellation or giving-up behaviours are also displayed by Tonkean macaque initiators [17,32]. This behaviour is however rarer than in capuchins and has less impact. This is probably because the two mechanisms observed—quorum response and selective mimetism—are enough for group synchronization and coordination in macaques, while no quorum response was seen in capuchin monkeys.

Quorum response is a simple and efficient way to lead to efficient collective decisions [44]. Several studies showed that this kind of mechanism allows speed-accuracy trade-off [22–24,27,45]. In the case of Tonkean macaques, it allows individuals to find a good compromise between the accuracy of the decision (i.e. the number of individuals satisfied by the decision or the truthfulness of the direction decision) and its timing (by not waiting until all individuals participate in the voting process, but deciding to move when a threshold is reached). Similar processes were also found in ants, bees or fishes [22–24,45]. Ward et al. [24] reported that in fishes, the greater the relative difference between the numbers of individuals in each direction was, the more the fishes tested showed a bias for the direction chosen by the majority. We obtained similar results for Tonkean macaques, but with a higher rate of discrimination. Tonkean macaques are highly sensitive to this difference, since they always choose the majority even if there is only a difference of one individual between the two directions [27]. Such variation in discrimination abilities between fishes and macaques is probably due to the complex cognitive abilities of the latter [46].

From ants to primates, complex collective decisions all seem to be ruled by similar mechanisms [1,22–24,26,27]. One mechanism—the quorum response—appears particularly present in these kinds of phenomena, probably because it allows a trade-off between the speed and the accuracy of a decision [45]. However, macaques appear to have a keen sense of discrimination when faced with collective decision patterns, especially as far as the number and the identities of individuals are concerned. Higher discrimination undoubtedly leads to better decisions in terms of accuracy and satisfaction of group members. This assumption may help us understand the development of brain size in animals, particularly in primates, and would be worth further investigation. Indeed, several authors suggest that brain development in primates may be mainly due to intra-group competition for food or alliances leading to the emergence of a ‘Machiavellian intelligence’ [47]. However, group cooperation and group decision may also contribute to the development of high cognitive abilities in order to have better discrimination and therefore better accuracy when deciding.