Abstract
Objectives
In old age, there are marked changes in both the structure of the liver sinusoidal endothelial cell and liver perfusion. The objective of this study was to determine whether there are also aging changes in the microvascular architecture and vascular dispersion of the liver that might influence liver function.
Methods
Vascular corrosion casts and light micrographs of young (4 mths) and old (24 mths) rat livers were compared. Fractal and Fourier analyses, and microcomputed tomography were used. Vascular dispersion was determined from the dispersion number for sucrose and 100 nm microspheres in impulse response experiments.
Results
Age did not affect sinusoidal dimensions, sinusoidal density or dispersion number. There were changes in the geometry and complexity of the sinusoidal network as determined by Fractal dimension and degree of anisotropy.
Conclusions
There are small age-related changes in the architecture of the liver sinusoidal network, which may influence hepatic function and reflect broader aging changes in the microcirculation. However sinusoidal dimensions and hepatic vascular dispersion are not markedly influenced by old age.
Keywords: aging, liver, microcirculation, liver sinusoid, vascular casts, Fractal dimensions, Fourier analysis, vascular dispersion, multiple indicator dilution
Introduction
Aging is associated with many changes in the cardiovascular system and old age is a major risk factor, if not the leading risk factor, for most vascular diseases [3, 13, 29, 30, 40, 45]. Age-related vascular changes are usually considered to include increased vascular stiffness, deposition of lipids and collagen in vessel walls, increased intimal thickness, reduced tissue perfusion and a decrease in endothelium-dependent vasodilatation [29, 30, 40]. Age-related changes in the microcirculation are less well understood [45] but have been identified, and most widely studied, in the microvasculature of skeletal muscle [3] and brain [12, 47]. It is of note that in his original exposition of the free radical theory of aging, Harman hypothesised that blood vessels were the key target for age-related oxidative stress [21] and, indeed, many systemic features of aging might reflect impaired tissue perfusion [46].
There have been a few reports on the effects of aging on the hepatic vasculature. In old age in humans and animals, there is a marked reduction in total hepatic blood flow [35, 51, 57] and tissue perfusion [24]. Ultrastructural aging changes have been reported in the liver sinusoidal endothelium and space of Disse from intact livers of the rat [25, 32], human [43], mouse [24, 54] and baboon [8]. Endothelial thickness is increased by about 50% in old age with a similar reduction in the porosity and number of fenestrations, which are pores within the liver sinusoidal endothelium. There is perisinusoidal basal lamina deposition in many old livers and some scattered collagen in the space of Disse. The endothelial marker, von Willebrand’s factor, which is not normally expressed in healthy young liver sinusoids, is upregulated in old age in most studies [37]. There is also reduced caveolin-1 expression [25] and increased ICAM-1 expression [24]. The expression of α-SMA and desmin is not upregulated indicating stellate cell activation is not present [8, 37]. Together these changes in the hepatic sinusoid have been termed pseudocapillarization and may have systemic implications because of their effect on the transfer of many substrates between blood and hepatocytes, most importantly lipoproteins such as chylomicron remnants [22, 23, 33, 34].
The potential effects of old age on the hepatic microcirculation are important because this might influence hepatic function, particularly hepatic clearance, through influencing hepatic perfusion. There is substantial reduction in hepatic clearance of many substrates in old age, which for medications is often in the range of a 30–50% reduction in metabolism [35]. The most robust explanation is that with old age there is a reduction in hepatic blood flow, which will reduce primarily the hepatic clearance of highly extracted substrates, according to the equation:
where Cl is clearance, Q is hepatic blood flow and E is the fractional extraction [35]. A mechanism for the age-related reduction in hepatic blood flow has not been forthcoming. A recent report by Ito et al. indicates that the reduction in hepatic perfusion may be secondary to increased expression of ICAM-1 on the sinusoidal endothelial cells with subsequent leukocyte adhesion and blocking of the sinusoids [24]. An alternative explanation is that there might be age-related changes in the sinusoidal microarchitecture including sinusoidal dimensions and branching. One purpose of this study was to determine whether there are such changes in the sinusoidal architecture that could contribute to the age-related reduction in hepatic perfusion.
In the past, hepatic clearance was considered to be determined primarily by hepatic blood flow, intrinsic clearance (a measure of enzyme capacity) and substrate protein binding. The effects of old age on all of these parameters have been investigated [35, 44, 51]. More recently, the dispersion model developed by Roberts and colleagues showed that mixing of substrates as they pass through the sinusoids also influences their clearance [48, 49]. The mixing of the substrates in the sinusoids is generated by sinusoidal branching, variations in flow velocity and path-lengths and turbulence, and is estimated by the dispersion number, DN. As the dispersion number increases, reflecting increased mixing in the sinusoids, the dispersion model predicts an increase in clearance according to the equation:
where Cl is clearance, Q is hepatic blood flow, DN is the dispersion number and is RN is the efficiency number [48, 49]. The effect of mixing is greatest for those substrates that undergo non-linear kinetics [55]. The effect of aging on the DN and sinusoidal mixing is unknown, but a reduction in DN with old age would contribute to the age-related reduction in hepatic clearance.
Fractal analysis has increasingly been used to study many microcirculatory networks because of their generally complex and iterative branching geometry [1, 41]. Usually the branching of vessels over several generations has been quantified using the box counting method to determine the Fractal dimension. The geometry of the liver circulation in health and disease has also been characterized using fractal analysis [6, 16, 26, 55]. Here Fourier analysis is more suitable to undertake to quantify the topography of the sinusoids because they do not undergo repeated branching to successively smaller vessels, but rather are a reticular branching network of vessels of a similar size [16]. It has been suggested that the fractal dimension of the vasculature may influence drug metabolism and hepatic clearance [15, 39], possibly through effects on mixing and dispersion [2, 55] therefore any age-related changes in the fractal geometry of the sinusoids may also contribute to altered hepatic function. Furthermore, the aging process appears to be associated with loss of complexity in many systems indicating that such analyses may be required in order to detect fundamental aging changes [18, 19, 28, 38].
In this study, vascular corrosion casts, scanning electron microscopy, micro-computed tomography, light microscopy and the multiple indicator dilution method were used to determine whether old age influences the geometry, fractal dimensions and mixing function of the liver sinusoidal network. As well as providing insight into the effects of aging on the microcirculation, the results may provide additional mechanisms for the reduction in hepatic function in old age.
Material and Methods
Animals
Young mature adult (aged 4–5 mths) and old adult (aged 24–26 mths) Fisher 344 male rats were obtained from the National Institute of Aging (Bethesda, MD). All animals were fed ad libitum (n=5 in each group). These animals have a median survival time of approximately 26 mths [17]. The study had the approval of the Sydney and Southwest Area Health Service Animal Welfare Committee.
Vascular corrosion casting
Rats were anaesthetized with ketamine (90 mg/kg) and xylazine (10 mg/kg) by intraperitoneal injection and livers were perfused via portal vein with heparinized buffer (PBS, 25000 U/l heparin, 35C) followed by 20 ml of fixative (4% formalin in PBS, 35°C) over approximately 5 mins at a pressure of 10 cmH2O. Polyurethane PU4ii resin (vasQtec, Zurich, Switzerland) was injected via portal vein at the same rate [27]. Livers were removed and allowed to polymerize for 48 hours and then macerated in 10% NaOH at 37°C for several days. Casts were incubated overnight in 5% formic acid solution at 37°C, extensively rinsed with water and dried in room air.
For scanning electron microscopy, only lobes that were completely perfused were selected. The cast was studied under a dissecting microscope where well perfused lobes appeared very thick with surface sinusoids present which outlined the shape of the lobe. At least five well-perfused cast sections were studied per lobe. Sinusoids were analysed that were distant from any larger vessels that would confound the analysis. For the fractal analysis, the images were taken from the uncut surface of the perfused livers because this is more suitable for the 3D volume-based analysis. Although aging might influence the quality and fixation of the casts, no age-related differences were observed in the quality of the cast perfusions. Zone 2 sinusoids, which lie midway between the periportal (zone 1) and pericentral (zone 3) sinusoids and were chosen for both light and electron microscopic analyses because they tend to be a reasonably homogeneous network between the more branching zone 1 sinusoids and more linear zone 3 sinusoids.
Scanning electron microscopy
Casts were sectioned, mounted on studs under a dissecting microscope and sputter coated with platinum. Casts were visualized and photographed using a Jeol JSM-6380LV scanning electron microscope (Jeol, Akishima-Shi, Japan). To estimate the sinusoidal diameter, ten micrographs from each cast were taken and studied under the same conditions (magnification ×500, working distance 8 mm and 15 kV). Each photograph was analysed using ImageJ software (http://rsb.info.nih.gov/ij/) and approximately 30 measurements of sinusoids taken.
Light Microscopy
Ten photographs were analysed from each rat liver and inter-sinusoidal distance and sinusoidal density calculated in zone 2 sinusoids using ImageJ. Inter-sinusoidal distance was defined as the shortest distance between the edges of two sinusoids. For the analysis of sinusoidal density, areas containing transversally sectioned sinusoids were selected and number of sinusoid was manually determined. Low magnification micrographs (×40) were also taken to allow measurements of the distance between adjacent central veins because this reflects lobular dimensions.
Micro-computed tomography
Micro-computed tomography was used to visualize the 3D geometry of the portal venous network and sinusoids. One well perfused section (0.5 mm diameter cylinder) of vascular cast from each liver was selected. Before the X-ray scans were performed, the vascular casts were treated with 2% osmium tetroxide for several days, in order to enhance contrast. After washing, casts were placed in plastic tubes filled with distilled water and mounted on a metal stub. Images were acquired with X-ray microcomputed tomography SKYSCAN-1072 (SkyScan, Aastselaar, Belgium) at high resolution (3.5 μm pixel size) and subsequently converted to bitmap images using Nrecon software. The bitmap image series were used for 3D quantitative morphometry analysis using Skyscan CT-analyser software. Within each corrosion cast, two representative and well perfused regions were analyzed (total volume 15 mm3). The percentage of the liver volume occupied by the blood vessels, degree of anisotropy and Fractal dimension were determined. The threshold set at either approximately 46 or 86, which allowed analysis either of the sinusoids or the larger vessels, respectively.
The degree of anisotropy determined by this software is a dimensionless parameter that varies between 0 and 1. When the degree of anisotropy is 1, there is perfect alignment of the blood vessels along a preferred axis. Conversely, when the degree of anisotropy is 0, there is no preferred axis of alignment. The Fractal dimension is determined by box counting and is a measure of the complexity of the network.
Fourier analysis of corrosion casts
For evaluation of the casts, both Fourier or Fractal analyses were undertaken as we have previously applied to the liver microcirculation [16].
For the Fourier analysis, each image is considered to be a superposition of a large amount of elementary diffraction graticules differing in their constance, i.e. number of lines per mm and the angular direction of the lines. This kind of analysis is based on the optical diffractograms. Using the fast Fourier transformation (FFT), transformation coefficients showing radial and spatial distribution of elementary harmonic elements of the images were computed, allowing for calculation of the spatial and angular distribution of light energy contained in the images. Indicating with I(r,c), the image function with r = row c = column where the image is N x N pixels, the Fourier transform algorithm is:
Amplitude was defined as:
The relative coefficients were computed using FFT algorithms. Based on Fourier coefficients, radial and spatial distributions were defined as follows. We defined n = 30 bands (Pn) of spatial frequency, the width of one band was Δf:
The spectral region of radial analysis was defined as rings. We measured the amplitude (A(Pn)) in a region of interest of spatial frequency by summing the amplitude over the chosen range:
Based on radial Fourier distribution the energy of the radial Fourier spectrum (E) and the entropy of the radial Fourier spectrum (ε)) were defined as follows:
- Energy (E):
- Entropy (ε):
Entropy is a particular form of energy related to the state of disorder of the material: higher entropy values indicate higher states of disorder in the system. E is the general amount of system energy, from a thermodynamic point of view, given by the addition of thermal and entropic energy. A normal system evolves to a minimum of total energy, corresponding to a maximum of stability, and at the same time to a maximal entropy, corresponding to a state of disorder. For our analysis, the algorithm was implemented in the program MATHCAD 6.0.
Two methods were used to estimate the Fractal dimension: Box Counting and the Fourier power spectrum method. The purpose of the Box Counting algorithm is to estimate the length of a complicated curve, which has several implications. Using this algorithm, Fractal dimension was obtained from the binarized images, which are a map of the vessel structure. A grid consisting of square boxes with size ε was superimposed on the extracted boundary of the vessel network to be quantified. In the Fourier power spectrum method of Fractal dimension estimation the two-dimensional (2D) Fourier transform of the digital image is calculated first and the 2D power spectrum is obtained. The latter is then reduced to a 1D power spectrum by averaging over circles. The average 1D power spectrum P(f) of the surface is a function of the frequency f.
The numerical data obtained by the use of Fractal and Fourier analyses of the images were used for the discriminant analysis. These data allowed the construction of multi-axial space and each image was positioned according to the measured values. In each analysed group of images a centroid was calculated and this allowed the distances between the centroids (the Mahalanobis distances) to be calculated. The Mahalanobis distances are in multi-axial space thus are not Euclidean lines. Evaluation of these distances permits calculation of differences between the compared groups of images and to estimate the statistical validity of differences. The discriminant analysis automatically computes the classification functions. The classification functions can be used to determine to which group each case most likely belongs. All statistical analyses were performed using STATISTICA software (StatSoft, Inc., Tulsa, OK, USA).
Impulse response experiments
Liver perfusions and impulse response experiments were performed as described previously [7, 22, 36]. The perfusate was Krebs-Henseleit bicarbonate buffer (10 mM glucose, pH 7.4, saturated with 95 % O2/5 % CO2, 2 % bovine serum albumin, 37°C). The perfusate flow rate was maintained at approximately 1 ml/min/g of liver using a cartridge pump (Masterflex L/S, Extech Equipment, Boronia, Australia) in a non-recirculating system. Viability was confirmed by macroscopic appearance, oxygen consumption, portal venous pressure, light microscopy and electron microscopy. The injectate was made to total 100 μl volume with Krebs-Henseleit bicarbonate buffer and contained 14C-sucrose (0.1 mCi/ml, Sigma Chemical Company, Sydney, Australia) and yellow-orange 100 nm Fluoresbrite polystyrene microparticles (Polysciences, Warrington, PA). Immediately after administration of the injectate as a bolus into the portal vein catheter, 30 outflow samples were collected using a Universal Fraction Collector (Extech Equipment, Boronia, Australia) at two-second intervals. Outflow samples were analyzed for 14C activity (Wallac 1410 Liquid Scintillation Counter, Pharmacia, Sydney, Australia) and fluorescence was quantified with a Hitachi F-4010 fluorimeter.
Analysis of outflow curves
Dose-normalized outflow time-activity curves were constructed, such that outflow concentrations were expressed as the fraction of the dose per mL of outflow [20]. The area under the curve (AUC), mean transit time (MTT) and variance of the transit time (VTT) were calculated directly from the outflow curves using the following equations:
MTT was corrected for the catheter and non-exchanging vessel transit time (t0), estimated from the time of first appearance of radioactivity above background levels. The recovery (F), volume of distribution (V), normalized variance (CV2) and dispersion number (DN) were then calculated as follows:
F is the fraction of substrate recovered in the outflow. V is the volume of distribution of the substrate within the liver and represents the space within which the substrate travels during the single pass. CV2 and DN are dimensionless markers of the dispersion of the substrate within the liver.
Statistical analysis
Data are presented as mean ± standard deviation. Comparison of sinusoidal dimensions and impulse response experiments was undertaken with the Students T-test. For Fractal analyses, the Wald-Wolfowitz Runs Test analysis was applied. Differences were considered significant when P < 0.05.
Results
Sinusoidal dimensions and density
Figures 1 and 2 show representative corrosion casts and light micrographs from young and old livers, respectively. The diameter of the sinusoids determined from the vascular casts was 9.4±3.6 μm in the young rats and 9.7±3.5 μm in the old rats. There was no significant effect of age on sinusoidal diameter (Table 1). Even though there was a slight reduction in the distance between sinusoids in old age of about 5%, there was no effect of aging on the number of sinusoids per unit area determined by light microscopy. The size of the lobules determined from the distance between adjacent central veins increased by 10% in the old livers (Table 1).
Figure 1.
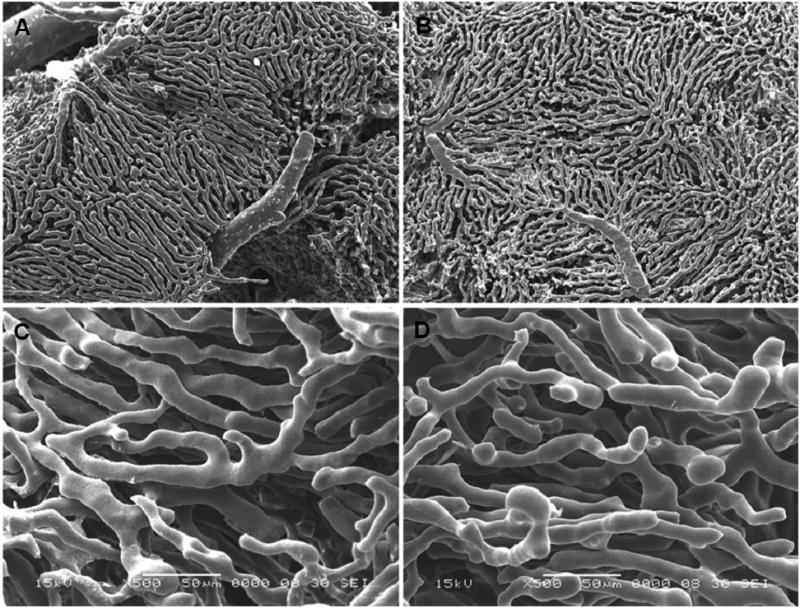
Low and high magnification scanning electron micrographs of vascular corrosion casts from young (A, C) and old (B, D) rat liver (A, B: 30 ×; C, D: 500× magnification).
Figure 2.
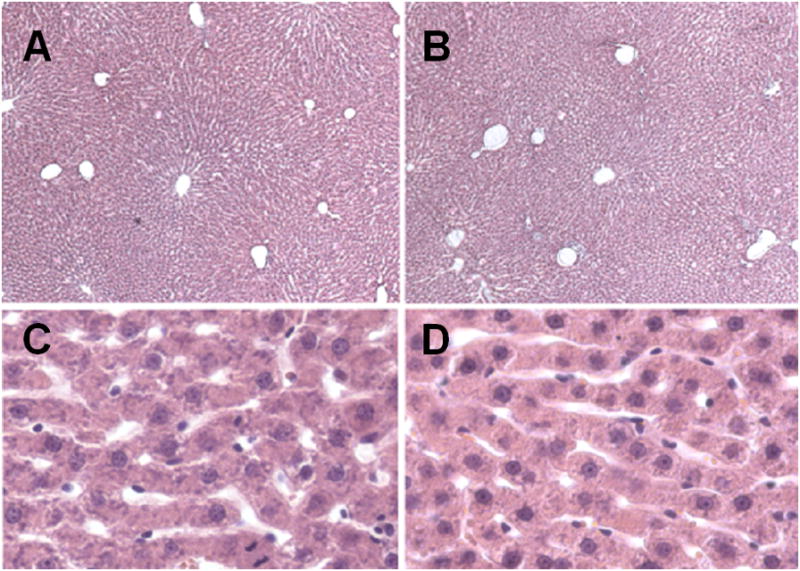
Light micrographs of the liver of a young (A, C) and old (B, D) rat (10 × magnification).
Table 1.
The effects of old age on the sinusoidal diameter (determined by electron microscopy) and sinusoidal density, intersinusoidal distance and distance between adjacent central veins (determined by light microscopy). The figures in parenthesis refer to the number of observations in livers from 4 young and 4 old rats.
| Parameter | Young | Old |
|---|---|---|
| Sinusoidal diameter (μM) | 9.4±3.6 (n=977) | 9.7±3.5 (n=1225) |
| Intersinusoidal distance (μM) | 16.1±3.9 (n=567) | 15.5±3.8* (n=558) |
| Number of sinusoids per 100 μM2 | 17.5±2.5 (n=56) | 17.4±4.1 (n=58) |
| Distance between central veins (μM) | 809±199 (n=79) | 891±190** (n=78) |
P<0.01
P<0.05.
Analysis of corrosion casts
The Fractal dimension of the sinusoidal network was lower in the old livers and this difference was greater and statistically significant when calculated using the FFT method, considered to be the more accurate method [16] (Table 2). The comparison of the Fourier radial distribution of the sinusoids in the young and old livers is shown in Figure 3. Based on this distribution, the energy, entropy and area of the radial Fourier spectrum were defined. Old age was associated with higher energy and lower entropy (Table 2).
Table 2.
The effects of age on the Fractal and Fourier analysis of the hepatic sinusoidal network. The figures in parentheses refer to the number of valid observations. All units are dimensionless.
| Parameter | Young (n=52) | Old (n=44) |
|---|---|---|
| Fractal dimension (Box counting method) | 1.891±0.011 | 1.888±0.019 |
| Fractal dimension (FFT) | 2.387±0.022 | 2.339±0.038* |
| Energy of Fourier radial distribution (×10−5) | 8.27±4.31 | 27.86±14.78* |
| Entropy of Fourier radial distribution (×10−4) | −2.78±0.89 | −4.99±1.67* |
| Area of Fourier radial distribution (×10−3) | 3.63±0.98 | 5.79±1.71* |
P < 0.0001
Figure 3.
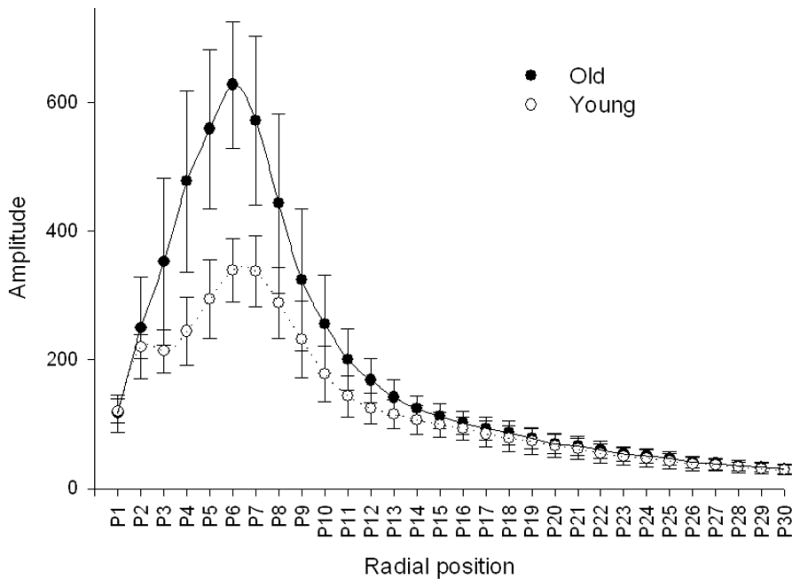
Radial distribution of analysed structures calculated by Fourier transformation corresponding to their dimensions. The x-axis represents defined bands of spatial frequencies. The y-axis represents the amplitude of particular frequency bands. 30 bands of spatial frequency were defined.
The Mahalanobis distance, corresponding to the distance between centroids of the images in multi-parameter space of the young versus the old sinusoidal networks was statistically significant (squared Mahalanobis distance 7.196, P<0.05). The sinusoidal networks could be classified as either young or old on the basis of their structure with an efficiency of 93%.
Analysis of micro-computed tomography
Figure 4 shows representative micro-computed tomographs from young and old livers. There was a significant age-related reduction in the degree of anisotropy when the image analysis included only the sinusoidal network. However, there were no other significant aging differences, including the percentage volume of the liver occupied by blood vessels and sinusoids (Table 3). The Fractal dimension of the large portal vessels was 1.9±0.1 in the old rats and 1.8±0.2 in the young rats.
Figure 4.
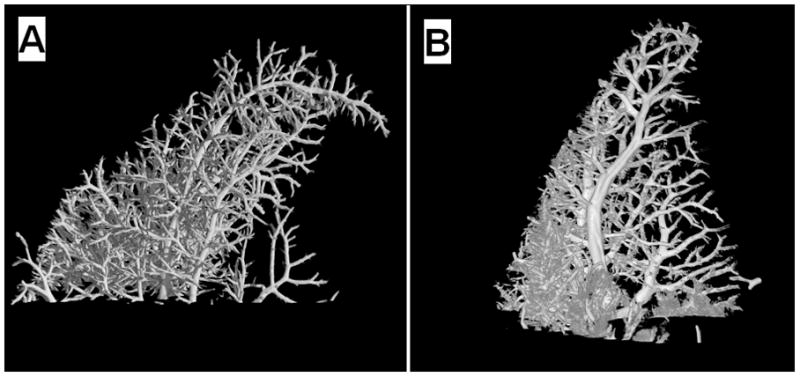
Micro-computed tomograph of the portal venous microcirculation of a young (A) and old (B) rat liver.
Table 3.
Analysis of the micro-computed tomography of the vascular corrosion casts. Analysis was undertaken of the sinusoids or just the larger vessels. There was a significant age-related reduction in the degree of anisotropy of the sinusoids
| Young | Old | |
|---|---|---|
| Sinusoids and large vessels | ||
|
| ||
| Relative volume (%) | 29.5±12.3 | 30.0±21.0 |
| Degree of anisotropy | 0.418±0.232 | 0.227±0.044* |
|
| ||
| Large vessels | ||
|
| ||
| Relative volume (%) | 2.7±1.4% | 3.4±1.3 |
| Degree of anisotropy | 0.836±0.344 | 0.603±0.108 |
P < 0.05.
Impulse response experiments
The results of the experiments are shown in Table 4 and representative outflow curves are shown in Figure 5. The values of the volumes of distribution of the microspheres are likely to be underestimated because the recoveries were less than unity. The DN for sucrose was approximately 0.4 and there were no differences in any of the parameters with age.
Table 4.
Results of impulse response experiments in the perfused livers of young and old rats for sucrose and 100 nm microspheres. There were no significant differences between young and old for any parameter.
| Young (n=10) | Old (n=8) | |
|---|---|---|
| Sucrose
| ||
| Volume of distribution (ml/g) | 10.9±3.1 | 14.4±7.9 |
| Recovery (%) | 90±15 | 86±10 |
| CV2 | 0.74±0.13 | 0.84±0.47 |
| Dispersion number | 0.37±0.07 | 0.42±0.24 |
|
| ||
| Microspheres
| ||
| Volume of distribution (ml/g) | 8.6±2.3 | 9.4±3.1 |
| Recovery (%) | 88±22 | 67±41 |
| CV2 | 1.29±1.05 | 1.07±0.51 |
| Dispersion number | 1.00±0.27 | 0.77±0.44 |
Figure 5.
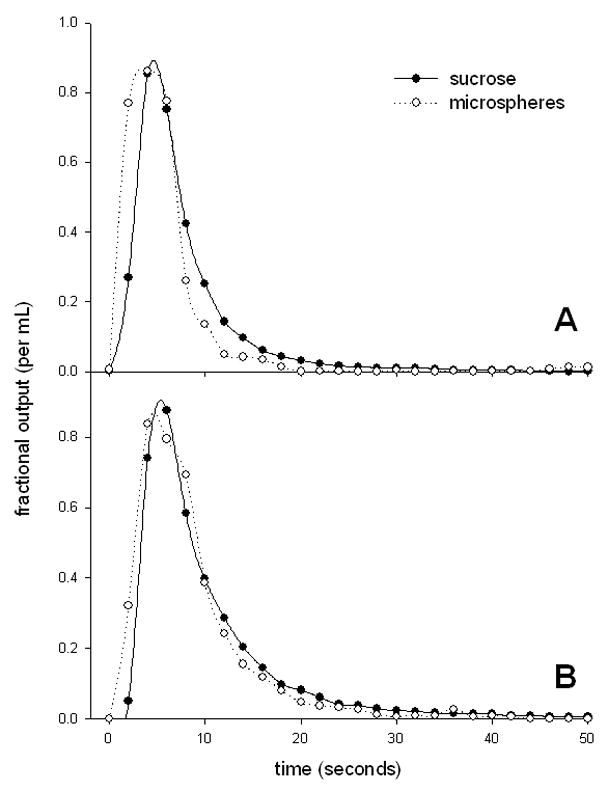
Impulse response outflow curves from perfused liver of a young (A) and old (B) rat (fitted with simple spline curves).
Discussion
There have been a few reports on the effects of aging on the architecture of the microcirculation in various tissues, primarily muscle and brain, and usually evaluated using either vascular corrosion casts or in vivo microscopy. For example, in F344 rats, capillaries in cremaster muscle did not change in diameter between 12 and 24 mths but there was a reduction in branching frequency in the distal vessels [9]. In C57BL/6 mice, there was an increase in branch angle and tortuosity in arterioles smaller than 30 μm in diameter, but no other differences in vascular topology in the gluteus maximus muscle [4]. The effects of age on the cerebral microcirculation have been more extensively studied and reviewed [12, 47]. Overall there is substantial age-related rarefaction of the surface arterioles and a limited reduction in the density of the parenchymal capillaries in some regions of the brain, particularly the hippocampus and cortex [47]. The cerebral capillaries undergo ultrastructural changes with old age including an increase in basement membrane and collagen, reduction in elastin and the deposition of flocculent material thought to be degenerative pericytes [47]. In addition there is increased tortuosity, looping and twisting of the cerebral microvessels [47]. In both cerebral and skeletal tissues, it has been concluded that age-related changes in the microcirculation will have an impact on tissue perfusion and transfer of substrates such as oxygen and glucose [45–47]
There have also been a few reports of aging changes in the hepatic microcirculation [34, 37] although it should be noted that the liver is not a post mitotic tissue and changes in its microcirculation might not reflect broader vascular changes. Total hepatic blood flow is reduced by 30–50% and although this is similar to the age-related reduction in liver mass as a fraction of body weight [35, 52] there appears to be some reduction in tissue perfusion. Determined by clearance of colloidal albumin, liver perfusion in rats was 1.30±0.13 ml/min/g at 3 mths, 1.54±0.19 ml/min/g at 6 mths and 1.33±0.28 ml/min/gram of liver at 36 mths, suggestive of a reduction in perfusion in old age [5]. Recently Ito et al. [24] used high resolution in vivo microscopy to investigate aging in mice. There was a 14% reduction in the numbers of perfused sinusoids between 0.8 and 27 mths of age and a 35% reduction in sinusoidal blood flow. Slightly narrower sinusoids with thickened LSECs and swollen stellate cells were observed. Vollmar et al. [53] used in vivo microscopy to study sinusoidal perfusion in the rat. They reported a minor reduction of sinusoidal density to 87% over life but concluded that there were no aging changes in sinusoidal perfusion or sinusoidal diameter. However there was a reduction in sinusoidal flow from 9.3±0.7 pL/s at 3 mths to 6.8±0.7 pL/s at 24 mths. Old age is associated with marked ultrastructural changes in the hepatic sinusoid called pseudocapillarization [8, 22, 24, 25, 32, 34, 54]. These include thickening of the liver sinusoidal endothelium and loss of fenestrations. There is some deposition of basal lamina, collagen and altered expression of some endothelial and extracellular matrix proteins and stains. Thus overall reports indicate there are morphological changes in the microcirculation in the liver, brain and muscle in old age.
In this study we found no major age-related changes in sinusoidal density (determined both from the number of sinusoids per unit area on light microscopy, and relative volume occupied by sinusoids on micro-computed tomography) or sinusoidal diameter (determined by vascular corrosion casts). Therefore the age-related reduction in hepatic perfusion requires alternative explanation. It is possible that the upregulation of ICAM-1 with subsequent leukocyte adhesion [24], swelling of stellate cells [8, 37, 54], or changes in production of or response to vasoactive substances in vivo contributes to impaired blood flow through the sinusoids. We did note a change in the size of the lobules determined by the distance between adjacent central veins, which increased by 10%. This is less than the 50% increase in lobule size between 3 and 24 mths detected by Vollmar et al. [53] but is consistent with the concept that lobule size increases in parallel with the increase in liver size in the growing animal.
The Fractal dimension estimated by the Fourier spectrum analysis, which is a measure of complexity of branching, was reduced with old age in the hepatic sinusoid. The higher complexity in young livers corresponds to a higher tortuousness, arborization and interconnections between adjacent sinusoids, compared to more linear and less ramified sinusoids in the aged liver. Aging has been reported to be associated with reduced complexity reported in many systems including bone architecture, dopamine release, lung structure, neuronal dendrites, heart rate variability, blood pressure variability, thyrotropin release, and electroencephalograms EEG [28, 38]. However Fractal analysis of renal artery [10] or retinal vessels [31] in humans did not show any clear relationship with age. We are not aware of any other studies of the effects of age on the Fractal dimension of the microcirculation. Our results in the hepatic sinusoidal microcirculation support the hypothesis that old age is associated with a loss of complexity [28, 38]. In addition, this result suggests that the age-related reduction in the hepatic clearance of some substrates (particularly those that undergo non-linear metabolism) might be in part secondary to an age-related reduction in the Fractal dimension of the sinusoids, although the magnitude of this effect is small.
The results obtained in this study with aging compare with those derived in the cirrhotic rat liver using similar methods [16]. Here, the Fractal dimension for the sinusoids was reduced from approximately 2.8 in control male Wistar rats to approximately 2.6 in rats rendered cirrhotic through bile duct ligation or administration of carbon tetrachloride. As with aging, this change in cirrhosis represents a loss of complexity of the sinusoidal network. However the squared Mahalanobis distance between aged and control livers was only about 7 therefore not as distinctly different from controls as cirrhotic livers, where Mahalanobis distances ranged from 28–51. Furthermore, the reduction in the Fractal dimension in old age was only about 0.05 compared with about 0.2 in cirrhosis. Overall, the effects of age on the branching structure of the sinusoid are not as marked as those seen in cirrhosis but in the same direction towards less complexity.
The values for the Fractal dimension obtained for the liver sinusoids both in this study and previously [16] are substantially higher than those reported in other microcirculations, typically around 1.6 or less [10, 42]. Other reports of Fractal dimensions in the liver include approximately 2.8 in normal rat liver and 2.6 in fibrotic rat liver derived from analysis of vascular casts [16], 1.8–1.9 derived from analysis of mibefradil pharmacokinetics in dog liver [15], and 2 from ultrasound analysis of calf livers [26]. Higher Fractal dimensions are linked with greater complexity, therefore, the results suggest that the hepatic sinusoid may have an unusually branched and complex architecture compared to other capillary systems. This presumably improves mixing and dispersion of substrates in the sinusoids, which increases the hepatic clearance [15, 55]. The degree of anisotropy of the sinusoids (approximately 0.4) was markedly less than that of the larger portal vessels (approximately 0.8) indicating the more aligned geometry of the large vessels as they branch from the central to peripheral regions of the liver. Interestingly, old age was associated with a decrease in the degree of anisotropy of the sinusoids suggesting that any alignment is diminished with aging. The functional implications of anisotropy on hepatic function are yet to be determined but the change with age is further evidence of altered sinusoidal geometry.
The impulse response method and dispersion model developed by Roberts and Rowland [49] was also used to study effects of aging the hepatic microcirculation. In this model the spread in the residence time distribution of substrates as they move through the liver is considered to be secondary to vascular dispersion, and is represented by the CV2 and DN. A higher value of DN indicates a greater degree of axial dispersion through the sinusoids, larger vessels and catheters. Various estimates of DN have been reported for non-eliminated reference markers such as sucrose in the isolated perfused rat liver. These estimates usually lie within the range of 0.2–0.5 [11, 48, 50] and are similar to the result of approximately 0.4 obtained for sucrose in our study. However, the results we obtained for the microspheres were much higher than this. It is possible that this is an artefact related to diminished sensitivity of fluorescence to detect the tail of the outflow curves, or alternatively there may indeed be greater mixing of microspheres because of their greater size. There was no age-related change in DN for sucrose or microspheres, which is consistent with our vascular corrosion cast data, which revealed only minor changes in vascular complexity and indicates that altered dispersion does not contribute to the age-related reduction in hepatic clearance. It is of interest that in cirrhosis of the liver, there are marked changes in the hepatic vasculature, yet the DN for oxygen was approximately 0.4 in both control and cirrhotic livers [14]. Likewise, following partial hepatectomy the CV2 of albumin was not altered despite expected changes in liver blood flow [56]. Together these results suggest that vascular dispersion in the liver is quite robust and resilient to various pathophysiological disruptions, or alternatively that the multiple indicator dilution method is not sensitive enough to detect changes that occur with liver pathology.
In conclusion, old age was not associated with any change in sinusoidal density, sinusoidal size or vascular dispersion. The liver sinusoidal network is highly complex and branched and there were age-related changes in the geometry and complexity of the sinusoidal microcirculation, which could impact on hepatic function and reflect patterns of aging in other structures.
Acknowledgments
Funding: This work was supported by the National Health and Medical Research Council of Australia grant number 352342 and 352343: National Institute Health/National Institute of Aging grant number R21 AG-02582: Ageing and Alzheimers Research Foundation.
We acknowledge the support and help of Tharani (Mimi) Sabaretnam, Dr Colin Dustan and Dr Robert Kalak from the ANZAC Research Institute.
References
- 1.Bassingthwaighte JB, King RB, Roger SA. Fractal nature of regional myocardial blood flow heterogeneity. Circ Res. 1989;65:578–90. doi: 10.1161/01.res.65.3.578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bassingthwaighte JB, King RB, Sambrook JE, van Steenwyk B. Fractal analysis of blood-tissue exchange kinetics. Adv Exp Med Biol. 1988;222:15–23. doi: 10.1007/978-1-4615-9510-6_2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bearden SE. Effect of aging on the structure and function of skeletal muscle microvascular networks. Microcirculation. 2006;13:279–88. doi: 10.1080/10739680600618892. [DOI] [PubMed] [Google Scholar]
- 4.Bearden SE, Payne GW, Chisty A, Segal SS. Arteriolar network architecture and vasomotor function with ageing in mouse gluteus maximus muscle. J Physiol. 2004;561:535–45. doi: 10.1113/jphysiol.2004.068262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brouwer A, Barelds RJ, Knook DL. Age-related changes in the endocytic capacity of rat liver Kupffer and endothelial cells. Hepatology. 1985;5:362–6. doi: 10.1002/hep.1840050304. [DOI] [PubMed] [Google Scholar]
- 6.Chelminiak P, Dixon JM, Tuszynski JA, Marsh RE. Application of a random network with a variable geometry of links to the kinetics of drug elimination in healthy and diseased livers. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73:051912. doi: 10.1103/PhysRevE.73.051912. [DOI] [PubMed] [Google Scholar]
- 7.Cogger VC, Hilmer S, Sullivan D, Muller M, Fraser R, Le Couteur DG. Surfactants and hyperlipidemia: the liver sieve is a link. Atherosclerosis. 2006;189:273–281. doi: 10.1016/j.atherosclerosis.2005.12.025. [DOI] [PubMed] [Google Scholar]
- 8.Cogger VC, Warren A, Fraser R, Ngu M, McLean AJ, Le Couteur DG. Hepatic sinusoidal pseudocapillarization with aging in the non-human primate. Exp Gerontol. 2003;38:1101–1107. doi: 10.1016/j.exger.2003.07.002. [DOI] [PubMed] [Google Scholar]
- 9.Cook JJ, Wailgum TD, Vasthare US, Mayrovitz HN, Tuma RF. Age-related alterations in the arterial microvasculature of skeletal muscle. J Gerontol. 1992;47:B83–8. doi: 10.1093/geronj/47.3.b83. [DOI] [PubMed] [Google Scholar]
- 10.Cross SS, Start RD, Silcocks PB, Bull AD, Cotton DW, Underwood JC. Quantitation of the renal arterial tree by fractal analysis. J Pathol. 1993;170:479–84. doi: 10.1002/path.1711700412. [DOI] [PubMed] [Google Scholar]
- 11.Evans AM, Hussein Z, Rowland M. A two-compartment dispersion model describes the hepatic outflow profile of diclofenac in the presence of its binding protein. J Pharm PharmacoL. 1991;43:709–714. doi: 10.1111/j.2042-7158.1991.tb03463.x. [DOI] [PubMed] [Google Scholar]
- 12.Farkas E, Luiten PG. Cerebral microvascular pathology in aging and Alzheimer’s disease. Prog Neurobiol. 2001;64:575–611. doi: 10.1016/s0301-0082(00)00068-x. [DOI] [PubMed] [Google Scholar]
- 13.Folkow B, Svanborg A. Physiology of cardiovascular aging. Physiol Rev. 1993;73:725–764. doi: 10.1152/physrev.1993.73.4.725. [DOI] [PubMed] [Google Scholar]
- 14.Froomes PR, Sachinidis J, Ghabrial H, Tochon-Danguy H, Scott A, Ching MS, et al. A novel method for determining hepatic sinusoidal oxygen permeability in the isolated perfused rat liver using [15O]O2. Nucl Med Biol. 2003;30:93–100. doi: 10.1016/s0969-8051(02)00386-4. [DOI] [PubMed] [Google Scholar]
- 15.Fuite J, Marsh R, Tuszynski J. Fractal pharmacokinetics of the drug mibefradil in the liver. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;66:021904. doi: 10.1103/PhysRevE.66.021904. [DOI] [PubMed] [Google Scholar]
- 16.Gaudio E, Chaberek S, Montella A, Pannarale L, Morini S, Novelli G, et al. Fractal and Fourier analysis of the hepatic sinusoidal network in normal and cirrhotic rat liver. J Anat. 2005;207:107–15. doi: 10.1111/j.1469-7580.2005.00436.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghirardi O, Cozzolino R, Guaraldi D, Giuliani A. Within- and between-strain variability in longevity of inbred and outbred rats under the same environmental conditions. Exp Gerontol. 1995;30:485–94. doi: 10.1016/0531-5565(95)00002-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goldberger AL, Amaral LA, Hausdorff JM, Ivanov P, Peng CK, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci U S A. 2002;99(Suppl 1):2466–72. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Goldberger AL, Peng CK, Lipsitz LA. What is physiologic complexity and how does it change with aging and disease? Neurobiol Aging. 2002;23:23–6. doi: 10.1016/s0197-4580(01)00266-4. [DOI] [PubMed] [Google Scholar]
- 20.Goresky CA, Pang KS, Schwab AJ, Barker Fd, Cherry WF, Bach GG. Uptake of a protein-bound polar compound, acetaminophen sulfate, by perfused rat liver. Hepatology. 1992;16:173–90. doi: 10.1002/hep.1840160129. [DOI] [PubMed] [Google Scholar]
- 21.Harman D. Aging: a theory based on free radical and radiation chemistry. J Gerontol. 1956;11:298–300. doi: 10.1093/geronj/11.3.298. [DOI] [PubMed] [Google Scholar]
- 22.Hilmer SN, Cogger VC, Fraser R, McLean AJ, Sullivan D, Le Couteur DG. Age-related changes in the hepatic sinusoidal endothelium impede lipoprotein transfer in the rat. Hepatology. 2005;42:1349–1354. doi: 10.1002/hep.20937. [DOI] [PubMed] [Google Scholar]
- 23.Huet PM, Villeneuve JP. Microcirculation of the aging liver: is getting old like having cirrhosis? Hepatology. 2005;42:1248–51. doi: 10.1002/hep.20991. [DOI] [PubMed] [Google Scholar]
- 24.Ito Y, Sorensen KK, Bethea NW, Svistounov D, McCuskey MK, Smedsrod BH, et al. Age-related changes in the hepatic microcirculation of mice. Exp Gerontol. 2007;48:789–797. doi: 10.1016/j.exger.2007.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jamieson H, Hilmer SN, Cogger VC, Warren A, Cheluvappa R, Abernethy DR, et al. Caloric restriction reduces age-related pseudocapillarization of the hepatic sinusoid. Exp Gerontol. 2007;42:374–8. doi: 10.1016/j.exger.2006.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Javanaud C. The application of a fractal model to the scattering of ultrasound in biological media. J Acoust Soc Am. 1989;86:493–6. doi: 10.1121/1.398228. [DOI] [PubMed] [Google Scholar]
- 27.Krucker T, Lang A, Meyer EP. New polyurethane-based material for vascular corrosion casting with improved physical and imaging characteristics. Microsc Res Tech. 2006;69:138–47. doi: 10.1002/jemt.20263. [DOI] [PubMed] [Google Scholar]
- 28.Kyriazis M. Practical applications of chaos theory to the modulation of human ageing: nature prefers chaos to regularity. Biogerontology. 2003;4:75–90. doi: 10.1023/a:1023306419861. [DOI] [PubMed] [Google Scholar]
- 29.Lakatta EG. Arterial and cardiac aging: major shareholders in cardiovascular disease enterprises: Part III: cellular and molecular clues to heart and arterial aging. Circulation. 2003;107:490–7. doi: 10.1161/01.cir.0000048894.99865.02. [DOI] [PubMed] [Google Scholar]
- 30.Lakatta EG, Levy D. Arterial and cardiac aging: major shareholders in cardiovascular disease enterprises: Part I: aging arteries: a “set up” for vascular disease. Circulation. 2003;107:139–146. doi: 10.1161/01.cir.0000048892.83521.58. [DOI] [PubMed] [Google Scholar]
- 31.Landini G, Misson GP, Murray PI. Fractal analysis of the normal human retinal fluorescein angiogram. Curr Eye Res. 1993;12:23–7. doi: 10.3109/02713689308999492. [DOI] [PubMed] [Google Scholar]
- 32.Le Couteur DG, Cogger VC, Markus AMA, Harvey PJ, Yin ZL, Ansselin AD, et al. Pseudocapillarization and associated energy limitation in the aged rat liver. Hepatology. 2001;33:537–543. doi: 10.1053/jhep.2001.22754. [DOI] [PubMed] [Google Scholar]
- 33.Le Couteur DG, Fraser R, Cogger VC, McLean AJ. Hepatic pseudocapillarisation and atherosclerosis in ageing. Lancet. 2002;359:1612–1615. doi: 10.1016/S0140-6736(02)08524-0. [DOI] [PubMed] [Google Scholar]
- 34.Le Couteur DG, Fraser R, Hilmer S, Rivory LP, McLean AJ. The hepatic sinusoid in aging and cirrhosis - Effects on hepatic substrate disposition and drug clearance. Clin Pharmacokinet. 2005;44:187–200. doi: 10.2165/00003088-200544020-00004. [DOI] [PubMed] [Google Scholar]
- 35.Le Couteur DG, McLean AJ. The aging liver - Drug clearance and an oxygen diffusion barrier hypothesis. Clin Pharmacokinet. 1998;34:359–373. doi: 10.2165/00003088-199834050-00003. [DOI] [PubMed] [Google Scholar]
- 36.Le Couteur DG, Rivory LP, Pond SM. Hepatic intracellular pH during the prereplicative period following partial hepatectomy. Am J Physiol. 1993;264:G767–G773. doi: 10.1152/ajpgi.1993.264.4.G767. [DOI] [PubMed] [Google Scholar]
- 37.Le Couteur DG, Warren A, Cogger VC, Smedsrod B, Sorensen K, de Cabo R, et al. Old age and the hepatic sinusoid. Anatomical Record. 2007 doi: 10.1002/ar.20661. (in press) [DOI] [PubMed] [Google Scholar]
- 38.Lipsitz LA, Goldberger AL. Loss of ‘complexity’ and aging. Potential applications of fractals and chaos theory to senescence. JAMA. 1992;267:1806–9. [PubMed] [Google Scholar]
- 39.Macheras P. A fractal approach to heterogeneous drug distribution: calcium pharmacokinetics. Pharm Res. 1996;13:663–70. doi: 10.1023/a:1016031129053. [DOI] [PubMed] [Google Scholar]
- 40.Marin J. Age-related changes in vascular responses: a review. Mech Ageing Dev. 1995;79:71–114. doi: 10.1016/0047-6374(94)01551-v. [DOI] [PubMed] [Google Scholar]
- 41.Marxen M, Henkelman RM. Branching tree model with fractal vascular resistance explains fractal perfusion heterogeneity. Am J Physiol. 2003;284:H1848–57. doi: 10.1152/ajpheart.00510.2002. [DOI] [PubMed] [Google Scholar]
- 42.Masters BR. Fractal analysis of the vascular tree in the human retina. Annu Rev Biomed Eng. 2004;6:427–52. doi: 10.1146/annurev.bioeng.6.040803.140100. [DOI] [PubMed] [Google Scholar]
- 43.McLean AJ, Cogger VC, Chong GC, Warren A, Markus AMA, Dahlstrom JE, et al. Age-related pseudocapillarization of the human liver. J Pathol. 2003;200:112–117. doi: 10.1002/path.1328. [DOI] [PubMed] [Google Scholar]
- 44.McLean AJ, Le Couteur DG. Aging biology and geriatric clinical pharmacology. Pharmacol Rev. 2004;56:163–184. doi: 10.1124/pr.56.2.4. [DOI] [PubMed] [Google Scholar]
- 45.Payne GW, Bearden SE. The microcirculation of skeletal muscle in aging. Microcirculation. 2006;13:275–7. doi: 10.1080/10739680600618710. [DOI] [PubMed] [Google Scholar]
- 46.Poole D, Behnke B, Musch T. Capillary hemodynamics and oxygen pressures in the aging microcirculation. Microcirculation. 2006;13:289–99. doi: 10.1080/10739680600618793. [DOI] [PubMed] [Google Scholar]
- 47.Riddle DR, Sonntag WE, Lichtenwalner RJ. Microvascular plasticity in aging. Ageing Res Rev. 2003;2:149–68. doi: 10.1016/s1568-1637(02)00064-8. [DOI] [PubMed] [Google Scholar]
- 48.Roberts MS, Donaldson JD, Rowland M. Models of hepatic elimination: comparison of stochastic models to describe residence time distributions and to predict the influence of drug distribution, enzyme heterogeneity, and systemic recycling on hepatic elimination. J Pharmacokinet Biopharm. 1988;16:31–83. doi: 10.1007/BF01061862. [DOI] [PubMed] [Google Scholar]
- 49.Roberts MS, Rowland M. A dispersion model of hepatic elimination: 1. Formulation of the model and bolus considerations. J Pharmacokinet Biopharm. 1986;14:227–260. doi: 10.1007/BF01106706. [DOI] [PubMed] [Google Scholar]
- 50.Sahin S, Rowland M. Evaluation of route of input on the hepatic disposition of diazepam. J Pharmacol Exp Ther. 2000;295:836–43. [PubMed] [Google Scholar]
- 51.Schmucker DL. Age-related changes in liver structure and function: implications for disease? Exp Gerontol. 2005;40:650–659. doi: 10.1016/j.exger.2005.06.009. [DOI] [PubMed] [Google Scholar]
- 52.Schmucker DL. Aging and the liver: an update. J Gerontol. 1998;53A:B315–B320. doi: 10.1093/gerona/53a.5.b315. [DOI] [PubMed] [Google Scholar]
- 53.Vollmar B, Pradarutti S, Richter S, Menger MD. In vivo quantification of ageing changes in the rat liver from early juvenile to senescent life. Liver. 2002;22:330–41. doi: 10.1034/j.1600-0676.2001.01631.x. [DOI] [PubMed] [Google Scholar]
- 54.Warren A, Bertolino P, Cogger VC, McLean AJ, Fraser R, Le Couteur DG. Hepatic pseudocapillarization in aged mice. Exp Gerontol. 2005;40:807–12. doi: 10.1016/j.exger.2005.06.012. [DOI] [PubMed] [Google Scholar]
- 55.Weiss M. A note on the interpretation of tracer dispersion in the liver. J Theor Biol. 1997;184:1–6. doi: 10.1006/jtbi.1996.0265. [DOI] [PubMed] [Google Scholar]
- 56.Weiss M, Ballinger LN, Roberts MS. Kinetic analysis of vascular marker distribution in perfused rat livers after regeneration following partial hepatectomy. J Hepatol. 1998;29:476–81. doi: 10.1016/s0168-8278(98)80068-8. [DOI] [PubMed] [Google Scholar]
- 57.Wynne HA, Cope LH, Mutch E, Rawlins MD, Woodhouse KW, James OFW. The effect of age upon liver volume and apparent liver blood flow in healthy man. Hepatology. 1989;9:297–301. doi: 10.1002/hep.1840090222. [DOI] [PubMed] [Google Scholar]


