Abstract
Many quantum mechanical calculations indicate water molecules in the gas and liquid phase have much larger quadrupole moments than any of the common site models of water for computer simulations. Here, comparisons of multipoles from quantum mechanical∕molecular mechanical (QM∕MM) calculations at the MP2∕aug-cc-pVQZ level on a B3LYP∕aug-cc-pVQZ level geometry of a waterlike cluster and from various site models show that the increased square planar quadrupole can be attributed to the p-orbital character perpendicular to the molecular plane of the highest occupied molecular orbital as well as a slight shift of negative charge toward the hydrogens. The common site models do not account for the p-orbital type electron density and fitting partial charges of TIP4P- or TIP5P-type models to the QM∕MM dipole and quadrupole give unreasonable higher moments. Furthermore, six partial charge sites are necessary to account reasonably for the large quadrupole, and polarizable site models will not remedy the problem unless they account for the p-orbital in the gas phase since the QM calculations show it is present there too. On the other hand, multipole models by definition can use the correct multipoles and the electrostatic potential from the QM∕MM multipoles is much closer than that from the site models to the potential from the QM∕MM electron density. Finally, Monte Carlo simulations show that increasing the quadrupole in the soft-sticky dipole-quadrupole-octupole multipole model gives radial distribution functions that are in good agreement with experiment.
INTRODUCTION
The unique properties of water as a pure liquid and as a solvent are a function of its hydrogen-bonded structure, specifically through the attraction between the partially positive hydrogen atoms and the electronegative oxygen atoms.1 Thus, the challenge in developing classical potential energy functions for computer simulations of liquid water is to find a simplified description of the charge distribution that accurately describes the hydrogen bonding in the liquid phase. Classical potentials typically represent the charge distribution of a water molecule as partial charges located at sites that are generally on the nuclei but may also include additional sites, with the electrostatic interactions between molecules given by charge–charge interactions between the partial charges. Alternatively, the charge distribution can be described by the electrostatic multipoles of the molecule, with electrostatic interactions between molecules given by a multipole expansion.2 The molecular point multipoles are centered on a single site of the molecule (as opposed to atomic multipoles on each atom, for instance in the AMOEBA model3), and thus reduce the number of interaction sites over site models. However, it is not strictly clear whether partial charges or multipoles are more accurate at a molecular level since although the charge of the nuclei can be considered as point charges, the electrons are best described as electron density rather than point charges.
Quantum mechanical (QM) calculations can be used to develop parameters for the electrostatic potential energy functions based on the location of the nuclei and electron density of a molecule. Unfortunately, partitioning electron density onto partial charge sites within the molecule is not a unique process. For instance, electrostatic potential (ESP) charges are obtained by fitting the electrostatic potential due to the electron density and nuclei by partial charges at designated sites. Alternatively, Mulliken population, natural bond orbital,4 atoms in molecules,5 and related analyses assign electron density to nuclei based on different criteria, and the total charge on an atom is then the sum of the assigned electron density and nuclear charge. On the other hand, the molecular electrostatic multipole moments are unique quantities that can be calculated from the electron density and nuclear charge, and the dipole and quadrupole moments can be measured experimentally in the gas phase. In fact, one indication of the inadequacy of partial charges is that the moments calculated from the partial charges usually differ from the exact moments computed from the electron density. For instance, even if the dipole moment of a molecule calculated from partial charges is constrained to the correct value from the electron density, the quadrupole moment may be quite different because the dipole depends on the distance of charge from the center of the expansion while the quadrupole depends on the square of the distance, generally leading to underestimation of the quadrupole by site models.
In addition, while high level QM calculations of the intramolecular geometry and electron density of a water molecule in the gas phase agree well with experiment,6 such calculations in the liquid phase are challenging because of fluctuating perturbations due to neighboring molecules. Ab initio molecular dynamics (AIMD) simulations generate multiple configurations of the liquid in which all of the waters are treated quantum mechanically but at a lower level.7, 8 Moreover, assigning electron density to specific molecules is problematic so that even calculating multipole moments is not unique. Alternatively, quantum mechanical∕molecular mechanical (QM∕MM) calculations in which properties are averaged for one QM water surrounded by MM water in configurations taken from classical simulations allow high-level calculations of the QM water.9 In addition, the problem of which molecule the electron density belongs to is averted since only one molecule is treated quantum mechanically, although charge exchange between molecules is thus not accounted for. However, both AIMD and QM∕MM calculations indicate a significant increase in the dipole and quadrupole moments over the gas phase due to electronic polarization. In addition, studies of ice via induction models also indicate increased multipole moments over the gas phase.10
For classical computer simulations, the most common models have rigid sites. The site models all have similar dipole moments but quite different quadrupole moments,11, 12, 13 and both the dipoles and especially the quadrupoles are smaller than the AIMD and QM∕MM calculations. SPC∕E (Ref. 14) and TIP3P (Ref. 15) are simple three-point models with a negative charge on the oxygen and a positive charge on each of the hydrogens. They yield remarkably good properties for pure water at room temperature, although the dielectric constant of SPC∕E is somewhat low and the self-diffusion constant of TIP3P is more than twice the experimental value, and the properties away from standard temperature and pressure are poor.11 TIP4P (Ref. 16) and the recent modifications, TIP4P-Ew (Ref. 17) and TIP4P∕2005 (Ref. 18), have a larger quadrupole because the negative charge is moved from the oxygen to a site near the center of mass as in the MCY model (Ref. 19). The two new TIP4P-type models differ slightly from TIP4P in the partial charges and the negative charge location and give excellent properties for pure water over a large range of temperatures although the dielectric constant is somewhat low. On the other hand, TIP5P (Ref. 20) and TIP5P∕Ew (Ref. 13), a modification of only the van der Waals parameters for better performance with Ewald sums, have two added charges representing “lone pairs” located tetrahedrally with respect to the oxygen and hydrogens at a distance of 0.7 Å from the oxygen, similar to the ST2 model (Ref. 21). Its pure liquid properties are also excellent over a large range of temperatures and the dielectric constant is good. However, the quadrupole moment is even smaller than the three-point models and the partial charge on the hydrogens is about half that of other models. In addition, no evidence for concentrated electron density at such large distances from the oxygen is seen in quantum mechanical calculations of a water molecule.
Recently, we have been developing the soft-sticky dipole-quadrupole-octupole (SSDQO) model,22, 23 which represents the entire charge distribution by a single point dipole, quadrupole, and octupole located on the oxygen. By utilizing an approximate multipole expansion (AME),22, 23 SSDQO is computationally faster than three-site models and the new parameters rival TIP4P-Ew, TIP4P∕2005, and TIP5P in accuracy.11 SSDQO is an improvement over the original soft-sticky dipole (SSD) model,24 which has a dipole and an arbitrary “sticky” hydrogen-bond potential. By replacing the arbitrary potential with a moment expansion, not only is the water–water interaction now physics based, but also solute–water electrostatics can be described by multipoles rather than requiring new arbitrary sticky potentials for each solute. The radial distribution functions, which are sensitive to the short-range interactions,25 of SSDQO compared with SPC∕E around simple ions,26N-methylacetamide, ethanol, and benzene,27 and sugars using CHARMM22 parameters28 are in good agreement. Thus, since multipole expansions are exact in the limit of infinite separations or number of multipole terms, these results show that the expansion up to the octupole is necessary and sufficient for molecules at contact.
These results lead to seeming confusion over the importance of correct multipoles. Many properties of pure liquid water and their temperature dependence appear to be largely dependent on obtaining good tetrahedral structure since the TIP4P-type models, TIP5P, and SSDQO1 have more ordered first shell neighbors than SPC∕E and TIP3P, and have better temperature dependent properties. Apparently, the TIP4P-type models and SSDQO1 may have better structure than TIP3P and SPC∕E because their multipole moments are closer to values from QM calculations. On the other hand, TIP5P may model the hydrogen bond interaction energy well even though the multipole moments and electrostatic potential for the molecule may not be accurate; in other words, although the hydrogens carry less charge, the “lone pairs” come very close to them at the hydrogen bonding distance so the interaction energy is good. In addition, the earlier SSD (Ref. 24), Yukagua (Ref. 29), and mW (Ref. 30) models also reproduce many liquid properties using different empirical orientation dependent functions that enforce tetrahedrality.
However, results also indicate that the correct multipoles are important for some properties. For instance, a dipole moment that is larger than the gas phase value but smaller than the AIMD and QM∕MM values appears necessary to get the correct dielectric constant. In addition, although the quadrupoles of TIP4P-Ew and TIP4P∕2005 are still significantly lower than the AIMD and QM∕MM calculations, interestingly TIP4P∕2005 has a slightly larger quadrupole than TIP4P-Ew and performs much better for the ice–liquid phase diagram.12 However, the MCY model, which has a quadrupole increased to the gas phase value, has a dielectric constant that is too much low, and more generally, the site models with large quadrupoles tend to have lower dielectric constants for the same dipole moment.13 Moreover, while the orientation of the first shell water around Cl− is quite similar for several site models and SSDQO1, the first shell around Na+ has a dipolar orientation for SPC∕E, TIP3P, and TIP4P-Ew, a “lone pair” orientation for TIP5P, and a range of values for SSDQO1, with SSDQO1 range in agreement with QM∕MM dynamics and neutron diffraction data.31 Furthermore, the orientation is shown to be dependent on the octupole moment.31
Here, we investigate how the multipole moments and electrostatic potentials from multisite models and moment expansions compare with results from QM and QM∕MM calculations of water molecules. Specifically, the physical origin of the large quadrupole moment of water as well as the contributing factors to the octupole moments are investigated. A cluster consisting of one QM water and four hydrogen bonded neighboring classical waters serves as a model for a water molecule in the liquid phase. In addition to examining the moments from several common site modes, the partial charges for different site models are optimized to fit moments from the QM electron density to understand where the charge lies. Also, the electrostatic potential calculated from various site models and the QM multipoles are compared to the potential from the QM electron density. Finally, the effects of the moments on the radial distribution functions of pure water are examined in Monte Carlo (MC) simulations.
THEORY
A molecular coordinate system for a water molecule is located with the center at the oxygen and the hydrogens with a OH bond length bOH in the positive z-direction in the yz plane with the bisector of the HOH bond angle θHOH along the z-axis. Note that other choices for the origin of the coordinate system such as the center of mass are possible, but for comparing different water models with different bOH and θHOH, the oxygen is a common reference point. In site models, partial charges qi for sites i are an approximate description of the net shielded charges, with typically sites at the O, the two Hs and sometimes a site M located at a distance OM along the positive z-axis or two sites L located at a distance bOL in the negative z-direction in the xz plane with the bisector of the LOL angle θLOL along the z-axis.
In this coordinate system, the elements of the traceless dipole D, quadrupole Q, and octupole O matrices are
| (1) |
| (2) |
| (3) |
The other elements of the O matrix can be obtained by symmetry. (Note, the relationship with slightly different constants used in our previous papers11, 22, 23, 26, 27, 31, 32 is given in the Appendix.) For a neutral molecule, the multipoles beyond the dipole are dependent on the origin of the coordinate system; the transformations to a coordinate system with the origin at a point (0,0,c) (i.e., the center of mass) are given in the Appendix. The charge of the oxygen does not contribute to the multipoles in this coordinate system except indirectly since it must be a value to maintain charge neutrality.
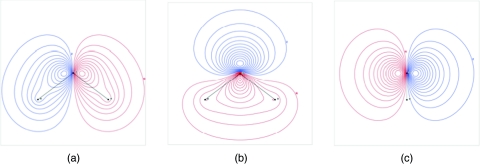
The multipoles represent the charge distribution with increasing degrees of complexity and each multipole corresponds to a different type of charge distribution, which can be illustrated as charge density (Fig. 1). The μ0 is a dipole along the z-axis due to separation of positive and negative charge along the z-axis and charge in the z = 0 plane does not contribute. The Θ0 is a linear quadrupole along the z-axis due to separation of like charge along the z-axis or in the z = 0 plane while the Θ2 is a square planar quadrupole in the xy-plane due to separation of like charge in the xy-plane. For any neutral molecule with similar symmetry, Θ2 is independent of the origin of the z-axis and the origin of the z-axis can be placed so that Θ0 = 0; for water with the coordinate system centered on the oxygen, Θ0 ≈ 0 so the focus is on the other moments. The Ω0 is a linear octupole along the z-axis due to separation of positive and negative charge along the z-axis, while the Ω2 is a cubic octupole due to separation of like charge not located on either the z-axis or the x- and y-axes.
Figure 1.
Charge distributions of moments, from left to right: μ0, a linear dipole; Θ0, a linear quadrupole; Θ2, a square quadrupole; Ω0, a linear octupole; and Ω2, a cubic octupole, in which positive charge is blue and negative charge is red.
CALCULATIONS
Quantum mechanical calculations were performed using Møller–Plesset perturbation theory (MP2) and density functional theory with B3LYP exchange–correlation functionals33 at extra fine grid levels of numerical integration. Dunning’s correlation consistent quadruple-ζ basis set with valence-polarization and diffuse functions (aug-cc-pVQZ) (Ref. 34) was utilized. Calculations for a water molecule in the gas phase were carried out at the MP2∕aug-cc-pVQZ level with geometry optimization and also at the MP2∕aug-cc-pVQZ level on a B3LYP∕aug-cc-pVQZ geometry (MP2∕aug-cc-pVQZ∕∕B3LYP∕aug-cc-pVQZ). In addition, calculations of a liquidlike cluster consisting one water surrounded by four tetrahedrally arranged hydrogen-bonded waters began with a B3LYP∕aug-cc-pVQZ optimization in which the dOO distances, the bOH bond lengths, and θHOH bond angles of all five molecules were constrained to be identical. Then, this geometry was used for all five water molecules in an MP2∕aug-cc-pVQZ level calculation in which the four surrounding waters were treated as MM waters with a partial charge of 0.33e on the hydrogens and –0.66e on the oxygen, approximately the ESP partial charges calculated for a gas phase molecule at the MP2∕aug-cc-pVQZ level. Although the surrounding waters will also be polarized, the lower gas phase values were chosen since the position and orientations of the surrounding waters will fluctuate. For additional comparisons, another cluster utilized the TIP5P geometry for all five waters and the intermolecular geometry was optimized at the B3LYP∕aug-cc-pVQZ level while constraining dOO to be identical, followed by an MP2∕aug-cc-pVQZ level calculation on the B3LYP∕aug-cc-pVQZ geometry with the four neighboring waters having TIP5P partial charges. Since all calculations used the aug-cc-pVQZ basis sets, henceforth the MP2∕aug-cc-pVQZ calculations will be referred to as simply MP2 level and the MP2∕aug-cc-pVQZ∕∕B3LYP∕aug-cc-pVQZ calculations will be referred to as MP2∕∕B3LYP level.
Quantum mechanical calculations were performed using NWCHEM (Ref. 35) and GAUSSIAN 03 (Ref. 36). All ESP charges were calculated using CHELPG (Ref. 37). The molecular orbital visualizations were performed using the extensible computational chemistry environment (ECCE) (Ref. 38) and MOLDEN (Ref. 39) application programs. The electron density and electrostatic potential contour plots were generated using the MOLDEN and GNUPLOT (Ref. 40) programs.
RESULTS AND DISCUSSION
The electrostatic description of a water molecule was investigated here by comparing results from quantum mechanical calculations of a water molecule in the gas phase and in a liquidlike cluster, gas phase experiments, and the partial charges of typical site potentials that successfully model liquid water in simulations. First, comparisons of the multipole moments from the quantum mechanical calculations and experiment with those from the partial charges of site models indicate the higher multipoles, particularly the quadrupole, of a water molecule in the liquid phase are not modeled accurately by site models. Next, examination of the electron density and variation of the partial charges in different site models to reproduce the quantum mechanical multipoles show that the large quadrupole arises from the strong p character of the highest occupied molecular orbital (HOMO) as well as from a shift in electron density toward the hydrogens away from the oxygen. Also, comparisons of the electrostatic potentials from the quantum mechanical electron density with those from the partial charges of the site models indicate that the electrostatic potential around a water molecule is not accurately modeled by site models. Finally, Monte Carlo simulations of the SSDQO multipole model of water indicate that reasonable short-range structure can be obtained with models with a large quadrupole.
Multipole moments
The ESP charge on the hydrogen qH, geometry, and multipole moments from QM calculations of a water molecule in the gas phase and of a simple water cluster model for the liquid phase were compared first to values in the literature (Table 1). Xantheas and co-workers have previously shown that the MP2∕aug-cc-pVQZ level gives excellent agreement with experimental results for the gas phase geometry, dipole, and quadrupole.6 Although the B3LYP geometry shows a slight increase in bOH and θHOH, the MP2∕∕B3LYP level can be considered a reasonable approximation in comparison to experiment. Furthermore, the water cluster consisting of a QM water surrounded by four tetrahedrally arranged hydrogen-bonded MM waters (QM∕4MM) calculated at the MP2∕∕B3LYP level (see Sec. 3) is a reasonable approximation for a water molecule in a liquid environment. The QM∕4MM geometry is similar to neutron diffraction measurements of liquid water,41 although somewhat underestimating the increase in bOH and underestimating θHOH in the liquid relative to the gas, and dOO = 2.85 Å, close to that in liquid water. The QM∕4MM moments show a general increase in the liquid relative to the gas, comparing well with those from AIMD simulations7, 8 and a QM∕MM calculation averaging a QM water in the TIP5P geometry surrounded by 230 MM TIP5P molecules (QM∕230TIP5P) using 50 snapshots from a Monte Carlo simulation at the MP2∕aug-cc-pVQZ∕∕TIP3P level.9 Furthermore, a cluster using the TIP5P geometry (QM∕4TIP5P) with dOO = 2.80 Å indicates that slight differences in bOH, θHOH, dOO, and partial charges lead to some of the differences of QM∕4MM from QM∕230TIP5P, with QM∕4MM having a better liquid phase geometry but perhaps slightly underestimating the dipole.
Table 1.
Multipoles and geometry from quantum mechanical calculations, site models, SSDQO, and experiment. All moments have been shifted to a molecular coordinate system centered on the oxygen.
| Model | qH | OH (Å) | HOH (deg) | μ0 (D) | Θ0 (DÅ) | Θ2 (DÅ) | Ω0 (DÅ2) | Ω2 (DÅ2) |
|---|---|---|---|---|---|---|---|---|
| Exp (gas) (Ref. 47) | NA | 0.957 | 104.5 | 1.86 | 0.11 | 2.57 | NA | NA |
| MP2 (gas) | 0.340 | 0.957 | 104.2 | 1.86 | 0.11 | 2.54 | –1.35 | 1.91 |
| MP2∕∕B3LYP (gas) | 0.341 | 0.961 | 105.1 | 1.85 | 0.06 | 2.58 | –1.40 | 1.94 |
| BLYP (gas) (Ref. 7) | NA | 0.972 | 104.4 | 1.87 | 0.12 | 2.51 | NA | NA |
| BLYP (gas) (Ref. 8) | NA | 0.972 | 104.4 | 1.85 | 0.09 | 2.49 | NA | NA |
| Exp (liquid) (Ref. 41) | NA | 0.976 | 105.1 | NA | NA | NA | NA | NA |
| QM∕4MM | 0.453 | 0.965 | 105.9 | 2.49 | 0.13 | 2.93 | –1.73 | 2.09 |
| QM∕4TIP5P | 0.504 | 0.957 | 104.5 | 2.69 | 0.26 | 2.95 | –1.70 | 2.08 |
| QM∕230TIP5P (Ref. 9) | NA | 0.957 | 104.5 | 2.55 | 0.20 | 2.81 | –1.52 | 2.05 |
| AIMD (Ref. 7) | NA | 0.991 | 105.5 | 2.95 | 0.18 | 3.27 | NA | NA |
| AIMD (Ref. 8) | NA | 0.970 | 104.7 | 2.43 | 0.10 | 2.72 | NA | NA |
| SPC∕E | 0.424 | 1.000 | 109.5 | 2.35 | 0.00 | 2.04 | –1.57 | 1.96 |
| TIP3P | 0.417 | 0.957 | 104.5 | 2.35 | 0.23 | 1.72 | –1.21 | 1.68 |
| TIP4P | 0.520 | 0.957 | 104.5 | 2.18 | 0.17 | 2.15 | –1.53 | 2.10 |
| TIP4P-Ew | 0.524 | 0.957 | 104.5 | 2.32 | 0.21 | 2.16 | –1.53 | 2.11 |
| TIP4P∕2005 | 0.556 | 0.957 | 104.5 | 2.31 | 0.18 | 2.30 | –1.64 | 2.24 |
| TIP4P∕Ice | 0.590 | 0.957 | 104.5 | 2.43 | 0.18 | 2.43 | –1.74 | 2.38 |
| TIP5P, TIP5P∕Ew | 0.241 | 0.957 | 104.5 | 2.29 | 0.13 | 1.56 | –1.01 | 0.59 |
| AST | 0.212 | 1.000 | 109.5 | 2.35 | 0.00 | 2.04 | –1.57 | 0.00 |
| SSDQO1 | NA | 0.957 | 104.5 | 2.12 | 0.28 | 2.13 | –1.34 | 1.15 |
Since both the molecular geometry and the charge distribution affect the multipole moments, various ratios of the moments were also compared (Table 2). The QM∕4MM moments agree even better with the liquid calculations when the relative values of the multipoles are considered, which should remove some bias in the different ways the multipoles were calculated. For instance, while the dipole moment varies considerably for the liquid calculations, the moments relative to the dipole moment are quite consistent for the same phase and are smaller for all of the liquid phase approximations (Θ2∕μ0 ≈ ∼1.1, Ω0∕μ0 ≈ ∼0.65, Ω2∕μ0 ≈ ∼0.8) than for the gas phase (Θ2∕μ0 ≈ ∼1.4, Ω0∕μ0 ≈ ∼0.71, Ω2∕μ0 ≈ ∼1.0). However, the QM octupole moments relative to the square planar quadrupole are about the same in the liquid phase as the gas phase (Ω0∕Θ2 ≈ ∼0.55, Ω2∕Θ2 ≈ ∼0.73). Thus, since μ0 measures the separation of positive and negative charge along the z-axis and Θ2 measures the separation of positive charges along the x-axis and negative charges along the y-axis, polarization enhances the moments more along the z-direction than the xy-direction. Furthermore, since Θ2∕μ0 is larger in the gas phase than the liquid phase, adding polarizability to a rigid model will not improve the quadrupole unless the model has a large quadrupole in the gas phase. Finally, the QM∕4MM agrees well with the AIMD and QM∕230TIP5P even though the thermal fluctuations of the first shell are neglected and no interactions beyond the first shell are considered so henceforth QM∕4MM will be used as a representative of a water molecule in the liquid phase.
Table 2.
Ratios of multipoles from quantum mechanical calculations, site models, SSDQO, and experiment. All moments have been shifted to a molecular coordinate system centered on the oxygen.
| Model | Θ0∕μ0 (Å) | Θ2∕μ0 (Å) | Ω0∕μ0 (Å2) | Ω2∕μ0 (Å2) | Ω0∕Θ2 (Å) | Ω2∕Θ2 (Å) | Ω2∕Ω0 |
|---|---|---|---|---|---|---|---|
| Exp (gas) | 0.07 | 1.38 | NA | NA | NA | NA | NA |
| MP2 (gas) | 0.06 | 1.36 | –0.72 | 1.03 | –0.53 | 0.75 | –1.42 |
| MP2∕∕B3LYP (gas) | 0.03 | 1.39 | –0.76 | 1.05 | –0.54 | 0.75 | –1.39 |
| BYLYP | 0.07 | 1.34 | NA | NA | NA | NA | NA |
| BYLYP | 0.05 | 1.34 | NA | NA | NA | NA | NA |
| QM∕4MM | 0.05 | 1.18 | –0.70 | 0.84 | –0.59 | 0.71 | –1.35 |
| QM∕4TIP5P | 0.10 | 1.10 | –0.63 | 0.77 | –0.57 | 0.71 | –1.23 |
| QM∕230TIP5P | 0.16 | 1.10 | –0.60 | 0.81 | –0.54 | 0.73 | –1.01 |
| AIMD | 0.07 | 1.11 | NA | NA | NA | NA | NA |
| AIMD | –0.04 | 1.12 | NA | NA | NA | NA | NA |
| SPC∕E | 0.00 | 0.87 | –0.67 | 0.83 | –0.77 | 0.96 | –1.25 |
| TIP3P | 0.10 | 0.73 | –0.52 | 0.72 | –0.70 | 0.98 | –1.39 |
| TIP4P | 0.08 | 0.99 | –0.70 | 0.96 | –0.71 | 0.98 | –1.37 |
| TIP4P-Ew | 0.09 | 0.93 | –0.66 | 0.91 | –0.71 | 0.98 | –1.38 |
| TIP4P∕2005 | 0.08 | 1.00 | –0.71 | 0.97 | –0.71 | 0.98 | –1.37 |
| TIP4P∕Ice | 0.07 | 1.00 | –0.72 | 0.98 | –0.71 | 0.98 | –1.37 |
| TIP5P, TIP5P∕Ew | 0.06 | 0.68 | –0.44 | 0.26 | –0.64 | 0.38 | –0.59 |
| AST | 0.00 | 0.87 | –0.67 | 0.00 | –0.77 | 0.00 | 0.00 |
| SSDQO1 | 0.00 | 1.00 | –0.63 | 0.54 | –0.63 | 0.54 | –0.86 |
The partial charge on the hydrogen qH, geometry, and moments of the site models were also examined (Table 1). The site models all have relatively similar μ0 but differ in the higher moments and all of the site models have slightly smaller μ0 than the QM∕4MM. The larger μ0 for QM∕4MM might be because significant electron density spreads beyond 1.4 Å of the oxygen, so that at the typical O–O distance of the liquid, some of the electron density at large distances is involved in charge exchange rather than contributing to the dipole–dipole interaction. Since electron density from another molecule would be closer to the oxygen than the electron density contributed to other molecule, this should systematically cause an increase in all of the multipoles of the QM∕4MM relative to a site model representation. Moreover, the most dramatic difference between the site models and QM∕4MM is the large Θ2 quadrupole of QM∕4MM.
The ratios of the multipoles of the site models were also compared (Table 2). Two site models that serve as useful references are the tetrahedral SPC∕E model with hydrogen sites at bOH = 1 Å, θHOH = 109.47°, and charge qH = 0.424e and a perfectly antisymmetric tetrahedral (AST) model with two additional sites L at bOL = bOH = 1 Å, θLOL = θHOL = θHOH = 109.47°, and charges qL = –qH = –0.212 e, so that the dipole μ0 is the same as SPC∕E. The AST multipoles are identical to SPC∕E multipoles for l odd, m = 0, 4, …, l–1 and l even, m = 2, 6, …, l where l is the order of the multipole and m is the subscript, but they are zero otherwise because AST is antisymmetric whereas they are (generally) nonzero for SPC∕E. Thus, AST and SPC∕E have identical Θ0∕μ0 = 0, Ω0∕μ0 = –(2∕3)bOH2, and Ω0∕Θ2 = –(4∕√3)bOH because the charge distribution along the z-axis is equivalent. Note that Ω0 is opposite in sign to μ0 so it decreases charge density along the z-axis and increases it along the tetrahedral directions to account for the separation of positive charge onto the hydrogens, which are off the z-axis. Also, AST and SPC∕E have identical Θ2∕μ0 = (√3∕2)bOH because the positive charge spread along the x- and z-axes and the negative charge spread along the y- and z-axes contribute equally. However, AST has Ω2∕μ0 = Ω2∕Θ2 = Ω2∕Ω0 = 0 while SPC∕E has Ω2∕μ0 = (5∕6)bOH2, Ω2∕Θ2 = (5∕3√3)bOH, and Ω2∕Ω0 = –(5∕4) because Ω2 enhances the lobes of positive charge near the hydrogens and decreases the lobes of negative charge in the lone pair direction, thus breaking the tetrahedral antisymmetry of the positive and negative of the AST model. Note that Ω2 is thus the lowest order multipole that differentiates SPC∕E and AST. Generally, –Θ0∕μ0, Θ2∕μ0, –Ω0∕μ0, and Ω2∕μ0 for TIP3P, SPC∕E, and the TIP4P-type become more positive with increasing θHOH or θHMH. TIP5P has somewhat smaller values of Θ2∕μ0 and Ω0∕μ0 than TIP3P because θLOL is not equal to θHOH as is the case for AST and SPC∕E, and it has a value of Ω2∕μ0 intermediate between AST and SPC∕E because the “lone pair” partial charges are slightly closer to the oxygen than the hydrogens are (bOL = 0.7 Å while bOH = 1.0 Å). In addition, TIP3P, SPC∕E, and the TIP4P-type have very similar Ω0∕Θ2, and Ω2∕Θ2 because Θ2 is a function of only the spread of the positive charge of the hydrogens in the xy-plane and Ω0 cancels charge along the z-axis from the dipole to account for the spread in the hydrogen charge and Ω2 cancels charge spread in the “lone pair” directions. TIP5P differs in Ω0∕Θ2 from the others because the θLOL and θHOH angles differ and Ω2∕Θ2 is small because of the lone pair charges.
Comparing the ratios of moments for the site models and QM∕4MM (Table 2) can give insight as to the origin of the large quadrupole. SPC∕E and TIP3P have much smaller Θ2∕μ0 than QM∕4MM, indicating that a three-site model cannot model the large quadrupole, while the TIP4P-type have closer Θ2∕μ0 to QM∕4MM, indicating that the movement of charge toward the hydrogens is consistent with the large quadrupole but does not account for all of it. On the other hand, TIP5P has a much smaller Θ2∕μ0 than even SPC∕E and TIP3P so that the lone pair charges are inconsistent with the large quadrupole. Moreover, the site models are similar to QM∕4MM for Ω0∕μ0 but consistently larger for Ω0∕Θ2, which indicates that the remaining contribution to the large quadrupole is due to charge that lies mainly in the z = 0 plane and thus contributes to increasing Θ2 but not Ω0 since charge that lies above or below that plane would contribute to increasing both. Also, the site models are similar to QM∕4MM for Ω2∕μ0 and very different for Ω2∕Θ2, which indicates that the remainder of the large quadrupole is not due to a greater shift in charge in the z or lone pair directions.
Thus, overall TIP5P is inconsistent with the QM∕4MM multipoles because it has too much tetrahedral antisymmetry. Moreover, the movement of negative charge in the positive z-direction in the TIP4P-type models is consistent with the QM∕4MM moments, although the quadrupole is still too small. Finally, the remainder of the large quadrupole appears to come from charge close to the z = 0 plane.
The large quadrupole moment in quantum mechanical calculations
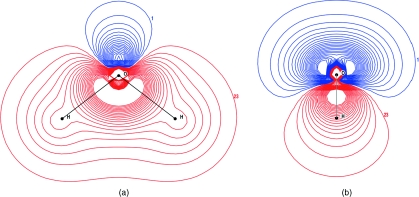
The origin of the large quadrupole moment can be seen by examining the electron density of the QM∕4MM cluster. The three highest occupied molecular orbitals all have strong p-orbital character (Fig. 2) and the HOMO has strong p character perpendicular to the plane of the molecule (referred to here as p⊥). Although the effects of these p-orbitals are hard to see in the total electron density, the difference in the electron density of the molecule versus the free atoms (Fig. 3) shows there is a net increase in electron density from the p⊥ orbital at ∼0.3 Å from oxygen and slightly below the x-axis; in comparison, the lone pair sites of TIP5P are 0.7 Å from the oxygen. In addition, there is less subtraction of electron density at a point similar to the M point in TIP4P-type models than other points equidistant around the oxygen.
Figure 2.
Electron density of three highest occupied MOs of QM∕4MM. (a) 1b2 (b) 3a1 (c) 1b1 (HOMO).
Figure 3.
Difference in electron density of the molecule from free atoms for QM∕4MM at the B3LYP∕6-31G** level (a) parallel and (b) perpendicular to the plane of the molecule.
To gain a better understanding of the QM moments based on the electron density, different site models were constructed with geometry and certain multipoles of the QM∕4MM cluster as well as the gas phase molecule (Table 3); only the QM∕4MM cluster will be discussed in detail. The simplest has sites only at the O and Hs, with partial charges qO = –2qH determined by μ0 from the QM∕4MM cluster (3P). The qH was close to the ESP value and the higher moments were fairly close to the QM∕4MM values except that Θ2 was only about 2∕3 of the QM∕4MM value. Thus, most of the basic features of the charge distribution of the QM∕4MM central water except for the large quadrupole are accounted for in this simple picture. Next, a TIP4Plike M site with charge qM = –2qH (qO = 0) was added along the positive z-axis with μ0 and Θ2 constrained to the QM∕4MM values (3P + M). The qH increased by ∼50% over the ESP value and Ω0 and Ω2 increased over the QM∕4MM values, indicating that moving negative charge along the z-axis accounts for some but not all of the large quadrupole. However, when two TIP5P-like L sites with charge qL = –qH and θLOL = 109.47° are added with μ0 and Θ2 constrained to the QM∕4MM values (3P + 2Ltet), qH is less than 40% of the ESP charge, the L sites are 1.65 Å from the oxygen, Ω0 is almost double the QM∕4MM value, and Ω2 has the wrong sign. However, when instead two L sites were added with θLOL = 180° to mimic the p⊥ orbital (3P + 2Lπ), qH is the same as the 3P value, the L sites are 0.56 Å from the oxygen, and the higher moments are reasonable except Θ0 is too large. Thus, adding charge to mimic the p⊥ orbital rather than an sp3 orbital is more consistent with the QM∕4MM moments, but the deviation in Θ0 indicates that moving negative charge in the positive z-direction is needed. Finally, adding an M site of charge qM = –1, two L sites of charge qL = –1, and qO = 2qH = 1 while varying θLOL but constraining μ0, Θ0, and Θ2 (3P + 2L + M) gives reasonable higher moments with θLOL = 139°.
Table 3.
Multipoles optimized to fit QM∕4MM moments. Multipoles free to vary indicated in boldface. Dipole for QM∕4MM is 2.49 D and for MP2(gas) is 1.86 D.
| Model | qH | qL | OL (Å) | qM | OM (Å) | Θ0∕μ0 (Å) | Θ2∕μ0 (Å) | Ω0∕μ0 (Å2) | Ω2∕μ0 (Å2) | Ω0∕Θ2 (Å) | Ω2∕Θ2 (Å) | Ω2∕Ω0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QM∕4MM | 0.45 | 0.05 | 1.18 | –0.70 | 0.84 | –0.59 | 0.71 | –1.21 | ||||
| 3P | 0.45 | 0.07 | 0.77 | –0.55 | 0.74 | –0.72 | 0.97 | –1.34 | ||||
| 3P+M | 0.69 | –1.37 | 0.20 | 0.00 | 1.18 | –0.87 | 1.14 | –0.74 | 0.97 | –1.31 | ||
| 3P+2Ltet | 0.17 | –0.17 | 1.65 | 0.03 | 1.18 | –1.34 | –1.13 | –1.13 | –0.96 | 0.84 | ||
| 3P+2Lπ | 0.45 | –0.45 | 0.56 | 0.35 | 1.18 | –0.55 | 0.74 | –0.47 | 0.63 | –1.34 | ||
| 3P+2L139+M | 0.50 | –1.00 | 0.35 | –1.00 | 0.31 | 0.05 | 1.18 | –0.75 | 0.77 | –0.63 | 0.65 | –1.03 |
| MP2(gas) | 0.34 | 0.06 | 1.36 | –0.72 | 1.03 | –0.53 | 0.75 | –1.42 | ||||
| 3P | 0.33 | 0.10 | 0.73 | –0.51 | 0.71 | –0.70 | 0.98 | –1.40 | ||||
| 3P+M | 0.62 | –1.24 | 0.27 | –0.05 | 1.36 | –1.02 | 1.33 | –0.75 | 0.98 | –1.31 | ||
| 3P+2Ltet | 0.11 | –0.11 | 1.96 | 0.04 | 1.36 | –1.85 | –1.85 | –1.36 | –1.36 | 1.00 | ||
| 3P+2Lπ | 0.33 | –0.33 | 0.70 | 0.53 | 1.36 | –0.51 | 0.71 | –0.37 | 0.52 | –1.40 | ||
| 3P+2L146+M | 0.45 | –1.00 | 0.32 | –1.00 | 0.33 | 0.06 | 1.36 | –0.85 | 0.91 | –0.63 | 0.67 | –1.07 |
Overall, considering 3P + M, 3P + 2L, and 3P + 2L + M, the increased Θ2 in the liquid phase is apparently due to the strong p⊥ character of the HOMO and the shift of electron density toward the hydrogens away from the oxygen. Of course, more sites could be added, but the utility of even a six-point model such as 3P + 2L + M is questionable since it entails adding partial charges at three more sites than TIP4P-type and one more than TIP5P since neither TIP4P-type nor TIP5P have any partial charge on the oxygen. Note that these site models were constructed to help understand the physical origins of the moments rather than to develop practical site models for simulations; thus, they have not been optimized for use in computer simulations of liquids.
Electrostatic potentials
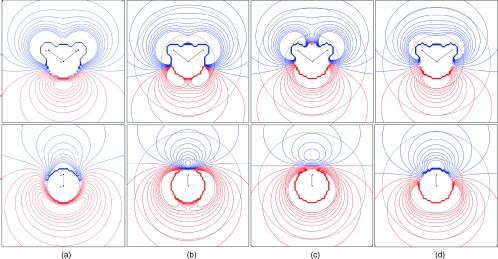
Contour maps of the electrostatic potential around the water molecule were compared for the QM∕4MM electron density, a multipole expansion to the octupole using QM∕4MM multipoles, TIP4P∕2005, and TIP5P (Fig. 4). The multipole expansion only to the quadrupole cannot give good liquid structure and the electrostatic potential for the expansion to the hexadecapole is almost identical to the potential of the expansion to the octupole at distances relevant to interatomic interactions.42 In addition, the electrostatic potentials for TIP4P∕Ew, SPC∕E, and TIP3P are similar to TIP4P∕2005 but successively in worse agreement with QM∕4MM in the p⊥ direction.42 In the plane of the molecule, the more important interactions are with the hydrogens (Fig. 4) and the greatest difference between the models is the “lumpiness” between the hydrogens.43 In comparison to the potential from the QM∕4MM electron density that from TIP4P∕2005 is too lumpy while those from TIP5P and the expansion to the octupole are slightly less lumpy. However, the potential at these distances are rarely relevant. Perpendicular to the plane of the molecule, the more important interactions are with the oxygen (Fig. 4). Here, one of the greatest differences between the models is in the nodal line as also noted before.43 In comparison to the potential from the electron density that from TIP5P is most different while those from TIP4P∕2005 and the QM∕4MM multipoles are closer. Moreover, the multipole expansion better mimics the greater negative potential in the p-orbital direction found in QM∕4MM electron density.
Figure 4.
Electrostatic potential around a water molecule parallel (top) and perpendicular (bottom) to the plane of the molecule for (a) the electron density for QM∕4MM, (b) a multipole expansion to the octupole for QM∕4MM, (c) TIP4P∕2005, and (d) TIP5P. Horizontal and vertical range from –6 to + 6 atomic units, contours from –0.1 to 0.1 at an interval of 0.01 au with positive contours in blue and negative in red, and the potential within 0.90 Å of the oxygen or 0.37 Å of either hydrogen is set equal to zero. Gray circles at 1.4 and 2.8 Å from the oxygen.
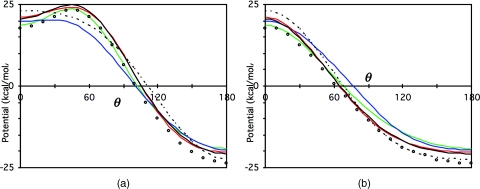
To compare further, the electrostatic potential at 2.75 Å from the oxygen was examined along the xz and yz planes, in arcs from the positive to negative z directions (Fig. 5). In the plane of the molecule, the potentials for all of the models are quite similar to the potential for the QM∕4MM electron density at the minima at 180° but there are differences near 0°. TIP4P and the QM∕4MM multipoles have maxima at the locations of the hydrogens as in QM∕4MM while TIP5P has a maximum only at 0° [Fig. 5a]. This indicates that the low quadrupole of TIP5P may lead to an inadequate description of water as a hydrogen donor with a greater preference for a bifurcated hydrogen bond donor orientation. Perpendicular to the plane of the molecule, neither the models nor QM∕4MM electron density have minima in the “lone pair” directions and the potentials for all of the multisite models are quite similar at the maxima at 0° and minima at 180° [Fig. 5b]. However, the potential for QM∕4MM crosses zero at about 65° while that for TIP5P crosses at about 80° presumably because of electron density in the p-type orbital of the oxygen in QM∕4MM; leading to a larger region of negative potential.
Figure 5.
Electrostatic potential at 2.8 Å from the central water molecule in QM∕4MM as a function of polar angle from the z-axis (a) parallel and (b) perpendicular to the plane of the molecule for the electron density at the MP2∕aug-cc-pVQZ level (×), a moment expansion to the quadrupole (dashed line), octupole (red line), hexadecapole (black line), TIP4P∕2005 (green line), TIP5P (blue line).
Radial distribution functions
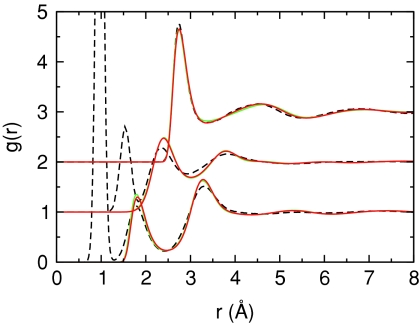
The effects of different multipoles on the radial distribution functions calculated from Monte Carlo simulations of the SSDQO model were also compared (Fig. 6). Using either the multipoles of TIP4P∕2005 or the multipoles of QM∕4MM scaled so that μ0 ≈ 2.12 D, the dipole moment of the SSDQO1 parameters, give good agreement with experimental radial distribution functions. Also, setting Ω2 = 0 in the SSDQO model while the rest of the moments are from either TIP4P∕2005 or SSDQO1 parameters gives almost identical radial distribution functions for the pure liquid as previously shown for the SSDQO model using SPC∕E moments,22 indicating the structure of first shell of the pure liquid as reflected in the radial distribution factor is relatively insensitive to the degree of charge antisymmetry of the water molecule. Since it is possible to obtain good radial distribution functions with large relative quadrupole moments, the effects of improving Θ2∕μ0 should be explored. Of course, the radial distribution functions primarily reflect the first shell structure and are not sensitive measures of the orientational correlations beyond the nearest neighbors so that structure-based quantities such as the dielectric constant and Kirkwood g-factor will be affected by changing the quadrupole as seen previously11 so that the all moments will need to be reoptimized. However, since the first shell of the pure liquid is relatively insensitive to Ω2 while the solvation structure around cations is very sensitive to Ω2, a value for Ω2 can be chosen to optimize the solvent properties of ions and then that value can be used in optimizing the pure liquid with the larger quadrupole without serious consequences on the pure liquid properties.31
Figure 6.
Radial distribution functions for the SSDQO model with QM∕4MM moments scaled to μ0 = 2.12 D with σ = 3.5 Å and ε = 0.145 kcal∕mol in a 9-6 Lennard-Jones potential (red line) and TIP4P∕2005 moments with σ = 3.5 Å and ε = 0.15 kcal∕mol in a 9-6 Lennard-Jones potential (green line).
CONCLUSIONS
Quantum mechanical studies of a single water and a waterlike cluster with a QM water and four hydrogen bonded classical waters indicate that the large quadrupole found in QM calculations of water in the gas and liquid phases is due mainly to a p-type orbital perpendicular to the plane of the molecule and a shift in electron density toward the hydrogens. Of several common site models, the TIP4P-type models account for the shift in electron density by moving the negative partial charge from the oxygen to a site further toward the hydrogens along the dipole vector. However, the electron density due to the p⊥-type orbital is not modeled well by the TIP5P model and is modeled better by points added along a vector perpendicular to the plane of the molecular through the oxygen. Overall, a six-site model with one site to model the electron density shift and two points for the p⊥-type orbital is necessary to model the large quadrupole with reasonable octupoles. Moreover, since the QM quadrupole even in the gas phase is larger than any of the site models, adding electronic polarizability to one of the existing site models will not resolve the large quadrupole problem. Instead, point multipole models such as SSDQO allow inclusion of the large quadrupole simply by increasing the value of the existing quadrupole, without any increase in computation as would be needed by a six-site model, and SSDQO is already computationally faster than three-site models because of the approximate multipole expansion. In addition, the electrostatic potential due to the electron density from the QM calculations is modeled better by a multipole expansion up to the octupole using QM moments calculated from the electron density than either the TIP4P-type or TIP5P models, particularly in the region near the p-type orbital. Finally, Monte Carlo calculations show that the SSDQO with QM moments scaled to a smaller dipole moment give good radial distribution functions, indicating that the large quadrupole does not disrupt the water structure.
Since the electrostatic potential in the p-orbital region should affect the interactions with cations, further studies of the effects of a quadrupole large enough to mimic both the p⊥-type orbital and the general shift in electron density toward the hydrogens in the SSDQO model are warranted. Moreover, although great progress has been made using nonpolarizable models for systems involving hydrophilic versus hydrophobic environments such as the free energies of transfer between water and organic phases,44 polarizability has been shown to be important for water near charged residues in proteins45 so that further investigations of adding polarizability to multipole models are also warranted. For instance, an approach for Ewald summation of multipole interactions including polarizability up to the quadrupolar level has been presented by Aguado and Madden,46 which could be extended to higher multipoles. Furthermore, the results here suggest that polarizing the quadrupoles and cubic octupole may not be necessary since they are relatively similar in the quantum mechanical calculations for the gas phase and the liquidlike cluster and that the linear octupole could be coupled to the dipole, thus reducing the degrees of freedom to be polarized.
ACKNOWLEDGMENTS
The authors are grateful to the National Science Foundation for the support of this work through Grant No. MCB-0544629. The calculations were performed on facilities provided by Georgetown University and administered by the division of Advanced Research Computing (ARC). Support was also provided by the William G. McGowan Foundation. In addition, this research was supported in part by the Intramural Research Program of the National Institutes of Health, National Heart, Lung, and Blood Institute (Laboratory of Computational Biology). T.I. also thanks Professor Sylvio Canuto for helpful discussions on his calculations and Professor Peter J. Rossky for insightful comments.
APPENDIX: TRANSFORMATION OF MULTIPOLES TO A DIFFERENT COORDINATE SYSTEM
To transform these moment parameters to a coordinate system at another point along the z-axis (0,0,c),
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
General expressions for the moments can be found in Stone.2 The values of the moment parameters for point charges and relationship to parameters in previous papers are in parentheses.
| (A6) |
| (A7) |
| (A8) |
| (A9) |
| (A10) |
References
- Maréchal Y., The Hydrogen Bond and the Water Molecule: The Physics and Chemistry of Water, Aqueous and Bio Media (Elsevier, Oxford, 2007). [Google Scholar]
- Stone A. J., The Theory of Intermolecular Forces (Clarendon, Oxford, 1996). [Google Scholar]
- Ren P. and Ponder J. W., J. Comput. Chem. 23, 1497 (2003). 10.1002/jcc.10127 [DOI] [PubMed] [Google Scholar]
- Reed A. E., Curtiss L. A., and Weinhold F., Chem. Rev. 88(6), 899 (1988). 10.1021/cr00088a005 [DOI] [Google Scholar]
- Bader R. W. F., Chem. Rev. 91, 893 (1991). 10.1021/cr00005a013 [DOI] [Google Scholar]
- Xantheas S. S. and T. H.DunningJr., J. Chem. Phys. 99(11), 8774 (1993). 10.1063/1.465599 [DOI] [Google Scholar]
- Silvestrelli P. L. and Parrinello M., J. Chem. Phys. 111(8), 3572 (1999). 10.1063/1.479638 [DOI] [Google Scholar]
- Site L. Delle, Alavi A., and Lynden-Bell R. M., Mol. Phys. 96(11), 1683 (1999). 10.1080/00268979909483112 [DOI] [Google Scholar]
- Coutinho K., Guedes R. C., Cabral B. J. Costa, and Canuto S., Chem. Phys. Lett. 369, 345 (2003). 10.1016/S0009-2614(02)02026-2 [DOI] [Google Scholar]
- Batista E. R., Xantheas S. S., and Jónsson H., J. Chem. Phys. 109(11), 4546 (1998). 10.1063/1.477058 [DOI] [Google Scholar]
- Te J. A. and Ichiye T., J. Chem. Phys. 132(11), 114511 (2010). 10.1063/1.3359432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abascal J. L. F. and Vega C., J. Phys. Chem. C 111, 15811 (2005). 10.1021/jp074418w [DOI] [Google Scholar]
- Rick S. W., J. Chem. Phys. 120, 6085 (2004). 10.1063/1.652434 [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C., Grigera J. R., and Straatsma T. P., J. Phys. Chem. 91, 6269 (1987). 10.1021/j100308a038 [DOI] [Google Scholar]
- Jorgensen W. L., J. Am. Chem. Soc. 103, 335 (1981). 10.1021/ja00392a016 [DOI] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Horn H. W., Swope W. C., Pitera J. W., Madura J. D., Dick T. J., Hura G. L., and Head-Gordon T., J. Chem. Phys. 120(20), 9665 (2004). 10.1063/1.1683075 [DOI] [PubMed] [Google Scholar]
- Abascal J. L. F. and Vega C., J. Chem. Phys. 123, 234505 (2005). 10.1063/1.2121687 [DOI] [PubMed] [Google Scholar]
- Matsuoka O., Clementi E., and Yoshimine M., J. Chem. Phys. 64, 1351 (1976). 10.1063/1.432402 [DOI] [Google Scholar]
- Mahoney M. W. and Jorgensen W. L., J. Chem. Phys. 112(20), 8910 (2000). 10.1063/1.481505 [DOI] [Google Scholar]
- Stillinger F. H. and Rahman A., J. Chem. Phys. 60, 1545 (1974). 10.1063/1.1681229 [DOI] [Google Scholar]
- Ichiye T. and Tan M.-L., J. Chem. Phys. 124, 134504 (2006). 10.1063/1.2161201 [DOI] [PubMed] [Google Scholar]
- Chowdhuri S., Tan M.-L., and Ichiye T., J. Chem. Phys. 125, 144513 (2006). 10.1063/1.2357117 [DOI] [PubMed] [Google Scholar]
- Liu Y. and Ichiye T., J. Phys. Chem. 100, 2723 (1996). 10.1021/jp952324t [DOI] [Google Scholar]
- Andrea T. A., Swope W. C., and Andersen H. C., J. Chem. Phys. 79, 4576 (1983). 10.1063/1.446373 [DOI] [Google Scholar]
- Tan M.-L., Lucan L., and Ichiye T., J. Chem. Phys. 124, 174505 (2006). 10.1063/1.2177240 [DOI] [PubMed] [Google Scholar]
- Te J. A., Tan M.-L., and Ichiye T., Chem. Phys. Lett. 486, 70 (2010). 10.1016/j.cplett.2009.12.089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- A. D.MacKerellJr., Bashford D., Bellot M., R. L.DunbrackJr., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph D., Kuchnir K., Kuczera K., Lau F. T. K., Mattos M., Michnick S., Nguyen D. T., Ngo T., Prodhom B., Roux B., Schlenkrich M., Smith J., Stote R., Straub J., Wiorkiewicz-Kuczera J., and Karplus M., J. Phys. Chem. B 102, 3586 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- Blum L., Vericat F., and Degrève L., Physica A 265, 396 (1999). 10.1016/S0378-4371(98)00436-1 [DOI] [Google Scholar]
- Molinero V. and Moore E. B., J. Phys. Chem. B 113, 4008 (2009). 10.1021/jp805227c [DOI] [PubMed] [Google Scholar]
- Te J. A., Tan M.-L., and Ichiye T., Chem. Phys. Lett. 499, 219 (2010). 10.1016/j.cplett.2010.09.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Te J. A., Tan M.-L., and Ichiye T., Chem. Phys. Lett. 491(4–6), 218 (2010). 10.1016/j.cplett.2010.04.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becke A. D., J. Chem. Phys. 98(2), 1372 (1993); 10.1063/1.464304 [DOI] [Google Scholar]; Lee C., Yang W., and Parr R. G., Phys. Rev. B 37(2), 785 (1988). 10.1103/PhysRevB.37.785 [DOI] [PubMed] [Google Scholar]
- T. H.DunningJr., J. Chem. Phys. 90, 1007 (1989). 10.1063/1.456153 [DOI] [Google Scholar]
- Straatsma T. P., Aprà E., Windus T. L., Bylaska E. J., Jong W. de, Hirata S., Valiev M., Hackler M., Pollack L., Harrison R., Dupuis M., Smith D. M. A., Nieplocha J., Tipparaju V., Krishnan M., Auer A. A., Brown E., Cisneros G., Fann G., Früchtl H., Garza J., Hirao K., Kendall R., Nichols J., Tsemekhman K., Wolinski K., Anchell J., Bernholdt D., Borowski P., Clark T., Clerc D., Dachsel H., Deegan M., Dyall K., Elwood D., Glendening E., Gutowski M., Hess A., Jaffe J., Johnson B., Ju J., Kobayashi R., Kutteh R., Lin Z., Littlefield R., Long X., Meng B., Nakajima T., Niu S., Rosing M., Sandrone G., Stave M., Taylor H., Thomas G., Lenthe J. van, Wong A., and Zhang Z., NW Chem, A Computational Chemistry Package for Parallel Computers, Version 4.6 (Pacific Northwest National Laboratory, Richland, WA, 2004). [Google Scholar]
- Frisch M. J., Trucks G. W., et al. , GAUSSIAN03, Revision C.02, Gaussian, Inc., Wallingford, CT, 2004.
- Breneman C. M. and Wiberg K. B., J. Comput. Chem. 11, 361 (1990). 10.1002/jcc.540110311 [DOI] [Google Scholar]
- Black G., Didier B., Elsethagen T., Feller D., Gracio D., Hackler M., Havre S., Jones D., Jurrus E., Keller T., Lansing C., Matsumoto S., Palmer B., Peterson M., Schuchardt K., Stephan E., Taylor H. T., Thomas G., Vorpagel E., Windus T., and Winters C., Ecce, A Problem Solving Environment for Computational Chemistry, Software Version 3.2.1 (Pacific Northwest National Laboratory, Richland, WA, 2004). [Google Scholar]
- Schaftenaar G. and Noordik J. H., J. Comput.-Aided Mol. Des. 14, 123 (2000). 10.1023/A:1008193805436 [DOI] [PubMed] [Google Scholar]
- Williams T. and Kelley T., Gnuplot 4.4.2 (2004).
- Soper A. K., Chem. Phys. 258, 121 (2000). 10.1016/S0301-0104(00)00179-8 [DOI] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3569563 for Fig. S1.
- Dykstra C. E., Chem. Rev. 93, 2339 (1992). 10.1021/cr00023a001 [DOI] [Google Scholar]
- Rose D. and Benjamin I., J. Phys. Chem. B 113, 9296 (2009). 10.1021/jp904470d [DOI] [PubMed] [Google Scholar]
- Kim B., Young T., Harder E., Friesner R. A., and Berne B. J., J. Phys. Chem. B 109, 16529 (2005). 10.1021/jp051569v [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguado A. and Madden P. A., J. Chem. Phys. 119(14), 7471 (2003). 10.1063/1.1605941 [DOI] [Google Scholar]
- Clough S. A., Beers Y., Klein G. P., and Rothman L. S., J. Chem. Phys. 65, 582 (1973). [Google Scholar]