Monodispersed magnetite nanoparticles optimized for magnetic fluid hyperthermia: Implications in biological systems

Abstract

Magnetite (Fe₃O₄) nanoparticles (MNPs) are suitable materials for Magnetic Fluid Hyperthermia (MFH), provided their size is carefully tailored to the applied alternating magnetic field (AMF) frequency. Since aqueous synthesis routes produce polydisperse MNPs that are not tailored for any specific AMF frequency, we have developed a comprehensive protocol for synthesizing highly monodispersed MNPs in organic solvents, specifically tailored for our field conditions (f = 376 kHz, H₀ = 13.4 kA∕m) and subsequently transferred them to water using a biocompatible amphiphilic polymer. These MNPs (σ_avg. = 0.175) show truly size-dependent heating rates, indicated by a sharp peak in the specific loss power (SLP, W∕g Fe₃O₄) for 16 nm (diameter) particles. For broader size distributions (σ_avg. = 0.266), we observe a 30% drop in overall SLP. Furthermore, heating measurements in biological medium [Dulbecco’s modified Eagle medium (DMEM) + 10% fetal bovine serum] show a significant drop for SLP (∼30% reduction in 16 nm MNPs). Dynamic Light Scattering (DLS) measurements show particle hydrodynamic size increases over time once dispersed in DMEM, indicating particle agglomeration. Since the effective magnetic relaxation time of MNPs is determined by fractional contribution of the Neel (independent of hydrodynamic size) and Brownian (dependent on hydrodynamic size) components, we conclude that agglomeration in biological medium modifies the Brownian contribution and thus the net heating capacity of MNPs.

INTRODUCTION

Magnetic fluid hyperthermia (MFH) is a promising approach toward improving cancer therapeutics.^{1, 2} In MFH, heat dissipated from superparamagnetic nanoparticles, in an alternating magnetic field (AMF) can be used to locally raise the temperature by ∼5 °C or more above the physiological temperature (37 °C), in targeted tumor tissues, thereby encouraging either cell damage or death. Alternatively, hyperthermia can be used in conjunction with conventional chemotherapy and radiation approaches to enhance their respective efficacies.^{3, 4} Currently, magnetite (Fe₃O₄) and maghemite (γ-Fe₂O₃) are the only FDA approved magnetic materials that can be used in humans,⁵ and thus we focus on the iron oxides for MFH application. The promise of transitioning MFH from the in vitro stage to the clinical stage faces several challenges including delivering a sufficient amount of nanoparticles required to raise the tumor temperature by 5 °C or more, without adversely affecting surrounding healthy tissue.¹ However, well-designed and optimized nanoparticles, tailored for a given AMF frequency can minimize the required nanoparticle volume. But since magnetite nanoparticles (MNPs) are often synthesized in aqueous solvents^{6, 7} to satisfy biocompatibility constraints, and a major disadvantage of aqueous routes is the inability to control size and size distribution, tailoring size to a specific AMF frequency is nearly impossible.

In this study we show that monodispersed MNPs (Fe₃O₄), synthesized in organic solvents and successfully transferred to water, can be tailored for strong size-dependent heating for any chosen combination of field frequency and amplitude. In order to establish biological relevance, heating rates were also measured in cell culture medium and the results interpreted in terms of changes in Brownian relaxation due to particle agglomeration.

We present a brief physical overview of magnetization relaxation dynamics and the related power losses. More details can be found elsewhere.^{8, 9} When magnetic nanoparticles are subject to an AMF frequency (f), the magnetization of the particles lags behind the ac field, and the relaxation or hysteresis losses result in a power dissipation (P) given by⁹

$$P=\pi {\mu }_0{H}_0^2\mathrm{\chi ″}f{\int }_0^{\infty }g(R)\mathit{dR},$$ (1)

where, μ₀ is the permeability of free space (4π × 10⁻⁷ H∕m), H₀ is the externally applied field amplitude (kA∕m), g(R) is the lognormal size distribution function, a material parameter, and χ″ is the out-of-phase susceptibility, given by

$$\mathrm{\chi ″}(\omega )={\chi }_0\frac{2\pi f\tau }{(2\pi f\tau ){}^2},$$ (2)

where, χ₀ is the dc susceptibility and τ is the effective relaxation time of the particles given by the Brownian (τ_B) and Néel (τ_N) components. Note that τ_N varies exponentially with the core volume, V_m [τ_N∝exp(V_m)], while τ_B varies linearly with the viscosity of the solvent, (η), and the hydrodynamic volume, V_H (τ_B∝ηV_H), of the particle.^{2, 8, 9} For an ensemble of ideally monodispersed and uniformly shaped particles, the crystalline or shape anisotropy is a constant, thus the particle volume determines which time component (the shorter one) dominates the effective relaxation time. In a real suspension, however, there is always a distribution of volumes, and thus a distribution of relaxation times. As a result, for an applied field frequency, only MNPs satisfying the condition, 2πfτ = 1, will contribute optimally to the power dissipation expressed in (1). Thus, monodispersed MNPs are crucial for optimization of MFH and in fact simulations show that an increase in standard deviation (σ) from 0 (ideal case) to 0.25 results in an ∼85% drop in heating capacity, emphasizing the incentive to use monodispersed MNPs.⁹ Magnetic particle imaging (MPI), an emerging imaging technology that works on the same basic operational principle of MFH,^{10, 11} will also benefit by using monodispersed MNPs as molecular probes. Due to the real-time imaging capability of MPI, the combination of MPI and MFH offers a unique opportunity for image-guided therapeutics.

METHODS

Nanoparticles were synthesized according to a procedure^{12, 13} based on pyrolysis of metal fatty acid salts; in this case, Fe³⁺-oleate. Fe³⁺-oleate was prepared and stored as a stock solution (conc. 18 wt. %) in 1-octadecene (ODE, technical grade 90%). Fe₃O₄ nanoparticles of desired sizes were synthesized by reacting predetermined amounts of Fe³⁺-oleate and oleic acid (tech. 90%) in ODE. For instance, synthesis of 15 nm particles required 0.2 mmol∕g of Fe³⁺-oleate and 3 mmol∕g of oleic acid in 2.5 g of reaction solvent (ODE). The mixture was refluxed overnight (≥24 h) at 320 °C under argon and vigorous stirring. The final product was collected and washed four times with a 1:1 (v∕v) mixture of chloroform and methanol to remove excess surfactant and solvent. MNP powder, obtained by drying in vacuum for 30 min, was hydrophobic and easily dispersed in organic solvents such as toluene or chloroform. Phase transfer to aqueous phase was achieved by coating oleic acid coated MNPs (MNP@OA) with poly(maleic anhydride-alt-1-octadecene)-poly(ethylene glycol) (PMAO-PEG), an amphiphilic polymer.¹⁴ Colloidal stability of PMAO-PEG coated MNPs (MNP@PMAO-PEG) was characterized using Dynamic Light Scattering (DLS – Zetasizer Nano, Malvern Instruments). Iron concentration was determined using an inductively coupled plasma atomic emission spectrophotometer (ICP-AES, Jarrell Ash 955). A room temperature vibrating sample magnetometer (VSM, Lakeshore) was used to obtain magnetization results.

Heating rates of MNPs in water and tissue culture medium (Dulbecco’s modified Eagle medium with 10% fetal bovine serum, DMEM + 10% FBS) was measured using a dedicated hyperthermia system (magneTherm, nanoTherics, UK). AMF frequency and amplitude were set at 376 kHz and 13.5 kA∕m, respectively. A fiber optic thermocouple (Luxtron, Lumasense Technologies) was used to probe temperature. The power dissipation or SLP was measured using the following equation:¹⁵

$$\mathrm{SLP}(\mathrm{watts}∕g{\mathrm{Fe}}_3{\mathrm{O}}_4)=c\frac{m_{{\mathrm{H}}_2{\mathrm{O}\mathrm{+}\mathrm{Fe}}_3{\mathrm{O}}_4}}{m_{{\mathrm{Fe}}_3{\mathrm{O}}_4}}\left(\frac{\mathit{dT}}{\mathit{dt}}\right),$$ (3)

where c is the specific heat capacity of water (4.186 J∕g °C), m_Fe3O4 and m_H2O+Fe3O4 are the mass of Fe₃O₄ MNPs and mass of whole sample in grams, respectively, and dT∕dt is the temperature ramp rate in °C∕s.

RESULTS AND DISCUSSION

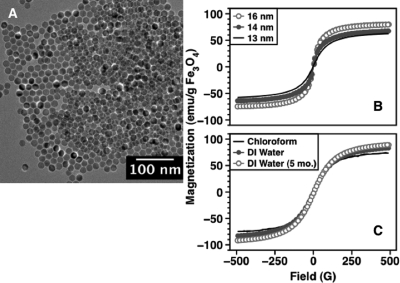
Transmission electron microscopy (TEM) imaging [Fig. 1a] shows that MNPs synthesized via the organic route are monodispersed (diameter of 16 ± 1 nm is shown). For superparamagnetic particles, size and the lognormal size distributions were also determined by fitting magnetization curves to the Langevin function.^{16, 17} Magnetization curves of MNP@PMAO-PEG in DI water for a range of sizes show increase in initial susceptibility and saturation with increasing particle size [Fig. 1b]. Depending on the particle size, saturation magnetization values reach up to 80% of the bulk saturation value of magnetite, i.e., 90 emu∕g.¹⁸ Due to spin disordering at the surface,¹⁹ saturation values of magnetite nanoparticles are often less than bulk values. Magnetization measurements before (MNP@OA) and after (MNP@PMAO-PEG) phase transfer show negligible change in the magnetic properties [Fig. 1c]. Finally, magnetic properties are consistent over the tested time period (5 months), suggesting excellent shelf life of MNP@PMAO-PEG.

Figure 1.

(Color online) (a) TEM image of ∼16 nm (diameter) magnetite nanoparticles. (b) Magnetization curves for a range of particle diameters. Initial magnetic susceptibility and saturation magnetization increase with size. (c) Magnetization curves before and after phase transfer for 12 nm MNPs and 5 months after phase transfer.

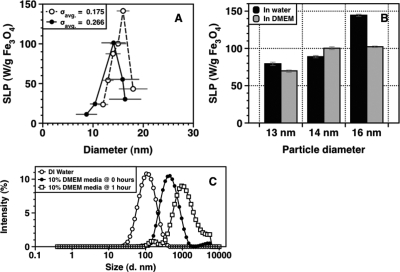
Heating rates measured as a function of MNP size show a sharp peak in SLP at a diameter of 16 nm for σ_avg. = 0.175 [Fig. 2a]. SLP values were calculated using equation 3. When particles of broader average size distribution (σ_avg. = 0.266) were used, the peak SLP value dropped from 144 to 100 W∕g Fe₃O₄ (30% drop). These results confirm that a small increase in polydispersity is detrimental to the heating capacity of MNPs.

Figure 2.

(Color online) (a) SLP of a range of MNP diameters. A sharp peak at 16 nm (open circles) is seen for MNPs with σ_avg. = 0.175. MNPs with larger average standard deviation, σ_avg. = 0.266, showed a significant drop in heating capacity (filled circles). (b) Heating capacity of MNP@PMAO-PEG as measured in DMEM with 10% FBS, and (c) DLS measurements of MNP@PMAO-PEG showing increase in size over time, due to agglomeration, after MNPs are dispersed in DMEM.

In order to simulate biologically relevant environment, heating rates of MNPs dispersed in (DMEM+10% FBS) were measured. Figure 2b shows that MNPs of sizes 13 and 14 nm do not show any significant changes in SLP; however, 16 nm MNPs show a 30% decrease. DLS measurements [Fig. 2c] show that hydrodynamic size of MNP@PMAO-PEG increase when dispersed in DMEM+10% FBS.²¹ According to the magnetization relaxation theory of superparamagnetic nanoparticles, increase in hydrodynamic volume prolongs Brownian relaxation while the relaxation via Néel mechanism is unaffected. Furthermore, models show that, in water, 16 nm MNPs lie within the transition region from Néel to Brownian relaxation.^{9, 20} Thus, based on our results, we infer that ∼30% of MNPs in the 16 nm sample were large enough to undergo Brownian relaxation and due to agglomeration in DMEM, the Brownian relaxation is blocked or too slow relative to the 376 kHz time window imposed by the AMF. The 13 and 14 nm samples did not show any significant change in SLP, even though they also agglomerated in DMEM (data not shown), suggesting primarily Néel relaxation. These measurements give significant insight into biological implications of hyperthermia. Even if MNPs are delivered in sufficient concentrations to target sites, adherence to cells and biomolecules is inevitable in in vivo situations and should be taken into consideration.

CONCLUSION

MFH can improve efficacy of conventional cancer therapeutics such as chemotherapy and radiation. We have synthesized monodisperse MNPs using organic routes and successfully transferred them to aqueous phase using an amphiphilic polymer. These size-optimized MNPs show a sharp peak in SLP at 16 nm for f = 376 kHz and H₀ = 13.5 kA∕m. With increased size distribution, SLP values dropped by 30%, emphasizing the importance of monodispersity. Finally, measurements in DMEM, which is representative of biological environments, showed substantial reduction in SLP. DLS measurements indicate increase in hydrodynamic volume or possible agglomeration of MNPs in DMEM, suggesting the reduced SLP is due to the blocking of Brownian relaxation contribution. Thus, for true optimization of MFH, it is preferable to use monodispersed MNPs that relax predominantly via Néel mechanism, which is unaltered by changes in hydrodynamic volume that are inevitable for foreign objects circulating in vivo.