Nonconvex prior image constrained compressed sensing (NCPICCS): Theory and simulations on perfusion CT

Abstract

Purpose: To present and evaluate a new image reconstruction method for dynamic CT based on a nonconvex prior image constrained compressed sensing (NCPICCS) algorithm. The authors systematically compared the undersampling potential, functional information recovery, and solution convergence speed of four compressed sensing (CS) based image reconstruction methods using perfusion CT data: Standard ℓ₁-based CS, nonconvex CS (NCCS), and ℓ₁-based and nonconvex CS, including an additional constraint based on a prior image (PICCS and NCPICCS, respectively).

Methods: The Shepp–Logan phantom was modified such that its uppermost ellipses changed attenuation through time, simulating both an arterial input function (AIF) and a homogeneous tissue perfusion region. Data were simulated with and without Poisson noise added to the projection data and subsequently reconstructed with all four CS-based methods at four levels of undersampling: 20, 12, 6, and 4 projections. Root mean squared (RMS) error of reconstructed images and recovered time attenuation curves (TACs) were assessed as well as convergence speed. The performance of both PICCS and NCPICCS methods were also evaluated using a kidney perfusion animal experiment data set.

Results: All four CS-based methods were able to reconstruct the phantoms with 20 projections, with similar results on the RMS error of the recovered TACs. NCCS allowed accurate reconstructions with as few as 12 projections, PICCS with as few as six projections, and NCPICCS with as few as four projections. These results were consistent for noise-free and noisy data. NCPICCS required the fewest iterations to converge across all simulation conditions, followed by PICCS, NCCS, and then CS. On animal data, at the lowest level of undersampling tested (16 projections), the image quality of NCPICCS was better than PICCS with fewer streaking artifacts, while the TAC accuracy on the selected region of interest was comparable.

Conclusions: The authors have presented a novel method for image reconstruction using highly undersampled dynamic CT data. The NCPICCS method takes advantage of the information provided by a prior image, as in PICCS, but employs a more general nonconvex sparsity measure [such as the ℓ_p-norm (0<p≤1)] rather than the conventional convex ℓ₁-norm. Despite the lack of guarantees of a globally optimal solution, the proposed nonconvex extension of PICCS consistently allowed for image reconstruction from fewer samples than the analogous ℓ₁-based PICCS method. Both nonconvex sparsity measures as well as prior image information (when available) significantly reduced the number of iterations required for convergence, potentially providing computational advantages for practical implementation of CS-based image reconstruction techniques.

INTRODUCTION

In recent years, there has been an increasing concern about radiation exposure in medical imaging procedures using ionizing radiation, such as computed tomography (CT).^{1, 2, 3} At the same time, several strategies have been developed to decrease radiation dose in CT, including improvements in the components of the acquisition systems, optimization of acquisition parameters (i.e., mA s or kilovoltage), and applying newer image reconstruction and postprocessing algorithms.^{4, 5} Higher radiation doses are associated with time-series CT studies such as dynamic CT angiography, perfusion CT (PCT), or CT-guided interventional procedures.^{6, 7} During a PCT examination, for example, the same anatomy is scanned several times to follow the transient arrival and washout of a contrast agent, which provides direct measurement of the time attenuation curve (TAC). Given these data, it is then possible to calculate functional parameters for perfusion analysis, such as mean transit time, blood volume, blood flow, and vascular permeability. Sufficient radiation dose is required in order to provide adequate signal to noise ratio (SNR), such that it is possible to fit a mathematical model to the data.⁸ Hence, it is desirable to find CT imaging strategies that reduce radiation dose but provide sufficient image quality and functional parameter accuracy, comparable to those acquired with conventional (and acceptable) radiation dose levels.

In time-series studies, the same anatomical region is scanned repeatedly. Since only parts of the regions change rapidly through time and a large percentage change slowly or are unchanged, much of the information contained within the time-series data is redundant. In PCT, for example, vessels and perfused tissues change their attenuation properties through time due to the arrival of intravascular contrast agent mixed with blood, while the nonperfused tissues are of largely constant intensity. Similarly, in interventional procedures, the background object for the most part remains unchanged, while instruments (e.g., biopsy needles or catheters) are inserted into the patient.⁹ Recently, strategies exploiting the aforementioned redundancies have been proposed, including both image-based^{10, 11} and projection space-based methods.^{12, 13, 14} In most cases, the methods assume there is no object motion. When this assumption is valid or motion can be corrected for, these methods have demonstrated that it is possible to reduce by up to ten fold the typical radiation dose used for perfusion like studies, while maintaining reasonable image quality and spatial resolution.¹⁰

Assuming no motion, two consecutive scans of a time-resolved study should not differ significantly (i.e., only from noise) except potentially at a compact set of locations. Thus, the resulting difference image can be described as “sparse” or “compressible.” A transformed version of the difference image (e.g., via finite spatial differences) may be even sparser or more compressible. Compressed sensing (CS) is a recently introduced sampling and reconstruction paradigm which asserts that the number of samples of a signal sufficient to guarantee accurate reconstruction is proportional to the signal’s complexity rather than its dimensionality. As such, signals that are sparse or compressible (either intrinsically or following mathematical transformation) can, in principle, be recovered from very limited data sets.^{15, 16} CS theory and its extensions were rapidly adopted for MRI imaging^{17, 18, 19} and several studies employing CS theory in CT have found that the number of x-ray projection views can be significantly reduced with little sacrifice in CT image quality.^{20, 21, 22, 23, 24} CS-based image reconstruction algorithms thus present significant potential for radiation dose reduction in CT, under the assumption that the dose is proportional to the number of x-ray projections.

The theoretical foundations of CS are based on the measurement of sparsity with the ℓ₀-quasinorm (a measure of the number of nonzero components) and the theory asserts that a signal of size N with S sparse components, with N⪢S, can be accurately reconstructed from as few as 2S measurements in a domain incoherent with the sparsity domain. However, the combinatorial search needed to directly solve the ℓ₀-minimization problem is intractable. It was shown in Refs. ^{15, 16} that by using the ℓ₁-norm as a surrogate for the ℓ₀-quasinorm, exact signal recovery can also be obtained, while instead solving a tractable convex ℓ₁-minimization problem. The cost of this relaxation is a modest oversampling above the theoretical minimum rate required by the ℓ₀-minimization problem (typically 3S–5S).²⁵ Most work in medical imaging has used such ℓ₁-minimization. Seeking to accurately recover signals from even fewer samples, some authors have tried nonconvex strategies that approximate the ℓ₀-minimization problem.^{26, 27, 28} For example, Trzasko and Manduca^{28, 29} incorporated nonconvex sparsity measures and a homotopic continuation scheme and demonstrated improved CS reconstructions of MR images and have also established theoretical advantages of such models. Chartrand²⁷ has demonstrated similar benefits, showing the increased undersampling possible with nonconvex minimization instead of ℓ₁-minimization. While nonconvex approaches are being investigated for MRI, little work has been reported in their use for x-ray based imaging modalities.^{30, 31}

Separately, Chen et al.^{12, 32} proposed a method called prior image constrained compressed sensing (PICCS) and showed that the application of CS to dynamic imaging applications can often be improved by auxiliary use of prior image constraints. This prior information is readily available in perfusion or interventional CT studies where the same anatomical region is scanned repeatedly. Using the PICCS algorithm, Chen and colleagues^{33, 34, 35} demonstrated significant improvements in image reconstruction quality for time-resolved studies compared to CS alone. Ongoing work on the PICCS algorithm has demonstrated its ability to increase temporal resolution in CT or perform dual-energy CT material decomposition.³⁶

The PICCS algorithm is based on ℓ₁-minimization. We hypothesized that the benefits of nonconvex sparsity measures over ℓ₁-minimization would also apply to the PICCS method, which simply includes additional constraints based on a prior image. We have therefore developed a technique we call nonconvex prior image constrained compressed sensing (NCPICCS). We describe the theory of NCPICCS and systematically compare the undersampling potential, functional information recovery, and solution convergence speed for four CS-based image reconstruction methods for time-resolved CT imaging: Standard ℓ₁-based CS, nonconvex CS (NCCS), and ℓ₁-based and nonconvex CS, including the additional constraint based on a prior image (PICCS and NCPICCS, respectively).

MATERIALS AND METHODS

NCPICCS

The NCPICCS method extends the PICCS algorithm by replacing all (convex) ℓ₁-norm terms with more general nonconvex sparsity measures ρ(⋅). Hence, the NCPICCS objective or cost functional is written as follows:

$$\underset{x}{\text{min}}\left[\alpha \cdot \rho \left(\left|{\Psi }_1\left(x-x_{pr}\right)\right|\right)+\left(1-\alpha \right)\cdot \rho \left(\left|{\Psi }_{2}x\right|\right)\right]s.t.\Phi x=f,$$ (1)

where Ψ₁ and Ψ₂ represent sparsifying transformations (e.g., the spatial gradient or a wavelet transform), x_pr is a prior image (to be discussed in Sec. 2C1), Φ is the forward projection operator, f is the measured data (i.e., the sinogram), and x is the reconstructed image.

The parameter α balances sparsity and fidelity to the prior image in the generated image estimate. While several functions are possible choices for ρ(⋅), such as Laplace, Geman, or ℓ_p functions (0<p≤1),²⁸ in this work we consider the latter, where the ℓ_p function is defined as

$${\parallel x\parallel }_p={\left(\sum _i\left|x_i^p\right|\right)}^{1∕p}.$$

Hence, the NCPICCS algorithm objective function using the ℓ_p function is

$$\underset{x}{\text{min}}\left\{\alpha {\parallel {\Psi }_1\left(x-x_{pr}\right)\parallel }_p^p+\left(1-\alpha \right){\parallel {\Psi }_{2}x\parallel }_p^p\right\}s.t\Phi x=f.$$ (2)

Setting p=1 with α=0 yields standard CS reconstruction, while setting α>0 yields an objective function identical to the PICCS model.¹² Similarly, setting p<1 in both cases yields NCCS and NCPICCS, respectively.

Numerical implementation using an inexact quasi-Newton method

For numerical simplicity, we consider minimization of the unconstrained variant of Eq. 2, namely,

$$\underset{x}{\text{min}}\left\{\alpha {\parallel {\Psi }_1\left(x-x_{pr}\right)\parallel }_p^p+\left(1-\alpha \right){\parallel {\Psi }_{2}x\parallel }_p^p+\frac{\lambda }{2}{\parallel \Phi x-f\parallel }_2^2\right\},$$ (3)

where λ is a non-negative regularization parameter. Notice that as λ→∞, exact data fidelity as in Eq. 1 is asymptotically promoted. In practice, for noisy data, inexact fidelity with an appropriate λ is known to give better results than exact fidelity to the measured data. Differentiating Eq. 3 with respect to the target signal x yields

$$L\left(x\right)=\alpha {\Psi }_1^{\ast }\Lambda \left({\Psi }_1\left(x-x_{pr}\right)\right){\Psi }_1\left(x-x_{pr}\right)+\left(1-\alpha \right){\Psi }_2^{\ast }\Lambda \left({\Psi }_{2}x\right){\Psi }_{2}x+\lambda {\Phi }^{\ast }\Phi x-\lambda {\Phi }^{\ast }f,$$ (4)

where elements of the diagonal matrix Λ are given by Λ_i,i(x)=1∕|x_i|⋅δρ(x_i)∕δ|x_i|.

As the targeted objective functional is not convex, only locally optimal solutions can be guaranteed by any nonexhaustive search. Nonetheless, in practice, nonconvex signal recovery models consistently perform at least as well as their convex analogs and often much better.^{26, 27, 28} Locally optimal solutions of Eq. 3 then satisfy L(x)=0. To find these signals, the following quasi-Newton iteration is used:

$$x^{t+1}=x^t-B^{-1}\left(x^t\right)L\left(x^t\right).$$ (5)

With the initial signal estimation x⁰=0 and the (linear) Hessian approximation,

$$B\left(x\right)=\left[\alpha {\Psi }_1^{\ast }\Lambda \left({\Psi }_1\left(x-x_{pr}\right)\right){\Psi }_1+\left(1-\alpha \right){\Psi }_2^{\ast }\Lambda \left({\Psi }_{2}x\right){\Psi }_2+\lambda {\Phi }^{\ast }\Phi \right].$$

A detailed account of the numerical implementation employed can be found in Ref. 28.

Numerical phantom simulations

Prior image data

For our simulation, we concentrated on dynamic data in PCT, which was acquired to follow the passage of contrast agent. As aforementioned, both PICCS and NCPICCS require a prior image. Common strategies to obtain this prior image include: (1) A background image (first time point in the data series) obtained using a conventional CT acquisition sampled with a predetermined number x-ray projections (e.g., ∼1000 projections) and employing sufficient radiation dose; (2) a composite image coming from a collection of several undersampled acquisitions at different time points, but with complementary angular projections;¹¹ or (3) an average of various time-point images acquired using a conventional CT acquisition regarding number of projections, but employing a lower radiation dose (e.g., lower mA s) at each time point. For the numerical simulations presented here, we assumed we had available an image with sufficient sampling and dose, corresponding to the background (before contrast agent arrival) as the prior image. Data with and without Poisson noise added to the projections were simulated. A value of 1×10⁴ photons per detector element was used to perform the noise addition. Simulations assumed ideal conditions (i.e., did not take into account polychromatic spectra, beam hardening, scattering, etc.) and employed parallel beam geometry.

Dynamic PCT phantom

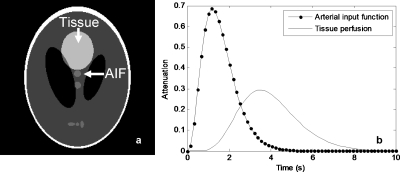
The Shepp–Logan phantom, with size 256×256, was modified such that the uppermost ellipses changed attenuation through time, simulating both an arterial input function (AIF) and a homogeneous tissue perfusion region (Fig. 1), each following a single gamma-variate function of the form

$$y=a\cdot t^b\cdot \text{exp}\left(-\frac{t}{c}\right),$$ (6)

where t is the time and the parameters a, b, and c, control the amplitude, width, and speed of decay of the gamma-variate function. Simulated values were a=8, b=3, and c=2.5 for the AIF and a=0.05, b=7, and c=2 for the tissue perfusion. A total of 20 time points were simulated, with time steps Δt=0.5 s.

Figure 1.

Dynamic phantom employed in simulations. (a) Detailed ellipses changing attenuation through time. (b) Time density curves of the simulated AIF and perfused tissue.

Noise-free phantom experiments

The simulated dynamic data were reconstructed using parallel beam geometry and four levels of undersampling, 4, 6, 12, and 20 projections, at evenly distributed angles. These numbers of projections were selected to illustrate the breaking points at which the different methods were no longer able to accurately reconstruct an image. Each level of undersampling was reconstructed using four methods: CS, NCCS, PICCS and NCPICCS; each condition was obtained by setting the appropriate p and α values in the NCPICCS objective function [Eq. 2] (Table 1). Note that our numerical implementation of PICCS differs from the original algorithm, which employs a modified gradient descent approach as in Ref. 37. In all four algorithm conditions, the filtered backprojection image was used for initialization.

Table 1.

Optimum λ selection for each simulated condition.

Method	Number of projections	λ
		Noise-free	Noise added
CS: p=1, α=0	20	75	50
	12	20	50
	6	20	50
	4	20	50
NCCS: p=0.7, α=0	20	75	50
	12	75	50
	6	20	50
	4	20	50
PICCS: p=1, α=0.7	20	75	50
	12	75	50
	6	50	20
	4	50	10
NCPICCS: p=0.7, α=0.7	20	75	50
	12	75	50
	6	50	50
	4	50	50

The NCPICCS formulation requires several free parameters to be defined. After empirical evaluation, we fixed α=0.7 for both prior image constrained methods (PICCS and NCPICCS), comparable to values previously used with the PICCS.³⁸ Similarly, we fixed p=0.7 for both nonconvex methods (NCCS and NCPICCS); this is to ease the comparison across methods. The results were found not too sensitive to the exact numbers chosen for the parameters α and p. However, the regularization parameter λ showed stronger dependence on its selection. To avoid unfair comparisons due to an inconsistent choice of λ, experiments were performed in which the optimal λ_opt for each of the four methods was selected based on the minimum calculated root mean squared (RMS) error after reconstructing the same data using different λ values [Eq. 3]. In other words, the optimal RMS error performance of each algorithm was compared.

Poisson noise added phantom experiments

Other than the use of added noise to the projection data, these simulations were similar to the noise-free conditions, including the search of λ_opt for each of the four methods.

Algorithm convergence experiments

We investigated the convergence benefits of using either nonconvex functions, prior images, or both. For these experiments, we chose λ_opt as explained previously. For all simulations, we used the same numerical solver and fixed the total number of iterations.

In vivo data simulation

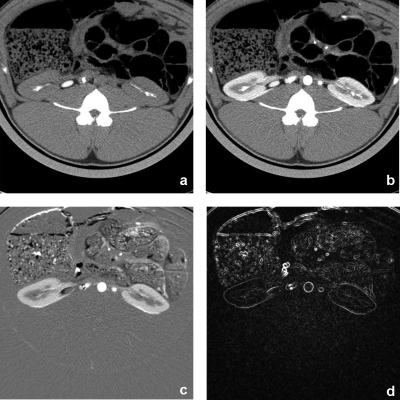
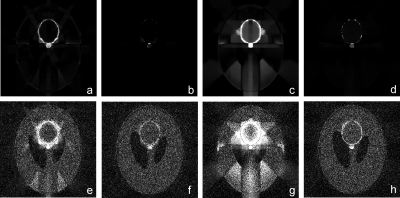
We performed a simulation using in vivo data acquired from a CT kidney perfusion animal study. Scans were performed at 80 kV, using 160 mA s, with 24×1.2 mm collimation and 0 mm table feed. Using a 0.33 s gantry rotation time, 70 exposures were acquired with 0.67 s interval, followed by another 70 exposures with 2 s interval, bringing the total scanning time to about 3 min. From these scans, we selected 17 exposures as representative time points of the time attenuation curve, with no loss in generality since reconstructed images for each time point are independent of each other. The first image of the data set was reconstructed using all available projections and served as the high SNR prior image x_pr. The remaining 16 images were reconstructed using all available projections (original data) and using 22 and 16 projections. TACs were calculated by tracing a manual region of interest (ROI) on the cortex of one of the kidneys and recording the mean CT numbers. Examples of the prior image and one of the other 16 images are provided (Fig. 2), in addition to examples demonstrating the sparsity of the difference image and image gradient transform. Reconstructions were also performed using 60 projections for a separate study of noise texture preservation.

Figure 2.

In vivo animal study. (a) Prior image with no contrast enhancement. (b) Sample target image to reconstruct. Demonstration of sparsity on (c) difference image (enhanced background) and (d) spatial gradient magnitude of difference image. Window levels were WL=40 HU and WW=350 HU for (a) and (b), WL=0 HU and WW=400 HU for (c), and WL=50 HU and WW=100 for (d).

RESULTS

Numerical phantom simulations

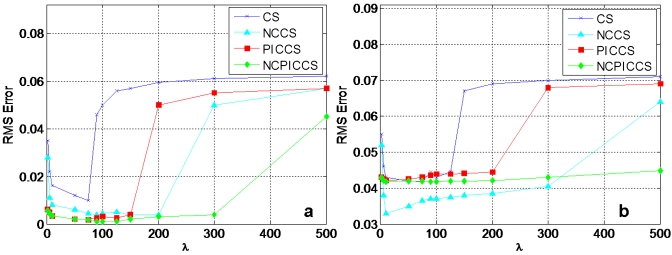
Reconstruction accuracy depended on appropriate selection of λ (Fig. 3) and λ_opt for each condition was established (Table 1). When the search of λ_opt had large areas of flatness (indicating several values giving similar results on RMS error), a common λ_opt was employed for each method to facilitate comparisons. Nonconvex methods had broader ranges of λ_opt that provided low RMS error compared to their convex counterparts, both in noise-free [Fig. 3a] and noise added [Fig. 3b] conditions.

Figure 3.

Example of numerical search of λ_opt at 20 projections. (a) Noise-free condition. (b) Poisson noise added.

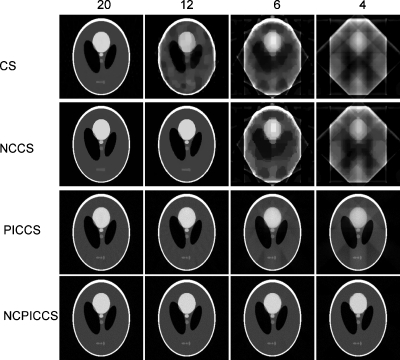
From the noise-free simulation, we observed that nonconvex methods (NCCS and NCPICCS) required fewer projections to accurately reconstruct the idealized dynamic Shepp–Logan phantom images than did their convex analogs (CS and PICCS). While CS required 20 projections to reconstruct the phantom, NCCS was able to reconstruct the phantom with only 12 projections, both with no use of prior images (Fig. 4). There was a significant gain in undersampling potential by using a prior image in the reconstruction process, requiring only six (PICCS and NCPICCS) or four projections (NCPICCS) for accurate reconstruction (Fig. 4).

Figure 4.

Noise-free reconstructed Shepp–Logan phantoms under four levels of undersampling: 20, 12, 6, and 4 (columns 1, 2, 3, and 4, respectively); and four compressed sensing based methods: CS, NCCS, PICCS, and NCPICCS (rows 1, 2, 3, and 4, respectively). Reconstructed image at time point t=2.5 s is shown.

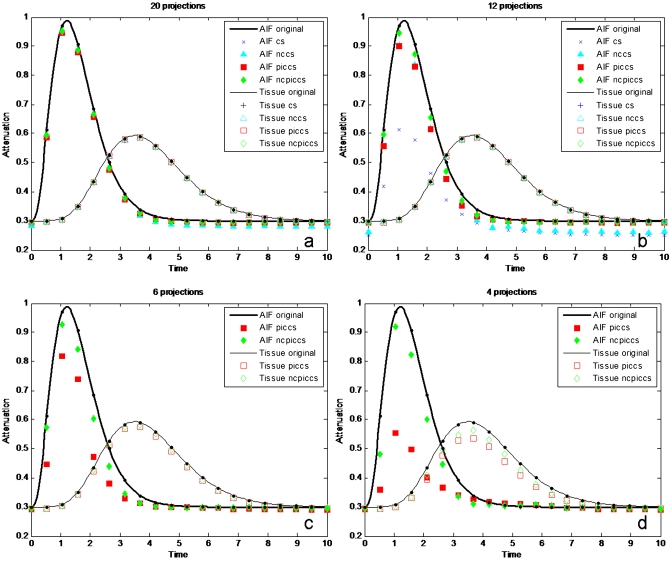
When the time density curves of the AIF and tissue ROIs were plotted, all methods reproduced the curves with a high degree of accuracy when enough projections were used (Fig. 5). NCPICCS provided high accuracy for as few as 4 projections, PICCS at 6 projections, and NCCS at 12 projections (Table 2).

Figure 5.

Accuracy of AIF and tissue perfusion (tissue) of simulated dynamic data under noise-free conditions. (a) 20 projections, (b) 12 projections, (c) six projections, and (d) four projections.

Table 2.

Measured RMS error of reconstructed images and time density curves using four CS-based methods.

Condition	Projections	RMS error
		Average reconstruction		Arterial input function		Tissue perfusion
		Noise-free	Noise added	Noise-free	Noise added	Noise-free	Noise added
Ideal	360	NA	0.0434	NA	0.00423	NA	0.00414
CS	20	0.0034	0.0396	0.000 86	0.013 86	0.000 16	0.003 90
NCCS	20	0.0023	0.0321	0.004 35	0.019 60	0.000 03	0.004 40
PICCS	20	0.0006	0.0424	0.001 02	0.015 60	0.000 04	0.003 66
NCPICCS	20	0.0003	0.0423	0.002 44	0.011 95	0.000 13	0.004 07
CS	12	0.0892	0.0975	0.081 73	0.137 23	0.001 99	0.002 27
NCCS	12	0.0021	0.0764	0.039 53	0.045 38	0.001 68	0.003 49
PICCS	12	0.0006	0.0474	0.002 60	0.035 79	0.000 07	0.003 74
NCPICCS	12	0.0003	0.0424	0.003 07	0.017 16	0.000 16	0.004 16
CS	6	0.1352	0.1362	0.213 83	0.233 68	0.013 03	0.019 43
NCCS	6	0.1429	0.1432	0.197 54	0.201 75	0.008 86	0.018 78
PICCS	6	0.0037	0.0429	0.014 76	0.085 42	0.000 80	0.010 16
NCPICCS	6	0.0006	0.0422	0.007 24	0.033 32	0.000 49	0.006 69
CS	4	0.1702	0.1667	0.247 14	0.262 16	0.076 59	0.084 09
NCCS	4	0.1754	0.1729	0.184 84	0.223 58	0.076 58	0.084 11
PICCS	4	0.0089	0.0625	0.036 85	0.159 45	0.010 47	0.031 53
NCPICCS	4	0.0028	0.0426	0.008 65	0.045 75	0.002 33	0.019 26

Results were similar to the above when Poisson noise was added to the simulated projections (Figs. 67). For the reconstructions with added noise and 20 or 12 projections, there was a significant difference between methods employing prior images (PICCS and NCPICCS) and methods that did not (CS and NCCS). Image noise was lower on CS and NCCS reconstructions, but some details of the smallest objects were lost (Fig. 6). PICCS and NCPICCS images preserved well both the large and small structures and also preserved the characteristic noise texture of CT images. As in the noise-free case, the performance of NCPICCS was superior at the highest degree of undersampling (4 projections), about the same as PICCS and NCCS at 12 projections, and all methods performed well at 20 projections (Table 2). Detailed absolute error for images reconstructed at four and six projections, under both noise-free and noise added conditions, illustrated a higher degree of accuracy of the NCPICCS in comparison to PICCS (Fig. 8).

Figure 6.

Poisson noise added and reconstructed Shepp–Logan phantoms under 4 levels of undersampling: 20, 12, 6, and 4 (columns 1, 2, 3, and 4, respectively); and four compressed sensing based methods: CS, NCCS, PICCS and NCPICCS (rows 1, 2, 3, and 4, respectively). Reconstructed image at time point t=2.5 s is shown.

Figure 7.

Accuracy of AIF and tissue perfusion (tissue) of simulated dynamic data under Poisson noise added conditions. (a) 20 projections, (b) 12 projections, (c) 6 projections, and (d) 4 projections.

Figure 8.

Absolute error comparison between Shepp–Logan phantom images reconstructed with PICCS [(a), (c), (e), and (g)] and NCPICCS [(b), (d), (f), and (h)]. Figures include noise-free conditions [(a)–(d)] and Poisson noise added to projections [(e)–(h)]. Figures (a), (b), (e), and (f) used six projections and (c), (d), (g), and (h) used four projections. Display window was [0, 0.05], range of original data [0, 1].

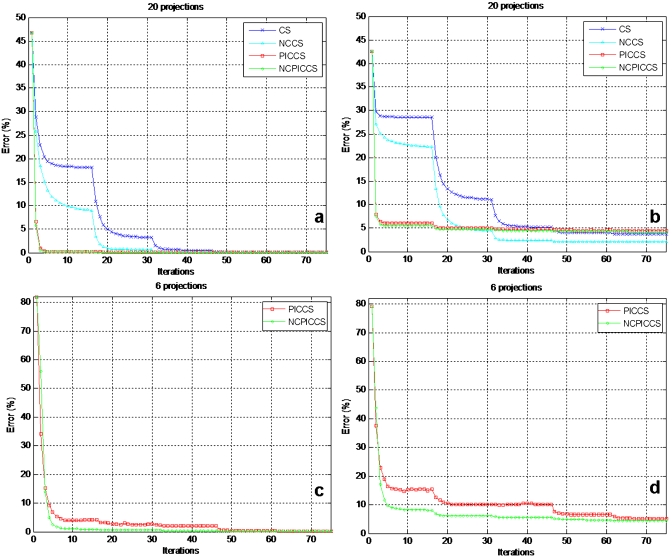
While all 4 methods provided good reconstructions at 20 projections, convergence speed was improved by the use of either nonconvex functions or prior images alone (Fig. 9). Reconstructions employing nonconvex functions consistently converged faster than those using convex ones and they usually converged to a lower RMS error as well. The greatest gain in convergence speed, however, was seen when prior image information was employed. This observation was consistent through all simulated undersampling levels with and without added noise. Fastest convergence was achieved, in all simulation conditions, when employing NCPICCS. The bumps in the RMS curves occur when an outer loop parameter is decreased in the optimization routine (Fig. 9).²⁸

Figure 9.

Convergence speed of CS-based image reconstruction methods under noise-free conditions [(a) and (c)] and Poisson noise added [(b) and (d)] at 20 projections [(a) and (b)] and 6 projections [(c) and (d)].

In vivo simulation

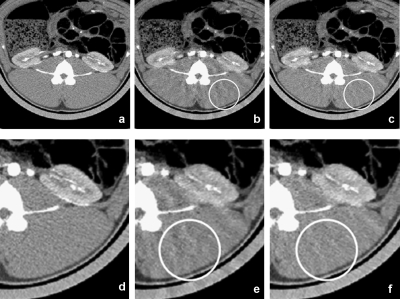
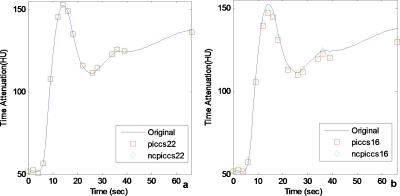
Both PICCS and NCPICCS were able to recover the TACs with either 22 or 16 projections, although accuracy started to decrease for the 16 projection case (Fig. 10). The results suggest that on real data, the difference in accuracy of perfusion TACs for the convex and nonconvex PICCS may be small, in contrast to the larger difference observed in the simulated phantom experiments. Although they provided similar TACs, the quality of images reconstructed with NCPICCS was less affected by streaking artifacts at the lowest number of projections (Fig. 11). NCPICCS also provided the advantage of faster convergence.

Figure 10.

TACs of in vivo data simulation. (a) Comparison using 22 projections. (b) Comparison using 16 projections. Performance of both convex and nonconvex PICCS decays with larger number of projections. Both show similar results on the TACs.

Figure 11.

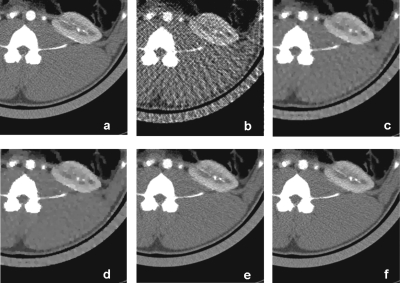
Images of in vivo data simulation reconstructed with [(a) and (d)] conventional filtered backprojection and using all available projections, [(b) and (e)] PICCS using only 22 projections, and [(c) and (f)] NCPICCS using only 22 projections. Images reconstructed with both methods were successful with little loss of image quality. However, the NCPICCS images have fewer artifacts (note circled area). Display window is WL=40 HU and WW=350 HU.

Another aspect of CS reconstructions that is relevant to CT is the depiction of noise texture. When evaluating image reconstructions from filtered backprojection and all four CS algorithms using 60 projections (Fig. 12), it was evident that only the PICCS and NCPICCS results maintained a noise texture similar to the original. These results agree with previous observations in which prior image constrained methods better preserve noise texture characteristics of CT images when compared to conventional CS methods, which can tend to oversmooth images, giving an artificial impression.³⁹

Figure 12.

Comparison of noise texture of (a) original data and reconstructed images using 60 projections and (b) filtered backprojection, (c) CS, (d) NCCS, (e) PICCS, and (f) NCPICCS. Notice both PICCS and NCPICCS preserve the characteristic noise texture of CT images [(e) and (f)] in comparison with smoother images provided by CS and NCCS [(c) and (d)]. Display window is WL=40 HU and WW=350 HU.

DISCUSSION

We have presented a novel image reconstruction method based on a nonconvex compressed sensing algorithm that employs a prior image constraint. NCPICCS expands on known methods such as compressed sensing and PICCS that employ the convex ℓ₁-norm. The main benefits of NCPICCS found using the dynamic Shepp–Logan phantom simulations were the higher undersampling potential compared to CS, NCCS, and PICCS, as well as faster convergence speed when solving the same reconstruction task with a fixed number of iterations. For this simulated perfusion data, NCPICCS provided the most accurate TAC at very high degrees of undersampling (i.e., four projections) and was the only method capable of accurately reconstructing the images at such undersampling levels. In general, all methods had similar TAC accuracy when the number of projections for a given method was high enough to allow accurate reconstruction.

NCCS outperformed CS when no prior image information was available, not only by allowing reconstruction of images with a lower number of projections, but also converging using fewer iterations. The use of prior image information (PICCS and NCPICCS) improved reconstructions over both CS and NCCS and also sped up convergence significantly. NCPICCS outperformed our implementation of PICCS in both image reconstruction and TAC accuracy at extremely low numbers of projections, with both methods employing the same numerical implementation.

The prior image constrained methods also did a better job at preserving the noise texture characteristics of CT images compared to the conventional CS methods, as shown by the animal experiments using 60 projections (Fig. 12). At 20 and 12 projections, image noise was lower in CS and NCCS reconstructions than in NCPICCS or PICCS (Fig. 6). Prior image constrained methods maintain fidelity to the noise-corrupted image; hence, some noise error is unavoidably propagated into the solution [Fig. 9b].

NCPICCS provided significant practical advantages using the numerical implementation described. First, NCPICCS typically performs better over a broader range of choices for the regularization parameter λ (Fig. 3). Second, because iterative reconstruction methods are computationally expensive, the faster convergence speed of NCPICCS can be an important advantage.

Limitations

Our studies had some limitations. First, we did not use true projection space data for the animal experiments, but rather we started with image space data and transformed back to projection space. However, because this was done for all four methods examined to solve an identical problem, the results found are expected to be equally valid in actual data. Furthermore, our results showed good agreement with previously published results using PICCS, NCCS, or CS.^{12, 22, 30} Second, in this paper we considered only the ℓ_p function as the nonconvex sparsity measure, with p=0.7. It is possible that different nonconvex functions or other values of p could lead to faster convergence or higher undersampling gains. Third, in this study we only considered a least-squares fidelity term rather than a Poisson likelihood model or a weighted least-squares approximation,^{39, 40} but since the fidelity term was common to the CS-based methods evaluated, one would expect the relative ranking of the methods (and thus the implications of this study) to remain the same. A final limitation, common to all methods investigated here, is that the collection of only a small number of projections would require a very fast pulsed x-ray system, allowing exposure at only selected projection angles. Although this might be technically feasible,⁴¹ it is not currently implemented in any commercial CT clinical scanner. CT scanners based on multiple x-ray sources, pioneered with the dynamic spatial reconstructor,⁴² and more recently stationary and multisource micro-CT systems using carbon nanotubes,⁴³ could benefit from CS-based reconstruction methods (including NCPICCS), as illustrated recently in small animal imaging.⁴⁴

Despite the great potential for dose reduction using x-ray angular undersampling, it is still uncertain if those strategies will be implemented in clinical systems, as discussed in Ref. 21. Alternatively, it is conceivable to seek strategies to further modulate the tube current during acquisition (somewhat emulating x-ray undersampling by using a very low exposure setting at certain angles) or to limit the angles of exposure.¹² A straightforward strategy for clinical implementation would be to lower the tube current during acquisition, but it remains to be investigated if either nonconvex or ℓ₁-based compressed sensing methods can offer any benefit in comparison to other iterative reconstruction methods,⁴⁰ since accurate image recovery then becomes a denoising problem rather than an undersampling problem.

CONCLUSION

We have presented a novel method for image reconstruction using highly undersampled dynamic data. The NCPICCS method takes advantage of the information provided by a prior image, as in the PICCS method, but employs a more general nonconvex sparsity measure (such as the ℓ_p-quasinorm) rather than the conventional convex ℓ₁-norm. Despite the lack of guarantees of a globally optimal solution, the proposed nonconvex extension of PICCS consistently allowed for image reconstruction from fewer samples than the analogous ℓ₁-based PICCS method, just as observed in other nonconvex compressed sensing applications.^{26, 27, 28}

In simulated perfusion phantoms and using identical numerical solvers, the NCPICCS method required a smaller number of projections compared to PICCS to successfully reconstruct an image and both were superior to methods without prior image constraints. In the in vivo data, NCPICCS and PICCS showed little difference in the recovered TACs. However, at the highest degree of undersampling, images reconstructed with NCPICCS had better image quality with fewer artifacts and provided faster convergence.