Abstract
Quantifying the connectivity between arbitrary surface patches in the human brain cortex can be used in studies on brain function and to characterize clinical diseases involving abnormal connectivity. Cortical regions of human brain in their natural forms can be represented in surface formats. In this paper, we present a framework to quantify connectivity using cortical surface segmentation and labeling from structural magnetic resonance images, tractography from diffusion tensor images, and nonlinear inter-subject registration. For a single subject, the connectivity intensity of any point on the cortical surface is set to unity if the point is connected and zero if it is not connected. The connectivity proportion is defined as the ratio of the total connected surface area to the total area of the surface patch. By nonlinearly registering the connectivity data of a group of normal controls into a template space, a population connectivity metric can be defined as either the average connectivity intensity of a cortical point or the average connectivity proportion of a cortical region. In the template space, a connectivity profile and a connectivity histogram of an arbitrary cortical region of interest can then be derived from these connectivity quantification values. Results from the application of these quantification metrics to a population of schizophrenia patients and normal controls are presented, revealing connectivity signatures of specified cortical regions and detecting connectivity abnormalities.
Keywords: connectivity, quantification, DTI, cortical surface, tractography
Introduction
The human brain cortex is a highly organized structure in which neurons rely on about 100 trillion synaptic connections for their communications and white matter axons underlie corticocortical pathways by which different cortical regions exchange information. Understanding the connectivity of the cortex may contribute to both functional and clinical studies of the human brain [e.g. Catani and ffytche, 2005; Mesulam, 2005; Mesulam, 2008]. But it is not clear how to appropriately quantify cortico-cortico connectivity, and therefore new strategies and tools continue to be developed in order to further improve connectivity studies [e.g. Hagmann et al., 2008; Gong et al., 2009].
The cerebral cortex of the human brain can be represented as a surface, and therefore one potential way to characterize connectivity is through the quantification of connectivity between surface patches defined on the cortex. Tools to assist in this process have been recently developed. First, methods to segment the cortex and to parcellate and label different regions of the surface using structural MR images have been developed [Fischl et al., 2004; Han et al., 2004, Desikan et al., 2006, Wan et al., 2008]. Second, tractography based on diffusion imaging [e.g., Conturo et al., 1999; Jones et al., 1999; Mori et al., 1999; Basser et al., 2000; Behrens et al., 2003; Tuch et al, 2003; Wedeen et al., 2005; Behrens et al., 2007] has enabled the noninvasive tracing of white matter trajectories connecting different parts of the brain. Finally, intersubject nonlinear registration tools also became available [e.g., Miller et al., 2002; Shen et al., 2002], enabling group analysis across populations.
The major goal of this study is to establish surface-based connectivity metrics that can be used to define the connectivity of an arbitrary cortical surface region. The metrics can then be used to study and compare multiple subjects, for example between a normal control group and a disease group. Hence they can be applied to studies on brain function and clinical diseases involving abnormal connectivity. The underlying connectivity model we use comprises a starting region, a trajectory, and an ending region. Note that “starting” or “ending” statements mentioned in this article are only used to simplify the description and do not have physiological meanings, since diffusion-based tractography cannot differentiate anterograde from retrograde connections. A labeled cortical region, for example a lobe or gyrus, was used as a starting region of interest (ROI) to initiate tractography. The cortical voxels (ending region) in the rest of the cortical surface were defined to have a connectivity intensity value of 1 or 0 if the cortical voxel was reached or not by tracing from starting region.
The intersections between the cortical surface and the underlying trajectories can be established either by mapping from the white matter fibers to the cortical surface [Hua et al., 2009; Huang et al., 2009] (if tractography results are in streamline format) or by direct labeling of the cortical voxels (if the tractography results are in volume data format). We used the latter method in this study. The cortical surface connectivity proportion (CSCP) of any cortical surface region was defined as the ratio of the connected surface area over the area of this entire surface region in the native subject space. The CSCP is a fraction between 0 and 1. After nonlinearly registering the individual binary connectivity data to a template space, each cortical voxel in the template space was characterized by a connectivity profile based on the average connectivity intensity from a series of starting cortical regions. Average connectivity intensities range from 0 to 1 with 1 indicating all subjects have connection from a starting region to this voxel. The connectivity profile and connectivity histogram of an arbitrary cortical surface region can be derived based on the connectivity profile of individual cortical voxels of which the ending cortical region is composed. Unique signatures of connectivity of any arbitrary cortical surface from a group of normal subjects can be revealed with connectivity profile and connectivity histogram. These connectivity metrics can also be used to search and refine the cortical regions with abnormal connectivity when applied to disease study.
The defined metrics were tested with data of twelve normal controls and ten schizophrenia patients. Previous comparisons of DTI-derived metrics such as fractional anisotropy (FA) values indicated disrupted left arcuate [e.g. Douaud et al., 2007; Phillips et al., 2009] and left uncinate fasciculus [e.g. Szeszko et al, 2005] both of which connect the cortex of left frontal and left temporal lobes. We hypothesized that the connectivity between left frontal and left temporal lobe may be weaker in schizophrenia patients and this connectivity weakness can be reflected from the significant lower values of the proposed connectivity quantifications. Furthermore, we hypothesized that the connectivity weakness can be localized around the areas to which arcuate and uncinate fasciculi connect.
Method
Overview of the framework on surface-based connectivity quantification
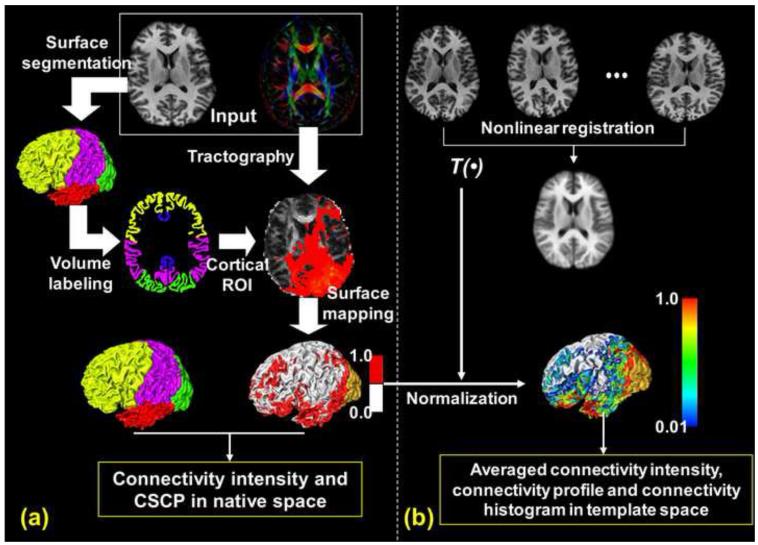
Fig. 1 illustrates the information flow of our connectivity quantification framework. In Fig. 1a, the input data is the diffusion tensor image (DTI) and T1-weighted structural image. The T1-weighted image is used for cortical surface segmentation and parcellation. In this study, the entire cortical surface is parcellated into cortical lobes with yellow, purple, green, red and dark blue representing the frontal, parietal, occipital, temporal, and limbic lobe, respectively. The parcellated lobes, after surface to volume transformation which is described in detail below, also serve as ROIs for tractography. Probabilistic tracking [Behrens et al., 2007] implemented by “probtrackx” in FDT of FSL (http://www.fmrib.ox.ac.uk/fsl/fdt, Oxford Centre for Functional Magnetic Resonance Imaging of the Brain, Oxford, UK), which resolves the well-known crossing fiber issues by constructing multi-orientation field allowing fiber crossing and then applying probabilistic tractography, was adopted for tracing corticocortical trajectories. For example, a connectivity result of tractography from the left occipital lobe is shown in Fig. 1a overlaid on an axial fractional anisotropy (FA) map. The tracking results were then thresholded and binarized with 1 indicating there is connectivity and 0 indicating there is no connectivity in the cortical surface other than regions where the tractography was initiated.
Fig. 1.
An overview of the workflow to obtain the connectivity metrics. (a) shows how to get connectivity intensity and CSCP in the native subject space with diffusion and T1-weighted images as input. (b) shows how the averaged connectivity intensity, connectivity profile and connectivity histogram were derived in the template space after normalization.
The cortical surface below the FA color map in Fig. 1a shows the distribution of binarized connectivity from the left occipital lobe. The red, silver, and gold colors on the cortical surface indicate the regions with connectivity, without connectivity, and the starting region (the left occipital lobe). In the native subject space, one of the connectivity metrics, the CSCP, could be calculated as the ratio of the connected surface area within this cortical surface region over the entire area of the surface region.
In Fig. 1b, the inter-subject transformation matrix T(β) was obtained by nonlinearly registering the individual T1 weighted volumetric images to a template T1 weighted volumetric image with large deformation diffeomorphic metric mapping (LDDMM) [Miller et al., 2002]. The averaged T1 weighted volumetric image after LDDMM transformation is shown below the individual T1 weighted volumetric images in Fig. 1b. The registered images after LDDMM transformation have Dice coefficient [Dice, 1945] of 0.967±0.004, demonstrating the high quality of inter-subject registration. Dice coefficient measures the quality of registration by calculating the fraction of volume overlap. The transformation matrix which registered the T1 weighted images was then applied to the binary connectivity data of individual subjects and warped the connectivity information into the template space. After normalization, connectivity profile of each cortical voxel in the template space, which includes the averaged connectivity intensities from a series of starting cortical regions, was established. As an example, the averaged connectivity intensities from left occipital lobe were mapped to the cortical surface and are shown in lower portion of Fig. 1b. More averaged connectivity intensity maps could be established with tractography initiated from other starting cortical regions.
With the average connectivity intensity of each cortical voxel, the connectivity profile and the connectivity histogram of any arbitrary cortical region can then be calculated. The connectivity intensity and CSCP in Fig. 1a and the averaged connectivity intensity, connectivity profile and connectivity histogram in Fig. 1b, highlighted with the yellow box, are the output of the connectivity quantification process with the DTI and T1-weigthed image in Fig. 1a, highlighted with the white box, as input.
Data acquisition
Data from twelve normal subjects (age=38.7±6.3, 7 male and 5 female) and ten schizophrenia patients (age=37.1±5.2, 6 male and 4 female) were used for testing the quantification of connectivity. All subjects gave written, informed consent for their participation after the risks and benefits of participation were explained to them prior to MRI scanning. A 3T Philips (Achieva) MR unit was used for MRI scans. Diffusion weighted images (DWI) were acquired using a single-shot EPI sequence with a SENSE parallel imaging scheme (SENSitivity Encoding, reduction factor = 2.3). The imaging matrix was 128 × 128, with a field of view of 256 × 256 mm (nominal resolution of 2mm), which was zero-filled to 256 × 256. Axial slices of 2.2 mm thickness were acquired parallel to the anterior–posterior commissure line. A total of 65 slices covered the entire brain and brainstem without gaps. The diffusion weighting was encoded along 30 independent orientations [Jones et al., 1999] and the b-value was 1000 s/mm2. Two additional images with minimal diffusion weighting were also acquired. TE and TR were 80ms and 6089ms without cardiac gating, respectively. The acquisition time per dataset was approximately 5 minutes. To enhance the SNR of DTI, two repetitions were used, resulting in a total acquisition time of 11 minutes. With the same field of view, co-registered magnetization-prepared rapid gradient-echo (MPRAGE) images with image matrix 256×256×143 (resolution 1mm) were also acquired. MPRAGE images have superior gray and white matter contrast and were used for cortical segmentation and parcellation. Co-registered axial T2-weighted images were acquired using a double spin echo sequence with the first echo time 40ms, the second echo time 100ms, and the repetition time 6084ms. The image matrix and resolution of T2 weighted image are the same as those of DWI. Twelve-parameter linear affine intra-subject registration was performed to correct geometric distortions caused by eddy currents during DWI acquisition using automated image registration (AIR) [Woods, et al., 1998]. The distortion caused by B0-inhomegeneity was corrected with LDDMM [Miller, et al., 2002]. In this nonlinear registration process, the averaged b0 image representing DWI data space was registered to the T2-weighted image which was used for anatomical guidance [Huang et al., 2008]. Since T1- and T2-weighted images were co-registered, distortion-corrected DWI data were then well registered to the T1-weighted images.
Cortical surface parcellation and surface-volume transformation
The cerebral cortex was segmented from the T1-weighted (MPRAGE) volumetric brain images having voxel size 1×1×1mm3. A topology preserving segmentation method [Han et al., 2004] was applied to generate three nested cortical surfaces, the outer, central, and inner surfaces. The inner cortical surface is at the boundary between gray and white matter; the outer cortical surface is at the boundary of pia mater and brain tissue; and the central cortical surface is positioned midway between the inner and outer surfaces.
A semi-automated process was used to generate accurate labeling of the cortical surface based on its geometry. In the first step, an RBF (radial basis function) based deformable registration method was used to determine a dense displacement field between the ICBM (International Consortium of Brain Mapping) T1-weighted (source) image and the subject T1-weighted (target) image. This displacement field was then applied to the ICBM gyral labels to get subject gyral labels. In order to correct for inevitable errors that occur due to the differences in gyral and sulcal geometries between the source and target, a second step comprising manual surface editing on a partially inflated surface was used to more accurately align the gyral label boundaries with their anatomically key sulci.
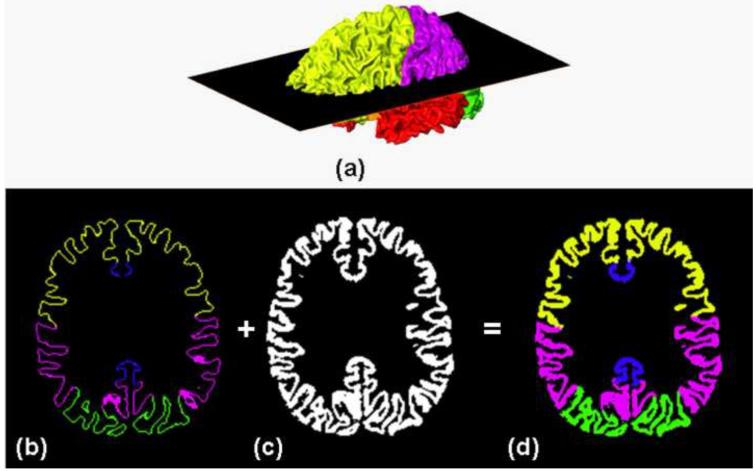
Fig. 2 demonstrates the transformation of cortical labeling from surface format to volume format. Fig. 2a shows a typical lobular labeling resulting from the semi-automated cortical parcellation. To initiate tracking, the inner cortical surface was shifted inward by 2 pixels (2mm) into the white matter (in the direction of the surface normal), and the voxels found between the (shifted) inner and outer cortical surfaces were used to create a binary mask representing the position of the cortical mantle, as shown in Fig. 2c. The volumetric labeling (Fig. 2d) was generated by extending the surface gyral labeling (Fig. 2b) into the binary mask (Fig. 2c). The labeled lobes in the volumetric space were also used to label the terminations of the trajectories.
Fig. 2.
Transformation of the surface labeling of cortical lobes to the lobular volume labeling. Surface cortical labeling (a) was transected with the 2D plane across the inferior-superior axis. The resultant 2D surface cortical labeling (b) was expanded to the volume format lobe labeling (d) with the segmented cortex (c) as a template.
Tractography and normalization
Both diffusion tensor fitting and probabilistic tracking [Behrens et al., 2007] were implemented by FDT of FSL. Parcellated volume format lobes were used as ROIs for tracing of white matter trajectories. Default parameters in FDT were used. After running FDT, a threshold value 10 was used to binarize the tracking results. This relatively low threshold was set to enable the trajectories initiated from starting region to better reach the cortex. From visual inspection, the traced white matter trajectories could well reach the shifted inner cortical surface described above. The binary volumetric connectivity data in the native subject space was obtained as follows. First, we set the cortical voxels with tracking results higher than the threshold equal to 1 and all others equal to 0. With the binary mask representing the cortical mantle (Fig. 2c) as the template, the voxels along the direction perpendicular to connected shifted inner surface in the cortical mantle were assigned value 1. In this way, the connectivity data from each subject was represented in volumetric format.
To warp the binary volumetric connectivity data to the template space, the transformation matrix T(β) was obtained by registering the skull stripped T1-weighted volumetric brain image of each of 12 subjects to a normal template using LDDMM. The same transformation from LDDMM process was applied to the binary volumetric connectivity data to obtain the averaged volumetric connectivity map from a group of subjects in the template space. By assigning the vertices of the template cortical surface the averaged connectivity intensities from their nearest cortical voxels, we could visualize of the averaged connectivity map on the template cortical surface.
Connectivity quantifications for cortical voxels and cortical surface regions
Connectivity quantification in our framework is defined based on connectivity intensity for cortical voxel and connectivity proportion for cortical surface region. Given an arbitrary cortical voxel, the connectivity intensity is 1 with connectivity from starting region and 0 if there is no connectivity. Given an arbitrary cortical surface region, part of this surface region is “covered” by projections from starting region. A measure of cortical connectivity can be defined by considering the fraction of covered surface region. Take the binary connectivity map shown in Fig. 1a as an example. If the total surface area of a lobe is Arealobe and the surface area painted red in this lobe is Areamapped, then we can define the cortical surface connectivity proportion (CSCP) from starting region to this lobe (ending region) as the ratio of mapped surface area over the total lobe surface area: CSCP= Areamapped / Arealobe. The cortical surface is represented by triangle meshes; therefore, by summing the areas of the triangles both Areamapped and Arealobe can be calculated. The CSCP ranged from 0 to 1 and was calculated in the native space. For group analysis, the average and standard deviation of CSCP of the group can be calculated with the correspondent CSCP of each subject.
In our study, binary cortical connectivity maps were generated with tracking initiated from every lobe surface. After normalization, the transformed cortical connectivity maps from individual subjects were then averaged in the template space. Hence, each of the four lobes (starting region of tractography) has the averaged connectivity map in the rest of the cortical surface (ending region of tractography) in the template space. The values in these averaged connectivity map range from 0 to 1 and are essentially the averaged connectivity intensity at the cortical voxels.
A profile or histogram of connectivity is an organized array based on two fundamental connectivity measures: connectivity intensity and CSCP. Combining the values of averaged connectivity intensity values from all lobes in any cortical voxel, we can get a quantified connectivity profile to characterize the connectivity property of this voxel. The horizontal axis of the connectivity profile of the cortical voxel is a series of starting regions from which the cortical voxel was connected. Take any voxel in the frontal lobe as an example. If a connectivity profile for this frontal lobe voxel can be described as “0 from frontal lobe, 0.6 from parietal lobe, 0.2 from occipital lobe and 0.25 from temporal lobe”, it means to this voxel 60% of subjects have connectivity from the parietal lobe, 20% of subjects have connectivity from the occipital lobe and 25% of subjects have connectivity from the temporal lobe. There is no connectivity to the frontal lobe itself for any frontal lobe voxel as intra-region connectivity is not accounted in this study. It should be noted that sum of the connectivity intensity measures of connectivity profile of a single voxel does not need to be 1.
With connectivity profiles from all voxels in any cortical region, the connectivity profile and connectivity histogram of this region is defined as follows. The connectivity profile of a cortical region is represented by the mean and standard deviation of the correspondent connectivity intensities of all cortical voxels in this cortical region. After dividing the connectivity quantification values into 10 subgroups, i*0.1 to i*0.1+0.1 as subgroup i with i from 0 to 9, the ratio of the voxel count in each subgroup over the total voxel count of the cortical region was calculated. The summation of all these ratios is 1. We used these ratios rather than direct voxel count to represent the connectivity histogram as the former representation can be used to compare the histogram of different cortical regions with different sizes. For each of the starting regions in the horizontal axis of the connectivity profile in a cortical region, there is a corresponding connectivity histogram. The integral of the connectivity histogram is the mean connectivity intensity displayed in the connectivity profile. Fig. 5 in the Results section below illustrates these connectivity metrics of cortical regions using real data.
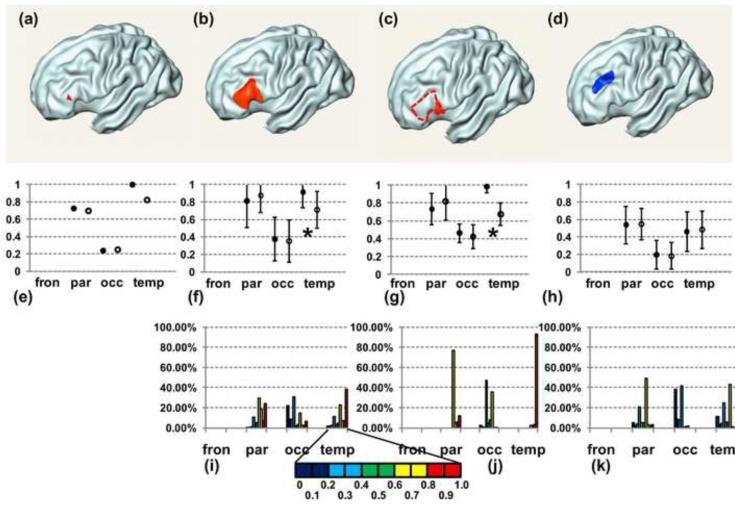
Fig. 5.
A single voxel (a), a cortical surface patch in left inferior frontal gyrus (b), an even smaller cortical surface patch in left inferior frontal gyrus (c) are painted red on the partially inflated cortical surface. A randomly chosen cortical surface patch distant from (b) is painted blue in (d). The cortical surface patch in (c) is part of that in (b), represented by dashed circle in (c). (e) to (h) show the connectivity profiles of the ending cortical regions (a) to (d), respectively. The horizontal axes of connectivity profile consist of a series of starting cortical regions. Solid black circles indicate averaged connectivity intensities (e) or CSCPs (f-h) from control subjects and empty circles indicate those from schizophrenia patients. The error bars in (f) to (h) are the standard deviations of connectivity intensities of all cortical voxels of which the cortical surface patch (b), (c) or (d) is composed. Significantly lower averaged connectivity intensities, indicated by asterisks, were found from temporal lobe to these cortical surface regions. No significant difference of connectivity (h) was found between two groups for connectivity from temporal lobe to blue patch in (d). Detailed connectivity distribution of connectivity intensities of all cortical voxels in patch (b), (c) and (d) can be found in connectivity histogram in (i), (j) and (k), respectively. The color bar encoding the connectivity histogram scales is enlarged below (i).
Relationship between the measures of cortical surface connectivity proportion and connectivity intensity
From the discussion on CSCP above, it suggests that CSCP can be potentially used to imply connectivity strength from a given starting cortical area. It will be useful if the CSCP measure can be obtained from an arbitrarily chosen cortical surface region. Below we discuss the possibility of getting CSCP of any cortical region from the connectivity intensity for a group of subjects.
The connectivity intensity and CSCP are intrinsically related. After transforming the binary connectivity data into a template space, we can obtain the average connectivity intensity. The connectivity proportion of an arbitrary cortical surface can be obtained by calculating the mean of these connectivity intensities of the cortical voxels of which this cortical surface is composed.
Given a starting region where tractography is initiated, let Si and sci be the area of any region of cortical surface and area of the connected surface region within this certain region of cortical surface for any subject i, where i is from 1 to N and N is the number of subjects. The CSCP of this cortical region for the group of subjects is calculated as
| (1) |
This is the same mathematical description with different symbols as that explained in the method section. After registration, we assume that all cortical correspondent surface regions with the area Si from different subjects have been transformed to be the same cortical surface region with the area St in the template space. And let be the correspondent connected surface area in the template space from different subjects. If we consider the case of linear affine transformation,
| (2) |
is the scaling factor after transforming this cortical surface region. Let mi (i=1 to N) be the voxel count of connected cortical region of each subject i in the native subject space. In the template space, let M be the cortical voxel count of the transformed entire cortical surface region the area St and be the voxel count of transformed connected surface region with area from different subjects. Define a constant . Connectivity intensities of all the cortical voxels in this area are Ij, (j=1 to M). Then the following relationship can be derived:
| (3) |
Combining equations (1) to (3), we can get the following relationship between the CSCP and summation of the connectivity intensities:
| (4) |
In another word, CSCP is essentially the mean of connectivity intensities of cortical voxels in an arbitrarily selected cortical surface region. It should be noted that equations (2) were derived with the assumption of linear affine transformation. For nonlinear registration we used in our study, the mean of the connectivity intensities also served as close estimate of the CSCP.
Comparison of the connectivity metrics between the control group and schizophrenia patients
The above analyses were applied to the connectivity data of ten schizophrenia patients. The CSCP and connectivity profile were calculated for these patients. For comparison of these connectivity metrics between the control group and schizophrenia patients, a student t-test was used to find the statistical difference. CSCP measurements of cortical lobes and smaller cortical regions within the cortical lobe were compared to reveal the connectivity difference between the two groups at these regions. Note that as proved from the previous section, the CSCP of an arbitrary smaller cortical region within the cortical lobe can be obtained by calculating the mean of the connectivity intensities of cortical voxels within this certain cortical region. FDR (False Discovery Rate) corrections for multiple comparisons were made for comparing connectivity metrics of control group and schizophrenia patients.
Results
Cortical surface connectivity proportion
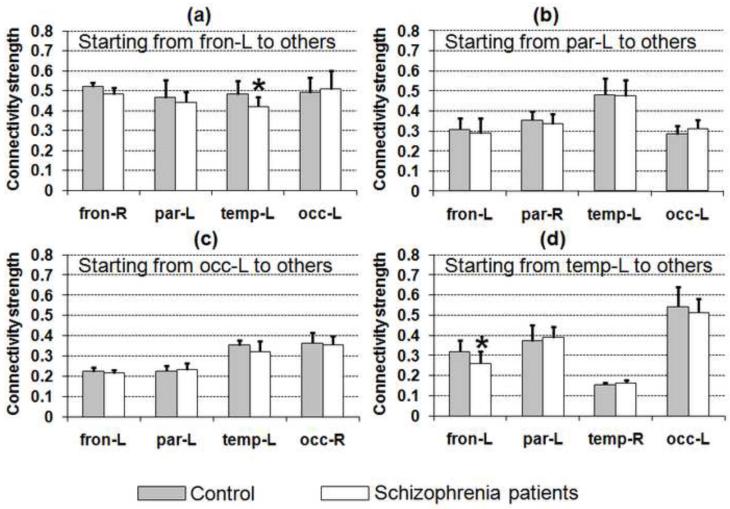
The mean and standard deviation of CSCP from normal subjects are shown as shaded bars in Fig. 3. The CSCP for each subject was calculated in the native space. For these normal subjects, except for the temporal lobe, the contralateral CSCP from the left cortical lobe to its right counterpart is relatively high. The profile of ipsilateral CSCP is quite unique for each lobe (Figs. 3a-3d). Among all normal CSCPs, left occipital lobe has the highest CSCP projecting from the left temporal lobe, shown in Fig. 3d. CSCP from left frontal lobe to all other lobes is relatively high. Left parietal, temporal and occipital lobes have similar CSCP from left frontal lobe and the values are all above 0.4 (Fig. 3a). On the contrary, CSCP from the left occipital lobe to other cortical areas is relatively low. Shown in Fig. 3c, left temporal lobe has the highest CSCP from left parietal lobe.
Fig. 3.
CSCP values from frontal (a), parietal (b), occipital (c), and temporal lobes (d) are shown for normal controls (shaded bar) and schizophrenia patients (white bar). Unique CSCP measures from different lobes can be observed. The CSCP is also sensitive to the structural connectivity changes and significantly smaller CSCPs between the temporal lobe and the frontal lobe, highlighted with asterisk in (a) and (d), can be identified in the schizophrenia group.
The results of the CSCP calculated for schizophrenia patients are shown in the white bars in Fig. 3. Among all CSCP values, the student t-test showed that differences of CSCPs between left frontal and left temporal lobes (Fig. 3a and Fig. 3d) are significant after FDR correction for multiple comparisons (corrected p=0.035 from left frontal to left temporal and corrected p=0.027 from left temporal to left frontal). The lower CSCPs clearly indicated weaker than normal connectivity between these two lobes in schizophrenia patients. In general, we found smaller contralateral CSCP for schizophrenia patients compared to that of the control group.
Averaged connectivity intensity maps
After nonlinear normalization, all cortical voxels in the template space were characterized with the connectivity profile that has the averaged connectivity intensity values from a series of cortical regions (cortical lobes in this study), ranging from 0 to 1. The connectivity intensity is 0 for the cortical voxels of the starting region.
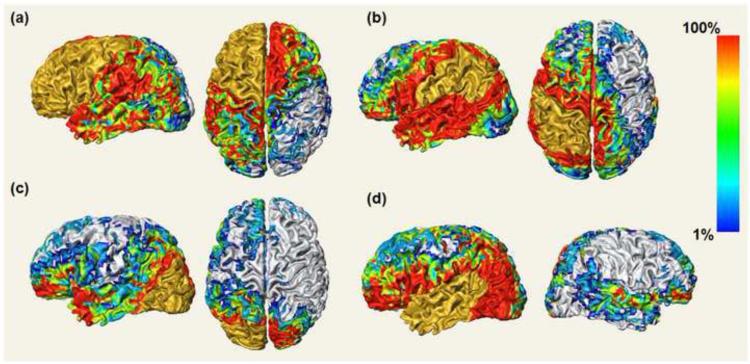
Averaged connectivity intensity maps from left lobes are shown in Fig. 4. They are direct mapping of the averaged connectivity intensities, the four components of the connectivity histogram for each cortical voxel in the template space. Therefore, four panels are shown in Fig. 4. The tractography starting region is painted gold in each panel of Fig. 4. The silver colored surface has no direct cortical connections from the gold region; otherwise, the color of the surface indicates the averaged connectivity intensity values with that position on the cortex that are connected to the gold region. For example, pure red indicates that all subjects have connection to the gold region at that point on the cortex.
Fig. 4.
Averaged connectivity intensity maps from frontal (a), parietal (b), occipital (c), and temporal lobes (d). Averaged connectivity intensity maps directly display the values of the connectivity intensities of every cortical voxel after normalization of connectivity data from 12 control subjects. The color bar encodes the scales for connectivity intensities mapped on the cortical surface.
It is observed in Fig. 4 that the contralateral projections are nearly symmetric in Fig. 4a and Fig. 4c. The contralateral projections in these two panels are composed of forceps minor (Fig. 4a) and forceps major (Fig. 4c) of the corpus callosum [Huang et al., 2005; Wakana et al., 2007]. Note that the lateral parts of the contralateral cortex are also covered with connectivity by the lateral trajectories of corpus callosum which are difficult to be traced due to crossing of corpus callosum, cortico-spinal tract, and other tracts. This lateral coverage of the contralateral cortex clearly indicates well traced lateral corpus callosum with the adopted probabilistic tracking. For ipsilateral connections, unique connectivity patterns can be observed for different panels of Fig. 4. The frontal lobe has most widely distributed connected surface areas (Fig. 4a) while the occipital lobe has two remotely connected areas located at the temporal pole and lateral prefrontal cortex in addition to a relatively small area proximal to itself (Fig. 4c). The connections with high connectivity intensity from parietal lobe are localized in its surrounding areas (Fig. 4b). The temporal lobe has some connections to the adjacent parietal lobe, but the majority of its projections map to the frontal lobe and occipital lobe (Fig. 4d).
Connectivity profile and connectivity histogram
Fig. 5 shows the connectivity profiles (Fig. 5e-5h) of an individual voxel (Fig. 5a) and three different cortical regions (Fig. 5b-5d). Connectivity histograms (Figs 5i-5k) are also demonstrated below the correspondent connectivity profiles of the three cortical regions. The red point in a partially inflated cortical surface of Figs 5a represents a cortical voxel. The connectivity profile of this cortical voxel in the left frontal lobe, shown in Fig. 5e, is simply composed of the values of the averaged connectivity intensity from left parietal, occipital and temporal lobe indicated by horizontal axis. Cortical regions in partially inflated cortical surfaces in Fig. 5b to Fig. 5d, highlighted with red (Fig. 5b and 5c) and blue (Fig. 5d), contain a group of cortical voxels. For a cortical region, the connectivity profile shows the mean (solid circle) and standard deviation (error bar) of connectivity intensities of all cortical voxels within this cortical region. Fig. 5f and Fig. 5i are the correspondent connectivity profile and connectivity histogram of the cortical region shown in Fig. 5b. This cortical region is located at the inferior frontal gyrus. The connectivity for this area is featured with a low connectivity from occipital lobe and similar high connectivity from parietal and temporal lobe, demonstrated in Fig. 5f. For this same cortical region, connectivity histogram in Fig. 5i helps differentiate temporal connectivity from parietal connectivity by revealing detailed information of distribution of connectivity from each lobe. Specifically, most of the parietal connectivity is in the range of 0.6 to 0.7 while most of the temporal connectivity is in the range of 0.9 to 1.0 (Fig. 5i). For a segment shown in Fig. 5c and within the cortical region of Fig. 5b, a higher temporal connectivity profile is found (Fig. 5g) and the correspondent connectivity histogram (Fig. 5j) also shows this cortical region is composed of cortical voxels with almost homogeneous high temporal connectivity. With comparison of Fig. 5f and Fig. 5g, it is clear that the smaller the cortical region is, the smaller the standard deviation of the components of the connectivity profile are. Figs. 5f to 5h show the comparison of connectivity profile of the control group indicated by solid black circles and schizophrenia patients indicated by empty black circles. The blue cortical patch of the partially inflated surfaces of Figs. 5d is a randomly chosen cortical region of interests in the left frontal lobe which is completely separate from the red region shown in Fig. 5b. Significantly lower averaged connectivity intensities from temporal lobe (corrected p=0.0085 for Fig. 5f and corrected p=0.012 for Fig. 5g) in schizophrenia group have been found for cortical regions shown in Figs. 5b and 5c while no statistical difference of the averaged connectivity intensity from temporal lobe has been found for cortical region shown in Fig. 5d.
Discussion
This paper describes a framework for quantifying connectivity in the human brain cortex. In the past, cortical connectivity information from tractography initiated from starting cortical region has been used to map and subdivide other neural structures, for example, the thalamus [Behrens et al., 2003] or mid-sagittal corpus callosum [Huang et al., 2005]. Without differentiating the starting or ending cortical region of connectivity, connectivity information has also been used to explore the brain network [e.g., Hagmann et al., 2008; Gong et al., 2009] after modeling the parcellated cortical regions as connectivity nodes. In this framework, we explored cortical connectivity from a different angle by establishing a surface-based quantification of connectivity. In particular, the metrics connectivity intensity for cortical voxels and CSCP for cortical surface regions were introduced. CSCP (Fig. 3) implies a global measure on connectivity strength. For detailed characterization of connectivity, each cortical voxel is featured with a unique connectivity profile consisting of connectivity intensities as demonstrated in Fig. 5e. Based on that, the connectivity profile and connectivity histogram of an arbitrary cortical surface area were established (Fig. 5). In addition, this framework was based on surface format which is the natural form of the human cortex. It may be potentially used for studies on the brain function and clinical diseases where connectivity information plays an important role. For example, these connectivity metrics has been tested by comparing connectivity data of normal controls and schizophrenia patients in our study. The comparison demonstrates that it has a potential to detect small differences in connectivity that may be present in disease. With data from more subjects and with a finer partitioning of the cortical surface, the framework can be used to build up a new modality of the atlas representing brain connectivity.
Cortical surface connectivity proportion
CSCP was defined as the ratio of the connected ending cortical area divided by a standard partitioned surface area. As shown in Fig. 1a, it was measured in the native space. This measurement quantifies, in some sense, the connectivity strength from a given starting cortical area where the tractography is initiated. It used the inverse of a standard partitioned cortical surface area as a scaling factor because the impact of the same trajectories on the two regions with different areas can be different. So when applied to cortical lobes, the CSCP values of the same two lobes do not have the same value if we swap starting and ending region. This is because the underlying lobe areas are different from each other and the mapped cortical surface areas from the same tracts are different at their terminations in two lobes (Fig. 3). For example, the left occipital lobe has the CSCP of 0.49 from the left frontal lobe (Fig. 3a) but the left frontal lobe only has much smaller CSCP of 0.22 from the left occipital lobe (Fig. 3c). This implies that with the same connecting trajectories, the frontal lobe has larger impact on the occipital lobe. In fact, with the largest cortical surface area, the CSCP starting from frontal lobe to any other lobe (Fig. 3a) is higher than that from any other lobe to the frontal lobe (Figs. 3b-3d). For group comparison, the mean of the CSCPs of individual subjects represents the connectivity metrics of the whole group.
Application of connectivity metrics to schizophrenia patients
From the previous comparisons of FA values of schizophrenia patients and control subjects at the major white matter tracts connecting left frontal and left temporal lobes [e.g., Szeszko et al., 2005; Douaud et al., 2007; Rosenberger et al., 2008; Phillips et al., 2009], they were found lower in schizophrenia patients. Based on these findings, we hypothesized that the proposed connectivity metrics could also be significantly lower and sensitive enough to detect the connectivity changes in schizophrenia patients. The measured CSCP in Fig. 3 shows that the schizophrenia patients have significantly weaker connectivity between left temporal lobe and left frontal lobe. Segmentation of starting regions was bounded by the cortical lobe parcellation we used in this study. However, the ending region could be an arbitrary cortical surface. By refining the ending region to a portion of the frontal lobe which is close to the mapped areas from arcuate fasciculus and shown in Fig. 5b or 5c, we could find a statistically significant connectivity difference between schizophrenia patients and control subjects. However, another randomly chosen cortical region (Fig. 5d) in frontal cortex demonstrated no significant difference of averaged connectivity intensities between the two groups (Fig. 5h). It may be due to the fact that this cortical region is not close to the mapped area of either arcuate fasciculus or uncinate fasciculus connecting frontal and temporal lobes. The comparison between the control and patient groups shows the potential of applying presented connectivity metrics to the clinical studies. Especially, the flexibility of our connectivity measurements on arbitrary cortical region made the searching and refining of cortical regions, which are sensitive to abnormal connectivity, possible.
Methodological issues
Tractography based on diffusion imaging has been promising to delineate the corticocortical connectivity. However, technical issues such as selection of tractography methods, the starting ROIs where the tractography should be initiated and how to affiliate the corticocortical trajectories to the ending cortical areas can all influence the quantification results. We have tried two different strategies to trace the white matter connecting different cortical areas. Previously, a streamline propagation method [Mori et al., 1999] was used. Only the long association tracts which have been revealed with DTI tractography by several groups [e.g. Catani et al., 2002; Mori et al., 2002; Wakana et al., 2004], namely inferior/superior longitudinal fasciculus (ILF/SLF), inferior fronto-occipital fasciculus (IFO), uncinate fasciculus (UNC) and corpus callosum (CC), and reproducibly traced short association tracts were included for the account of corticocortical connectivity, following a standard tractography protocol [Wakana et al., 2007] which is based on previous multicenter efforts. The mapping from corticocortical white matter trajectories to the cortex was conducted following the method described in the previous publication [Hua et al., 2009]. The averaged connectivity map obtained with our previous strategy and published in an abstract [Huang et al., 2009] tends to have false negative results which cannot completely represent the entire corticocortical connectivity. For example, our previous strategy [Huang et al., 2009] could not reveal lateral contralateral connectivity as shown in the right panels of Figs 4a to 4d. An improved strategy in this paper adopted the tractography method capable of resolving the crossing fiber issue [Behrens et al., 2007]. The gray-white matter surface was shifted inwards so that tracking could be initiated from pure white matter rather than the gray-white matter mixed areas close to the cortex. In addition, thresholding the tractography results directly labeled the cortical voxels with connectivity. By comparing Fig. 4 and the averaged connectivity map generated from mapping of known and reproducibly traced tracts [Huang et al., 2009], we found that the averaged connectivity maps generated with two different strategies are quite similar, while Fig. 4 has larger coverage on cortical connectivity. From visual inspection, it seems that the added coverage in Fig. 4 of this paper mostly comes from lateral projection of corpus callosum, increased connectivity to the cortical areas immediately around starting cortical region and increased prefrontal connectivity from parietal lobe. As the cortical areas with increased connectivity coverage are related to the projection of white matter trajectories which are known to have crossing fiber issues, this comparison provided cross-validation to our approach of delineating corticocortical connectivity to some extent. Since the averaged connectivity map of Fig. 4 directly reveals the connectivity intensities of every cortical voxel, it suggests that the tractography strategy adopted in this paper is appropriate for the quantifications of connectivity metrics. However, further validation is still needed with the connectivity information revealed by more robust chemical tracing results from monkey studies [e.g. Schmahmann and Pandya 2006].
The quality of inter-subject and intra-subject registration plays an important role in this study. For both registrations, we used LDDMM (Miller et al., 2002) as a nonlinear registration tool. Dice coefficient measuring volume overlap of the T1 weighted images in the template space after inter-subject registration is up to 0.967. The intra-subject registration with LDDMM can effectively correct B0-induced distortion and has been discussed in details in our previous publication (Huang et al., 2008).
Difference of surface-based connectivity metrics from fiber count
Fiber count with its absolute value or scaled value has been used to imply connectivity strength and served as an important metric of connectivity. While fiber count is comparable with the data acquired from same scanner and having same SNR and same resolution, it will be biased to use this metric for comparison with data of different SNR and different resolution. In fact, a recent study [Mishra et al., 2010] has found that fiber count is significantly affected by these two factors. Moreover, resolution plays a much more significant role to fiber count than SNR and fiber count reaches a plateau after SNR is higher than around 40dB with the same resolution. To build a connectivity atlas which can be reference for data from all kinds of sources, connectivity metrics which are not sensitive to SNR or resolution would be preferred. The DWIs acquired from the modern scanners usually have sufficient SNR. Hence, the surface-based connectivity measures all defined as relative ratios in this paper are in their native forms more robust against the influence of resolution and can serve as connectivity metrics for a connectivity atlas.
Conclusion
In conclusion, a surface-based connectivity quantification framework including connectivity intensity for cortical voxels and connectivity proportion for cortical surface regions has been presented. Connectivity profile and connectivity histogram could be derived from these two measures for an arbitrary cortical surface region. The CSCP can be used to imply the quantification of the connectivity strength from one cortical area to another. Connectivity intensity and CSCP can be used in both native space for a single subject and the template space after averaging. In the latter case, the averaged values of these two metrics for a group of subjects on a certain cortical surface region were mathematically proven to be equal to each other with perfect inter-subject registration. Data of applying these connectivity metrics to revealing connectivity signatures of specified cortical regions and detecting connectivity abnormality of schizophrenia disease are also presented. These connectivity metrics can be potentially used for functional studies and to detect connectivity abnormality in diseased brains.
Research highlights.
We present a surface-based connectivity quantification framework.
It is based on cortical surface labeling and diffusion tensor tractography.
It quantifies connectivity strength for arbitrary cortical regions.
It was validated to use these quantifications to detect connectivity abnormality.
Connectivity abnormality of schizophrenia patients was revealed with the framework.
Acknowledgement
This study was supported by NIH grants R01AG020012, P41 RR015241 and R21 EB009545. Peter van Zijl is a paid lecturer for Philips Medical Systems and has technology licensed to this company. This arrangement has been approved by Johns Hopkins University in accordance with its conflict of interest policy.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. 2003;50:1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Johansen-Berg H, Woolrich MW, Smith SM, Wheeler-Kingshott CAM, Boulby PA, Barker GJ, Sillery EL, Sheehan K, Ciccarelli C, Thompson AJ, Brady JM, Matthews PM. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat Neurosci. 2003;6:750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- Catani M, Howard RJ, Pajevic S, Jones DK. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. NeuroImage. 2002;17:77–94. doi: 10.1006/nimg.2002.1136. [DOI] [PubMed] [Google Scholar]
- Catani M, ffytche DH. The rises and falls of disconnection syndromes. Brain. 2005;128:2224–2239. doi: 10.1093/brain/awh622. [DOI] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci USA. 1999;96:10422–10427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Wendt GJ, Turski PA, Moritz CH, Quigley MA, Meyerand ME. Mapping functionally related regions of brain with functional connectivity MR imaging. AJNR Am J Neuroradiol. 2000;12:1636–1644. [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maquire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- Douaud G, Smith S, Jenkinson M, Behrens T, Johansen-Berg H, Vickers J, James S, Voets N, Watkins K, Matthews PM, James A. Anatomically related grey and white matter abnormalities in adolescent-onset schizophrenia. Brain. 2007;130:2375–2386. doi: 10.1093/brain/awm184. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM. Automatically parcellating the human cerebral cortex. Cereb Cortex. 2004;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb Cortex. 2009;19:524–536. doi: 10.1093/cercor/bhn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. Mapping the structural core of human cerebral cortex. PLOS Bio. 2008;6:e159. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han X, Pham DL, Tosun D, Rettmann ME, Xu C, Prince JL. CRUISE: cortical reconstruction using implicit surface evolution. NeuroImage. 2004;23:997–1012. doi: 10.1016/j.neuroimage.2004.06.043. [DOI] [PubMed] [Google Scholar]
- He Y, Chen Z, Evans AC. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 2007;17:2407–2419. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- Hua K, Oishi K, Zhang J, Wakana S, Yoshioka T, Zhang W, Akhter KD, Li X, Huang H, Jiang H, van Zijl PCM, Mori S. Mapping of functional areas in the human cortex based on connectivity through association tracts. Cereb Cortex. 2008;19:1889–1895. doi: 10.1093/cercor/bhn215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H, Zhang J, Jiang H, Wakana S, Poetscher L, Miller MI, van Zijl PCM, Hillis AE, Wytik R, Mori S. DTI tractography based parcellation of white matter: application to the mid-sagittal morphology of corpus callosum. NeuroImage. 2005;26:195–205. doi: 10.1016/j.neuroimage.2005.01.019. [DOI] [PubMed] [Google Scholar]
- Huang H, Ceritoglu C, Li X, Qiu A, Miller MI, van Zijl PCM, Mori S. Correction of B0 susceptibility induced distortion in diffusion-weighted images using large-deformation diffeomorphic metric mapping. Magn Reson Imaging. 2008;26:1294–1302. doi: 10.1016/j.mri.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H, Prince JL, Carass A, Landman B, van Zijl PC, Mori S. Probabilistic corticocortical connectivity maps of human brain based on DTI tractography and cortical parcellation; Proceedings of ISMRM; Honolulu. 2009. [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusin in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
- Jones DK, Simmons A, Williams SC, Horsfield MA. Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magn Reson Med. 1999;42:37–41. doi: 10.1002/(sici)1522-2594(199907)42:1<37::aid-mrm7>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Mesulam M. Imaging connectivity in the human cerebral cortex: the next frontier? Ann Neurol. 2005;57:5–7. doi: 10.1002/ana.20368. [DOI] [PubMed] [Google Scholar]
- Mesulam M. Representation, inference, and transcendent encoding in neurocognitive networks of the human brain. Ann Neurol. 2008;64:367–378. doi: 10.1002/ana.21534. [DOI] [PubMed] [Google Scholar]
- Miller MI, Trouve A, Younes L. On the metrics and euler-lagrange equations of computational anatomy. Annu Rev Biomed Eng. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
- Mishra VR, Fan X, Huang H. Systematic assessment of effects of noise and resolution on metrics of DTI tractography; Proceedings of ISMRM; Stockholm. 2010. [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Mori S, Kaufmann WE, Davatzikos C, Stieltjes B, Amodei L, Fredericksen K, Pearlson GD, Melhem ER, Solaiyappan M, Raymond GV, Moser HW, van Zijl PCM. Imaging coritcal association tracts in human brain. Magn Reson Med. 2002;47:215–223. doi: 10.1002/mrm.10074. [DOI] [PubMed] [Google Scholar]
- Moseley ME, Cohen Y, Kucharczyk J, Mintorovitch J, Asgari HS, Wendland MF, Tsuruda J, Norman D. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology. 1990;176:439–445. doi: 10.1148/radiology.176.2.2367658. [DOI] [PubMed] [Google Scholar]
- Phillips OR, Nuechterlein KH, Clark KA, Hamilton LS, Asarnow RF, Hageman NS, Toga AW, Narr KL. Fiber tractography reveals disruption of temporal lobe white matter tracts in schizophrenia. Schizophrenia Res. 2009;107:30–38. doi: 10.1016/j.schres.2008.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberger G, Kubicki M, Nestor PG, Connor E, Bushell GB, Markant D, Niznikiewicz M, Westin CF, Kikinis RJ, Saykin A, McCarley RW, Shenton ME. Age-related deficits in fronto-temporal connetions in schizophrenia: a diffusion tensor imaging study. Schizophr Res. 2008;102:181–188. doi: 10.1016/j.schres.2008.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmahmann JD, Pandya DN. Fiber pathways of the brain. Oxford Univ. Press; USA: 2006. [Google Scholar]
- Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Szeszko PR, Ardekani BA, Ashtari M, Kumra S, Robinson DG, Sevy S, Gunduz-Bruce H, Malhotra AK, Kane JM, Bilder RM, Lim KO. White matter abnormalities in first-episode schizophrenia or schizoaffective disorders: a diffusion tensor imaging study. Am J Psychiatry. 2005;162:602–605. doi: 10.1176/appi.ajp.162.3.602. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of complex neural architecture. Neuron. 2003;40:885–895. doi: 10.1016/s0896-6273(03)00758-x. [DOI] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PCM, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, Hua K, Zhang J, Jiang H, Dubey P, Blitz A, van Zijl PCM, Mori S. Reproducibility of quantitative tractography methods applied to cerebral white matter. NeuroImage. 2007;36:630–644. doi: 10.1016/j.neuroimage.2007.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan J, Carass A, Prince JL. Automated reliable labeling of the cortical surface; Proc. Int’l Symp Biomed Imag (ISBI); Paris. 2008; pp. 440–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. General methods and intrasubject, intramodality validation. J Comput Assist Tomogr. 1998;22:139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]