Testing and Validating Machine Learning Classifiers by Metamorphic Testing

Abstract

Machine Learning algorithms have provided core functionality to many application domains - such as bioinformatics, computational linguistics, etc. However, it is difficult to detect faults in such applications because often there is no “test oracle” to verify the correctness of the computed outputs. To help address the software quality, in this paper we present a technique for testing the implementations of machine learning classification algorithms which support such applications. Our approach is based on the technique “metamorphic testing”, which has been shown to be effective to alleviate the oracle problem. Also presented include a case study on a real-world machine learning application framework, and a discussion of how programmers implementing machine learning algorithms can avoid the common pitfalls discovered in our study. We also conduct mutation analysis and cross-validation, which reveal that our method has high effectiveness in killing mutants, and that observing expected cross-validation result alone is not sufficiently effective to detect faults in a supervised classification program. The effectiveness of metamorphic testing is further confirmed by the detection of real faults in a popular open-source classification program.

1. Introduction

Machine Learning algorithms have provided core functionality to many application domains - such as bioinformatics, computational linguistics, etc. As these types of scientific applications become more and more prevalent in society (Mitchell, 1983), ensuring their quality becomes more and more crucial.

Quality assurance of such applications presents a challenge because conventional software testing techniques are not always applicable. In particular, it may be difficult to detect subtle errors, faults, defects or anomalies in many applications in these domains because it may be either impossible or too expensive to verify the correctness of computed outputs, which is referred to as the oracle problem (Weyuker, 1982).

The majority of the research effort in the domain of machine learning focuses on building more accurate models that can better achieve the goal of automated learning from the real world. However, to date very little work has been done on assuring the correctness of the software applications that implement machine learning algorithms. Formal proofs of an algorithm’s optimal quality do not guarantee that an application implements or uses the algorithm correctly, and thus software testing is necessary.

To help address the quality of machine learning programs, this paper presents a technique for testing implementations of the supervised classification algorithms which are used by many machine learning programs. Our technique is based on an approach called “metamorphic testing” (Chen et al., 1998), which uses properties of functions such that it is possible to predict expected changes to the output for particular changes to the input. Although the correct output cannot be known in advance, if the change is not as expected, then a fault must exist.

In our approach, we first enumerate the metamorphic relations that classifiers would be expected to demonstrate, then for a given implementation determine whether each relation is a necessary property for the corresponding classifier algorithm. If it is, then failure to exhibit the relation indicates a fault; if the relation is not a necessary property, then a deviation from the “expected” behavior has been found. In other words, apart from verification, our approach also supports validation.

In addition to presenting our technique, we describe a case study on a real-world machine learning application framework, Weka (Witten and Frank, 2005), which is used as the foundation for many computational science tools such as BioWeka (Gewehr et al., 2007) in bioinformatics. Additionally a mutation analysis is conducted on Weka to investigate the effectiveness of our method. We also discuss how our findings can be of use to other areas.

The rest of this paper is organized as follows. Section 2 provides background information about machine learning and introduces the specific algorithms that are evaluated. Section 3 discusses the metamorphic testing approach and the specific metamorphic relations used for testing machine learning classifiers. Section 4 presents the results of case studies demonstrating that the approach can find faults in real-world machine learning applications. Section 5 discusses empirical studies that use mutation analysis to systematically insert faults into the source code, and measures the effectiveness of metamorphic testing. Section 6 presents related work, and Section 7 concludes.

2. Background

In this section, we present some of the basics of machine learning and the two algorithms we investigated (k-Nearest Neighbors and Naïve Bayes Classifier), as well as the terminology used (Alpaydin, 2004). Readers familiar with machine learning may skip this section.

One complication in our work arose due to conflicting technical nomenclature: “testing”, “regression”, “validation”, “model” and other relevant terms have very different meanings to machine learning experts than they do to software engineers. Here we employ the terms “testing”, “regression testing”, and “validation” as appropriate for a software engineering audience, but we adopt the machine learning sense of “model”, as defined below.

2.1. Supervised Machine Learning Fundamentals

In general, input to a supervised machine learning classifier consists of a set of training data that can be represented by two vectors of size k. One vector is for the k training samples S = <s₀, s₁, ..., s_k−1> and the other is for the corresponding class labels C = <c₀, c₁, ..., c_k−1>. Each sample s ∈ S is a vector of size m, which represents m attributes from which to learn. Each label c_i in C is an element of a finite set of class labels, that is, c_i ∈ L = {l₀, l₁, ..., l_n−1}, where n is the number of possible class labels.

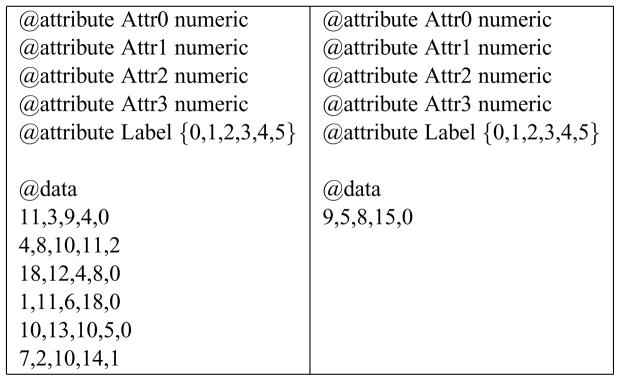
Figure 1 shows a small portion of a training data set that could be used by supervised learning applications. The rows represent samples from which to learn, as comma-separated attribute values; the last number in each row is the label.

Figure 1.

Example of part of a data set used by supervised machine learning classifier algorithms

Supervised machine learning classifiers consist of two phases. The first phase (called the training phase) analyzes the training data; the result of this analysis is a model that attempts to make generalizations about how the attributes relate to the label. In the second phase (called the testing phase), the model is applied to another, previously unseen data set (the testing data) where the labels are unknown. In a classification algorithm, the system attempts to predict the label of each individual example. That is, the testing data input is an unlabeled test case t_s, and the aim is to determine its class label c_t based on the data-label relationship learned from the set of training samples S and the corresponding class labels C, where c_t ∈ L.

2.2. Algorithms Investigated

In this paper, we only study the k-Nearest Neighbors Classifier and the Naïve Bayes Classifier, because of their popularity in the machine learning community. However, it should be noted that the oracle problem description and techniques described below are not specific to any particular algorithm, and as shown in our previous work (Chen et al., 2009; Murphy et al., 2008), our results are applicable to the general case.

In k-Nearest Neighbors (kNN), for a training sample set S, suppose each sample has m attributes, <att₀, att₁, ..., att_m−1>, and there are n classes in S, {l₀, l₁, ..., l_n−1}. The value of the test case t_s is <a₀, a₁, ..., a_m−1>. kNN computes the distance between each training sample and the test case. Generally kNN uses the Euclidean Distance: for a sample s_i ∈ S, suppose the value of each attribute is <sa₀, sa₁, ..., sa_m−1>, and the distance between s_i and t_s is as follows:

$$\mathit{dist}(s_i,t_s)=\sqrt{\sum _j^{m-1}{({sa}_j-a_j)}^2}.$$

After sorting all the distances, kNN selects the k nearest ones which are considered as the k nearest neighbors. Then kNN calculates the proportion of each label in the k nearest neighbors, and the label with the highest proportion is assigned as the label of the test case.

In the Naïve Bayes Classifier (NBC), for a training sample set S, suppose each sample has m attributes, <att₀, att₁, ..., att_m−1>, and there are n classes in S, {l₀, l₁, ..., l_n−1}. The value of the test case t_s is <a₀, a₁, ..., a_m−1>. The label of t_s is called l_ts, and is to be predicted by NBC.

NBC computes the probability of l_ts to be of class l_k, when each attribute value of t_s is <a₀, a₁, ..., a_m−1>. NBC assumes that attributes are conditionally independent with one another given the class label, therefore we have the equation:

$$P(l_{ts}=l_k\mid a_0{a}_1\dots a_{m-1})=\frac{P(l_k){\displaystyle \prod _j}P(a_j\mid l_{ts}=l_k)}{{\sum }_{i}P(l_i){\prod }_{j}P(a_j\mid l_{ts}=l_i)}$$

After computing the probability for each l_i ∈ {l₀, l₁, ..., l_n−1}, NBC assigns the label l_k with the highest probability, as the label of test case t_s.

Generally NBC uses a normal distribution to compute P(a_j | l_ts = l_k). Thus NBC trains the training sample set to establish a distribution function for each element att_j of vector <att₀, att₁, ..., att_m−1> in each l_i ∈{l₀, l₁, ..., l_n−1}, that is, for all samples with label l_i ∈ {l₀, l₁, ..., l_n−1}, it calculates the mean value μ and mean square deviation σ of att_j in all samples with l_i. Then a probability density function is constructed for a normal distribution with μ and σ.

For test case t_s with m attribute values <a₀, a₁, ..., a_m−1>, NBC computes the probability of P(a_j | l_ts = l_k) using a small interval δ to calculate the integral area. With the above formulae NBC can then compute the probability of l_ts belonging to each l_i and choose the label with the highest probability as the classification of t_s.

2.3. Oracle Problem in Supervised Machine Learning Classifiers

As described above, supervised machine learning classifiers “learn” knowledge from the given “training data”, based on which they give prediction for the “test data”. For a particular classifier, whose specification is fixed, the prediction result must be deterministic. However the prediction always involves very complicated logical and computational process, and brings difficulties in figuring out the expected result, for any arbitrary training data and test data, unless we can repeat the whole process with a “perfect” version of the program. Obviously such a “perfect” version never exists in the real-world. This makes the supervised machine learning classifiers fall into the category of programs having the oracle problem.

Usually testers for classifier software just utilize some special test cases which were acquired from previous studies or domain knowledge, and seldomly conduct comprehensive testing, due to the oracle problem. Such an approach is unsatisfactory because these classifiers usually serve as the kernel and fundamental components in many applications. For example, a popular tool called BioWeka (Gewehr et al., 2007) just adopts the algorithms implemented in the famous machine learning algorithm package Weka (Witten and Frank, 2005), for further computation in bioinformatics. Consequently the quality of these machine learning programs is very crucial.

Therefore in this paper, we propose a method to test such programs, based on the technique called metamorphic testing. We do not directly verify the correctness of each individual testing result; instead we check whether they satisfy certain expected properties with respect to multiple but related inputs.

3. Our Approach

Our approach is based on a testing technique called metamorphic testing (Chen et al., 1998). In the rest of this section, we will first briefly summarize its concept, introduce some guidelines in metamorphic relation (MR) selection, and then give the definitions to all the MRs for the two target classifiers.

3.1. Metamorphic Testing

The oracle problem has been one of the biggest difficulties in software testing during the past decades, and several attempts have been conducted to alleviate it. One attempt for testing programs without a test oracle is to use a “pseudo-oracle” (Davis and Weyuker, 1981), in which multiple implementations of an algorithm process the same input and the results are compared; if the results are not the same, then one or both of the implementations contains a fault. This is not always feasible, though, since multiple implementations may not exist, or they may have been created by the same developers, or by groups of developers who are prone to making the same types of mistakes (Knight and Leveson, 1986).

However, even without multiple implementations, often these applications exhibit properties such that if the input were modified in a certain way, it should be possible to predict some characteristics of the new output, given the output of the original input. This approach is known as metamorphic testing. Metamorphic testing can be implemented easily in practice. The first step is to identify a set of properties (“metamorphic relations”, or MRs) that relate multiple inputs and their outputs of the algorithm for the target program. Then, the source test cases and their corresponding follow-up test cases are constructed based on these MRs. We then execute all these test cases using the target program, and check whether the outputs of the source and follow-up test cases satisfy their corresponding MRs.

A simple example to which metamorphic testing could be applied would be one that calculates the standard deviation of a set of numbers. Certain transformations of the set would be expected to produce the same result. For instance, permuting the order of the elements should not affect the calculation; nor would multiplying each value by −1, since the deviation from the mean would still be the same.

Furthermore, there are other transformations that will alter the output, but in a predictable way. For instance, if each value in the set is multiplied by 2, then the standard deviation should be twice as much as that of the original set, since the values on the number line are just “stretched out” and their deviation from the mean becomes twice as great. Thus, given one set of numbers (the source test cases), we can use these metamorphic relations to create three more sets of follow-up test cases (one with the elements permuted, one with each multiplied by −1, and another with each multiplied by 2); moreover, given the outputs of the source test cases, we can predict the outputs of the follow-up test cases.

3.2. Guidelines for Defining Metamorphic Relations

It is obvious that metamorphic testing is simple in concept, easy to implement, automatable, and independent of any particular programming language. In metamorphic testing, the most crucial step is the identification of the MRs. In previous studies which focus on verification, MRs are specifically enumerated for each individual algorithm under test. Actually we can also harness the domain knowledge, as a form of MR repository. This knowledge can either be specific to a particular algorithm, or a general anticipation in that domain. The former can be used to construct MRs which are necessary properties and can then be used for the purpose of verification. And though the latter may not always be the necessary properties for all peer algorithms, can still be used for the purpose of validation.

With respect to selecting a good MR, there are several principles that can be followed, from both white-box and black-box perspectives, such as logical hierarchy, difference in execution traces, user’s profiles, etc (Chen et al., 2004). For example, based on the principle of “difference in execution traces”, we should select MRs with more differences between the execution traces of source test cases and follow-up test cases. Here is an illustration. The Shortest-Path program SP accepts 3 parameters as inputs: a given graph G, a starting node s, and an ending node e. SP(G, s, e) returns the shortest path between s and e and | SP(G, s, e)| denotes the length of SP(G, s, e). Let us consider the two following MRs. MR1 is | SP(G, s, e)| = | SP(G, s, m)| + | SP(G, m, e)|, where m denotes a visited node between s and e returned by SP(G, s, e); and MR2 is | SP(G, s, e)| = | SP(G, e, s)|. Apparently, these two MRs will execute different path-pairs (source path and follow-up path), and a path pair with more difference is preferred as a better MR. Of course in order to decide which MR will result in more execution difference, we can just run the program and collect the real coverage information. But we also can acquire this information simply by analysing the mechanism of the algorithm, without any execution. Supposing the algorithm is a forward-search algorithm, obviously MR2 is likely to be associated with more execution difference than MR1. However if the algorithm is a 2-way search method, MR2 will not necessarily yield more execution difference than MR1.

Apart from the above principles, there are also some other features that may affect the fault detection ability of certain MR. One important feature is about the type of the relation among the relevant outputs for an MR. Intuitively speaking, an equality relation is preferred to a non-equality one. Here by “equality relation”, we mean in a metamorphic group, the source and the follow-up outputs are expressed in an equality expression. This kind of relation is preferred because an equality expression is tighter than a non-equality one. Consequently an MR with equality relation is more easily violated than a non-equality relation. Therefore in this study, we use MRs with such characteristics.

3.3. Metamorphic Relations for Supervised Classifiers

In previous work (Murphy et al., 2008), we broadly classified six types of metamorphic relations (MRs) applicable to many different types of machine learning applications, including both supervised and unsupervised machine learning. In this work, however, our approach focuses on the supervised machine learning classifiers. According to the general anticipated behaviors of these algorithms, we define our MRs formally as follows.

MR-0: Consistence with affine transformation

The result should be the same if we apply the same arbitrary affine transformation function, f(x) = kx + b, (k ≠ 0) to the values of any subset of attributes for each sample in the training data set S and the test case t_s.

MR-1.1: Permutation of class labels

Assume that we have a class-label permutation function Perm() to perform one-to-one mapping between a class label in the set of labels L to another label in L. If the source case result is l_i, applying the permutation function to the set of corresponding class labels C for the follow-up case, the result of the follow-up case should be Perm(l_i).

MR-1.2: Permutation of the attribute

If we permute the m attributes of all the samples and the test data, the output should remain unchanged.

MR-2.1: Addition of uninformative attributes

An uninformative attribute is one that is equally associated with each class label. For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we add an uninformative attribute to each sample in S and respectively a new attribute in t_s. The choice of the actual value to be added here is not important as this attribute is equally associated with the class labels. The output of the follow-up test case should still be l_i.

MR-2.2: Addition of informative attributes

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we add an informative attribute to each sample in S and t_s such that this attribute is strongly associated with class l_i and equally associated with all other classes. The output of the follow-up test case should still be l_i.

MR-3.1: Consistence with re-prediction

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we can append t_s and c_t to the end of S and C respectively. We call the new training dataset S’ and C’. We take S’, C’ and t_s as the input of the follow-up case, and the output should still be l_i.

MR-3.2: Additional training sample

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we duplicate all samples in S with label l_i, as well as their associated labels in C. The output of the follow-up test case should still be l_i.

MR-4.1: Addition of classes by duplicating samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we duplicate all samples in S and C that do not have label l_i and concatenate an arbitrary symbol “*” to the class labels of the duplicated samples. That is, if the original training sample set S is associated with class labels <A, B, C> and l_i is A, the set of classes in S in the follow-up input could be <A, B, C, B*, C*>. The output of the follow-up test case should still be l_i. Another derivative of this metamorphic relation is that duplicating all samples from any number of classes which do not have label l_i should not change the result of the output of the follow- up test case.

MR-4.2: Addition of classes by re-labeling samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we re-label some of the samples in S with labels other than l_i, through concatenating an arbitrary symbol “*” to their associated class labels in C. That is, if the original training set S is associated with class labels <A, B, B, B, C, C, C> and c₀ is A, the set of classes in S in the follow-up input may become <A, B, B, B*, C, C*, C*>. The output of the follow-up test case should still be l_i.

MR-5.1: Removal of classes

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we remove one entire class of samples in S of which the label is not l_i. That is, if the original training sample set S is associated with class labels <A, A, B, B, C, C> and l_i is A, the set of classes in S in the follow-up input may become <A, A, B, B>. The output of the follow-up test case should still be l_i.

MR-5.2: Removal of samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we remove part of some of the samples in S and C of which the label is not l_i. That is, if the original training set S is associated with class labels <A, A, B, B, C, C> and l_i is A, the set of classes in S in the follow-up input may become <A, A, B, C>. The output of the follow-up test case should still be l_i.

3.4. Analysis of Relations for Classifiers

It can be seen from the above discussion that, for machine learning classifiers, the MRs can be derived either from the specification of a particular algorithm under test, or from the users’ general expectation for the classifiers. Obviously the former group of properties, which are necessary properties to the relevant algorithm, can be used for the purpose of verification, that is, if the implementation does not exhibit this property, then there is a fault. While the latter ones, which may not be necessary properties for all the classifiers, can still be adopted to support validation, that is, whether the selected algorithm can satisfy the user’s expected/potential requirements.

The discussion on the necessary properties for kNN and NBC will be detailed in Appendix A. Here we are going to demonstrate some of the relations that are not necessary properties for the algorithms being implemented, which can still be used for the purpose of validation.

For kNN, five of the metamorphic relations given above are not its necessary properties but can be used for validation purposes instead. MR-1.1 (Permutation of class labels) is not a necessary property because of tiebreaking between two labels for prediction that are equally likely: permuting their order may change which one is chosen by the tiebreaker.

Additionally, MR-5.1 (Removal of classes) is not a necessary property. Suppose the predicted label of the test case is l_i. MR-5.1 removes a whole class of samples without label l_i. Consequently this will remove the same samples in the set of k nearest neighbors, and thus some other samples will be included in the set of k nearest neighbors. These samples may have any labels except the removed one, and so the likelihood of any label (except the removed one) may increase. Therefore there are two situations: (1) If in the k nearest neighbors of the source case, the proportion of l_i is not only the highest, but also higher than 50%, then in the follow-up prediction, no matter how the k nearest neighbors change, the prediction will remain the same, because no matter which labels increase, the pro-portion of l_i will still be higher than 50% as well. Thus the prediction remains l_i. Now consider situation (2), in which in the k nearest neighbors of the source case, the proportion of l_i is the highest but lower or equal to 50%. Since the number of each survived label may increase, and the original proportion of l_i is lower or equal to 50%, it is possible that the proportion of some other label increases and becomes higher than l_i: thus, the prediction changes.

Similarly MR-2.2 (Addition of informative attributes), MR-4.1 (Addition of classes by duplicating samples), and MR-5.2 (Removal of samples) may not hold if the predicted label has a likelihood of less than 50%.

For the NBC, three of the metamorphic relations are not considered necessary properties, but can still be used for validation. They are MR-3.1 (Consistence with re-prediction), MR-4.2 (Addition of classes by re-labeling samples), and MR-5.2 (Removal of samples). We could neither prove nor disprove MR-3.1 as a necessary property of NBC. Hence MR-3.1 is not treated as a necessary property of NBC in this study. While for the other two MRs, since both of them actually introduce noise to the data set, which could affect the result, we can prove that they are not necessary properties.

4. Case Studies

To demonstrate the effectiveness of metamorphic verification and validation in machine learning classifiers, we applied the approach to Weka 3.5.7 (Witten and Frank, 2005). Weka is a popular open-source machine learning package that implements many common algorithms for data preprocessing, classification, clustering, association rule mining, attribute selection and visualization. Due to its large range of functionality, it is normally used as a “workbench” for applying various machine learning algorithms. Furthermore, Weka is widely used as the back-end machine learning engine for various applications in computational science, such as BioWeka (Gewehr et al., 2007) for machine learning tasks in bioinformatics.

4.1. Experimental Setup

We adopted a random data model in our experiments as follows. In one source test suite, there are x inputs. Each input_i has two parts: tr_i and t_i, in which tr_i represents the training sample set, and t_i represents the test case. In each training sample set tr_i and test case t_i, there are four attributes: <A₀, A₁, A₂, A₃>, and a class label L with three possible nominal values {L₀, L₁, L₂}. Since the two classifiers under investigation are specific to numeric attributes, in order to conform to this, in our study we assign a numeric value within a valid range [a, b] to each attribute, as well as a nominal value to the class label, for each tr_i and t_i in the suite. All the assignments are random. Besides the number of samples in tr_i is also randomly decided with a maximum of k.

This randomly generated data model does not encapsulate any domain knowledge, that is, we do not use any meaningful, existing training data for testing: even though those data sets are more predictable, they may not be sensitive to detecting faults. Random data may, in fact, be more useful at revealing faults (Duran and Ntafos, 1984).

Based on each MR-j, x follow-up inputs are constructed from the x source inputs. After conducting classification with both the source and the follow-up inputs, we compare their results against each MR-j. A revealed violation in an MR implies either faults (verification), or a deviation between the actual behaviors of the current algorithm and the users’ general anticipation of a machine learning classifier (validation), which highlights that the current algorithm may not be appropriate for use.

For each MR-j, we conducted several batches of experiments, and in each batch of experiments we changed the value of x (size of source suite) and k (max number of training samples). Intuitively the more inputs we tried (the higher is x), the more likely we are to encounter violations. Also, we would expect that with fewer samples in the training data set (the less is k), the less predictable the data are.

In our case study, we instantiate the random model with inputs number k from 20 to 300, maximal number of training sample k from 20 to 50, and the valid value range [a, b] for each atrribute of [1, 20].

4.2. Experimental Results and Findings

All the MRs that derived from the commonly expected behaviors of a machine learning classifier in Section 3.3 are adopted in our experimental study, for both kNN and NBC. Table 1 summarizes the experimental results. In this table, for each algorithm, MRs that are its necessary properties are marked as NP, otherwise they are unmarked; VP indicates the percentage of violations found in the corresponding MR. Obviously MRs marked with NP are used for verification, and a non-zero VP indicates the existence of faults. On the other hand, unmarked MRs are used for the purpose of validation, and a non-zero VP implies faults or a deviation between the actual behaviors of this algorithm and the users’ general anticipation on machine learning classifiers. Such deviation indicates that for users with the anticipation described by the corresponding MR, the current algorithm is not an appropriate one for use.

Table 1.

Result of testing KNN and NBC

MR	kNN		NBC
	NP	VP	NP	VP
0	Y	0	Y	7.4%
1.1		15.9%	Y	0.3%
1.2	Y	0	Y	0
2.1	Y	0	Y	0.6%
2.2		4.1%	Y	0
3.1	Y	0		0
3.2	Y	0	Y	0
4.1		25.3%	Y	0
4.2	Y	0		3.9%
5.1		5.9%	Y	5.6%
5.2		2.8%		2.8%

It can be seen from Table 1 that NBC of Weka has violations in some necessary properties, indicating faults. For both kNN and NBC, metamorphic relations that could be used for validation are also violated, perhaps not indicating an actual fault but showing that the implementations could yield unexpected results and deviate from the behavior anticipated by the users.

4.2.1. k-Nearest Neighbors

None of the necessary properties of kNN were violated in our experiment, but we did uncover violations in some of the other properties that are not necessary properties to kNN. Although these violations are not necessarily indicative of faults per se, they do demonstrate a deviation from what would normally be expected. Followings are examples of such violations.

1. Calculating distribution

In the Weka implementation of kNN, a vector distance with the length of numOfSamples is used to record the distance between each sample from the training data and the test case to be classified. After determining the values in distance, Weka sorts it in ascending order, to find the nearest k samples from the training data, and then puts their corresponding labels into another vector k-Neighbor with the length of k.

Weka traverses k-Neighbor, computes the proportion of each label in it and records the proportions into a vector distribution with the length of numOfClasses as follows: Each element of vector distribution is initialized as 1/numOfSamples. It then traverses the array k-Neighbor, and for each label in k-Neighbor, it adds the weight of its distribution value (in our experiments, the weight is 1), that is, for each i, distribution[k-Neighbor[i].label] + 1. Finally, Weka normalizes the whole distribution vector.

Figure 2 shows two data sets, with the training data on the left, and the test case to be classified on the right. For the test case to be classified, the (unsorted) values in the vector distance are <11.40, 7.35, 12.77, 10.63, 13, 4.24>, and the values in k-Neighbor are <1, 2, 0>, assuming k = 3. The vector distribution is initialized as <1/6, 1/6, 1/6, 1/6, 1/6, 1/6>. After traversing the vector k-Neighbor, we get distribution = <1+1/6, 1+1/6, 1+1/6, 1/6, 1/6, 1/6> = <1.167, 1.167, 1.167, 0.167, 0.167, 0.167>. After the normalization, distribution = <0.292, 0.292, 0.292, 0.042, 0.042, 0.042>.

Figure 2.

Sample data sets

The issue here, as revealed by MR-5.1 (Removal of classes), is that labels which never existed in the training data samples have non-zero probability of being chosen in the vector distribution. By common sense, one might expect that if a label did not occur in the training data, there would be no reason to classify a test case with that label. However, by initializing the distribution vector so that all labels are equally likely, even non-existent ones become possible. Although this is not necessarily an incorrect implementation, it does deviate from what one would normally expect.

2. Choosing labels with equal likelihood

Another issue is about the choice of the label when there are multiple labels with the same probability. Our testing indicated that in some cases, this method may lead to the violation in some MR transformations, particularly MR-1.1 (Permutation of class labels), MR-2.2 (Addition of informative attributes), and MR-4.1 (Addition of classes by duplicating samples).

Consider the same example in Figure 2. To perform the classification, Weka chooses the first highest value in distribution, and assigns its label to the test case. For this example, l₀, l₁, and l₂ all have the same highest proportion in distribution, so based on the order of the labels, the final prediction is l₀, since it is first.

However, if the labels are permuted (as in MR-1.1, for instance), then another label with equal probability might be chosen if it happens to be first. This is not a fault per se (after all, if there are three equally-likely classifications and the function needs to return only one, it must choose somehow) but rather it represents a deviation from expected behavior (that is, the order of the data set shall not affect the computed outputs), which could have an effect on an application expecting such a scenario.

4.2.2. Naïve Bayes Classifier

Our investigation into NBC revealed violations in both the necessary MRs indicating faults, and the MRs that are not necessary properties to NBC, indicating faults or unexpected behaviors.

1. Loss of precision

Precision can be lost due to the treatment of continuous values. In a pure mathematical model, a normal distribution is used for continuous values. Obviously it is impossible to realize true continuity in a digital computer. To implement the integral function, for instance, it is necessary to define a small interval δ to calculate the area. In Weka, a variable called precision is used as the interval. The precision for att_j is defined as the average interval of all the values. For example, suppose there are 5 samples in the training sample set, and the values of att_j in the five samples are 2, 7, 7, 5, and 10 respectively. After sorting the values we have vector <2, 5, 7, 7, 10>. Thus precision = [(5−2) + (7−5) + (10−7)] / (1 + 1 + 1) = 2.67.

However, Weka rounds all the values x in both the training samples and test case with precision pr by using round(x / pr) * pr. These rounded values are used for the computation of the mean value μ, mean square deviation σ, and the probability P(l_ts = l_k | a₀a₁...a_m−1). This manipulation means that Weka treats all the values within ((2k−1)* pr/2, (2k+1)* pr/2] as k*pr, in which k is any integer.

This may lead to the loss of precision and hence may result in the violation of some MR transformations, particularly MR-0 (Consistence with affine transformation) and 5.1 (Removal of classes). As a reminder, both of these are necessary properties.

There are also related problems of calculating integrals in Weka. A particular calculation determines the integral of a certain function from negative infinity to t = x - μ / σ. When t > 0, a replacement is made so that the calculation becomes 1 minus the integral from t to positive infinity. However, this may raise an issue because in Weka, all these values are of the Java datatype “double”, which only has a maximum of 16 bits for the decimal fraction. It is very common that the value of the integral is very small, thus after the subtraction by 1.0, there may be a loss of precision. For example, if the integral I is evaluated to 0.0000000000000001, then 1.0 - I =0.9999999999999999. Since there are 16 bits of the number 9, in Java the double value is treated as 1.0. This also contributed to the violation of MR-0 (Consistence with affine transformation).

2. Calculating proportions of each label

In NBC, to compute the value of P(l_ts = l_k | a₀a₁...a_m−1), we need to calculate P(l_k). Generally when the samples are equally weighted, P(l_k) = (number of samples with l_k) / (number of all the samples). However, Weka uses Laplace Accuracy by default, that is, P(l_k) = (number of samples with l_k + 1) / (number of all the samples + number of classes).

For example, consider a training set with six classes and eight samples, with labels as follows: <l₀, l₀, l₁, l₁, l₁, l₂, l₃, l₃>. Following the probability theory, the vector of proportions for l₀ to l₅ is <2/8, 3/8, 1/8, 2/8, 0/8, 0/8> = <0.25, 0.375, 0.125, 0.25, 0, 0>. However in Weka, using Laplace Accuracy, the vector of proportions for l₀ to l₅ becomes <(2+1)/(8+6), (3+1)/(8+6), (1+1)/(8+6), (2+1)/(8+6), (0+1)/(8+6), (0+1)/(8+6)> = <0.214, 0.286, 0.143, 0.214, 0.071, 0.071>. This difference caused a violation of MR-2.1 (Addition of uninformative attributes), which was also considered a necessary property.

3. Choosing labels

Finally, there are problems in the principle of “choosing the first label with the highest possibility”, as seen above for kNN. Usually the probabilities are different among different labels. However in Weka, since the non-existent labels in the training set have non-zero probability, those non-existent labels may conceivably share the same highest probability. This caused a violation of MR-1.1 (Permutation of class labels), which was considered a necessary property.

4.3. Discussion

4.3.1. Addressing Violations of Properties

Our experiments reported the violation of four MRs in kNN; however, none of these were necessary properties and are mostly related to the situation where the algorithm must return one result but more than one “correct” answers are available. However, in NBC, we uncovered violations of some necessary properties, which indicate faults. Our experience of this study shall be valuable to those who are developing similar applications.

To address the issues in NBC related to the precision of floating point numbers, we suggest using the BigDecimal class in Java rather than the “double” datatype. A BigDecimal represents immutable arbitrary precision decimal numbers, and consists of an arbitrary precision integer unscaled value and a 32-bit integer scale. If zero or positive, the scale is the number of digits to the right of the decimal point. If negative, the unscaled value of the number is multiplied by ten to the power of the negation of the scale. The value of the number represented by the BigDecimal is therefore (unscaledValue * 10^−scale). Thus, it can help to avoid the loss of precision when doing “1.0 − x”.

The use of Laplace Accuracy also caused some violations in the NBC implementation. The reason is as follows. Since Weka treats the label as a nominal attribute, the label will then be processed by Laplace Accuracy as a nominal attribute in the training data set. However, the label should not be treated in such a way. As noted, the side effect of using Laplace Accuracy is that the labels that never show up in the training set also have non-zero probability, and thus they may interfere with the prediction, especially when the size of the training sample set is quite small. In some cases the predicted results are the non-existent labels. We suggest that the label should be treated as a special-case nominal attribute, to which the use of Laplace Accuracy should be disabled.

4.3.2. More General Applications

Our technique has been shown to be effective for the two particular algorithms. More importantly, it is actually feasible for other areas of machine learning.

First, our previous studies have shown the effectiveness of using MT for the purpose of verification in some other types of machine learning areas (ranking, unsupervised learning, etc.) (Murphy et al., 2008, 2009; Murphy and Kaiser, 2010).

Secondly, our technique actually introduces a general process to verify and validate a machine learning algorithm, based on metamorphic testing. In this process, MRs are defined based on the general domain knowledge, and can be adopted in any of the peer algorithms for the same application domain. That is, if an MR can be proved as the necessary property to a specific algorithm, it will serve for the purpose of verification, otherwise, for validation. In particular, this study focuses on supervised classification algorithms, and the experience from this study should be of broad applicability to many other algorithms in this field. The kNN and NBC algorithms described in this paper are representatives of two major algorithmic approaches to supervised classification: instance-based learning algorithms and generative model-based algorithms, respectively. The list of MRs in Section 3.3 is just part of the MR repository in the whole machine learning domain.

More importantly, the approach can be used to validate any application that relies on machine learning techniques. For instance, bioinformatics tools such as Medusa (Middendorf et al., 2005) use classification algorithms. If the underlying machine learning algorithms are not correctly implemented, or do not behave as the user expects, then the overall application likewise will not perform as anticipated. As long as the user of the software knows the expected metamorphic relations, then the approach is simple and powerful to validate the implementation.

One emerging application of these supervised classifiers is in the area of clinical diagnosis using a combination of systems-level biomolecular data (e.g., microarrays or sequencing data) and conventional pathology tests (e.g., blood count, histological images, and clinical symptoms). It has been demonstrated that a machine learning approach of multiple data types can yield more objective and accurate diagnostic and prognostic information than conventional clinical approaches alone. However, for clinical adoption of this approach, these programs that implement machine learning algorithms must be rigorously verified and validated for their correctness and reliability (Ho et al., 2010). A mis-diagnosis due to a software fault can lead to serious, even fatal, consequences. Our case studies clearly demonstrated the importance of rigorous and systematic testing of this type of machine learning algorithm. Thus our proposed testing strategy based on metamorphic testing becomes even more crucial to improve the quality of one of the most critical parts in these kinds of applications.

5. Mutation Analysis

In the case study presented in Section 4, we applied the metamorphic relations in Section 3.3 to the kNN and NBC classifiers implemented in Weka-3.5.7. Through the violations of the necessary properties of NBC, we discovered faults in its implementation. Even though these real-world faults illustrate the effectiveness of our method in verification of programs that do not have test oracles, they cannot empirically show how effective our method is. Thus, in this section, we conduct further experiments with mutation analysis, aiming to investigate the effectiveness of our method in verification.

5.1. Experimental Setup

To gain an understanding of how effective metamorphic testing is at detecting faults in applications without test oracles, we use mutation analysis to systematically insert faults into the applications of interest. Mutation analysis has been shown to be suitable for evaluation of effectiveness, as experiments comparing mutants to real faults have suggested that mutants are a good proxy for comparisons of testing techniques (Andrews et al., 2005).

5.1.1. Mutant Generation

In our mutation analysis, we applied MuJava (Ma et al., 2005) to systematically generate mutants for Weka-3.5.7. MuJava is a powerful and automatic mutation analysis system, which allows user to select related source files to be mutated. Since Weka is large-scale software (the total source code is about 16.4M), and our experiments only focused on certain major functions of kNN and NBC, in order to exclude the equivalent mutants, we only selected files related to these two classifiers according to their hierarchy structure. Table 2 lists all the selected files in our mutation analysis for both kNN and NBC.

Table 2.

Selected files for mutation analysis.

kNN	NBC
weka.classifiers.lazy.IBk.java	weka.classifiers.bayes.NaiveBayes.java
weka.core.Attribute.java	weka.core.Attribute.java
weka.core.Instance.java	weka.core.Instance.java
weka.core.Instances.java	weka.core.Utils.java
weka.core.Utils.java	weka.core.Statistics
weka.core.neighboursearch.LinearNNSearch.java	weka.estimators.DiscreteEstimator.java
weka.core.neighboursearch.NearestNeighbourSearch.java	weka.estimators.Estimator.java
weka.core.NormalizableDistance.java	weka.estimators.KernelEstimator.java
weka.core.EuclideanDistance.java	weka.estimators.NormalEstimator.java

With respect to the types of faults, MuJava provides two levels of mutation operators: method-level operators (also known as “traditional operators” that were originally designed for structured programs (Offutt et al., 1996)) and “class-level operators” (particularly designed for object-oriented programs) (Ma et al., 2005).

Usually MuJava can generate many more syntactically correct mutants using method-level operators than using the class-level ones. Hence in our experiments, we targeted these traditional method-level mutants, which may induce both intra-method and inter-method failures. For both kNN and NBC, we randomly selected 30 valid mutants generated by MuJava, and the operators covered by these mutants are listed in Table 3.

Table 3.

Mutation operators covered by selected mutants.

Operator	Description
AOR	Arithmetic Operator Replacement
ROR	Relational Operator Replacement
COR	Conditional Operator Replacement
SOR	Shift Operator Replacement
LOR	Logical Operator Replacement
ASR	Short-Cut Assignment Operator Replacement

5.1.2. Selection and Modification of MRs

Since the mutation analysis serves for the purpose of verification, in this experiment, we need to adopt those MRs which are necessary properties for the classifier. For each necessary MR, if we find violations in certain mutants, we can declare that this mutant is killed by the MR, that is, the fault has been detected. The goal of the experiment is to calculate what percentage of the mutants are killed by the MRs, as a measure of the fault-detection effectiveness.

For kNN, apart from the necessary MRs, we also modify other MRs to make them become necessary properties, to fit for our mutation analysis. As for NBC, we only select 8 MRs from Section 3.3 that have been proved as necessary properties, and define a new MR (MR-NBC) which is a necessary property of NBC, according to its specification. The definition of MR-NBC, as well as the detailed discussion of the necessity for all MRs are presented in the Appendix. Table 4 and Table 5 summarize the MRs used for kNN and NBC respectively in the mutation analysis for verification.

Table 4.

Metamorphic relations for kNN used in mutation analysis.

k = 1	k = 3
MR-1.1 Permutation of class labels	MR-0 Consistence with affine transformation
MR-2.2 Addition of informative attributes	MR-1.2 Permutation of the attribute
MR-4.1 Addition of classes by duplicating samples	MR-2.1 Addition of uninformative attributes
MR-5.1 Removal of classes	MR-3.1 Consistence with re-prediction
MR-5.2 Removal of samples	MR-3.2 Additional training sample
	MR-4.2 Addition of classes by re-labeling samples

Table 5.

Metamorphic relations for NBC used in mutation analysis.

MR-0 Consistence with affine transformation

MR-1.1 Permutation of class labels

MR-1.2 Permutation of the attribute

MR-2.1 Addition of uninformative attributes

MR-2.2 Addition of informative attributes

MR-3.2 Additional training sample

MR-4.1 Addition of classes by duplicating samples

MR-5.1 Removal of classes

MR-NBC Consistence with value permutation

5.2. Empirical Results and Analysis

5.2.1. Metamorphic Testing Results

In the mutation analysis, we adopted 300 randomly generated inputs as source test inputs. Each test input consists of one training dataset and one test case, following the same model used in Section 4.

In the previous experimental study, we found some real faults in the source code of the NBC classifier of Weka-3.5.7. Thus in the mutation analysis, in order to exclude the violations that are due to these real faults, we eliminated the test inputs which violated MRs in the original version of Weka-3.5.7. And we check the violated test pairs in mutants to make sure that they are really due to the modification, instead of the real faults.

We applied MuJava to all the selected files in Table 2, and randomly selected 30 valid mutants for both kNN and NBC. Obviously our method targets the non-crash failures. Hence after excluding the mutants that cause runtime exceptions, we obtained 24 mutants for kNN and 26 mutants for NBC.

Table 6 lists the results for all mutants that were killed by at least one MR in Table 4 for kNN. Each cell except the last line of Table 6 records the percentage of violated input pairs among all valid input pairs, for the relevant metamorphic relation and mutant version. The last line records the total number of killed mutants of the corresponding MR.

Table 6.

Effectiveness of metamorphic relations for kNN

	Metamorphic Relation
Mutant	0	1.1	1.2	2.1	2.2	3.1	3.2	4.1	4.2	5.1	5.2
original	0	0	0	0	0	0	0	0	0	0	0
v1	0	1.7	7.7	27.0	5.7	0	0	0	0	6.7	3.7
v2	0	0	0	0	0	0	0	0	0	4.7	3.0
v3	0	0	0	0	42.7	0	0	0	0	4.7	3.7
v5	0	2.3	0	0	0	0	0	2.3	0	6.7	3.0
v6	0	11.3	0	26.3	37.0	0	0	0	0	2.0	0
v7	0	9.7	0	0	1.7	0	0	0	0	4.0	1.7
v9	0	9.0	0	0	3.3	8.3	0	41.7	0	5.0	2.0
v10	0	1.3	22.7	34.3	94.7	0	0	0	0	4.3	5.3
v12	0	10.3	0	0	1.7	0	0	0	0	4.0	1.7
v13	0	0.3	22.3	0	0	0	0	0	0	3.0	3.0
v15	0	0	16.3	0	13.7	0	0	0	0	3.3	2.3
v16	0	10.0	0	26.3	37.0	0	0	0	0	2.0	0
v17	0	13.7	0	0	0	0	0	0	0	0	0
v18	0	11.0	0	0	0	0	0	0	0	0	0
v19	0	9.3	0	26.3	37.0	0	0	0	0	2.0	0
v20	0	0	0	0	43.7	0	0	0	0	2.3	1.7
v21	0	1	0	42.7	24.0	0.7	0	0	0	3.7	4.0
v22	0	68.3	0	0	0	0	0	0	0	0	0
v24	0	62.7	0	0	0	0	0	0	0	0	0
TOTAL	0	15	4	6	12	2	0	2	0	15	16

It can be seen from Table 6 that our method is very effective in killing mutants: 19 out of 24 mutants have been killed by some of the current source inputs and their follow-up inputs generated with these 11 metamorphic relations. After examining the five surviving mutants, we discovered that three out of the five mutants are equivalent mutants with respect to the current source inputs, the parameters in the command line, and all the 11 metamorphic relations. The reason for the equivalent mutants is that Weka is a large-scale program; even though we have selected the related program files for mutation analysis, we do not target all the functionality in these files. The parameters we used in the command line and the metamorphic relations that we have enumerated are only related to certain properties of the target algorithm. Thus in the three mutants, the modified statements are not executed using the current source inputs, the parameters in command line, and all the 11 metamorphic relations. Hence the actual effectiveness is 90.5%(19 out of 21 mutants).

The results in Table 6 also show that different metamorphic relations have different performance in detecting program faults. Among all 11 MRs, MR-1.1 and MR-5.1 had the highest killing rate (15 out of 21, 71.4%), while MR-0, MR-3.2 and MR-4.2 had the lowest killing rate (0 out of 21).

We also inspected the average violation percentage of all MRs. Since we enumerated all the metamorphic relations only by means of the background knowledge of the classifier without referring to the source code of the Weka implementation, and we also generated all mutants and test inputs randomly, our metamorphic relations are hence unbiased to any mutants under investigation. In this way, the average violation percentage for the MRs over all mutants (including all the survived mutants) can be used as an effectiveness measurement of metamorphic testing, that is, how likely a test input pair (source test input and follow-up test input) on average will reveal a violation. From Table 6, we can calculate that for kNN, the average percentage is 4.2% for the 21 non-equivalent mutants.

Similarly, we investigated the effectiveness of each selected metamorphic relation in the mutation analysis for NBC. The results are presented in Table 7, which lists all mutants violating at least one MR in Table 5. Each cell except the last line records the percentage of violated input pairs among all valid input pairs and the last line of the table records the total number of killed mutants of the corresponding MR.

Table 7.

Effectiveness of metamorphic relations for NBC

	Metamorphic Relation
Mutant	0	1.1	1.2	2.1	2.2	3.2	4.1	5.1	NBC
original	0	0	0	0	0	0	0	0	0
v1	6.7	7.7	7.3	6.7	7.3	6.3	7.3	18.9	7.0
v2	0.7	0	0.3	0	0	0	0	0	0
v4	3.3	0	0	0	0	0	0	1.4	0
v5	45.6	30.9	29.7	25.6	28.3	37.7	52.3	68.0	29.3
v6	0.4	1.7	0.3	0	0	0	0.3	0	0
v7	4.8	10.1	1.3	2.4	1.0	1.3	1.3	7.1	1.3
v9	0.4	0	0	0	0	0	0	1.4	0
v11	0.4	1.3	0	0	0	0	0.3	0	0
v12	17.4	5.0	47.0	66.4	2.3	2.7	2.7	16.4	2.7
v15	81.9	80.5	79.0	90.3	87.0	79.0	79.0	89.3	79.0
v16	0.7	10.7	0	0	0	0	0	0.7	0
v17	50.7	53.0	50.3	41.6	50.0	51.3	50.3	63.7	50.3
v18	6.3	6.4	1.7	1.7	1.3	10.3	20.3	15.0	1.0
v19	7.4	8.7	0.7	1.3	0.3	4.0	8.3	11.4	0.7
v20	19.3	0.3	0.3	1.3	1.0	8.3	12.0	11.0	0.3
v21	33.3	0.7	0.3	0.7	0.7	0.3	0.3	13.9	0.3
v22	40.0	4.0	4.0	3.7	2.7	2.7	4.0	19.2	3.3
v24	0	2.4	0	0	0	0	0.3	0	0
v25	49.3	53.4	50.0	42.0	60.7	53.3	50.0	63.0	50.0
v26	0	2.0	0	0	0	0	0.3	0	0
TOTAL	18	17	14	12	12	12	16	15	12

For NBC, our method demonstrates a very good performance: 20 out of 26 mutants have been killed by some of the current source inputs and nine metamorphic relations. And among the six surviving mutants, four are equivalent mutants with respect to the current source inputs, the parameters in the command line, and all the nine metamorphic relations. Hence the actual effectiveness is 20 out of 22 mutants (90.9%).

Different from kNN, where some MRs kill none or a small number of mutants, in NBC, about half of the mutants are killed by any given MR. For example, MR-0, which kills no mutants in kNN, can kill 18 mutants in NBC. And consequently in NBC, the average violation percentage of the nine MRs is much higher than that in kNN. This average percentage is 13.2% among all the 22 non-equivalent mutants.

5.2.2. Cross-validation Analysis

Apart from metamorphic testing, we also conducted cross-validation on these mutants. In the machine learning community, cross-validation is commonly used to assess how well the classification algorithms can model the classification process. Normally its results are affected by three main factors: (1) the predictive power of the underlying classification algorithm, (2) the correctness of the implementation of the algorithm, and (3) the characteristic of the training dataset.

Cross-validation is primarily used to validate the appropriateness of the classification algorithm to the given problem. Hence it is often implicitly assumed that the implementation of the algorithm is correct. Since kNN and NBC are extensively used classification algorithms, their predictive power is expected to be reliable. For example, given a reasonable training dataset, they should perform well in cross-validation. For the training dataset, we have used a range of simulated datasets, with which the predictive results of cross-validation can be estimated beforehand for a reasonable classification algorithm. Therefore in our experiments, for these two classifiers under investigation, a correct implementation should perform consistently with the predicted results. Correspondingly an unexpected performance of cross-validation is an alarm of software faults in their implementation.

We say that a mutant is being “killed” by the cross-validation strategy if the observed error-rate patterns using the simulated datasets deviates significantly from our expected error-rate patterns given the knowledge of data simulation process. And in our experiments, we did find some mutants that “survive” the cross-validation procedure. This observation implies that the systematic software testing is indispensable for these kinds of machine learning applications. Furthermore, due to the frequent occurrence of the oracle problem in this application domain, our proposed method becomes particularly critical.

In our experiments, we conducted k-fold cross-validation, which is a typical cross-validation method. In k-fold cross-validation, the original sample set is randomly partitioned into k subsets (k > 1). Among the k subsets, a single subset is retained as the validation data for testing the classifier model, and the remaining subsets are used as training data. The cross-validation process is then repeated k times. The k results from the k folds then can be averaged or summarized (or otherwise combined) to produce a single estimation (McLachlan et al., 2004). In cross-validation, a classifier is simply evaluated in terms of its respective fraction of misclassified instances, noted as the error-rate. A lower error-rate means a better performance of a classifier.

In the cross-validation analysis, we used some simulation datasets that contain signals that allow samples from each class to be readily distinguishable from one another using any reasonable classification algorithms. These simulated datasets have similar sizes and formats as the randomly generated training sample sets used in the mutation analysis. They were produced and used in another bioinformatics study (Ho et al., 2008) that simulates microarray gene expression data containing realistic noise characteristics. All the samples in the simulated datasets have five attributes. And each dataset contains 100 samples comprising five classes (class 1, 2, ..., 5) of 20 samples each. The expression level of each attribute in each sample is simulated by a normal distribution N(μ_c, σ) where μ_c is the mean expression level characteristics to class c ∈ {1, 2, 3, 4, 5}. The same value is used for variance (σ² = 2) in all simulated datasets. Three different ways of the assignment of μ_c for every class c (referred to as Rule-1, Rule-1.5 and Rule-2) are defined in our experiments, which result in different amounts of signals for class discrimination. In Rule-1, the mean expression value of successive class is different by a factor of one, that is, μ₁ = μ₂ =, …, = μ₅ =1 for every attribute. Then all the samples drawn from all five classes would have the same signal distribution, and therefore contain no discriminative attributes for classification. While in Rule-1.5 and Rule-2, we simulated datasets for the case where the mean feature values from successive classes differ by a factor of 1.5, and 2, respectively.

Actually for any correct implementation of the two classifiers under investigation, the error-rate with these three groups of simulated dataset can be roughly estimated based on their corresponding generation process. For a dataset generated by Rule-1 which contains no signals for class discrimination, we expect to observe a cross-validation accuracy of about 1/5=20%, and thus a cross-validation error-rate of a Rule-1 dataset around 80%, because this is the chance of observing a false positive in a five-class classification problem by a random classifier (i.e., the worst possible classifier). While datasets generated by Rule-1.5 and Rule-2 contain discriminatory signals, therefore a cross-validation analysis usually yields very low error-rate for both of them. Furthermore, the error-rate for the Rule-2 dataset could be even smaller than the Rule-1.5 dataset in most cases, because better class separation can be obtained by Rule-2.

Accordingly, in our experiment, a mutant is said to have been “killed” by cross-validation if the observed error-rate patterns using the simulated datasets deviate significantly from the expected error-rate patterns (error-rate of Rule-1≃80%, and the error-rates of Rule-1.5 and Rule-2 are progressively smaller).

In our experiments we conducted 10-fold cross-validation for each simulated dataset, and utilized 300 datasets simulated from each rule. Hence, we have a total of 900 datasets for the cross-validation experiment. Table 8 presents the results for kNN, while Table 9 shows the performance of NBC. In each table, we list both the original version and the mutants that were killed by metamorphic testing. Each cell from column 2 to column 4 records the average error-rate among all 300 datasets for the corresponding rule. The cell in the last column, “Result”, indicates whether the corresponding mutant “is killed” or “survives” in cross-validation, by using K for the killed mutant and S for the survival.

Table 8.

Cross-validation error-rate for kNN.

Mutants	Rule-1	Rule-1.5	Rule-2	Result
original	80.1	4.0	0.1	-
v1	79.8	10.6	1.6	S
v2	80.1	4.0	0.1	S
v3	80.0	80.0	80.0	K
v5	80.1	6.8	0.2	S
v6	80.0	80.0	80.0	K
v7	79.7	5.8	1.2	S
v9	80.0	44.4	40.8	K
v10	80.1	100.0	100.0	K
v12	79.7	5.8	1.2	S
v13	80.1	5.7	0.2	S
v15	80.1	100.0	100.0	K
v16	80.0	80.0	80.0	K
v17	80.0	80.0	80.0	K
v18	80.0	80.0	80.0	K
v19	80.0	80.0	80.0	K
v20	80.2	80.0	80.0	K
v21	79.9	80.0	80.0	K
v22	100.0	100.0	100.0	K
v24	100.0	100.0	100.0	K

Table 9.

Cross-validation error-rate for NBC.

Mutants	Rule-1	Rule-1.5	Rule-2	Result
original	80.1	3.4	0.1	-
v1	80.6	49.7	60.0	K
v2	80.0	3.4	0.1	S
v4	80.2	3.4	0.1	S
v5	80.0	80.0	80.0	K
v6	80.0	3.4	0.1	S
v7	80.0	80.0	80.0	K
v9	80.0	3.3	0.1	S
v11	80.0	3.4	0.1	S
v12	80.2	18.2	3.5	S
v15	100.0	100.0	100.0	K
v16	80.0	80.0	80.0	K
v17	80.2	81.1	91.2	K
v18	80.0	80.0	80.0	K
v19	80.0	80.0	80.0	K
v20	79.9	27.2	39.9	K
v21	80.0	80.0	5.4	K
v22	80.0	80.0	60.0	K
v24	80.0	3.4	0.1	S
v25	80.2	81.1	91.0	K
v26	80.0	3.4	0.1	S

It can be seen from Tables 8 and 9 that, for both kNN and NBC, there are some survivals in the cross-validation.

Obviously, in the original program version, the cross-validation performs within our expectation, that is, the error-rate in Rule-1 is around 80%, and in Rule-1.5 and Rule-2, the error-rates become progressively smaller. However there are also some mutants whose error-rates of the three rules have the same expected trend as the original program version, which are considered as survivals in our experiments. It can be seen that for kNN, there are 6 out of 19 (31.6%) of the mutants survive the cross-validation. And for NBC, using cross-validation alone will miss 8 out of 20 (40.0%) of the mutants.

These experimental data reveal that there do exist some mutants that can achieve expected performances in cross-validation, despite the fact that these mutants are faulty implementations of the algorithms. Given the lack of systematic testing strategies for machine learning algorithms, cross-validation has been commonly adopted as an informal method for evaluating a supervised classifier algorithm for decades, even thought it was never designed for the purpose of either verification or validation. Nevertheless, most practitioners in the machine learning field have relied on the cross-validation method to check the correctness of the implementation of the algorithm. In other words, our observations imply that an additional way to verify the correctness of the implementation is necessary. Because of the oracle problem, metamorphic testing becomes appealing and suitable in testing these supervised machine learning programs. In fact, metamorphic testing is very powerful in detecting faults even in mutants that cannot be readily identified by cross-validation. For example, mutant v1 in the kNN experiment has an ASR mutant in the EuclideanDistance.java file, line 182. The modification is:

result = diff * diff; //correct: result += diff * diff;

According to the cross-validation error-rates in our experiment (Table 8), this mutant would likely not be detected since the error-rate patterns from the simulated data falls within the expected range. On the other hand, metamorphic testing is able to kill this mutant. Table 6 shows that MR-1.1, MR-1.2, MR-2.1, MR-2.2, MR-5.1 and MR-5.2 all reveal this mutant.

As a result, our experiment shows that the cross-validation technique is not sufficiently effective to detect faults in a supervised classification program. It is strongly recommended to adopt MT as the supplement to this technique in order to provide more confidence of the software quality.

6. Related Work

Machine learning has aroused the interest of more and more people in software engineering. Currently there has been much work that applies machine learning techniques to software engineering, in particular, to software testing (e.g., (Briand, 2008; Cheatham et al., 1995; Zhang and Tsai, 2003)). However we are not aware of any work in the reverse sense: applying software testing techniques to machine learning applications, particularly to those that have no reliable test oracle.

Despite the fact that the machine learning programs have been widely utilized, there is no systematic testing method to guarantee their quality. Apart from the testing objective (Weka) in this study, Orange (Demsar et al., 2004) is another famous framework that aids machine learning developers. But the testing functionality provided by these two frameworks is only focused on comparing the quality of the results, but not evaluating the correctness of the implementations. Though there are repositories of reusable data sets being collected (e.g., the UCI Machine Learning Repository (Newman et al., 1998)) for the purpose of comparing result quality, such as the accuracy of the prediction, they are not for testing. Furthermore there are also many other applications which contain machine learning components, such as some intrusion detection systems (Mell et al., 2003; Puketza et al., 2002), intrusion tolerant systems (Madan et al., 2004), and other security systems (Balzarotti et al., 2008). However testing in these systems has typically addressed quantitative measurements like overhead, false alarm rates, or ability to detect zero-day attacks, rather than the detection of faults in the implementation as studied in this paper.

On the other hand, applying metamorphic testing to situations in which there is no test oracle was first suggested in (Chen et al., 1998) and is further discussed in (Chen et al., 2002; Gotlieb and Botella, 2003; Guderlei and Mayer, 2007). Currently the studies in MT include two main directions. The first one is to apply MT to verify software in various application domains without a test oracle. Up to now the application domains in which MT has been shown to be effective include service-oriented software (Chan et al., 2007), context-sensitive middleware-based software (Tse et al., 2004), stochastic optimisation algorithms (Yoo, 2010), feature models (Segura et al., 2010), bioinformatics (Chen et al., 2009), etc. However none of these works has explicitly focused on the machine learning area, which should be more complicated due to its nature of a discipline rather than a simple group of peer algorithms. Actually, our previous studies provided several MRs to test some machine learning applications (Murphy et al., 2008). But they only focused on the verification with quite simple MRs. The study in this paper has provided a more comprehensive MR repository. More importantly, we also extend the role of MT beyond the verification, demonstrating that it can also be adopted for the purpose of validation.

The other research direction that has recently been explored is the integration of MT with other testing and analysis techniques. One representative study in this direction is the method called semi-proving, which integrates MT with symbolic execution, for program proving, testing, and debugging (Chen et al., 2010). And another study is the proposal of a novel concept, mice, which is based on the integration of metamorphic relation and program slices, to support various software testing and analysis purposes, such as spectrum-based fault localization (Xie et al., 2010).

7. Conclusion and Future Work

Our contribution in this study is a systematic approach, which enables users and programmers to easily and effectively verify and validate the machine learning components of their software. Neither sound knowledge nor experience of software testing is required in our proposed method. This study has successfully demonstrated the feasibility of MT as a verification and validation method for classification algorithms. The effectiveness of our proposed method is demonstrated by its detection of real faults in a popular open-source software, Weka, and by the technique of mutation analysis. Despite the fact that we use simple MRs without referring to deep domain knowledge; our proposed method has demonstrated a high rate of effectiveness. Furthermore, we also demonstrate that cross-validation alone is not sufficient to verify these classification algorithms.

Since our proposed method is basically a testing method, it inherits one limitation from software testing, that is, if there is no violation revealed by any MR, we can neither conclude the correctness nor the appropriateness of the algorithm under investigation. Actually this is the common limitation for all the testing techniques, thus for any software with critical safety requirements, a supplementary verification method should be adopted, apart from using our method.

Similar to other applications of MT, the most important activity of our method is the identification of MRs, as the effectiveness of our method is critically determined by the choice of MR. Since this paper is focused on illustrating the applicability of our method with sample MRs for representative classifiers, a more comprehensive investigation on the performance of different MRs will be conducted in our future study.

Moreover as discussed in previous sections, our method has actually provided a general process. In view of the simplicity in concept and easiness of automation, our method can be easily adopted in various machine learning application domains, with a continually building MR repository in the future.

Appendix A

In the appendix, we discuss the necessity of MRs for both kNN and NBC.

Appendix A.1. Necessary MRs for k-Nearest Neighbors

In our previous study (Xie et al., 2009), we adopted a total of 11 MRs on kNN, and 6 of them can be proved as necessary properties for kNN with any value of k.

1. MR-0: Consistence with affine transformation

Each value in the training sample set and in the test case is transformed in this way: kx+b (k ≠ 0). Thus, this MR does not change the distance between s_i and t_s. The distance is:

$$\mathit{dist}(s_i\text{'},t_s\text{'})=\sqrt{\sum _j^m{[(k\ast {sa}_j+b)-(k\ast a_j+b)]}^2}=k\sqrt{\sum _j^m{({sa}_j-a_j)}^2}.$$

Therefore MR-0 does not change the order in the k nearest neighbors and will still give the same prediction.

2. MR-1.2: Permutation of the attribute

It can be seen from the formula for calculating the distance that the result is not related to the order of the attributes. Thus, the permutation of the attributes will not affect the prediction result.

3. MR-2.1: Addition of uninformative attributes

In this MR, we add a new attribute att_m to both the samples and the test case and assign them with the same value. Suppose the value of att_m is a. It is obvious that MR-2.1 will not change the distance between any sample s_i and test case t_s. The new distance is:

$$\mathit{dist}(s_i\text{'},t_s\text{'})=\sqrt{\sum _j^{m-1}{({sa}_j-a_j)}^2+{(a-a)}^2}=\sqrt{\sum _j^{m-1}{({sa}_j-a_j)}^2}.$$

Therefore MR-2.1 does not change anything in the k nearest neighbors and will still give the same prediction.

4. MR-3.1: Consistence with re-prediction

Suppose the label of a test case is l_i. We put the test case back into the training sample set, and from the distance formula we can know that the distance between the new sample and the test case is 0. Thus, the number of samples with label l_i in the k nearest neighbors increases by 1, and obviously the proportion of samples with label l_i will increases. Therefore, the follow-up prediction remains the same, l_i, as the source prediction.

5. MR-3.2: Additional training sample

Suppose the label of a test case is l_i. MR-3.2 duplicates the samples with label l_i in the training sample set. These new samples have the same value as the old ones, thus the number of samples with label l_i increases in the k nearest neighbors (maximum is being doubled). Meanwhile, the samples with other labels are excluded from the k nearest neighbors. Thus, the proportion of samples with label l_i increases (maximum is being doubled). Therefore the follow-up prediction remains the same, l_i, as the source prediction.

6. MR-4.2: Addition of classes by re-labelling samples

Suppose the label of a test case is l_i. MR-4.2 renames parts of the samples, which have labels other than l_i. This will not change the value of the distance between each sample and test case. It just changes the label of the distance. Thus it changes the label in the k nearest neighbors. This will not result in any changes in the number and proportion of samples with label l_i. It only may decrease the number and the pro- portion of samples which have labels other than l_i; therefore it will not affect the follow-up prediction.

The remaining MRs can be proved as not necessary properties for any k. Actually, those MRs usually lead to changing the distance between the training samples and the test case, thus the ranking of all distances and the proportion in the k nearest neighbors also change correspondingly. However if we fix k as 1, these MRs all become necessary properties.

The reason is apparent. Since all the samples are sorted ascendingly by the distance to test case (no duplicated samples in our experiments), when k = 1, the kNN classifier just picks up the first sample, and makes its label as the predicted result. Even though the MRs may change the distance between the samples and the test case, and consequently change the ranking, they do not affect the top position of all the sorted distances. Thus if we assign k = 1, these MRs become necessary properties and can be adopted in our mutation analysis.

Appendix A.2. Necessary MRs for Naïve Bayes Classifier

For NBC, we adopted 12 MRs in our previous study, and 9 of them can be proved as necessary properties.

1. MR-0: Consistence with affine transformation

To implement the calculation of an integral in a digital computer, it is necessary to define a small interval δ to calculate the area. In Weka, they use a variable called Precision as the interval. The Precision for att_j is defined as the average interval of all the values. For example, suppose there are five samples in the training sample set, and the values of att_j in the five samples are 2, 7, 7, 5, and 10. After sorting the values we have 2, 5, 7, 7, 10. Thus, Precision = [(5–2) + (7–5) + (10-7)]/(1+1+1) = 2.67. If all the values are the same, Precision (abbreviated pr) equals its default value, 0.01. In the computation, Weka rounds all the values x in both the training samples and the test case with pr as rint(x/pr) * pr, in which rint is the function to round to the nearest integer. This manipulation means that Weka treats all the values within ((2k-1)* pr/2, (2k+1)* pr/2] as k*pr, in which k is any integer. This manipulation may lead to a loss of precision; however, it provides a mechanism to disperse the continuous values in the mathematic model, in order to be make the model suitable for computer implementation.

In Weka, the small interval δ is the magnitude of precision. According to formula for calculating area, we have:

$$P(a_j\mid l_{ts}=l_k)=\frac{1}{\sigma \sqrt{2\pi }}{\int }_{a_j-pr/2}^{a_j+pr/2}{e}^{-{(x-\mu )}^2/2{\sigma }^2}dx.$$

In MR-0, each value x in the training set and the test case are transformed in this way: ϕ= k*x+b (k ≠ 0). According to the calculation of pr, pr’ is set to be k*pr + b. According to the formula of mean value μ and mean square deviation σ, we have μ’ = k*μ + b, and σ’ = k*σ. And the formula for probability is as follows:

$$P(k\ast a_j+b\mid l_{ts}=l_k)=\frac{1}{{\sigma }^{\prime }\sqrt{2\pi }}{\int }_{k\ast a_j+b-k\ast pr/2}^{k\ast a_j+b+k\ast pr/2}{e}^{-{(\varphi -\mu \text{'})}^2/2\sigma {\text{'}}^2}d\varphi$$

by substituting σ′ with k * σ, and σ′ with k * μ + b, we have:

$$P(k\ast a_j+b\mid l_{ts}=l_k)=\frac{1}{k\sigma \sqrt{2\pi }}{\int }_{k\ast a_j+b-k\ast pr/2}^{k\ast a_j+b+k\ast pr/2}{e}^{-{(\varphi -k\mu -b)}^2/2k{\sigma }^2}d\varphi$$

by substituting ϕ with k * x + b, we have:

$$P(k\ast a_j+b\mid l_{ts}=l_k)=\frac{1}{k\sigma \sqrt{2\pi }}{\int }_{a_j-pr/2}^{a_j+pr/2}{e}^{-{(kx+b-k\mu -b)}^2/2k^2{\sigma }^2}d(kx+b)\Rightarrow P(k\ast a_j+b\mid l_{ts}=l_k)=\frac{1}{\sigma \sqrt{2\pi }}{\int }_{a_j-pr/2}^{a_j+pr/2}{e}^{-{(x-\mu )}^2/2{\sigma }^2}dx=P(a_j\mid l_{ts}=l_k).$$

It can be seen from the above formula that after the transformation, the probability will not change, thus the prediction result will not change either.

2. MR-1.1: Permutation of class labels

This MR reflects a key property of mathematical function such as NBC that the output of the classifier is deterministic, and is not affected by random permutation.

3. MR-1.2: Permutation of the attribute

It is known that in NBC, we assume all the attributes are independent, thus we have the following formula:

$$P(l_{ts}=l_k\mid a_0{a}_1\dots a_{m-1})=\frac{P(l_k){\displaystyle \prod _j}P(a_j\mid l_{ts}=l_k)}{{\sum }_{i}P(l_i){\prod }_{j}P(a_j\mid l_{ts}=l_i)}$$

Therefore, changing the attribute order will not affect the prediction result.

Actually, it can be concluded that all classifiers should have a consistent result in this MR, assuming the attributes are independent to each other.

4. MR-2.1: Addition of uninformative attributes

In this MR, we add a new attribute att_m with identical value to both the samples and the test case. Suppose the value of att_m is a. For each l_k ∈ {l₀, l₁, ..., l_n-1}, the probability P(l_ts = l_k | a₀a₁...a_m-1) can be re-written in the following way:

$$P(l_{ts}=l_k\mid a_0{a}_1\dots a_m)=\frac{P(l_{ts}=l_k){\displaystyle \prod _j}P(a_j\mid l_{ts}=l_k)\ast P({\mathit{att}}_m=a\mid l_{ts}=l_k)}{{\sum }_{i}P(l_{ts}=l_i){\prod }_{j}P(a_j\mid l_{ts}=l_i)\ast P({\mathit{att}}_m=a_m\mid l_{ts}=l_i)}$$

Since the new attribute att_m has the same value a in all the samples, the mean value μ = a and the mean square deviation σ = 0. Thus the P(att_m = a | l_ts = l_k) part is equal to 1 for all the l_k ∈{l₀, l₁, ..., l_n-1}.

In Weka, since it is infeasible for computer to deal with the normal distribution with σ = 0, they give σ a default minimum of pr/2*3. Thus for each l_k ∈{l₀, l₁, ..., l_n-1}, the numerator in the formula above will be changed by multiplying a constant value P(att_m = a | l_ts = l_k), which is a little less than 1.

It follows that the probability for each l_k ∈{l₀, l₁, ..., l_n-1} changes in the same way. Thus the order of the probabilities will not change; consequently the prediction in the follow-up cases will remain the same as the one in the source cases.

5. MR-2.2: Addition of informative attributes

In this MR, we add a new attribute att_m to both the samples and the test case and assign the samples having the same label with the same value; meanwhile, we assign the new attribute’s value in the test case as the one of its predicted label. For example, suppose there are three classes in the training samples, {l₀, l₁, l₂}, and the predicted label of the test case is l₀. In the MR-2.2 transformation, we add a new attribute and make it different among different classes, that is, for samples with l₀, the att_m = a; for samples with l₁, the att_m = b; for samples with l₂, the att_m = c; and for the test case, the att_m = a.

Since the denominator in the formula for each l_k ∈{l₀, l₁, ..., l_n-1} are the same, only the numerator will affect the result.

For l₀, the mean value of att_m is μ = a; the mean square deviation of att_m is σ= δ (since it is hard to deal with a normal distribution with σ = 0, we assign a very small number to σ).

For l₁, the mean value of att_m is μ= b; the mean square deviation of att_m is σ = δ.

For l₂, the mean value of att_m is μ = c; the mean square deviation of att_m is σ = δ.

Thus the numerator in the formula for l₀ is multiplied by a value of P(att_m = a | l_ts = l₀), which is quite close to 1. Also, the numerator in the formula for l₁ is multiplied by a value of P(att_m = b | l_ts = l₁), which is quite close to 0. Last, the numerator in the formula for l₂ is multiplied by a value of P(att_m = c | l_ts = l₂), which is quite close to 0.

Therefore the former highest possibility almost remains the same, while the other two decrease dramatically. Consequently the follow-up prediction will remain the same as in the source case.

6. MR-3.2: Additional training sample

Suppose the label of test case is l_i. MR-3.2 duplicates the samples with label l_i in the training data set. Those new samples have the same value as the old ones, thus the mean value and the mean square deviation of each attribute in l_i will not change. Meanwhile, the mean square deviation of each attribute in other labels will not change either. The only change is the proportion of each l_k ∈{l₀, l₁, ..., l_n-1}: P(l_ts = l_k); that is, P(l_ts = l_i) increases, while P(l_ts = l_k) for the other labels decreases.

Therefore the probability of t_s belonging to l_i increases, while the probability of t_s being one of the other labels decreases. The prediction is still l_i, as in the source case.

7. MR-4.1: Addition of classes by duplicating samples

Suppose we have labels {l₀, l₁, ..., l_n-1}, the number of each distinct label l_i ∈{l₀, l₁, ..., l_n-1} in the training sample set is count[i], and its corresponding proportion is proportion[i]. For each l_i ∈{l₀, l₁, ..., l_n-1}, the mean value of att_j is μ_ij; the mean square deviation is σ_ij. Suppose the prediction in source case is l_k. Thus in the MR-4.1 transformation, we duplicate all samples with l_i ∈{l₀, l₁, ..., l_n-1} (i ≠ k) and re- name them as l_i’. After duplication the μ_ij and σ_ij for the original labels remain the same value as the ones in the source case. The only change is the proportion[], which is as follows:

$$\mathit{proportion}\text{'}[i]=\mathit{proportion}[i]\ast \frac{{\displaystyle \sum _0^{m-1}}\mathit{count}[i]}{\mathit{count}[0]+2{\sum }_1^{m-1}\mathit{count}[i]}$$

And for the new added label l_i’, their μ, σ and proportion[] values are all the same for l_i. Therefore proportion[0] remains the highest value, and the prediction will not change in the follow-up case.

8. MR-5.1: Removal of classes

This MR transformation only changes the proportion of each class, rather than changing the distribution in each survived class. Suppose we have labels {l₀, l₁, ..., l_n-1}, the number of each distinct label l_i ∈{l₀, l₁, ..., l_n-1} in the training sample set is count[i], and its corresponding proportion is proportion[i]. For each l_i ∈{l₀, l₁, ..., l_n-1}, the mean value of att_j is μ_ij; the mean square deviation is σ_ij. Suppose the prediction in the source case is l₀, and l₂ is the label being removed. Thus, after transformation, the μ and σ for each survived label remain the same as in the source case. The only change is the count[i] and the proportion[i], which changes as follows: