Multilevel Confirmatory Factor Analysis of a Scale Measuring Interagency Collaboration of Children's Mental Health Agencies

Abstract

Multilevel confirmatory factor analysis was used to evaluate the factor structure underlying the 12-item, three-factor Interagency Collaboration Activities Scale (IACS) at the informant level and at the agency level. Results from 378 professionals (104 administrators, 201 service providers, and 73 case managers) from 32 children's mental health service agencies supported a correlated three-factor model at each level and indicated that the item loadings were not significantly (p < .05) different across levels. Reliability estimates of the three factors (Financial and Physical Resource Activities, Program Development and Evaluation Activities, and Collaborative Policy Activities) at the agency level were .81, .60, and .72, respectively, while these estimates were .79, .82, and .85 at the individual level. These multilevel results provide support for the construct validity of the scores from the IACS. When the IACS was examined in relation to level-1 and level-2 covariates, results showed that participants' characteristics (i.e., age, job role, gender, educational level, and number of months employed) and agency characteristics (i.e., state location and number of employees) were not significantly (p > .05) related to levels of interagency collaboration.

Interagency collaboration has been defined broadly as “mutually beneficial and well-defined relationships entered into by two or more organizations to achieve common goals” (Mattessich, Murray-Close, & Monsey, 2001, p. 4). Additional defining characteristics of interagency collaboration have included: (a) developing and agreeing to a set of common goals and directions, (b) sharing responsibility for obtaining those goals, and (c) working together at all levels of an organization to achieve those goals (Bruner, 1991; Cumblad, Epstein, Keeney, Marty, & Soderlund, 1996).

In the past two decades, the call for collaboration among child-serving organizations has increased as many believe that important problems faced by children that result from being served by multiple agencies (e.g., service fragmentation, gaps, barriers) cannot be resolved effectively by single entities working alone (Bergstrom et al., 1995; Mattessich et al., 2001; Salmon, 2004). For example, recent reforms in children's mental health service delivery, such as the systems of care approach, have emphasized interagency collaboration as an important element in providing comprehensive services to children with serious emotional disturbance (Stroul & Friedman, 1986). Interagency collaboration may provide a way to cope with increasing complexity; meet expanding expectations, needs, and demands of human services; maximize human resources; share facilities and program resources; and improve utilization of funds and personnel (Jones, Thomas, & Rudd, 2004; Lippitt & Van Til, 1981).

While many agree about the value of interagency collaboration, others have identified potential negatives associated with interagency collaboration. These negatives include diffusion of responsibility, reduced service quality, and either negative or weak relationships with positive child outcomes (see Glisson & Himmelgarn, 1998 and Longoria, 2005 for a discussion of the potential downside associated with inter-organizational collaboration in human service organizations). Longoria has cautioned policymakers and administrators about diverting scarce resources towards the promotion of interagency collaboration and away from other organizational activities (e.g., direct services that would benefit clients), until more empirical evidence has accumulated that supports the positive impact of collaboration on service recipients' and organizational outcomes.

Notwithstanding the different viewpoints on the value of interagency collaboration, there is even less agreement about how the construct of interagency collaboration should be conceptualized and measured, and what research approaches are best suited to understanding interagency collaboration. Some researchers have distinguished among collaboration, cooperation, coordination, and networking while others have used these terms interchangeably (Hodges, Nesman, & Hernandez, 1999). Still others have viewed interagency collaboration as an aspect of organizational culture or “the way things are done in an organization” (Glisson, 2007, p. 739) versus organizational climate or “the way people perceive their work environment” (Glisson, 2002, p. 235). As an organizational cultural variable, interagency collaboration is viewed as reflecting the organization's norms and values of how the agency responds to and works with other organizations. These norms and values are manifested in the organization's policies, practices, and activities.

Guided by these various conceptualizations as the boundaries for the interagency collaboration construct, several approaches have been used to measure collaboration including: (a) network analysis, which involves mapping formal and informal links between collaborators (Calloway, Morrissey, & Paulson, 1993; Friedman, Reynolds, Quan, Call, Crusto, & Kaufman, 2007; Wasserman & Faust, 1994); (b) semi-structured interviews of staff by knowledgeable experts who then make global ratings of interagency collaboration (Macro International, 2000); and (c) self-report questionnaires that measure informants' perceptions of their organization's level of collaboration. Although each of these approaches has strengths and limitations and use of one of these approaches does not preclude the use of other approaches, self-report questionnaires have emerged as one of the more widely used methods for measuring interagency collaboration. Questionnaires can be used in large scale studies to collect data across a wide geographic area and can be administered repeatedly to monitor collaborative processes over time.

Currently, there are a number of questionnaires that measure various aspects of collaboration. These include Morrissey et al.'s (1994) questionnaire that measures service coordination (e.g., “Creating opportunities for joint planning”); Harrod's (1986) instrument that measures collaborative activities such as joint needs assessment, planning, program development and or program evaluation; Darlington, Feeney, and Rixon's questionnaire (2005) that measures interagency collaboration practices involving child protection and mental health services (e.g., “Providing information or guidance for managing cases”); Smith and Mogro-Wilson's (2007) questionnaire that measures child welfare and substance use workers' inter-agency collaborative behavior (“I have telephoned a child welfare caseworker about one of my clients in the last month”); Brown, Hawkins, Arthur, Abbott, and Van Horn's (2008) measure of community prevention collaboration (e.g., “Organizations [in community] share money or personnel when addressing prevention issues”); and Greenbaum and Dedrick's (2007) Interagency Collaboration Activities Scale (ICAS) that measures specific organizational collaborative practices and activities (e.g., “shared staff training”) in three areas (i.e., Financial and Physical Resources, Program Development and Evaluation, and Collaborative Policies) focused on delivering services to children with mental health challenges.

For researchers using these questionnaires to measure interagency collaboration, there are two predominant approaches to data collection. One approach has been to administer the questionnaire to a single informant within the organization (usually the director) with the score from the questionnaire being used to represent the organization's level of collaboration. This approach has been guided by the assumption that interagency collaboration is a construct that is a “relatively objective, descriptive, easily observable characteristic of a unit that originates at the [organizational] level” (Kozlowski & Klein, 2000, p. 29). A second approach has been to administer questionnaires to multiple informants within an organization, with data being aggregated to represent the organization's level of collaboration. Chan (1998, p. 235) has described this approach as elemental composition (i.e., “data from a lower level are used to establish the higher level construct”) and has provided a typology of five compositional models (see Chan, 1998). The multiple informant approach assumes that the activities and practices related to interagency collaboration are diverse and are manifested in multiple forms within an agency. This diversity may result in varying perceptions of interagency collaboration, therefore demanding input from multiple constituencies to determine the degree of consensus or disagreement across the group. Using information from multiple informants, rather than a single informant, has been argued to provide a more comprehensive and reliable assessment of organizational variables such as an agency's level of collaboration (Bliese, 2000). Proponents of using multiple informants have argued that individuals within an organization may share common information about formal collaborations involving their organization but they may also have unique information, based on their position in the organization, about instances of informal interagency collaborative activities.

The single versus multiple informant data collection approaches imply different conceptualizations and measurement of interagency collaboration and require different approaches to evaluating the psychometric qualities of the measures of interagency collaboration. When data are collected from a single informant within an organization, psychometric analysis of the data is relatively straightforward. Analysis can proceed using a single-level of analysis approach with analyses such as confirmatory factor analysis (CFA) providing evidence of construct validity (e.g., factorial validity; American Educational Research Association, American Psychological Association, National Council on Measurement in Education, 1999). In contrast, when data are collected from multiple individuals nested within organizations and the data from these individuals are used to measure organizational constructs, psychometric analysis of the data becomes more complex. The added complexity is a result of the fact that the measures of interagency collaboration can vary within organizations as a result of individuals' perceptions of the degree to which their organization is collaborating with other organizations and between organizations as a result of characteristics of the organizations (e.g., state location). Data collection designs that involve using multiple informants within an organization across multiple organizations produce a multilevel or nested structure that needs to be taken into account in the psychometric analysis of the data.

Currently, techniques and statistical software are available to analyze multilevel data (e.g., HLM, MLwin, Mplus), but these techniques have been used mostly to analyze relationships between variables at different levels of analysis rather than the psychometric properties of the data collected at multiple levels. Psychometric analyses of measures of organizational variables such as climate and collaboration that have been collected using two-level nested designs (e.g., individuals nested in organizations) have frequently ignored the multilevel structure of the data (Darlington, Feeney, & Rixon, 2005; Glisson & Hemmelgarn, 1998; Morrissey et al., 1994). These analyses have been conducted at the individual level (i.e., single-level of analysis) using the informant as the unit of analysis. Single-level psychometric analyses such as confirmatory factor analysis with nested data are problematic for a number of reasons. First, these analyses assume that the data are independent. This assumption is not realistic when the data have been collected from individuals clustered in groups such as an organization. Violation of the independence assumption leads to incorrect standard errors and inaccurate statistical inferences. Secondly, and perhaps more importantly for establishing the structure of the measurement model, single level CFA operates on a single covariance matrix that does not take into account the multiple levels and ignores the fact that the factor structure of an organizational measure and its psychometric properties (e.g., reliability) may not be the same at each level of the analysis. By using single-level CFA with multilevel data, there is the potential of committing either an atomistic fallacy (incorrectly assuming that the relationship between variables observed at the individual level holds for group-level versions of the variables) or an ecological fallacy (incorrectly assuming that the relationship between variables aggregated at the group level holds for individual-level versions of the variables, Robinson, 1950).

To date there has been only one psychometric study of a collaboration measure that has been conducted using a multilevel framework. Brown et al. (2008) analyzed a nine-item questionnaire that measured the construct of prevention collaboration, which was defined as “a set of activities that relate to the shared efforts of organizations, agencies, or groups and individuals within a community to prevent youth health and behavior problems” (pp. 116-117). Data for the psychometric analysis of the Prevention Collaboration Scale were collected from 599 community leaders nested in 41 communities and analyzed using multilevel (two-level) confirmatory factor analysis (MCFA). Results of Brown et al.'s study supported a one-factor model at both the individual and the community level with significant variances of the prevention collaboration construct at each level.

Multilevel confirmatory factor analysis (MCFA) has the potential of providing new insights into the construct of interagency collaboration. To realize this potential there is a need for more analyses of existing measures of interagency collaboration that use a multilevel framework for data collection. In view of this need, the present study used MCFA to examine the psychometric properties of the Interagency Collaboration Activities Scale, an instrument designed by Greenbaum and Dedrick (2007) to measure specific collaborative activities in children's mental health agencies. This study extends the previous work of Greenbaum, Lipien, and Dedrick (2004) by examining the factor structure of the interagency collaboration scale at the individual respondent level and at the agency level. Relationships between the domains of interagency collaboration at each level of the analysis (i.e., individual and agency) and reliability of the scores at each level also were examined. Specific research questions included:

1. Is the factor structure (i.e., number of factors and factor loadings) underlying the Interagency Collaboration Activities Scale at the individual informant level similar or different from the structure at the agency level?

2. How much variability in the factors (Financial and Physical Resources, Program Development and Evaluation, Collaborative Policies) underlying the Interagency Collaboration Activities Scale is there between- and within-agencies?

3. What is the reliability of the scores from the Interagency Collaboration Activities Scale at the individual and agency levels?

4. What is the relationship between selected individual level covariates (i.e., mental health professionals' age, job role, gender, educational level, and number of months employed) and the Interagency Collaboration Activities Scale at the individual level?

5. What is the relationship between selected agency level covariates (i.e., state location, number of agency employees) and the Interagency Collaboration Activities Scale at the agency level?

To address these questions, multilevel confirmatory factor analysis (Questions 1 to 3) and multilevel structural equation modeling with covariates (Questions 4 to 5) were used. These analyses were intended to add to the knowledge base of interagency collaboration and illustrate the methodology used to examine the psychometric properties of the Interagency Collaboration Activities Scale.

Method

Instrument

The Interagency Collaboration Activities Scale (ICAS) consists of 12 items covering three domains of collaborative activities. These domains were viewed as aspects of an organization's culture. The first collaborative activity scale, Financial and Physical Resources (4 items), covered interagency sharing of funding, purchasing of services, facility space, and record keeping and management information system data. The second scale, Program Development and Evaluation (4 items), covered interagency collaboration related to developing programs or services, program evaluation, staff training, and informing the public of available services. The third scale, Collaborative Policy Activities (4 items), covered interagency collaboration involving case conferences or case reviews, informal agreements, formal written agreements, and voluntary contractual relationships (see Table 1 for a listing of the items).

Table 1.

Descriptive Statistics for Items from the Interagency Collaborative Activities Scale (ICAS)

Scale	n	M	SD	Skewness	Kurtosis	ICC
Financial and Physical Resources
1. Funding	205	3.09	1.27	−0.12	−0.89	.30
2. Purchasing of services	173	2.79	1.23	0.13	−0.91	.23
3. Facility space	287	2.63	1.33	0.37	−0.90	.21
4. Record keeping and management information systems data	240	2.62	1.34	0.28	−1.15	.08
Program Development and Evaluation
5. Developing programs or services	277	3.55	1.11	−0.25	−0.74	.11
6. Program evaluation	234	3.13	1.16	−0.15	−0.68	.07
7. Staff training	312	3.09	1.11	0.15	−0.56	.11
8. Informing the public of available services	306	3.58	1.12	−0.36	−0.61	.13
Collaborative Policy Activities
9. Case conferences or case reviews	308	3.30	1.15	−0.15	−0.87	.18
10. Informal agreements	246	3.46	1.09	−0.40	−0.27	.12
11. Formal written agreements	242	3.49	1.13	−0.44	−0.38	.14
12. Voluntary contractual relationships	218	3.37	1.33	−0.28	−0.55	.21

Note. ICC = intraclass correlation coefficient. Response scale ranged from 1 (Not at all) to 5 (Very much).

The IACS is what Chan (1998) has described as a referent-shift measure. In the present case, the referent for the questionnaire items was shifted from the individual's level of collaboration to the agency's level of collaboration. So, rather than asking the participant to report his or her own level of collaboration, the participant was asked about the extent his or her agency collaborated with other agencies. The response scale ranged from 1 (Not at all) to 5 (Very much). A Don't Know response category also was included for each collaborative activity as it was not clear that all participants, which included administrators, case managers, and service providers, would have sufficient knowledge of the extent their organization was involved in the specific activities that were surveyed. While the use of a Don't Know option, which was treated as missing data, decreased the number of responses used in the analysis, research (Andrews, 1984) has shown that a Don't Know option decreases the amount of random responding and therefore increases the reliability of the responses. Analyses of the Don't Know responses are provided in the results.

Items for the ICAS were generated from a review of the literature on interagency collaboration and face-to-face interviews with personnel directly involved in collaborative activities. Subsequently, as part of the content validation process, a five-member expert panel reviewed the items for clarity and alignment to the construct of collaboration. Finally, the items were pilot tested with 175 mental health workers from four children's mental health agencies to exam internal consistency and test-retest reliability. Internal consistency reliability estimates were: .84 for Financial and Physical Resource Activities, .83 for Program Development and Evaluation Activities, and .86 for Collaborative Policy Activities. A subsample of 75 from the 175 mental health workers was used to evaluate two week test-retest reliability. Test-retest reliability estimates were .76 for Financial and Physical Resource Activities, .77 for Program Development and Evaluation Activities, and .82 for Collaborative Policy Activities. These pilot study results supported the use of the scales for the present study (see Greenbaum, Lipien, & Dedrick, 2004 for additional details of instrument development). In the present study, Cronbach's alphas for the three scales, based on the sample of 378 participants, were .79, .82, and .85, respectively.

Sample of Agencies and Mental Health Professionals

A two-level, multilevel design was used to collect data to evaluate the psychometric properties of the Interagency Collaboration Activities Scale. Level-2 consisted of the target group of agencies defined as those funded by the public mental health service sector that served children 18 years of age or younger. Level-1 consisted of multiple employees (informants) within an agency.

Agencies

To obtain the sample of agencies, directors of mental health agencies were recruited at a national conference on children's mental health services to participate in the study. In an attempt to broaden the sample, personal contacts also were used to recruit directors from multiple states. The results of the recruitment efforts were 32 child-serving mental health agencies that agreed to participate, with 23 from California, six from Michigan, and three from Ohio. The 23 agencies from California were located in five counties. These counties ranged in population size from 361,907 to 9.1 million. The percentage of the population living in poverty in these counties ranged from 7% to 23%. The percentage of the county population under 18 years of age ranged from 23% to 30%. In Michigan, the six agencies came from four counties that ranged in population size from 61,234 to 1.2 million. In these counties, the percentage of the population living in poverty ranged from 6% to 11% and the percentage of the county population under 18 years of age ranged from 21% to 28%. The three agencies from Ohio were located in three counties. These counties ranged in population size from 23,994 to 61,276. Here, the percentage of the counties' population living in poverty ranged from 18% to 21% and the percentage of the county population under 18 years of age ranged from 20% to 27% (Health Resources and Services Administration, 2000). We aimed for diversity in the sample of agencies to insure variability on the construct of interagency collaboration. This variability was necessary to assess the psychometric properties of the Interagency Collaboration Activities Scale.

Mental Health Professionals

Once agencies were selected, multiple mental health professionals within each agency were recruited to participate in the study. To be included, mental health professionals needed to have a job title of administrator, case manager, or service provider and have been employed at their current agency for at least one month. Participants were recruited with the assistance of a site coordinator, an agency employee who received instructions for delivering, administering, collecting, and returning the surveys. The site coordinator was instructed to distribute the questionnaire to individuals meeting study eligibility requirements. For 29 agencies, two research associates from the project visited the agencies to facilitate data collection. Research associates reviewed the administration procedures including informed consent and addressed any questions from the agency contact person. For the three agencies in Ohio, video conferencing was used in lieu of a site visit at the request of agency personnel. Given that it was unclear how many agency personnel who met study eligibility requirements at all 32 agencies received questionnaires, a response rate could not be calculated.

Three hundred and seventy eight mental health professionals from 32 agencies agreed to participate. Participants consisted of 104 administrators, 201 service providers, and 73 case managers. Informants were primarily female (74%) and White (60%; African American, 5%; Hispanic, 27%, Asian American, 4%; Native American, 1%, Mixed, 1%; Other, 3%), with a mean age of 41.2 years (SD = 11.1). The sample consisted of 4% with less than a bachelor's degree, 14% with a bachelor's degree, 74% with a master's degree, and 9% with a post-master's degree (e.g., doctorate). The mean length of employment was 65.7 months (SD = 70.9) and ranged from 1 month (n = 5) to 360 months (n = 2). To examine the potential effect of length of employment on subsequent analyses, analyses were conducted with all cases and were then repeated excluding those cases who were employed for less than three months (n = 10). Results from both analyses were virtually indistinguishable. In this paper, we report the analyses with all participants.

The number of participants at the 32 participating agencies ranged from 1 to 53, with the mean number by agency equal to 11.81. Ten agencies (31%) had fewer than five participants; eight (25%) had between five and nine, seven (22%) had between 10 and 19 (22%); and seven (22%) had 20 or more participants.

Procedures

All participants were told that the IACS questionnaire was for research purposes and was not intended as an evaluation of their individual agency. Participants were told that the anonymous questionnaire would take about 20 minutes to complete and were asked to complete the items in terms of how their organization collaborates to provide services to children and their families. Participants first answered the Respondent Information section, which asked about individual demographic characteristics (e.g., gender, age, length of employment) and then completed the IACS.

Multilevel Confirmatory Factor Analysis

Whereas confirmatory factor analysis (CFA) at a single level of analysis analyzes the total variance-covariance matrix of the observed variables, multilevel CFA decomposes the total sample covariance matrix into pooled within-group and between-group covariance matrices and uses these two matrices in the analyses of the factor structure at each level. With multilevel CFA, it is possible to evaluate a variety of models including those that have the same number of factors and loadings at each level, the same number of factors but different loadings at each level, or models that have a different number of factors at the two levels.

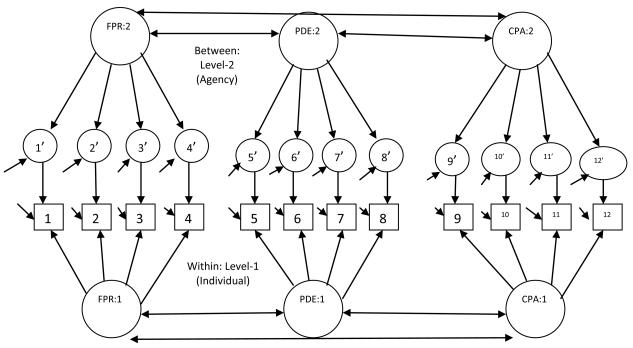
In the present study, we examined five multilevel measurement models. The first model consisted of three factors at each level with item loadings freely estimated across levels (see Figure 1). Next, we examined a three-factor model at each level with item loadings constrained to be equal across levels (Model 2). Model 3 consisted of one level-2 factor and three level-1 factors. The rationale for looking at this model was that previous research using MCFA has tended to find a smaller number of level-2 factors relative to level-1 (Hox, 2002). Model 4 consisted of one factor at each level (i.e., level-1 and level-2) with loadings freely estimated. Model 5 consisted of one factor at each level but with loadings constrained to be equal across levels. Each of the level-1 factors and level-2 factors was scaled by fixing the first factor pattern coefficient (i.e., loading) to 1.0. Items were specified to load on only one factor and error covariances were fixed to zero.

Figure 1.

Multilevel confirmatory factor model for the Interagency Collaboration Activities Scale. Item number with prime represents the agency-level version of the item (intercept). FPR = Financial and Physical Resources, PDE = Program Development and Evaluation, CPA = Collaborative Policy Activities.

Next, the multilevel measurement model was expanded to include multilevel structural relations between covariates and the level-1 and level-2 factors of the ICAS. In view of the demographic diversity of the mental health professionals, we examined if these differences were associated with differences in their perceptions of interagency collaboration. Level-1 covariates included participant's age, length of employment in the agency, gender, educational level, and job role (case worker, provider, and administrator). Level-2 covariates also were included to see if the diversity in the agencies was related to differences in the agencies' level of collaboration. Level-2 covariates included state location (OH, MI, CA) and number of employees in the agency, which ranged from 8 to 385 with a mean of 128.0 (SD = 119.4). State was included because agency policies often differ as a function of state mental health policies; number of employees was believed to be a proxy for size of the agency and number of clients served. These variables were included as part of the exploratory analyses as we had no specific hypotheses about how they might relate to collaboration.

Analyses, conducted using Mplus version 5.1 (Muthén & Muthén, 1998-2007), were based on the pooled within-group and between-group covariance matrices, and parameters were obtained using full information maximum likelihood (FIML) estimation that allows for missing data under the missing at random assumption (MAR, i.e., after conditioning on observed covariates and outcomes, but not on unobserved variables, any remaining missingness is assumed to be completely at random; Graham, 2009; Little & Rubin, 2002).

Overall goodness-of-fit for the models was evaluated using the χ² likelihood ratio statistic, Bentler's (1992) normed comparative fit index (CFI), root mean square error of approximation (RMSEA; Steiger & Lind, 1980) and the standardized root mean square residual (SRMR). Acceptable fit was judged by CFI values greater than .95 and SRMR and RMSEA values less than or equal to .08 (Hu & Bentler, 1999). Multiple fit statistics were used because each has limitations, and there is no agreed upon method for evaluating whether the lack of fit of a model is substantively important. To compare alternative models, such as a three-factor model at each level versus a one-factor model at level-2 and three factors at level-1, the Bayesian Information Criterion (BIC, Schwartz, 1978) was used. For the BIC, smaller values are indicative of better fitting models.

Results

Descriptive statistics

Item means ranged from 2.62 (SD = 1.34) for Record keeping and management information systems data (Financial and Physical Resources) to 3.58 (SD = 1.12) for Informing the public of available services (Program Development and Evaluation) with sample sizes for the items varying from 173 for Purchasing services to 312 for Staff training. Responses were approximately normally distributed with skewness ranging from 0.37 to −0.44 and kurtosis values ranging from −0.27 to −1.15 (see Table 1). Respondents were given the option of responding Don't Know to each of the 12 ICAS items, which was treated as missing data in the analyses. The Don't Know responses ranged from 15% for Item 7 (Staff Training) to 53% for Item 2 (Purchasing of Services), with an overall mean of 32% and a median of 34%.

Examination of Don't Know responses indicated that the participants' educational level and gender were not significantly (p > .05) related to the proportion of Don't Know responses to the items in the three IACS factors. There were, however, statistically significant (p < .01), but small negative relationships between participants' length of employment at their current agency and the proportion of Don't Know responses to the items in the Financial and Physical Resources (r = −.34), Program Development and Evaluation (r = −.31), and Collaborative Policies (r = −.30) scales (i.e., those who were employed for a longer period of time had fewer Don't Know responses). Age also had a statistically significant (p < .01), but small negative relationship, to the proportion of Don't Know responses but only for the items in the Financial and Physical Resources (r = −.17). Lastly, job role had a statistically significant (p < .01) and moderate relation to each of the three IACS factors (Financial and Physical Resources, eta-squared = .079; Program Development and Evaluation, eta-squared = .046; and Collaborative Policies, eta-squared = .053). For each IACS factor, providers had the greatest percentage of Don't Know responses, followed by case managers, and administrators. The potential implications of including the Don't Know category in the IACS questionnaire are addressed in the Discussion.

Confirmatory factor analysis with corrected standard errors for nested data

Researchers have suggested that because of the complexity of multilevel confirmatory factor analysis (MCFA) models, simpler models are recommended as a preliminary step in conducting MCFA. Therefore, initially, a single-level confirmatory factor analysis (CFA) with robust maximum likelihood estimation and standard errors adjusted to take into account cluster sampling (i.e., nested data) was used to examine the three-factor measurement model underlying the Interagency Collaboration Activities Scale. The single-level CFA does not take into account the two-level structure of the data and is based on the total covariance matrix of the observed variables (i.e., the total covariance matrix is not decomposed into between– and pooled within-agency covariance matrices, which is the case for the multilevel CFA).

The chi-square value, for the single-level, three-factor CFA model, χ² (51, N = 360) = 89.66, p < .001, indicated a significant lack of fit. However, alternative measures of fit, less sensitive to sample size, suggested that the fit was acceptable. The standardized root mean square residual (SRMR) of .04 and the root mean square error of approximation (RMSEA) of .05 were less than Hu and Bentler's (1999) cutoff value of .08 that has been used as a general indicator of acceptable fit and the comparative fit index (CFI) of .97 was greater than the cutoff value for this index (cutoff = .95). All factor pattern coefficients (loadings) were significantly different from zero (p < .01). The standardized loadings for the items within the Financial and Physical Resources factor ranged from .59 to .84; .64 to .80 for Program Development and Evaluation; and from .66 to .85 for Collaborative Policy Activities. The correlations between the factors were positive and significantly different from zero (ps < .01) with Program Development and Evaluation and Policy Activities, Financial and Physical Resources and Policy Activities, and Financial and Physical Resources and Program Development and Evaluation correlating .69, .71, and .79, respectively. Comparisons of the latent variable means revealed that the highest level of collaboration involved Program Development and Evaluation (M = 3.55), followed by Collaborative Policies (M = 3.32), and Financial and Physical Resources (M = 3.10). The pairwise comparison between the lowest two means was not statistically significant (p > .05).

An alternative one-factor model also was considered. This model did not fit as well as the three-factor model based on the chi-square value, χ² (54, N = 360) = 209.15, p < .001, the nested model chi-square value, Δχ² (3, N = 360) = 119.49, p < .001, and the other fit indices, SRMR (.07), RMSEA (.09), and CFI (.86). Standardized item loadings on the one factor ranged from .52 to .74.

Multilevel confirmatory factor analysis

Prior to conducting the MCFA, the variability between and within agencies on each item was examined by computing the intraclass correlations (ICC) for each of the 12 items on the questionnaire. The ICCs for the observed variables provide a measure of the amount of variability between agencies and the degree of non-independence or clustering of the data within agencies. Using a random effects model, the ICC for an item represents the variation between agencies in the intercepts (means) of the item divided by the total variation (sum of the variation between agencies in the intercepts and the variation within agencies). ICCs can range from 0 to 1.0 with larger values indicating greater clustering effects within agencies. Although there are no firm guidelines for deciding how large the ICC has to be to warrant multilevel analyses, most of the published multilevel CFAs have reported ICCs greater than .10 (e.g., Dyer, Hanges, & Hall, 2005; Hox, 2002).

Table 1 displays the ICCs for the 12 items. The ICCs for each of the observed items ranged from .07 (item 6 within the Program Development and Evaluation factor) to .30 (item 1 within the Financial and Physical Resources factor) and averaged .16 with a median of .13. These values indicated that there was sufficient between-agency variability to warrant multilevel analysis.

Results of the two-level, correlated three-factor multilevel model (Model 1) with loadings freely estimated across levels indicated a reasonable fit of the model to the data. The root mean square error of approximation (RMSEA) of .029 and CFI of .972 indicated acceptable fit overall. The SRMR fit indices at each level indicated that the fit of the level-1 (within) part of the model was better than at level-2 or between (SRMR-within = .047 vs. SRMR-between .182, see Table 2 for measures of fit).

Table 2.

Multilevel Confirmatory Factor Analysis: Fit Indices for Five Models

Fit Index	Model 1: Three Factors at Level-1 and Three Factors at Level-2: Loadings Freely-Estimated	Model 2: Three Factors at Level-1 and Three Factors at Level-2: Loadings Constrained to be Equal	Model 3: Three Factors at Level-1 and One Factor at Level-2	Model 4: One Factor at Level-1 and One Factor at Level-2: Loadings Freely-Estimated	Model 5: One Factor at Level-1 and One Factor at Level-2: Loadings Constrained to be Equal
χ 2	141.82	160.00	144.54	291.51	309.80
(df)	(109)	(118)	(112)	(115)	(124)
CFI	.972	.964	.972	.850	.842
RMSEA	.029	.031	.028	.065	.065
SRMR:
Within	.047	.046	.048	.081	.082
Between	.182	.218	.219	.224	.234
BIC	8,666.78	8,631.98	8,651.84	8,781.15	8,746.47

Note. CFI = normed comparative fit index, RMSEA = root mean square error of approximation, SRMR = the standardized root mean square residual, and BIC = Bayesian Information Criterion. Δχ² comparing Model 2 with Model 1 = 18.172 (Δ df = 9), p = .03.

At level-1, all factor pattern coefficients (loadings) were significantly different from zero (p < .01). At level-2, all loadings were statistically significant except for item 4 Record keeping and management information data (p = .35) for the Financial and Physical Resources factor. Table 3 displays the unstandardized factor loadings and residual variances for Model 1. It should be noted that seven residual variances for the level-2 intercepts (averages) were fixed to zero. Hox (2002) states that fixing residual variances to zero at the between-level is often necessary in MCFA when sample sizes at level-2 are small and the true between–group variance is close to zero, which were the case in the current study. Interfactor correlations were .80 (p < .001) between Financial and Physical Resources and Program Development and Evaluation at level-1 and .80 (p > .05) at level-2; .65 (p < .001) between Program Development and Evaluation and Policy Activities at level-1 and .90 (p > .05) at level-2; and .64 between Financial and Physical Resources and Policy Activities at level-1 and .98 at level-2 (p < .001).

Table 3.

Unstandardized Parameter Estimates for Model 1: Three Factors at Level-1 and Three Factors at Level-2 with Loadings Freely Estimated

		Level-1 (Individuals)				Level-2 (Agencies)
Item	Financial and Physical Resources	Program Development and Evaluation	Collaborative Policy Activities	Residual Variance	Financial and Physical Resources	Program Development and Evaluation	Collaborative Policy Activities	Residual Variance
FPR 1	1.00b (---)			0.56 (0.08)	1.00b (---)			0.13 (0.09)
FPR 2	1.06 (0.12)			0.46 (0.08)	0.98 (0.27)			0.00a (---)
FPR 3	0.89 (0.12)			0.96 (0.10)	0.76 (0.29)			0.11 (0.07)
FPR 4	1.06 (0.14)			0.99 (0.12)	0.25 (0.27)			0.07 (0.07)
PDE 5		1.00b (---)		0.47 (0.060		1.00b (---)		0.00a (---)
PDE 6		1.09 (0.10)		0.46 (0.07)		0.47 (0.23)		0.00a (---)
PDE 7		0.80 (0.09)		0.64 (0.06)		1.16 (0.26)		0.00a (---)
PDE 8		0.79 (0.09)		0.70 (0.07)		0.88 (0.31)		0.07 (0.04)
CPA 9			1.00b (---)	0.68 (0.07)			1.00b (---)	0.07 (0.05)
CPA 10			1.22 (0.13)	0.42 (0.06)			0.79 (0.24)	0.00a (---)
CPA 11			1.21 (0.14)	0.53 (0.06)			0.93 (0.30)	0.00a (---)
CPA 12			1.35 (0.16)	0.37 (0.06)			1.01 (0.36)	0.00a (---)

Note. FPR = Financial and Physical Resource; PDE = Program Development and Evaluation; CPA = Collaborative Policy Activities. See Table 1 for item content. All loadings were significant at p < .05 except for item 11 on the between factor. Standard errors are in parentheses.

^aResidual variances were fixed to zero.

^bFactor loading fixed to 1.0.

To test the equality of the factor loadings across levels, a second MCFA model (Model 2) was estimated where the loadings across level-1 and level-2 were constrained to be equal. This constrained model was nested within the earlier freely estimated model and, therefore, a nested chi-square difference test was used to evaluate the hypothesis of equal factor loadings across levels. The Δχ2 was 18.17 (Δdf = 9, p = .03) indicating that the overall hypothesis of equal loadings should be rejected. However, follow up Δχ2 tests of each loading (Δdf = 1) found that none was statistically significant after adjusting the significance level for multiple testing (i.e., p < .01). Additionally, the overall BIC index for the constrained model (equal loadings) was smaller (BIC = 8,631.98) than that for the freely estimated model (BIC = 8,666.78) indicating better fit for the equal loadings model (see Table 2).

Using the equal loadings model, it was possible to calculate the intraclass coefficients (ICC) for the three latent variables and, subsequently, the reliability of each factor when aggregated at the agency level. The ICC is the variation between-agency divided by the total variation. Total variation equals the combined within- and between-agency variation. Financial and Physical Resources had the greatest amount of between-agency variability (ICC = .273) followed by Collaborative Policy Activities (ICC = .182) and Program Development and Evaluation (ICC = .118). Using these ICCs with the Spearman-Brown formula, [k(ICC) ] / [ (k-1)(ICC )+ 1],where k is the average number of informants per agency, the estimated reliabilities for the factors in this study, with approximately 11 respondents per agency were .81 for Financial and Physical Resources, .60 for Program Development and Evaluation, and .72 for Collaborative Policy Activities.

Because of the high interfactor correlations at level-2 (i.e., .90 or greater), an alternative model with one factor at level-2 instead of three factors, was considered; three factors were specified at level-1 (Model 3). This model provided a reasonable fit to the data. The standardized root mean square residual (SRMR) was .048 for level-1 (within) and .219 for level-2 (between); the root mean square error of approximation (RMSEA) was .028; and the CFI was .972. All of the indices were indicators of acceptable fit with the exception of the SRMR-between. The BIC was 8,651.84, smaller than the BIC from Model 1, which had three factors at each level and loadings free to vary across levels. For Model 3, all level-2 loadings on the single factor were significantly different from zero except for Record keeping and management information data (p = .41) and Program evaluation (p = .09).

To further explore whether a one-factor model at each level was tenable, two additional models were evaluated. Models 4 and 5 each contained one factor at each level; the major difference between these two models was that in Model 4 the factor loadings were freely estimated across levels whereas in Model 5 the loadings were constrained equal across levels. Overall, the fit of these models was not good and all of these models had poorer fit indices than any of the three-factor models (see Table 2).

Covariate models

Finally, to examine the relationship between selected individual level characteristics of the mental health professionals (i.e., employee's age, job role, gender, educational level, and number of months employed) and characteristics of the agencies (i.e., state location and number of agency employees) and variation in the scores from the Interagency Collaboration Activities Scale, Model 2 (three-factors at each level with loadings constrained equal across levels) was expanded to include level-1 and level-2 covariates. At level-1, none of the mental health professionals' characteristics was significantly related to the IACS factors. At level-2, state location of the agency and the number of employees were not significantly related to the three level-2 factors (see Table 4). State location and number of employees also were not significantly related to interagency collaboration when conceptualized as a single latent factor at level-2 (i.e., Model 3, three factors at level-1, one-factor at level-2).

Table 4.

Standardized Coefficients for Interagency Collaboration Activity Scale Factors and Level-1 and Level-2 Covariates

	Interagency Collaboration Activity Scale Factors
	Financial and Physical Resources		Program Development and Evaluation		Collaborative Policies
Covariates	Coefficient	Standard Error	Coefficient	Standard Error	Coefficient	Standard Error
Level-1 (Within Agency)
Age	−.087	.086	−.130	.081	−.061	.081
Length in Organization (months)	−.108	.080	.047	.074	.033	.077
Female	−.019	.071	.077	.066	.000	.068
Education Level	.010	093	−.138	.092	−.018	.089
Role
Case Worker	.014	.108	.053	.102	−.056	.100
Provider	.155	.094	.051	.086	.076	.088
Level-2 (Between Agency)
State
Ohio	−.231	.214	−.271	.249	.025	.247
Michigan	−.094	.230	.021	.284	−.042	.260
Employees	−.304	.205	−.118	.259	−.226	.230

Note. None of the coefficients was statistically significant (p > .05).

Discussion

As policy makers continue to debate the positives and negatives of interagency collaboration, researchers have been developing measurement instruments designed to provide empirical data to inform the debate. One of these instruments is the Interagency Collaboration Activities Scale (ICAS), a self-report questionnaire designed to be used in large-scale quantitative studies to measure the extent to which individuals perceive their agency is collaborating with other agencies.

The ICAS focuses on collaboration in three domains—Financial and Physical Resources, Program Development and Evaluation, and Collaborative Policy Activities—and uses a multi-informant, multilevel data collection design in which administrators, case managers, and service providers report information about their agency's level of collaboration with other agencies. To date, most researchers have evaluated the psychometric properties of instruments measuring organizational variables such as interagency collaboration using factor analysis (i.e., exploratory and confirmatory) conducted at the individual informant level despite the fact that the relationships between the variables at the individual or lower level may not be the same as those at the organizational or higher level (Zyphur, Kaplan, & Christian, 2008). The present study represents one of the first to analyze the psychometric properties of an interagency collaboration instrument using a multilevel analysis approach and explicitly test the equivalence of the three-factor structure (i.e., Financial and Physical Resources, Program Development and Evaluation, and Collaborative Policy Activities) across levels. If the factor structures are different at each level, using an individual level measurement model to represent agency level factors may produce distorted structural relationships with other external variables in subsequent analyses (e.g., relationship between an agency's level of collaboration and children's mental health outcomes).

Results of the multilevel CFA supported the three-factor model at each level and indicated that the relationships of the IACS items to their corresponding factor (i.e., pattern coefficients) were not different at the individual and agency levels. These results support the construct validity of the IACS scores. However, the strength of the relationships between the three factors as revealed by the interfactor correlations did show differences across the two levels. The interfactor correlations at the agency level (level-2) were generally stronger than those at the individual level (level-1). These correlations led us to consider an alternative model, three-factors at level-1, but a single factor at level-2. A test of the one-factor model at level-2 was found acceptable. When we considered a one-factor model at both levels, model fit deteriorated and was statistically unacceptable.

Taken together these results support three factors at the individual informant level. Results for the factor structure at the agency level are more equivocal with either one or three factors being plausible. The advantage of the one-factor solution at level-2 is that it provides a parsimonious summary measure of an agency's level of collaboration, as perceived by the individuals within the agency. The disadvantage of the one-factor solution is that there is some loss of information on the three dimensions of collaboration. Additional research with a larger sample of agencies (level-2 units) is necessary to distinguish between these two alternative models that differ in the number of factors at the agency level. The current study had 32 agencies as level-2 units and although this number is within the minimal range of between 30-50 level-2 units recommended for multilevel factor analysis (Muthén & Muthén, 2007), more level-2 units would provide greater power to discriminate between alternative models. The issue of adequate sample size in multilevel analyses, especially at level-2, has not been fully resolved. In the handful of studies that have used MCFA, the number of level-2 units has ranged from approximately 30 to 200. Simulation work that examines such conditions as model complexity (i.e., number of observed and latent variables), level of intraclass correlation, estimation methods, and scale and distributions of observed variables, is needed to establish more refined guidelines for sample sizes at level-1 and level-2.

A strength of the multilevel latent variable approach is that by partitioning the variance in the scores into within- and between-agency components, the reliability of the agency scores for the three factors can be obtained at each level. Many researchers evaluating the reliability of the scores from organizational measures have ignored the nested data structure and have computed Cronbach's alpha. These reliability coefficients, however, do not reflect the reliability at the organizational level. As shown in this study, the reliability of the scores of the Financial and Physical Resources, Program Development and Evaluation, and Collaborative Policy Activities factors were different at the organizational level (.81, .60, and .72, respectively) compared to the reliability estimates obtained when ignoring the nesting of individual informants within agencies (.79, .82, and .85, respectively).

Reliabilities of the Financial and Physical Resources and Collaborative Policy Activities factors were acceptable while the Program Development and Evaluation factor fell below the .70 criterion used by many (Nunnally, 1978). Based on the intraclass correlation coefficients obtained in the present study and the Spearman-Brown prophecy formula, at least 17 informants per agency would be needed to obtain reliabilities above .70 on that factor. The large number of informants needed is due to the fact that individuals within the same agency differed substantially in their perceptions of how much their agency collaborated with other agencies on the Program Development and Evaluation factor and also because there was limited true score variability between agencies on this factor (i.e., Program Development and Evaluation factor had the lowest ICC of .118). One implication of this finding of large within-agency variability is that researchers studying interagency collaboration who use either a single or a few informants within an agency will produce scores with very low reliabilities at the agency level resulting in attenuated relationships with other variables (e.g., outcomes).

In view of the large amount of within-agency variability, we explored potential participant characteristics that might be related to these different perceptions. Results revealed that employee's age, job role, gender, educational level, and number of months employed were not significantly related to perceptions of interagency collaboration. One explanation for the lack of significant results may be that a referent-shift approach was used in the questionnaire. In this approach, participants were asked to self-report for their agency as a whole rather than their own individual level of collaboration. To test the plausibility of this explanation, future research would need to compare the relationships between participants' demographic characteristics and their perceptions of collaboration under the conditions of a self- versus agency-referent. A second possible explanation for the lack of significant relationships between participants' characteristics and their perceptions of interagency collaboration is that the questionnaire contained a Don't Know response category that eliminated those who did not have sufficient knowledge of their agency's level of collaboration. Thus, for example, although service providers had the greatest level of Don't Know responses, followed by case managers, and administrators, results from those who reported that they had sufficient knowledge of their agency's level of collaboration showed that these three groups did not differ in their ratings on the IACS. To test the effect of the Don't Know option on the relationships between participants' characteristics and their perceptions of interagency collaboration, future research would need to compare these relationships when the Don't Know option was included in the questionnaire and when this option was not available. A third explanation for the lack of significant differences may derive from reduced statistical power due to the relatively small sample sizes at level-1 (approximately 11 participants at each agency). Future research with larger sample sizes at level-1 would provide greater statistical power and would permit expanding the level-1 model to include a wider range of characteristics as explanatory variables of the within-agency variability (e.g., personal beliefs about the value of collaboration).

Analysis of the level-2 covariates of state location and number of employees also revealed no significant relationships with Financial and Physical Resources, Program Development and Evaluation, and Collaborative Policy Activities despite the fact that there was between-agency variability on these factors as measured by the intraclass correlation coefficient. The lack of statistically significant relationships may be due in part to a lack of statistical power resulting from the small sample size at level-2 (32 agencies) and the choice of predictors. The present study had few level-2 predictors and, therefore, it is recommended that future research include a larger number of level-2 units and additional level-2 predictor variables that are either direct measures of agency characteristics (e.g., budget size, case loads, number of interagency collaborations, characteristics of the client population served) or represent aggregated level-1 or compositional measures of agency characteristics (e.g., organizational climate, agency collective efficacy).

Longoria (2005) has argued that to achieve a better understanding of interorganizational collaboration among human-service agencies, there is a need for better operational definitions of the construct, along with data-driven evaluations of how interagency collaboration affects service recipients. The Interagency Collaboration Activities Scale represents one operational definition of collaboration and when analyzed within a multilevel framework has the potential to provide new insights into the construct of collaboration. Additional research with a large number of agencies, randomly selected from across the United States, is needed to evaluate the generalizability of the present findings. Larger sample sizes at both level-2 and at level-1 also would provide opportunities to conduct multilevel, multigroup confirmatory factor analyses to evaluate the metric and scalar invariance of the measurement model (e.g., factor loadings and intercepts) underlying the IACS for different groups of respondents (e.g., administrators, service providers, and case managers). These DIF (differential item functioning) analyses would provide additional insight into potential systematic measurement error related to the measurement of interagency collaboration.

More research also is needed to examine the relation between the scores on the Interagency Collaboration Activities Scale and other methods used to measure collaboration (e.g., network analysis, interviews) and ultimately to outcome measures for service recipients. The multilevel latent variable framework that was used in the present study to examine the measurement of interagency collaboration can be expanded to include predictors of collaboration and also examine the effects of collaboration on proximal (e.g., worker satisfaction) and distal (e.g., client mental health status) outcomes. Ludtke et al. (2008) have referred to this approach as the multilevel latent covariate model (MLC) approach to contrast it with the multilevel manifest covariate (MMC) model that uses observed group means. The use of latent variables versus manifest observed agency means provides estimates of the effects of interagency collaboration on outcomes that are corrected for the unreliability of the measurement of the latent agency mean. Continued use of these advanced analytical methods should provide a more solid basis for informing the discussion of the positives and negatives associated with interagency collaboration in the area of human services.