Abstract
In the companion paper, we presented a set of induced dipole interaction models using four types of screening functions, which include the Applequist (no screening), the Thole linear, the Thole exponential model, and the Thole Tinker-like (another form of exponential screening function) functions. In this work, we evaluate the performance of polarizability models using large set of amino acid analog pairs that are frequently observed in protein structures as a benchmark. For each amino acid pair we calculated quantum mechanical interaction energies at the MP2/aug-cc-pVTZ//MP2/6-311++G(d,p) level with the basis set superposition error (BSSE) correction and compared them with molecular mechanics results. Encouragingly, all the polarizable models significantly outperform the additive F94 and F03 models (mimicking AMBER ff94/ff99 and ff03 force fields, respectively) in reproducing the BSSE-corrected quantum mechanical interaction energies. Particularly, the root-mean-square errors (RMSE) for three Thole models in Set A (where the 1–2 and 1–3 interactions are turned off and all 1–4 interactions are included) are 1.456, 1.417 and 1.406 kcal/mol for Model AL (Thole Linear), Model AE (Thole exponential) and Model AT (Thole Tinker-like), respectively. In contrast, the RMSE are 3.729 and 3.433 kcal/mol for F94 and F03 models, respectively. A similar trend was observed for the average unsigned errors (AUE), which are 1.057, 1.025, 1.011, 2.219 and 2.070 kcal/mol for AL, AE, AT, F94/ff99 and F03, respectively. Analyses based on the trend line slopes indicate that the two fixed charge models substantially underestimate the relative strengths of non-charge-charge interactions by 24% (F03) and 35% (F94), respectively, whereas the four polarizable models over-estimate the relative strengths by 5% (AT), 3% (AL, AE) and 13% (AA), respectively. Agreement was further improved by adjusting the van der Waals parameters. Judging from the notably improved accuracy in comparison to the fixed charge models, the polarizable models are expected to form the foundation for the development of high quality polarizable force fields for protein and nucleic acid simulations.
Keywords: Polarizable force field, Polarizability, Dipole interaction, Thole’s model, Applequist’s model, Force field parameterization, interaction energy
1. Introduction
Accuracy of molecular mechanical force field has become an increasingly important issue with the growing ability to model long-time and large-scale events. A key component that can potentially lead to substantial improvement is the atomic polarization to enable responses to the changes in dielectric environment.1 Among several possible models to represent molecular polarization,2–5 the most studied model is the induced dipole model in which the induced dipole moment μi at atom i is proportional to its atomic polarizability αi and electrostatic field acting on it. This model has been employed in several force fields, including OPLS/PFF,6 AMOEBA7,8 and AMBER ff02, ff02EP 9and ff02r1.10
In the AMBER polarizable force fields, the total potential energy is a sum of the intramolecular bonded terms (Vbonded, calculated by Eq. 1) and intra- and intermolecular non-bonded terms (Vnonbonded, calculated by Eq. 2) and the polarization energy Vpol calculated using an induced dipole model (Eq. 3).
| (1) |
| (2) |
| (3) |
In Eq. 1, the three terms represent contribution to the total energy from bond stretching, bond angle bending and torsion angle twisting, respectively. In Eq. 2, Vnonbonded is the sum of van der Waals (vdW) and electrostatic energies. In Eq. 3, Vpol is calculated for each pair of point charge and induced point dipole moment. μi is the induced dipole of the ith atom, and is the electrostatic field at the ith atom generated by all other point charges qj. For a collection of N point polarizable dipoles placed in a homogeneous electric field E, the induced dipole moment at point i (μi) is calculated by Eqs. (4–7).
| (4) |
| (5) |
| (6) |
| (7) |
where, αi is the atomic polarizability, rij is the distance vector between interaction points i and j, and Tij is the dipole field tensor, I is the unit matrix. In the original Applequist’s model, fe=1 and ft=1.11 To avoid “polarization catastrophe” 12–14, Thole12,13 proposed distance-dependent screening functions to replace the constants fe and ft. There are several widely used forms of fe and ft depending on the way the electron density is represented. Three forms, one linear, one exponential and another exponential form adopted by Ren and Ponder are studied in this work. 7,8 The functional forms of fe and ft for the three Thole models are presented in the companion paper and Ref.1.
In the companion paper, we optimized the isotropic atom polarizability parameters αi to reproduce the experimental molecular polarizabilities. In this work, we focus on evaluating the three types of Thole polarization models by analyzing their performance in reproducing the interaction energies between amino acids side chain analogs computed with high-level quantum mechanical theories.
Theoretically, the contribution from nearby atoms that are linked through one to three consecutive bonds should be included in polarization energy calculation. However, in almost all the polarizable force fields, especially those utilizing the Applequist model (such as AMBER ff02/ff02EP9 and ff02r115) the short-range 1–2 (bonded) and 1–3 (separated by two bonds) interactions are excluded to avoid the so-called “polarization catastrophe”.12 The argument behind this treatment is that the 1–2 and 1–3 interactions are modeled by the bond stretching and bond angle bending (Eq. (1)) and the short-range polarization can be effectively taken into account by the long-range polarization through proper atomic polarizability parameterization, and the leftover is further absorbed by the effective partial charges that are obtained by fitting to the electrostatic potential of the molecules. Given the explicit use of screening functions, the effect due to exclusion of the short-range interactions is expected to be small. In fact, as shown in the companion paper 16, fitting of the atomic polarizability degraded notably when 1–2 and 1–3 terms were included. Our attempt to include 1–2 and 1–3 interactions frequently leads to the divergence of the induced dipoles during the charge fitting. Thus, we focus our effort to evaluate the models in which the 1–2 and 1–3 interactions are excluded. Specifically, we will evaluate three sets of polarizability models, including Set A, B, and C in which the 1–4 interactions are scaled down by 1.0, 1.2, and 2.0, respectively. These scaling factors have been used before to decrease the magnitude of the 1–4 electrostatic interactions in various AMBER force fields. Each individual polarizable model within a set is denoted by additional letter describing screening method. For example symbols AA, AL, AE, AT means polarizable models belonging to set A with Applequist, Thole-linear, Thole-exponential and Thole-Tinker-like screening method, respectively. For comparison, we will also evaluate the two fixed charge models in Set F, in which the atomic partial charges are derived in manner consistent with either AMBER ff94/ff9917–19 (model F94) or AMBER ff0320 (model F03). The objective of this work is to identify the polarizable models that outperform the other polarizable and the two fixed charge models to pave the way to the development of high quality polarizable force fields for proteins and nucleic acids.
2. Methods
The main goal of the force field development is to derive a consistent set of parameters that reproduces both experimental properties of the condensed matter and high-level ab initio results for intermolecular interaction energies, conformational energies and geometries. However, the purpose of this study is to develop and evaluate polarizability models described in the first paper of this series. Therefore, we focus here on assessing how well the intermolecular interaction energies can be reproduced.
In order to evaluate the polarizability models systematically, we constructed a set of amino acid side chain analog pairs that are frequently observed in protein crystal structures. The intermolecular interaction energy between a pair of amino acid analogs, which is defined as a energy difference between the dimer (EAB) and the two monomers (EA and EB), is calculated at the MP2/aug-cc-pVTZ//MP2/6-311++G(d,p) level. The above notation indicates that geometrical optimization is performed at MP2/6-311++G(d,p) level followed by a single point energy calculation at MP2/aug-cc-pVTZ level. The other notions of QM models can be interpreted in a similar way. The interaction energies were corrected for the basis set superposition error using the counterpoise method.21,22 The molecular mechanical interaction energies calculated using point dipole interaction models were then compared to the respective ab initio values and the errors were evaluated.
Amino acid side chain analog pairs
A set of amino acid side chain analog pairs that frequently occurred in the protein crystal structures were selected from PDB (www.rcsb.org).23 Here only structures of resolution better than 2.0 Å were selected. A total of 6,244 proteins were identified, excluding redundant sequences that share 70% or higher sequence identity. After removal of non-amino acid residues, (water, ions, cofactors and small ligands, etc.), the missing atoms (e.g., hydrogens) were added using the Leap program from the AMBER simulation package24. The configurations of amino acid analog pairs that have residue-based distances smaller than 5.0 Å were generated. These pairs were then clustered based on a scoring function , where N is the number of configurations for a particular amino acid pair and f (rmsdij)is a step function of the heavy atom root-mean-square displacements (rmsd) between the two configurations, i and j, after alignment through rigid body rotation and translation. The function f (rmsd) takes discrete values from f = 10 (rmsd <= 0.5) to f = 1 (4.5 < rmsd <= 5.0) and decreases by 1 when rmsd increases by 0.5 Å (f = 0.5 for rmsd > 5.0 Å). A configuration with a higher score would have more similar configurations to it and, therefore, is more representative. The configurations were then grouped together iteratively. In each cycle, the configuration with the highest score was chosen as the ‘centroid’ of a cluster and an ungrouped configuration enters the cluster if rmsdij is within a preset criterion (1.0 Å). Note that an amino acid pair is qualified as a ‘centroid’ of the cluster only if the rmsd between itself and any other ‘centroid’ is not larger than the criterion. The representative structures from the top clusters were then selected for ab initio calculations after the main chain atoms were removed and the open valences were filled in with hydrogen atoms. A set of in-house programs was developed to conduct the above clustering analysis and to generate the Gaussian input files.25
For the set of charged side chain analogs we investigated the change of the interaction energies as a function of separating distance between two charged residues. For Asp/Arg and Glu/Arg, the separation d is defined as a distance between the carbon of the carboxyl group of Asp or Glu and the sp2 carbon of the guanidine of Arg; for Asp/Lys and Gly/Lys, d is defined as a distance between the carbon of the carboxyl group of Asp or Glu and the positively charged nitrogen of Lys. This subset includes the following amino acid analog pairs: Asp/Arg separated by 5.02, 5.32, 5.62, 6.02, 6.42, 6.82, 7.42, 8.02 and 8.82 Å; Asp/Lys, Glu/Arg and Glu/Lys separated by 5.02, 5.52, 6.02, 6.52, 7.02, 7.52, 8.02, 8.52, 9.52 Å. Partial optimizations of the charged amino acid analog pairs were performed by Gaussian 0325 program.
Main chain analogs
Besides the amino acid side chain analogs, we also investigated the role of interactions between the main chains of two amino acid residues (not necessary linked by the peptide bond). We constructed several configurations of the NMA (N-methylacetamide) pairs to mimic the amino acid main chain interaction. Two sets of NMA-NMA pairs were generated. In the first set, comprising 18 pairs, the NMA-NMA pairs were constructed using the structures of the glycines dipeptide, tripeptide and tetrapeptide. The conformations of six types of secondary structures, which include C5, C7ax, C7eq, CIS, Helix and Sheet were taken into account for all three kinds of polyglycines.26,27 In the second set of 13 pairs, we generated the NMA-NMA pairs from glycine dipeptide that adopts either alpha helix or beta-sheet conformation and the two carbonyl carbon atoms are separated by certain distances. A total of 13 NMA-NMA configurations were finally constructed. For the 7 helical pairs, the separating distances are 4.4, 4.8, 5.0, 12.0, 17.3, 20.7 and 24.2 Å, respectively; for the 6 sheet pairs, the separating distances are 7.5, 10.3, 13.8, 17.3, 20.7 and 24.2 Å, respectively. The NMA-NMA pairs in the first set were optimized with the full degrees of freedom using Gaussian 0325 while those in the second set were optimized with positional restraints (applied only to several selected atoms that can maintain the overall conformations of the monomers, setting the force constants of harmonic constraints to 50.00 kcal/mol/Å2) using the Jaguar program.28
BSSE-Corrected Interaction Energy Calculation
Each amino acid analog pair was first optimized using the B3LYP/6-31G*.29 Then all the amino acid analog pairs, except those in the second set of 13 NMA-NMA pairs that were optimized at B3LYP/6-31G* level using Jaguar 28, were optimized at the MP2/6-311++G(d,p) theory level. Finally, the MP2/aug-cc-pVTZ single point calculations were performed for all the amino acid analog pairs. Given the fact that geometries are much less sensitive to the ab initio models than the energies, as such, a widely used strategy in ab initio calculations is to perform geometry optimization at a low level followed by a single point calculation using a more advanced model. This strategy well balances the accuracy of the energy calculation and computational efficiency. The basis set superposition errors (BSSE) were corrected for all calculated dimers through the counterpoise corrections.21,22 The interaction energies were calculated using Eqs (8) and (9).
| (8) |
| (9) |
Where Eint is the interaction energy between A and B, EAB, EA and EB are the quantum mechanical energies of dimer AB, and monomers A and B, respectively; the BSSE (basis set superposition error) corrected interaction energy, is calculated with Eq (9), where EBSSE is the BSSE energy, are the quantum mechanical energies of A and B in the dimer centered basis set, respectively.
Charge fitting
In molecular mechanical force fields, charge model plays a key role in determining their accuracy. In the existing AMBER polarizable force fields, parametrization of the permanent point charges depend on the polarization model, because both permanent charges and induced dipoles contribute to the electrostatic potential in the vicinity of a molecule. Consistent with this strategy, in this study, the charges were obtained by fitting them to high level ab initio electrostatic potentials with the designated polarizable models and parameters. For model F94, the partial point charges were derived to fit the HF/6-31G* electrostatic potentials of the analog monomers by RESP (Restrained Electrostatic Potential)18,30, consistent with the AMBER ff94 charge set18,19. For model F03, the charges were fit to reproduce the electrostatic potentials derived at the B3LYP/cc-pVTZ//HF/6-31G** level. In this case quantum mechanical calculations included the reaction field approach 31–33 to account for the solvent treated as a polarizable continuum medium (the solvent is ether). This approach is consistent with AMBER ff03 charge set derivation method.20 For the current polarizable models, the ab initio molecular electrostatic potentials were calculated at the MP2/aug-cc-pVTZ level for the geometries of the amino acid analog monomers optimized at the MP2/-6-311++G(d,p).
Since both the permanent charges and the induced dipoles generate electrostatic field the charges fitted by the conventional RESP method are thus no longer applicable. Cieplak and Kollman9 developed an iterative procedure for fitting point charges that takes into account self polarization of the molecule. In this procedure, the point charges are iteratively fit to the difference between the QM electrostatic potential field and that generated by the induced dipoles (i.e. ESPQM-ESPinduced). The induced electrostatic potential is calculated by Eq. (10) where rip is a distance vector. Summation runs over all atoms i, to derive an electrostatic potential at site p.
| (10) |
At every iteration step, the point dipoles are induced by interaction with permanent atomic charges and other induced dipoles. The procedure is iterated until the change in the total dipole moment is less or equal to 0.001Debye. The induced dipole of an atom due to other point charges and other point dipoles are computed by the i_RESP program.1 Consistent with the polarizability model under evaluation the atomic charges used in this study were derived for every polarization model. During the charge fitting the 1–2 and 1–3 interactions were excluded and the 1–4 interactions between induced dipoles were either not scaled or scaled down, depending on the specific model set.
Molecular mechanical energy calculations
To calculate the molecular mechanical energies with the three Thole polarizable models, the sander program from the current version of the AMBER package (AMBER11)24 was extended by introducing fe and ft to calculate the distance-dependent dipole-dipole interaction tensor. Single point interaction energies were calculated using the ab initio geometries and no cutoff for the non-bonded interactions. The 1–4 vdW energies were scaled down by 2.0, and 1–4 electrostatic energies were scaled down only whenever required by the models. Besides the polarizable models, we also evaluated interaction energies using two non-polarizable models whose charges were obtained in a manner consistent with ff94/ff9917–19 and ff03.20 These two non-polarizable models are designated as F94 and F03, respectively.
3. Results and discussion
In this section, we first discuss the interaction energies of amino acid analog pairs calculated by ab initio models; then both the polarizable and non-polarizable molecular mechanical models are assessed by comparing their interaction energies to those calculated by the high-level ab initio model. Next, we identify the ‘outliers’ that have predicted errors larger than 2.5 kcal/mol. Attempts are also made to explore adjusting vdW parameters to improve the agreement.
3.1 Interaction Energies of Amino acid analogs Calculated by High-level Ab Initio Models
Amino acid analog pairs
A pool of 450 amino acid side chain analog pairs was selected from the top clustered configurations, covering most types of interactions which can be found in real protein structures. They can be grouped into several categories: 86 pairs of non-polar residues (Ala, Cys, Ile, Leu, Met, Val), 35 pairs of polar residues (Asn, Gln, His, Ser and Thr), 21 pairs of aromatic pairs (Phe, Tyr and Trp), 41 pairs of charged residues (Asp, Glu, Arg and Lys), and 267 pairs of mixed types. Note that Gly and Pro are not included in the 450 amino acid pairs. In addition to the side chain analog pairs, 31 NMA-NMA pairs were constructed to mimic the main chain conformations. Thus, a total of 481 amino acid analog pairs were studied in this work.
Interaction energies
the BSSE-corrected QM interaction energies are listed in Table S1 of the supporting materials. For a subset of nonpolar pairs, Nos 94–163, the interaction energies were also calculated at MP2/aug-cc-pVQZ (quadruple-zeta including diffuse functions) level; for selected charged-charged residue pairs (Nos 32–68), the interaction energies were calculated with a variety of QM models including MP2/aug-cc-pVTZ (triple-zeta including diffuse functions), MP2/aug-cc-pVDZ (double-zeta including diffuse functions), MP2/cc-pVTZ (triple-zeta) and MP2/cc-pVDZ (double-zeta). The calculated interaction energies using different ab initio models, the BSSE energies, are also listed in Table S1. The comparison between different QM models is summarized in Table 1.
Table 1.
Comparisons between different QM models.
| No. | QM Model 1 | QM Model 2 | # of data | AUEc | RMSEc |
|---|---|---|---|---|---|
| 1 | Aug-cc-pVQZ + BSSE | aug-cc-pVQZ | 70a | 0.1159 | 0.1434 |
| 2 | Aug-cc-pVTZ + BSSE | aug-cc-pVTZ | 70a | 0.2836 | 0.3482 |
| 3 | Aug-cc-pVTZ + BSSE | aug-cc-pVTZ | 481 | 1.0576 | 1.2643 |
| 4 | Aug-cc-pVTZ + BSSE | aug-cc-pVTZ | 37b | 0.1080 | 0.1777 |
| 5 | Aug-cc-pVDZ + BSSE | aug-cc-pVDZ | 37b | 0.2185 | 0.3384 |
| 6 | cc-pVTZ + BSSE | cc-pVTZ | 37b | 0.5058 | 0.9246 |
| 7 | cc-pVDZ + BSSE | cc-pVDZ | 37b | 0.8049 | 1.7964 |
| 8 | Aug-cc-pVTZ + BSSE | aug-cc-pVQZ + BSSE | 70a | 0.0276 | 0.0397 |
| 9 | Aug-cc-pVTZ + BSSE | aug-cc-pVDZ + BSSE | 37b | 0.0302 | 0.0363 |
| 10 | Aug-cc-pVTZ + BSSE | cc-pVTZ + BSSE | 37b | 0.5007 | 0.5419 |
| 11 | Aug-cc-pVTZ + BSSE | cc-pVDZ + BSSE | 37b | 0.8504 | 0.9350 |
| 12 | Aug-cc-pVDZ + BSSE | cc-pVDZ + BSSE | 37b | 0.8750 | 0.9543 |
For the first 37 charged analog pairs, the BSSE-corrected interaction energies were calculated using all four QM methods. As shown in Table 1, with BSSE corrections (Nos 9–11), the root-mean-square errors (RMSE) errors in comparison to MP2/aug-cc-pVTZ are 0.04, 0.54 and 0.94 for MP2/aug-cc-pVDZ, MP2/cc-pVTZ and MP2/cc-pVDZ, respectively. Furthermore, with diffuse functions (Nos 4–5), the RMSE between the BSSE-corrected and uncorrected are 0.18 and 0.34 kcal/mole for aug-cc-pVTZ and aug-cc-pVDZ, respectively. In contrast, the RMSE between the BSSE-corrected and uncorrected (Nos 6–7) are 0.92 and 1.80 kcal/mole for cc-pVTZ and cc-pVDZ, respectively. Clearly, the diffuse functions are critical for obtaining reliable quantum mechanical energies. In fact, for the 70 non-polar pairs, the aug-cc-pVQZ and aug-cc-pVTZ data shows remarkable agreement. For the BSSE-corrected energies (No 8), the RMSE is 0.04 kcal/mol between aug-cc-pVTZ and aug-cc-pVQZ. This is notably smaller than the RMSE between the BSSE-corrected and uncorrected energies at the aug-cc-pVQZ level. The small difference between aug-cc-pVQZ+BSSE and aug-cc-pVTZ+BSSE data indicates that our choice of using the MP2/aug-cc-pVTZ model with BSSE-correction is adequate since it achieves a good balance between accuracy and efficiency. Interestingly, for the 37 charged analogs pairs, the RMSE between the BSSE-corrected aug-cc-pVTZ and BSSE-corrected aug-cc-pVDZ (No 9) is also small, suggesting that one might choose aug-cc-pVDZ for these dimers.
3.2 Polarizable models are significantly more accurate than the fixed charge models
The polarizable models tested in this paper are summarized in the Table 1 of the companion paper. As stated earlier, the purpose of this paper is to evaluate the dipole interaction models for their ability to reproduce the high-level ab initio energies of amino acid analog pairs. To eliminate the errors caused by different conformations optimized by QM and MM, the MM energies were calculated for the QM-optimized geometries without further optimization. Since no MM optimization was performed, the internal energies, i.e. the bond stretching, bond angle bending, torsional twisting, as well as intramolecular non-bonded energies are precisely cancelled out. The interaction energies were calculated using Eq. (9) and are listed in Table S2 of the supporting materials. Table 2 is a statistical summary of Table S2 in which the maximum errors (MAXE), AUE and RMSE of the 12 polarizable models are listed. Table 3 is a summary of the errors for different interaction types (main chain, charged, aromatic, nonpolar, polar, mixed). Figure 1 shows the scatter plots of MM versus QM energies are shown for the Sets A and Set F models; the left panels are those of the full data set and the right hand panels are those without the 41 charged amino acid analog pairs.
Table 2.
Performance of the molecular mechanical models*
| No. | Model | BSSE-corrected MP2/aug-cc-pVTZ | MP2/aug-cc-pVTZ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| With original VDW parameters |
With adjusted VDW parameters* |
With original VDW parameters |
||||||||
| MaxE | AUE | RMSE | MaxE | AUE | RMSE | MaxE | AUE | RMSE | ||
| 1 | AA | 6.71 | 1.13 | 1.67 | 6.84 | 0.85 | 1.54 | 7.45 | 1.82 | 2.30 |
| 2 | AL | 4.99 | 1.06 | 1.46 | 4.70 | 0.73 | 1.19 | 7.44 | 1.86 | 2.36 |
| 3 | AE | 5.76 | 1.03 | 1.42 | 5.47 | 0.70 | 1.12 | 7.44 | 1.86 | 2.35 |
| 4 | AT | 5.10 | 1.01 | 1.41 | 4.81 | 0.70 | 1.16 | 7.43 | 1.81 | 2.28 |
| 5 | BA | 7.35 | 1.17 | 1.80 | 7.40 | 0.93 | 1.73 | 7.35 | 1.74 | 2.26 |
| 6 | BL | 5.20 | 1.10 | 1.54 | 5.33 | 0.81 | 1.36 | 7.34 | 1.78 | 2.26 |
| 7 | BE | 5.80 | 1.06 | 1.48 | 5.51 | 0.78 | 1.28 | 7.35 | 1.76 | 2.23 |
| 8 | BT | 5.24 | 1.08 | 1.56 | 5.26 | 0.83 | 1.42 | 7.34 | 1.71 | 2.18 |
| 9 | CA | 8.38 | 1.41 | 2.22 | 8.73 | 1.26 | 2.25 | 7.31 | 1.83 | 2.38 |
| 10 | CL | 6.70 | 1.18 | 1.75 | 7.09 | 1.00 | 1.70 | 7.08 | 1.73 | 2.19 |
| 11 | CE | 6.35 | 1.23 | 1.83 | 6.81 | 1.06 | 1.81 | 7.09 | 1.70 | 2.17 |
| 12 | CT | 6.65 | 1.20 | 1.80 | 7.00 | 1.03 | 1.78 | 7.07 | 1.70 | 2.16 |
| 13 | F94 | 12.50 | 2.22 | 3.73 | 11.99 | 1.75 | 3.40 | 14.44 | 3.25 | 4.70 |
| 14 | F03 | 12.40 | 2.07 | 3.43 | 12.18 | 1.62 | 3.10 | 13.42 | 3.02 | 4.39 |
The following adjustments were made to the van der Waals parameters in MM including HO (the hydroxyl hydrogen) from (r0 = 0, ε = 0) to (r0 = 0.25, ε = 0.028), H (amine or amide hydrogen) from (r0 =0.6, ε = 0.0157) to (r0 = 0.65, ε = 0.0055), and CA (aromatic carbon) from (r0 = 1.908, ε = 0.086) to (r0 = 1.908, ε = 0.180).
MaxE: maximum error; AUE: average unsigned error; RMSE: root-mean-square error. All energies are in kcal/mol.
Table 3.
Comparison between molecular mechanical models and QM data for the six individual subsets*
| Model | MainChain | Charged | Aromatic | Nonpolar | Polar | Mixed | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MaxE | AUE | RMSE | MaxE | AUE | RMSE | MaxE | AUE | RMSE | MaxE | AUE | RMSE | MaxE | AUE | RMSE | MaxE | AUE | RMSE | |
| AA | 0.77 | 0.17 | 0.24 | 2.21 | 0.56 | 0.83 | 3.20 | 2.25 | 2.33 | 2.14 | 0.23 | 0.47 | 2.01 | 0.72 | 0.89 | 6.71 | 1.59 | 2.07 |
| AL | 0.75 | 0.17 | 0.23 | 2.20 | 0.55 | 0.83 | 3.20 | 2.25 | 2.33 | 2.14 | 0.23 | 0.47 | 2.01 | 0.74 | 0.91 | 4.99 | 1.45 | 1.76 |
| AE | 0.82 | 0.19 | 0.28 | 2.05 | 0.46 | 0.74 | 3.23 | 2.24 | 2.32 | 2.12 | 0.23 | 0.47 | 1.96 | 0.76 | 0.94 | 5.76 | 1.40 | 1.71 |
| AT | 0.74 | 0.16 | 0.22 | 2.19 | 0.55 | 0.82 | 3.20 | 2.24 | 2.32 | 2.14 | 0.23 | 0.47 | 2.01 | 0.73 | 0.91 | 5.10 | 1.37 | 1.69 |
| BA | 1.43 | 0.49 | 0.65 | 1.10 | 0.33 | 0.43 | 3.21 | 2.17 | 2.26 | 2.08 | 0.24 | 0.47 | 1.74 | 0.61 | 0.78 | 7.35 | 1.68 | 2.28 |
| BL | 3.09 | 1.42 | 1.87 | 1.14 | 0.31 | 0.43 | 3.21 | 2.17 | 2.26 | 2.09 | 0.23 | 0.47 | 1.75 | 0.64 | 0.80 | 5.20 | 1.45 | 1.81 |
| BE | 3.02 | 1.38 | 1.83 | 1.14 | 0.31 | 0.42 | 3.23 | 2.18 | 2.27 | 2.09 | 0.23 | 0.47 | 1.77 | 0.66 | 0.83 | 5.80 | 1.38 | 1.73 |
| BT | 3.12 | 1.43 | 1.88 | 1.13 | 0.31 | 0.43 | 3.21 | 2.17 | 2.26 | 2.10 | 0.23 | 0.47 | 1.75 | 0.63 | 0.79 | 5.24 | 1.41 | 1.84 |
| CA | 3.57 | 1.38 | 1.78 | 2.04 | 0.91 | 1.00 | 3.23 | 2.04 | 2.14 | 1.99 | 0.24 | 0.47 | 2.38 | 0.63 | 0.82 | 8.38 | 1.92 | 2.80 |
| CL | 3.35 | 1.32 | 1.69 | 1.78 | 0.82 | 0.90 | 3.23 | 2.04 | 2.14 | 2.01 | 0.24 | 0.47 | 2.16 | 0.63 | 0.79 | 6.70 | 1.52 | 2.14 |
| CE | 3.27 | 1.31 | 1.68 | 1.86 | 0.85 | 0.93 | 3.23 | 2.04 | 2.15 | 2.01 | 0.24 | 0.47 | 2.12 | 0.62 | 0.79 | 6.35 | 1.62 | 2.25 |
| CT | 3.34 | 1.30 | 1.68 | 1.75 | 0.81 | 0.89 | 3.23 | 2.03 | 2.14 | 2.01 | 0.24 | 0.47 | 2.12 | 0.61 | 0.78 | 6.65 | 1.56 | 2.21 |
| F94 | 3.10 | 0.41 | 0.80 | 5.80 | 1.13 | 1.84 | 4.13 | 2.71 | 2.81 | 2.08 | 0.24 | 0.46 | 2.57 | 0.94 | 1.16 | 12.50 | 3.36 | 4.86 |
| F03 | 1.52 | 0.68 | 0.88 | 3.95 | 0.92 | 1.24 | 3.63 | 2.60 | 2.68 | 2.11 | 0.23 | 0.46 | 2.68 | 0.79 | 1.01 | 12.40 | 3.13 | 4.49 |
The reference QM data are the BSSE-corrected MP2/aug-cc-pVTZ energies. MaxE: maximum error; AUE: average unsigned error; RMSE: root-mean-square error. All energies are in kcal/mol.
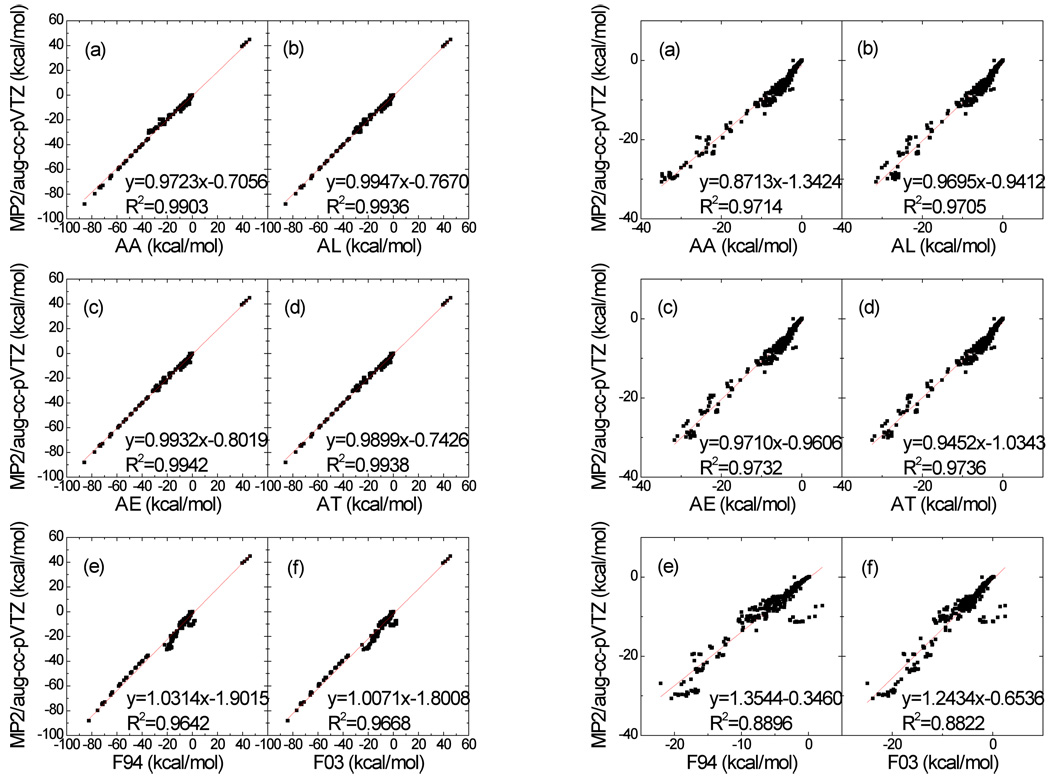
Figure 1.
Correlation between QM interaction energies and those obtained from Set A polarizable models and two fixed charge models. QM energies were the BSSE-corrected MP2/aug-cc-pVTZ energies. Left panel: all pairs, including the charged analog pairs; right panel: charged analog pairs excluded. (a) Model AA, (b) Model AL, (c) Model AE, (d) Model AT, (e) Model F94 (ff94/ff99 − HF/6-31G* RESP charges) and (f) Model F03 (ff03 − B3LYP/cc-pVTZ (solvent = ether) RESP charges).
Several interesting conclusions can be drawn from Table 2 and Table S2. First of all, all the polarizable models outperform the two additive models (F94 and F03). The best model is AT, which achieved a RMSE of 1.406 kcal/mol. The worst polarizable model, CA, has an RMSE of 2.220 kcal/mol. Yet, both are significantly better than the F94 and F03 additive models (3.729 and 3.433 kcal/mol, respectively). The fact that the polarizable models perform much better than the additive ones justifies our effort of developing polarizable force fields.
Further comparisons are made for six of the MM models (AA, AL, AE, AT, F94 and F03) and are shown in Figure 1. On average, the MM interaction energies are less attractive than the QM interaction energies and the average difference are −0.41, −0.71, −0.73, −0.64, −2.18, and −1.87 kcal/mol for Models AA, AL, AE, AT, F94 and F03, respectively. In particular, the interaction energies of the two fixed charge models were notably less attractive in comparison to the QM energies. In contrast, all polarizable models showed substantial improvement over both fixed charge models. We conclude that the deficiency of the fixed charge model is mainly caused by the missing polarization terms.
As illustrated in Figure 1, for all pairs, including the charge-charge interaction pairs (shown in left panels), consistent with the average differences discussed above, all trend lines have negative intercepts, indicating that the MM energies are somewhat less attractive than the QM energies by 0.7 to 1.9 kcal/mole. The slopes of the trend lines are all close to unity, with those of the polarizable models slightly smaller than unity and those of the two fixed charge models slightly greater than unity whereas the correlation coefficients are also close to unity. It is understandable that the two fixed charge models have larger negative intercepts to compensate the underestimated interaction energies (−2.18 and −1.87 kcal/mol for F94 and F03, respectively)
Because the interactions between the charged analogs are dominated by electrostatic force between the formal charges, their interaction energies are notably stronger than those between two neutral groups. Excluding the charge-charge pairs, the correlation for neutral groups is illustrated on the right hand side panels of Figure 1. In comparison to the full set, the ranges are notably smaller and the deviations between QM and MM data can be visualized clearly. Consistent with the full set, all models have negative intercepts. Yet, the slopes now deviate notably from the unity with two clear trends: all slopes of the polarizable models are smaller than unity and the slopes of both fixed charge models are greater than unity. Thus, in terms of relative strengths between the pairs, all polarizable models have stronger interactions and both fixed charge models have weaker interactions. For the two fixed charge models, the slopes exceed the unity by 24% and 35% for F03 and F94, respectively. These large slopes are compensated by the much smaller negative intercepts, and the average differences do not change significantly (−2.27 and −2.04 for F94 and F03, respectively).
It should be noted that the relative strengths are directly correlated to the preference of molecules to form contacts. Therefore, the relative strengths are some of the most critical measurements of the accuracy of the models. This is particularly true for models that are intended to represent heterogeneous environment in which molecules constantly compete against neighbors to gain close contacts. For example, a drug compound may compete with water molecules to gain access to the binding site or two hydrophobic molecules may come together to form a complex by releasing surface water molecules. In our case, the slopes are important indicators of the accuracy of representing the relative strengths of the interactions.
Using the slopes as the measurements, we may conclude that the two fixed charge models underestimate the relative strengths by 24% (F03) and 35% (F94), respectively. Evidently, the fixed charge models substantially underestimate the relative strengths of different interactions. In contrast, the four polarizable models over-estimate the relative strengths by 5% (AT), 3% (AL, AE) and 13% (AA), respectively. Thus, the polarizable models are significantly more accurate in representing the relative strengths of the interactions and have crucial advantage over the fixed charge models in their ability to represent the heterogeneous environment and process. In terms of correlation between QM and MM data, all four polarizable models have R2=0.97, much better than the two fixed-charge models (0.89 and 0.88, for F94 and F03, respectively). This is a remarkable improvement. Thus, the polarizable models are expected to notably improve the interaction energies.
Scaling on 1–4 interactions also has appreciable impact to the performance of the model. In fact, poorer performance in the polarizable models was observed when the 1–4 interactions are scaled down. The best performance was achieved when the 1–4 interactions were fully included (i.e., Set A models). Within the individual model sets, the three Thole models performed similarly, judging from their similar errors from the QM data, and the best models are AT of Set A, BE of Set B and CL of Set C, respectively. Table 2 also shows that the RMSE of the three best models are slowly increased from 1.406 kcal/mol for AT to 1.482 kcal/mol for BE and 1.752 kcal/mol for CL. The 1–4 interaction scaling factors for the three model sets are: 1.0 for Set A (interactions not scaled), 1.2 for Set B and 2.0 for Set C, respectively.
The Thole models consistently out-performed the Applequist models within the same set when the same 1–4 scaling scheme and exclusion of 1–2 and 1–3 interactions. In the same model set, the prediction errors for the Applequist model, with the identical fitting data set, was about 15–20% higher than those of the Thole models. The fact that Applequist models only has 15–20% larger errors than the Thole models is understandable as pointed out by Cieplak et al.,1 because both the fe and ft parameters of the three Thole models approach to 1.0 when the distance between two polarization sites goes beyond 3–4 Å. In other words, the polarization catastrophe is well avoided when 1–2 and 1–3 interactions are omitted in the Applequist models. Nevertheless, the 15%–20% larger errors of the Applequist models indicate that the Thole models consistently performed better than the Applequist models. Thus, in addition to the ability to prevent polarization catastrophe that may take place between two molecules or two parts of a molecule interacting through space while the Applequist models cannot guarantee that, the Thole models also have accuracy advantage over the Applequist models. Therefore, we conclude that the Thole models are the better choices than the Applequist models.
For comparison, the non-BSSE corrected MP2/aug-cc-pVTZ quantum mechanical interaction energies are also listed in Table 2. Better agreement with the BSSE-corrected QM data is observed for all MM models, including ff94 and ff03. In fact, the RMSE significantly increased when MM results are compared to the MP2/aug-cc-pVTZ data without BSSE correction. All the 12 polarizable models in Sets A, B and C perform very similarly and the RMSE range from 2.16 to 2.38 kcal/mol when compared to the MP2/aug-cc-pVTZ interaction energies without BSSE correction; the two fixed charge models had considerably larger errors and the RMSE’s are 4.39 kcal/mole (F03) and 4.7 kcal/mole (F94), respectively. The substantially larger errors are consistent with the observation that the fixed charge models have notable larger errors than the polarizable models when compared to the BSSE-corrected energies. In fact, in both cases, the RMSE of the fix models are about 2.0 kcal/mole larger than the polarizable models, re-enforcing the notion that polarizable models are significantly more accurate than the fixed charge models. Thus, explicit inclusion of the atomic polarizability and the refinement of the polarizability parameters improved the agreement from RMSE ~3.5 kcal/mole of the fixed charge models to ~1.4 kcal/mole level of the polarizable models when compared to the BSSE-corrected QM interaction energies.
More detailed information can be obtained from Table 3 in which the comparison is grouped by the types of interaction pairs. As discussed earlier, we grouped the pairs into mainchain, charged, aromatic, nonpolar, polar, and mixed types. The 31 NMA-NMA pairs constitute the mainchain group, the non-polar group comprises 86 pairs of non-polar residues whereas 35 pairs of polar residues form the polar group, 21 pairs of aromatic pairs form aromatic group, 41 pairs of charged residues form charged group. The remaining 267 pairs are mixed types.
Among the six groups, the nonpolar group stands out as the group of the smallest error between MM and QM energies. This is likely due to the fact that interactions between nonpolar analogs are weak interactions. In fact, the strongest interaction within the group had the interaction energy of −3.8 kcal/mole. For the mainchain group, the A set models outperformed all other models. Interestingly, except F94 model, all MM models were more attractive than the QM models for this group. It is also noteworthy that the fixed charge models outperformed both B and C sets polarizable models in this group.
For the charged-charged group, the B set models outperformed all other sets. Interestingly, the C set models have tendency to over estimate the attractive energies between the charged analogs whereas the A set models tend to under estimate such interactions. It is important to note the agreement between the polarizable and QM models within this group. Because of the presence of the formal charges, the polarization effect in this group can be considerably stronger than any other groups. Thus, the agreement clearly shows that the induced dipole model is adequate to represent the strong polarization effect.
The aromatic group stands as the most challenging group. In fact, all MM models performed poorly in the aromatic group and the RMSE’s were all in the range of 2.2 to 2.8 kcal/mole. The MM models have tendency to under estimate the attractive force between the aromatic analogs. On average, the underestimation ranged from 2.0 to 2.3 kcal/mole of the polarizable models and 2.6 to 2.7 kcal/mole for the fixed charge models. In contrast, all MM models performed well in the polar group with the RMSE ranged from 0.8 to 0.9 kcal/mole of the polarizable models and 1.0 to 1.2 kcal/mole for the fixed charge models. The mixed group is the largest group comprising 267 pairs. Within this group, the two fixed charge models performed notably worse than the polarizable models. The RMSE of the fixed models are 4.86 (F94) and 4.49 kcal/mole (F03), respectively, notably greater than the typical RMSE of 1.7 kcal/mole to 2.3 kcal/mole of the polarizable models (CA has a RMSE of 2.8 kcal/mole). This is a clear indication that polarizable models have significant advantage over the fixed charge models in representing heterogeneous interactions. Taken together, the comparison between the groups suggests that the polarizable models can significantly improve the accuracy of interaction energy calculations and the aromatic group remains challenge targets, despite the notable improvement over the fixed charge models.
3.3 Analyses of the outliers
Despite the remarkable improvement summarized earlier, large differences exist between the QM and MM interaction energies. Although these large differences are limited only to relatively small number of pairs, it is imperative to provide detailed analyses on these “outliers”. Insight from these analyses may shed light toward further improvement. Since Model AT is the best-performing model, our following analysis is based on this model. Among the 481 amino acid analog pairs, there were 44 outliers whose MM and QM energy difference is greater than 2.5 kcal/mol. These 44 outliers can be classified into five groups based on the structural features.
The first group of outliers contains dimers characterized by stacked or T-shaped aromatic rings. The second group, contains dimers forming a strong hydrogen bond between charged residues. The third group of outliers is characterized by the in-plane ion-ring interactions. The fourth group of outliers is characterized by the off-plane ion-ring interaction. Finally, some outliers involve sulfur-containing molecules: cysteine and methionine. The first four groups of outliers correspond to four types of molecular interactions: the π-π interactions of stacked/T-shaped rings, the hydrogen-bonds involving charged residues, the n-σ* interactions of the in-plane ion-ring structures, the cation-π interactions of the off-plane ion-ring structures. The representatives of the five groups of outliers are shown in Figure S1.
The MM energies of outliers and the differences from the QM data are listed in Table S3 for five MM models, which are AL, AE, AT and F94 and F03. Table 4 summarizes the statistical results of the interaction energies of the 44 outliers. Overall, the three polarizable models significantly outperform the two non-polarizable models. The RMSE are 3.179, 3.133, 3.257, 6.368 and 6.668 kcal/mol for AL, AE, AT, F94 and F03, respectively. Thus, on average, the RMSE was improved by more than 3.0 kcal/mole. This result suggests that for the ‘difficult’ molecules, the induction energies are helpful in improving the model accuracy. As to the specific group of outliers, the polarizable models excel in modeling the π-π, n-σ* and cation-π interactions. In fact, accuracy of the fixed charge models is unacceptable; with RMSE of the n-σ* was more than 10 kcal/mole! Interestingly, the F94 and F03 models outperform the three polarizable models for the four outliers that form strong hydrogen-bonds between charged residues. One possible explanation could be because the van der Waals parameters of hydrogen have been well tuned to facilitate the formation of hydrogen bonds in the additive force fields. As such, different van der Waals parameters of hydrogen may be needed for the polarizable models to better describe hydrogen bonding.
Table 4.
Statistics of the 44 outliers*
| Interaction Type | AL | AE | AE | F94 | F03 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| AUE | RMSE | AUE. | RMSE | AUE | RMSE | AUE | RMSE | AUE | RMSE | |
| With original van der Waals parameters | ||||||||||
| π-π | 3.090 | 3.121 | 3.104 | 3.135 | 3.086 | 3.117 | 3.723 | 3.791 | 3.511 | 3.555 |
| H-bonding | 2.818 | 2.874 | 2.831 | 2.844 | 3.740 | 3.751 | 2.234 | 2.234 | 1.786 | 1.795 |
| n-σ* | 3.513 | 3.587 | 3.918 | 4.021 | 3.562 | 3.641 | 10.009 | 10.030 | 10.783 | 10.829 |
| Cation-π | 3.158 | 3.186 | 2.557 | 2.593 | 3.110 | 3.138 | 6.844 | 6.942 | 7.193 | 7.269 |
| Sulfur-containing | 2.725 | 2.729 | 2.780 | 2.784 | 2.717 | 2.721 | 3.011 | 3.015 | 2.717 | 2.725 |
| Total | 3.131 | 3.179 | 3.047 | 3.133 | 3.208 | 3.257 | 5.714 | 6.368 | 5.839 | 6.668 |
| With adjusted van der Waals parameters | ||||||||||
| π-π | 0.825 | 1.084 | 0.829 | 1.083 | 0.822 | 1.079 | 1.370 | 1.724 | 1.173 | 1.448 |
| H-bonding | 2.814 | 2.883 | 2.827 | 2.847 | 3.735 | 3.751 | 2.239 | 2.242 | 1.791 | 1.795 |
| n-σ* | 3.178 | 3.259 | 3.582 | 3.696 | 3.226 | 3.314 | 9.674 | 9.698 | 10.448 | 10.499 |
| Cation-π | 3.625 | 3.655 | 3.025 | 3.066 | 3.578 | 3.608 | 6.376 | 6.543 | 6.725 | 6.848 |
| Sulfur-containing | 2.135 | 2.152 | 2.190 | 2.202 | 2.127 | 2.144 | 2.420 | 2.423 | 2.127 | 2.156 |
| Total | 2.463 | 2.784 | 2.377 | 2.684 | 2.541 | 2.870 | 4.746 | 5.821 | 4.875 | 6.151 |
AUE: average unsigned error; RMSE: the root-mean-square error. All energies are in kcal/mol.
The π-π interaction is associated with stacking configuration of π-electron systems. There are many factors contributing to the formation of this unique structural feature, which include the intermolecular overlapping of p-orbitals between two or more π-conjugated systems, the vdW interactions, the charge-transfer interactions and dipole-dipole interactions. Since the RMSE of the polarizable models are smaller than those of the fixed charge models by ~0.5 kcal/mol, polarization energy does stabilize the aromatic stacking. For five stacked pairs (Phe_Trp_1, Phe_Trp_5, Phe_Tyr_7, Trp_Trp_4, Tyr_Trp_2 and Tyr_Tyr_3) the interaction energies were also calculated at the B3LYP/aug-cc-pVTZ level with BSSE correction. The B3LYP interaction energies are significantly underestimated in comparison with our BSSE-corrected MP2/aug-cc-pVTZ Energies with the prediction errors ranging from 10.4 to 16.1 kcal/mol. This is consistent with the notion that the dispersion energy is not well described in the B3LYP method.34–36
In the case of strong hydrogen bonds formed with the carboxyl oxygen atoms, the three polarizable models overestimated the interaction energies but the two fixed charge models underestimated them. Hydrogen bond involves the delocalization of the lone pair (n) of the hydrogen bond acceptor (here the carboxyl oxygen) over the anti-bonding orbital (σ*) of the hydrogen bond donor.37,38 Thus, the result suggests that it could be possible to reduce the MM errors by adjusting the relevant vdW parameters.
For the hydrogen-bond-like interactions between carboxyl oxygen atoms and aromatic carbon atoms, all of the MM models, both polarizable and additive models underestimated the interaction energies. In fact, in this group the fixed charge models (F94 and F03) performed extremely poorly with RMSE greater than 10 kcal/mole! To investigate the mechanism that leads to the strong interaction between a charged residue and an aromatic residue observed in quantum mechanical results, we conducted natural bond orbital (NBO) analysis for five outliers in this category.39,40 As a control, the NBO analysis was also performed for three amino acid analog pairs that form hydrogen bonds. The MP2/6-311++(d,p) optimized conformations of the eight amino acid pairs are shown in Figure S2. The dashed lines designate where the hydrogen bonds are formed. All the NBO analysis were performed in a separate single point calculation after the MP2/6-311++(d,p) optimization. The calculated delocalization energies of the eight amino acid analog pairs are listed in Table 5. The components of the degenerated orbitals of the lone pairs of the carbonyl or hydroxyl oxygen are listed in the table. Clearly, the lone pair orbitals are degenerated and the s-rich lone pair (ns) has ~ 60% s and ~ 40 % p character, whereas, the p-rich lone pair (np) has nearly 100% p character.
Table 5.
The delocalization energies of the amino acid analog pairs involved in n→σ* interactions*
| Analog Pairs |
Edeloc (kcal/mol) | ns | np | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ns→σ* | np→σ* | Total | Occup. | s (%) | p (%) | d (%) | Occup. | s (%) | p (%) | d (%) | |
| Asp_Phe_1 | 1.45 | 3.58 | 5.03 | 1.97640 | 61.70 | 38.28 | 0.02 | 1.91797 | 0.31 | 99.64 | 0.06 |
| Asp_Trp_3 | 1.94 | 3.44 | 5.38 | 1.97585 | 61.76 | 38.22 | 0.02 | 1.91707 | 0.29 | 99.66 | 0.06 |
| Asp_Tyr_4 | 3.55 | 0.29 | 3.84 | 1.97385 | 61.89 | 38.09 | 0.02 | 1.92029 | 0.00 | 99.94 | 0.06 |
| Glu_Phe_5 | 3.00 | 4.14 | 7.14 | 1.97522 | 61.20 | 38.78 | 0.02 | 1.91665 | 0.76 | 99.18 | 0.06 |
| Glu_Tyr_3 | 1.55 | 3.59 | 5.08 | 1.97642 | 61.76 | 38.22 | 0.02 | 1.91695 | 0.14 | 99.80 | 0.06 |
| Ser_Glu_2 | 6.74 | 22.8 | 29.54 | 1.96815 | 55.53 | 44.45 | 0.02 | 1.90472 | 6.75 | 93.21 | 0.04 |
| Ser_Asn_1 (O-H···O) | 1.63 | 5.50 | 7.13 | 1.97611 | 59.15 | 40.83 | 0.02 | 1.90207 | 0.22 | 99.71 | 0.07 |
| Ser_Asn_1 (N-H···O) | 1.92 | 1.91 | 3.83 | 1.98275 | 44.82 | 55.16 | 0.03 | 1.96724 | 1.60 | 98.37 | 0.03 |
| Ser_Asn_2 | 4.90 | 0.00 | 4.9 | 1.98104 | 48.20 | 51.78 | 0.02 | ||||
Edeloc is calculated through NBO analysis. ns and np are the degenerated orbitals of lone pairs of the carboxyl oxygen, σ* is the antibonding orbital of H-D (D is the hydrogen bond donor). For each lone pair degenerated orbital, the occupancy and the s, p and d components are shown. All energies are in kcal/mol.
It is obvious that the hydrogen-bond-like interactions (Nos 1–5 in Table 5) are as strong as hydrogen bonding interactions not involved in charged residues (Nos 7–9), although the delocalization energies of hydrogen-bond-like interactions are only 17 to 25% of that of a very strong hydrogen bond forming between the hydroxyl group of Ser and the carboxyl group of Glu. Thus the deficiency of the proposed polarizable models that systematically underestimate the interaction energies of the second group of pairs can be remedied by taking the strong n→σ* interaction into account. A possible way to account for the strong n→σ* interaction is to reoptimize the vdW parameters.
The investigation on the geometrical parameters of the third group outliers further confirms the formation of hydrogen-bond-like interactions. The distances between A (carboxyl oxygen of charged residues) and D (an aromatic carbon) ranges from 3.174 to 3.317 Å and the hydrogen bond angles (A···H-D) ranges from 156 to 179° for the five outliers listed in Table 5 (Nos 1–5).
Given the n→σ* interaction is as strong as normal hydrogen bonds, we conducted a survey to find out how abundant this structure feature is in protein crystal structures. We used a similar criterion for defining a hydrogen bond to do the database search: the distance between A and D must be 3.3 Å or less; the hydrogen bond angle must be 120° or larger. For the 6244 filtered protein structures, 2310 have at least one such kind of hydrogen-bond-like structural feature. Some twenty years ago, Levitt and Perutz pointed out that aromatic rings can act as hydrogen bond acceptor.41 Until today, it is still a controversial issue. Evidently, our NBO analysis indicates that the delocalization energies arise from the delocalization of the electron pair of carboxyl oxygen into anti-bonding orbital of the aromatic H-C bond, a mechanism that is similar to hydrogen bonding. Delocalization energies of the outliers in this category are as big as those of the normal hydrogen bonds.
The fourth group of outliers is characterized by presence of the cation-π interaction. Similar to the outliers that form strong hydrogen bonds, the polarizable models systematically overestimate, while the fixed charge models systematically underestimate the interaction energies. The RMSE of the 13 outliers, which are in the range from 2.59 to 3.19 kcal/mol, are significantly smaller than those of fixed charge models (6.94 and 7.3 for the Models F94 and F03, respectively). It is clear that the polarization energy makes a significant contribution to the cation-π interaction. In recent publication, Tateno and Hagiwara 36 evaluated the stabilization energies in π-π and cation-π interactions by ab initio calculations. Our calculation results are consistent with theirs in that the MM energies of additive models are significantly underestimated for the cation-π interactions.
The overestimation of the cation-π interaction may be caused by the underestimation of the polarizabilities of aromatic systems using the Thole's parameters. In the AMOEBA force field, larger values of the atomic polarizabilities of the aromatic systems than those suggested by Thole are used to overcome this problem.42 We have examined the data for 38 aromatic molecules in the data set. For the four Set A models, the molecular polarizabilties are only slightly overestimated (0.24, 0.20, 0.29 and 0.23% for AA, AL, AE and AT, respectively) and the average percent errors are about 1.24% for all the four models. Therefore, our polarizable models have satisfactory performance for aromatic systems.
The overestimation of the cation-π interaction for our models is likely caused by the fact that ions have more smeared charge distribution than neutral organic molecules as characterized by the damping factor in Thole models.43–45Besides the van der Waals parameterization, a potential remediation of this problem could be different screening factors or atomic polarizabilities for ions.
3.4 The role that the vdW parameters play in MM models
We shall note that the vdW parameters applied in this study were originally parameterized for the fixed charge models based on simulations of pure liquid. Despite the remarkable accuracy and transferability, inclusion of the explicit polarization terms may require reoptimization of the vdW parameters. In addition, Tateno et al. suggested that the use of effective vdW potential, which is a functional of the electron density of the system, could significantly improve the interaction energies of stacked rings.46 Exploration of new functional forms to account for those interactions is another direction to improve our polarizable models. For example, the more elaborate polarizability models, as the one proposed by Ponder and Ren, 7,8 which takes the interaction between induced dipoles and higher permanent electric moments into account, may be helpful in reducing certain prediction errors, for example those observed in the systems with overlapping of p-orbitals of the π- conjugated systems. Bartlett et al. recently found that the n→π* interaction, which arises from electron delocalization analogous to that of the hydrogen bond, plays an important role in stabilizing many secondary structures of proteins.47 The n→π* interaction has not been taken explicitly into account in the current molecular mechanical force fields.
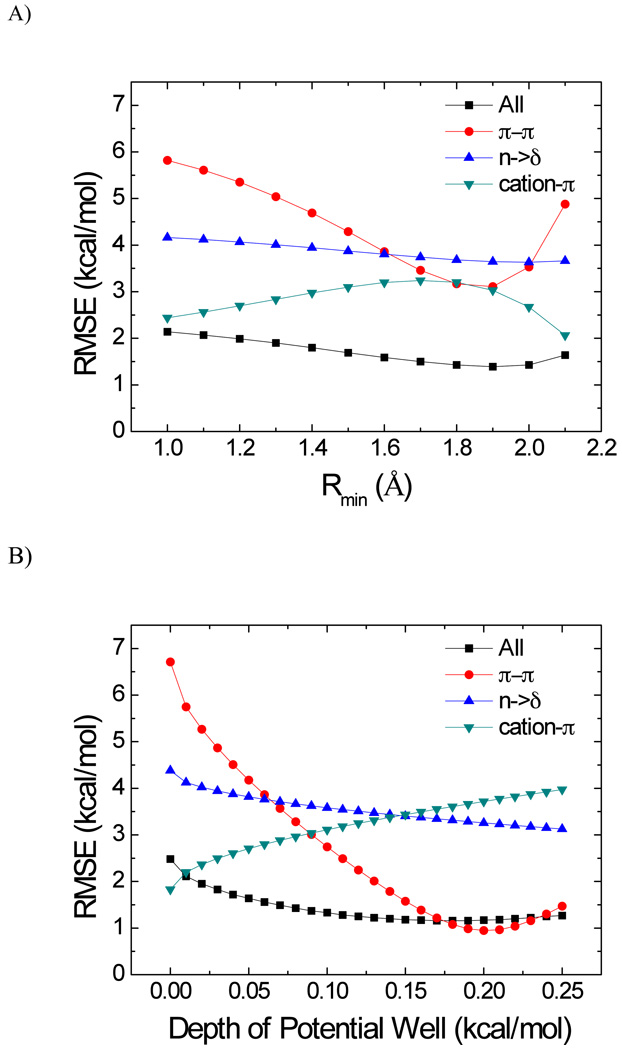
Motivated by the substantial deviation between QM and MM models in the hydrogen bonding, π-π, cation-π and n→π* interactions, we focus on the optimization of the vdW parameters of three atom types: CA (sp2 carbon in an aromatic ring), HO (a hydrogen atom bonded to oxygen) and H (a hydrogen atom bonded to nitrogen) in order to reduce the errors between the QM and MM energies. Our goal is to illustrate the principle that minor adjustments to key vdW parameters may lead to notable improvement in model accuracy. Thus, we will focus on Model AT.
By an adaptive systematic search, we found that the following adjustments to the vdW parameters: CA from (r0 = 1.908, ε = 0.086) to (r = 1.908, ε = 0.180), HO from (r0 = 0, ε = 0) to (r0 = 0.25, ε = 0.028), H from (r0 =0.6, ε = 0.0157) to (r0 = 0.65, ε = 0.0055). In this search protocol, a large searching step was applied to search a large range of the potential well depth or radius at the first stage, and then in the following focus searching stage a smaller search step and searching range were applied. Dependence of the RMSE on the vdW parameters of CA is illustrated in Figure 2. When radius parameter (rmin) was optimized, the potential well depth took the original value (0.086); similarly, the original value of the radius parameter (1.908 Å) was used when the potential well depth was optimized. The adjustments reduced the RMSE of the Model AT from 1.41 to 1.16 kcal/mol in comparison to the original parameters and the AUE dropped from 1.01 to 0.70 kcal/mol. In fact, the adjustments also reduced the RMSE of all MM models except Model CA, for which the RMSE slightly increases from 2.22 to 2.25 kcal/mol.
Figure 2.
The dependence of RMSE as functions of van der Waals parameters of the aromatic carbon. (a) radius parameters − rmin (ε= 0.086 kcal/mol), (b) potential well depth (rmin = 1.908 Å).
The interaction energies calculated using new vdW parameters are listed in Table S4 of the supporting materials and are summarized in Table 2 in the columns under the title “with adjusted VDW parameters”. Table S5 summarizes the performance using new vdW parameters for the six different groups (main chain, charged, aromatic, nonpolar, polar, mixed). In comparison to the data obtained using original vdW parameters, the minor adjustments notably improved the RMSE of the aromatic group from greater than 2.0 to 2.7 kcal/mole to 0.6 to 0.9 kcal/mole. Another group that was notably improved was the polar group with the RMSE of the polarizable models reduced from 0.8 to 0.9 kcal/mole range to 0.5 to 0.8 kcal/mole range. The energies and residuals of the 44 outliers calculated using the new vdW parameters are listed in Table S6. For the 13 outliers that form π-π interactions, the RMSE of Model AT is significantly reduced from 3.117 kcal/mol for the original parameters to 1.079 kcal/mol for the new parameters.
We want to emphasize that the van der Waals optimization presented here is rather exploratory. The sole purpose is to show that the van der Waals parameters do have notably influence to the quality of the polarizable models. Therefore, the new vdW parameters may not be suitable to use in a polarizable or additive force field, simply because they have not been developed to reproduce the liquid properties. These vdW parameters will be optimized systematically to reproduce various properties and systems in both the gas and liquid phases in our effort of developing highly accurate and reliable polarizable force fields. Nevertheless, the minor adjustment clearly shows that the accuracy of the MM model can be improved by adjusting key vdW parameters.
To thoroughly evaluate our polarizable models, we also need to study interactions associated with water, including water and ions, water and amino acids, ion and amino acids, etc. In certain situations, these interaction energies are more sensitive to a polarizable model, as illustrated by Ponder and Ren and their co-workers.7,43,48,49 Indeed, a polarizable water model is under development that is consistent with the polarization schemes presented in this work. Once we have satisfactory models for water and ions, we will test our polarizable models on various properties and systems in both gas and condensed phases. Indeed, such evaluation will be an important step in the development of any force field.
4. Conclusions
We created a benchmark data set for evaluating molecular mechanics models. The data set comprises 481 amino acid main chain and side chain analog pairs in configurations observed in real protein structures and covers most of the types of intermolecular interactions. These pairs were optimized using MP2/6-311G++(d,p) quantum mechanical approaches and the ab initio interaction energies were calculated at the MP2/aug-cc-pVTZ with BSSE correction. Using the BSSE-corrected ab initio interaction energies as the reference, we attempted to provide a quantitative assessment on the performance and accuracy of four types of polarizable models: the Applequist, Thole linear, Thole exponential and Thole Tinker-like exponential. The models are grouped into several model sets based on how 1–2, 1–3 and 1–4 interactions were treated. Encouragingly, we found out that all the polarizable models perform better than the two non-polarizable models Amber force fields: F94/ff99 and F03. The best performing model, AT achieves a root-mean-square error of 1.406 kcal/mol, less than half of the errors for F94/ff99 (3.729 kcal/mol) and F03 (3.433 kcal/mol). Furthermore, using the trend line slopes as indicators of accuracy in representing the relative strengths of the interactions, we found that the two fixed charge models substantially underestimate the relative interaction strengths by 24% (F03) and 35% (F94), respectively. In contrast, the four polarizable models over-estimate the relative strengths by 5% (AT), 3% (AL, AE) and 13% (AA), respectively. Evidently, the polarizable models are significantly more accurate than the fixed charge models. Thus, our effort in developing polarizable models has been paid off by their significantly improved accuracy in the ability to reproduce the ab initio data. In addition, we have identified outliers that are grouped in five groups including: aromatic ring parallel stacking and T-shaped, strong hydrogen bonds formed by charged residues, in plane and out of plane ion-ring interactions and sulfur-containing molecules. We have demonstrated that the errors caused by the π-π interactions can be greatly reduced through proper vdW parameters optimization. Our vdW energy component exploration study provides guidance on how to conduct parameterization of this term in the future. We believe that the best performing polarizable models tested here (AL, AE and AT) have a potential to become reliable and accurate molecular mechanical models in studying protein structures and energies, especially after optimization of the vdW terms.
Supplementary Material
Acknowledgments
We are grateful to acknowledge the research support from NIH (R01GM79383, Y. Duan, P.I.) and the TeraGrid for the computational time (TG-CHE090098, J. Wang, P.I. and TG-CHE090135, P.Cieplak, P.I.). We thank Professor Tom Cundari at University of North Texas and Dr. Arne Strand at University of Texas Southwestern Medical Center for the instructive discussions on the hydrogen bond-like interactions between a carboxyl group and an aromatic ring.
Abbreviations
- AUE
average unsigned errors
- RMSE
root-mean-square errors
- APE
average percent errors
- R2
correlation coefficient square
- vdW
van der Waals
- NMA
N-methylacetamide
Footnotes
Supporting Information Available:
The BSSE corrected MP2/aug-cc-pVTZ energies as well as the interaction energies calculated by a variety of polarizable models are listed in Tables S1, and S4. The statistical analysis on the performance of 12 polarizable models and two fixed charge models with adjusted vdW parameters is presented in Table S5. The interaction energies of the outliers are listed in Table S3 and those using the adjusted vdW parameters are listed in Table S6. Representative structures of the outliers are shown in Figure S1 and those with strong n→σ* interactions are shown in Figure S2. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Cieplak P, Dupradeau FY, Duan Y, Wang JM. Journal of Physics-Condensed Matter. 2009:21. doi: 10.1088/0953-8984/21/33/333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Xie WS, Pu JZ, MacKerell AD, Gao JL. J Chem Theory Comput. 2007;3:1878. doi: 10.1021/ct700146x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Borodin O. Journal of Physical Chemistry B. 2009;113:11463. doi: 10.1021/jp905220k. [DOI] [PubMed] [Google Scholar]
- 4.Patel S, Mackerell AD, Brooks CL. Journal of Computational Chemistry. 2004;25:1504. doi: 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
- 5.Banks JL, Kaminski GA, Zhou RH, Mainz DT, Berne BJ, Friesner RA. Journal Of Chemical Physics. 1999;110:741. [Google Scholar]
- 6.Kaminski GA, Stern HA, Berne BJ, Friesner RA. Journal of Physical Chemistry A. 2004;108:621. [Google Scholar]
- 7.Ponder JW, Case DA. Adv. Protein Chem. 2003;66:27. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 8.Ren P, Ponder JW. J Comput Chem. 2002;23:1497. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 9.Cieplak P, Caldwell J, Kollman PA. J Comput Chem. 2001;22:1048. [Google Scholar]
- 10.Wang Z-X, Zhang W, Wu C, Lei H, Cieplak P, Duan Y. Journal of Computational Chemistry. 2006;27:781. doi: 10.1002/jcc.20386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Applequist J, Carl JR, Fung KK. Journal of the American Chemical Society. 1972;94:2952. [Google Scholar]
- 12.van Duijnen PT, Swart M. Journal of Physical Chemistry A. 1998;102:2399. [Google Scholar]
- 13.Thole BT. Chemical Physics. 1981;59:341. [Google Scholar]
- 14.de Vries AH, van Duijnen PT, Zijlstra RWJ, Swart M. J. elec. Spec. Rel. Phen. 1997;86:49. [Google Scholar]
- 15.Wang Z-X, Wu C, Lei H, Zhang W, Cieplak P, Duan Y. 2006 to be submitted. [Google Scholar]
- 16.Wang J, Cieplak P, Li J, Hou T, Luo R, Duan Y. J Phys Chem B. 2011 doi: 10.1021/jp112133g. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang JM, Cieplak P, Kollman PA. Journal of Computational Chemistry. 2000;21:1049. [Google Scholar]
- 18.Cieplak P, Cornell WD, Bayly C, Kollman PA. J. Comp. Chem. 1995;16:1357. [Google Scholar]
- 19.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. Journal of the American Chemical Society. 1995;117:5179. [Google Scholar]
- 20.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong GM, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang JM, Kollman P. Journal of Computational Chemistry. 2003;24:1999. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 21.Boys SF, Bernardi F. Molecular Physics. 1970;19:553. [Google Scholar]
- 22.Simon S, Duran M, Dannenberg JJ. Journal Of Chemical Physics. 1996;105:11024. [Google Scholar]
- 23.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. Nucleic Acids Res. 2000;28:235. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Case DA, Darden TA, Cheatham ITE, Simmerling C, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Wang B, Hayik S, Roitberg A, Seabra G, Kolossvary I, Wong KF, Paesani F, Vanicek J, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh MJ, Cui G, Roe DR, Mathews DH, Seetin MG, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. San Francisco: University of California; 2010. [Google Scholar]
- 25.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery J, J A, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Wallingford CT: Gaussian, Inc; 2004. [Google Scholar]
- 26.Gould IR, Kollman PA. Journal of Physical Chemistry. 1992;96:9255. [Google Scholar]
- 27.Beachy MD, Chasman D, Murphy RB, Halgren TA, Friesner RA. Journal of the American Chemical Society. 1997;119:5908. [Google Scholar]
- 28.Schrodinger LLC. New York, USA: 2004. [Google Scholar]
- 29.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J. Phys. Chem. 1994;98:11623. [Google Scholar]
- 30.Bayly CI, Cieplak P, Cornell WD, Kollman PA. Journal Of Physical Chemistry. 1993;97:10269. [Google Scholar]
- 31.Tomasi J, Mennucci B, Cammi R. Chem Rev. 2005;105:2999. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 32.Pascualahuir JL, Silla E, Tomasi J, Bonaccorsi R. Journal of Computational Chemistry. 1987;8:778. [Google Scholar]
- 33.Miertus S, Scrocco E, Tomasi J. Chemical Physics. 1981;55:117. [Google Scholar]
- 34.Meijer EJ, Sprik M. Journal Of Chemical Physics. 1996;105:8684. [Google Scholar]
- 35.Dobes P, Otyepka M, Strnad M, Hobza P. Chem-Eur J. 2006;12:4297. doi: 10.1002/chem.200501269. [DOI] [PubMed] [Google Scholar]
- 36.Tateno M, Hagiwara Y. Journal of Physics-Condensed Matter. 2009;21 doi: 10.1088/0953-8984/21/6/064243. [DOI] [PubMed] [Google Scholar]
- 37.Weinhold F. Adv Protein Chem. 2005;72:121. doi: 10.1016/S0065-3233(05)72005-2. [DOI] [PubMed] [Google Scholar]
- 38.Khaliullin RZ, Cobar EA, Lochan RC, Bell AT, Head-Gordon M. Journal of Physical Chemistry A. 2007;111:8753. doi: 10.1021/jp073685z. [DOI] [PubMed] [Google Scholar]
- 39.Reed AE, Weinstock RB, Weinhold F. Journal Of Chemical Physics. 1985;83:735. [Google Scholar]
- 40.Foster JP, Weinhold F. Journal of the American Chemical Society. 1980;102:7211. [Google Scholar]
- 41.Levitt M, Perutz MF. Journal of Molecular Biology. 1988;201:751. doi: 10.1016/0022-2836(88)90471-8. [DOI] [PubMed] [Google Scholar]
- 42.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Jr, Head-Gordon M, Clark GN, Johnson ME, Head-Gordon T. J Phys Chem B. 2010;114:2549. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jiao D, King C, Grossfield A, Darden TA, Ren P. J Phys Chem B. 2006;110:18553. doi: 10.1021/jp062230r. [DOI] [PubMed] [Google Scholar]
- 44.Piquemal JP, Perera L, Cisneros GA, Ren P, Pedersen LG, Darden TA. J Chem Phys. 2006;125 doi: 10.1063/1.2234774. 054511. [DOI] [PubMed] [Google Scholar]
- 45.Wu JC, Piquemal JP, Chaudret R, Reinhardt P, Ren P. J Chem Theory Comput. 2010;6:2059. doi: 10.1021/ct100091j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hagiwara Y, Tateno M. Journal of Physics-Condensed Matter. 2009;21 doi: 10.1088/0953-8984/21/6/064243. [DOI] [PubMed] [Google Scholar]
- 47.Bartlett GJ, Choudhary A, Raines RT, Woolfson DN. Nature Chemical Biology. 2010;6:615. doi: 10.1038/nchembio.406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ren PY, Ponder JW. J. Phys. Chem. B. 2004;108:13427. [Google Scholar]
- 49.Ren PY, Ponder JW. J. Phys. Chem. B. 2003;107:5933. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.