Impact of 2′-hydroxyl sampling on the conformational properties of RNA: Update of the CHARMM all-atom additive force field for RNA

Abstract

Here, we present an update of the CHARMM27 all-atom additive force field for nucleic acids that improves the treatment of RNA molecules. The original CHARMM27 force field parameters exhibit enhanced Watson-Crick (WC) base pair opening which is not consistent with experiment while analysis of MD simulations show the 2′-hydroxyl moiety to almost exclusively sample the O3′ orientation. Quantum mechanical studies of RNA related model compounds indicate the energy minimum associated with the O3′ orientation to be too favorable, consistent with the MD results. Optimization of the dihedral parameters dictating the energy of the 2′-hydroxyl proton targeting the QM data yielded several parameter sets, which sample both the base and O3′ orientations of the 2′-hydroxyl to varying degrees. Selection of the final dihedral parameters was based on reproduction of hydration behavior as related to a survey of crystallographic data and better agreement with experimental NMR J-coupling values. Application of the model, designated CHARMM36, to a collection of canonical and non-canonical RNA molecules reveals overall improved agreement with a range of experimental observables as compared to CHARMM27. The results also indicate the sensitivity of the conformational heterogeneity of RNA to the orientation of the 2′-hydroxyl moiety and support a model whereby the 2′-hydroxyl can enhance the probability of conformational transitions in RNA.

Introduction

RNA is a versatile macromolecule^1–3 involved in a range of biological processes. These processes include roles in maintaining, regulating, processing, and transmitting genetic information throughout the cell. In addition, selected RNA molecules are capable of performing enzymatic activity and it is known that a given RNA sequence can assume different conformations. RNA conformations may be separated into two classes of structural forms, the canonical A-form, similar to that observed in DNA, and the non-canonical forms.⁴ Non-canonical structures of RNA vary and involve motifs such as hairpins, junctions, and bulges ^5–7, which display variety of different intramolecular interactions between nucleotides such as mismatched base pairs and Hoogsteen interactions ^5–7.

Molecular dynamics (MD) simulations and associated empirical force field based methods are important techniques for the investigation of atomic details of the structure-function relationships of biological macromolecules ⁸. In the case of RNA, a number of systems have been studied using force field methods. Nilsson and coworkers have extensively used the CHARMM27 force field to study non-canonical forms of RNAs ^9–13 including the stability and flexibility of a series of RNA molecules that contain internal loops of variable lengths ¹⁰ or different tetraloops ^9,12. The base flipping process in a duplex RNA has been studied using umbrella sampling simulations, from which free energy profiles were obtained ¹³. Pan et al have also used the force field to study the helicoidal parameters in the GU mismatches regions of RNA molecules, with the obtained results in agreement with experimental data^14,15. In addition, the CHARMM27 force field has been shown to give insights on DNA-RNA hybrid structures, explaining their differential biochemical profiles with respect to their sequence ¹⁶ and, more recently, insights into the mechanism by which urea denatures RNA has been presented ¹⁷.

The AMBER force field has been employed by Sponer and coworkers to study canonical and non-canonical RNA molecules ¹⁸. Kierzek et al. have studied the differential flexibilities of DNA and RNA duplexes showing the base stacking and hydrogen bonding interactions to enhance the stability of canonical RNA molecules ¹⁹. Csaszar et al. applied the AMBER force field to investigate the importance of the C8 nucleotide for maintaining the tertiary structure of the pseudoknot Beet Western Yellows Virus RNA ²⁰. They concluded that the N3 of C8 was protonated in the native structure and that upon mutating C8 to U8 the pseudoknot junction was destabilized. Beyond the above studies, both the CHARMM and the AMBER force fields have shown utility in explaining experimental observations reasonably well for a range of RNA molecules ^21–29.

Results obtained from MD simulations greatly depend on the quality of force field parameters that are employed in addition to other factors such as sampling issues and the particular simulation methodology adopted ^18,30,31. While a range of MD simulations of RNAs have been performed using the CHARMM or AMBER force fields, only recently have the force fields begun to be systematically evaluated. For example, Deng and Cieplak examined the behavior of two hairpin RNA molecules for both force fields and saw subtle differences in the unfolding of the molecules ³². In another study Bessova et. al. showed that the AMBER Parmbsc0 force eld makes the A-RNA duplex more compact in comparison to the Parm99³³. The Parmbsc0 force field represents an adjustment of the Parm99 force field with respect to dihedral parameters associated with the alpha and gamma dihedrals ^28,31. In addition, improvements in the AMBER FF with respect to χ dihedral parameters have been presented ³⁴. In the latest parametrization of the AMBER RNA force field (parmbsc0+OL), Banas et. al. showed that adjustments of χ dihedral parameters lead to improvements in the treatment of non-canonical RNA regions as well as avoiding the formation of “ladder-like” conformations in tetraloop simulations³⁵.

The CHARMM27 all-atom nucleic acid force field was originally developed based on a combination of data from quantum mechanical (QM) calculations of small molecules representative of nucleic acids and MD simulations of canonical DNA and RNA ^25,26. While CHARMM27 has been successfully applied to a number of RNAs, as described above, a tendency for local opening of the Watson-Crick base pairs is known ¹⁴. While imino proton exchange NMR experiments indicate that such openings for the AU base pairs occur in the sub-microsecond time range, possibly indicating that the opening events are consistent with experiment, such an observation was not made in the case of GC base pairs ³⁶ though the opening events were present in the simulation. This local opening appears to contribute to a haripin with a UUCG tetraloop being predicted to be unstable based on potential of mean force unfolding calculations ³². Notably, the opening behavior has not been observed in MD simulations of DNA using the CHARMM27 ^25,26,37 force field even though all aspects of the DNA and RNA force field are identical with the exception of the sugar dihedral parameters. This situation and the main difference between RNA and DNA being the 2′-hydroxy groups, leads one to assume that the base-pair opening events observed only in RNA are related to the behavior of the 2′-hydroxyl group.

The above observations motivated the present study of improvements in the CHARMM27 nucleic acid force field with respect to the modeling of RNA structures. As this is only observed when simulating RNA molecules and not DNA molecules ¹⁴, a series of model compounds were design to analyze the energetics of rotation of the 2′-hydroxyl using QM calculations. That data was then used to develop several sets of new parameters associated with the dihedrals impacting rotation of the 2′-hydroxyl. The optimized parameters were then applied to a variety of RNA structures in MD simulations. The types of RNA structures considered here include duplexes, bulged bases, mismatches, hairpin structures, base triples, and a junction (Table 1). These structures were selected to maximize the structural diversity of the RNAs, thereby providing a suitable test set for validating the force field. In addition, the present results further indicate the orientation of the 2′-hydroxyl moiety in RNA impacts the conformational properties, a phenomenon that may contribute to the known conformational heterogeneity of RNA ^38,39.

Table 1.

RNA structures utilized for this study

RNA type	Conditions	PDB ID	Chains	Size	Reference
Canonical	Crystallography	1SDR	AB, CD	24	Schindelin et. al.43
Canonical	Crystallography	1RNA	AB	28	Dock-Bregeona et. al.44
Canonical	Modelled	RNA4 **	--	36	Faustino et. al. 56
Canonical (GA Mismatch)	Crystallography	1SA9	AB, CD	16	Jang et. al. 45
Canonical (GA Mismatch)	Solution NMR	1YFV	AB	16	SantaLucia et. al. 46
Bulge	Crystallography	1DQH	AB	19	Xiong et. al. 47
Pseudoknot	Crystallography	1L2X	A	28	Egli et. al. 52
Hairpin	Solution NMR	1K5I	A	23	Nagaswamy et. al.49
Hairpin	Crystallography	1MSY	A	27	Correll et. al.51
Hairpin	Solution NMR	1UUU	A	19	Sich et. al. 50
Hairpin	Crystallography	1F7Y*	A	10	Ennifar et. al.54
Hairpin	Crystallography	1MME*	A	10	Scott et. al. 53
Hairpin	Solution NMR	1EOR	A	22	Rüdisser et. al.48
Aptamer	Crystallography	1Y26	Apo/Holo	71	Serganov et. al.55

^*modified structures based on sequence used by Deng and Cieplak

^**indicates that structure was not take from PDB rather the structure was modeled based on the sequence identification used by Faustino et. al. ⁵⁶

Methodology

Model Compound Calculations

QM calculations were performed using the program Gaussian03⁴⁰ to obtain an estimate of the potential energy associated with rotation of the 2′-hydroxyl moiety. The RNA backbone dihedrals (α: P-O5′, β: O5′-C5′, γ: C5′-C4′, δ: C4′-C3′, ε: C3′-O3′, and ζ: O3′-P) or the RNA glycosidic linkage dihedral (χ: C1′-N1/N9) were fixed while dihedral potential energy scans were performed for the 2′-hydroxyl as previously described ⁴¹. Scans were performed at the MP2/6-31+G(d) level of theory followed by single point calculations at the RIMP2/cc-pVTZ level performed using the Q-Chem program ⁴². This level of theory has previously been shown to be sufficiently accurate for a number of systems.^25,43 For this study, the 2′-hydroxyl dihedral angle is defined with the respect to C1′-C2′-O2′-H2′ (note that the atom names are representative of those in the CHARMM27 all-atom additive nucleic acid force field). The dihedral was scanned at 15° intervals from 0° to 360° for each of the compounds. Analogous potential-energy scans were performed using the original CHARMM27 all-atom additive force field and several trial revisions of the force field developed in the present study. Empirical scans were performed using the same constraints as in the QM scans, implemented as a harmonic potential with force constant 10,000 kcal/mol/rad² on the respective backbone and glycosidic linkage dihedrals, with the remaining degrees of freedom optimized using the Newton-Raphson algorithm to a final root-means-square (RMS) gradient of 10⁻⁶ kcal/mol/Å. All nonbonded interactions were included in the calculations.

RNA Simulations

Four canonical ^44–47 and nine non-canonical RNA structures ^48–56 obtained from the protein databank and one computationally-modeled canonical RNA structure ⁵⁷ were considered for the force field assessment (Table 1). MD simulations and analysis were done using the CHARMM⁵⁸ or NAMD⁵⁹ programs using the published CHARMM27 all-atom additive nucleic acid force field parameters^25,26 with subsequent revisions associated with changes the 2′-hydroxyl parameters as part of the present work (Table SI1 of the supporting information). After the addition of missing hydrogen atoms to the crystallographic coordinates using the Hbuild ⁶⁰ facility in CHARMM, the RNAs were immersed in a pre-equilibrated truncated octahedron shaped water box (1MSY, 1UUU, and 1Y26) or a cubic shaped water box (all additional RNA molecules). The length of each box was extended approximately 9 Å beyond all dimensions defined by the RNA non-hydrogen atoms. Overlapping water molecules with their oxygen atoms within 1.9 Å of the non-hydrogen RNA atoms were deleted. Sodium ions or potassium ions (Tables SI2 and SI3 of the supporting information) were randomly placed in the water box to make the system electrically neutral except in the riboswitch (1Y26), where Mg²⁺ ions were used in addition to the Mg²⁺ ions identified in the crystal structure. The resultant configurations for each of the RNAs in solution were used as the initial structures for further minimizations and MD simulations.

For the minimizations and MD simulations, the CRYSTAL utility in CHARMM was used to implement periodic boundary conditions, and the particle mesh Ewald summation method ^61,62 was used for the calculation of electrostatic interactions. Lennard-Jones (LJ) interactions were truncated at 12 Å, with a force switch smoothing function from 8 to 12 Å. The non-bonded interaction lists were updated heuristically, and similar to LJ interactions, the real space electrostatic interactions were also truncated at 12 Å. Other than the SHAKE algorithm ⁶³ that was employed to constrain all the covalent bonds involving hydrogen atoms, the production simulations did not involve any other constraints or restraints. Initially, the systems underwent a 500-step adopted basis Newton-Raphson minimization followed by a 200 ps MD simulation in the NPT ensemble with mass weighted restraints with force constant 5 kcal/mol/Ų on all RNA non-hydrogen atoms. This enabled the equilibration of the solvent molecules and ions around the RNAs, filling any voids created by deleting the water molecules. The resultant structures were used as the initial structures for the production MD simulations.

Overall, 50 ns of production simulation, unless noted, was performed on each system in the NPT ensemble employing the Leapfrog integrator for CHARMM simulations and MTS algorithm integrator for NAMD simulations. All the simulations used an integration time step of 2 fs and coordinates were saved every 2 ps for analysis. The Langevin piston algorithm⁶⁴ was used for maintaining the pressure at 1 atm and Hoover chains were employed to maintain the temperature at 298 K. On 1Y26, the presented results from CHARMM27 are from a previously reported simulation of 40 ns where the frequency of saving the coordinates was 5 ps ²³. The double-stranded 18-mer RNA (SEQ4 from Faustino et. al. ⁵⁷) was simulated in the NVE ensemble using CHARMM with the CHARMM27 and CHARMM27d parameter sets using spherical force-shift cutoff scheme with a 12 Å cutoff ^65–67, and with PME in a rhombic dodecahedron (58.8 Å distance across) containing 34 Na⁺ and 4481 TIP3P water molecules. Nonbonded interactions were evaluated using fast lookup tables. ⁶⁸ For parameter set CHARMM27d, four independent simulations were performed, two with (50 ns) and two without (100 ns) PME (Table SI3 of the supporting information).

Water Probability Distribution Analysis

A probability distribution map of water in the vicinity of RNA nucleotide WC pairs was created from a survey of 22 high-resolution Protein DataBank (PDB) RNA crystal structures with < 2.6 Å resolution that included 179 WC base pairs. The crystallographic data was generated by doing an RMS alignment of each set of WC base pairs with template base pairs taken from a high-resolution crystal structure ⁴⁴ and by selecting waters within 5 Å of the nucleotides, with the results summed over all GC, CG, AU and UA base pairs. Probability maps were generated on a 1 ų grid using the MDAnalysis ⁶⁹ and the Hops ⁷⁰ python libraries. The densities were normalized relative to CHARMM bulk solvent hydration value (0.0313 molecules/ų for TIP3P water molecules). The simulation water probability distribution maps were generated in a similar fashion to the crystal map determination. The probabilities were normalized relative to the bulk solvent hydration within each simulation. This procedure was performed for four different RNA molecules (1SDR, 1K5I, 1L2X, 1DQH).

The simulation probability distribution maps were then overlapped with the crystal maps. The extent of overlap for each simulation map with the crystal map was calculated using the following equation:

$$P=\sum _{i=1}^{N}min\{{\rho }_x(i),{\rho }_y(i)\}$$ [1]

where P is the overlap integral, i is the individual grid point, N is the total number of grid points, ρ_x (i) and ρ_y (i) are the normalized density values of grid point i from the simulation and crystal maps, respectively.

PMF Calculations

Unfolding free energy determinations, based on one-dimensional potential mean force (PMF) calculations, were performed on two hairpin structures (1F7Y and 1MME). These two structures were chosen based on the previous study of Deng and Cieplak ³² in which similar end-to-end 1D PMFs were performed. The PMF simulation protocol is similar to that described above for the production equilibrium simulations. A harmonic restraint was placed on the C1′ – C1′ distance of the terminal nucleotides. The force constant values and the end-to-end distance values used to restrain the distance were similar to those used by Deng and Cieplak (Table SI4 of the supporting information) ³².

The initial conformation in each window of the PMF was taken from a preliminary orthogonal sampling random walk (OSRW) simulation ⁷¹. The OSRW method was used to increase sampling along our 1D reaction coordinate and provide sensible starting conformations and conditions for each umbrella window. Each window was then run for a total of 12 ns with data from the last 10 ns used for the PMF determination. The free energy surface along our end-to-end distance reaction coordinate was estimated using the weighted histogram analysis method (WHAM) ^72,73. The free energy of folding, ΔG_fold, was then calculated for each RNA molecule:

$$\mathrm{\Delta }{G}_{\mathit{fold}}=-k_{B}Tln\left[\sum _{i,\mathit{folded}}p(r_i)/\sum _{i,\mathit{unfolded}}p(r_i)\right]$$ [2]

where p(r_i) is the probability distribution of the end-to-end distance, r_i, and an end-to-end distance cutoff value of 20 Å used to define the folded and unfolded states.

Results and Discussion

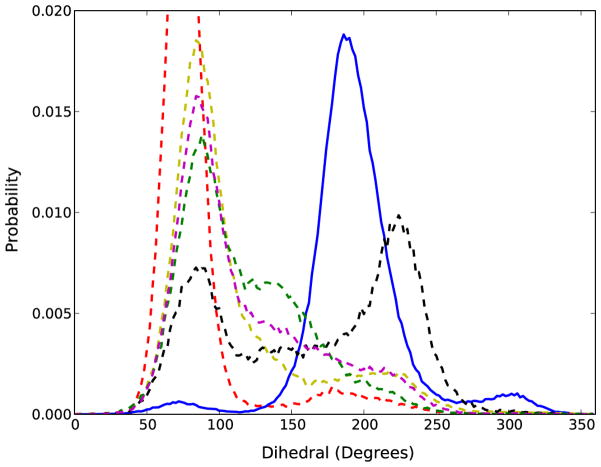
Previous RNA simulation studies observed local Watson-Crick base-pair opening events, corresponding to N1-N3 distances between 4Å and 8Å ¹⁴. Here, we calculated probability distributions of the N1-N3 distances (the WC distribution) and orientation of the 2′-hydroxyl proton for canonical base pairs in our RNA test set using the CHARMM27 force field (Figure 1). The peaks in the WC distribution beyond 3.5Å indicate the presence of local base-pair opening. Figure 1 also shows that a specific 2′-hydroxyl orientation is dominant when the CHARMM27 force field is used.

Figure 1.

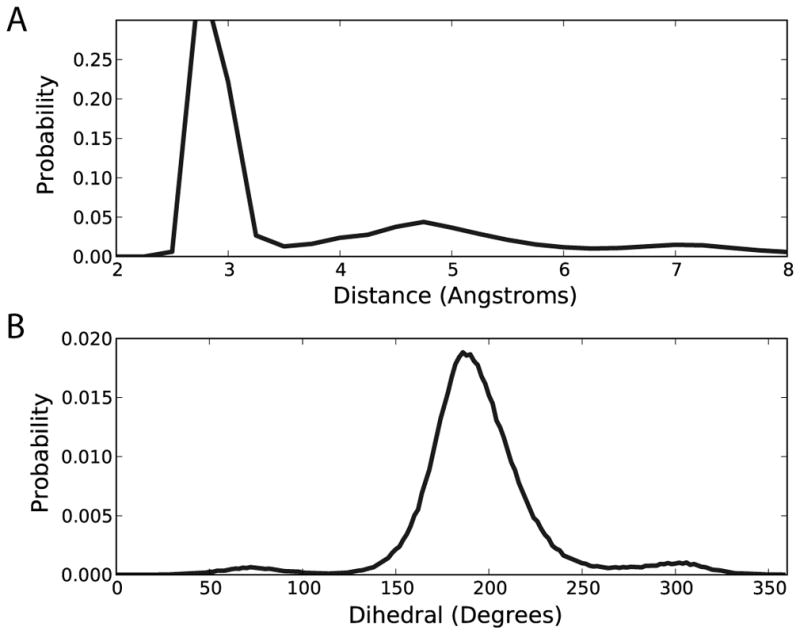
RNA behavior exhibited when using original CHARMM27 parameters. (A) distribution of the N1-N3 WC base-pair distance and (B) 2′-hydroxyl torsion distribution.

Experimental studies have shown that there are three favorable regions for the 2′-hydroxyl dihedral and they are described by the direction in which the O2′-H2′ bond points: the base region (30° to 98°), the O4′ region (305° to 360°), and the O3′ region (190° to 280°) ^74,75. The base orientation involves the 2′-hydroxyl proton hydrogen bonding with a water molecule that also hydrogen bonds with the base moiety, the O3′ orientation involves the hydroxyl proton hydrogen bonding with the O3′ atom on the same sugar moiety, and O4′ orientations have the H2′ atom pointing in the direction of the O4′ atom on the same sugar moiety. Notably, experimental studies on the orientation of the hydroxyl moiety suggest that the base orientation should dominate^38,74,75, though the extent of sampling of the different orientations is currently not resolved. When comparing these experimental results ^38,74,75 to results when using the CHARMM27 force field (Figure 1), these behaviors suggest that to reduce the RNA base-pair opening, the optimization of the 2′-hydroxyl dihedral parameter should be targeted.

Parameter Optimization

To understand the 2′-hydroxyl behavior, QM calculations were performed on the rotation of the 2′-hydroxyl in the model compounds shown in Figure 2. The QM data shows favorable dihedral values for the 2′-hydroxyl ranging from 200° to 300° for all the model compounds (Figure 3). This corresponds approximately to the maximum in the 2′-hydroxyl probability distribution in Figure 1b. In all cases, the location of the minimum in the CHARMM27 surface (blue solid lines) is in good agreement with the QM data; however, the region for the CHARMM27 surface from 0° to 150° is systematically too high in all model compounds, suggesting that sampling of the base, and possibly the O4′ orientations, of the hydroxyl may be disallowed. This motivated the creation of a series of RNA parameter sets in which the torsion parameters dictating the orientation of the 2′-hydroxyl moiety were systematically varied to alter the energy in the region of 0° to 150°. It should be noted that the development of multiple parameter sets was necessary due to the inability of any given parameter set to reproduce the QM energy surfaces of all the model compounds.

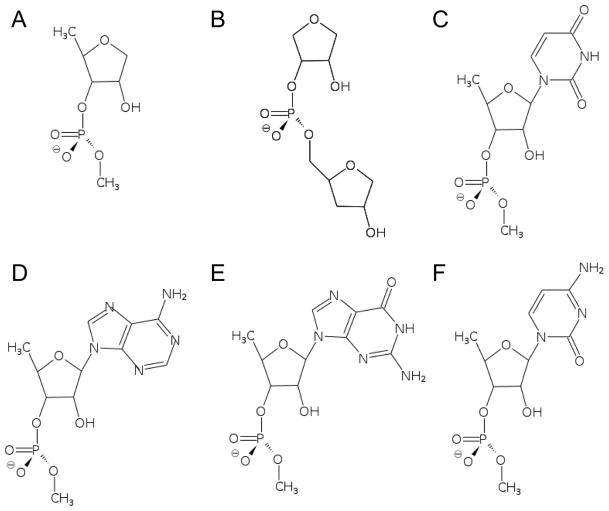
Figure 2.

Diagram of of model compounds to study the energetics of the 2′-hydroxyl group. The compounds include different moieties present in RNA oligonucleotides. (A) ribose (B) double-ribose (C) ribose with uracil base (D) ribose with adenine base (E) ribose with guanine base (F) ribose with cytosine base.

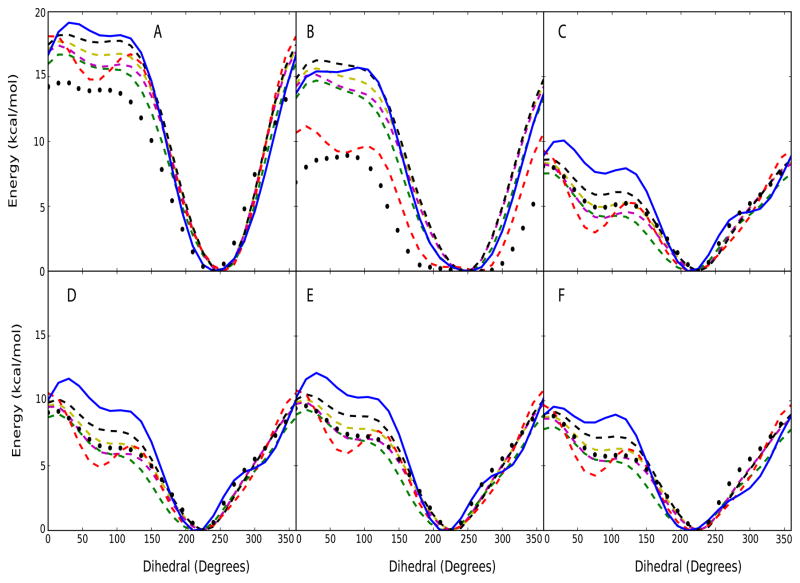
Figure 3.

2′-hydroxyl potential energy surfaces for six model compounds from CHARMM and QM level calculations. Model compounds shown in Figure 2 are (A) ribose (B) double-ribose (C) ribose with uracil base (D) ribose with adenine base (E) ribose with guanine base and (F) ribose with cytosine base. [Note: the dihedral is taken with respect to C1′-C2′-O2′-H2′]. Solid-blue line represents the original CHARMM27 parameters; Dash-dot lines represent CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e]; Black circles represent the QM data.

The MM energy surfaces from the newly generated torsion parameter sets (specified as CHARMM27a through CHARMM27e) are included in Figure 3. The initial modification, CHARMM27a (red dashed line in Figure 3) was designed to alter the energy surface to yield agreement for the 0° to 150° region with model compound 2, the model with two ribose moieties. While this was approximately achieved, a local energy well is created at ~70°, which significantly underestimates that seen in the QM surfaces, especially with the model compounds that include the base moieties (compounds 3 to 6).

Accordingly, additional test parameters were generated to lower the energy for the 0° to 150° region without creating a local energy well around ~70°. These additional parameters reproduced the QM surfaces for the model compounds with a base reasonably well while they overestimate the energies in the 0° to 150° region for compounds 1 and 2. The one significant exception is the CHARMM27e parameters, which results in energies higher than sets CHARMM27b, c, and d in the 0° to 150° region for compounds 3 to 6. Sets CHARMM27b, c and d differ only slightly in the curvature of the surfaces in the region of the broad energy minimum (the 200° to 300° region) and these are differences that could impact sampling during MD simulations. These five parameter sets were subjected to a series of simulations of RNA in aqueous solution (Tables SI2 and SI3 of the supporting information) to select the optimal set for the new model. The new parameters, which only differ in the torsional terms for the 2′-hydroxyl, are listed in Table SI1 of the supporting information.

RNA Parameter Evaluation

A comparison of the structural and dynamical properties for twelve RNA molecules was used to evaluate the five modified parameter sets (1RNA and the 18mer RNA were excluded from these calculations). The overall structure of the RNA molecules during the simulations were evaluated based on the average heavy-atom root mean square deviation (RMSD), the Watson-Crick base pairing, the phosphodiester backbone torsion angles, and the 2′-hydroxyl dihedral. As discussed above, several studies show three energetically favorable 2′-hydroxyl orientations: the O4′, O3′, and base states ^8,38,74,75. Fohrer et al. suggest that the hydroxyl orientation alternates between the O3′ and base domain ⁷⁵. These biophysical studies suggest the main role of the 2′-hydroxyl orientation is to stabilize the C3′-endo pucker of the ribose ^38,75,76. This suggests that differential sampling by the 2′hydroxyl may have a subtle impact on the sugar conformation, a property that may be monitored by NMR J-coupling constant measurements. Accordingly, NMR data was considered as additional target data for parameter set selection.

It has been suggested that the 2′-hydroxyl orientation impacts an extended water/hydrogen bond network and differences in this network can possibly lead to differences in the overall RMSD and differences in the behavior of WC base-pairing, backbone torsion angles, and the 2′-hydroxyl orientation ^{8,38,39,76,77}. Accordingly, the force field should be able to reproduce the solvation pattern around the RNA. Given that the experimental solvation pattern may be obtained from high-resolution crystal structures, such data was considered as target data for selection of the optimal parameters.

The RMSD values were calculated based on the alignment of the (A) non-hydrogen atoms of the RNA molecules in the canonical regions, and (B) non-hydrogen atoms involved in the non-canonical regions (Tables SI5 and SI6 of the supporting information). The terminal bases were excluded from the RMSD calculations in this analysis. In general, the RMSD for the CHARMM27 parameters are in satisfactory agreement with the experimental structures, with a maximum deviation of 3.8 Å in the canonical region and a maximum deviation of 4.9 Å for the non-canonical regions. However, the modified CHARMM27 parameter MD simulations show marked improvements in their agreement with the experimental structures. The RMSD for the modified parameters for both canonical and non-canonical regions for all RNA molecules on average are significantly lower, with the maximum deviation of 3.2 Å in the canonical region and a maximum deviation of 5.0 Å in the non-canonical region (Tables SI5 and SI6 of the supporting information). Notably, differences in the overall RMSD among the modified parameters are not large enough to distinguish among the parameter sets emphasizing that additional assessments are necessary to provide more insights into the parameter set that maximizes RNA behavioral improvements.

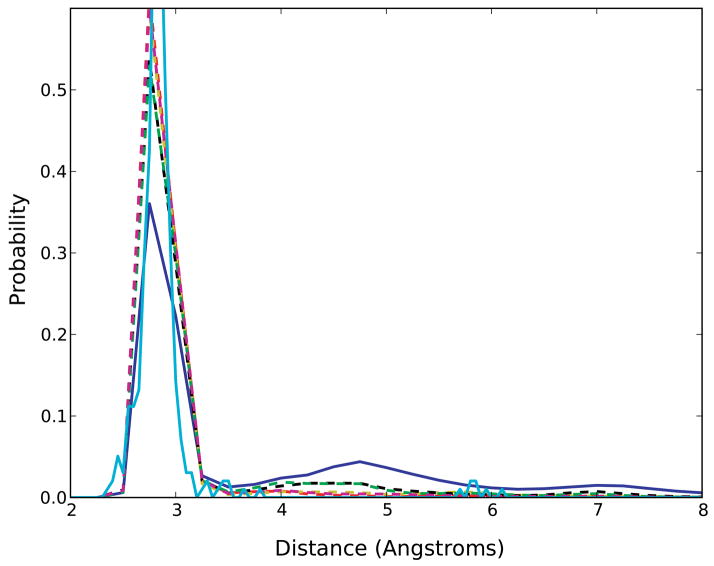
The WC hydrogen bonding represents one of the dominant types of interactions influencing the structure of RNA ^78,79. To determine if the updates to the force field parameters exhibit an improvement in Watson-Crick base-pairing, the hydrogen bonding of GC and AU base pairs was assessed by calculating the probability distributions corresponding to the WC base-pair N1-N3 distances in the canonical regions of all the RNA molecules (Figure 4). The results show the CHARMM27 parameters exhibit three peaks at distances 2.8 Å, 4.8 Å, and 6.9 Å while the parameters optimizing the 2′-hydroxyl dihedral yield a larger peak associated with the WC base-pairing maximum at 2.8 Å and reduced sampling at distances > 3.5 Å. Thus, the modified sets exhibit a reduction in WC base opening over the CHARMM27 parameters.

Figure 4.

The probability distributions of the N1-N3 distances obtained for the Watson-Crick (WC) hydrogen-bond interactions for all RNA molecules. Solid-blue line represents the original CHARMM27 parameters; Solid cyan represents experimental survey-data; Dash-dot lines represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e].

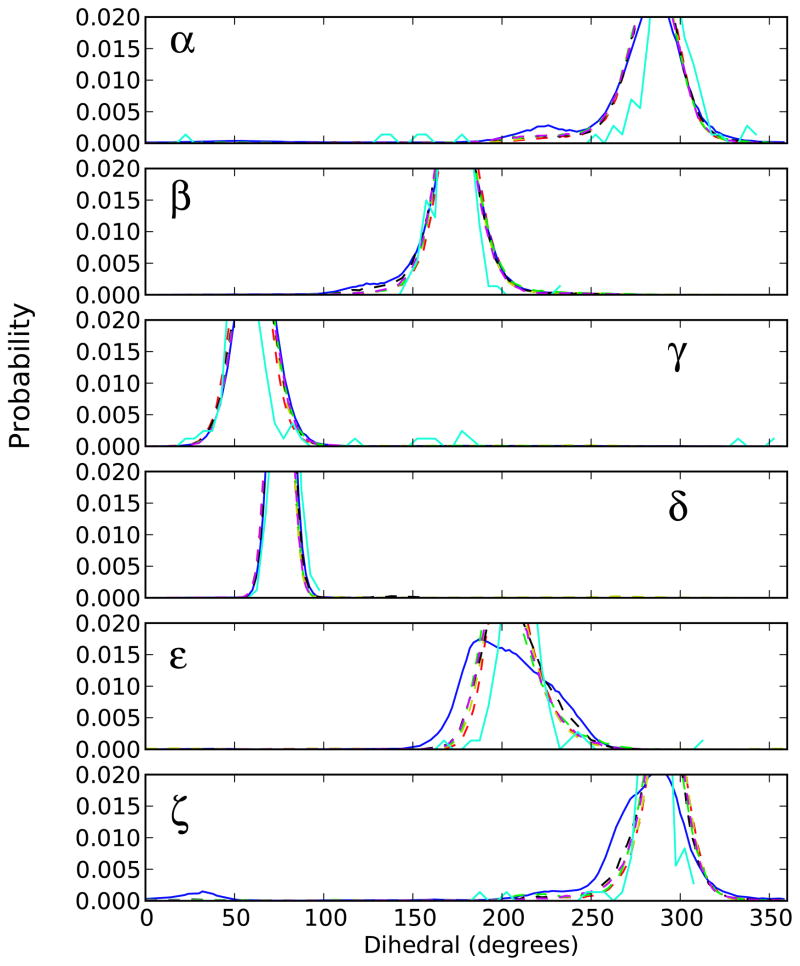
Numerous studies have documented the relationship of the backbone torsion angles with the different forms of DNA and canonical RNA molecules (α: P-O5′, β: O5′-C5′, γ: C5′-C4′, δ: C4′-C3′, ε: C3′-O3′, and ζ: O3′-P) ³⁷. Non-canonical RNA structures sample slightly different regions in backbone torsion-angle space ^11,16,33,80. To evaluate the different parameter sets, the probability distributions for the seven torsions were calculated and compared to survey data taken from crystallographic structures with a resolution < 2.6 Å. Figure 5 shows the distributions calculated based on the backbone torsion angles for the canonical regions exhibiting Watson-Crick pairing excluding the terminal base pairs. The distributions obtained from all the MD simulations are consistent with the experimental distributions for the α, β, γ, and δ dihedral angles for all parameter sets, but qualitative differences are observed for the ε and ζ torsion angles between the CHARMM27 and the modified parameter sets.

Figure 5.

The probability distributions obtained for the phosphodiester backbone dihedral angles (α, β, γ, δ, ε, and ζ) for all canonical RNA regions of the canonical regions. Solid-blue line represents the original CHARMM27 parameters; Solid cyan represents experimental survey-data; Dash-dot lines represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e].

The distribution curves for the ε and ζ torsions are broader for the CHARMM27 parameters compared to the histogram obtained using the NDB survey (Figure 5). Additionally, the ζ dihedral angle samples certain regions (around 30°) inconsistent with the experimental data. It has previously been shown that flipping of a base from its helical position may be achieved by altering the ζ dihedral angle ^13,81,82. Thus, one could assume that wider ranges sampled by the ε and ζ torsions might be facilitating base opening (Figure 4 and Figure 5) with the CHARMM27 parameters. The modified parameters reduce the sampling of ζ in the 30° region and the results are in good agreement with the NDB survey data for the ε and ζ torsion curves. Given that the ε and ζ torsions both involve the O3′ atom, it is not surprising that sampling of the O3′ orientation of the 2′-hydroxyl torsion angle (Figure 1) is related to the difference in sampling for ε and ζ.

Figure 6 shows the probability distribution of the 2′-hydroxyl dihedral when comparing the original and modified parameters sets. The CHARMM27 parameter set yields high sampling for the O3′-hydroxyl-orientation, as shown above. The modified parameter sets, however, exhibit significant sampling for the base orientation of the 2′-hydroxyl (Figure 6). Sampling predominantly within the base-orientation versus significant sampling of the O3′-orientation is in good agreement with NMR data ^74,83,84 Thus, the modified parameters improve sampling of the phosphodiester backbone conformations and decreased WC base-pair opening by enhancing sampling of the 2′-hydroxyl dihedral within the base orientation and decreasing sampling of the O3′ orientation. However, given current experimental knowledge of the orientation of the 2′OH moiety, it was still not possible to select among the 5 modified parameter sets based on sampling of the 2′OH occurring in the simulations.

Figure 6.

The probability distributions obtained for the 2′-hydroxyl dihedral for all RNA molecules. Solid-blue line represents the original CHARMM27 parameters; Dash-dot lines represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e].

Water Probability Distribution Comparison

Water molecules play an important role in maintaining the three-dimensional (3D) structure of biological macromolecules in general, and oligonucleotides in particular due to their polyanionic nature. Semiquantitative NOE NMR studies of duplex RNA structures reveal structured arrangements of water molecules in both the major and minor groove ⁸⁵. A number of experimental studies suggest that an extended hydration network underlies long-range intra- and inter- molecular RNA interactions ^39,86, specifically the correlation between the 2′-hydroxyl orientation and the degree of RNA hydration ^{76,83–85,87}. In particular, Egli et. al. and Olsen et. al. suggest the 2′-OH group also provides a scaffold for the water networks near RNA molecules ^76,85. Thus, the hydration pattern around RNA offers a potential, though indirect, approach for evaluating the modified force field parameters.

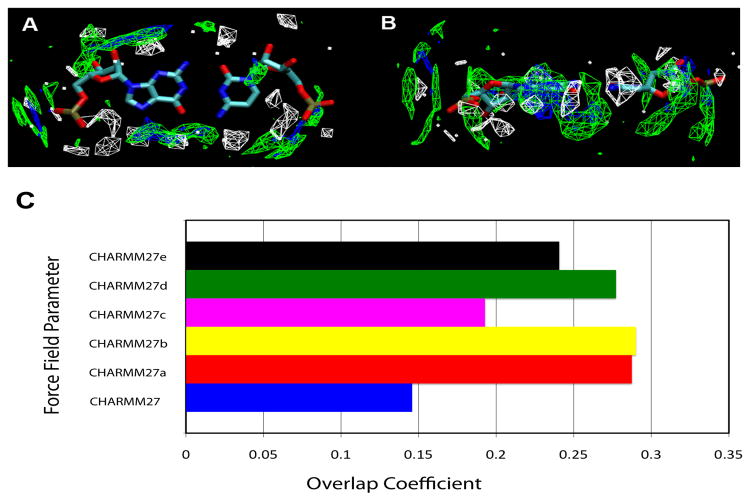
To exploit hydration patterns for force field evaluation a survey of the distribution of water around WC pairs of nucleotides in canonical regions of RNA was performed. This goes beyond published studies of RNA hydration based on single x-ray structures^77,88. The distribution of water summed over all base pair types is shown in Figure 7a and b. From the crystal survey high probability regions are evident adjacent to the hydrogen bonding moieties on the bases, sugars and phosphates ⁷⁷. This includes regions of high probability in both the major and minor grooves, with minor groove densities adjacent to the 2′-hydroxyl moieties present. In addition, as the goal of the present work was identification of a parameter set that best reproduces a range of experimental data, including hydration, it was deemed appropriate to perform the analysis over all base pair types, and thus finer details of the hydration pattern are not discussed, though future studies will address these details (E.J. Denning and A.D. MacKerell, Jr., work in progress).

Figure 7.

Water 3D probability distribution within 3 Å of RNA Watson-Crick nucleotide pairs for the crystal survey (white) and the CHARMM27 (blue), and CHARMM27d (green) MD simulations. (A) Top-down view and (B) Side view of the probability distributions and (C) Overlap of the survey and simulation water probability distributions. Blue represents the original CHARMM27 parameters; the others represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e].

Quantification of the reproduction of the survey hydration pattern by the parameter sets was performed by calculating the overlap integral, P, of the survey data with that obtained from the simulations (Equation 1). Results from this analysis are shown in Figure 7c. Taken in conjunction with the above 2′-hydroxyl data, we observe that the degree of overlap with crystallographic water changes with respect to the probability distribution of the 2′-hydroxyl orientation (Figures 6 and 7c). The CHARMM27 parameter set, which predominantly results in a O3′ orientation for the 2′-hydroxyl, shows a low overlap with the crystallographic water density with the values being significantly larger for all the modified CHARMM27 parameter sets. These results further indicate that sampling of the O3′ orientation of the 2′-hydroxyl in CHARMM27 is not correct, and that in general the 2′-hydroxyl states in crystal structures reflect a high ratio of base to O3′ orientation, as previously discussed ^74,85. In particular, the CHARMM27a, CHARMM27b, and CHARMM27d sets exhibit the highest degree of overlap. Thus, one can assume the 2′-hydroxyl behavior in these modified CHARMM27 parameter sets more accurately reflects the hydration behavior of RNA molecules ^{38,74,76,77,85}.

NMR J-coupling Comparison

The final method for evaluating the modified parameter sets involved a comparison to experimental NMR data associated with sugar related J-couplings in non-canonical regions of RNA. This part of the study was motivated by preliminary analysis suggesting that the couplings for the non-canonical RNA regions may be sensitive to the sampling of the torsional 2′-hydroxyl. The two experimental structures 1UU ⁵¹ and 1K5I⁵⁰ were chosen based on available NMR data, thereby offering a comparison of experimental NMR J-coupling data obtained in solution and calculated J-couplings from the appropriate dihedral angles in the simulations using the Karplus equation ⁸⁹ with parameters from Lankhorst et. al. ⁹⁰ and Marino et al ⁹¹:

$$\begin{array}{l}{{}^3\text{J}}_{\text{HCCH}}=13.7{cos}^2\theta -0.73cos\theta +\sum \mathrm{\Delta }{\chi }_i\{0.56-2.47{cos}^2(z_i\theta +16.9\mid \mathrm{\Delta }{\chi }_i\mid )\}\\ {{}^3\text{J}}_{\text{POCH}}=15.3{cos}^2\theta -6.1cos\theta +1.6\\ {{}^3\text{J}}_{\text{CCOP}}=6.9{cos}^2\theta -3.4cos\theta +0.7\end{array}$$ [3]

where θ is the torsion angle (in units of degrees) and Δχ depends on the electronic character of non-proton substituents attached to the carbon atoms (Δχ = O, 1.3; C, 0.4; N, 0.85; P, −0.05) and z_i = ±1. The J -coupling values were calculated for each snapshot from the simulations and the results presented as histograms.

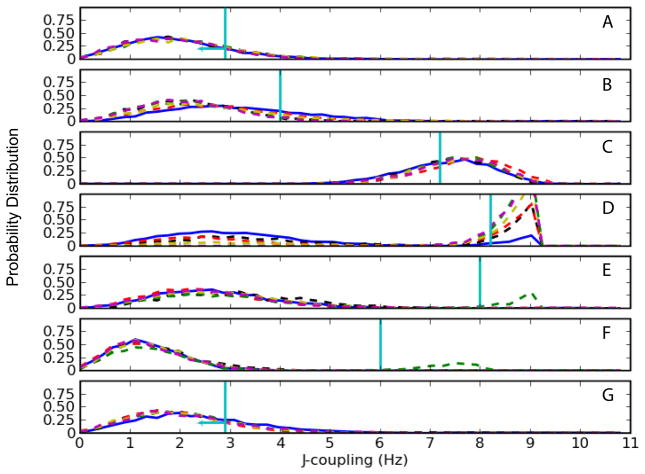
Figure 8 shows the 1K5I J-coupling distributions for the following ribose proton-proton coupling constants: ³J _H1′-H2″, ³J _H2″-H3′, and ³J _H3′-H4′ (note the atom names are defined with respect to the CHARMM topology). The ³J _H1′-H2″ coupling data for nucleotides G9, C10, and C15 and the C10 ³J _H3′-H4′ coupling exhibit similar distributions independent of the parameter set and are in relatively good agreement with the experimental values (Figures 8a,b,c,g). For U11, the ³J _H1′-H2″ simulation results all exhibit bimodal behavior but the profiles differ depending on the parameters (Figure 8d). The sampling of the ³J _H1′-H2″ around 8.2 Hz for the CHARMM27 is reduced compared to the modified parameter sets. In particular, the CHARMM27d (green) parameter set abolishes sampling around the 3 Hz region (Figure 8d).

Figure 8.

Comparison of NMR J-coupling data with CHARMM parameters for the 1K5I structure. Solid-blue line represents the original CHARMM27 parameters; Dash-dot lines represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e]. Horizontal-cyan line represents the experimental ³J-coupling value. (A) G9 ³J _H1′-H2″ (B) C10 ³J _H1′-H2″ (C) C10 ³J _H3′-H4′ (D) U11 ³J _H1′-H2″ (E) C12 ³J _H1′-H2″ (F) C12 ³J _H2″-H3′ (G) A14 ³J _H1′-H2″ (H) C15 ³J _H1′-H2″.

The parameter updates also improve sampling for the C12 nucleotide both for the ³J _H1′-H2″ and the ³J _H2″-H3′ couplings (Figure 8e and 8f). The experimentally determined values for the ³J _H1′-H2″ and ³J _H2″-H3′ coupling constants are 8.0 Hz and 6.0 Hz, respectively. The sampling within these regions is non-existent for the CHARMM27 force field and many of the modified parameters. The CHARMM27d (green) modified parameter set allows the C12 to sample near the experimentally determined values for the ³J _H1′-H2″ and the ³J _H2″-H3′ coupling constants.

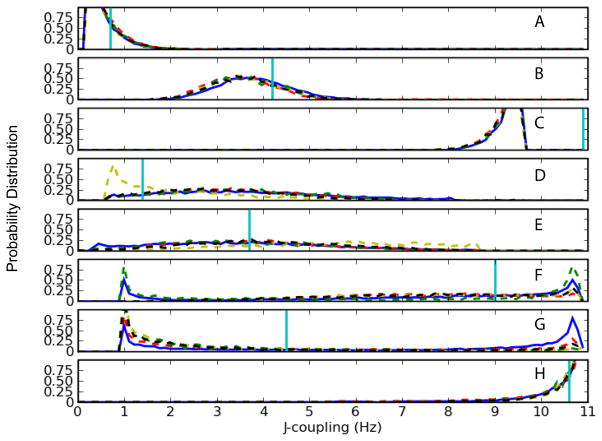
Similar J-coupling results were obtained for the 1UUU structure. The results for nucleotides U5 and C19 are in good agreement with experiment and exhibit similar behavior independent of force field parameters (Figure 9a,b,c,h). The backbone proton-phosphate data for ³J_H5″-P (U11) and ³J_H3′-P (C18) exhibits bimodal behavior (Figure 9f,g) but improved sampling near the experimental value is only observed in the C18 using the CHARMM27b (yellow) and d (green) parameter sets. Some improvement is also observed with those parameter sets for ³J _H4′-H5′ C12 (Figure 9d).

Figure 9.

Comparison of NMR J-coupling data with CHARMM parameters for the 1UUU structure. Solid-blue line represents the original CHARMM27 parameters; Dash-dot lines represent variants of CHARMM27 parameters [Red: CHARMM27a, yellow: CHARMM27b, magenta: CHARMM27c, green: CHARMM27d, black: CHARMM27e]. Horizontal-cyan line represents the experimental J-coupling value. (A) U5 ³J _H1′-H2″ (B) U5 ³J _H2″-H3′ (C) U5 ³J _H3′-H4′ (D) C12 ³J _H4′-H5′ (E) C12 ³J _H4′-H5″ (F) C18 ³J _H3′-P (G) U11 ³J _H5′-P (H) C19 ³J _C4′-P.

Overall, the J-coupling results show that none of the parameter sets captures the exact coupling behavior for all the nucleotides. This may be due to the fact the nucleotides are located within or near a loop region making it difficult to fully sample all the necessary conformations present in the NMR studies on a simulation timescale of 50 ns. In addition, the loop region for each system may be dependent on the salt or other experimental conditions that are not fully accounted for in the present simulations. However, the CHARMM27d parameter set did improve reproduction of the experimentally determined J-coupling constant values for both RNA molecules. This improvement in the reproduction of the J-coupling values is associated with more balanced sampling of the C2′-endo and C3′-endo ribose conformations in the hairpin loop region while maintaining the dominant C3′-endo ribose conformation in the canonical region (Figure SI3 of the supporting information). These results, in conjunction with the hydration analysis, further suggest that the 2′-hydroxyl orientation samples a mixture of base and O3′ orientations and indicate that the CHARMM27d set best reproduces the investigated experimental observables.

Unfolding free energies from end-to-end PMF calculations

Previous studies using the CHARMM27 force field indicate the free energies associated with unfolding of two hairpin-containing RNA molecules are in good agreement with experiment ⁹². Hairpin structures are a common secondary motif of RNA structure, the motif is often involved in protein-RNA recognition ⁹³ and their unfolding can be conveniently model based on end to end distance allowing for 1D PMF calculations to be applied. To determine if the modified parameter sets are in agreement with the experimental free energy of folding for the 1F7Y structure (a UUCG tetraloop) ⁵⁵ and a modified 1MME structure (to create a UUUU tetraloop) ^32,54, several of the modified parameter sets, as well as CHARMM27, were used in PMF unfolding calculations.

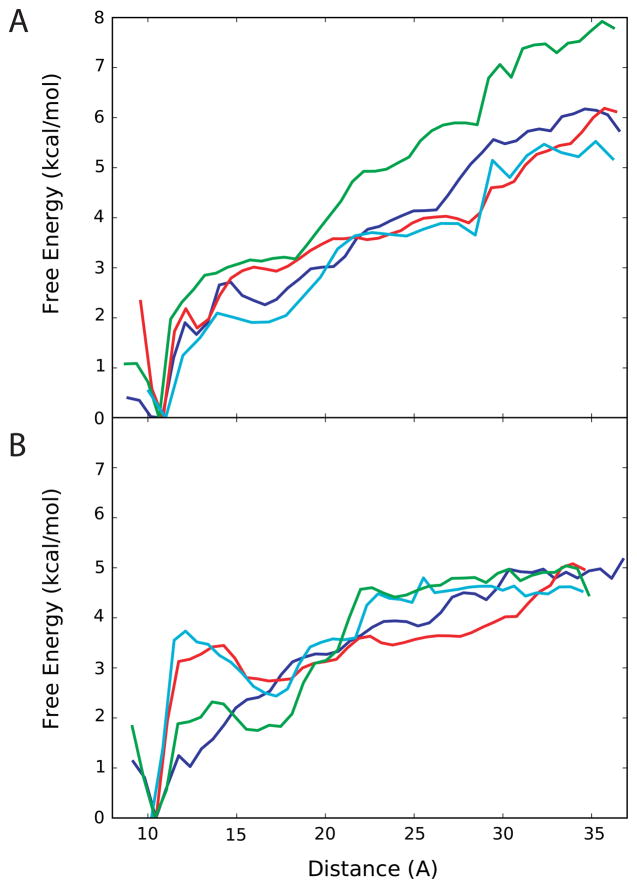
Free energy profiles for unfolding the UUCG and UUUU hairpins are shown in Figure 10. Experimental studies indicate that the UUCG hairpin is more stable than the UUUU hairpin by approximately −2 kcal/mol ^92,94. Only the CHARMM27, the CHARMM27a (2′-OH base-orientation), CHARMM27b, and the CHARMM27d parameter sets (the optimal parameter sets determined from the hydration and NMR data) were used for these calculations. The reaction coordinate for unfolding used the end-to-end distance based on the C1′ atoms of terminal nucleotides; the use of this reaction coordinate allowed for a comparison with the previous study on these structures³².

Figure 10.

Relative free energy profiles based on the end-to-end (C1′-C1′-) distance for two small hairpin RNA molecules. [Note: Solid-blue line represents the original CHARMM27 parameters; the other lines represent variants of CHARMM27 parameters [red: CHARMM27a; cyan: CHARMM27b; green: CHARMM27d]. (A) 1F7Y structure which contains a UUCG-loop (B) 1MME structure that has a UUUU-loop.

In general, all the tested parameter sets produce similar free energy profiles (Figure 10). Free energies of unfolding were obtained by defining the folded state as an end-to-end distance of 20 Å or less and the unfolded state as > 20 Å (Equation 2). Small changes in the selection of the folded-state distance did not significantly impact the obtained free energy and the selected distance of 20 Å is consistent with the loss of base stacking (Figures SI4 and SI5 of the supporting information), which is assumed to correspond with the loss of the hypochromic shift used to monitor RNA folding in the experimental studies. Notably, the free energy of folding values are approximately those obtained experimentally ^92,94 (Table 2). The ΔΔG_UUCG→UUUU value for each of our parameter sets is also in satisfactory agreement the −2 kcal/mol experimental ΔΔG value ⁹⁴. Beyond the excellent level of agreement with experiment an important observation is that the change in the parameters does not lead to over-stabilization of the RNA. Consistent with this are the RMS fluctuations of the RNAs (Figure SI7) indicating only minor changes in the overall flexibility of the molecules. This is important, as there is a high likelihood that increased stabilization of the WC interactions would stabilize the folded state. However, this is clearly not occurring suggesting that if the modified parameters are leading to stabilization of the folded state, they are also impacting the unfolded state such that the overall folding equilibrium is not significantly changed.

Table 2.

Folding free energy values based on the respective PMF calculations (error analysis was performed using random block analysis).

RNA	Charmm27	Charmm27a	Charmm27b	Charmm27d	Experiment
ΔGfold: UUCG	−3.3 ± 0.3	−4.2 ± 0.5	−2.2 ± 0.4	−2.5 ± 0.4	−3.7 ± 0.2 91
ΔGfold: UUUU	−2.2 ± 0.2	−2.2 ± 0.3	−1.5 ± 0.2	−2.0 ± 0.2	−1.5 ± 0.1 91
ΔGfold: UUCG-UUUU	−1.1	−2.0	−0.7	−0.5	−2.2

It should be noted that the free energy profiles shown here differ from those presented by Deng and Cieplak using the CHARMM27 parameters ³². These differences may be due to the use of slightly different cutoff values for the nonbond interactions. The CHARMM27 nucleic acid force field was originally parameterized based on LJ-interactions being truncated at 12 Å with smoothing using a force switch function from 8 to 12 Å ^41,66, while in the Deng and Cieplak study LJ-interactions being truncated at 10 Å ³². Another possible explanation may be the use of the OSRW method in the present study to generate unfolded conformations. This approach may yield a wider range of conformations of the unfolded states that were then used to initiate the PMF calculations thereby impacting the obtained free energy surfaces.

Selection from the modified CHARMM27 parameter sets

Five modifications of the CHARMM27 force field with respect to the dihedral parameters impacting sampling of the orientation of the 2′-hydroxyl were developed to reproduce QM data on model compounds to varying degrees. All of the modified sets led to a decrease in the opening of WC interactions, a problem that motivated the present work. In addition, all the modified sets lead to a significant decrease in RMSD from the starting structure for the RNAs included in the test set and they all lead to significant sampling of the base orientation of the 2′-hydroxyl, consistent with NMR data. However, these sets did show differences in the extent of sampling of the base versus O3′ conformations of the 2′-hydroxyl. Given the lack of conclusive experimental data allowing for one of these sets to be selected based on sampling by the 2′hydroxyl, two indirect measures were used. The ability of the parameter sets to improve the treatment of hydration of RNA showed a clear limitation in CHARMM27 and allowed for elimination of set CHARMM27c. Reproduction of J-coupling data in noncanonical regions was then considered. Both the CHARMM27b and d sets show improved agreement with experiment, with the level of agreement deemed greater with CHARMM27d. This result and the similar unfolding free energies of the b and d sets, both of which are in excellent agreement with experiment, led to selection of CHARMM27d. This set will be referred to as CHARMM36.

Large Duplex RNA Simulations

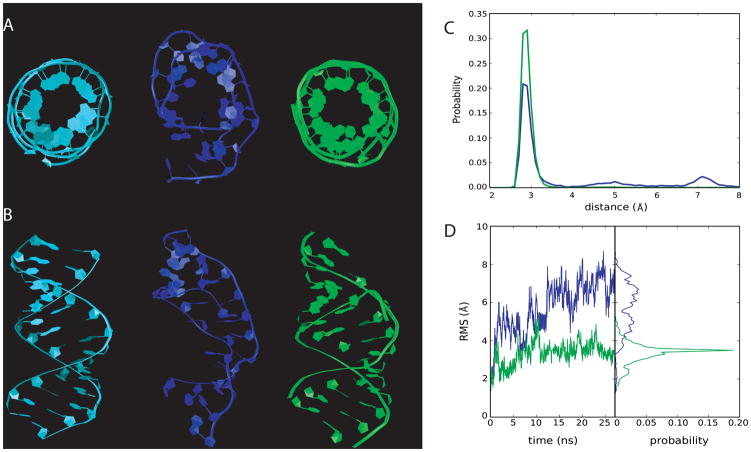
As an additional validation of the CHARMM36 parameter set, two additional RNA molecules were tested: a 14mer AU-duplex (1RNA) and a model 18mer duplex⁵⁷. These particular RNA molecules were used as they are rather large duplex structures and problems were encountered in simulations using both CHARMM and AMBER. The AU-duplex was reported to be unstable (J. Sponer, personal communication), which was reproduced by us with CHARMM27 and is reflected in the RMSD values (Table SI4), the WC interactions and visualization of its structure (Figure 11). The CHARMM36 parameter set significantly improves the overall behavior of this duplex, with respect to all three properties.

Figure 11.

AU base-pair RNA duplex structure (PDB: 1RNA). cyan: crystal structure; blue: CHARMM27; green: CHARMM27d (A) Top-down view of the structures after 27 ns (B) Side-view of the structures after 27 ns (C) WC base-pair distance distribution (D) RMS difference timeseries and RMS difference probability distributions.

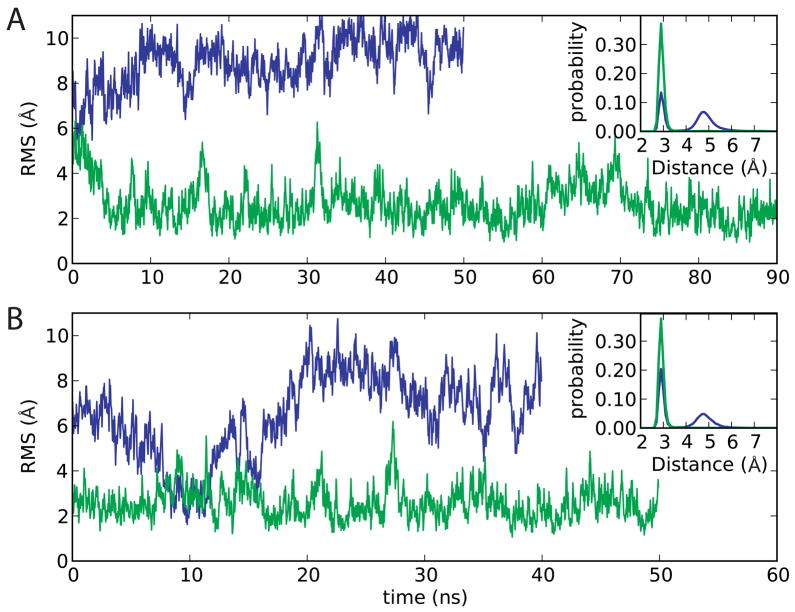
As a final test, the CHARMM27 and CHARMM36 parameter sets were applied to a18-mer RNA duplex with a high CG content (RNA sequence GGCGCGCACCACGCGCGG) both with and without PME. The simulations in the absence of PME were performed to verify that the force field may be used when electrostatic interactions are truncated using an appropriate truncation distance (12 Å) and smoothing function (force switch).⁹⁵ Overall, the structural results obtained were similar to those obtained for the other RNA systems when comparing the CHARMM27 and CHARMM36 parameter sets. With CHARMM27, the N1-N3 distance distributions have a high population of states where the distance is > 4Å (Figure 12 and Figure SI9 of the supporting information), indicating local opening of the Watson-Crick base pairs, whereas with CHARMM36 the N1-N3 distributions are unimodal, with the peak at 3Å corresponding to a Watson-Crick base pair. The 2′-hydroxyl dihedral distributions (Figure SI10 of the supporting information) are virtually identical to the corresponding distributions obtained with the other RNA systems (Figure 6).

Figure 12.

18mer RNA duplex structure. RMS differences in relation to the starting structure versus time and an inlay figure representing the probability distribution of the N1-N3 distance for the fourteen central WC base pairs are shown. [Blue: original CHARMM27; green: CHARMM27d] (A) No PME conditions (B) PME conditions

Importantly, the RMSD from the canonical A-RNA starting structure of the 14 central base pairs (Figure 12) clearly indicates structural deformation for the CHARMM27 simulations as previously observed ⁵⁷, whereas with the CHARMM36 parameter set both simulation methods give RMSDs that are very stable over the entire trajectories. All these results are very similar for the PME and the electrostatic cutoff simulations; additional equally long independent simulations give identical results (data not shown). Finally, motivated by Faustino et al ⁵⁷ the configurational entropy was determined based on quasiharmonic analysis ⁹⁶ (Table SI7 of supporting information) as a measure of the flexibility of the central 14 base pairs. The configurational entropy is larger for the two CHARMM27 simulations than for the CHARMM36 simulations. This is consistent with the decreased local base pair opening with CHARMM36. Given that the overall RMS fluctuations of the RNAs are not significantly altered (Figure SI7), though the RMS fluctuations of the bases are enhanced relative to the remainder of the structures, the results suggest that the change in configurational entropy is dominated by the bases alone. Moreover, given that the free energy of folding is not significantly altered in the modified parameter sets, the change is entropy may be occurring to a similar extent in both the folded and unfolded states, though additional studies are required to verify this suggestion.

Conclusions

To overcome a known limitation associated with local opening of WC base pairs, additional optimization of the CHARMM27 nucleic acid force field was undertaken focusing on the 2′-hydroxyl dihedral parameters. Five sets of modified CHARMM27 parameters were generated based on the reproduction of QM potential energy surfaces for hydroxyl rotation in a series of small model compounds. These parameter sets were then subjected to condensed phase simulations to determine an optimal CHARMM36 force field parameter set (Table 3). The final set was chosen based on structural properties, hydration analysis, reproduction of ³J-couplings and assessment of thermodynamic stability through free energy calculations. The new CHARMM36 force field reduces the probability of sampling WC hydrogen bonding distances > 5 Å associated with the 2′-hydroxyl torsion sampling primarily the base orientation, though sampling of O3′ orientations occurs. This leads to increased sampling of the C2′endo conformation in noncanonical regions (Figure SI3 of the supporting information) which is associated with improved agreement with NMR J-coupling data. Moreover, distributions of selected helicoidal parameters are in better agreement with experimental survey data (Figure SI6 of the supporting information). Additional comparison of the simulations to experimental hydration data indicates the force field to more accurately model solvation of the RNA molecules. Accordingly, it is anticipated that the presented RNA force field will allow for more accurate modeling of RNA alone, including both canonical and non-canonical structures, and in complexes with proteins and other molecules given the compatibility of the present force field with the remainder of the CHARMM all-atom additive force field for biological and medicinal molecules.

Table 3.

The updated CHARMM36 force field parameters describing the 2′-hydroxyl torsion.

Torsion	Vn/2	Multiplicity	Phase
HN5 ON5 CN7B CN7B	0.400	3	0.0
HN5 ON5 CN7B CN7B	0.400	2	0.0
HN5 ON5 CN7B CN7B	0.800	1	0.0
HN5 ON5 CN7B CN7	0.200	3	0.0
HN5 ON5 CN7B CN7	0.000	2	180.0
HN5 ON5 CN7B CN7	2.000	1	0.0

While the goal of the present study was to improve the CHARMM RNA force fields the results support the phenomenon of a “conformational switch” in RNA that enhances its conformational heterogeneity ¹⁴. It was proposed that the presence of the hydroxyl moiety along with the conformational properties of the sugar moiety and glycosidic linkages in RNA facilitated base pair opening and, ultimately, conformational heterogeneity. The present results are consistent with that model. Though the improved force field leads to enhanced sampling of the base orientation of the 2′-hydroxyl along with more stable WC interactions, the results with the different force field (CHARMM27 versus CHARMM36) clearly show that when the 2′-hydroxyl is in an O3′ orientation, there is a greater probability of base pair opening as well as sampling of a wider range of the ε and ζ dihedrals. This increased conformational sampling when the 2′-hydroxyl is in the O3′ orientation may facilitate conformational transitions in RNA, thereby acting as lubricant to allow for different conformations in different environments to be sampled. Further studies are required to address this issue in more details.