Abstract
The aim of this study was to determine whether the differences in timing of the peak growth velocity (PGV) between sitting height, total body height, subischial leg length, and foot length can be used to predict whether the individual patient with adolescent idiopathic scoliosis is before or past his or her PGV of sitting height. Furthermore, ratios of growth of different body parts were considered in order to determine their value in prediction of the PGV of sitting height in the individual patient. Ages of the PGV were determined for sitting height (n = 360), total body height (n = 432), subischial leg length (n = 357), and foot length (n = 263), and compared for the whole group and for the individual child in particular. Furthermore, the ages of the highest and lowest ratios between the body length dimensions were determined and compared to the age of the PGV of sitting height. The mean ages of the highest and lowest ratios were significantly different from the mean age of the PGV of sitting height in 3 out of 12 ratios in girls and 8 out of 12 ratios in boys. The variation over children was large and the ratios were too small, leading to a too large influence of measurement errors. The mean ages of the PGV all differed significantly from the mean age of the PGV of sitting height. However, the variation over individual children of the age differences in PGV between body dimensions was large, and the differences in timing of the PGV were not useful to predict whether the individual child is before or past his or her PGV of sitting height.
Keywords: Adolescent idiopathic scoliosis, Peak growth velocity, Sitting height, Total body height, Ratio
Introduction
Successful treatment of adolescent idiopathic scoliosis remains a complex challenge for the orthopedic surgeon. For planning of the complete therapeutic pathway, it is essential to understand the spinal growth of the patient since rapid longitudinal growth is likely to cause an increase in the spinal curvature [1–3]. Furthermore, the timing of possible surgical treatment is dependent on the timing of the pubertal growth spurt of the spine. Surgical fusion is still the golden standard in severe scoliosis and for the prevention of complications like the crankshaft phenomenon [4], the operation, if possible, has to be postponed until the peak growth velocity (PGV) of the spine has passed. The accurate measurement of spinal length is only possible on X-ray; however, sitting height is a good substitute. The main question in decision making regarding the treatment of adolescent idiopathic scoliosis is therefore whether the patient is before or past his or her PGV of sitting height, as a substitute of spinal length.
To answer this question longitudinal growth data of the individual patient are needed. Unfortunately it takes years to gather this information and conclusions can only be drawn retrospectively. A useful tool for prediction of the timing of the PGV can possibly be found in the combination of length growth of different body parts. Tanner et al. [5] described the distal-to-proximal growth gradient in adolescents: distal body parts have their pubertal growth spurt earlier in adolescence in comparison to more proximal body parts. This theory from the 1960s was investigated by other researchers and indeed different ages were found for the PGV of the different body length dimensions [6–8]. The peak growth of, for example, foot length or subischial leg length preceded the peak growth of sitting height and this might be useful in determining the age of the PGV of sitting height in advance. However, it is still unclear whether this theory is applicable to individual children, since the ages of the PGV were compared between body dimensions for the mean over the whole group of children. Therefore, the individual variations in growth patterns were not taken into account.
In addition to timing of the peak growth velocity of distal body parts, ratios of growth of body length dimensions could give an early indication for the timing of the pubertal growth spurt of children as well. Since different body parts grow fastest in different periods, the ratios should change as well. The advantage of using ratios is that, at least in theory, less data points are needed to notice whether the ratio is increasing or decreasing. Growth velocity is based on the difference between two data points and therefore at least three measurements are needed in order to be able to determine whether the velocity is increasing or decreasing. Using ratios, only two measurements in time are needed. Again, this theory regarding change in ratios during adolescence should be applicable in general, but the question remains whether it holds for the individual child.
The aim of this study was to determine whether the differences in ages of PGV between sitting height, total body height, subischial leg length, and foot length can be used to predict whether the patient is before or past his or her PGV of sitting height. The existence of the distal-to-proximal growth gradient was tested for the whole group in general, and for the individual child in particular. Furthermore, ratios of growth of different body parts were considered in order to determine their value in prediction of the PGV of sitting height in the individual patient.
Materials and methods
Data for this study were collected in the South of the Netherlands from 1995 to 1999. Children were measured every 6 months in the last 4 years of primary school or the first 4 years of secondary school. In this way, two cohorts of children were obtained with longitudinal measurements of growth over a total range of 7.7–13.4 years and 11.0–17.3 years in girls, and 7.6–13.7 and 11.0–17.7 years in boys.
Parents and children were informed concerning the purposes of the study and their permission was obtained before use of their data. This study only included children without any signs of growth abnormalities.
Measurements
Total body height (TBH) was measured using a stadiometer with digital reading. The child was placed so that the heels and shoulders were in contact with the vertical plane of the stadiometer. The measurement was taken while a gentle manual upward pressure was exerted on the mastoid processes so that the child was fully extended. Sitting height (SH) was measured using a sitting height table. The child was sitting with a straight back on the rigid plate of the sitting height table and the feet on the footrest so that his or her full weight was on the table plate. Furthermore, sitting height was measured in a similar way as total body height. Subischial leg length (SLL) was defined as the arithmetic difference between total body height and sitting height. Foot length (FL) was measured with the child standing full weight bearing. The distance between the most posterior part of the heel and the tip of the longest toe was measured on the left foot using a Harpenden anthropometer. All length dimensions were recorded to the nearest millimeter.
A customized program in Matlab® (Mathworks, Natick MA, USA) was used to plot the longitudinal growth data of each individual child for sitting height, total body height, subischial leg length, and foot length. The program plotted the derivative of the individual growth curve as well (i.e., growth velocity curve), and the timing of the largest peak in this growth velocity curve was calculated. Therefore, each child had four ages of the PGV for sitting height, total body height, subischial leg length, and foot length, respectively.
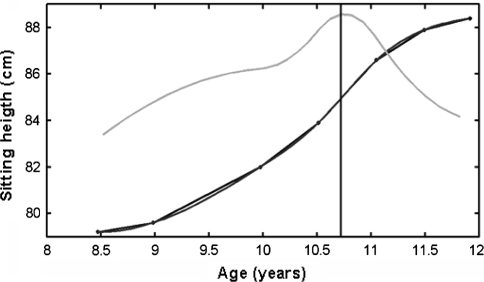
For each different body length dimension, only data of children were used for analysis where the course of the individual growth was clear, i.e., growth curves of children were used which showed a clear peak in the growth velocity curve. A typical example is shown in Fig 1. Furthermore, the children should have at least five measurements, including one measurement in the range between 11.5 and 12.5 years for girls, and one measurement in the range between 13.5 and 14.5 years for boys. This last criterion was applied to make sure the data would include the expected average age for the pubertal growth spurt, which would reduce the chance of identifying a secondary peak as the primary growth velocity peak.
Fig. 1.
Example of a growth curve of sitting height of an individual girl. The grey line is the derivative of the growth curve, i.e. the growth velocity curve. The vertical black line represents the age of the peak growth velocity of sitting height of this particular child
Due to the two cohorts of children, many children showed a largest growth velocity at the start or the end of their growth velocity curve. In these cases, the peak was considered to be an unreliable estimate of the actual PGV and therefore these data were not used in the analysis of that body length dimension. Since the ages of the PGV of, for example, foot length or sitting height are often different in an individual child, it was possible that a child had a useful growth curve for, e.g., foot length, but not for sitting height. Therefore, different numbers of children could be included in the analysis of the different body length dimensions (Table 1).
Table 1.
The number of children included for each body length dimension
| Body length dimension | Number of children (n) | |
|---|---|---|
| Girls | Boys | |
| Sitting height | 181 | 179 |
| Total body height | 213 | 219 |
| Subischial leg length | 147 | 210 |
| Foot length | 212 | 125 |
The original database included longitudinal growth data of 714 girls and 815 boys. The numbers of children with useful growth curves and growth velocity curves for the different body length dimensions ranged from 21 to 30% for girls, and 15–27% for boys (Table 1).
For calculation of the ratios between different body length measures, the data of the children in the selected group for sitting height were used, since the goal was to evaluate whether the ratios could have value for prediction of the PGV of sitting height.
The following six ratios between body length measures were calculated at each measured age in each individual child:
Total body height/sitting height (TBH/SH)
Total body height/subischial leg length (TBH/SLL)
Total body height/foot length (TBH/FL)
Sitting height/subischial leg length (SH/SLL)
Sitting height/foot length (SH/FL)
Subischial leg length/foot length (SLL/FL).
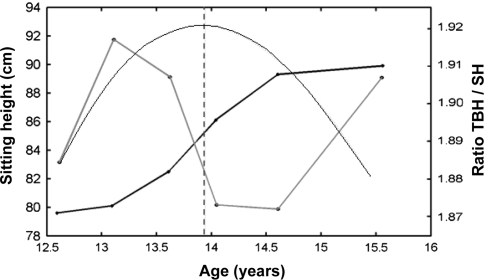
The ratios between different body length measures were plotted as well for each individual and the ages of the highest and lowest ratios were calculated. Therefore, each child had six graphs showing the different ratios during the measured age range. The age of the PGV of sitting height of that particular individual was shown in the graphs as well. An example is shown in Fig. 2.
Fig. 2.
Example of a growth curve of sitting height of a boy, as well as the ratio of that same boy for total body height/sitting height. The smooth black line represents the growth velocity curve of the fitted growth curve (fitted growth curve is not shown in this graph). The vertical dotted line represents the age of the PGV of sitting height of this particular boy
The individual ages of the PGV of the different body length measures were acquired and the mean age of the PGV for the group of selected children was calculated for each body length dimension in order to check whether the expected distal-to-proximal growth gradient would be present in the current data. The mean ages of the PGV for the different body length dimensions were statistically compared using an independent t test where p values <0.05 were considered significant.
Furthermore, the percentages of children were calculated where the PGV of total body height (TBH), subischial leg length (SLL), and foot length (FL) occurred before their own PGV of sitting height (SH) in order to determine whether the pattern was consistent for all individuals. This was repeated calculating the percentages of children having the PGV of a body length dimension more than 0.5 years earlier than their own age of the PGV of sitting height since the difference of 0.5 year was determined to be clinically relevant.
A similar method was used for the ratios between the different body length dimensions. The mean ages of the highest and lowest ratios between body length dimensions were compared to the mean age of the PGV of sitting height. A paired t test was used and P values <0.05 were considered significant. Furthermore, the percentages of children were calculated where the highest and lowest ratios occurred before, and at more than 0.5 years before their own age of the PGV of sitting height in order determine whether the ratios could be used as a predictor in the individual children.
Results
The mean ages of the PGV of the different body length measures are shown in Table 2. In both girls and boys, the mean ages of the PGV of total body height, subischial leg length, and foot length were all significantly lower than the mean age of the PGV of sitting height (Table 2). Furthermore, the distal body parts experienced the growth spurt on average earlier during adolescence, although the difference between the mean age of the PGV of subischial leg length and total body height in boys was minimal. The ages in all other possible pairs of length measures in girls and boys were significantly different (p < 0.05).
Table 2.
Results of mean ages and magnitudes of peak growth velocities of different body length dimensions in girls and boys
| Body length dimension | Age of the PGV (years) | |
|---|---|---|
| Girls | Boys | |
| Sitting height (SD) | 12.12 (1.12) | 14.33 (0.82) |
| Total body height (SD) | 11.70 (1.09)a | 14.01 (0.83)a |
| Subischial leg length (SD) | 11.34 (1.00)a | 14.00 (0.63)a |
| Foot length (SD) | 10.99 (0.68)a | 13.09 (1.10)a |
aSignificantly different from the age at peak growth velocity of sitting height
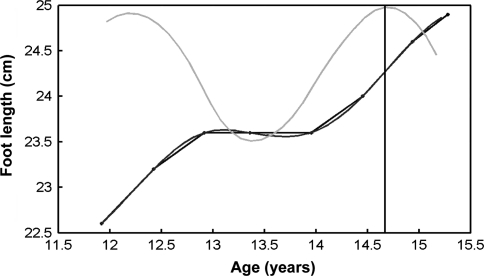
Many boys showed a growth curve of foot length with two almost equal peaks, one around the age of 12 years and the other around the age of 15 years. A typical example was shown in Fig. 3. This resulted in a mean age of the PGV of 13.1 years and a relatively large SD of 1.1.
Fig. 3.
Example of a common growth curve of foot length of a boy with two peaks in the growth velocity curve. The grey line is the derivative of the growth curve, i.e., the growth velocity curve. The vertical black line represents the age of the highest growth velocity
The distal-to-proximal growth gradient did not hold for each individual child as was illustrated by the low percentages of girls and boys having their PGV of TBH, SLL, and FL before their own PGV of sitting height (Table 3).
Table 3.
Percentage of children having their PGV of a body length dimension earlier than their own PGV of sitting height (first value in each cell)
| Body length dimension | Percentage of children (%) | |
|---|---|---|
| Girls | Boys | |
| PGV total body height | 43.7–14.9 | 60.7–23.1 |
| PGV subischial leg length | 68.6–65.7 | 66.7–50.0 |
| PGV foot length | 68.7–32.8 | 65.5–43.1 |
The second value in each cell is the percentage of children having their PGV of a body length dimension more than 0.5 years earlier than their own age of the PGV of sitting height
PGV peak growth velocity
In girls, significant differences were only found between the mean age of the lowest ratios involving foot length and the mean age of the PGV of sitting height. In boys, 5 out of 6 mean ages of the highest ratios were significantly different from the mean age of the PGV of sitting height, as well as 4 out 6 mean ages of the lowest ratios (Table 4).
Table 4.
Mean ages of the highest and lowest value of the different ratios between body length measures of girls and boys
| Ratio | Girls | Boys | ||
|---|---|---|---|---|
| Age at highest ratio (years) | Age at lowest ratio (years) | Age at highest ratio (years) | Age at lowest ratio (years) | |
| TBH/SH (SD) | 11.94 (1.46) | 12.26 (1.57) | 14.24 (0.77) | 14.92 (1.25)a |
| TBH/SLL (SD) | 12.32 (1.55) | 11.96 (1.47) | 15.02 (1.18)a | 14.19 (0.77) |
| TBH/FL (SD) | 12.28 (1.33) | 11.26 (1.53)a | 15.28 (0.94)a | 13.68 (0.87)a |
| SH/SLL (SD) | 12.28 (1.55) | 11.96 (1.47) | 14.96 (1.25)a | 14.21 (0.77) |
| SH/FL (SD) | 11.94 (1.65) | 11.36 (1.21)a | 15.31 (0.95)a | 13.85 (0.84)a |
| SLL/FL (SD) | 12.13 (1.75) | 11.49 (1.17)a | 14.94 (0.84)a | 13.81 (1.02)a |
SH sitting height, TBH total body height, SLL subischial leg length, FL foot length
aSignificantly different from the age of the PGV of sitting height
The percentages of individual children having their highest or lowest value of a ratio more than 0.5 years before their own age of the PGV of sitting height varied between 4.7 and 61.8% (Table 5). Again, the variability between individual children was large and the predictive value of the ages of the highest and lowest ratios was low.
Table 5.
Percentage of children having their age of the highest or lowest ratio between two body length measures earlier than their own age of the PGV of sitting height (first value in each cell)
| Ratio | Girls | Boys | ||
|---|---|---|---|---|
| % highest ratio (>0.5 year) before PGV SH | % lowest ratio (>0.5 year) before PGV SH | % highest ratio (>0.5 year) before PGV SH | % lowest ratio (>0.5 year) before PGV SH | |
| TBH/SH | 70.7–31.7 | 43.5–40.6 | 71.1–42.2 | 17.7–15.3 |
| TBH/SLL | 41.7–38.9 | 69.7–29.5 | 12.4–11.2 | 71.4–41.2 |
| TBH/FL | 46.1–34.8 | 71.0–48.4 | 15.5–9.1 | 83.5–57.7 |
| SH/SLL | 42.5–38.4 | 78.4–54.5 | 14.6–14.6 | 71.9–43.8 |
| SH/FL | 50.7–49.3 | 81.9–45.7 | 8.4–4.7 | 86.3–61.8 |
| SLL/FL | 56.0–31.0 | 60.0–45.0 | 29.1–16.5 | 66.7–48.6 |
The second value in each cell is the percentage of children having their highest or lowest ratio between two body length measures more than 0.5 years earlier than their own age of the PGV of sitting height
PGV peak growth velocity. Other abbreviations are explained in Table 4
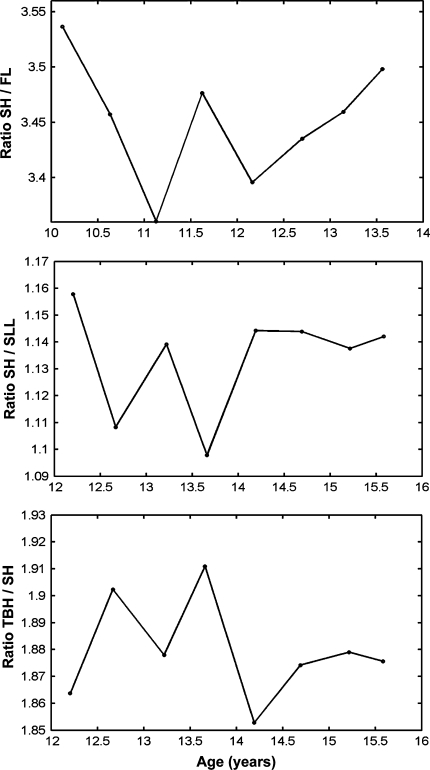
A large variability was observed as well in the graphs concerning the ratios. The range of the magnitude of the ratios in an individual child was very small in general, with an average difference between the highest and lowest values in all ratios of only 0.11 (SD 0.046). Some typical examples of graphs of different ratios are shown in Fig. 4.
Fig. 4.
Three typical examples of graphs of individual children showing the variability in the ratios between TBH/SH, SH/SLL, and SH/FL, respectively. TBH total body height, SH sitting height, SLL subischial leg length, FL foot length
Discussion
This study determined whether the differences in ages of the PGV between different body length dimensions could be used to determine whether the individual child was before or after his or her PGV of sitting height. It was shown before that distal body parts have their peak growth earlier in adolescence and therefore the growth velocity of foot length, for example, could be an early predictor for the timing of the peak growth of sitting height. This study indeed showed a lower age of the PGV of distal body parts when taking the average ages of the PGV of the whole group. When the peak growth of the foot takes place, the peak growth of sitting height should on average take place 1.1 years later in girls and 1.2 years later in boys. However, this study showed that the variation between individual children was too large to apply this fact for early prediction of the PGV of sitting height, as the peak growth velocity of foot length still occurred after the PGV of sitting height in over 31% of the girls and 34% of the boys. Furthermore, the percentage of children having their PGV of a body length dimension more than 0.5 years before their own age of the PGV of sitting varied between only 14.9 and 65.7%. Therefore, the predictive value in the individual child was very low.
Similar results were found for the ratios between the growths of different body parts. The advantage of using ratios was explained earlier in the “Introduction” section. However, no more than 61.8% of the individual children had a highest or lowest value of a ratio at least 0.5 years before their own age of the PGV of sitting height. Therefore, the ages of the highest and lowest ratios and the age of the PGV of sitting height were not considered useful for the clinical practice. Furthermore, the ratios themselves were too variable and the differences between consecutive ratios were too small to be useful as a predictive tool. As a consequence, the influence of measurement errors will probably be too large.
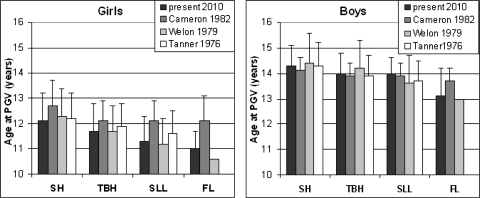
Several other studies measured longitudinal growth in different body parts [9–11]. When comparing the present results to these studies, striking agreements were found for the average ages of the PGV of the four body length dimensions (Fig 5). Only Cameron et al. [9] showed higher ages at all four PGV’s in girls, and at PGV of foot length in boys. Possibly the fitting of a Preece–Baines 1 model to their data caused different results.
Fig. 5.
Comparison of the mean age of the PGV of sitting height, total body height, subischial leg length, and foot length in the present study with 3 other studies using longitudinal growth data (Cameron et al. [9], Welon and Bielicki [11], and Tanner et al. [10]). Tanner et al. did not measure foot length, and Welon and Bielicki did not provide an SD for foot length. Vertical bars represent the SD
One limitation of the present study was the data collection at primary and secondary schools. Therefore, two cohorts of children were present in the available database and the data of a relative large amount of children could not be used for analysis. Due to this split up in two cohorts, only 21–30% of the data for girls, and 15–27% of the data for boys were included in the final analysis. Data of children with a PGV around the age of 12 years were probably less available and since this was near to the mean age of the PGV, an overestimate of the standard deviation was feasible. However, a study design with a comparable study group and longer follow-up was logistically unachievable.
In particular, the data regarding foot length in boys were largely decreased. In these growth curves an unexpected pattern was seen. As seen earlier in the results section, many boys showed a growth curve with two almost equal peaks, around the age of 12 and 15 years. Because of this pattern, many of the growth curves of foot length of boys could not be used in the analysis. This presence of two peaks in the growth velocity curve of foot length in boys should be taken into account when interpreting the mean age of the PGV of 13.1 years and the SD of 1.1.
A second limitation of this study was that the measurements were performed in healthy children and not in children with adolescent idiopathic scoliosis. However, Veldhuizen et al. [12] and Duval-Beaupere [13] failed to demonstrate any deviation of total body height or sitting height in scoliotic children in comparison to healthy children. Furthermore, Willner [14] showed that the legs and the spine in children with scoliosis have similar length proportions in relationship to total body height as in healthy children. Therefore, it is believed that results of present study are applicable as well for children with adolescent idiopathic scoliosis.
In conclusion, the distal-to-proximal growth gradient as described by several researchers, should be interpreted as a reflection of the group mean. However, this gradient cannot be used for predictions in the individual child since the variation between children is too large. Furthermore, the use of ratios between growth of different body parts is not useful for predictions in the individual child since the variation is too large as well, and the influence of measurement errors in the clinical practice is probably too large to obtain reliable results.
Acknowledgments
This research was supported by the Dutch Technology Foundation STW, applied science division of NWO and the Technology Program of the Ministry of Economic Affairs.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Escalada F, Marco E, Duarte E, et al. Growth and curve stabilization in girls with adolescent idiopathic scoliosis. Spine. 2005;30:411–417. doi: 10.1097/01.brs.0000153397.81853.6a. [DOI] [PubMed] [Google Scholar]
- 2.Hagglund G, Karlberg J, Willner S. Growth in girls with adolescent idiopathic scoliosis. Spine (Phila Pa 1976.) 1992;17:108–111. doi: 10.1097/00007632-199201000-00016. [DOI] [PubMed] [Google Scholar]
- 3.Sanders JO, Browne RH, Cooney TE, et al. Correlates of the peak height velocity in girls with idiopathic scoliosis. Spine. 2006;31:2289–2295. doi: 10.1097/01.brs.0000236844.41595.26. [DOI] [PubMed] [Google Scholar]
- 4.Sanders JO, Little DG, Richards BS. Prediction of the crankshaft phenomenon by peak height velocity. Spine. 1997;22:1352–1356. doi: 10.1097/00007632-199706150-00013. [DOI] [PubMed] [Google Scholar]
- 5.Tanner JM. Growth at adolescence. 2. Oxford: Blackwell; 1962. [Google Scholar]
- 6.Cheng JC, Leung SS, Chiu BS, et al. Can we predict body height from segmental bone length measurements? A study of 3, 647 children. J Pediatr Orthop. 1998;18:387–393. doi: 10.1097/00004694-199805000-00022. [DOI] [PubMed] [Google Scholar]
- 7.Rao S, Joshi S, Kanade A. Growth in some physical dimensions in relation to adolescent growth spurt among rural Indian children. Ann Hum Biol. 2000;27:127–138. doi: 10.1080/030144600282244. [DOI] [PubMed] [Google Scholar]
- 8.Fredriks AM, Van Buuren S, van Heel WJ, et al. Nationwide age references for sitting height, leg length, and sitting height/height ratio, and their diagnostic value for disproportionate growth disorders. Arch Dis Child. 2005;90:807–812. doi: 10.1136/adc.2004.050799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cameron N, Tanner JM, Whitehouse RH. A longitudinal analysis of the growth of limb segments in adolescence. Ann Hum Biol. 1982;9:211–220. doi: 10.1080/03014468200005701. [DOI] [PubMed] [Google Scholar]
- 10.Tanner JM, Whitehouse RH, Marubini E, et al. The adolescent growth spurt of boys and girls of the Harpenden growth study. Ann Hum Biol. 1976;3:109–126. doi: 10.1080/03014467600001231. [DOI] [PubMed] [Google Scholar]
- 11.Welon Z, Bielicki T. The timing of adolescent growth spurts of 8 body dimensions in boys and girls of the Wroclaw growth study. Stud Phys Anthropol. 1979;5:75–79. [Google Scholar]
- 12.Veldhuizen AG, Baas P, Webb PJ. Observations on the growth of the adolescent spine. J Bone Jt Surg Br. 1986;68:724–728. doi: 10.1302/0301-620X.68B5.3782232. [DOI] [PubMed] [Google Scholar]
- 13.Duval-Beaupere G (1970) Pathogenic relationship between scoliosis and growth. In: Zorab PA (ed) Scoliosis and growth, vol 1. Churchill Livingstone, Edinburg, pp 58–64
- 14.Willner S. The proportion of legs to trunk in girls with idiopathic structural scoliosis. Acta Orthop Scand. 1975;46:84–89. doi: 10.3109/17453677508989195. [DOI] [PubMed] [Google Scholar]