Fast and accurate reconstruction of HARDI data using compressed sensing

Abstract

A spectrum of brain-related disorders are nowadays known to manifest themselves in degradation of the integrity and connectivity of neural tracts in the white matter of the brain. Such damage tends to affect the pattern of water diffusion in the white matter – the information which can be quantified by means of diffusion MRI (dMRI). Unfortunately, practical implementation of dMRI still poses a number of challenges which hamper its wide-spread integration into regular clinical practice. Chief among these is the problem of long scanning times. In particular, in the case of High Angular Resolution Diffusion Imaging (HARDI), the scanning times are known to increase linearly with the number of diffusion-encoding gradients. In this research, we use the theory of compressive sampling (aka compressed sensing) to substantially reduce the number of the diffusion gradients without compromising the informational content of HARDI signals. The experimental part of our study compares the proposed method with a number of alternative approaches, and shows that the former results in more accurate estimation of HARDI data in terms of the mean squared error.

1 Introduction

The human brain consists of about 10¹¹ nerve cells which can be further sub-divided into about 1000 different cell types, a complexity that far exceeds that of other organs of the body. An additional complexity is evident in the way in which the component cells of the brain interconnect and function. In contrast to other types of the cells, each neuron communicates with many target cells by means of its peculiar protoplasmatic protrusion, called axon. Moreover, axons with similar destinations tend to form bundles, known as neural fiber tracts. Taken together, these fibers play a pivotal role in the determination of brain connectivity, which is presently far from being completely understood. Consequently, by reconstructing the pattern of connectivity of the neural tracts in both healthy and diseased subjects, it is possible to obtain an abundance of valuable diagnostic information that could be used for early diagnostics of brain-related disorders, for assessing the damage caused to the brain by stroke, tumors or injuries, as well as for planning and monitoring of neurosurgeries [1],[2]. In this regard, diffusion MRI (dMRI) appears to be an unparalleled tool of diagnosis imaging of the brain, as it is the only imaging modality which can “sense” the local orientation of neural fibers tracts.

Diffusion tensor imaging (DTI) is the most widespread type of dMRI, which describes the local diffusion of water molecules using a unimodal Gaussian model [3],[4],[5]. Unfortunately, the performance of DTI is known to deteriorate considerably at the spatial locations where neural tracts cross, touch upon each other, or diverge [6],[7],[8],[9]. To overcome this intrinsic limitation of DTI, the High Angular Resolution Diffusion Imaging (HARDI) technique has been proposed [10],[8],[11],[12] which is capable of capturing multi-modal diffusion patterns through sampling the corresponding diffusion signals over a spherical shell in k-space.

The superiority of HARDI over DTI suggests the possibility of further improvement of the diagnostic value of dMRI [13]. Unfortunately, this superiority comes at a significant price: HARDI requires using a substantially larger number of diffusion-encoding gradients N, with a typical N being in the range between 60 and 100 (as compared to N ∈ [25, 30] in the case of DTI). As the total scanning time increases linearly with N, HARDI-based analysis is currently deemed to be “too slow” to be used in clinical applications involving children or patients with dementia.

The above deficiency of HARDI can be overcome using the theory of compressive sampling (aka compressed sensing) (CS) [14],[15],[16], which provides a framework to recover HARDI signals from a much smaller number of measurements as compared to the standard range of N. Formalizing such a reconstruction approach constitutes the main contribution of this work. It should be noted that there already exists a body of works in which the theory of CS has been used for reconstruction of grayscale MR images from their sub-critical samples in k-space [17],[18],[19]. The proposed method, on the other hand, is different in that it applies the tools of CS in the diffusion domain (rather than in the spatial domain), as is detailed in the sections that follow.

2 Compressed Sensing

A continuum of all possible orientations in IR³ can be identified with the points of the unit sphere 𝕊² := {u ∈ IR³ | ‖u‖₂ = 1}. Let p = (x, y, z) be the spatial coordinate of an arbitrary voxel within a volume of interest. Then, the diffusion signal S(u) at p can be formally described as a real-valued function defined over 𝕊². In practical settings, the signal S(u) can only be measured along N discrete orientations ${\{{\mathbf{u}}_k\}}_{k=1}^N$ . The most fundamental question in this regard has always been: what is the minimum number of diffusion directions N required to unambiguously represent the signal S in terms of its discrete values S_k?

A particularly important answer to the above question is offered by the theory of CS. To summarize some fundamental results of the theory, we consider S to be a member of a Hilbert space, endowed with a standard inner product. Since diffusion measurements are linear, the discrete measurements S_k := S(u_k) can be expressed in the form of inner products S_k = 〈S, φ_jk〉, with ${\{{\phi }_{\mathit{\text{jk}}}\}}_{k=1}^N$ being a subset of a sampling basis {φ_i}_i∈ℐ. Moreover, let {ψ_j}_j∈𝒥 be another basis in the signal space, such that any S can be expressed according to

$$S(\mathbf{u})={\displaystyle \sum _{j\in 𝒥}}{c}_j{\psi }_j(\mathbf{u}),\forall \mathbf{u}\in {𝕊}^2,$$ (1)

where 𝒥 denotes the set of indices over which the basis functions ψ_j are counted. Note that, in a more general setup, the set {ψ_j}_j∈𝒥 may be overcomplete, in which case it becomes a frame. However, independently of whether it is a basis or a frame, in what follows, the set {ψ_j}_j∈𝒥 is assumed to be finite, with the total number of its elements being equal to M.

Using the above definitions, we make the following two assumptions:

1. S is assumed to be sparsely representable by {ψ_j}_j∈𝒥, which implies that the number K of non-zero coefficients c_j in (1) is significantly less than M.

2. The bases {φ_i}_i∈ℐ and {ψ_j}_j∈𝒥 are assumed to be incoherent, implying that the value of μ = sup_i,j |〈φ_i(u), ψ_j(u)〉| is relatively small.

On Conditions (a) and (b), the theory of CS proves that an accurate approximation of S is possible from only 𝒪 (μ² log(M)K) of its measurements, as opposed to 𝒪(M) in the case of standard sampling theory. Moreover, this approximation is computable through solution of a convex optimization problem [14],[15],[16].

The above considerations suggest that the applicability of CS to HARDI depends on the availability of a basis/frame {ψ_j}_j∈𝒥 for which the assumptions (a) and (b) above would be valid. Such a basis has been recently introduced in [20], where it is called a basis of spherical ridgelets – the functions which have been specifically designed to provide sparse representation of HARDI signals. Moreover, as the energy of spherical ridgelets is distributed alongside the great circles of 𝕊², the ridgelets appear to be very incoherent with respect to the Dirac sampling basis. All this makes spherical ridgelets an ideal candidate to be used for CS-based recovery of HARDI signals, as it is demonstrated next.

3 Spherical Ridgelets

Spherical ridgelets are constructed using the fundamental principles of wavelet theory. Let κ_ρ(x) = exp{−ρ x (x + 1)}, where 0 < ρ < 1 and x > 0. Also, let κ_j(x) = κ_ρ(2^−jx) be a scaled version of κ_ρ, where j ∈ IN. Then, the Gaussian-Weierstrass scaling function K_j,v : 𝕊² → IR at resolution j ∈ IN and orientation v ∈ 𝕊² is given by

$$K_{j,\mathbf{v}}(\mathbf{u})={\displaystyle \sum _{n=0}^{\mathrm{\infty }}}\frac{2n+1}{4\pi }{\kappa }_j(n)P_n(\mathbf{u}·\mathbf{v}),\forall \mathbf{u}\in {𝕊}^2$$ (2)

where P_n denotes the Legendre polynomial of order n and the dot stands for the Euclidean inner product in IR³. Consequently, following [20], the semi-discrete frame IF of spherical ridgelets can be defined as

$$\text{IF}:=\{{\Psi }_{j,\mathbf{v}}|\mathbf{v}\in {𝕊}^2,j\in \text{IN}\cup \{-1\}\},$$ (3)

where

$${\Psi }_{j,\mathbf{v}}=\frac{1}{2\pi }\{\begin{array}{cc}ℛ\{K_{0,\mathbf{v}}\},\hfill & \text{if}j=-1,\hfill \\ ℛ\{K_{j+1,\mathbf{v}}-K_{j,\mathbf{v}}\},\hfill & \text{if}j\in \text{IN}\hfill \end{array}$$ (4)

with ℛ standing for the Funk-Radon transform (FRT) [21]. Note that, for an arbitrary j ∈ IN ∪ {−1} and v ∈ 𝕊², the FRT of K_j,v(u) can be computed as

$$ℛ\{K_{j,\mathbf{v}}\}(\mathbf{u})={\displaystyle \sum _{n=0}^{\mathrm{\infty }}}\frac{2n+1}{4\pi }{\lambda }_n{\kappa }_j(n)P_n(\mathbf{u}·\mathbf{v}),\forall \mathbf{u}\in {𝕊}^2$$ (5)

where

$${\lambda }_n=\{\begin{array}{cc}2\pi {(-1)}^{n/2\frac{1·3\cdots (n-1)}{2·4\cdots n},}\hfill & \text{if}n\text{is even}\hfill \\ 0,\hfill & \text{if}n\text{is odd}.\hfill \end{array}$$ (6)

The set IF in (3) is infinite-dimensional, and hence is not suitable for practical computations. To define a discrete counterpart of IF, one has first to restrict the values of the resolution index j to a finite set {−1, 0, 1,…, J}, where J defines the highest level of “detectable” signal details. Additionally, the set of all possible orientations v ∈ 𝕊² of spherical ridgelets needs to be discretized as well. To find a proper discretization scheme, we first note that the construction in (4) is dyadic, which suggests that the bandwidth of spherical ridgelets increases proportionally to 2^j. Owing to the fact that the dimension of the space of spherical harmonics of degree n is equal to (n + 1)², it is reasonable to define the number of discrete orientations to be a function of j. Specifically, let m₀ be the smallest spherical order resulting in κ₀(m₀) ≤ ε for some predefined 0 < ε ≪ 1 (e.g. ε = 10⁻⁶). Then, one can define the number of ridgelet orientations at resolution j to be equal to M_j = (2^j+1m₀ + 1)². Subsequently, for each M_j, let ${\{{\mathbf{v}}_{i,j}\}}_{i=1}^{M_j}$ be a set of M_j distinct points on 𝕊². A finite-dimensional set of spherical ridgelets can then be defined as

$${\text{IF}}_d={\displaystyle \underset{j=-1}{\overset{J}{\cup }}}{\{{\Psi }_{j,{\mathbf{v}}_{i,j}}\}}_{i=1}^{M_j},$$ (7)

where the subscript d stands for “discrete”. It should be emphasized that the set IF_d is finite, as it consists of a total of $M={\displaystyle {\sum }_{j=-1}^J}{(2^{j+1}{m}_0+1)}^2$ spherical ridgelets.

Given a measurement set of N diffusion-encoding orientations $U_N:={\{{\mathbf{u}}_k\}}_{k=1}^N$ , one can use (4) and (5) to compute the values of the spherical ridgelets in IF_d over U_N. The resulting vales can be then stored into an N × M matrix 𝒜. Subsequently, if c ∈ IR^M is defined to be a (column) vector of ridgelet coefficients and y := [S(u₁), S(u₂),…, S(u_N)]^T, then the measurement model can be formally expressed as 𝒜c = y + e, where e is an error vector that accounts for both measurement and model noises.

Assuming that ‖e‖₂ ≤ η, an optimal estimate c should satisfy ‖𝒜c−y‖₂ ≤ η. Unfortunately, since N < M, the above condition by itself falls short to define an optimal c. However, if the coefficients c are known to be sparse w.r.t. IF_d, then the theory of CS states that a useful estimate of the representation coefficients can be found by solving

$$c^{*}=\text{arg}\underset{c}{\text{min}}{\Vert c\Vert }_1\text{ subject to }{\Vert 𝒜c-y\Vert }_2\le \eta .$$ (8)

Note that (8) is a convex optimization problem, whose solution can be found using standard tools of optimization theory. In the present work, the problem has been solved using the ℓ₁-magic software freely available at http://www.acm.caltech.edu/l1magic/.

For the sake of comparison, we also estimate the representation coefficients c by computing the minimum ℓ₂-norm solution satisfying ‖𝒜c − y‖₂ ≤ η. It is important to point out that such solutions are typically not sparse, in which case there are no a priori guarantees of optimality of resulting estimates. It will be shown however that, in the case of spherical ridgelet analysis, the ℓ₂-solutions appear to be quite informative. Note that the ℓ₂-estimates are attractive for they admit a close form expression, which is

$$c^{*}={𝒜}^T{(𝒜{𝒜}^T)}^{-1}y.$$ (9)

4 Results

To test the performance of the proposed method, HARDI data acquired from an dMRI phantom [?] were used. Specifically, the data were acquired using 3 mm isotropic acquisition over a square field-of-view of size 19.2 cm, b = 2000 s=mm², and 128 diffusion orientations, uniformly distributed over the sphere. (For more details on the data acquisition setup see www.lnao.fr/spip.php?article107.) The acquired HARDI signals were low-pass filtered using the regularized estimation approach of [22] to suppress the effect of measurement noise. The signals thus obtained were regarded as the original HARDI signals against which their CS-based estimates were compared. In this work, normalized mean squared error (NMSE) has been used to assess the performance of different reconstruction methods.

To simulate CS acquisition, the full set of 128 diffusion directions was reduced to subsets of N = 16, 18, 20,…, 32 spherical points. These subsets were chosen in such a way that their points covered 𝕊² in a quasi-uniform manner (similarly to the original coverage by 128 points). For each value of N, its associated sensing matrix 𝒜 was constructed with J = 1, ρ = 0.5 and m₀ = 4. Subsequently, the optimal ridgelet coefficients were computed using two different approaches, namely by solving the minimum ℓ₁-norm problem (8) and using (9). (These two estimates will be referred to below as SR-L1 and SR-L2, respectively.) Note that, in the case of SR-L1, the value of η = 0:12 in (8) was found by trials and errors to result in the most accurate reconstruction in terms of NMSE. Finally, the estimated ridgelet coefficients were used to evaluate their associated HARDI signals at the points of the original data set according to (1), followed by the computation of NMSE.

As an alternative to spherical ridgelets, the applicability of spherical harmonics (SHs) to the problem of CS-based reconstruction of HARDI signals has been investigated as well [12],[23]. To this end, the orthogonal set of SHs of orders up to n = 8 inclusive was used to define the sensing matrix 𝒜. Note that, since the diffusion signals are symmetric and real-valued, only the even-ordered SHs have been employed. Analogously to the case of spherical ridgelets, the SH-based reconstruction was carried out twice, viz. using both (8) and (9). The respective estimates will be referred to below as SH-L1 and SH-L2, correspondingly.

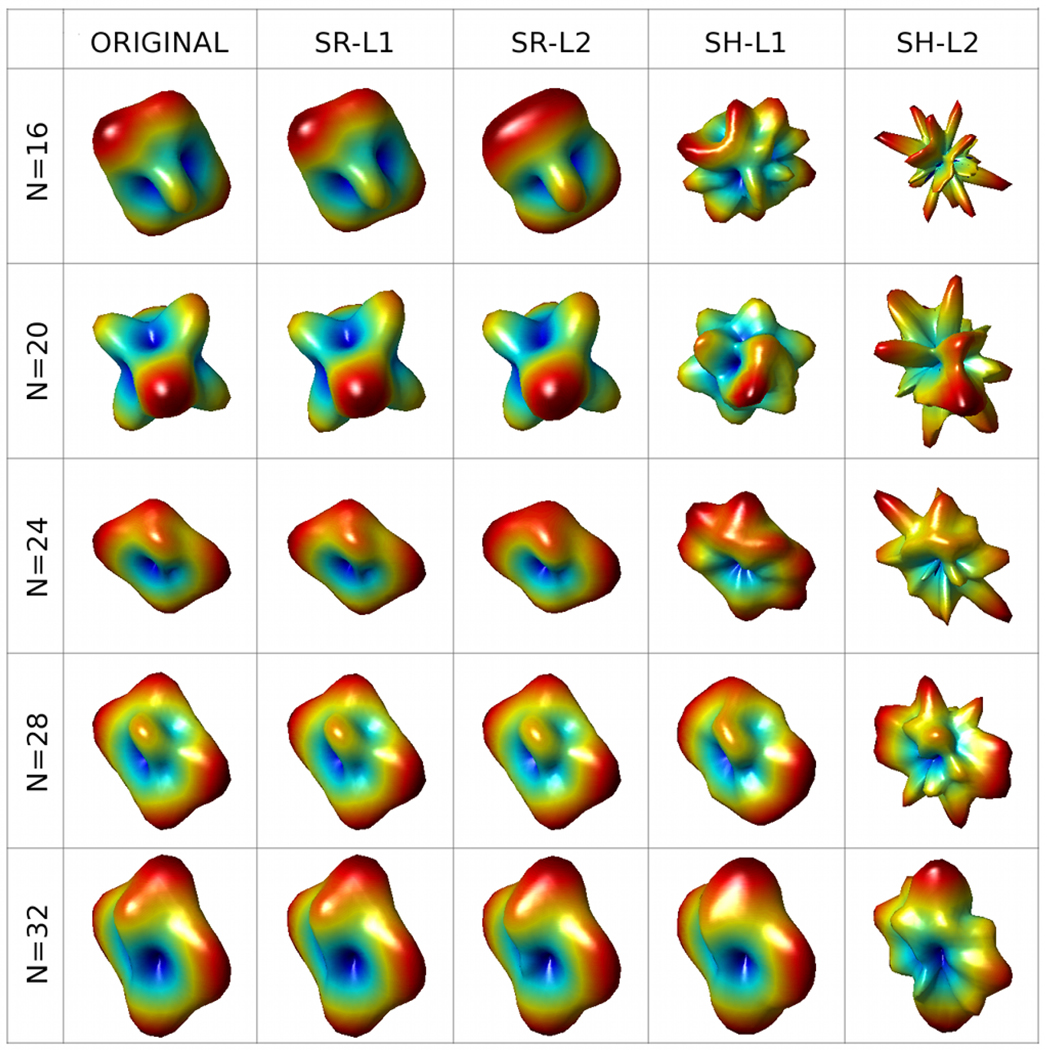
Table 1 summarizes the values of NMSE (± one standard deviation) obtained in the above experiments. Note that each value in the table has been computed by averaging the results of 500 independent estimations. One can clearly see that the ridgelets-based ℓ₁-reconstruction (SR-L1) performs incomparably better than SH-L1. Moreover, the SH-based approach is also outperformed by SR-L2, which performs surprisingly well in the case of spherical ridgelet analysis (despite the inability of ℓ₂-norm minimization to take advantage of the sparse nature of the ridgelet coefficients). The results of Table 1 are also supported by Fig. 1 which depicts a subset of the original HARDI signals together with their estimates computed by the compared algorithms for different values of N.

Table 1.

NMSE (±σ) obtained by different reconstruction methods.

	Spherical Ridgelets (SR)		Spherical Harmonics (SH)
N	ℓ1-minimization	ℓ2-minimization	ℓ1-minimization	ℓ2-minimization
16	0.0148 ± 0.0045	0.0176 ± 0.0047	0.0883 ± 0.0329	0.5145 ± 0.0211
18	0.0116 ± 0.0042	0.0147 ± 0.0039	0.0646 ± 0.0304	0.4011 ± 0.0257
20	0.0107 ± 0.0032	0.0127 ± 0.0034	0.0440 ± 0.0183	0.2774 ± 0.0319
22	0.0085 ± 0.0031	0.0120 ± 0.0031	0.0326 ± 0.0138	0.1976 ± 0.0257
24	0.0083 ± 0.0030	0.0118 ± 0.0028	0.0257 ± 0.0097	0.1411 ± 0.0252
26	0.0077 ± 0.0023	0.0115 ± 0.0026	0.0195 ± 0.0071	0.1130 ± 0.0246
28	0.0069 ± 0.0018	0.0113 ± 0.0024	0.0158 ± 0.0045	0.0790 ± 0.0230
30	0.0067 ± 0.0016	0.0112 ± 0.0020	0.0146 ± 0.0037	0.0651 ± 0.0145
32	0.0066 ± 0.0015	0.0109 ± 0.0019	0.0121 ± 0.0033	0.0566 ± 0.0140

Fig. 1.

HARDI signals recovered by different reconstruction algorithms.

5 Discussion and Conclusions

Central to the theory of compressed sensing is the notion of sparse representation. In particular, if a signal of interest is known to have a sparse representation in the domain of a linear transform, then it can be accurately reconstructed from a much smaller number of its discrete measurements, as it is required by the classical sampling theory. In the case of HARDI data analysis, the most frequently used representation basis is that of spherical harmonics (SHs). Unfortunately, SHs do not provide sparse representation of HARDI signals, which makes them inappropriate for the use in CS-based estimation. The basis of spherical ridgelets, on the other hand, can represent HARDI signals using a relatively small number of representation coefficients. As demonstrated by Table 1, the above fact allows one to reconstruct HARDI signals from as few as 20 of their measurements with the reconstruction error being about 1%. This result suggests that the CS-based acquisition of HARDI signals has a potential of substantially shortening the scanning times in dMRI, which is known to be a major bottleneck in clinical applications of this important tool of diagnostic imaging.