Towards a genome-wide transcriptogram: the Saccharomyces cerevisiae case

Abstract

Analysis of genome-wide expression data poses a challenge to extract relevant information. The usual approaches compare cellular expression levels relative to a pre-established control and genes are clustered based on the correlation of their expression levels. This implies that cluster definitions are dependent on the cellular metabolic state, eventually varying from one experiment to another. We present here a computational method that order genes on a line and clusters genes by the probability that their products interact. Protein–protein association information can be obtained from large data bases as STRING. The genome organization obtained this way is independent from specific experiments, and defines functional modules that are associated with gene ontology terms. The starting point is a gene list and a matrix specifying interactions. Considering the Saccharomyces cerevisiae genome, we projected on the ordering gene expression data, producing plots of transcription levels for two different experiments, whose data are available at Gene Expression Omnibus database. These plots discriminate metabolic cellular states, point to additional conclusions, and may be regarded as the first versions of ‘transcriptograms’. This method is useful for extracting information from cell stimuli/responses experiments, and may be applied with diagnostic purposes to different organisms.

INTRODUCTION

Genome-wide expression data consist of expression levels of thousands of genes and the joint analysis of the whole data represents a challenge. The usual approaches compare expression levels of modified cellular stages relative to those of a pre-established control. The genes are then ranked by the variations in expression relative to the control and those genes that present the most significant alterations (highest or lowest) are chosen to be further analyzed. However, genes have their expression dynamics determined by a network of other genes and moderate alterations on many interacting genes may cause measurable effects on cell metabolism. These effects may be overlooked when using the maximally altered level criterion but, on the other hand, the great amount of data may prevent a more accurate analysis.

From a broader point of view, however, analysis of a great amount of information is not a novelty in scientific research. Even in everyday life events, people deal with amounts of data that largely exceeds their capacity to process. Indeed, data filtering to process only the most relevant information is an ability that saves time and energy and, probably, it has been repeatedly selected during evolution. A common example of data filtering can be given by a high-resolution photograph: although the digital file contains information on a huge number of pixels, much higher than the number of pixels in a computer screen, a picture of the whole object can still be produced on the screen. Image processing tools assign to each screen pixel some average of the information stored in a neighboring group of digital pixels, reducing the total information sent to the computer screen but still preserving global information. Observe that zooms may be applied to these pictures to obtain partial images such that, after a zoom, each screen pixel is assigned with the average of the information stored by a number of neighboring digital pixels. In other words, a huge collection of data relative to a whole phenomenon may be presented either by a coarser, global image or by a finer but partial image of the whole. In this example, the key point is the average of information stored on neighboring pixels. Furthermore, the averaging over neighboring pixels also acts in the sense of neutralizing spurious fluctuations caused by some random external effect.

In this article we present a method to produce ‘images’ of gene expression data of whole genomes, by producing expression profiles for transcriptomes. The idea of the method is to consider averages of expression data over neighboring genes disposed on a line, as in the metaphoric example of the high-resolution photograph. In one hand, this procedure targets a global assessment of expression data of whole genomes. On the other hand, it requires the definition of gene neighborhood when disposed on a line, which is not straightforward.

Expression levels of different genes may differ by large amounts. Consequently a random list of genes generates plots of relative gene expression levels that fluctuate so wildly that very few, if some information, can be gathered from them. Techniques to extract information from wildly fluctuating general profiles consider averages taken over intervals of neighboring points. In the case where genes are ordered on a list following some criterion that favors clustering together interacting genes, the distance between any two genes on the list may correlate with the probability of mutual interaction, yielding then a natural criterion to define gene neighborhood on the list.

Many algorithms exist that find clusters of nodes in complex networks. These algorithms have been successfully applied to gene networks based on protein–protein interactions [see, for example, refs (1–4)]. However, they do not order genes on a list, but rather present the genes that belong to the same cluster in an arbitrary order. An exception is the clustering algorithm proposed by Barabási and collaborators (5,6), as we discuss in the following sections. Also, analysis of trancriptomes often cluster together genes by their co-expression, or co-variation in time, which implies that these cluster definitions depend on the stage the cell is going through or on the protocol used to produce the assessed sample.

Here we present a method for ordering a list of genes using the computational physics method known as Monte Carlo (7), that we call Cost Function Method (CFM). The aim is to cluster on a line interacting genes, such that the distance between two genes on the list correlates with the probability that they interact, that is, the probability that their protein products are associated in protein–protein association data bases as STRING (8). A first advantage is that the definition of these clusters is independent from the specific stage the cells are at a given moment, or the protocol they have suffered. The genome ordering we propose here defines a mathematical metric that correlates the distance between two genes on the list with their mutual influence. In this sense, the probability that two genes interact decreases with the distance between their localization on the ordered list, and an average of the expression levels over neighboring genes on this list dumps fluctuations and produces a smooth profile—that we call ‘transcriptogram’. As we show in the following, the ordering is capable of clustering together genes belonging to terms of Gene Ontology: Biological Processes (9). Furthermore, expression profiles projected on the ordering give enough information on the global performance of a cell to discriminate different metabolic or biosynthetic processes, rendering a global assessment of cellular metabolism.

MATERIALS AND METHODS

We retrieved protein–protein interactions from STRING database (8th version) (http://string.embl.de/) (8), using ‘experimental’ and ‘database’ (95% of these interactions) added with ‘neighbourhood’, ‘fusion’, ‘co-expression’, and ‘co-occurrence’ evidences, String-score ≥0.800, comprising 4655 genes and 47 415 interactions.

Gene Ontology (GO) term enrichment was performed using DAVID bioinformatics resources (http://david.niaid.nih.gov) (10) to determine whether particular gene ontology terms occur more frequently than expected by chance in a given set of genes. We used default settings for the category GOTERM_BP_ALL, and selected those terms with P < 0.05 (for FDR no greater than 5%) representing central biochemical pathways/metabolic functions. From bit strings where the ith bit is set to 1(0) whenever the ith gene of an ordering is (not) listed in the GO term, we obtain smooth profiles by assigning to every gene the fraction of bits with value 1 in a window of size w, centred on the gene.

Yeast transcript expression data were obtained from YG_S98 array platforms (Affymetrix, Inc.), available at GEO database, Series GSE3431 (11) and GSE423 (12) (http://www.ncbi.nlm.nih.gov/projects/geo/). The transcriptograms are obtained by assigning to the ith gene the average of the expression values of its neighbors in a window of size w centred at the gene.

RESULTS

The starting point for the method is a randomly enumerated list of genes and the corresponding matrix specifying the interaction between the proteins. Here we consider gene or protein interaction as the physical and/or functional association presented by any pair of protein products. This body of information has been produced along the years by different researchers around the world and is magnificently organized and available at STRING database (8). We retrieved all protein–protein interactions described in that database inferred by ‘experimental’ and ‘database’ evidences for the organism Saccharomyces cerevisiae. Our final list comprises 4655 genes and 47 415 interactions.

For an ordered list with N genes, the interaction data may be organized in an 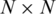matrix 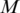, where the matrix elements, 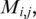are 1 or 0 depending on whether or not the ith and jth genes on the list interact. The result is a symmetric matrix of zeroes and ones with a null diagonal. We propose here an ordering algorithm that favors the proximity of interacting genes by minimizing a cost function E assigned to each ordering, given as

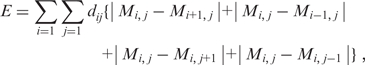(1)

where, |..| stands for the positive value of the difference of the matrix elements located at neighboring sites and 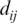is proportional to the distance from the point (i,j) to the diagonal, that is, 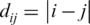. This cost function increases with the number of interfaces between one and zero elements on the matrix and increases further when these interfaces are far from the diagonal. We remember that points (i,j) far from the diagonal present very different values for i and j, implying then interactions between distant genes on the ordering.

After starting with a randomly ordered gene list and its corresponding interaction matrix, the algorithm proceeds by randomly choosing a pair of genes and swapping their positions on the ordering. A new interaction matrix is produced for this new ordering and its cost is recalculated using Equation (1). If the cost decreases, the change is accepted. If the cost is increased by ΔE, the change is accepted with probability exp [–ΔE /T], where T is a virtual temperature. We started with T = 6 × 10⁵ and every 100 Monte Carlo Steps (MCS) the temperature is lowered to 20% of its previous value. A MCS is a number of random choices equal to the number of elements in the system. This procedure is known as a ‘simulated annealing’ (13), and is intended to escape from metastable states. When changes are not accepted, they are discarded and a new gene pair is chosen to repeat the process. This procedure is repeated until the calculated value of cost is stabilized. See Supplementary Figure S1 for the plot of the cost function versus number of changes.

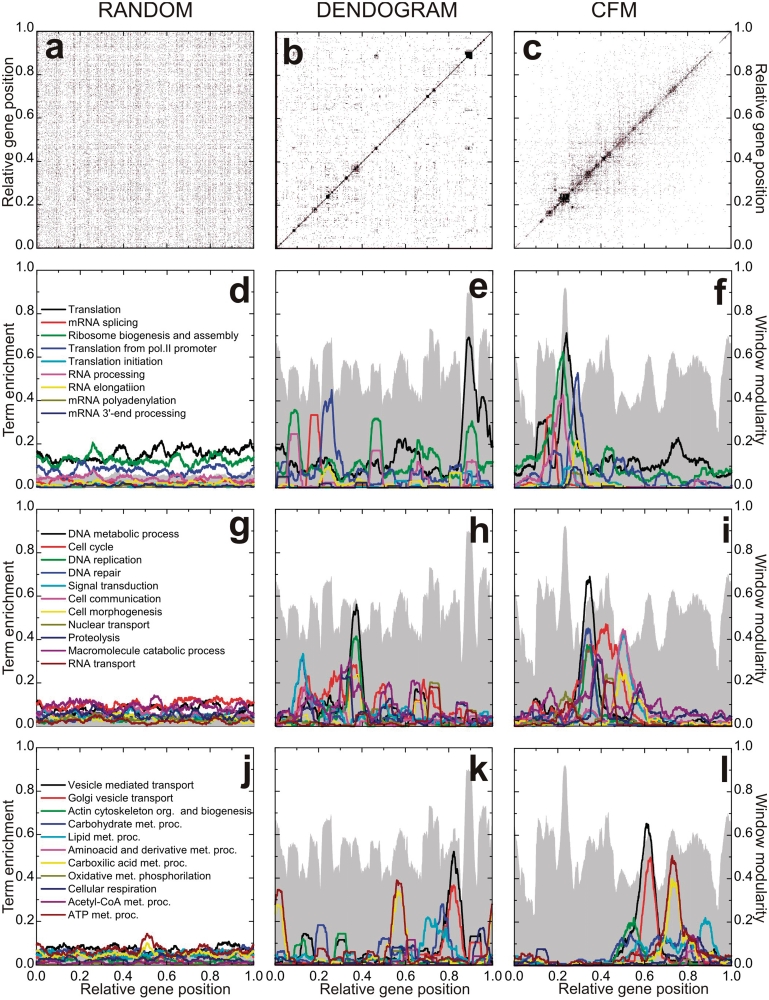
Figure 1 presents the interaction matrices relative to S. cerevisiae for the initial random gene ordering (Figure 1a), after ordering following the Dendogram clustering algorithm as proposed by Barabási and collaborators (5) (Figure 1b), and following the algorithm described above (Figure 1c). For each figure, vertical and horizontal axes give the relative gene positions on the ordering. See also Supplementary Data for the details for the Dendogram ordering. These positions are normalized, such that the ith gene on the list is assigned the position 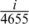on both vertical and horizontal axes. In these figures a black dot located at (i,j) indicates an association between the gene in position i on the horizontal axis with the gene on position j on the vertical axis such that 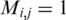. All three configurations present the same number of black dots and represent the same information on protein–-protein association.

Figure 1.

Protein–protein interaction matrix analysis algorithms. The axes relative to gene position have been divided by the total number of genes: 4655. (a) Random ordering. (b) Dendogram ordering algorithm. (c) Cost Function Minimizing (CFM) algorithm. (d–l) Projection of diverse terms of the Gene Ontology: Biological Process, as indicated in the right hand frame of each row. Gray landscape backgrounds: window modularity for the orderings. The maxima at the window modularity plots correspond to larger concentrations of black dots on the matrix representation, that is, intra-module interactions are more intense in these regions.

The difference between the figures stems in the different localizations of the genes on the axes. The randomly ordered gene list distributes uniformly the interaction-representing-dots over the whole matrix surface. After Dendogram ordering, some black dots are concentrated on the main diagonal with some large clusters, while after CFM ordering the black dots concentrate even nearer the diagonal, leaving the top left and bottom right corners free of black dots. These two corners represent interactions between genes located far apart on the list, since they represent matrix elements 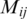for which i and j are very different. Furthermore, the black dot clusters far from the diagonal, which are present in the interaction matrix representing the Dendogram ordering, indicate that there are many interacting genes belonging to clusters located far apart on that ordering.

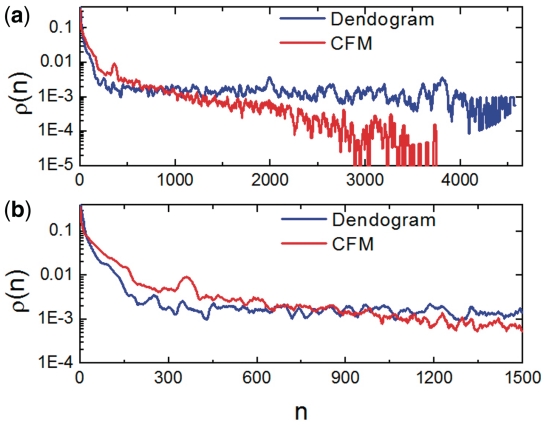
A way of quantitatively characterizing the orderings is using the interaction probability 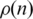for two genes that are separated by n positions on an ordering. This probability is given by the relative number of black dots on diagonals distant by n pixels from the main diagonal on the interaction matrix and may be calculated as

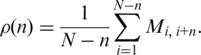(2)

Figure 2 presents 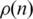versus n for the Dendogram and CFM algorithms in log-linear plots. Observe that the Dendogram algorithm stabilizes 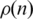at a finite value as n increases, but the CFM algorithm yields an exponential decay (represented by a straight line in a log linear plot) for this probability. It implies that the probability that two genes interact decays exponentially with the distance between their locations on the CFM ordering, while stabilizing at a finite value (∼10⁻³) in the case of the Dendogram ordering. For very short ranges, however, Figure 2b shows that the Dendogram algorithm concentrates more on the interacting genes, up to 20 genes distant; between 20 and approximately 600 genes apart the CFM concentrates more, between 600 an 1000 they present roughly the same interaction probability and, after that, the CFM ordering presents exponentially decreasing 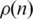. We interpret this exponential decay in 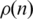for the CFM ordering as a correlation between interaction and localization of the genes on the ordering. This correlation yields to adequate averages over neighboring genes, allowing the smoothing out of wild fluctuations in the diverse profiles. For comparison we considered four artificially constructed networks whose results are presented on Supplementary Materials Online.

Figure 2.

Interaction probability 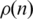as a function of n. This gives information on the quantity of links between genes as a function of their distance on the ordering. (a) On a log-linear plot and the whole interval, to evince the exponential decay of dot density on the CFM plots and (b) for a smaller interval in n to evince the behaviour near the main diagonal.

Gene ordering on a line is a frustrated process, in the sense that conflicts appear on how to order genes. It may happen that a gene interacts with two different clusters, say cluster A and B. This gene could be located near any one of the clusters or in some place in between. A criterion must be provided to resolve these conflicts. When favoring putting this gene together with, for example, cluster A, the blocks near the diagonal are more compact, but the price for that is the appearance of dots far from the diagonal, representing the interactions of the gene with cluster B. On the other hand, when the ordering method favors putting the gene in some place between clusters A and B on the ordering, the locations far from the main diagonal on the interaction matrix are free from black dots (there is no interaction M_ij such that i and j are very different) but the blocks near the diagonal are less compact.

While ordering, CFM algorithm acts to reduce a cost function by penalizing configurations with interactions between genes located far apart in the ordering. This is done by the factor in Equation (1) that depends on the distance of a black dot (representing interaction between two genes) from the main diagonal. The consequence is reflected in the probability that two genes located n positions apart on the ordering, 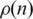, decays exponentially with n.

The Dendogram method, on its turn, does not penalize strongly enough interactions between genes far apart on the ordering, favoring compact blocks near the main diagonal. The consequence is an interaction probability between genes, 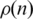, that is large for small n, decreases fast for intermediate distances and then stabilizes at a constant value, as shown in Figure 2.

Window modularity

To further characterize the orderings, we have considered the window modularity for each gene on an ordering, defined as follows. For each gene on the ordering consider its w/2 neighbors to the left and its w/2 neighbors to the right, comprehending an interval of w + 1 genes. The window modularity W_w(i) for a gene, located at the ith position of the ordering, is defined as the ratio between the number of interactions that link any two genes in the interval (window) of size w + 1 list, centered at the ithgene, and the number of interactions involving at least one gene in that window (14). That is,

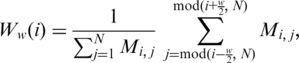(3)

where,

(4)

accounts for periodic boundary conditions to deal with genes near the ends of the list.

Window modularity strongly depends on the window size w. For example, for a window containing all genes of an ordered list, window modularity is one for every gene. However, when a gene is at the center of an interval that describes a highly interconnected cluster, its modularity decreases for windows smaller than the cluster size. This happens due to interactions connecting genes inside the window with genes outside the window but still belonging to the cluster. Also, genes that link different clusters present low modularity. On Figure 1d–l window modularity is represented as gray landscapes. There we have chosen w = 251. Plots for other values of window size are presented in Supplementary Data, as well as for other artificial networks for didactic purposes. The choice of the window size w depends on the desired accuracy for the peaks. In fact, as window size increases, the rugosity of the window modularity profile varies. It first increases, passes to a maximum and then decreases as w increases. Rugosity of a profile is defined as the standard deviation of the profile height and gives a measure of the amount of peaks and valleys. (See Supplementary Figure S4c and S4d). Here we choose w = 251 to have a more global description of the GO: BP terms. However, smaller windows may enhance accuracy for the modularity profile, as well as for expression data analysis (See Supplementary Figure S13 and S14 and discussion below).

Observe that window modularity in both Dendogram and CFM orderings present well defined peaks and valleys, indicating interacting modules. The random list presents a very low modularity for all genes. Taking random fluctuations as a null hypothesis, and estimating the standard deviations of random fluctuations from the random ordering modularity (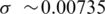), the probability that both CFM and Dendogram window modularity peaks and valleys are random is virtually zero, that is, peaks and valleys of heights of order 0.5 are more distant from the random average than 50 standard deviations of the window modularity distribution in a random ordering. The magnitude of both average and standard deviations for the window modularity may be directly estimated from the figures.

Although, the peaks in CFM and Dendogram orderings are similar in height, in the CFM ordering the valleys are deeper and the number of peaks separated by deep valleys is smaller. In fact, since there are valleys with different depth in the CFM ordering the peaks may be hierarchically defined: smaller clusters composing larger clusters.

Biological characterization

To assess the biochemical meaning of the orderings we have projected on the ordering information regarding the Biological Process terms from the Gene Ontology (GO) Database (9). We used ‘DAVID’ Bioinformatics Resources (10), as described in Materials and Methods, to obtain the GO terms of Biological Process Ontology that best represent each window modularity peak. After obtaining the representing terms, we calculated for each one a profile over the whole ordering. These GO term profiles are smooth functions of gene localization and give the fraction of genes that belong to the GO term in windows of 251 sites around a given gene. See Figure 1d–l. For the randomly ordered list, no peaks are seen and no information can be gathered from these plots. For the ordering obtained using Dendogram algorithm, some peaks appear, but the ontology terms are not as concentrated as for the CFM algorithm. Again, having a null hypothesis of random fluctuations whose standard deviation is estimated from the random ordering projections, the probability that the peak values of the terms profiles presented by both CFM and Dendogram algorithm are random fluctuation is virtually zero, since they lay more distant from the random average than tens of standard deviations. See Supplementary Figures S8–S10 . Also, the CFM ordering successively locates classes of GO terms in an order that reproduces cell cycle: from right to left we first find terms associated with energy metabolism, followed by cell morphogenesis and cell communication, then GO terms related to vesicle transport and Golgi vesicle transport, then DNA replication and repair, and finally GO terms associated with RNA production and translation.

Network properties

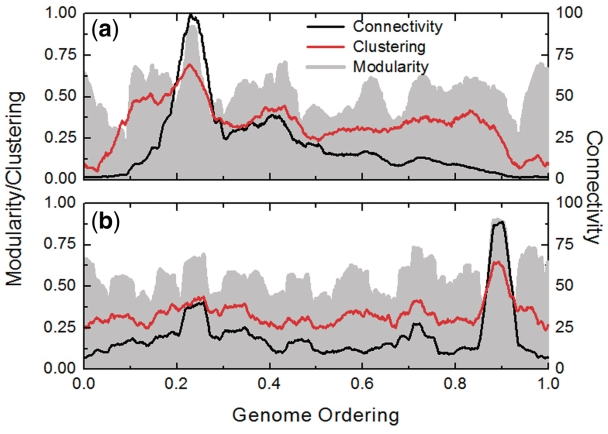
The orderings may be characterized using the connectivity k(i) and the clustering coefficient c(i) of the ith gene on the ordering (15). The interaction matrix gives information on which pairs of genes interact. The connectivity k(i) of the ith gene on the ordering is defined as the number of genes with which it interacts. On its turn, the clustering coefficient c(i) is defined as the fraction of existing links between any two of the k(i) neighbors of the ith gene, relative to the maximum possible number k(i)[k(i)-1]/2 of such links. Figure 3a and 3b presents the connectivity and clustering coefficient profiles for, respectively, the CFM and Dendogram orderings, obtained by taking the average of these quantities over windows of 251 sites. The connectivity profile of the CFM ordering shows that (i) genes with higher connectivity are more concentrated than the Dendogram ordering, presenting a high peak around the window modularity maximum at the region located at 0.2–0.3 on the horizontal axis. This region of the CFM ordering is rich with genes belonging to GO terms associated with translation, while the poorly connected genes are found at the ordering extremities. Also Figure 3 shows that (ii) the clustering coefficient decreases to very small values at the ordering extremities for the CFM ordering.

Figure 3.

Connectivity and clustering coefficient for (a) CFM and (b) Dendogram ordering. The gray landscapes are relative to the window modularity. The window size is 251.

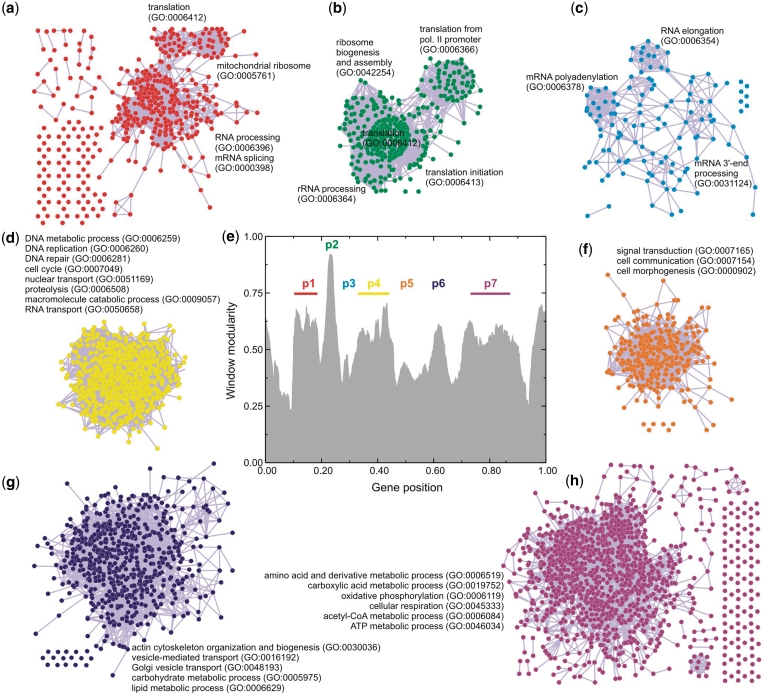
From now on we concentrate in analyzing the results for the CFM ordering. We sliced the CFM ordering in seven pieces, using the window modularity peaks as a guide (Figure 4e). The genes of each piece, together with the information on the interaction between these genes, are fed to Medusa application (16) and partial network graphs were produced, shown in Figure 4. The biological functions are mapped with GO terms. Observe that in this figure we are able to discriminate gene networks of related functions.

Figure 4.

Graph representation of the CFM ordering. The axes relative to gene position have been divided by the total number of genes: 4655. (e) CFM ordering was sliced in seven pieces, using the window modularity peaks as a guide for this division. The genes of each piece, together with the information on the interaction between these genes, were fed to Medusa application to produce the network graphs. (a–c,e–h) Network graphs associated with each peak, whose biological functions are mapped with GO terms using ‘DAVID’ bioinformatics resources.

For example, networks p1, p2 and p3 (Figure 4a–c) are all associated with transcription and translation processes, as rRNA/mRNA processing and ribosome biogenesis and assembly. Network p4, also overlaps these functions (Figure 4d), represented by DNA repair/replication and cell-cycle regulation. All these four gene networks have in common the synthesis of biological polymers. By contrast, network p5 seems to be a single cluster, shifting the ordering to other biochemical classes (Figure 4f), such as cell communication and morphogenesis. The last two gene networks (Figure 4g–h) present a variety of functions, from actin cytoskeleton organization and vesicle transport to carbohydrate, lipid and amino acid metabolic processes.

A feature of the right side of CFM ordering is the presence of several intermediate products and ATP-producing pathways (e.g. carboxylic acid cycle and cellular respiration). The network structure is enriched with highly interconnected anabolic and catabolic pathways, which is consistent with the basic strategy of central metabolism to form ATP, electron carriers and precursors for the biosynthesis of more-complex molecules. Therefore, gene networks p6 and p7 are related to the production of both energy and the building blocks from which other biomolecules are made.

At the other end of the CFM ordering (the left side), the functional boundaries of the network structure seems to be better discriminated. There are sub-clusters associated with several processing steps that control the flow of genetic information in cells.

In summary, the metabolic pattern as organized by the CFM algorithm gives rise to a sound biochemical and functional ordering, where the closest gene networks are more interrelated than the distant ones.

The transcriptogram: projection of gene expression data

Now we analyze gene expression data for the yeast genome. We focus on experimental data available at Gene Expression Omnibus database, regarding microarrays presenting probes for almost all genome components. We have then projected the expression on the CFM ordering, always considering window averages, obtaining expression profiles that we call transcriptograms. Here we present transcriptograms for S. cerevisiae using data obtained from two different experiments.

The first one, as explained in a very nice paper by Tu et al. (11), considers expression data obtained from yeast continuous culture, in controlled conditions, where the concentration levels of dissolved O₂ are constantly monitored. These levels vary periodically in time and the transcription levels were measured for 12 different stages in three different dissolved O₂ concentration oscillation periods, summing up 36 transcription profiles.

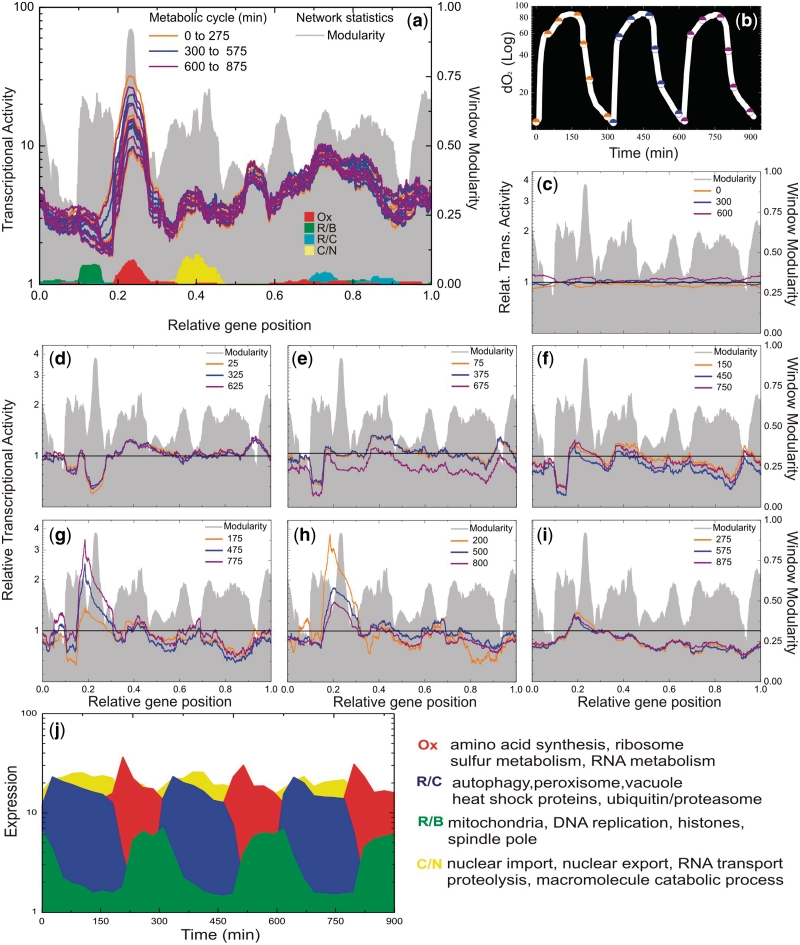
Figure 5 presents the results concerning transcriptograms obtained using the CFM ordering. A movie presenting all 36 snapshots is available at Supplementary Materials Online, as well as the results for the Dendogram ordering. Figure 5a presents 21 transcriptograms (7 per cycle), taken at the instants represented by the colored (orange, blue and purple) dots on the plot of dissolved oxygen versus time in log-linear plot (Figure 5b). Each color is associated with one cycle. Figure 5a also presents the window modularity as a landscape, to guide the eye, and the distribution of three gene clusters as defined in Tu et al. paper based on sentinels genes: Ox (oxidative), R/B (reductive, building) and R/C (reductive, charging). Figure 5c–i present the relative expression profiles at different instants. The relative profiles were calculated taking as reference the average of the expression intensity for each gene presented at times equal to 0, 300 and 600 min, which represent the first stages of each cycle. We have divided each gene expression intensity for its respective average, and projected over the ordering after performing a 251-window average, as done for other quantities.

Figure 5.

Saccharomyces cerevisiae transcriptograms. The axes relative to gene position have been divided by the total number of genes: 4655. (a) Microarray data available at Gene Expression Omnibus database were projected on CFM ordering to obtain the expression profiles, or transcriptograms. Each color is associated with one cycle, as shown in (b). Projections on the ordering were performed always considering window averages. To guide the eye, the window modularity is depicted as a landscape, together with the distribution of three gene clusters, as described previously, based on sentinels genes: Ox, oxidative; R/B, reductive, building; R/C, reductive, charging. Also, the distribution of the 40 genes whose expressions are maximally altered in the interval 0.35–0.45 of the CFM ordering. As discussed in the text, these genes are mainly related to catabolism of macromolecules and nuclear transport. (b) Plot of dissolved Oxygen versus time in log linear. Transcriptograms (seven per cycle), were taken at the instants represented by the colored (orange, blue and purple) dots. (c–i) Relative expression profiles. Transcriptograms were divided by the average expression values of the first state of the cycles (Time = 0, 300 and 600 min). c: represents the relative expression profile corresponding to the first dot of each cycle; d: represents the second dot of each cycle and so on. (j) Oscillations in expression levels of the sentinels genes: Ox, oxidative; R/B, reductive, building; R/C, reductive, charging, together with the most altered genes for the interval 0.35–0.45 of CFM ordering (yellow). These are average levels of the 40 most altered genes in each case.

The expression profiles show different behaviours for the left and right hand side portions: the expression profile of left side peaks extremely abruptly at the intense burst of oxygen consumption, while the right side gradually rises when cells begin to cease oxygen consumption. According to the gene networks mapped in Figures 1 and 4, the left side embraces several energy-demanding processes, essentially represented by the synthesis of biological polymers. It requires abundant amounts of adenosine triphosphate (ATP), which is available in profusion at the respiratory phase. This interplay of metabolic pathways for energy production is compatible with the time ordering through the phases Ox, R/B and R/C as described in the original article (11).

Our results support the conclusion drawn by the authors based on the expression of 40 genes for each cluster, a small gene fraction available in yeast transcriptomes. Here, by the use of transcriptograms, we present the dynamic changes during the metabolic cycle assessing the complete information.

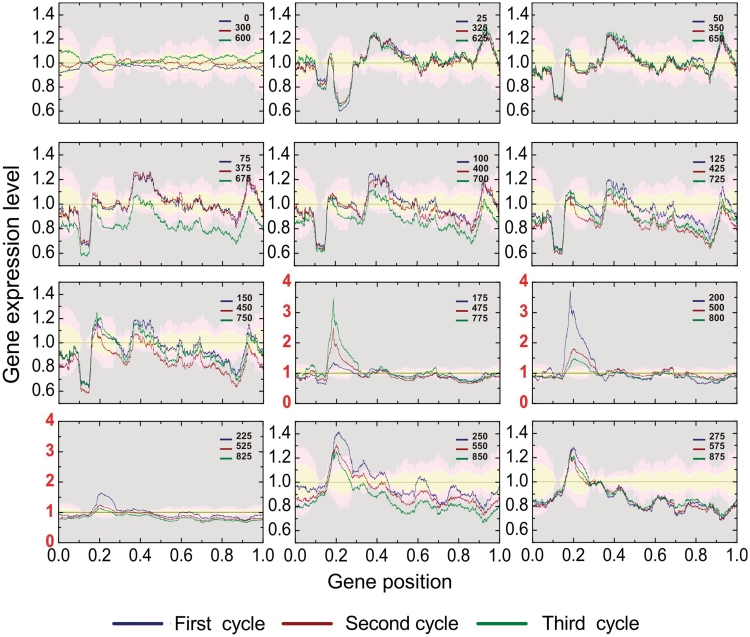
Moreover, the transcriptograms allow going further. There are more regions in the ordering that are significantly varying during the yeast life cycle. Figure 6 presents the transcriptograms together with the significance intervals for each point, given as the colored irregular bands. These significance bands have been calculated as follows. Taking the points at T = 0, 300 and 600 min as the reference (the initial stage of each respiratory cycle), we estimated the variation from the standard deviation of relative expression levels for each gene. The yellow band stands for relative gene expression levels that deviate from the initial stage average from 0 to 2 SDs. The pale pink band stands for regions where the relative expression levels deviates from the initial values from 2 to 4 SDs and the gray regions stand for deviations larger than 4 SDs. Because the expression levels of each gene present different values of standard deviations, these bands present irregular interfaces. Besides the regions pointed by Tu et al. the transcriptograms point to the interval from 0.35 to 0.45 as significantly varying during the respiration cycle (several standard deviations). See Figure 6 for times from 25 to 125 min. For illustration, we present in Figure 5j the average expression levels of the 40 genes that present the highest variations in this interval, together with the average expression levels of the three groups of 40 genes presented by Tu et al. Although the oscillations in the expression levels are less intense than those found by Tu et al., they are still largely significant.

Figure 6.

The respiration cycle transcriptograms and an estimate of the confidence intervals. The reference averages and their variations are estimated from the average and standard deviation for the relative expression level of each gene i in the initial state of the three respiration cycles. The yellow bands represent values that deviates from the average from 0 to 2 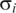; pink bands stand for deviations from 2 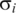to 4 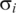, and the gray area stands for deviations larger than 4 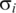. Each panel presents data relative to corresponding states of the three cycles. The ordering region in the interval 0.35–0.45 presents variations that are clearly in the gray region, mainly in times corresponding to T = 150, 450 and 4750 min, and T = 175, 475 and 775 min, which correspond to the final fermentation phase and the beginning of high consumption of O₂.

The density profiles for these 40 genes are represented in Figure 5a by the yellow peak. This is a group rich in genes belonging to macromolecule catabolic process terms or nuclear transport. In fact, these 40 genes belong to two different sub-peaks of peak 4 in Figure 6, that are made visible when we use a smaller window (w = 101 instead of w = 251), as shown in Supplementary Figures S13 and S14. The complete list of genes in the interval between 0.35 and 0.45 of the ordering may be found in Supplementary Table S1 and Supplementary Table S2 indicates the 40 genes that are maximally expressed in this interval.

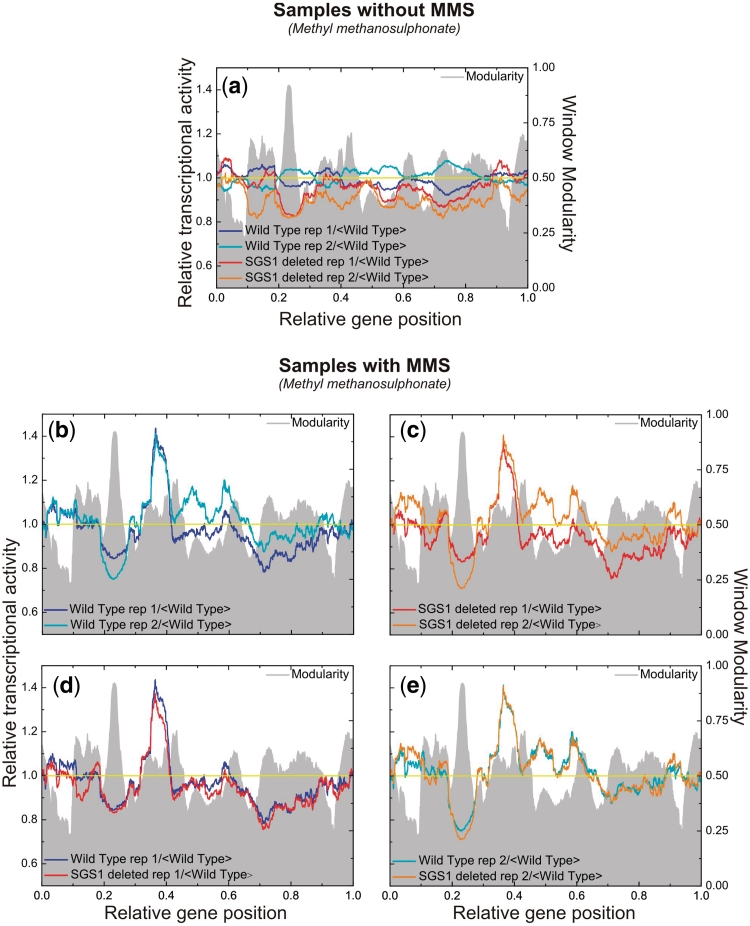
The second experiment is the one by Fry, Sambandan and Rha (12), where the authors compare the transcription levels of S. cerevisiae wild-type with those of sgs1 mutants, when the samples are submitted or not to stress represented by the direct addition of 0.1% methyl methanesulfonate (MMS) and the cultures were incubated at 30°C for 1 h. Their conclusions from the results are that (i) under normal conditions the mutant present 4% of the genes with transcriptional levels altered by 2-fold or more and (ii) under the stressed conditions there is not any difference between the different lineages. Figure 7 presents the transcriptograms for their samples, always having the modularity as a background, to guide the eye. In those figures we have considered the expression levels relative to the average of each transcript of the wild-type under normal conditions.

Figure 7.

Saccharomyces cerevisiae transcriptograms: wild-type and sgs1 mutant. The axes relative to gene position have been divided by the total number of genes: 4655. (a) Transcriptograms for two replicates of wild-type and sgs1 mutant prior to addition of MMS. (b) Transcriptograms for two replicates of wild-type after MMS treatment. (c) Transcriptograms for two replicates of sgs1 mutants after MMS treatment. (d) Transcriptograms of one replicate of wild-type and one replicate of sgs1 mutant, to evince that both samples have been arrested at the same state of cell cycle. (f) Same as (d), but for the other pair of replicates, that have been arrested at a different state of cell cycle. All transcriptograms are taken relative to the average values of the replicates of wild-type, prior to the addition of MMS. Averages of windows of 251 have been taken.

Fugure 7a presents the transcriptogram for the normal, control condition for both wild-type and sgs1 mutants, in two replicates each, as obtained from Gene Expression Omnibus, GSE423, related to the experiment by Fry et al. We first observe that although there is not a very large peak, the transcriptogram of sgs1 mutants present an overall depression as compared to the wild-type replicate: sgs1 mutant relative transcription levels are consistently below the wild-type ones, possibly indicating a generalized reduction of cellular metabolism due to the knockout of sgs1 gene. Figure 7b and c present the transcriptograms for, respectively, wild-type and sgs1 mutants in two replicates each, after the treatment with MMS. The transcription levels were again taken in relation to the wild-type levels under normal conditions. Observe that each one of the figures present two very different transcriptograms. These differences are noticeable due to peaks and depressions as compared to the wild-type. However, taking into account the transcriptograms for respiration cycle presented in Figures 5 and 6, we can assume that in each case the replicates were arrested in different stages of the respiration cycle. In fact, addition of MMS can cause cell arrest in different stages of cell cycle (17). To evince further, Figure 7d and e present the superposition of transcriptograms of one replicate of the wild-type and one replicate of the sgs1 Mutant: the plots are now almost identical. This corroborates Fry and collaborators conclusions that, under MMS stress, the sgs1 mutant performs as the wild-type. However, it also indicates that care should be taken in what regards the cell cycle stage, by either synchronizing cell cycle stages as done by Tu et al. or assessing in which stage the cells are at the moment of measuring the transcription levels.

DISCUSSION

In summary, we propose here the transcriptogram as a tool for assessing cell metabolism, which is capable of discriminating the stage the cell is going through at a given instant, as well as pointing metabolic changes in altered cellular states as compared to a control state. The transcriptogram is capable of evincing these features due to the gene ordering that correlates the distance between any two genes in the ordering with the probability that they interact. Since for the ordering obtained using the CFM method this interaction probability decays exponentially with the distance between the genes, the neighborhood on the ordering may be used to obtain averages that smooth out too wild fluctuations presented by gene expression data. This correlation also allows the identification of different regions of the ordering with well defined metabolic functions, endowing the dynamics of expression levels with biological meaning. Furthermore, transcriptograms allow whole genome assessment of expression data, dispensing the clustering genes by their (maximally) altered expression levels, which may vary from a cell metabolic state to another.

Dendogram-like methods are capable of ordering the genome and may also be used to produce transcriptograms. However, they are less efficient in ordering at long-range neighborhood, and hence compromise the quality of the information evinced by the averages over neighboring sites, besides rendering more difficult the biological interpretation of the expression levels variations.

Further improvements on the algorithm should specifically consider window size, which ultimately reflects the functional correlation between genes. In fact, the transcriptogram opens the possibility of a tool that works as a telescope, where the focus is tuneable and may be adjusted to the desired level of detail: when passing from a wide genome overview to smaller functional modules analysis, the observation window may be narrowed down, discriminating more functional modules at greater detail. In this case, projecting smaller sets of functionally related genes as some KEGG pathways (18) may bring further information. On the other hand, the method is readily applicable to any species, including Homo sapiens, which will be presented elsewhere.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, partially); Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES, partially); Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul (FAPERGS, partially). Funding for open access charge: Brazilian agencies CNPq.

Conflict of interest statement. None declared.