Abstract
Measuring parameters such as stability and conformation of biomolecules, especially of nucleic acids, is important in the field of biology, medical diagnostics and biotechnology. We present a thermophoretic method to analyse the conformation and thermal stability of nucleic acids. It relies on the directed movement of molecules in a temperature gradient that depends on surface characteristics of the molecule, such as size, charge and hydrophobicity. By measuring thermophoresis of nucleic acids over temperature, we find clear melting transitions and resolve intermediate conformational states. These intermediate states are indicated by an additional peak in the thermophoretic signal preceding most melting transitions. We analysed single nucleotide polymorphisms, DNA modifications, conformational states of DNA hairpins and microRNA duplexes. The method is validated successfully against calculated melting temperatures and UV absorbance measurements. Interestingly, the methylation of DNA is detected by the thermophoretic amplitude even if it does not affect the melting temperature. In the described setup, thermophoresis is measured all-optical in a simple setup using a reproducible capillary format with only 250 nl probe consumption. The thermophoretic analysis of nucleic acids shows the technique’s versatility for the investigation of nucleic acids relevant in cellular processes like RNA interference or gene silencing.
INTRODUCTION
Nucleic acids play a fundamental role in cellular processes and are the subject of intense biological research. Short non-coding RNA is expected to be an especially versatile target for new drugs or pharmaceuticals. Measuring the stability of these nucleic acids is especially important and typically measured with melting curve analysis. In such experiments, the sample is heated through a range of temperatures, while typically fluorescence or UV absorbance is continuously collected (1–4). Although well established, UV absorption measurements of melting curves require a considerable amount of DNA sample. As a result fluorescence approaches have gained momentum (5–7). However, these techniques often suffer from the missing sequence specificity of the fluorescence signal and are less sensitive to detect transitions which do not change the number of closed base pairs. This is due to the use of an intercalating fluorescent dye, which predominantly reflects the amount of double-stranded DNA in the sample. Thus, an analysis of purely tertiary DNA structures like for example G-quadruplexes are difficult to access. These restrictions can be reduced by separating the molecular recognition from the signal transduction, which is achieved using specially designed primers like scorpion primers or probes with fluorophore-acceptor pairs (8). However, these primers are complex in design and dramatically increase the cost for a melting curve analysis.
Another approach that measures the stability of nucleic acids or proteins is thermal gradient electrophoresis (9,10). It uses standard gel electrophoresis with an additionally applied thermal gradient perpendicular to the electric field. According to the position in the temperature gradient, the molecules experience different temperatures. When the molecules melt, they show a change in size or effective charge and thus show a different movement in the gel matrix. The advantage of this technique is that it records the motion of the molecules at all temperatures at once and can thus reduce the time to record a melting curve. On the other hand, the gel matrix does not represent the molecules’ native environment and gel preparation is time-consuming.
When using thermophoresis to monitor the melting of molecules, the sample is heated through a range of temperatures as it is the case for UV and fluorescence melting curves. But the information about the melting of the probe is provided by the movement of molecules and not by a change in absorbance or fluorescence. Hence, the thermophoretic approach requires only one unspecific tag to monitor the melting behaviour. The movement of particles in a temperature gradient (11) known as thermophoresis, or Soret effect depends on the size of a molecule, its charge and other surface properties such as ionic shielding and the hydration shell of the molecule (12,13). Thus, when one property of the monitored particles changes, for example, by changing its conformation or interacting with another molecule, the Soret coefficient changes. Recently, it was confirmed that binding events can be monitored with thermophoresis (14,15). Since the hybridization of DNA strands dramatically alters the molecular properties of the labelled primer, thermophoresis measurements are suitable for monitoring the melting of nucleic acids.
EXPERIMENTAL SECTION
Basics of thermophoresis
When an aqueous solution is locally heated, particles start to move in the given temperature gradient  . The resulting movement is described by a linear thermophoretic drift
. The resulting movement is described by a linear thermophoretic drift 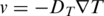 which is then counteracted by a diffusive backflow
which is then counteracted by a diffusive backflow 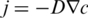 with diffusion coefficient D and the concentration gradient
with diffusion coefficient D and the concentration gradient 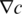 . These two fluxes lead to a steady state molecule distribution, which is characterized by the Soret coefficient. The Soret coefficient is defined as the ratio ST = DT/D and determines the magnitude of the change in concentration. In steady state, a temperature difference ΔT results in a change in concentration Δc, which can be derived from the following Equation (16).
. These two fluxes lead to a steady state molecule distribution, which is characterized by the Soret coefficient. The Soret coefficient is defined as the ratio ST = DT/D and determines the magnitude of the change in concentration. In steady state, a temperature difference ΔT results in a change in concentration Δc, which can be derived from the following Equation (16).
| (1) |
The concentration in the heated region c is normalized against the initial concentration c0 before applying the temperature gradient. In our experiments, the depletion is small (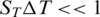 ) and thus, a linear function of the temperature increase. While the microscopic basis of thermophoresis is still under debate, experiments indicate that interfacial properties such as size, charge and hydrophobicity affect the Soret coefficient (12,13).
) and thus, a linear function of the temperature increase. While the microscopic basis of thermophoresis is still under debate, experiments indicate that interfacial properties such as size, charge and hydrophobicity affect the Soret coefficient (12,13).
Temperature dependence of thermophoresis
Iacopini et al. (17) investigated the temperature dependence of the Soret effect through measuring the thermophoretic properties of various biomolecules. They found a characteristic dependence, which is described well with an empirical fitting function:
| (2) |
Here 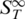 represents the thermophoretic limit for high temperatures T, while
represents the thermophoretic limit for high temperatures T, while 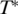 is the temperature where ST switches its sign and T0 is a rate of exponential growth that embodies the strength of the temperature effect. Our experiments showed that the temperature dependence differs for double- and single-stranded molecules, which is reflected in the index i. In previous experiments (12) the sign switching temperature
is the temperature where ST switches its sign and T0 is a rate of exponential growth that embodies the strength of the temperature effect. Our experiments showed that the temperature dependence differs for double- and single-stranded molecules, which is reflected in the index i. In previous experiments (12) the sign switching temperature 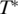 was found to be at ∼4°C for DNA strands of different length. The following analysis confirmed this finding, and we fixed
was found to be at ∼4°C for DNA strands of different length. The following analysis confirmed this finding, and we fixed 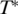 = 277 K throughout the analysis.
= 277 K throughout the analysis.
Analysis of thermophoretic melting curves
To determine the melting temperatures from the Soret coefficient, we corrected for the temperature dependence of 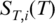 and used Equation (2) to infer the high temperature limit
and used Equation (2) to infer the high temperature limit 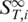 . This
. This 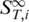 is constant for each conformational state
is constant for each conformational state 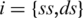 of the nucleic acid. Due to the linearity of thermophoretic depletion [Equation (1)], the experimentally measured apparent
of the nucleic acid. Due to the linearity of thermophoretic depletion [Equation (1)], the experimentally measured apparent 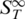 is a linear superposition of the closed and melted state, showing a transition from
is a linear superposition of the closed and melted state, showing a transition from 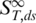 to
to 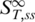 given by:
given by:
| (3) |
The parameter x represents the fraction of molecules in the single-stranded state. 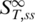 is the high temperature limit
is the high temperature limit 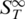 for single-stranded DNA,
for single-stranded DNA, 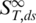 for double-stranded DNA. The melting temperature Tm represents the temperature at which x = 0.5 holds (18).
for double-stranded DNA. The melting temperature Tm represents the temperature at which x = 0.5 holds (18).
Presenting the thermophoretic melting curve in terms of the high temperature limit 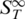 allows an analysis of the melting temperature combined with a quantification of the thermophoretic properties. These properties contain additional information about the molecular size and conformation.
allows an analysis of the melting temperature combined with a quantification of the thermophoretic properties. These properties contain additional information about the molecular size and conformation.
The melting of nucleic acids is mostly interpreted as a two-state process, where double-stranded molecules are transferred into a single-stranded state. Such an interpretation ignores intermediate states (e.g. due to the unfolding of tertiary structures) but still is a good approximation for many DNA melting curves. An intermediate state with 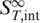 leads to an expanded equation:
leads to an expanded equation:
| (4) |
At the temperature with 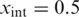 , the double-stranded structure melts into the intermediate conformation, at
, the double-stranded structure melts into the intermediate conformation, at 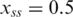 the intermediate structure melts into single-stranded DNA. To infer Tm from the melting curve, the data was analysed using a sigmoidal fitting function:
the intermediate structure melts into single-stranded DNA. To infer Tm from the melting curve, the data was analysed using a sigmoidal fitting function:
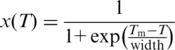 |
(5) |
If intermediate states were observed, the data was fitted with an additive superposition of two sigmoidal curves.
Experimental setup
In our experiments, temperature gradients in solution were generated by a local absorption of an infrared laser in the sample (19). At a wavelength of 1480 nm, water strongly absorbs the radiation and a local increase in temperature is obtained. An epi-fluorescence microscope was modified by adding an IR laser (Furukawa FOL1405-RTV-617-1480, 1480 nm, 320 mW maximum power, AMS Technologies AG, Martinsried, Germany) to the microscope. The setup is shown schematically in Figure 1A. The IR laser was coupled into the beam of light by inserting a dichroic mirror (NT46-386, Edmund Optics, Barrington, USA) between microscope (AxioTech Vario, Zeiss, Oberkochen, Germany) and objective (40 × magnification, NA = 0.8, Partec GmbH, Münster, Germany). The dichroic mirror deflects infrared radiation and is transparent for visible light. Using this setting, the IR laser is focused in the sample plane and allowed simultaneous monitoring of the fluorescence inside the sample. Fluorescence was excited with Luxeon high-power LEDs (Luxeon V-star, cyan; Luxeon III-star, red; Luxeon, Calgary, Canada). The LEDs were built into a standard halogen lamp housing and driven at a current of 10–200 mA by an ILX Lightwave LD-3565 constant current source, providing low illumination noise levels. Fluorescence images were recorded with a Sensicam QE CCD camera (PCO AG, Kelheim, Germany). Measurement chambers were capillaries made of fused silica with an inner diameter of 100 µm (Polymicro Technologies, Phoenix, USA), resulting in a low sample consumption of ∼250 nl per measurement. To obtain a more facile handling when preparing the samples and filling the capillaries, we typically used a priming volume of ∼5 µl. This could be further reduced by using automated sample preparation.
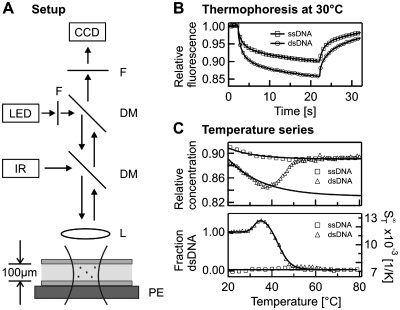
Figure 1.
Thermophoresis assay. (A) The solution inside a capillary was locally heated with a focused infrared laser (IR), coupled into an epi-fluorescence microscope using a dichroic mirror (DM). A capillary was used as a sample compartment and placed on top of a peltier stage (PE), which allowed adjustment of the overall sample temperature. L, lens; LED, light emitting diode; F, fliter; CCD, CCD camera. (B) The data obtained with our setup was the relative concentration inferred from the recorded fluorescence signal. Single- and double-stranded DNA showed different depleted concentrations in the heated laser spot. (C) When repeated for different temperatures, single-stranded DNA (ssDNA) as well as double-stranded DNA (dsDNA) showed a pronounced temperature dependence, which was fitted using Equation (3). Correcting the data for this temperature dependence, a typical DNA melting curve appeared.
The IR laser heating gave a Gaussian temperature profile with a 1/e2 diameter of 25 µm and a peak temperature of typically 15 K. The temperature profile was obtained using the temperature dependence of the fluorescent dye Cy5 in 1 × saline sodium citrate (1 × SSC), which was determined independently by a fluorometer experiment (20). The temperature profile inside the capillaries was highly reproducible with a precision of ±0.1 K (13). The overall sample temperature was controlled with a peltier element beneath the capillary, which allows to scan a broad range of sample temperatures with the precision of ±0.1 K. The effective sample temperature was corrected for the additional temperature increase due to the laser heating. For better thermal contact, a thin layer of oil was used between the surface of the peltier element and the capillary.
Measurements
For recording a melting curve, the overall sample temperature was increased stepwise with an equilibration time of 60 s at each temperature. Typically a step size between 0.6 and 2°C was used but it could be lowered to 0.2°C depending on the desired accuracy. At every temperature, a thermophoretic time trace was recorded (Figure 1B). First, the fluorescence of the sample was acquired for several seconds and then the IR-Laser was switched on to create a temperature gradient and trigger the thermophoretic movement. Due to the small dimensions of the local heating, the spatial distribution of DNA molecules in the heated spot came close to its steady state within the measurement time of 20 s. After this time the IR-laser was switched off again and the molecules re-established their initial homogeneous molecule distribution. Throughout the measurement, the fluorescence is recorded with the CCD-camera. To infer the relative change in concentration from the fluorescence signal, the curve was normalized with a fluorescence image 500 ms after switching on the IR laser. At this time, the temperature profile in the capillary was already established, while the concentration profile was almost unchanged (7). This allowed correcting the fluorescence signal for the temperature dependence of the fluorescent dye. For the fluorophore HEX, the temperature dependence was in the order of 0.0–0.24%/K depending on the nucleic acid molecule attached. The Soret coefficient ST was obtained from the magnitude of the depleted concentration according to Equation (1). When plotting the Soret coefficient over temperature a transition from the double-stranded state to the single-stranded state was observed (Figure 1C, top). This curve was then corrected with the temperature dependence of the Soret coefficient according to Equation (2) resulting in a melting curve presented in the high temperature limit 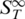 (Figure 1C, bottom). Using Equation (3) or (4) allowed to determine the fraction of double-stranded and single-stranded DNA. To derive the exact melting temperatures the temperature used for plotting was corrected for the additional heating by the IR-laser. All experiments were compared to UV absorbance melting curves that were obtained with a temperature controlled spectrometer (Jasco GmbH, Gross-Umstadt, Germany) using the same DNA concentrations and equal buffer conditions.
(Figure 1C, bottom). Using Equation (3) or (4) allowed to determine the fraction of double-stranded and single-stranded DNA. To derive the exact melting temperatures the temperature used for plotting was corrected for the additional heating by the IR-laser. All experiments were compared to UV absorbance melting curves that were obtained with a temperature controlled spectrometer (Jasco GmbH, Gross-Umstadt, Germany) using the same DNA concentrations and equal buffer conditions.
Molecules
The oligomers (Metabion AG, Martinried, Germany) used in this study are shown in Table 1. All molecules were diluted to a concentration of 1 µM in 1 × SSC (15 mM sodium citrate, pH 7.4, 150 mM NaCl) except for the DNA thrombin aptamer which was diluted in its selection buffer. (20 mM Tris–HCl pH 7.4, 150 mM NaCl, 5 mM KCl, 1 mM CaCl2, 1 mM MgCl2, 0.01% Tween-20). For duplex formation, the single-stranded nucleic acids were mixed in a ratio of 1:1 and annealed by heating the sample to 95°C and then gradually cooling it to room temperature. This procedure favours the energetically most likely conformation. Aptamer and hairpin were heated to 95°C, as well, but then rapidly cooled on ice to prevent homodimer formation and trap the molecules in their tertiary structure.
Table 1.
Sequences of nucleic acids. The underlined bases represent mutated or modified bases or dangling ends
| Sequence (5′–3′) | |
|---|---|
| Reference DNA #1 | HEX-ATTGAGATACACATTAGAACTA |
| Reference DNA #2 | HEX-ATTGAGATATACATTAGAATTA |
| Reference DNA #3 | HEX-AGTGAGATAGACAGTAGAACTA |
| Perfect match | TAGTTCTAATGTGTATCTCAAT |
| Single nucleotide mismatch | TAGTTCTAATGTCTATCTCAAT |
| Methylated perfect match | TAGTTCTXATGTGTATCTCXAT where X is a N6-Methyl-dA |
| 22 nt dangling ends random | TTTATATTTGTAGTACTTCAGATAGTTCTAATGTGTATCTCAATACTTTTGTTACTG TTTACTATT |
| 11 nt dangling ends random | AGTACTTCAGATAGTTCTAATGTGTATCTCAATACTTTTGTTAC |
| 11 nt dangling ends polyA | AAAAAAAAAAATAGTTCTAATGTGTATCTCAATAAAAAAAAAAA |
| 11 nt dangling ends polyT | TTTTTTTTTTTTAGTTCTAATGTGTATCTCAATTTTTTTTTTTT |
| 5 nt dangling ends random | TCAGATAGTTCTAATGTGTATCTCAATACTTT |
| 11 nt dangling ends polyA – Duplex #2 | AAAAAAAAAAATAATTCTAATGTATATCTCAATAAAAAAAAAAA |
| 11 nt dangling ends polyA – Duplex #3 | AAAAAAAAAAATAGTTCTACTGTCTATCTCACTAAAAAAAAAAA |
| Hairpin DNA | Cy3–TTTACAACGGTTTAGCGTTGTA |
| DNA thrombin aptamer | Cy5–TGGTTGGTGTGGTTGGT |
| DNA thrombin aptamer mutant | Cy5–TGGTTGTTGTGGTTTGT |
| Reference RNA | HEX–UAGUUCUAAUGUGUAUCUCAAU |
| RNA perfect match | AUUGAGAUACACAUUAGAACUA |
RESULTS
In the following, we used thermophoresis to perform various types of melting analysis. The experiments cover the melting of DNA duplexes and RNA structures like RNA-RNA duplexes. We further used the technique to analyse the melting of DNA tertiary structures and to investigate the influence of methylation on the melting properties. All results are compared to UV absorbance melting curves and to calculations estimating the melting temperature on the basis of nearest neighbour thermodynamics (21–24).
Standard DNA melting
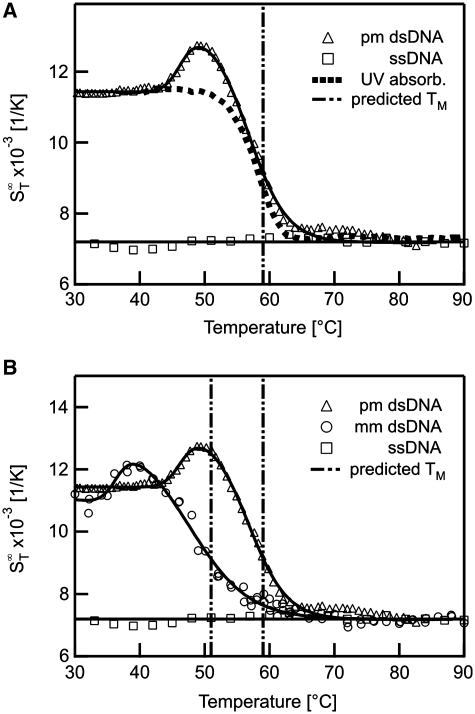
First we analysed DNA–DNA melting using short DNA oligonucleotides in a range typical for antisense DNA (25). These nucleic acids can selectively inhibit the expression of a single protein when internalized into a cell (26). Thermophoresis is capable of acquiring standard melting curves with high precision and can distinguish between single point mutations. The 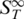 of the sample was measured in a temperature range from 30 to 90°C (Figure 2A). As double-stranded DNA melts into single-stranded molecules, the thermophoretic properties change significantly. When comparing the thermophoretic melting curve with the expected sigmoidal shape of a melting transition, an unexpected initial increase of the thermophoretic amplitude before the actual melting into single-strands was observed (Figure 2A, triangles). This may reflect a change in DNA size or indicate an intermediate conformation of the DNA duplex. For control, single-stranded DNA without complementary DNA was measured which showed neither transition and reproduced the
of the sample was measured in a temperature range from 30 to 90°C (Figure 2A). As double-stranded DNA melts into single-stranded molecules, the thermophoretic properties change significantly. When comparing the thermophoretic melting curve with the expected sigmoidal shape of a melting transition, an unexpected initial increase of the thermophoretic amplitude before the actual melting into single-strands was observed (Figure 2A, triangles). This may reflect a change in DNA size or indicate an intermediate conformation of the DNA duplex. For control, single-stranded DNA without complementary DNA was measured which showed neither transition and reproduced the 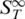 of completely melted DNA (Figure 2A, squares). The obtained melting temperature was Tm = 56.3 ± 0.1°C, the melting temperature for the transition into the intermediate state was Tm = 49.7 ± 0.2°C. This melting analysis was compared to theoretically predicted melting temperatures and control experiments performed with UV absorbance spectroscopy. The UV control yielded Tm = 56.4 ± 0.1°C for the perfect match, but did not show an intermediate state before the melting. For the theoretically predicted value we found 56.3 ± 1.4°C (21–24) (Figure 2A, vertical bar). Both, the melting temperature obtained with UV absorbance and Tm obtained from thermodynamic calculations are in very good agreement with the results gained from the thermophoretic signal. This demonstrates that the thermophoresis signal is well suited to quantify the stability of nucleic acids.
of completely melted DNA (Figure 2A, squares). The obtained melting temperature was Tm = 56.3 ± 0.1°C, the melting temperature for the transition into the intermediate state was Tm = 49.7 ± 0.2°C. This melting analysis was compared to theoretically predicted melting temperatures and control experiments performed with UV absorbance spectroscopy. The UV control yielded Tm = 56.4 ± 0.1°C for the perfect match, but did not show an intermediate state before the melting. For the theoretically predicted value we found 56.3 ± 1.4°C (21–24) (Figure 2A, vertical bar). Both, the melting temperature obtained with UV absorbance and Tm obtained from thermodynamic calculations are in very good agreement with the results gained from the thermophoretic signal. This demonstrates that the thermophoresis signal is well suited to quantify the stability of nucleic acids.
Figure 2.
DNA melting curves. Thermophoresis allows the measurement of the melting curve of DNA molecules. (A) The melting of a 22 bp long DNA oligonucleotide was analysed with thermophoresis and UV absorbance and compared to thermodynamic calculations. (B) DNA containing a single base mismatch was compared to perfectly matching DNA. The mismatch showed a changed melting temperature Tm due to the lower thermal stability by the base mismatch.
We further tested if we could monitor the effect of a single point mutation on the melting behaviour with thermophoresis. The melting analysis of DNA containing such a mutation compared to the melting of a perfectly matching DNA is shown in Figure 2B. For DNA with a mismatch in the sequence a transition before the melting into two strands was observed at Tm = 36.3 ± 0.4°C. The mismatch resulted in a lower melting temperature Tm = 47.7 ± 0.9°C compared to the perfect match. This is in good agreement with thermodynamic calculations which yield a melting temperature of 47.9 ± 1.4°C. The measurement with UV absorbance also showed a deviation from the two-state model with melting temperatures Tm = 37.7 ± 0.5°C for the first transition and Tm = 44.9 ± 0.1°C for melting (data not shown). This is in fair agreement with the thermophoretic and calculated melting temperature. The deviation in the UV absorbance may be caused by the correction of the curves with sloping baselines (18).
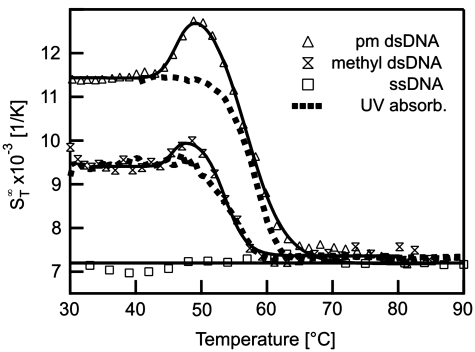
The thermophoretic stability analysis was then applied to DNA with methylated bases to analyse the influence of this modification on the stability. DNA methylation is essential for cell differentiation and viability and seems to function as a tool for partitioning the genome into active and inactive parts (27–29). Methylation is further incorporated in various diseases like cancer (30) and heart disease as well as aspects of ageing (31). To test the thermophoretic analysis, two adenosines in the sequence of perfectly matching DNA were replaced with N6-Methyl-2′-dA. The modification led to a decrease in the melting temperature by 2.7°C to Tm = 53.6 ± 0.4°C (Figure 3). Before the melting an initial transition was measured at 45.5 ± 0.7°C. The reference experiment with UV absorbance spectroscopy yielded Tm = 53.3 ± 0.2°C. Interestingly, the Soret coefficient showed a strong difference of 2.0 × 10−3 1/K in 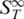 between normal and the methylated DNA at low temperatures and allowed for a discrimination of the two species by the Soret signal alone. Such a difference was still observable when comparing the perfect match and the single mismatch at low temperatures. Here, a difference in
between normal and the methylated DNA at low temperatures and allowed for a discrimination of the two species by the Soret signal alone. Such a difference was still observable when comparing the perfect match and the single mismatch at low temperatures. Here, a difference in 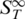 of 0.4 × 10−3 1/K was found. This underlines the high sensitivity of thermophoresis for the analysis of various surface properties of biomolecules (12–15).
of 0.4 × 10−3 1/K was found. This underlines the high sensitivity of thermophoresis for the analysis of various surface properties of biomolecules (12–15).
Figure 3.
Methylated DNA. The effect of methylated bases on the stability of DNA was analysed with thermophoresis and compared to UV absorbance. Beside monitoring the melting of the two strands, the Soret coefficient at low temperatures showed a significant reduction in the thermophoretic amplitude resulting from the modified bases.
In contrast to standard melting techniques, the thermophoretic melting data also contains information about possible intermediate states or conformational changes. A transition prior to melting has been observed for all measured samples. Such information may be of importance as cellular functions of nucleic acids not only rely on the sequence but also on their structure.
Additional transitions upon melting
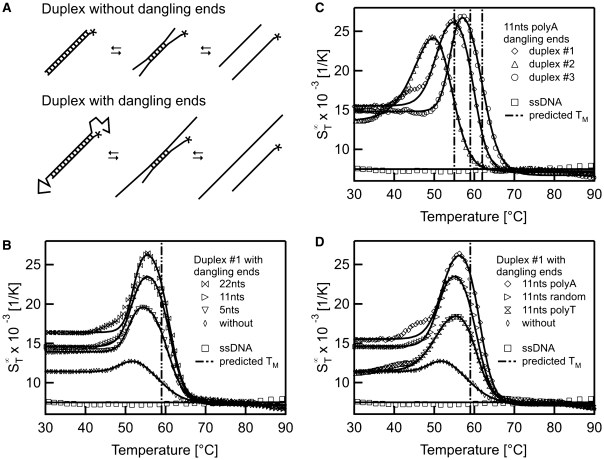
The initial transitions before the actual melting were unexpected at first glance but appeared in all thermophoretic melting experiments. Hence, it seems to be a general process which occurs in the melting process. A possible explanation for the increase in 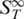 is shown in Figure 4A. We propose that partial unfolding of the duplex at the two ends increases the surface area of the duplex. This leads to a rise in the
is shown in Figure 4A. We propose that partial unfolding of the duplex at the two ends increases the surface area of the duplex. This leads to a rise in the 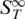 (12). To test this hypothesis, the effect was tested by adding dangling ends at both sides of the duplex which should then result in an increase of the thermophoretic amplitude. Such overlaps are important in biology as they are known to determine the stability of codon–anticodon associations (32,33). They may also play a role in modulating biological processes involving DNA (34). Concerning the stability of a duplex, dangling ends often alter the melting temperature but may also have no effect on the stability (23).
(12). To test this hypothesis, the effect was tested by adding dangling ends at both sides of the duplex which should then result in an increase of the thermophoretic amplitude. Such overlaps are important in biology as they are known to determine the stability of codon–anticodon associations (32,33). They may also play a role in modulating biological processes involving DNA (34). Concerning the stability of a duplex, dangling ends often alter the melting temperature but may also have no effect on the stability (23).
Figure 4.
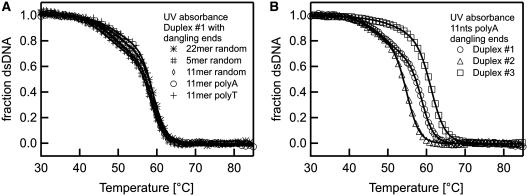
Effects of dangling ends. The melting of DNA double strands with dangling ends was analysed with thermophoresis. (A) As a hypothesis for the transition before the actual melting of the two DNA strands we propose an unbinding of the duplex-ends in a pre-melting transition. This ‘end effects’ should increase when adding overlapping DNA strands to both sides of one duplex strand. (B) The data for dangling ends of various length showed an increase of the Soret coefficient due to a change in the conformation before the actual melting transition. The final melting temperature matches the situation without dangling ends. (C) When changing the composition of the duplex forming sequence a shift in the melting temperature but also in the first transition was observed. (D) To rule out any potential structures of the dangling ends, duplex #1 was analysed with 11 nt overhangs of random sequence and compared to dangling ends with polyA and polyT sequence. Irrespective of the dangling ends, the melting temperature remained constant.
In Figure 4B the melting of a perfect match with dangling ends of various length is shown. For this experiment the sequence was kept constant but only the length of the dangling ends was varied. At low temperatures around 30°C a distinct difference in the 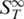 was found for the perfect match and the asymmetric probes with dangling ends. With the addition of the dangling ends, the Soret coefficient raises as the molecule becomes larger. When melting a duplex with a 22 nt overhang on both sides the initial increase in the Soret coefficient was observed at 51.9 ± 0.1°C beside the melting into two single DNA strands at Tm = 60.9 ± 0.1°C. These pre-melting transitions were obtained for dangling ends of all lengths at similar transition temperatures but with varying amplitude. Nearly no shift in the final melting temperatures was observed (11 nt: Tm = 50.5 ± 0.2°C and Tm = 60.0 ± 0.1°C; 5 nt: Tm = 50.8 ± 0.1°C and Tm = 60.6 ± 0.1°C). The height of the first transition increased with the length of the dangling ends. This indicates that the dangling ends form a more elongated structure prior to melting. This increases the surface of the molecules and thus the Soret coefficient.
was found for the perfect match and the asymmetric probes with dangling ends. With the addition of the dangling ends, the Soret coefficient raises as the molecule becomes larger. When melting a duplex with a 22 nt overhang on both sides the initial increase in the Soret coefficient was observed at 51.9 ± 0.1°C beside the melting into two single DNA strands at Tm = 60.9 ± 0.1°C. These pre-melting transitions were obtained for dangling ends of all lengths at similar transition temperatures but with varying amplitude. Nearly no shift in the final melting temperatures was observed (11 nt: Tm = 50.5 ± 0.2°C and Tm = 60.0 ± 0.1°C; 5 nt: Tm = 50.8 ± 0.1°C and Tm = 60.6 ± 0.1°C). The height of the first transition increased with the length of the dangling ends. This indicates that the dangling ends form a more elongated structure prior to melting. This increases the surface of the molecules and thus the Soret coefficient.
To check whether the duplex forms a tertiary structure which melts at a given temperature, the analysis was performed with duplexes of changed composition (Figure 4C). In this case the dangling ends consisted of 11 nt polyA overlaps. The change of the duplex sequences led to a shift of the melting temperature from Tm = 60.1 ± 0.1°C for duplex #1 to Tm = 54.8 ± 0.3°C for duplex #2 and Tm = 62.3 ± 0.2°C for duplex #3. These melting temperatures are in accordance with predicted values of 59 ± 1.4°C, 55 ± 1.4°C and 62 ± 1.4°C, respectively. Interestingly, a similar pre-melting transition is found for all duplexes, however shifted in accordance with the melting transition temperature (duplex #1: Tm = 51.0 ± 0.3°C, duplex #2: Tm = 45.6 ± 0.4°C, duplex #3: Tm = 53.6 ± 0.5°C). This indicates that the rise in 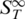 is not due to a special tertiary structure only of duplex #1, but a sequence-independent common feature.
is not due to a special tertiary structure only of duplex #1, but a sequence-independent common feature.
Finally, a possible special structure of the dangling ends itself could be ruled out. The sequence of a 11nt overlap was varied from a random sequence to polyA and polyT dangling ends, respectively (Figure 4D). Both transition temperatures remained constant (11 nt polyT: Tm = 50.6 ± 0.9°C and Tm = 60.5 ± 0.4°C; 11 nt polyA: Tm = 51.0 ± 0.3°C and Tm = 60.1 ± 0.1°C; 11 nt random: Tm = 50.5 ± 0.2°C and Tm = 60.0 ± 0.1°C). This indicates that no (unpredicted) secondary or tertiary structure in the dangling ends exists. The height of the first transition was of comparable magnitude (random: 8.9 × 10−3 1/K, polyA: 10.9 × 10−3 1/K, polyT: 7.0 × 10−3 1/K) but polyA dangling ends showed a slightly stronger signal than polyT dangling ends. This is in accordance with findings that polyA strands show a much higher persistence length compared to polyT strands and thus form more rigid dangling ends (35). Hence, the rise in 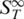 before the actual melting appears to be a natural intermediate state in the denaturing process.
before the actual melting appears to be a natural intermediate state in the denaturing process.
In Figure 5 control experiments of above probes with dangling ends using UV absorbance are presented. The controls for duplex #1 with dangling ends of various length and composition showed a similar shape (Figure 5A). The curves also showed a deviation from a typical two state melting, but the tendency was less pronounced than in the thermophoretic melting curve. When fitting the UV curves with a three-state model, melting temperatures were obtained in a similar range as for the thermophoretic melting analysis. (random 22 nt: 50.6 ± 0.3°C and 59.3 ± 0.1°C; random 11 nt: 49.4 ± 0.3°C and 59.0 ± 0.1°C; random 5 nt: 47.4 ± 0.3°C and 58.4 ± 0.1°C; polyA 11 nt: 49.4 ± 0.2°C and 58.8 ± 0.1°C; polyT 11 nt: 50.2 ± 0.4°C and 59.1 ± 0.1°C). When measuring 11 nt polyA dangling ends with varying duplex sequences a shift in the melting temperature was observed. This is in agreement with the thermophoretic melting curves (Figure 5B; duplex #1: 49.4 ± 0.2°C and 58.8 ± 0.1°C; duplex #2: 46.1 ± 0.5°C and 54.9 ± 0.1°C; duplex #3: 54.9 ± 0.4°C and 61.2 ± 0.1°C). Deviations from a two-state behaviour were noticeable but less pronounced. Without the prior knowledge of a pre-melting transition, the rather small deviations from a two state model in the UV absorption signal would have been too insignificant to be analysed.
Figure 5.
UV melting controls. Measurements with various dangling ends and duplex sequences confirm the thermophoretic melting curves. (A) The melting of double-stranded DNA (Figure 4) with dangling ends of various compositions was analysed with UV absorbance. As in the thermophoretic melting analysis, a deviation from the two-state model was observed although the first transitions were less pronounced than in the thermophoresis signal. Both melting transitions occurred at similar melting temperatures. (B) The duplex composition is varied while keeping the overlap of 11 nt fixed to a polyA structure. Both melting temperatures shift with the varied duplex sequence in accordance to the thermophoresis measurement of Figure 4C.
Conformational information
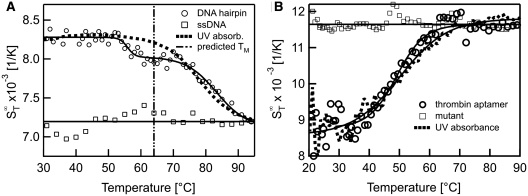
Tertiary structures formed by DNA often have a strong effect on possible interactions. They are known to enhance the affinity to the binding partner but can also reduce the binding strength due to steric shielding of the binding site (36). Hence, information on the stability of tertiary structures is desirable. In Figure 6, we show examples of obtaining purely conformational information from thermophoretic melting curves of structure-forming ssDNA molecules. In Figure 6A we show the melting of a hairpin with a double-stranded stem. In the thermophoretic melting curve, the Soret coefficient showed a first transition at Tm = 55.8 ± 0.8°C, followed by a second transition at Tm = 83.3 ± 1.1°C. The first transition could be attributed to an initial change of the tertiary structure while the second transition is likely due to the complete melting of the hairpin stem. The second transition was also observed with UV absorbance spectroscopy, but a different melting temperature of Tm = 78.0 ± 0.4°C was obtained. Compared to the theoretical prediction of Tm = 64.3 ± 1.4°C (21), the experimentally observed melting temperatures are considerably higher. This may be due to uncertainties of the thermodynamic calculations when analysing hairpin structures. Nevertheless, the melting of the DNA hairpin is measurable with thermphoresis. In Figure 6B the melting of a thrombin DNA aptamer is presented. This aptamer is known to form a G-quadruplex, but no duplex structures (37). When analysing the melting behaviour of this structure a clear transition was observed. The 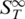 increased when unfolding the quadruplex structure at Tm = 49.2 ± 0.4°C. Such an increase was expected as the molecules change from a compact form in the G-quadruplex state to a more elongated form after melting which leads to an increased surface of the molecule. A control experiment with a mutated DNA sequence which does not form a quadruplex structure (14) showed no transition (Figure 6B, squares). The UV absorbance measurement yielded a Tm = 50.1 ± 0.3°C which is in good agreement with the thermophoretic measurement and literature (37). As expected, the change in conformation was readily detectable in the thermophoretic melting curve although no changes in mass or charge occured. The sensitivity to these kinds of conformational changes is attributed to the dependence of thermophoresis on changes in size or hydrophobicity.
increased when unfolding the quadruplex structure at Tm = 49.2 ± 0.4°C. Such an increase was expected as the molecules change from a compact form in the G-quadruplex state to a more elongated form after melting which leads to an increased surface of the molecule. A control experiment with a mutated DNA sequence which does not form a quadruplex structure (14) showed no transition (Figure 6B, squares). The UV absorbance measurement yielded a Tm = 50.1 ± 0.3°C which is in good agreement with the thermophoretic measurement and literature (37). As expected, the change in conformation was readily detectable in the thermophoretic melting curve although no changes in mass or charge occured. The sensitivity to these kinds of conformational changes is attributed to the dependence of thermophoresis on changes in size or hydrophobicity.
Figure 6.
Structural information of DNA molecules. (A) The change in conformation of a DNA hairpin was resolved by evaluating its thermophoretic behaviour with temperature. We found a distinct deviation from a two-state behaviour, attributed to a breakage or re-orientation of the duplex structure. (B) As an example for a pure conformational melting signal, a DNA aptamer which is known to form a G-quadruplex was analysed with thermophoresis. It showed a clear transition without deviations from a two-state model.
RNA melting
The melting of RNA can be equally analysed with thermophoresis. Short non-coding RNA, for example, plays a fundamental role in cellular processes and regulates gene expression. It is the target of antisense oligonucleotides, which are primarily designed because of their ability to hybridize with the mRNA of interest (38,39). This mRNA has a complex secondary and tertiary structure that restricts the accessibility of certain segments. Therefore, it is interesting to investigate the stability of RNA duplexes used for RNA silencing and in parallel gather information about possible tertiary structures.
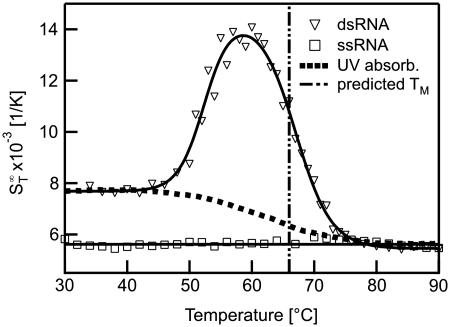
The shape of the thermophoretic melting curve for double-stranded RNA (Figure 7) also showed a deviation from standard two-state melting. A significant increase in the 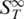 in an initial transition (Tm = 52.4 ± 0.4°C) was followed by a second transition to the single-stranded state (Tm = 67.0 ± 0.4°C). In comparison to DNA the increase for RNA was considerably more pronounced. This could be attributed to the higher flexibility of single-stranded RNA which is significantly more polymorphic than DNA (40).
in an initial transition (Tm = 52.4 ± 0.4°C) was followed by a second transition to the single-stranded state (Tm = 67.0 ± 0.4°C). In comparison to DNA the increase for RNA was considerably more pronounced. This could be attributed to the higher flexibility of single-stranded RNA which is significantly more polymorphic than DNA (40).
Figure 7.
Melting of RNA duplexes. The melting of RNA showed a strong change in 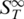 before the actual melting occurs. This increase in
before the actual melting occurs. This increase in 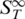 prior to melting for dsRNA was attributed to a partial melting of the double strand beginning at the ends of the RNA duplex. It was significantly larger for RNA as compared to DNA.
prior to melting for dsRNA was attributed to a partial melting of the double strand beginning at the ends of the RNA duplex. It was significantly larger for RNA as compared to DNA.
As for the case of DNA, the second downward transition was close to the theoretically predicted melting temperature of Tm = 66 ± 1.3°C. Under close examination, the UV absorbance also revealed deviations from a two-state melting (Figure 7, filled squares). We found melting temperatures at Tm = 54.1 ± 1.4°C and Tm = 65.0 ± 0.9°C, in close accordance to the results from the more pronounced thermophoresis signal.
Thermophoretic properties of nucleic acids
The presented data showed that the stability analysis of nucleic acids can be performed with thermophoresis. We found that the thermophoretic signal is not only sensitive to the hybridization state of nucleic acids. Moreover, the magnitude of the Soret coefficient provides information about the conformation, size and modification of the polynucleotides. The sensitivity readily allows the resolution of a single nucleotide mismatch for short ssDNA (13). Each of the investigated molecules featured a distinct 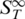 and yielded information about its molecular properties (Table 2). This implies that differences in the composition of DNA strands lead to different
and yielded information about its molecular properties (Table 2). This implies that differences in the composition of DNA strands lead to different 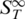 signals and thus are distinguishable with thermophoresis.
signals and thus are distinguishable with thermophoresis.
Table 2.
The Soret coefficient 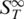 and melting temperatures for various types of nucleic acids
and melting temperatures for various types of nucleic acids
| Molecule | 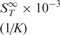 |
Tm pre-melting transition (°C) | Tm melting transition (°C) |
|---|---|---|---|
| ssDNA | 7.2 ± 0.1 | – | – |
| 22-mer hairpin | 8.3 ± 0.1 | 55.8 ± 0.8 | 83.3 ± 1.1 |
| Thrombin aptamer | 8.7 ± 0.5 | – | 49.2 ± 0.4 |
| Thrombin aptamer mutant | 11.7 ± 0.1 | – | – |
| Perfect match dsDNA | 11.4 ± 0.1 | 49.7 ± 0.2 | 56.3 ± 0.1 |
| Mismatched dsDNA | 11.0 ± 0.4 | 36.3 ± 0.4 | 47.7 ± 0.9 |
| Methylated dsDNA | 9.4 ± 0.1 | 45.5 ± 0.7 | 53.6 ± 0.4 |
| Duplex #1 with 22 nt random | 16.4 ± 0.1 | 51.9 ± 0.1 | 60.9 ± 0.1 |
| Duplex #1 with 11 nt random | 14.6 ± 0.1 | 50.5 ± 0.2 | 60.0 ± 0.1 |
| Duplex #1 with 5 nt random | 13.8 ± 0.1 | 50.8 ± 0.1 | 60.6 ± 0.1 |
| Duplex #1 with 11 nt polyT | 11.6 ± 0.4 | 50.6 ± 0.9 | 60.5 ± 0.4 |
| Duplex #1 with 11 nt polyA | 15.7 ± 0.6 | 51.0 ± 0.3 | 60.1 ± 0.1 |
| Duplex #2 with 11 nt polyA | 13.7 ± 0.2 | 45.6 ± 0.4 | 54.8 ± 0.3 |
| Duplex #3 with 11 nt polyA | 14.8 ± 0.2 | 53.6 ± 0.5 | 62.3 ± 0.2 |
| ssRNA | 5.5 ± 0.1 | – | – |
| dsRNA | 7.7 ± 0.2 | 52.4 ± 0.4 | 67.0 ± 0.4 |
The thermophoretic effect provides information about the molecular properties of nucleic acids, both for DNA and RNA. Thus, thermophoresis not only discriminates molecules of different sizes but is sensitive to various conformations or modifications. The error in 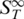 represents the standard deviation of each data point calculated from five measurement points in the double-stranded regime.
represents the standard deviation of each data point calculated from five measurement points in the double-stranded regime.
This sensitivity to size, charge and conformational structure can be used to identify a molecule only based on its Soret coefficient when compared to a calibration curve of a known species. Hence the Soret coefficient, together with the pre-melting and melting temperature can serve as a molecule’s fingerprint, which can allow the identification of species in an unknown sample.
CONCLUSION
The experiments herein demonstrated that thermophoresis is a versatile tool for analysing the stability of nucleic acids. Beside the standard melting temperature Tm, the data showed that additional information about conformational states is accessible. This provides insights into the behaviour prior to melting. This additional information is especially important for RNA, where functionality highly relies on its tertiary structure. Due to its sensitivity to conformations, thermophoresis may thus help in the investigation of complex structures of nucleic acids and provide more detailed information about molecular processes.
Recently, Mast et al. (41) showed that the thermophoretic analysis of DNA is possible using intercalating fluorophores and that thermophoresis can be employed to quantify the length of PCR products. Based on these measurements, we expect that the presented thermophoretic measurements are also accessible with intercalating dyes.
To conclude, we have developed a sensitive, sample-efficient method for the analysis of the thermal stability of nucleic acids. Using 250 nl of sample, the cost for an analysis is low and thus, expensive or rare samples can be used sparingly. The technique requires only one fluorescently labelled oligonucleotide probe and no complex FRET probe pairs, further decreasing the cost and complexity of mutation-specific analysis. Furthermore, no special buffers are required to record thermophoresis signals and the buffer conditions can be chosen freely. The duration of the experiment is comparable to UV absorbance melting curve experiments. However, the experiment times could be shortened by reducing the equilibration time of the peltier elements and by acquiring thermophoretic depletion without recording the back-diffusion of the molecules.
The sensitivity of thermophoresis offers the possibility to resolve complex melting behaviours, and due to its additional information, the technique can provide more detailed insights into the interactions of nucleic acids. With its sensitivity for conformational states of the nucleic acids thermophoresis provides a promising experimental approach for testing biological models and allows for a more detailed understanding of the melting behaviour of biologically relevant nucleic acids.
FUNDING
The LMU initiative Functional NanoSystems (FuNS); the Excellence Cluster NanoSystems Initiative Munich (NIM); NanoTemper Technologies GmbH. Funding for open access charge: Center for NanoScience (CeNS) and Ludwig-Maximilians-Universität München.
Conflict of interest statement. P.B. and S.D. are founders of the University Spin Off Company NanoTemper Technologies GmbH which provides services and devices based on thermophoresis. D.B. and C.J.W. declare no conflict of interests.
ACKNOWLEDGEMENTS
The authors thank Hubert Krammer for help with the UV absorbance melting curves and Uta Steinbach and Ann Fornof for helpful discussions and for comments on the article. We also want to express our gratitude to the Center for Nanoscience (CeNS).
REFERENCES
- 1.Doty P. The physical chemistry of deoxyribonucleic acids. J. Cell Comp. Physiol. 1957;49:27. doi: 10.1002/jcp.1030490405. [DOI] [PubMed] [Google Scholar]
- 2.Marmur J, Doty P. Heterogeneity in deoxyribonucleic acids: I. Dependence on composition of the configurational stability of deoxyribonucleic acids. Nature. 1959;183:1427–1429. doi: 10.1038/1831427a0. [DOI] [PubMed] [Google Scholar]
- 3.Marmur J, Doty P. Determination of the base composition of deoxyribonucleic acid from its thermal denaturation temperature. J. Mol. Biol. 1962;5:109–118. doi: 10.1016/s0022-2836(62)80066-7. [DOI] [PubMed] [Google Scholar]
- 4.Ansevin AT, Vizard DL, Brown BW, McConathy J. High-resolution thermal denaturation of DNA. I. Theoretical and practical considerations for the resolution of thermal subtransitions. Biopolymers. 1976;15:153–174. doi: 10.1002/bip.1976.360150111. [DOI] [PubMed] [Google Scholar]
- 5.Mergny JL, Maurizot JC. Fluorescence resonance transfer as a probe for G-quartet formation by a telomeric repeat. ChemBioChem. 2001;2:124–132. doi: 10.1002/1439-7633(20010202)2:2<124::AID-CBIC124>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 6.Reed GH, Kent JO, Wittwer CT. High-resolution DNA melting analysis for simple and efficient molecular diagnostics. Pharmacogenomics. 2007;8:597–608. doi: 10.2217/14622416.8.6.597. [DOI] [PubMed] [Google Scholar]
- 7.Baaske P, Duhr S, Braun D. Melting curve analysis in a snapshot. Appl. Phys. Lett. 2007;91:133901. [Google Scholar]
- 8.Lyon E. Mutation detection using fluorescent hybridization probes and melting curve analysis. Expert Rev. Mol. Diagn. 2001;1:92–101. doi: 10.1586/14737159.1.1.92. [DOI] [PubMed] [Google Scholar]
- 9.Thatcher DR, Hodson B. Denaturation of proteins and nucleic acids by thermal-gradient electrophoresis. Biochem. J. 1981;197:105–109. doi: 10.1042/bj1970105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rosenbaum V, Riesner D. Temperature-gradient gel electrophoresis thermodynamic analysis of nucleic acids and proteins in purified form and in cellular extracts. Biophys. Chem. 1987;26:235–246. doi: 10.1016/0301-4622(87)80026-1. [DOI] [PubMed] [Google Scholar]
- 11.Ludwig C. Diffusion zwischen ungleich erwärmten Orten gleich zusammengesetzter Lösungen. Sitzungsber. Akad. Wiss. Wien: Math.-Naturwiss. 1856;20:539. [Google Scholar]
- 12.Duhr S, Braun D. Why molecules move along a temperature gradient. Proc. Natl Acad. Sci. USA. 2006;103:19678–19682. doi: 10.1073/pnas.0603873103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reineck P, Wienken CJ, Braun D. Thermophoresis of single stranded DNA. Electrophoresis. 2010;31:279–286. doi: 10.1002/elps.200900505. [DOI] [PubMed] [Google Scholar]
- 14.Baaske P, Wienken CJ, Reineck P, Duhr S, Braun D. Optical thermophoresis for quantifying the buffer dependence of aptamer binding. Angew. Chem. Int. Ed. 2010;49:2238–2241. doi: 10.1002/anie.200903998. [DOI] [PubMed] [Google Scholar]
- 15.Wienken CJ, Baaske P, Rothbauer U, Braun D, Duhr S. Protein binding assays in biological liquids using microscale thermophoresis. Nat. Commun. 2010;1:100. doi: 10.1038/ncomms1093. [DOI] [PubMed] [Google Scholar]
- 16.Duhr S, Braun D. Thermophoretic depletion follows Boltzmann distribution. Phys. Rev. Lett. 2006;96:168301. doi: 10.1103/PhysRevLett.96.168301. [DOI] [PubMed] [Google Scholar]
- 17.Iacopini S, Rusconi R, Piazza R. The “macromolecular tourist”: universal temperature dependence of thermal diffusion in aqueous colloidal suspensions. Phys. J. E. 2004;19:59–67. doi: 10.1140/epje/e2006-00012-9. [DOI] [PubMed] [Google Scholar]
- 18.Mergny J, Lacroix L. Analysis of thermal melting curves. Oligonucleotides. 13:515–537. doi: 10.1089/154545703322860825. [DOI] [PubMed] [Google Scholar]
- 19.Duhr S, Arduini S, Braun D. Thermophoresis of DNA determined by microfluidic fluorescence. Eur. Phys. J. E. 2004;15:277. doi: 10.1140/epje/i2004-10073-5. [DOI] [PubMed] [Google Scholar]
- 20.Skirtach AG, Déjugna C, Braun D, Susha AS, Rogach AL, Parak WJ, Möhwald H, Sukhorukov GB. The role of metal nanoparticles in remote release of encapsulated materials. Nano Lett. 2005;7:1371–1377. doi: 10.1021/nl050693n. [DOI] [PubMed] [Google Scholar]
- 21.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.SantaLucia J, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 23.Bommarito S, Peyret N, Santa Lucia J. Thermodynamic parameters for DNA sequences with dangling ends. Nucleic Acids Res. 2000;28:1929–1934. doi: 10.1093/nar/28.9.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Allawi H, SantaLucia J. Nearest neighbor thermodynamic parameters for internal G-A mismatches in DNA. Biochemistry. 1998;36:10581–10594. doi: 10.1021/bi9724873. [DOI] [PubMed] [Google Scholar]
- 25.Patil SD, Rhodes DG, Burgess DJ. DNA-based therapeutics and DNA delivery systems: a comprehensive review. AAPS J. 2005;7:E61–E77. doi: 10.1208/aapsj070109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Crooke ST. Molecular mechanisms of action of antisense drugs. Biochim. Biophys. Acta. 1999;1489:31–43. doi: 10.1016/s0167-4781(99)00148-7. [DOI] [PubMed] [Google Scholar]
- 27.Robertson KD, Wolffe AP. DNA methylation in health and disease. Nat. Rev. Gen. 2000;1:11–19. doi: 10.1038/35049533. [DOI] [PubMed] [Google Scholar]
- 28.Li E, Bestor TH, Jaenisch R. Targeted mutation of the DNA methyltransferase gene results in embryonic lethality. Cell. 1992;69:915–926. doi: 10.1016/0092-8674(92)90611-f. [DOI] [PubMed] [Google Scholar]
- 29.Okano M, Bell DW, Haber DA, Li W. DNA methyltransferases Dnmt3a andDnmt3b are essential for de novo methylation and mammalian development. Cell. 1999;99:247–257. doi: 10.1016/s0092-8674(00)81656-6. [DOI] [PubMed] [Google Scholar]
- 30.Baylin SB, Herman JG, Herman JR, Vertino PM, Issa J-P. Alterations in DNA methylation: a fundamental aspect of neoplasia. Adv. Cancer Res. 1998;72:141–196. [PubMed] [Google Scholar]
- 31.Post WS, Goldschmidt-Clermont PJ, Wilhide CC, Heldman AW, Sussman MS, Ouyang P, Milliken EE, Issa JJ. Methylation of the estrogen receptor gene is associated with aging and atherosclerosis in the cardiovascular system. Cardiovasc. Res. 1999;43:985–991. doi: 10.1016/s0008-6363(99)00153-4. [DOI] [PubMed] [Google Scholar]
- 32.Grosjean H, Soll DG, Crothers DM. Studies of the complex between transfer RNAs with complementary anticodons: I. Origins of enhanced affinity between complementary triplets. J. Mol. Biol. 1976;103:499. doi: 10.1016/0022-2836(76)90214-x. [DOI] [PubMed] [Google Scholar]
- 33.Yoon K, Turner DH, Tinoco I, von der Haar F, Cramer F. The kinetics of binding of U-U-C-A to a dodecanucleotide anticodon fragment from yeast tRNAPhe. Nucleic Acids Res. 1976;3:2233–2242. doi: 10.1093/nar/3.9.2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Senior M, Jones RA, Breslauer KJ. Influence of dangling thymidine residues on the stability and structure of two DNA duplexes. Biochemistry. 1988;27:3879–3885. doi: 10.1021/bi00410a053. [DOI] [PubMed] [Google Scholar]
- 35.Millsa JB, Vacanoa E, Hagerman PJ. Flexibility of single-stranded DNA: use of gapped duplex helices to determine the persistence lengths of Poly(dT) and Poly(dA) J Mol. Biol. 1999;285:245–257. doi: 10.1006/jmbi.1998.2287. [DOI] [PubMed] [Google Scholar]
- 36.Travers AA. DNA conformation and protein binding. Annu. Rev. Biochem. 1989;58:427–452. doi: 10.1146/annurev.bi.58.070189.002235. [DOI] [PubMed] [Google Scholar]
- 37.Kankia BI, Marky LA. Folding of the thrombin aptamer into a G-quadruplex with Sr(2+): stability, heat, and hydration. J. Am. Chem. Soc. 2001;123:10799–10804. doi: 10.1021/ja010008o. [DOI] [PubMed] [Google Scholar]
- 38.Kim VN. MicroRNA biogenesis: coordinated cropping and dicing. Nat. Rev. Mol. Cell Biol. 2005;6:376–385. doi: 10.1038/nrm1644. [DOI] [PubMed] [Google Scholar]
- 39.He L, Hannon GJ. MicroRNAs: small RNAs with a big role in gene regulation. Nat. Rev. Genet. 2004;5:522–531. doi: 10.1038/nrg1379. [DOI] [PubMed] [Google Scholar]
- 40.Pan YP, MacKerell AD. Altered structural fluctuations in duplex RNA versus DNA: a conformational switch involving base pair opening. Nucleic Acids Res. 2003;31:7131–7140. doi: 10.1093/nar/gkg941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mast CB, Braun D. Thermal trap for DNA replication. Phys. Rev. Lett. 2010;104:188102. doi: 10.1103/PhysRevLett.104.188102. [DOI] [PubMed] [Google Scholar]