Time-reversed ultrasonically encoded optical focusing into scattering media

Abstract

Light focusing plays a central role in biomedical imaging, manipulation, and therapy. In scattering media, direct light focusing becomes infeasible beyond one transport mean free path. All previous methods^1–3 to overcome this diffusion limit lack a practical internal “guide star.”⁴ Here we proposed and experimentally validated a novel concept, called Time-Reversed Ultrasonically Encoded (TRUE) optical focusing, to deliver light into any dynamically defined location inside a scattering medium. First, diffused coherent light is encoded by a focused ultrasonic wave to provide a virtual internal “guide star”; then, only the encoded light is time-reversed and transmitted back to the ultrasonic focus. The TRUE optical focus–defined by the ultrasonic wave–is unaffected by multiple scattering of light. Such focusing is especially desirable in biological tissue where ultrasonic scattering is ~1000 times weaker than optical scattering. Various fields including biomedical and colloidal optics can benefit from TRUE optical focusing.

Manipulating light propagation has always been a subject of intense research^1–6. The motivations are obvious: as the only electromagnetic wave sensitive to molecular conformation, light is an essential tool to probe the structure and properties of matter, and monitor physical, chemical or biological processes; light instead of harmful x-rays is an ideal nonionizing radiation for imaging and treating biological tissues; light is also a basic tool in communication and computing. A better understanding and control of light propagation in matter has both immediate benefits and far reaching impacts–indeed, any advance in this subject can be readily transferred to other fields dealing with wave phenomena^7–9.

Of particular interest is the problem of focusing light into a scattering medium. For example, high-resolution optical imaging relies on precisely focusing light into the medium at desired depths; photodynamic therapy and optogenetics require light be delivered to specific regions of interest inside tissue. However, multiple scattering imposes a fundamental optical diffusion limit on direct light focusing in scattering media. Consequently, the imaging depth of all forms of focusing optical microscopy such as confocal microscopy is limited to less than one transport mean free path. A number of technologies have been developed to address this problem. For example, light can be focused through biological tissue by optical phase conjugation³, or focused into a static scattering medium by iterative wave front shaping that maximizes the signal strength of a blurred yet visible implanted target². However, it is desirable to focus light into (instead of through) a scattering medium, to tolerate dynamic microstructures, and to rapidly adjust the focal position. These challenges have not been met by previous research endeavours. Our method shows great promise in filling this gap.

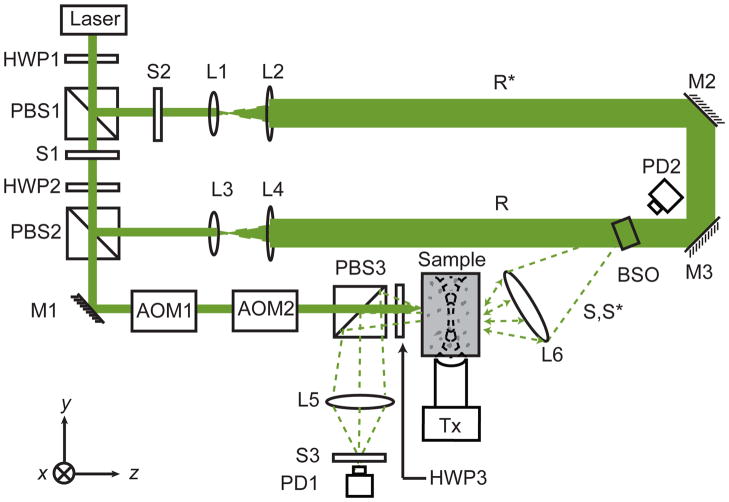
Our technique, called Time-Reversed Ultrasonically Encoded (TRUE) optical focusing, combines ultrasonic modulation of diffused coherent light^10,11 with optical phase conjugation^12,13 to achieve dynamic focusing of light into a scattering medium (Fig. 1). The light from a laser source (λ = 532 nm) with long coherence length was split into three parts, a sample beam S and two mutually conjugated reference beams R and R*. S was transmitted through two acousto-optic modulators (AOM) in series to tune its optical frequency to f_s = f₀ − f_a before propagating diffusively through the medium, where f₀ was the laser frequency and f_a was the frequency shift due to the two AOMs. A focused ultrasonic wave of the same frequency f_a traversed the medium and modulated the diffused light. The ultrasonically modulated light could be regarded as emanating from a virtual source that was defined by the ultrasonic focus and was frequency shifted by ± f_a , resulting in two sidebands S(f_±) with frequencies f₊ = f₀ and f₋= f₀ − 2f_a . This virtual source serves as the internal “guide star.” ⁴ Outside the medium, the diffused light was holographically recorded onto a phase-conjugate mirror, here a photorefractive Bi₁₂SiO₂₀ (BSO) crystal. The only stationary hologram that could be recorded was from the interference between R and S(f)^14–16. Then, the hologram was read by R* to generate a time-reversed (TR) copy of S(f₊), denoted as S^*(f₊). By reversibility, S^*(f₊) back-traced the trajectory of S(f₊) and converged to its virtual source, thereby achieving optical focusing into the scattering medium. The energy in S^*(f₊) did not exceed that in S(f₊) as the hologram was read without fixing. However, an intensity gain can be achieved with a higher-intensity shorter-duration readout beam R* . Further, an energy gain much greater than unity is attainable with hologram fixing or two-step recording.^{14, 17}

Fig. 1.

Schematic of the experimental setup for TRUE optical focusing. HWPi, ith half-wave plate; PBSi, ith polarizing beam splitter; Si, ith shutter; Mi, ith mirror; AOMi, ith acousto-optic modulator; Li, ith lens; PDi, ith photodiode; R, reference beam; R*, conjugated reference beam; S, signal light; S*, time-reversed signal light; BSO, Bi₁₂SiO₂₀; Tx, ultrasonic transducer with centre frequency f_a= 3.5 MHz, focal length = 38 mm, and focal width = 0.87 mm. Coordinates: x = sample scanning axis, y = acoustical axis, and z = optical axis. The time-reversal procedure consisted of recording and readout of a hologram. To record a hologram, S1 was opened, and S2 and S3 were closed for 190 ms; to read the hologram, S1 was closed, and S2 and S3 were opened for 10 ms.

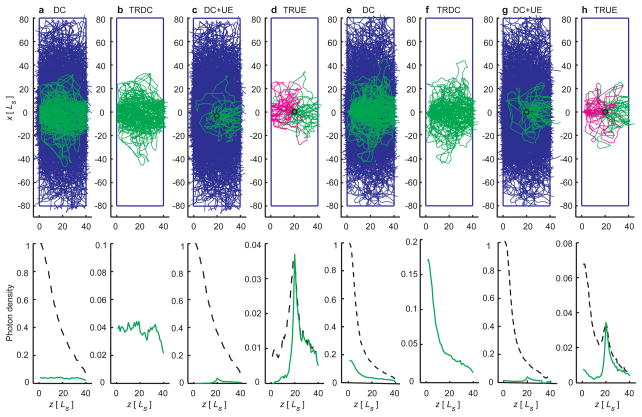
To illustrate the concept of TRUE optical focusing in a scattering medium, we used a Monte Carlo model¹⁸ to simulate the propagation of the sample light S(f_s) and the ultrasonically encoded S(f₊). The light–medium interaction, dominated by elastic scattering, is characterized by the scattering mean free path L and scattering anisotropy g . For example, L_s ≈ 0.1 mm and g ≈ 0.9 in human breast.¹⁹ Optical absorption is much weaker than scattering in typical biological tissue and was neglected here. At depths beyond one transport mean free path L_s′ = L /(1 − g) , light propagation is sufficientlyrandomized. In our simulation, a photon was scattered ~70 times on average before exiting a scattering layer of thickness L= 40L_s . With increasing optical thickness, the intensity of the multiple-scattered light decreases much more slowly than the ballistic light, consistent with our experimental observation. The light that can be holographically recorded and time-reversed is therefore predominantly multiple-scattered.

The trajectories of S(f_s), S(f₊), S^*(f_s) and S^*(f₊), shown in Fig. 2, appeared to be random walks. However, in ideal time reversal, S^*(f_s) and S^*(f₊)would trace back the trajectories of S(f_s) and S(f₊) owing to the deterministic nature of the medium at any instant, leading to the convergence to their sources (see Supplementary Videos). Without ultrasonic encoding, S^*(f_s) converged to the incident location of S(f_s). With ultrasonic encoding, S^*(f₊) converged to the ultrasonic focus instead, which is the source of S(f).

Fig. 2.

2D Monte Carlo simulation of light propagation inside a scattering slab whose dimensions were x=160 L and z= 40 L . Initially, a broad (a–d) or a narrow (e–h) light beam was normally incident at the origin of the coordinates. In each panel, the top plot shows the trajectories while the bottom plot shows the photon density distribution(s) along the optical axis (total density shown in black). a & e, diffusive trajectories of S(f_s) propagating through the slab: some (shown in green) reach the phase-conjugate mirror and the others (shown in blue) do not. b & f, trajectories of S* ( f_s ) propagating back through the slab and converging to the incident point. c & g, trajectories of S( f ) (shown in blue) and the ultrasonically encoded component S(f₊) (shown in green) inside the slab. d & h, trajectories of S^*(f₊) converging back to the ultrasonic focus (shown in green) then back to the incident point (shown in magenta). The black circles in the middle of the slab denote the ultrasonic focus. UE: Ultrasonically Encoded light.

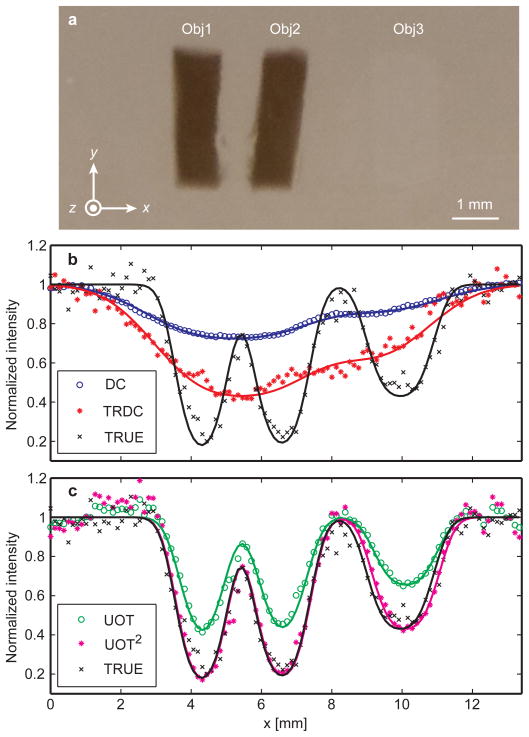
The TRUE optical focusing was validated with imaging experiments (Fig. 3). The imaging sample was a 10-mm thick scattering slab, made from a mixture of porcine gelatine, distilled water, and 0.25% Intralipid, resulting in L_s≈ 0.4 mm, g≈ 0.9 , and absorption length L_a≈ 79 mm. The light beam started with a 2-mm diameter on the incident plane of the sample and diffused to ~4 mm (FWHM) in the middle plane, which contained three objects with different compositions: two dyed with black ink (Obj1 and Obj2), resulting in an optical absorption coefficient μ_a ≈ 0.8 mm⁻¹, and one having 1%-concentration Intralipid (Obj3) resulting in L_s ≈ 0.1 mm. When the sample was laterally scanned along the x axis, four 1D images were acquired (Fig. 3b and 3c). The first two were acquired without either AOM tuning or ultrasonic modulation. To form the first image–a “DC” image, S( f_s) was detected by a photodiode at the BSO position. To form the second image–a “TRDC” image, S* ( f_s) was transmitted back through the sample and detected by a photodiode PD1. To form the third image–a “UOT” image based on conventional Ultrasound-modulated Optical Tomography (UOT)^15,16, S(f₊) was spectrally filtered by the BSO and was then detected by PD2. To form the fourth image–a “TRUE” image, S^*(f₊) was transmitted back through the sample and detected by PD1.

Fig. 3.

Results from four imaging experiments validating TRUE optical focusing. a, photograph of the imaged sample dissected at the middle plane containing two absorbing objects (Obj1 and Obj2) and one scattering object (Obj3). The object dimensions were x = 1.3 mm, y = 4.5 mm, and z = 1 mm for the two absorbing objects and x = 1.7 mm, y = 4.5 mm, and z = 0.6 mm for the scattering object, while the full dimensions of the sample were x = y = 60 mm and z = 10 mm. b, comparison of the normalized DC, TRDC, and TRUE images of the sample. The absolute strengths of the TRDC and TRUE signals were ~3,000 mV and ~30 mV, respectively. The objects could not be distinguished in the DC and TRDC images, while in the TRUE image the objects were clearly shown against the background with 61% contrast for the absorbing objects and 31% contrast for the scattering object. c, comparison of the UOT and TRUE images of the sample to demonstrate the square law: the TRUE signal is proportional to the square of the UOT signal (UOT²). The FWHMs of the point-spread functions were 0.89 mm (UOT) and 0.63 mm (TRUE), whose ratio is 1.4 (≈ $\sqrt{2}$ ). In b and c, the symbols represent experimental data while the solid curves represent Gaussian fitting.

The salient differences in the apparent image resolution and contrast among the four imaging methods stem from the distinct inherent imaging mechanisms. The DC and TRDC imaging methods, suffering from optical diffusion, lacked spatial resolution to resolve the three objects. The optical diffusion, approximated as a Gaussian profile, was convolved with the object profile to fit the experimental data. The full widths at half maxima (FWHM) of the Gaussian profiles, defined as the image resolutions, were 3.4 mm for DC imaging and 3.2 mm for TRDC imaging. By contrast, the UOT and TRUE imaging methods, based on imaging signals emanating from the internal virtual sources, both adequately depicted the profiles of the objects. The ultrasonic focus, approximated as a Gaussian profile, was convolved with the object profile to fit the data. The resolutions were 0.89 mm and 0.63 mm for UOT and TRUE imaging, respectively.

A square law exists if S^*(f₊) indeed converges to the ultrasonic focus: the TRUE signal is proportional to the square of the UOT signal. On the one hand, the optical field for the UOT image S(x, f₊)|_BSO ∝C(x)·S_in(f_s), where C(x) is a virtual source term and S_in(f_s) is the incident optical field. On the other hand, for the TRUE image, S*(x, f₊)|_BSO ∝ S(x, f₊)|_BSO . As S^*(f₊) inversely traverses the sample, the virtual source term in its conjugated form C^*(x) operates on S*(x, f₊)|_BSO . As a result, the optical field detected by PD1 S*(x, f_s) |_PD1 ∝C* (x)·, S*(x, f₊)|_BSO ∝ |C (x)|² S_in (f_s) Therefore, the detected light intensities in UOT and TRUE imaging are related by |S *(x, f_s) |_PD1|² ∝|S(x, f₊)|_BSO|⁴. This prediction was verified by the normalized amplitudes of the UOT and TRUE images in Fig. 3c. Furthermore, if the point-spread functions in UOT and TRUE imaging follow Gaussian profiles, their widths–defining the spatial resolutions–have a $\sqrt{2}$:1 ratio. This second prediction agrees with the ratio of 1.4 between the image resolutions of UOT (0.89 mm) and TRUE (0.63 mm) imaging. In addition, the resolution of UOT is in agreement with the ultrasonic focal diameter of 0.87 mm.

Focusing into a scattering medium is much more valuable than focusing through it. In fact, the former can be reduced to the latter by moving the focal position. Focusing through a medium was used to image a target only outside a scattering medium, which can be either viewed directly from the target side or scanned by a collimated laser beam. Focusing into the medium must be invoked to image or treat a target embedded inside a scattering medium. For example, when a tumour inside biological tissue is optically imaged or treated, light must be focused to the tumour.

Focusing light into a scattering medium dynamically, with the desired speed and localization, can profoundly benefit studies involving photophysical, photochemical, and photobiological processes. This work has demonstrated the feasibility of TRUE optical focusing by combining two key mechanisms–localized ultrasonic encoding of the diffused light and selective time reversal of the encoded light–to suppress the scattering effect. The focal spot size can be flexibly scaled with the ultrasonic frequency, and the experimental system can be adapted for reflection or other configurations according to the application. Improvement can be made by using faster photorefractive materials, time-reversal techniques with energy gains greater than unity, and more efficient time-reversal configurations. TRUE optical focusing–effectively bringing order to the chaotic scattering process–sees potential impact on imaging technologies such as fluorescence microscopy, diffuse optical tomography, and photoacoustic tomography; manipulation technologies such as optical tweezers and optogenetics; and therapeutic technologies such as photodynamic therapy and photothermal therapy.