Abstract
The kinetics of aromatic nucleophilic substitution of the nitric oxide generating diazeniumdiolate ion, DEA/NO, by thiols, (L-glutathione, L-cysteine, DL-homocysteine, 1-propanethiol, 2-mercaptoethanol and sodium thioglycolate) from the prodrug, DNP-DEA/NO, has been examined in aqueous solution and in solutions of cationic DOTAP vesicles. Second-order rate constants in buffered aqueous solutions (kRS- = 3.48 – 30.9 M-1s-1; 30 °C) gave a linear Brønsted plot (βnuc = 0.414 ± 0.068) consistent with rate-limiting SNAr nucleophilic attack by thiolate ions. Cationic DOTAP vesicles catalyze the thiolysis reactions with rate enhancements between 11 and 486-fold in Tris-HCl buffered solutions at pH 7.4. The maximum rate increase was obtained with thioglycolate ion. Thiolysis data are compared to data for nucleophilic displacement by phenolate (kPhO- = 0.114 M-1s-1) and hydroxide (kOH- = 1.82 × 10-2 M-1s-1, 37 °C) ions. The base hydrolysis reaction is accelerated by CTAB micelles and DODAC vesicles with vesicles being ca 3-fold more effective as catalysts. Analysis of the data using pseudophase ion-exchange formalism implies that the rate enhancement of the thiolysis and base hydrolysis reactions is due primarily to reactant concentration in the surfactant pseudophase.
Keywords: Diazeniumdiolates, nitric oxide, surfactant vesicles, catalysis, Brønsted plots
Introduction
Diazeniumdiolates (NONOates) are widely used nitric oxide generating agents in biomedical research studies both in ionic forms, R1R2NN(O)NO-, that undergo spontaneous acid-catalyzed dissociation at physiological pH and as O2-protected prodrugs, R1R2NN(O)NOR, that are stable until activated for NO release by enzymes at targeted biological sites. [1-4] Prodrug strategies involving O2-arylated diazeniumdiolates, in particular, have been of recent interest because of their success at delivering NO to acute myeloid leukemia cells on activation by glutathione/glutathione S-transferase [5-7] and this process is believed to be responsible for the anticancer properties that they display. Key to the effectiveness of O2-arylated diazeniumdiolate as prodrugs is their stability under physiological conditions until nucleophilic attack by glutathione frees the diazeniumdiolate ion resulting in its spontaneous hydrolysis and release of NO. To better understand the reactivity of diazeniumdiolates of the O2-arylated class, we have studied reactions of a model diazeniumdiolate prodrug, O2-(2,4-Dinitrophenyl) 1-(N,N-Diethylamino)diazen-1-ium-1, 2-diolate (DNP-DEA/NO, 1) with different thiols (RSH) in buffered aqueous solutions and have compared the nucleophilicity of thiol anions towards 1 with that of hydroxide and phenolate ions.

Because of the interest in the activation of 1 in different microenvironments, we have also examined the effect of cationic CTAB micelles and DODAC and DOTAP vesicles on thiolysis and base hydrolysis reactions of 1 and have compared the effectiveness of the surfactant aggregates as catalytic media for the reactions. To assess factors influencing the reactions at the aqueous interfaces of the micellar and vesicle systems, we have employed pseudophase ion-exchange (PIE) formalism, with consideration of ion-exchange between the OH- and RS- nucleophiles and the bound halide counter ions of the surfactant head groups in the interfacial region.
Experimental
Materials
O2-(2,4-Dinitrophenyl) 1-(N,N-Diethylamino)diazen-1-ium-1,2-diolate (DNP-DEA/NO, 1) was synthesized by reaction of DEA/NO (sodium (Z)-1-(N,N-diethylamino)diazen-1-ium-1,2-diolate) with 2,4-dinitrofluorobenzene (Acros Organics) in dimethylsulfoxide. [8] The structure was confirmed using UV-vis (λmax= 304 nm, ε = 14.2 mM-1 cm-1) and by 1H NMR in CDCl3 (300 MHz, Bruker). DOTAP (1,2-dioleoyl-3-trimethylammonium-propane) was obtained as a chloroform solution from Avanti Polar Lipids (Alabaster, Alabama). L-Glutathione, L-cysteine, DL-homocysteine. 1-propanethiol, 2-mercaptoethanol, CTAB, cetyltrimethylammonium bromide and DODAB, dimethyldioctadecylammonium bromide were obtained from Sigma-Aldrich. D-penicillamine and sodium thioglycolate were obtained from Acros. All were used as received.
Preparation of vesicle solutions
Unilamellar DOTAP vesicles were prepared from chloroform solutions of the lipid by removal of the solvent on a rotorvap under a N2 flux followed by hydration in buffer and bath sonication, as described in detail elsewhere. [9] The size of the DOTAP vesicles, prepared as above in 0.050 M Tris-HCl buffer, has been previously determined by dynamic light scattering. Their mean diameter (38.8 ± 0.20 nm) showed no significant change over the time period (20 – 90 min) that they were examined. [9] Dimethyldioctadecylammonium chloride (DODAC) was prepared by passing a methanol-chloroform (70:30, v/v) solution of the bromide salt, DODAB, through a Dowex 1X8-100 anion-exchange resin, followed by evaporation of the solvent and recystallization of the solid obtained two times from acetone-water (95:5, v/v). DODAC vesicles (ca. 10 mM) were prepared in a thermostated cell at 55 °C by probe sonication with an Ace Glass sonicator (Model GEX 750-5B,) operated at 20 kHz for 5s on/5s off for a 1 hr period. Total sonication time was 30 minutes. Titanium particles were removed from the resulting solution by passage through a PTFE 0.20 μm filter (Fisher). All vesicle solutions were prepared daily prior to their use in rate studies and used in kinetic runs immediately after preparation.
Rate measurements
Rate constants for the thiolysis reactions were measured spectrophotometrically by following the formation of the S-(2,4-dinitrophenyl)-conjugates at ∼350 nm, using a Hewlett Packard 8453 Diode Array UV-visible spectrophotometer. Stock solutions of 1 were prepared in DMSO and added to aqueous buffer to obtain substrate concentrations in kinetic runs (0.50-1.0 × 10-4 M) that contained 0.5-1% DMSO. All thiol stock solutions (0.15 – 0.40 M) were prepared immediately before use in the kinetic experiments and were stored in capped vials with a small head-space. Series of rate measurements were typically completed within 30-60 min and replicate rate measurements routinely made at the beginning and end of this period, showed no indication of variability due to thiol oxidation over the time period the experiments were conducted. Data obtained in duplicate sets of experiments, carried out on different days with freshly prepared thiol solutions also showed good reproducibility. During preparation of glutathione stock solutions, additional NaOH was needed to bring glutathione solutions to pH 7.4. The 1-propanethiol stock solution was prepared in acetonitrile. For liposome experiments, variable amounts of 0.050 M Tris buffer (pH 7.42) and 0.010 M DOTAP vesicle solution in 0.050 M Tris buffer were mixed in a 1 mL cuvette and thermostated before reaction was initiated by the addition of consecutive 10-μL aliquots of thiol and substrate. For buffer experiments, thiol stock solutions were prepared in a Tris-HCl, or glycine/NaOH buffer. pH values were checked against standard buffer solutions using an Orion 350 pH meter (Thermo Electron Corporation). Base hydrolysis rate constants were measured by monitoring the decrease in absorbance of the diazeniumdiolate chromophore at 305 nm. For runs with short half-lives requiring more rapid mixing, reaction was initiated by delivering 1.0-mL aliquots of a previously thermostated buffer to 10 μL of diazeniumdiolate substrate in the thermostated cell.
Measurement of thiol association constants
Values for the vesicle association constants, KRSH, for glutathione and thioglycolic acid were determined spectrophotometrically from changes in thiol absorbance (A) at 210 nm in the presence of variable amounts of sonicated DOTAP using reported procedures. [10] Solutions containing variable amounts of DOTAP (0 – 6.0 × 10-3 M) in 0.050 M Tris-HCl buffer were thermostated, blanked and treated with the same amount of thiol. Spectral scans (200 – 250 nm) showed the thiol absorbance decreasing progressively with increase in DOTAP concentration and the thiol absorption maximum shifting to longer wavelengths. Measured absorbance values were fitted to the equation A = (Aw + AvesKRSH[DOTAP])/(1 + KRSH[DOTAP]), where Aw and Aves are the absorbance values for thiol in water and in the vesicle pseudo-phase, respectively. KRSH values were obtained from a non-linear regression fit of the data to the above equation using SigmaPlot (Systat Software Inc., 2007) (See Supporting Information; Table E and Figure A).
Results and Discussion
Effect of pH on the thiolysis of 1 in buffered aqueous media
The nucleophilicity of different thiols (RSH) towards 1 in aqueous media was determined by measurement of thiolysis rate constants as a function of pH in 0.050 M Tris-HCl or glycine-NaOH buffered aqueous solutions at 30 °C. With the concentration of the thiol in 20-50 fold excess of the substrate, pseudo-first-order rate constants increased with increase in pH, consistent with nucleophilic attack by the thiolate anion, RS-. The dependence of the measured first-order rate constant on pH, is described by Eqns (1-3) and individual values for the second- order rate
| (1) |
| (2) |
| (3) |
constant, kRS-, and the apparent Ka of the thiol under the experimental conditions were obtained from plots of [RSH]T/kobs versus [H+] (Figure 1). The excellent linearity of the reciprocal plots obtained and the close agreement between the measured and literature pKa values [11-13] is consistent with reaction involving nucleophilic attack by the thiol anion in each case. When the nucleophilicity of the anions were compared through a Brønsted plot of log kRS- against pKa, the nucleophilicity increased with increasing basicity of the thiol and (with the exception of penicillamine) was described by a linear relation log kRS- = βnuc · pKRSH + C, where βnuc = 0.414 ± 0.068 and C = -2.83 ± 0.60 (see Figure 2). The finding is consistent with the thiolysis reactions proceeding through rate-limiting SNAr nucleophilic attack of the thiolate anion on the ipso carbon of the O2-protected prodrug in each case. [14] Diazeniumdiolate ions, R2N[N(O)NO]-, have been shown to be good leaving groups in SNAr reactions with a displacement rate by hydroxide between that of chloride and fluoride ions, [8] and the O2 oxygen of the diazeniumdiolate ion (pKa ≤ 4.5) [15] is less basic than that of the thiols employed in the study. Spectral evidence of a solvent stabilized intermediate Meisenheimer complex has been reported for reaction of 1 with sodium methoxide in dimethylsulfoxide. [8]
Figure 1.
Plot of [GSH]/kobs versus [H+] for reaction of glutathione with 1 in 0.050 M Tris-HCl buffer (pH 8.5-9.7) at 30 °C
Figure 2.
Dependence of second-order rate constant for thiolysis of 1 in aqueous solution on thiol pKa. (○) k2 = kRS-: log kRS- = 0.414 pKRS- - 2.83; R2 = 0.959. (□) k2 = k2o: log k2o = -0.566 pKa + 0.0466; R2 = 0.973.
Of interest also is the thiol-mediated reactivity of 1 at physiological pH where reaction rates are determined not only by the inherent strengths of the thiolate ions as nucleophiles, but also by their relative concentrations in the reaction solutions. A comparison was obtained through values of the second-order rate constant k2o for reaction at pH 7.4 that were estimated using Eq (4).
| (4) |
In contrast to the kRS- values, k2o is negatively correlated with the pKa of the thiols (Figure 2), and although thiols with higher pKa values are intrinsically better nucleophiles, their reactivity with 1 at pH 7.4 is offset by their lower tendency to generate thiolate anions, making the cellular thiols glutathione, cysteine and homocysteine, the most effective at activating 1 for NO release at physiological pH. Data are summarized in Table 1. The much smaller kRS- value obtained with penicillamine and its failure to follow the Brønsted reactivity pattern established for the other thiols may be tied to steric constraints arising from the methyl groups adjacent to the sulfhydryl group of penicillamine and the fact that its thiol group is the only one attached to a tertiary carbon. Similar irregular rate behavior by penicillamine in Brønsted plots has been reported for the thiol-mediated decomposition of S-nitrosothiols.[16]
Table 1.
Dependence of nucleophilic rate constants (kRS-) and apparent second-order rate constants at pH 7.4 (k2o) on the pKa of the thiol for the thiolysis of 1 at 30 °C.
| Thiol | kRS- (M-1s-1) | k2o (M-1s-1) | pKa |
|---|---|---|---|
| L-Cysteine a | 3.48 | 0.431 | 8.25 |
| DL-Homocysteine a | 5.62 | 0.215 | 8.80 |
| L-Glutathione a | 10.4 | 0.292 | 8.94 |
| 2-Mercaptoethanol b | 22.7 | 0.0638 | 9.95 |
| Sodium thioglycolate b | 28.4 | 0.0284 | 10.4 |
| 1-Propanethiol b | 30.9 | 0.0245 | 10.5 |
| D-Penicillamine a | 0.18 | 0.0329 | 8.05 |
0.050 M Tris-HCl buffer.
0.050 M glycine/NaOH buffer. [Thiol] = 1.5–5.0 mM. [1] = 0.10 mM.
Nucleophilic displacement by phenolate and hydroxide ions
The rate of nucleophilic displacement of the diazeniumdiolate ion, DEA/NO, by thiol anions has been compared to that obtained by phenolate and hydroxide ions. A value for the second-order rate constant for nucleophilic attack by the phenolate ion was determined from rate measurements carried out in glycine/NaOH buffer (pH 9.3-10.8) through a plot of [phenol]/kobs versus [H+]. Data was again obtained under pseudo-first-order conditions with [phenol] = 5.0 mM and [1] = 1 × 10-4 M. The slope and intercept of the plot yielded a value for of 0.114 M-1s-1 for kPhO- and a pKa value for phenol of 10.0 consistent with the phenolate ion as the effective nucleophile in the reaction.
The second-order rate constant for the base hydrolysis of 1 was obtained from reactions carried out with [NaOH] = 2.0 – 10.0 mM. Nucleophilic displacement of the diazeniumdiolate ion by hydroxide occurred readily in basic solution with formation of the diazeniumdiolate and dinitrophenolate ions.

Our data established a first-order dependence on hydroxide ion, kobs = kOH- [OH-], and a second-order rate constant, kOH- = 1.82 × 10-2 ± 1.04 × 10-3 M-1s-1 at 37 °C, in good agreement with the value 7.4 × 10-3 M-1s-1, previously determined at 25 °C by HPLC. [8] The second-order rate constants for nucleophilic attack by phenolate (kPhO- = 0.114 M-1s-1) and hydroxide (kOH- = 1.82 × 10-2 M-1s-1) ions compare to the values, kRS- = 3.48 – 30.9 M-1s-1 obtained in the thiolysis reactions. The kPhO- and kOH- values are consistent with the slower rates typically found with oxygen nucleophiles in SNAr reactions compared to those of sulfur anions.
Thiolysis of 1 in Cationic DOTAP Vesicle Media
The effect of cationic DOTAP liposomes on the thiolysis of 1 was examined in 0.050 M Tris-HCl buffer at pH 7.42 with [RSH]T = 5.0 mM and [DOTAP] = 0.10 – 10.0 mM. kobs – [DOTAP] rate profiles obtained were typical of bimolecular reactions catalyzed by vesicle interfaces, with pseudo-first-order rate constants increasing to a maximum at ca 4 mM lipid. A measure of the liposome catalysis is provided by catalytic factors, kcat, the ratio of the rate constant in the buffered liposome solution (kobs) to that in the buffer solution alone (kw), plotted as a function of lipid concentration. kw values were estimated for the conditions of the DOTAP experiments (pH 7.42, [thiol] = 5.0 mM) using kw = k2o[thiol]. Values for kcat were found to depend on the thiol employed, ranging from 486 for sodium thioglycolate to 11 for homocysteine. Data is summarized in Table 2.
Table 2.
Rate data for thiolysis of 1 in 0.050 M Tris/HCl buffer and in Tris-buffered DOTAP vesicle media at pH 7.42 and 30 °C.
| kmax (s-1) | kw (s-1) | kcat = kmax/kw | |
|---|---|---|---|
| Sodium thioglycolate | 0.0690 | 0.000142 | 486 |
| 1-Propanethiol | 0.0175 | 0.000123 | 143 |
| L-Glutathione | 0.122 | 0.00146 | 84 |
| 2-Mercaptoethanol | 0.0207 | 0.000319 | 65 |
| L-Cysteine | 0.0250 | 0.00215 | 12 |
| DL-Homocysteine | 0.0120 | 0.00108 | 11 |
[Thiol] = 5.0 mM. [1] = 0.10 M mM. [DOTAP] = 1.0 – 10.0 mM.
Assuming that the liposome catalysis is due predominantly to the concentration of the reactants in the vesicle pseudo-phase, as has been established for the vast majority of micellar and vesicle-catalyzed organic reactions, the differences in kcat values in our study must arise in large part from differences in thiol association with DOTAP vesicles. Although such associations will involve differing degrees of electrostatic and hydrophobic interaction, electrostatic binding is expected to dominate at the cationic vesicle interface. The most pronounced catalysis that was observed with sodium thioglycolate, is presumably due to strong electrostatic interaction between thioglycolate's carboxylic acid group (pKa = 3.68) [17] and the cationic DOTAP surface bringing the small thioglycolate ion in close proximity to the diazeniumdiolate substrate in vesicle bilayer. Similar considerations apply to the bulkier glutathione molecule, with its two carboxylate groups (pKa = 2.12, 3.59) [17] effectively orienting the thiol for reaction at the vesicle surface. In contrast, hydrophobic association must predominate for 1-propanethiol and 2-mercaptoethanol, while the relatively modest catalysis found with the two amino acids cysteine and homocysteine is consistent with the weaker vesicle interactions expected for those two zwitterions.
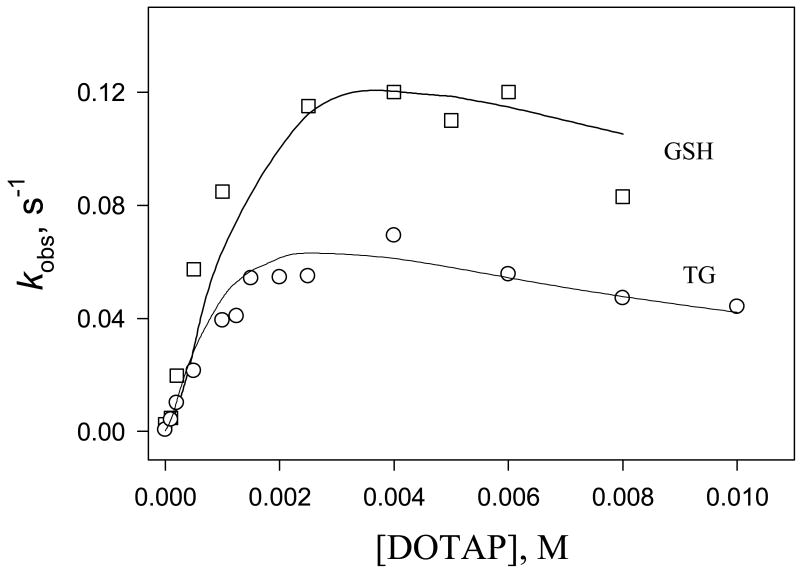
Aside from differences in thiol binding, additional contributions to the catalysis are also expected to arise from enhanced ionization of the thiol groups at the cationic surface and possibly from changes in intrinsic nucleophilic reactivity in the vesicle pseudo-phase. A rate enhancement of over a million-fold has been observed for p-nitrophenyl octanoate thiolysis by 1-heptanethiol in cationic DODAC vesicles.[18] We applied the same PIE model (Eqn (5)), developed for reactions between a neutral substrate and a nucleophilic anion derived from a weak acid [19], to the relatively modest catalysis we have observed for the thiolysis of 1 by glutathione, the thiol of relevance to the enzymatic activation of O2-arylated prodrugs in vivo, and thioglycolate, the thiol that exhibited the greatest catalysis in our DOTAP studies.
| (5) |
In Eqn (5), k2o and k2v are the second-order rate constants for thiolysis in the aqueous and vesicle phases, respectively, KRS/Cl and Kap are the selectivity constant for thiolate-chloride ion-exchange and the apparent thiol acidity constant at the cationic vesicle interface, and KRSH is the vesicle association constant for the protonated thiol. We used values of 0.20 for α, the degree of counter-ion dissociation at the vesicle surface, 0.58 for V, the effective volume of the vesicle pseudo-phase, [19] and 710 M-1, for Ks, obtained from the binding of 1 to DPPC and DOPE vesicles.[20] Values of 263 and 693 M-1, respectively, that we determined for glutathione and thioglycolic acid association with DOTAP vesicles were used for KRSH. These compare to values of 1200 M-1 reported for 1-heptanethiol association with DODAC vesicles [21] and 150 M-1 for benzyl thiol association with CTAB micelles.[22] [Cl-]b and [Cl-]f, the concentrations of bound and free chloride ions in the Tris-HCl buffered DOTAP vesicle solutions were calculated using equations 6 and 7, where [RS-]b and [OH-]b are the concentrations of vesicle-bound thiolate [23]
| (6) |
| (7) |
and hydroxide [24] ions. Since Kap is expected to vary as a function of [DOTAP], we used values for Kap calculated by Eqn (8). [19] We have previously observed a lowering of the pKa of
| (8) |
glutathione by 0.5 units in the presence of DOTAP vesicles.[20]
In treating our data, the equations defining [RS-]b, [OH-]b, [Cl-]f, [Cl-]b, Kap, and kcalc, were linked in an Excel spreadsheet (MS Office, 2007) and values of KGS/Cl and k2v were left as adjustable parameters and systematically varied to achieve the closest fit between kobs and curves generated by kcalc for [DOTAP] between 0 and 0.010 M. Shown in Figure 3 are the best fits obtained for the thiolysis of 1 by glutathione and thioglycolate that we obtained using KGS/Cl = 10 and 45, respectively. The corresponding k2v/k2o values were 1.2 and 1.6. Although we recognize that such k2v/k2o ratios are subject to some uncertainty due to the compensatory nature of the values used for KGS/Cl and k2v, we believe they are indicative of only a small increase in the intrinsic reactivity of the substrates in DOTAP media. Such changes compare to a k2v/k2o ratio of 38 and a rate enhancement in excess of 106 that were reported for the thiolysis of p-nitrophenyl octanoate by heptanethiol in cationic DODAC vesicle media.[18, 21] This clearly indicates that the electrostatic binding of thiols at the DOTAP vesicle interface is not as effective in modifying the intrinsic reactivity of our substrates as is the hydrophobic solubilization of p-nitrophenyl octanoate and heptanethiol in the tetraalkylammomium DODAC bilayer. In contrast to the DODAC vesicles, the polarity of the acetate bridges in the dioleoyl chains of DOTAP would appear to inhibit penetration of the thiol reactants into the hydrophobic core of the DOTAP vesicles to an extent that is apparently necessary to achieve the local concentration of reactants and the greater catalysis obtained with DODAC.
Figure 3.
Plot of kobs versus [DOTAP] for reaction of 1 with glutathione (□) and sodium thioglycolate (○) in 0.050 M TRIS-HCl buffer at pH 7.4 and 30 °C. Solid line (kcalc) is calculated with Eqn (5) using best fit values indicated in text.
Catalysis of base hydrolysis by CTAB micelles and DODAC Vesicles
Our examination of the hydrolysis of 1 in NaOH solutions was extended to microenvironments provided by the cationic interfaces of both CTAB micelles and DODAC vesicles. Reactions were conducted at NaOH concentrations between 2.0 and 10.0 mM in large excess of the substrate (1 × 10-4 M). When the base hydrolysis reaction was examined in CTAB solutions as a function of added surfactant, rate profiles typical of micellar-catalyzed bimolecular reactions were observed (Fig. 4) with the measured first-order rate constant increasing with added [CTAB] to a maximum at ca 3mM surfactant before decreasing sharply at higher surfactant concentrations. The acceleration of pseudo-first-order rate constants was also noted in the presence of the bilayer vesicles provided by the synthetic surfactant DODAC, with greater rate enhancements being apparent with DODAC vesicles than with CTAB micelles. The rate profiles obtained in NaOH solutions are compared in Figure 4 and Figure 5. A comparison of the catalytic efficiency of the two surfactant media was obtained through the ratio, kmax/kw, where kmax was the maximum rate constant observed in the surfactant solutions and kw was that for base hydrolysis in the absence of surfactant. In 5.0 mM NaOH solution, kmax/kw was 290 for DODAC vesicles compared to 93 for CTAB micelles.
Figure 4.
Plots of kobs versus [Dn] for hydrolysis of 1 in 0.010M (△) and 0.0050 M (○) NaOH solution at 37°C. The solid lines are calculated with Eqn (9).
Figure 5.
Plots of kobs versus [DODAC] for hydrolysis of 1 at 37°C in 0.010 M NaOH (○), 0.005 M NaOH (◊) and 0.002 M NaOH (□) The solid lines are calculated with Eqn (9).
Quantitative analysis of rate-surfactant profiles in sodium hydroxide solutions was made using the pseudophase ion-exchange (PIE) formalism developed by Quina and Chaimovich [25] with explicit consideration of ion-exchange between the bound halide counter ions, X-, of the surfactant head groups and OH- ions in the interfacial region. Although the PIE model has been shown to have limitations at high base concentrations, it has found wide application in treating kinetic data for base-hydrolysis reactions catalyzed by surfactant micelles and vesicles. [10, 24-30] The kinetic data obtained for the hydrolysis of 1 in NaOH solutions in CTAB and DODAC solutions were fitted to Eqn (9) where KOH/X is the ion-exchange constant between
| (9) |
hydroxide and the halide at the micellar or vesicle surface, k2m is the second-order rate constant in the surfactant phase, k2w is the second-order rate constant in the aqueous phase and Dn and V are the concentration and effective volume of the micellized surfactant. The concentrations of the bromide ions (CTAB) or chloride ions (DODAC) in the aqueous and surfactant pseudophases, [X]w and [X-]m, respectively, were calculated using the ion-exchange equations described in detail elsewhere. [23-25] The value of α (0.20), the degree of counter-ion dissociation at both the micelle and vesicle surface was assumed independent of the surfactant concentration and cmc values of 5.0 × 10-4 M and 6 × 10-6 M were used for CTAB and DODAC. In treating our data we used V = 0.37 M-1 for CTAB micelles [26] and 0.58 M-1 for DODAC vesicles,[25] and values of 0.08 [24, 25] and 1.6 [10] for KOH/Br and KOH/Cl. With these assumptions, rate-surfactant profiles were fitted to Eqn (9) to provide best fit values for k2m and k2v. The agreement between the experimental data and the theoretical line calculated with Eqn (9) is shown in Figures 4 and 5 and the rate and equilibrium parameters obtained are summarized in Table 3.
Table 3.
Comparison of rate and equilibrium parameters for micelle- and vesicle-catalyzed hydrolysis of 1 in NaOH solutions at 37°C
| Surfactant | [NaOH], M | k2m/k2w | Ks (M-1) | kmax/kw | k2m,2v (M-1 s-1) |
|---|---|---|---|---|---|
| CTAB | 0.010 | 1.43 | 350 | 76 | 2.10 × 10-2 |
| CTAB | 0.0050 | 1.21 | 340 | 97 | 2.20 × 10-2 |
| DODAC | 0.010 | 0.63 | 730 | 250 | 1.1 × 10-2 |
| DODAC | 0.0050 | 0.46 | 770 | 279 | 8.0 × 10-3 |
| DODAC | 0.0020 | 0.25 | 756 | 334 | 4.0 × 10-3 |
The finding that the larger DODAC vesicles are more effective at enhancing base hydrolysis rates than are CTAB micelles has been observed previously for other CTAB and DODAC-catalyzed reactions [10, 26]. Such size-dependent differences in catalytic efficiency for alkylammonium micelles and vesicles has generally been attributed to differences in substrate binding to the surfactant aggregates, with the increased hydrophobicity and fluidity of the vesicle bilayers [31] making them more effective at concentrating hydroxide ions at the interface. [21] Although in our study, both CTAB micelles and DODAC vesicles accelerate the rate of alkaline hydrolysis of 1, the increased reaction rate is not reflected in values calculated for the intrinsic second-order rate constants, k2v and k2m for reaction in the two pseudo-phases. The value obtained for k2v is lower than k2w and those of k2m and k2w are more comparable in magnitude. Such findings have been previously observed in other reactions catalyzed by micelles and vesicles, where a reduction in the intrinsic reactivity is more than compensated by an increase in the local concentration of the reactants at the interface. The lowering of the intrinsic reactivity in the presence of DODAC vesicles and CTAB micelles, compared to that in water is generally attributed to differences in the polarity of the media, particularly the lower dielectric at the surface of the surfactant aggregates and the diminished hydrogen bonding ability of the DODAC interface compared to that in CTAB micelles.[10, 21, 25]
Although the vesicle bilayers of DODAC and DOTAP provide both internal and external surfaces as potential reaction sites, we have found no evidence of biphasic kinetic behavior resulting from differences in reactivity at the inner and outer interfaces or rate limiting permeation of reactants through the membrane. This may suggest that the rate of transmembrane equilibration of reactants is fast compared to the vesicle catalyzed reaction and, if so, this implies similar reaction behavior at the outer and inner vesicle interfaces.
Conclusions
The linear Brønsted plot obtained for the thiolysis reactions is consistent with rate-limiting SNAr nucleophilic attack of the thiolate anion on the ipso carbon of the O2-protected prodrug. Although weaker nucleophiles, the cellular thiols employed in the study are the most effective at activating 1 for NO release at physiological pH. The intrinsic nucleophilic reactivity of glutathione, the active thiol for the thiolysis of 1 in vivo, is 570 times that of hydroxide ion and at physiological pH and typical intracellular concentrations (1.0 – 10.0 mM), free glutathione is estimated to react with DNP-DEA/NO a million times more rapidly than hydroxide ion, even without the participation of the enzyme. Vesicle-mediated catalysis of the thiolysis and base hydrolysis reactions is due mostly to substrate concentration in the surfactant pseudo-phase, with the smaller size of OH- and thioglycolate ions giving them a rate advantage for catalysis by cationic vesicle interfaces.
Supplementary Material
Acknowledgments
Support of this work by the National Institutes of Health (Grant number R15-HL078750-01) is gratefully acknowledged.
References
- 1.Keefer LK, Nims RW, Davies KM, Wink DA. Methods Enzymol. 1996;268:281–293. doi: 10.1016/s0076-6879(96)68030-6. [DOI] [PubMed] [Google Scholar]
- 2.Keefer LK. Annu Rev Pharmacol Toxicol. 2003;43:587–607. doi: 10.1146/annurev.pharmtox.43.100901.135831. [DOI] [PubMed] [Google Scholar]
- 3.Valdez CA, Saavedra JE, Showalter BM, Davies KM, Wilde TC, Citro ML, Barchi JJ, Deschamps JR, Parrish D, El-Gayar S, Schleicher U, Bogdan C, Keefer LK. J Med Chem. 2008;51:3961–3970. doi: 10.1021/jm8000482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Showalter BM, Reynolds MM, Valdez CA, Saavedra JE, Davies KM, Klose JR, Chmurny GN, Citro ML, Barchi JJ, Merz SI, Meyerhoff ME, Keefer LK. J Am Chem Soc. 2005;127:14188–14189. doi: 10.1021/ja054510a. [DOI] [PubMed] [Google Scholar]
- 5.Shami PJ, Saavedra JE, Wang LY, Bonifant CL, Diwan BA, Singh SV, Gu Y, Fox SD, Buzard G, Citro ML, Waterhouse DJ, Davies KM, Keefer LK. Mol Canc Ther. 2003;2:409–417. [PubMed] [Google Scholar]
- 6.Shami PJ, Saavedra JE, Bonifant CL, Chu J, Udupi V, Malaviya S, Carr BI, Kar S, Wang M, Jia L, Ji X, Keefer LK. J Med Chem. 2006;49:4356–4366. doi: 10.1021/jm060022h. [DOI] [PubMed] [Google Scholar]
- 7.Chakrapani H, Kalathur RC, Maciag AE, Citro ML, Ji X, Keefer LK, Saavedra JE. Bioorg Med Chem. 2008;16:9764–9771. doi: 10.1016/j.bmc.2008.09.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Saavedra JE, Srinivasan A, Bonifant CL, Chu J, Shanklin AP, Flippen-Anderson JL, Rice WG, Turpin JA, Davies KM, Keefer LK. J Org Chem. 2001;66:3090–3098. doi: 10.1021/jo0016529. [DOI] [PubMed] [Google Scholar]
- 9.Dinh BT, Price SE, Majul A, El-Hajj M, Morozov V, Hrabie JA, Davies KM. Nitric Oxide. 2008;18:113–121. doi: 10.1016/j.niox.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hervés P, Leis JR, Mejuto JC, Pérez-Juste J. Langmuir. 1997;13:6633–6637. [Google Scholar]
- 11.Huskey SEW, Huskey WP, Lu AYH. J Am Chem Soc. 1991;113:2283–2290. [Google Scholar]
- 12.Tang SS, Chang GG. Biochem J. 1995;309:347–353. doi: 10.1042/bj3090347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lange's Handbook of Chemistry and Physics. 13th. McGraw-Hill; 1985. [Google Scholar]
- 14.Hupe DJ, Jencks WP. J Am Chem Soc. 1977;99:451–464. [Google Scholar]
- 15.Davies KM, Wink DA, Saavedra JE, Keefer LK. J Am Chem Soc. 2001;123:5473–5481. doi: 10.1021/ja002899q. [DOI] [PubMed] [Google Scholar]
- 16.Hu TM, Chou TC. The AAPS Journal. 2006;8:485–E492. doi: 10.1208/aapsj080357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pitman IH, Morris IJ. Aust J Chem. 1979;32:1567–1573. [Google Scholar]
- 18.Cuccovia IM, Quina FH, Chaimovich H. Tetrahedron. 1982;38:917–90. [Google Scholar]
- 19.Chaimovich H, Bonilha JBS, Zanette D, Cuccovia IM. In: Surfactants in Solution. Mittal KL, Linderman B, editors. Vol. 2. Plenum Press; New York: 1984. pp. 1121–1138. [Google Scholar]
- 20.Dinh BT, Zanbrakji MN, Dove K, Price SE, Peterson M, Davies KM. Nitric Oxide. 2008;19:326–332. doi: 10.1016/j.niox.2008.07.004. [DOI] [PubMed] [Google Scholar]
- 21.Kawamuro MK, Chaimovich H, Abuin EB, Lissi EA, Cuccovia IM. J Phys Chem. 1991;95:1458–1463. [Google Scholar]
- 22.Correia VR, Cuccovia IM, Chaimovich H. J Phys Org Chem. 1993;6:7–14. [Google Scholar]
- 23.Triboni ER, Politi MJ, Cuccovia IM, Chaimovich H, Filho PB. J Phys Org Chem. 2003;16:311–317. [Google Scholar]
- 24.Quina FH, Politi MJ, Cuccovia IM, Baumgarten E, Martins-Franchetti SM, Chalmovich H. J Phys Chem. 1980;84:361–365. [Google Scholar]
- 25.Quina FH, Chaimovich H. J Phys Chem. 1979;83:1844–1850. [Google Scholar]
- 26.Fendler JH, Hinze WL. J Am Chem Soc. 1981;103:5439–5447. [Google Scholar]
- 27.García-Rio L, Hervés P, Leis JR, Mejuto JC, Perez-Juste J. J Phys Org Chem. 1998;11:584–588. [Google Scholar]
- 28.Nascimento MD, Lezdcano MA, Nome F. J Phys Chem. 1992;96:5537–5540. [Google Scholar]
- 29.Scarpa MV, Araujo PS, Schreier S, Sesso A, Anselmo GO, Chaimovich H, Cuccovia IM. Langmuir. 2000;16:993–999. [Google Scholar]
- 30.Broxton TJ, Christie JR, Chung RPT. J Org Chem. 1988;53:3081–3084. [Google Scholar]
- 31.Kunitake T, Okahata Y, Ando R, Shinkai S, Hirakawa S. J Am Chem Soc. 1980;102:7877–7881. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.