Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2011 May;21(5):768–774. doi: 10.1101/gr.115972.110

Maximum-likelihood estimation of recent shared ancestry (ERSA)

Chad D Huff 1,5, David J Witherspoon 1,5, Tatum S Simonson 1, Jinchuan Xing 1, W Scott Watkins 1, Yuhua Zhang 1, Therese M Tuohy 2, Deborah W Neklason 2, Randall W Burt 2, Stephen L Guthery 3, Scott R Woodward 4, Lynn B Jorde 1,6
PMCID: PMC3083094  PMID: 21324875

Abstract

Accurate estimation of recent shared ancestry is important for genetics, evolution, medicine, conservation biology, and forensics. Established methods estimate kinship accurately for first-degree through third-degree relatives. We demonstrate that chromosomal segments shared by two individuals due to identity by descent (IBD) provide much additional information about shared ancestry. We developed a maximum-likelihood method for the estimation of recent shared ancestry (ERSA) from the number and lengths of IBD segments derived from high-density SNP or whole-genome sequence data. We used ERSA to estimate relationships from SNP genotypes in 169 individuals from three large, well-defined human pedigrees. ERSA is accurate to within one degree of relationship for 97% of first-degree through fifth-degree relatives and 80% of sixth-degree and seventh-degree relatives. We demonstrate that ERSA's statistical power approaches the maximum theoretical limit imposed by the fact that distant relatives frequently share no DNA through a common ancestor. ERSA greatly expands the range of relationships that can be estimated from genetic data and is implemented in a freely available software package.

Knowledge about the recent shared ancestry between individuals is fundamental to a wide variety of genetic studies. Detecting cryptic relatedness is a valuable technique for mapping disease-susceptibility loci and for identifying other at-risk individuals (Neklason et al. 2008; Thomas et al. 2008). For case-control association studies and population-based genetic analyses, related individuals must be identified and removed from samples that are intended to be random representatives of their populations (Voight and Pritchard 2005; Pemberton et al. 2010; Simonson et al. 2010; Xing et al. 2010). Using genetic data to correct pedigree errors increases the power of disease mapping in families (Cherny et al. 2001). Genetic identification of relatives has also proven invaluable in forensic identification of missing persons, victims of mass disasters, and suspects in criminal investigations (Biesecker et al. 2005; Bieber et al. 2006; Zupanic Pajnic et al. 2010). Studies of conservation biology, quantitative genetics, and evolutionary biology are greatly illuminated when the recent shared ancestry between individuals can be reconstructed, especially in agricultural and wild populations (DeWoody 2005; Slate et al. 2010).

Most established methods for detecting and estimating genetic relationships are based on genome-wide averages of the estimated number of alleles shared identically by descent (IBD) between two individuals (Weir et al. 2006). These methods are accurate and efficient for relationships as distant as third-degree relatives (e.g., first cousins) but cannot identify more distant relationships. Here we present ERSA, a novel method for estimation of recent shared ancestry. Our method builds on recently developed algorithms (Thomas et al. 2008; Gusev et al. 2009; Browning and Browning 2010) that use high-density SNP data to detect the number, lengths, and locations of chromosomal segments identical by descent (IBD) between two individuals (for a depiction of IBD segment inheritance, see Fig. 1). ERSA uses a likelihood ratio test to compare the null hypothesis that the two individuals are unrelated with the alternative hypothesis that the individuals share recent ancestry. Because of the qualitative difference between genome-wide averages of relatedness and the information contained in IBD segments, our method greatly expands the range of relationships that can be detected from genetic data. ERSA accurately estimates the degree of relationship for up to eighth-degree relatives (e.g., third cousins once removed), and detects relationships as distant as twelfth-degree relatives (e.g., fifth cousins once removed).

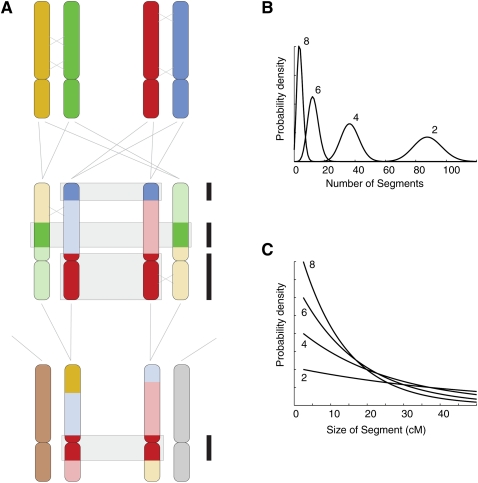
Figure 1.

Figure 1.

Open in a new tab

Expected distributions of IBD chromosomal segments between pairs of individuals. (A) The process underlying the pattern of IBD segments. Two homologous autosomal chromosomes are shown for two parents, each colored differently. Meiosis and recombination occur, and two sibling offspring inherit recombinant chromosomes (just one crossover per homologous pair for each meiosis event is depicted, marked by an X). For some segments of the chromosome in question, the siblings share a stretch that was inherited from one of the four parental chromosomes. The three IBD segments are identifiable as regions that share the same color (boxed and marked at right by black bars). The siblings mate with unrelated individuals, and the offspring each inherit an unrelated chromosome (tan or gray) and one that is a recombinant patchwork of the grandparental chromosomes. These first cousins share one segment IBD at this chromosome (red, boxed). (B) The number of segments that a pair of individuals shares IBD, across all chromosomes, is approximately Poisson-distributed with a mean that depends on the number of meioses d on the path relating the individuals (d = 2, 4, 6, 8, corresponding to siblings through third cousins). (C) The lengths of the IBD segments are approximately exponentially distributed, with mean length depending on the relationship between individuals (theoretical distributions shown for d = 2, 4, 6, 8).

Methods

Estimation of recent ancestry

Our method uses a likelihood ratio test for which the data are the number and lengths of autosomal genomic segments shared between two individuals, with segment length measured in centiMorgans (cM). The null hypothesis is that the individuals are no more related than two persons picked at random from the population; the alternative hypothesis is that the two individuals share recent ancestry. When the alternative model is not significantly more likely than the null model, we conclude that there is no evidence for recent shared ancestry. Otherwise, we obtain the maximum-likelihood estimate for the degree of relationship between two individuals by maximizing the likelihood over all possible relationships in the alternative model. We determine significance levels and confidence intervals from standard chi-square approximations for the likelihood ratio test.

Null hypothesis

We estimate the likelihood of the null hypothesis from the empirical distribution of autosomal shared segments in the population. We are only interested in shared segments longer than a given threshold t because shorter segments are more difficult to detect and provide little information about recent ancestry. Let s equal the set of segments shared between two individuals and n equal the number of elements in s. For this calculation, we assume that the number of segments shared and the length of each segment are independent, which is approximately true for the HapMap CEU population (see Fig. 2D). The likelihood of the null hypothesis is:

graphic file with name 768equ1.jpg

where

graphic file with name 768equ2.jpg

NP(n|t) is the likelihood of sharing n segments, SP(s|t) is the likelihood of the set of segments s, and FP(i|t) is the likelihood of a segment of length i. We approximate NP(n|t) from a Poisson distribution with mean equal to the sample mean of the number of segments shared in the population (Fig. 2B). Under a model of random mating and complete ascertainment of shared segments, FP(i|t) specifies a geometric distribution, for which we substitute an exponential approximation.

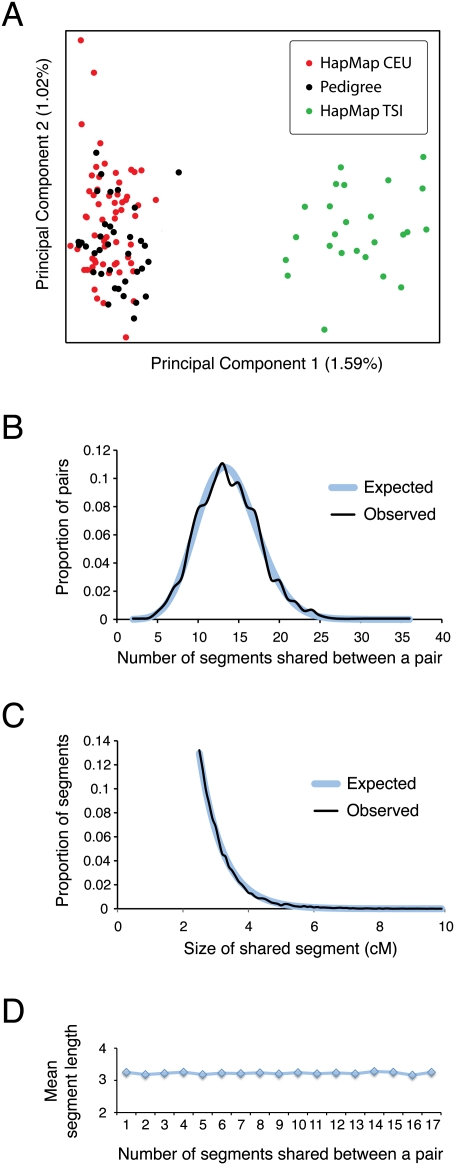
Figure 2.

Figure 2.

Open in a new tab

Characteristics of HapMap CEU parents as a background reference population. (A) Principal Components Analysis comparing 36 individuals from our three pedigrees (no pair closer than seventh-degree relatives) to 85 unrelated individuals from three European populations (60 HapMap CEU parents from 30 parent–offspring trios and 25 HapMap TSI individuals) based on pairwise allele-sharing distances computed from ∼247,000 SNPs typed on the Affymetrix SNP array (for additional details on data and methods, see Xing et al. 2010). The percentage of genetic variation explained by each component is given on the corresponding axis. (B) Distribution of the number of segments with length >2.5 cM that are inferred to be shared IBD by Germline in pairs of CEU individuals (Observed), with fitted Poisson distribution (Expected). (C) Distribution of the lengths of IBD segments longer than 2.5 cM in CEU pairs (Observed), with fitted exponential distribution (Expected). (D) Scatterplot of the number of IBD segments per pair versus the mean length of segments in the pair.

We recommend setting t to the smallest value that can achieve a false-negative rate of 1% or lower. This setting maximizes the use of available data while ensuring that the exponential approximation to the distribution of segment lengths in the population holds. Our choice of t = 2.5 cM was based on Germline's previously reported false-negative rate of 1% for segments 2.5 cM and longer (Gusev et al. 2009). In the HapMap CEU population, the distribution of segments detected by Germline that are longer than 2.5 cM is approximately exponential, with the exception of a few significant outliers (Fig. 2C). We exclude these outlying segments (those longer than h = 10 cM) when estimating the population distribution of shared segment lengths, for two reasons. First, the outliers are inconsistent with the assumption of random mating used in the approximation. Second, the outliers are examples of shared recent ancestry, and including them in the population distribution would decrease our power to detect recent ancestry. Therefore, we approximate FP(i|t) from the maximum likelihood estimate of the mean of a truncated exponential distribution:

graphic file with name 768equ3.jpg

where θ is equal to the mean shared segment length in the population for all segments of size >t and <h. For HapMap CEU with t = 2.5 cM and h = 10 cM, our estimate of θ is 3.12 cM.

Alternative hypothesis

The alternative hypothesis is that the pair of individuals shares either one or two recent ancestors. Let a represent the number of ancestors shared, and let d equal the combined number of generations separating the individuals from their ancestors(s), e.g., d = 6 and a = 1 for half-second cousins. Under the alternative hypothesis, segments shared by two individuals come from two sources: recent ancestry and the population background (denoted by subscripts A and P, respectively). Let nP + nA = n, where nA is equal to the number of shared segments inherited from recent ancestors, and nP is the number of segments shared due to the population background. sP and sA are two mutually exclusive subsets of s, with sA equal to the subset of segments inherited from recent ancestor(s) with nA elements and sP equal to the subset of segments shared due to the background with nP elements. The likelihood of the alternative hypothesis of recent ancestry, LR, is then:

graphic file with name 768equ4.jpg

Because sP is distributed according to the population distribution, LP follows the description in Equation 1. LA is the likelihood that two individuals share n autosomal segments from recent ancestor(s) specified by d and a, with the segment lengths specified by sA. LA can be expressed as the product of likelihoods of the number of shared segments and the length of each segment, which parallels Equations 1 and 2 :

graphic file with name 768equ5.jpg
graphic file with name 768equ6.jpg

Equation 6 assumes that, for a given value of d, the lengths of segments are independent. This assumption is not strictly true. One might imagine that the presence of a particularly long segment would reduce the genomic space available for additional segments. However, because the length of any one segment is small relative to the genome and because the genome is physically divided into chromosomes, the segment lengths are approximately independent (Thomas et al. 1994).

For two individuals who are related by an inheritance path that is d meioses long, the probability that they will inherit any particular autosomal segment from a common ancestor on that path is equal to 1/2(d − 1). The expected number of shared autosomal segments that could potentially be inherited from a common ancestor is equal to rd + c, where c is the number of autosomes and r is the expected number of recombination events per haploid genome per generation. Therefore, the expected number of shared segments is equal to a(rd + c)/2(d − 1) (Thomas et al. 1994). In humans, c is equal to 22 and r is ∼35.3 (McVean et al. 2004). Given d, the expected value of i is 100/d. Without conditioning on t, the distribution of segment length is exponential with mean 100/d. Conditioning on t,

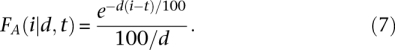graphic file with name 768equ7.jpg

The probability p(t) that a shared segment is longer than t is equal to e−dt/100 (Thomas et al. 1994). Because the distribution of the number of shared segments is approximately Poisson (Thomas et al. 1994),

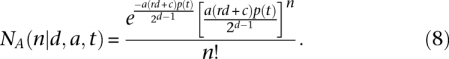graphic file with name 768equ8.jpg

Given nA and nP, the maximum value of the likelihood function (Eq. 4) is equal to:

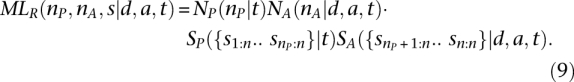graphic file with name 768equ9.jpg

where sx:n is equal to the xth smallest value in s. Equation 9 asserts that the likelihood is maximized when the set of segments resulting from recent ancestry is equal to the longest nA segments in s, with the remaining nP segments being due to the population background. In the Supplemental Methods section, we show that Equation 9 holds as long as θ < a(rd + c), which is true whenever a and d specify shared ancestry that is recent relative to pairs of individuals selected at random from the population.

The alternative model contains three additional parameters relative to the null model, d, a, and nA (nP = n − nA). However, when we evaluated the behavior of d and a empirically, we found that they effectively act as a single parameter (see Supplemental Fig. S6). Therefore, we evaluate the ratio of Equations 1 and 9 using a χ2 approximation with two degrees of freedom (−2 ln[LR/LN] ∼ χ22). For closely related individuals, the distribution of NP(nP|t) should theoretically be adjusted to account for segments shared from the population background that could not be observed because they occur within longer segments shared due to recent ancestry. Although ERSA optionally includes this adjustment, our experience has been that the algorithm performs slightly better without the adjustment due to the occasional imprecise definition of very long IBD segments in Germline. To identify the maximum value of the likelihood function (Eq. 4) given d, a, and t, we evaluate all possible values of nP and nA in Eq. 9:

graphic file with name 768equ10.jpg

Individuals ascertained based on a shared genetic variant

If the two individuals have been ascertained because they both share the same genetic variant, as in the case of a shared disease-causing variant, then the likelihood calculation must be conditioned on this ascertainment. In the case of such ascertainment, the shared segment that contains the variant is equivalent to two shared segments, with the segment boundaries defined by the original boundaries and the location of the ascertained variant. Thomas et al. (1994, 2008) have shown that the lengths of these segments, g1 and g2, are exponentially distributed, with mean equal to the unconditional length of a segment. Excluding the ascertained segment from n and s, the maximum value of the likelihood function is equal to:

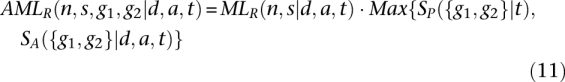graphic file with name 768equ11.jpg

Genotyping and inference of IBD segments

We applied our method to three well-defined pedigrees with predominantly northern European ancestry (Table 1). Informed consent was obtained from all study subjects, and all procedures were approved by the Western Institutional Review Board. DNA samples were collected and purified from blood as in Xing et al. (2010). Affymetrix 6.0 SNP arrays were used to genotype 169 individuals selected from these pedigrees (Table 1), per the manufacturer's instructions (see Xing et al. 2010). Beagle 3.2 (Browning and Browning 2010) was used to phase and impute missing genotypes, using the Affymetrix 6.0 SNP genotypes of the 30 HapMap CEU trios as a reference (CEL files provided by Affymetrix). Of 868,155 autosomal SNP loci with unique positions on the array (not including controls, whose probe set IDs begin with “AFFX-SNP”), 18,610 were excluded from the final data set because they exhibited more than three Mendelian inheritance errors in the CEU trios or >10% missing data in either the CEU or pedigree individuals. On the basis of the pedigree genotypes, Germline 1.4.1 (Gusev et al. 2009; http://www1.cs.columbia.edu/∼gusev/germline/) inferred the locations and extents of IBD segments for all pairs of individuals (parameters err_het = 2, err_hom = 1, and min_m = 1cM, with marker positions given on the HapMap r22 genetic map). Germline identifies short regions of exact matches between haplotypes using a library of short seeds, then extends and merges those regions using an efficient hashing and matching algorithm. ERSA was applied to the output of Germline. The program fastIBD in Beagle version 3.3 (http://faculty.washington.edu/browning/beagle/beagle.html) was also used to generate IBD segments for analysis by ERSA (default options). Although Principal Component Analysis (Fig. 2A) can distinguish the closely related HapMap CEU and TSI sample sets, the pedigree and HapMap CEU samples are indistinguishable.

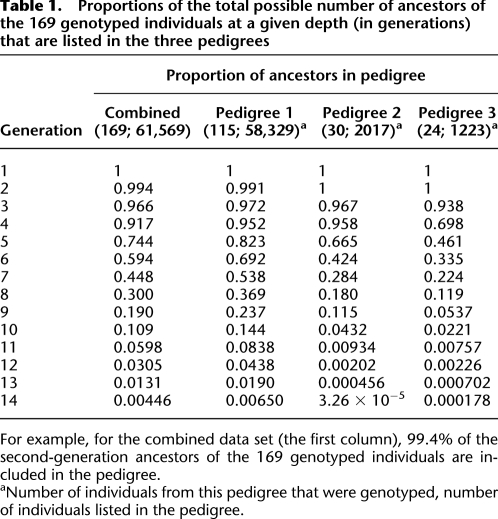
Table 1.

Proportions of the total possible number of ancestors of the 169 genotyped individuals at a given depth (in generations) that are listed in the three pedigrees

graphic file with name 768tbl1.jpg

Open in a new tab

For example, for the combined data set (the first column), 99.4% of the second-generation ancestors of the 169 genotyped individuals are included in the pedigree.

aNumber of individuals from this pedigree that were genotyped, number of individuals listed in the pedigree.

Results

We evaluated the performance of ERSA by analyzing high-density SNP microarray data on three deep, well-defined pedigrees composed of 24, 30, and 115 individuals (Table 1). The output from this analysis was a maximum-likelihood estimate and confidence interval (C.I.) for the degree of relationship of each pair of individuals in the sample. The computation time taken by ERSA to analyze all 14,196 pairs of individuals in this sample was ∼9 min running on one core of a 2.3-GHz AMD Opteron processor. In Figure 3, we present results for all 2802 known pairs of first- through fourteenth-degree relatives with exactly two known common ancestors in the pedigree and for which the two inheritance paths between the individuals have the same length (e.g., full siblings, full cousins). Results for relatives with exactly one common ancestor (e.g., half cousins) were qualitatively similar (see the Supplemental material).

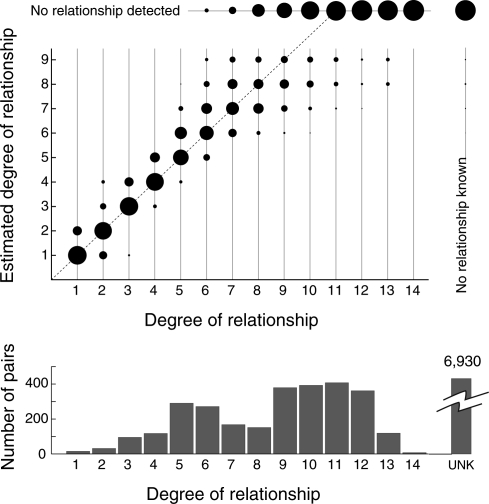
Figure 3.

Figure 3.

Open in a new tab

Estimated degree of relationship between pairs of individuals versus known degree of relationship. Pedigree information was used to identify 2802 pairs of genotyped individuals that share exactly two common ancestors (a mated pair) and classify them according to the degree of their relationship (horizontal axis). The number of pairs in each category is indicated by the histogram below. Within each category, the areas of the filled circles indicate the proportion of those pairs with various estimated degrees of relationship between a pair (vertical axis; two ancestors, two degrees of freedom, α = 0.001). The total area within a category is a constant across categories. Pairs with a known but undetected relationship are represented across the top. Pairs with no known relationship are represented on the right.

For pairs of individuals as distantly related as eighth-degree relatives, ERSA's estimates are generally accurate to within one degree of the known relationship. ERSA predicted the exact degree of relationship for 66% of the 549 pairs of first-degree through fifth-degree relatives and was accurate to within one degree of relationship for 97% of those pairs (Fig. 3; Supplemental Table S1). Point estimates were accurate to within one degree of relationship for >80% of sixth-degree and seventh-degree relatives, and 60% of eighth-degree relatives (Fig. 3), but accuracy drops off rapidly beyond this point (Fig. 3).

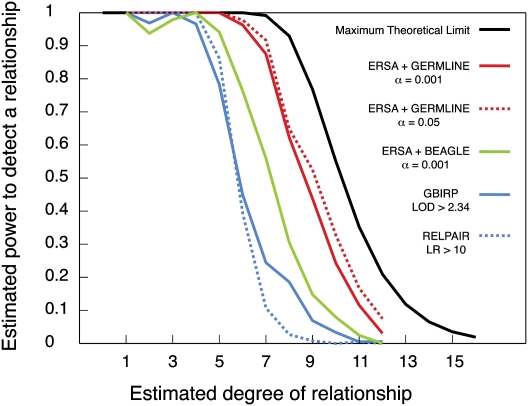
ERSA has nearly 100% power to detect first-degree through fifth-degree relatives and substantial power to detect ancestry as distant as eleventh-degree relatives. We detected a significant relationship among all 549 pairs of first-degree through fifth-degree relatives in our sample (α = 0.001, where the null hypothesis is no relationship) (Fig. 4). Although the power to detect more distant ancestry is constrained by the fact that distant relatives often share no genetic material (Donnelly 1983), ERSA retains relatively high power for these relationships. We detected 88% of seventh-degree relatives, 44% of ninth-degree relatives, and 12% of eleventh-degree relatives at a significance level of 0.001 (red line in Fig. 4), which closely approaches the maximum theoretical power (black line in Fig. 4).

Figure 4.

Figure 4.

Open in a new tab

Power to detect recent common ancestry between pairs of individuals known to be related at varying degrees. Each pair of individuals has exactly two known ancestors in the pedigree, and both inheritance paths connecting the pair (one through each ancestor) have the same number of meioses in them. (Black) Maximum theoretical power (the probability that a pair of individuals with the given relationship is genetically related at all, calculated from Eq. 7 with a = 2 and t = 0). The power of ERSA using IBD segments estimated by Germline, with α = 0.05 (red dotted line) and α = 0.001 (red solid line) (two degrees of freedom, d.f.). (Green line) Using IBD segments estimated by fastIBD of the Beagle 3.3 package, ERSA achieves the power shown (α = 0.001, 2 d.f.). (Blue dotted line) The power of RELPAIR (Epstein et al. 2000) to detect a relationship (using 9990 evenly spaced autosomal markers with minor allele frequency MAF > 0.4, default likelihood ratio LR threshold of 10 for reporting a relationship as significant). (Blue solid line) The power of GBIRP (Stankovich et al. 2005) (10,028 evenly spaced autosomal markers with MAF > 0.4, LOD threshold of 2.34 for significance as in Stankovich et al. 2005, corresponding to α = 0.001 with 1 d.f.).

For comparison, we analyzed the same relationships by applying RELPAIR (Epstein et al. 2000) and GBIRP (Stankovich et al. 2005) to subsets of our SNP loci (see Fig. 4; Supplemental material). Both methods had high power to detect third-degree and fourth-degree relatives (dotted and solid blue lines in Fig. 4), although RELPAIR reports all relationships beyond second degree as simply “cousins” (i.e., more distant than second degree). The power of RELPAIR and GBIRP drops off rapidly beyond fourth-degree relationships, approximately three degrees before ERSA's power begins to decline (Fig. 4).

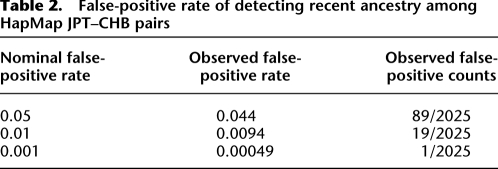
As shown in Table 2, ERSA's probability of detecting a significant relationship between unrelated individuals (the empirical false-positive rate) is approximately equal to the nominal significance level (α). To estimate the empirical false-positive rate, we needed high-density SNP data on a set of individuals with no recent shared ancestry. Given the sensitivity of ERSA to distant relationships, acquiring an appropriate data set from pedigree data would require complete ancestry information for each individual in the sample extending back at least seven generations. Because such pedigrees are extremely rare, we estimated our false-positive rate from two closely related populations, the CHB (45 Han Chinese in Beijing) and JPT (45 Japanese in Tokyo) samples, using the HapMap phase 2 SNP genotype data (International HapMap Consortium 2005). Because these populations can be distinguished genetically (International HapMap Consortium 2005), estimating the false-positive rate from the CHB–JPT comparison is not ideal. However, the allele frequency and haplotype distributions of these populations are very similar (International HapMap Consortium 2005), and pairs of CHB and JPT individuals are unlikely to have shared an ancestor in the past 200 years. Therefore, we estimated false-positive rates from the proportions of CHB–JPT pairs in which significant recent ancestry was detected. The estimated false-positive rates closely matched the nominal rates (Table 2). For the significance level of α = 0.001 used in Figures 3 and 4, our estimated false-positive rate was 0.0005 (95% C.I. = 1.3 × 10−5 to 0.0028).

Table 2.

False-positive rate of detecting recent ancestry among HapMap JPT–CHB pairs

graphic file with name 768tbl2.jpg

Open in a new tab

ERSA can also accurately detect relationships between individuals who share a disease-causing mutation transmitted from a common founder. The process of ascertaining individuals based on a shared mutation introduces biases in the estimation of recent ancestry, but this bias can be taken into account (see Methods). Our test case was composed of seven previously described individuals who are affected with attenuated familial adenomatous polyposis (AFAP) due to a single disease-causing mutation (c.426_427delAT in the APC gene) (Neklason et al. 2008). The available pedigree information identified four pairs of these individuals as sixth-degree relatives and one pair as eighth-degree relatives. The point estimates from ERSA were accurate to within one degree of relationship for all five of these pairs.

Discussion

The number, lengths, and locations of chromosomal segments that are shared IBD by a pair of individuals constitute essentially all of the genetic information that bears on their recent shared genetic ancestry. Figure 1 illustrates the process that generates IBD segments and shows how the expected distributions of segment number and length depend on the relationship between two individuals.

Some methods of detecting relatedness (e.g., the method implemented in PLINK) (Purcell et al. 2007) rely on genome-wide averages of genetic identity coefficient estimates. These statistics incompletely summarize the information contained in the IBD segment data: Genetic identity coefficients can be calculated from IBD segment data, but the reverse is not true. To illustrate the importance of this difference, consider the typical amount of genetic sharing between a pair of fourth cousins. The probability that fourth cousins share at least one IBD segment is 77%, and the expected length of this segment is 10 cM (Donnelly 1983). Because a 10-cM segment represents <0.3% of the genome, this excess of IBD has very little effect on estimates of relatedness averaged over the genome. However, because unrelated individuals are unlikely to share a 10-cM segment in most populations, ERSA is capable of detecting many fourth cousin relationships (Fig. 4). For relationships as distant as third cousins, there are typically enough IBD segments throughout the genome to allow strong inferences (Fig. 3).

Another family of methods for detecting relationships models the IBD states between haplotypes as a Markov process along a chromosome, with different transition probability matrices corresponding to different hypothesized relationships. The likelihoods of various relationship models are then estimated from the data. Examples of these methods include RELPAIR (Boehnke and Cox 1997; Epstein et al. 2000), PREST (which extended the methods in Boehnke and Cox 1997; McPeek and Sun 2000; Sun et al. 2002), and GBIRP (which extended PREST to the problem of general relationship estimation) (Stankovich et al. 2005). These tools were initially designed for use with hundreds of microsatellite loci spaced at intervals of several centimorgans, but they have also been applied to high-density SNP data (e.g., Berkovic et al. 2008; Pemberton et al. 2010). However, they do not model the patterns of linkage disequilibrium (LD) that exist between very closely spaced SNP markers and instead assume that markers are not in strong LD. High-density SNP data sets must be thinned to approximately 10,000 markers before they can be used (see, e.g., Berkovic et al. 2008; Pemberton et al. 2010). The key information used by such Markov-process methods is the match between the hypothesized transition probability matrix and the pattern of IBD state transitions induced by the genotype data.

In contrast, ERSA uses explicit IBD segment information to estimate the relationships between pairs of individuals in a maximum-likelihood framework. This makes better use of the information present in high-density SNP genotyping data, as shown by the power curves in Figure 4. Our power to detect relationships between second cousins or closer relatives is essentially perfect and exceeds 85% for third cousins even at the α = 0.001 level. ERSA is also more accurate than RELPAIR or GBIRP (Supplemental Fig. S2; Supplemental Table 1.) Beyond third cousins, genetic methods inherently become more limited by the fact that two individuals with a common genealogical ancestor frequently do not share any genetic material inherited from that ancestor: Such genealogical links cannot be directly detected by genetic methods. This limitation is illustrated in Figure 4, which demonstrates that ERSA's power decreases in lock step with the maximum theoretical power as the degree of relationship increases.

Because denser and more accurate genetic data will improve the ability to detect and delineate IBD segments, we expect the accuracy of IBD segment inference to improve as whole-genome sequencing becomes more affordable and as higher-density microarrays become available. In addition, while the IBD segment detection methods we used here (Germline; Gusev et al. 2009; fastIBD in Beagle 3.3) perform well, we expect further improvements as phasing and imputation methods advance (e.g., Genovese et al. 2010).

ERSA detects recent shared ancestry by identifying an excess of IBD segment sharing relative to the population background. Therefore, the power to detect shared ancestry between individuals depends on the demographic history of the population to which those individuals belong. If the population size is small, or if the population has experienced a founder effect or recent bottleneck, then the level of IBD segment sharing among unrelated individuals will increase. In such populations, ERSA's power to detect distant relationships will be diminished. The pedigree samples analyzed here are from a homogeneous population, and population admixture may affect ERSA's performance. However, there is reason to believe that ERSA will retain its high detection power in admixed populations (see the Supplemental material).

ERSA will be immediately applicable to a number of problems. It can be used to identify cryptic relatedness between individuals with the same rare genetic disorder. In analyzing large pedigrees, ERSA can verify distant relationships without genotyping of intervening family members. This can sharply reduce sample collection and genotyping requirements.

In the forensic field, the most common DNA-based method for identifying the remains of missing persons is based on comparisons of kinship statistics computed from a modest number (13–17) of STR loci, with useful comparisons generally limited to second-degree relationships (Alonso et al. 2005) (e.g., MDKAP [Leclair et al. 2007]; M-FISys [Budimlija et al. 2003; Cash et al. 2003]). The International Commission on Missing Persons (ICMP, http://www.ic-mp.org) has generated matches for more than 18,000 persons missing from armed conflicts or mass disasters at a significance level exceeding 99.95% (TJ Parsons, ICMP, pers. comm.). However, this level of certainty requires typing multiple first-degree or second-degree relatives. Such close relatives are often unavailable, due either to disasters and conflicts that disperse entire families or to the passage of time (Leclair 2004; Brenner 2006). For example, DNA profiles exist for more than 2000 individuals killed in the armed conflict in Bosnia for which identifications cannot be made due to insufficient family reference samples (TJ Parsons, ICMP, pers. comm.) ERSA would allow the use of a much larger pool of distant relatives (Bieber et al. 2006) and would also enable definitive conclusions to be drawn based on single closer relatives. For the first time, with ERSA, even a single individual searching for a family member would be able to provide a definitive reference.

The methods described here are computationally efficient, make near-optimal use of the genetic signal of relatedness between individuals, achieve a statistical power very close to the theoretical maximum, and have multiple applications. These methods are implemented in the software program ERSA, which is freely available for academic use at http://jorde-lab.genetics.utah.edu/ersa.

Acknowledgments

We thank the reviewers, whose thorough and insightful comments substantially improved this work. This research was supported by grants from the National Institutes of Health (GM-59290 to L.B.J.) and the Sorenson Molecular Genealogy Foundation. C.D.H. is supported by the University of Luxembourg – Institute for Systems Biology Program. C.D.H. and S.L.G. are supported by the Primary Children's Medical Center Foundation National Institute of Diabetes and Digestive and Kidney Diseases (DK069513). J.X. is supported by the National Human Genome Research Institute, National Institutes of Health (K99HG005846). Additional partial support was provided by P01-CA073992 (to R.W.B., PI), R01-CA040641 (to R.W.B., PI), and by the Huntsman Cancer Foundation. Collection of the AFAP pedigree was supported in part by the Utah Population Database and the Utah Cancer Registry. Partial support for all data in the Utah Population Database was provided by the University of Utah and Huntsman Cancer Institute. The Utah Cancer Registry is funded by contract N01-PC-35141 from the NCI SEER program with additional support from the Utah State Department of Health and the University of Utah.

Footnotes

[Supplemental material is available for this article. The software program ERSA is freely available for academic use at http://jorde-lab.genetics.utah.edu/ersa.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.115972.110.

References

  1. Alonso A, Martin P, Albarran C, Garcia P, Fernandez de Simon L, Jesus Iturralde M, Fernandez-Rodriguez A, Atienza I, Capilla J, Garcia-Hirschfeld J, et al. 2005. Challenges of DNA profiling in mass disaster investigations. Croat Med J 46: 540–548 [PubMed] [Google Scholar]
  2. Berkovic SF, Dibbens LM, Oshlack A, Silver JD, Katerelos M, Vears DF, Lullmann-Rauch R, Blanz J, Zhang KW, Stankovich J, et al. 2008. Array-based gene discovery with three unrelated subjects shows SCARB2/LIMP-2 deficiency causes myoclonus epilepsy and glomerulosclerosis. Am J Hum Genet 82: 673–684 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bieber FR, Brenner CH, Lazer D 2006. Finding criminals through DNA of their relatives. Science 312: 1315–1316 [DOI] [PubMed] [Google Scholar]
  4. Biesecker LG, Bailey-Wilson JE, Ballantyne J, Baum H, Bieber FR, Brenner C, Budowle B, Butler JM, Carmody G, Conneally PM, et al. 2005. Epidemiology. DNA identifications after the 9/11 World Trade Center attack. Science 310: 1122–1123 [DOI] [PubMed] [Google Scholar]
  5. Boehnke M, Cox NJ 1997. Accurate inference of relationships in sib-pair linkage studies. Am J Hum Genet 61: 423–429 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brenner CH 2006. Some mathematical problems in the DNA identification of victims in the 2004 tsunami and similar mass fatalities. Forensic Sci Int 157: 172–180 [DOI] [PubMed] [Google Scholar]
  7. Browning SR, Browning BL 2010. High-resolution detection of identity by descent in unrelated individuals. Am J Hum Genet 86: 526–539 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Budimlija ZM, Prinz MK, Zelson-Mundorff A, Wiersema J, Bartelink E, MacKinnon G, Nazzaruolo BL, Estacio SM, Hennessey MJ, Shaler RC 2003. World Trade Center human identification project: Experiences with individual body identification cases. Croat Med J 44: 259–263 [PubMed] [Google Scholar]
  9. Cash HD, Hoyle JW, Sutton AJ 2003. Development under extreme conditions: Forensic bioinformatics in the wake of the World Trade Center disaster. Pac Symp Biocomput 2003: 638–653 [PubMed] [Google Scholar]
  10. Cherny SS, Abecasis GR, Cookson WO, Sham PC, Cardon LR 2001. The effect of genotype and pedigree error on linkage analysis: Analysis of three asthma genome scans. Genet Epidemiol (Suppl 1) 21: S117–S122 [DOI] [PubMed] [Google Scholar]
  11. DeWoody JA 2005. Molecular approaches to the study of parentage, relatedness, and fitness: Practical applications for wild animals. J Wildl Manage 69: 1400–1418 [Google Scholar]
  12. Donnelly KP 1983. The probability that related individuals share some section of genome identical by descent. Theor Popul Biol 23: 34–63 [DOI] [PubMed] [Google Scholar]
  13. Epstein MP, Duren WL, Boehnke M 2000. Improved inference of relationship for pairs of individuals. Am J Hum Genet 67: 1219–1231 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Genovese G, Leibon G, Pollak M, Rockmore D 2010. Improved IBD detection using incomplete haplotype information. BMC Genet 11: 58 doi: 10.1186/1471-2156-11-58 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gusev A, Lowe JK, Stoffel M, Daly MJ, Altshuler D, Breslow JL, Friedman JM, Pe'er I 2009. Whole population, genome-wide mapping of hidden relatedness. Genome Res 19: 318–326 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. International HapMap Consortium 2005. A haplotype map of the human genome. Nature 437: 1299–1320 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Leclair B 2004. Large-scale comparative genotyping and kinship analysis: Evolution in its use for human identification in mass fatality incidents and missing persons databasing. Prog Forensic Genet 10: 42–44 [Google Scholar]
  18. Leclair B, Shaler R, Carmody GR, Eliason K, Hendrickson BC, Judkins T, Norton MJ, Sears C, Scholl T 2007. Bioinformatics and human identification in mass fatality incidents: The World Trade Center disaster. J Forensic Sci 52: 806–819 [DOI] [PubMed] [Google Scholar]
  19. McPeek MS, Sun L 2000. Statistical tests for detection of misspecified relationships by use of genome-screen data. Am J Hum Genet 66: 1076–1094 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. McVean GAT, Myers SR, Hunt S, Deloukas P, Bentley DR, Donnelly P 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584 [DOI] [PubMed] [Google Scholar]
  21. Neklason DW, Stevens J, Boucher KM, Kerber RA, Matsunami N, Barlow J, Mineau G, Leppert MF, Burt RW 2008. American founder mutation for attenuated familial adenomatous polyposis. Clin Gastroenterol Hepatol 6: 46–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pemberton TJ, Wang C, Li JZ, Rosenberg NA 2010. Inference of unexpected genetic relatedness among individuals in HapMap Phase III. Am J Hum Genet 87: 457–464 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, et al. 2007. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81: 559–575 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Simonson TS, Yang Y, Huff CD, Yun H, Qin G, Witherspoon DJ, Bai Z, Lorenzo FR, Xing J, Jorde LB, et al. 2010. Genetic evidence for high-altitude adaptation in Tibet. Science 329: 72–75 [DOI] [PubMed] [Google Scholar]
  25. Slate J, Santure AW, Feulner PGD, Brown EA, Ball AD, Johnston SE, Gratten J 2010. Genome mapping in intensively studied wild vertebrate populations. Trends Genet 26: 275–284 [DOI] [PubMed] [Google Scholar]
  26. Stankovich J, Bahlo M, Rubio JP, Wilkinson CR, Thomson R, Banks A, Ring M, Foote SJ, Speed TP 2005. Identifying nineteenth century genealogical links from genotypes. Hum Genet 117: 188–199 [DOI] [PubMed] [Google Scholar]
  27. Sun L, Wilder K, McPeek MS 2002. Enhanced pedigree error detection. Hum Hered 54: 99–110 [DOI] [PubMed] [Google Scholar]
  28. Thomas A, Skolnick MH, Lewis CM 1994. Genomic mismatch scanning in pedigrees. Math Med Biol 11: 1–16 [DOI] [PubMed] [Google Scholar]
  29. Thomas A, Camp NJ, Farnham JM, Allen-Brady K, Cannon-Albright LA 2008. Shared genomic segment analysis. Mapping disease predisposition genes in extended pedigrees using SNP genotype assays. Ann Hum Genet 72: 279–287 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Voight BF, Pritchard JK 2005. Confounding from cryptic relatedness in case-control association studies. PLoS Genet 1: e32 doi: 10.1371/journal.pgen.0010032 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Weir BS, Anderson AD, Hepler AB 2006. Genetic relatedness analysis: Modern data and new challenges. Nat Rev Genet 7: 771–780 [DOI] [PubMed] [Google Scholar]
  32. Xing J, Watkins WS, Shlien A, Walker E, Huff CD, Witherspoon DJ, Zhang Y, Simonson TS, Weiss RB, Schiffman JD, et al. 2010. Toward a more uniform sampling of human genetic diversity: A survey of worldwide populations by high-density genotyping. Genomics 96: 199–210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zupanic Pajnic I, Gornjak Pogorelc B, Balazic J 2010. Molecular genetic identification of skeletal remains from the Second World War Konfin I mass grave in Slovenia. Int J Legal Med 124: 307–317 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES