Skip to main content
PMC home page
Journal of Synchrotron Radiation logoLink to Journal of Synchrotron Radiation
. 2011 Mar 15;18(Pt 3):338–345. doi: 10.1107/S0909049511005504

Energy dependence of site-specific radiation damage in protein crystals

Christina Homer a, Laura Cooper a, Ana Gonzalez a,*
PMCID: PMC3083911  PMID: 21525641

The energy dependence of specific radiation damage to sulfur sites in tetragonal HEWL lysozyme is studied.

Keywords: specific radiation damage, disulphide bridges, methionine sulphur, cystein suphur, X-ray energy

Abstract

It is important to consider radiation damage to crystals caused by data collection when solving structures and critical when determining protein function, which can often depend on very subtle structural characteristics. In this study the rate of damage to specific sites in protein crystals cooled at 100 K is found to depend on the energy of the incident X-ray beam. Several lysozyme crystals were each subjected to 3–26 MGy of cumulative X-ray exposure by collecting multiple data sets from each crystal at either 9 keV or 14 keV. The integrated electron density surrounding each S atom in the structure was calculated for each data set and the change in electron density was evaluated as a function of dose at the two energies. The rate of electron density decrease per cubic Å per MGy was determined to be greater at 14 keV than at 9 keV for cysteine sulfurs involved in disulphide bridges; no statistically significant differences in the decay rates were found for methionine sulfurs. These preliminary results imply that it might be possible to minimize certain types of specific radiation damage by an appropriate choice of energy. Further experiments studying a variety of photolabile sites over a wider range of energies are needed to confirm this conclusion.

1. Introduction  

X-ray diffraction is a powerful tool for structural biology studies; the determination of the precise location of atoms in a protein is extremely important for functional studies but the structural information obtained can be compromised as a consequence of radiation damage.

Photoabsorption is the main contributor to radiation damage at the energies commonly used for macromolecular diffraction experiments. For very small crystals it has been suggested that the photoelectron could escape, causing less damage than if all the energy was deposited in the crystal (Nave & Hill, 2005 ▶; Cowan & Nave, 2008 ▶); however, in larger samples the photoelectron scatters inelastically off surrounding atoms, creating several hundred secondary electrons and positively charged centers (O’Neill et al., 2002 ▶). These secondary electrons are mobile, even at 100 K (Jones et al., 1987 ▶), and are directed preferentially to sites of high electron affinity. These electrons add specifically to electron-deficient functional groups throughout the protein and cause secondary damage such as breakage of disulphide bridges, reduction of metal centers, recarbonization and bond cleavage of heavy atoms. These phenomena are all frequently described in radiation damage studies (for example, Burmeister, 2000 ▶; Ravelli & McSweeney, 2000 ▶; Weik et al., 2000 ▶; Berglund et al., 2002 ▶; Carugo & Carugo, 2005 ▶; Fioravanti et al., 2007 ▶; Corbett et al., 2007 ▶; Yano et al., 2005 ▶) and collectively named ‘specific radiation damage’, as opposed to ‘global damage’ which is commonly used to refer to radiation-induced changes on a global scale [e.g. loss of resolution, changes in the unit cell and mosaicity (Murray & Garman, 2002 ▶; Ravelli et al., 2002 ▶)].

It has been experimentally determined that, at 100 K, protein crystals can absorb up to a dose of 43 MGy before losing half of their diffraction power (Owen et al., 2006 ▶). This relatively high tolerance to radiation at cryo-temperatures means that, for a reasonably large number of samples, it is possible to collect enough data to determine the structure using only one or very few crystals. Unfortunately the effects of photoreduction often take place much earlier than detectable damage at the global level and, if one does not take these changes into account, it can lead to an erroneous interpretation of the structure (Weik et al., 2000 ▶; Berglund et al., 2002 ▶; Yano et al., 2005 ▶). This makes it important to determine ways to slow down the damage during the data collections. Some potentially useful ways to do this include the use of scavengers (Murray & Garman, 2002 ▶; Kauffmann et al., 2006 ▶; Macedo et al., 2009 ▶) or data collection at lower temperatures (Corbett et al., 2007 ▶; Meents et al., 2010 ▶).

Another potential avenue for reducing X-ray damage involves exploring the effects of data collection at different energies. The possible X-ray energy dependence of radiation damage has already been investigated based on theoretical and experimental approaches (Arndt, 1984 ▶; Gonzalez et al., 1994 ▶; Polikarpov, 1997 ▶; Polikarpov et al., 1997 ▶; Teplyakov et al., 1998 ▶; Mueller-Dieckmann et al., 2005 ▶; Weiss et al., 2005 ▶; Shimizu, 2007 ▶). Experimental studies have shown no significant dependence in global radiation damage rates on X-ray energy. This is consistent with radiation damage being proportional to the energy deposited on the crystal per diffracted photon, as first suggested by Arndt (1984 ▶).

Most experimental studies on the energy dependence of the rate of radiation damage have focused on using global metrics to quantify the effects of the damage. This requires a careful calibration of the detector response as a function of X-ray energy that has not, to date, been carried out in these types of experiments. An alternative method to quantify radiation damage consists of concentrating on the specific structural effects radiation damage has on the electron density of the sample. This method is perhaps less experimentally demanding, requiring only a careful calculation of the dose deposited on the sample at each energy. Weiss et al. (2005 ▶) have already used this approach when comparing the effects of radiation damage on cadmium metals sites at 6.2 and 12.4 keV. In that experiment, although relative peak height decreased slightly more slowly for 2F o − F c and F o − F c difference maps calculated at the lower energy, an opposite trend was observed for the anomalous difference maps, which led to the conclusion that there was no clear discernible difference in damage rate at the two energies. A rate of decay per unit of dose was not available in the Weiss et al. study.

The present study examines specific damage to S—S bonds and S—C bonds in tetragonal hen egg-white lysozyme (HEWL). HEWL contains four disulphide bridges, which have been shown to break when exposed to radiation in the tetragonal crystal form (Weik et al., 2000 ▶; Murray & Garman, 2002 ▶; Borek et al., 2007 ▶), and two methionines. We attempt to ascertain whether the rate of this breakage is energy-dependent, beyond the factors already considered in dose calculations, at 9 and 14 keV. These energies were chosen because they are within reach of most tunable macromolecular crystallography beamlines and are at the limits of energies most commonly considered for data collection when the choice of energy is somewhat open (e.g. for phasing via an existing model or when selecting the remote energy for MAD experiments). The question is addressed by analyzing the rate of decrease of electron density around S atoms of cysteine and methionine residues as a function of the dose absorbed by the sample, as described below.

2. Methods  

Four pairs of lysozyme crystals were used for the experiment. Four of the lysozyme crystals (the A and B pairs) were grown in 1.5 mM sodium acetate buffer and 1.3 M NaCl (pair A) and 0.9 M NaCl (pair B); the C and D pairs were grown in 50 mM sodium acetate buffer, 1 M NaCl and 25% (v/v) ethylene glycol. All the crystals belonged to the space group P43212, with unit-cell dimensions a = b = 78.5 and c = 37.4 Å (the unit-cell dimensions varied very slightly between crystals). For each crystal, data were collected at either 9 keV (crystals A-9, B-9, C-9, D-9) or 14 keV (crystals A-14, B-14, C-14, D-14). For each pair of crystals (A, B, C and D), collection at the two energies was carried out back-to-back at SSRL macromolecular crystallography beamlines (Soltis et al., 2008 ▶) on the same day and on the same beamline. The data collection for the crystal pairs A and B was carried out on beamline BL9-2. Data from pairs C and D were collected on beamline BL12-2. All crystals were mounted in nylon loops and cryo-protected in paratone oil; care was taken to flip the crystals in the oil to completely remove the mother liquor around them prior to cooling in liquid nitrogen. The crystals were kept in a cold nitrogen stream at 100 K during data collection.

The flux at the beamlines was calibrated prior to data collection with a Hamamatsu photodiode, using the model described by Owen et al. (2009 ▶). To ensure that the dose calculations were as accurate as possible, care was taken to choose crystals smaller than or the same size as the beam for the experiment (see Table 1 ▶). The crystal size was estimated visually, or, in the cases where the edges of the crystal were not visible, by using the diffraction-based crystal centering method developed at SSRL (Song et al., 2007 ▶). This method uses an extremely attenuated beam to center the crystal and therefore does not contribute significantly to the dose received by the crystal (no more than the equivalent of collecting two diffraction images at full beam strength).

Table 1. Data collection parameters per data set.

The exposure time given is for the first image in the data series.

Crystal Exposure per image (s) Beam attenuation (%) Beam size (horizontal, vertical) (mm) Largest crystal dimension (mm) Oscillation per image () Number of images per data set Dose rate (kGy s1) Dose per data set (MGy)
A-9 2.0 0 0.17, 0.17 0.15 1.0 360 6.3 4.45
A-14 2.0 0 0.17, 0.17 0.12 1.0 360 2.8 2.04
B-9 2.5 61.7 0.2, 0.2 0.14 1.0 360 5.2 4.72
B-14 7.2 54.9 0.2, 0.2 0.11 1.0 360 2.4 6.16
C-9 0.5 71.0 0.2, 0.2 0.11 0.85 106 51.7 3.23
C-14 1.0 75.7 0.2, 0.2 0.12 0.95 380 8.6 3.26
D-9 0.5 67.1 0.2, 0.2 0.10 0.75 120 52.9 3.11
D-14 1.5 44.8 0.2, 0.2 0.12 0.85 106 12.5 1.99
Open in a new tab

Several data sets were collected consecutively from each crystal, taking care that the same crystal zone was irradiated on all of the data sets; the data were collected back-to-back at each energy, to ensure that day-to-day changes in the beam characteristics did not affect the comparison. The exposure time was adjusted for each image to ensure that the total number of photons through the sample per image remained constant, based on the readings on an ion chamber in the beam collimation system. The dose was calculated using the program RADDOSE, version 2 (Paithankar et al., 2009 ▶; Murray et al., 2004 ▶). The data collection strategy was calculated with the program Web-Ice (González et al., 2008 ▶), using the program BEST (Popov & Bourenkov, 2003 ▶) for determination of the exposure time required to measure data to a similar resolution for the two paired crystals. However, the time finally used for data collection was also adjusted to make the total dose per data set more comparable. For the crystals collected on BL12-2, fewer images per data set were collected to compensate for the higher intensity of this beamline, except for crystal C-14, which diffracted very well; for this crystal the number of images was increased to make the dose per data set similar to that of crystal C-9. The data collection parameters are summarized in Table 1 ▶.

The data were processed with MOSFLM [Collaborative Computational Project, Number 4, 1994 ▶ (hereafter CCP4); Leslie, 1992 ▶] and SCALA (CCP4, 1994 ▶; Evans, 2006 ▶). Data sets A-9 and A-14 contained some reflections with overloaded pixels (less than 0.05% of the total number of observations), which were removed before scaling. All the data sets for each crystal were processed to the same resolution, although the diffraction limit of the crystal decreased during the course of the experiment. Structure-factor amplitudes were calculated with TRUNCATE (CCP4). Data statistics for all the data sets are shown in Table 2 ▶. The Protein Data Bank (PDB) entry 1W6Z (HEWL) was used as the refinement model; the coordinates were refined using REFMAC5 (Murshudov et al., 1997 ▶). The starting model was refined against each data set independently, in order to ensure that the phases corresponded to a model with the appropriate level of radiation damage. The refinement protocol consisted of ten cycles of rigid-body refinement followed by ten cycles of restrained refinement.

Table 2. Data processing statistics for all the data series used. R meas and R pim are calculated as proposed by Diederichs Karplus (1997 ▶) and Weiss (2001 ▶), respectively. R merge and Mean[I/(I)] are defined by Evans (2006 ▶). The values in parentheses refer to the highest-resolution shell. The R-factor for amplitudes with respect to the first data set was calculated with the program SCALEIT (CCP4, 1994 ▶). The temperature factor is estimated from the Wilson plot. The dose refers to the total accumulated dose at the end of the data set.

(a).

Statistics for the data sets collected from crystals A-9 and A-14 for data between 29 and 1.76 resolution.

E = 9.0keV
R merge 0.07 (0.21) 0.07 (0.26) 0.07 (0.37) 0.07 (0.57) 0.06 (0.94)
R meas 0.07 (0.21) 0.07 (0.27) 0.07 (0.38) 0.07 (0.58) 0.07 (0.96)
R pim 0.01 (0.04) 0.01 (0.05) 0.01 (0.07) 0.01 (0.11) 0.01 (0.19)
Total number of observations 322679 (23235) 322876 (23177) 323451 (23304) 324017 (23281) 324428 (23382)
Total number unique 11985 (870) 11999 (870) 12020 (876) 12030 (873) 12048 (877)
Mean[(I)/(I)] 37.9 (15.0) 37.3 (12.2) 34.8 (9.2) 33.1 (6.3) 30.6 (3.8)
Completeness 99.9 (100) 99.9 (100) 99.9 (100) 99.9 (100) 100 (100)
Multiplicity 26.9 (26.7) 26.9 (26.6) 26.9 (26.6) 26.9 (26.7) 26.9 (26.7)
R-factor against first data set   0.06 0.11 0.15 0.20
B (2) 20.2 22.9 25.4 28.8 32.4
Dose (MGy) 4.54 9.08 13.62 18.16 22.7
Open in a new tab
E = 14.0keV
R merge 0.13 (0.21) 0.13 (0.25) 0.13 (0.28) 0.14 (0.32) 0.13 (0.36)
R meas 0.12 (0.21) 0.13 (0.25) 0.13 (0.29) 0.14 (0.32) 0.13 (0.36)
R pim 0.02 (0.04) 0.03 (0.05) 0.02 (0.05) 0.03 (0.06) 0.03 (0.07)
Total number of observations 326886 (24790) 324827 (24427) 329247 (24735) 305268 (23125) 327206 (24915)
Total number unique 12044 (876) 12026 (872) 12155 (876) 12074 (873) 12208 (884)
Mean[(I)/(I)] 22.9 (12.5) 21.4 (11.6) 20.7 (10.3) 18.1 (8.5) 25 (6.3)
Completeness 99.9 (100) 99.9 (100) 99.9 (100) 99.9 (100) 100 (100)
Multiplicity 27.1 (28.3) 27.0 (28.0) 27.1 (28.2) 25.3 (26.5) 26.8 (28.2)
R-factor against first data set   0.05 0.08 0.11 0.14
B (2) 16.2 17.4 18.9 19.7 21.5
Dose (MGy) 2.04 4.08 6.12 8.16 10.2
Open in a new tab

(b).

Statistics for the data sets collected from crystals B-9 and B-14 for data between 40 and 2.0 resolution.

E = 9.0keV          
R merge 0.11 (0.30) 0.12 (0.39) 0.13 (0.60) 0.15 (1.16) 0.16 (2.07)
R meas 0.12 (0.31) 0.12 (0.39) 0.13 (0.61) 0.15 (1.12) 0.16 (2.11)
R pim 0.02 (0.06) 0.02 (0.07) 0.03 (0.12) 0.03 (0.23) 0.03 (0.40)
Total number of observations 225654 (16398) 226181 (16498) 224543 (16295) 222813 (16111) 219944 (16133)
Total number unique 8332 (606) 8370 (602) 8377 (599) 8383 (601) 8406 (604)
Mean[(I)/(I)] 28 (13.6) 27.5 (10.3) 25.6 (6.1) 24.5 (3.2) 23.2 (1.8)
Completeness 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Multiplicity 27.1 (27.1) 27 (27.4) 26.8 (27.2) 26.6 (26.8) 26.2 (26.7)
R-factor against first data set   0.08 0.15 0.21 0.27
B (2) 18.1 21 26.2 33.3 39
Dose (MGy) 4.72 9.44 14.16 18.88 23.6
Open in a new tab
E = 14.0keV
R merge 0.07 (0.12) 0.07 (0.18) 0.08 (0.39) 0.1 (0.93) 0.13 (2.49) 0.19 (6.01)
R meas 0.07 (0.12) 0.07 (0.18) 0.09 (0.40) 0.1 (0.95) 0.13 (2.53) 0.19 (6.12)
R pim 0.01 (0.02) 0.01 (0.03) 0.02 (0.07) 0.02 (0.18) 0.03 (0.47) 0.04 (1.13)
Total number of observations 234900 (17675) 236119 (17402) 236652 (17345) 236375 (17170) 236778 (17486) 235945 (17419)
Total number unique 8360 (613) 8394 (603) 8423 (601) 8445 (595) 8470 (604) 8486 (603)
Mean[(I)/(I)] 45.2 (28.6) 42.9 (19.9) 35.1 (10.1) 28.8 (4.0) 24.0 (1.5) 18.8 (0.5)
Completeness 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Multiplicity 28.1 (28.8) 28.1 (28.9) 28.1 (28.9) 28.0 (28.9) 28.0 (29.0) 27.8 (28.9)
R-factor against first data set   0.10 0.18 0.24 0.29 0.34
B (2) 14.8 18.6 24 31.8 40.7 47.4
Dose (MGy) 6.16 12.32 18.48 24.64 30.8 36.96
Open in a new tab

(c).

Statistics for the data sets collected from crystals C-9 and C-14 for data between 40 and 1.9 resolution.

E = 9.0keV
R merge 0.11 (0.33) 0.11 (0.35) 0.11 (0.40) 0.12 (0.45) 0.12 (0.50) 0.13 (0.57) 0.15 (0.65) 0.17 (0.70)
R meas 0.12 (0.37) 0.12 (0.40) 0.13 (0.47) 0.14 (0.52) 0.14 (0.57) 0.15 (0.65) 0.17 (0.75) 0.19 (0.80)
R pim 0.06 (0.14) 0.06 (0.15) 0.07 (0.18) 0.07 (0.20) 0.07 (0.22) 0.08 (0.25) 0.09 (0.28) 0.10 (0.30)
Total number of observations 67292 (4933) 67248 (4925) 67228 (4917) 67075 (4936) 67113 (4917) 67253 (4931) 67076 (4951) 67417 (5034)
Total number unique 9840 (722) 9854 (721) 9863 (721) 9867 (722) 9878 (718) 9886 (719) 9898 (725) 9919 (735)
Mean[(I)/(I)] 15.2(4.8) 15.4 (4.9) 14.8 (4.4) 14.0 (4.0) 13.7 (3.8) 12.6 (2.7) 12.1 (2.9) 11.1 (2.1)
Completeness 99.9 (99.5) 99.9 (99.5) 99.9 (99.5) 99.9 (99.5) 99.9 (99.7) 99.9 (99.7) 99.9 (99.5) 99.9 (99.7)
Multiplicity 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.9) 6.8 (6.8) 6.8 (6.8)
R-factor against first data set   0.05 0.06 0.07 0.08 0.09 0.10 0.11
B (2) 14.2 15.3 15.7 16.6 16.3 16.9 17.1 14.2
Dose (MGy) 3.23 6.46 9.69 12.92 16.15 19.38 22.61 25.84
Open in a new tab
E = 14.0keV
R merge 0.08 (0.23) 0.09 (0.25) 0.09 (0.29) 0.09 (0.33) 0.09 (0.37) 0.10 (0.43) 0.11 (0.50) 0.11 (0.58)
R meas 0.08 (0.23) 0.09 (0.26) 0.09 (0.29) 0.09 (0.34) 0.10 (0.38) 0.11 (0.43) 0.11 (0.51) 0.12 (0.60)
R pim 0.02 (0.04) 0.02 (0.05) 0.02 (0.05) 0.02 (0.06) 0.03 (0.07) 0.03 (0.08) 0.03 (0.10) 0.03 (0.11)
Total number of observations 272701 (20082) 272072 (19498) 272070 (19504) 271968 (19365) 272318 (19565) 272604 (19556) 272844 (19851) 273406 (19956)
Total number unique 9675 (702) 9689 (688) 9691 (688) 9711 (687) 9720 (694) 9736 (694) 9754 (704) 9764 (708)
Mean[I/(I)] 36.6 (18.7) 35.0 (18.2) 33.5 (16.5) 31.9 (15.2) 30.3 (13.3) 29.0 (12.2) 27.4 (10.5) 25.9 (9.2)
Completeness 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Multiplicity 28.2 (28.6) 28.1 (28.3) 28.1 (28.3) 28.0 (28.2) 28.0 (28.2) 28.0 (28.2) 28.0 (28.2) 28.0 (28.2)
R-factor against first data set   0.04 0.07 0.09 0.11 0.13 0.15 0.16
B (2) 13.3 13.9 14.6 16.3 17.4 18.0 18.7 19.4
Dose (MGy) 3.26 6.52 9.78 13.04 16.30 19.53 22.82 26.08
Open in a new tab

(d).

Statistics for the data sets collected from crystals D-9 and D-14 for data between 40 and 1.9 resolution.

E = 9.0keV
R merge 0.08 (0.12) 0.08 (0.13) 0.08 (0.14) 0.08 (0.14) 0.08 (0.15) 0.09 (0.16) 0.09 (0.17) 0.0 9(0.18)
R meas 0.09 (0.13) 0.09 (0.14) 0.09 (0.15) 0.09 (0.15) 0.09 (0.16) 0.09 (0.17) 0.10 (0.18) 0.1 0(0.20)
R pim 0.03 (0.05) 0.03 (0.05) 0.03 (0.06) 0.03 (0.06) 0.04 (0.06) 0.04 (0.07) 0.04 (0.07) 0.04 (0.08)
Total number of observations 66549 (66549) 66696 (4930) 66586 (4933) 66886 (4936) 66707 (4909) 66731 (4910) 66896 (4954) 66855 (4930)
Total number unique 9777 (711) 9792 (718) 9805 (721) 9818 (721) 9820 (722) 9825 (718) 9840 (727) 9836 (723)
Mean[(I)/(I)] 20.8 (13.2) 21.0 (13.1) 20.1 (11.8) 20.4 (12.1) 19.6 (11.4) 19.2 (11.0) 18.7 (10.3) 18.5 (9.8)
Completeness 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Multiplicity 6.8 (6.8) 6.8 (6.9) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8) 6.8 (6.8)
R-factor against first data set   0.04 0.05 0.06 0.07 0.09 0.10 0.11
B (2) 13.3 13.7 14.1 14.6 15.0 15.5 16.1 16.3
Dose (MGy) 3.11 6.22 9.33 12.44 15.55 18.66 21.77 24.88
Open in a new tab
E = 14.0keV
R merge 0.06 (0.15) 0.06 (0.15) 0.06 (0.16) 0.06 (0.17) 0.06 (0.18) 0.07 (0.20) 0.07 (0.21) 0.07 (0.23)
R meas 0.07 (0.16) 0.07 (0.16) 0.07 (0.17) 0.07 (0.18) 0.07 (0.20) 0.07 (0.21) 0.08 (0.23) 0.08 (0.25)
R pim 0.03 (0.06) 0.03 (0.06) 0.03 (0.06) 0.03 (0.07) 0.03 (0.07) 0.03 (0.08) 0.03 (0.09) 0.03 (0.09)
Total number of observations 69188 (5114) 68372 (5016) 69120 (5135) 68980 (5125) 69102 (5089) 69294 (5094) 69169 (5076) 69400 (5168)
Total number unique 9836 (727) 9843 (721) 9822 (726) 9830 (728) 9840 (724) 9851 (723) 9850 (722) 9870 (731)
Mean[I/(I)] 22.6 (14.4) 22.5 (13.9) 22.5 (13.9) 22.2 (13.3) 21.5 (12.6) 20.7 (11.5) 19.7 (10.6) 19.1 (10.3)
Completeness 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Multiplicity 7.0 (7.0) 6.9 (7.0) 7.0 (7.1) 7.0 (7.0) 7.0 (7.0) 7.0) (7.0) 7.0 (7.0) 7.0 (7.1)
R-factor against first data set   0.03 0.04 0.05 0.07 0.08 0.09 0.10
B (2) 12.3 12.5 12.6 13.1 13.5 13.9 14.2 14.6
Dose (MGy) 1.99 3.98 5.97 7.96 9.95 11.95 13.94 15.93
Open in a new tab

In order to evaluate radiation damage, the cysteine and methionine side-chains were omitted from the refinement. The occupancy of the cysteine and methionine S atoms was estimated by integrating the weighted coefficient difference map m F o − DF c over a 1 Å sphere around the sulfur positions using MAPMAN (Kleywegt & Jones, 1996 ▶). The use of this type of map further reduces bias of the electron density to the initial model that might still be present after omitting the atoms of interest from the refinement (Read, 1986 ▶). Because the overall electron density level tends to change, owing to the decrease in resolution of the diffraction as the crystals were increasingly irradiated, we also omitted a buried N atom with a low atomic temperature factor from the refinement and used the integrated intensity level around the nitrogen to correct for loss of intensity around the sulfurs owing to global radiation damage effects. Thus we expected to separate the specific effects around the S atoms from other radiation-induced changes taking place in the crystal.

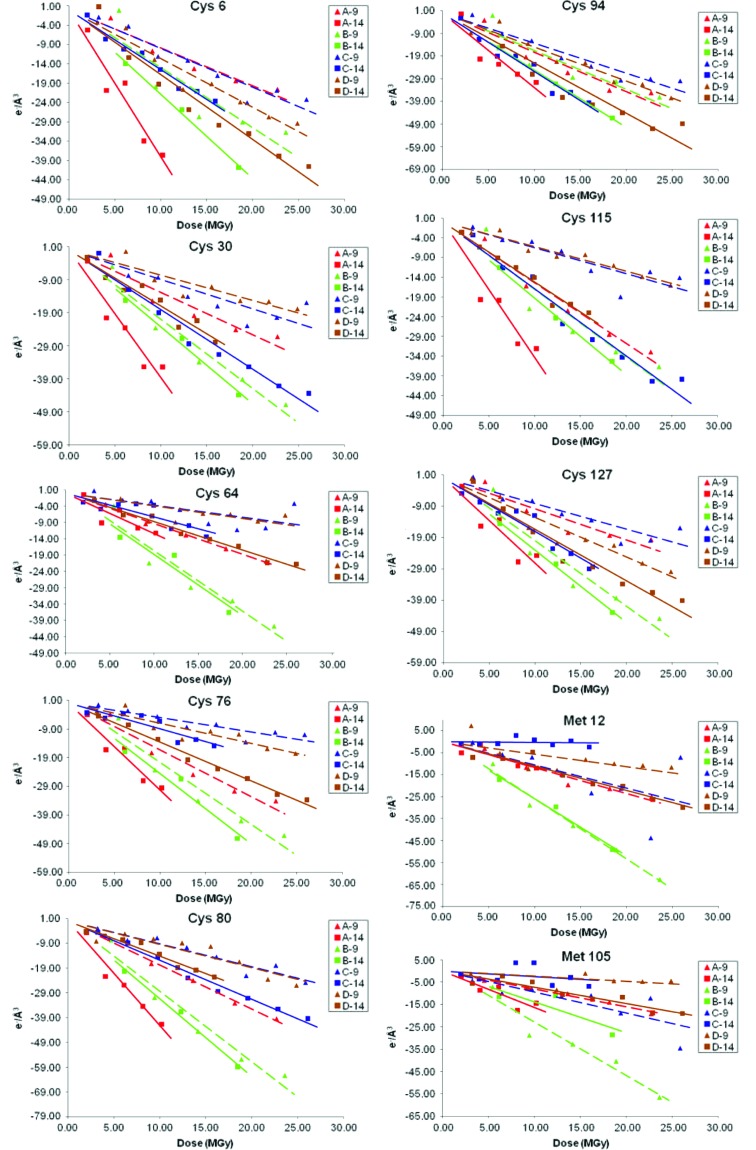
The rate of density loss as a function of dose was obtained by linear regression fitting of the integrated intensity about the site as a function of dose (Fig. 1 ▶). A steeper slope indicates a higher rate for the disordering of the atom in question, which in turns suggests faster onset of damage in response to irradiation.

Figure 1.

Figure 1

Open in a new tab

Integrated intensity (electrons per cubic Å) for each sulfur site as a function of dose absorbed by the crystal. The data points shown as triangles and squares correspond to the crystals exposed at 9 keV and 14 keV, respectively; the discontinuous lines and solid lines were fitted to the 9 keV and 14 keV data, respectively. Each crystal pair used for the comparison is shown in the same color. All the data have been normalized so that the integrated intensity is zero at zero dose.

3. Results and discussion  

3.1. Factors affecting the decay rate  

The decay rate depends on the beamline and circumstances of the experiment. There is a relatively large spread in the calculated damage between samples and sites. Variation in the data quality and resolution between samples (and also between data sets from the same sample as it gets progressively damaged) undoubtedly affect the electron density maps and introduces a certain amount of noise.

Differences in sample size and orientation of the crystals in the beam are otherwise not expected to impact the results, since the crystals were all smaller or about the same size as the beam and, at the energies considered, the absorbed dose is not very sensitive to variations of the crystal size. The variation between the rates of decay at a particular energy at the same beamline is relatively small (about 10%) and could be explained by small errors in the dose calculation (e.g. variations in the beam intensity between the time of the flux calibration and the time of the experiment). However, the cysteine sulfur decay rates for the data collected on BL12-2 (crystals C-9, C-14, D-9 and D-14) are consistently much smaller for both energies than those measured on BL9-2 (A-9, A-14, B-9 and B-14). A parameter in the dose calculation that could account for this discrepancy is the difference in the beam profiles. For the typical conditions used in this study the absorbed dose per second is 1.5 times higher if the beam profile is assumed to be Gaussian than if it is a flat-top beam. Neither beam can be adequately described fully as a Gaussian or flat top, which limits somewhat the capability to directly compare results across beamlines.

The different crystallization conditions for the C and D crystals are not expected to contribute to the observed difference in rate between the beamlines, since the concentration of the precipitant NaCl is already accounted for in the dose calculation, and ethylene glycol, absent from the buffer for crystals A and B, is predominantly a radical scavenger (O’Neill, 2002 ▶), while electron trapping is thought to contribute predominantly to the reduction of disulphide bridges (Weik et al., 2002 ▶).

A relationship between the rate of decay and the site environment, as characterized by the atomic temperature factor and solvent accessibility of the side-chain, could not be found.

3.2. Energy dependence  

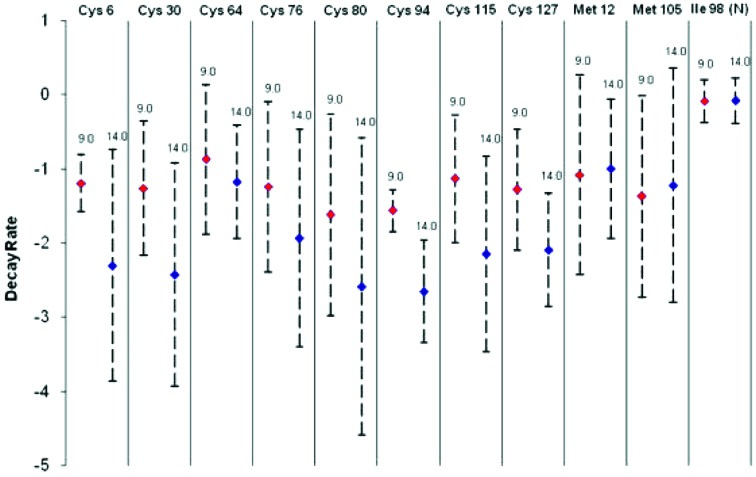
When comparing the data collected at different energies back-to-back on the same day, it is observed that the sulfurs in disulphide bridges in crystals irradiated with the 14 keV beam tend to decay faster than the corresponding ones in the crystals exposed to the 9 keV beam. Fig. 2 ▶ plots the decay rates for all the sulfur sites, across all the experiments, and shows a consistent average difference of approximately one electron per cubic Å per MGy in the decay at both beam energies used; although the error for each individual site is large (this is due to the variations between experiments discussed above), inspection of the decay rate plots for each pair of crystals collected on the same day (Fig. 1 ▶) shows a systematic difference at the two energies for these atoms. It is worth noting that the temperature factor calculated from the Wilson plot increases as a function of dose at roughly the same rate for both energies in most crystal pairs (see Table 2 ▶). Because the temperature factor has been shown to increase linearly as a function of dose (Bourenkov et al., 2006 ▶; Kmetko et al., 2006 ▶), this suggests that the energy dependence is confined to specific secondary radiation damage and cannot be attributed to systematic differences in the dose received by the crystals at the two energies.

Figure 2.

Figure 2

Open in a new tab

Average decay rate (electrons per cubic Å per MGy) for each atom site examined in the study. The decay rate for the N atom used for normalization is also shown. The average is calculated over all four crystals used for data collection at each energy. Error propagation is used to determine the error of the average rate from the calculated error in the slope of the fitted lines shown in Fig. 1 ▶.

It is difficult to explain the results by photoelectron trapping or chemical reactions with radicals using the current simple models. The Compton scattering contribution, which is not taken into account in the RADDOSE version used for the dose calculation, is not enough to account for the differences in decay in the experiment. Dose-rate effects, which could be present at flux rates close to or above 1012 photons s−1 (Leiros et al., 2006 ▶), would predominantly affect data collected at 9 keV, since the flux was always higher at this energy for all the experiments; the highest dose rate (about 0.5 MGy s−1) was suffered by crystals C-9 and D-9; in comparison, C-14 and D-14 absorbed about 0.1 MGy s−1 (see Table 1 ▶).

The S—C bond decay in methionines, on the other hand, does not show a clear energy dependency. A likely explanation for this is the existence of different mechanisms for the attack of different species in the protein, with different sensitivities to experimental conditions. It is also worth noting that the rate of decay for these sites is, on average, less than that found for sulfurs involved in disulphide bridges, and the S—C bonds appear to be more resistant to breakage than the disulphide bridges, which confirms previous well established results.

4. Summary and conclusions  

In this study we found what appears to be an energy dependence in the rate of radiation-induced damage to specific sites, with the integrated electron density around the cysteine S atoms in HEWL decreasing faster at 14 keV than 9 keV. A similar dependence in the specific damage to the methionine sulfur sites could not be clearly ascertained. These results cannot be easily explained by our current models of specific radiation damage mechanisms, but, if they are not artifacts, it would be possible to mitigate the radiation damage to important sites in proteins by selection of the energy for data collection where damage is minimized. Further experiments need to be carried out to confirm these preliminary results and to explore the sensitivity of different sites at different energies.

Acknowledgments

This research was carried out at the Stanford Synchrotron Radiation Lightsource, a national user facility operated by Stanford University on behalf of the US Department of Energy, Office of Basic Energy Sciences. The SSRL Structural Molecular Biology Program is supported by the Department of Energy, Office of Biological and Environmental Research, and by the National Institutes of Health, National Center for Research Resources, Biomedical Technology Program, and the National Institute of General Medical Sciences. LC was supported by the Science Teacher and Researcher (STAR) program. The authors thank the SSRL Molecular Crystallography group for their support and, in particular, Irimpan Mathews for the help preparing the crystals used in the experiment. The project described was supported by Award Number P41 RR001209 from the National Center for Research Resources, a component of the National Institutes of Health, and its contents are solely the responsibility of the authors and do not necessarily represent the official view of NCRR or NIH.

References

  1. Arndt, U. W. (1984). J. Appl. Cryst. 17, 118–119.
  2. Berglund, G. I., Carlsson, G. H., Smith, A. T., Szoke, H., Henriksen, A. & Hajdu, J. (2002). Nature (London), 417, 463–468. [DOI] [PubMed]
  3. Borek, D., Ginell, S. L., Cymborowski, M., Minor, W. & Otwinowski, Z. (2007). J. Synchrotron Rad. 14, 24–33. [DOI] [PubMed]
  4. Bourenkov, G. P., Bogomolov, A. & Popov, A. N. (2006). Fourth International Workshop on X-ray Damage to Biological Crystalline Samples, SPring-8, Japan.
  5. Burmeister, W. P. (2000). Acta Cryst. D56, 328–341. [DOI] [PubMed]
  6. Carugo, O. & Djinovic Carugo, K. (2005). Trends Biochem. Sci. 30, 213–219. [DOI] [PubMed]
  7. Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760–763.
  8. Corbett, M. C., Latimer, M. J., Poulos, T. L., Sevrioukova, I. F., Hodgson, K. O. & Hedman, B. (2007). Acta Cryst. D63, 951–960. [DOI] [PubMed]
  9. Cowan, J. A. & Nave, C. (2008). J. Synchrotron Rad. 15, 458–462. [DOI] [PubMed]
  10. Diederichs, K. & Karplus, P. A. (1997). Nat. Struct. Biol. 4, 269–275. [DOI] [PubMed]
  11. Evans, P. (2006). Acta Cryst. D62, 72–82. [DOI] [PubMed]
  12. Fioravanti, E., Vellieux, F. M. D., Amara, P., Madern, D. & Weik, M. (2007). J. Synchrotron Rad. 14, 84–91. [DOI] [PubMed]
  13. Gonzalez, A., Denny, R. & Nave, C. (1994). Acta Cryst. D50, 276–282. [DOI] [PubMed]
  14. González, A., Moorhead, P., McPhillips, S. E., Song, J., Sharp, K., Taylor, J. R., Adams, P. D., Sauter, N. K. & Soltis, S. M. (2008). J. Appl. Cryst. 41, 176–184.
  15. Jones, G. D. D., Lea, J. S., Symons, M. C. R. & Taiwo, F. A. (1987). Nature (London), 330, 772–773. [DOI] [PubMed]
  16. Kauffmann, B., Weiss, M. S., Lamzin, V. S. & Schmidt, A. (2006). Structure, 14, 1099–1105. [DOI] [PubMed]
  17. Kleywegt, G. J. & Jones, T. A. (1996). Acta Cryst. D52, 826–828. [DOI] [PubMed]
  18. Kmetko, J., Husseini, N. S., Naides, M., Kalinin, Y. & Thorne, R. E. (2006). Acta Cryst. D62, 1030–1038. [DOI] [PubMed]
  19. Leiros, H.-K. S., Timmins, J., Ravelli, R. B. G. & McSweeney, S. M. (2006). Acta Cryst. D62, 125–132. [DOI] [PubMed]
  20. Leslie, A. G. W. (1992). Joint CCP4+ESF-EAMCB Newsl. Protein Crystallogr. 26
  21. Macedo, S., Pechlaner, M., Schmid, W., Weik, M., Sato, K., Dennison, C. & Djinović-Carugo, K. (2009). J. Synchrotron Rad. 16, 191–204. [DOI] [PubMed]
  22. Meents, A., Gutmann, S., Wagner, A. & Schulze-Briese, C. (2010). Proc. Natl Acad. Sci. USA, 107, 1094–1099. [DOI] [PMC free article] [PubMed]
  23. Mueller-Dieckmann, C., Panjikar, S., Tucker, P. A. & Weiss, M. S. (2005). Acta Cryst. D61, 1263–1272. [DOI] [PubMed]
  24. Murray, J. & Garman, E. (2002). J. Synchrotron Rad. 9, 347–354. [DOI] [PubMed]
  25. Murray, J. W., Garman, E. F. & Ravelli, R. B. G. (2004). J. Appl. Cryst. 37, 513–522.
  26. Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. [DOI] [PubMed]
  27. Nave, C. & Hill, M. A. (2005). J. Synchrotron Rad. 12, 299–303. [DOI] [PubMed]
  28. O’Neill, P., Stevens, D. L. & Garman, E. (2002). J. Synchrotron Rad. 9, 329–332. [DOI] [PubMed]
  29. Owen, R. L., Holton, J. M., Schulze-Briese, C. & Garman, E. F. (2009). J. Synchrotron Rad. 16, 143–151. [DOI] [PMC free article] [PubMed]
  30. Owen, R. L., Rudiño-Piñera, E. & Garman, E. F. (2006). Proc. Natl Acad. Sci. USA, 103, 4912–4917. [DOI] [PMC free article] [PubMed]
  31. Paithankar, K. S., Owen, R. L. & Garman, E. F. (2009). J. Synchrotron Rad. 16, 152–162. [DOI] [PubMed]
  32. Polikarpov, I. (1997). J. Synchrotron Rad. 4, 17–20. [DOI] [PubMed]
  33. Polikarpov, I., Teplyakov, A. & Oliva, G. (1997). Acta Cryst. D53, 734–737. [DOI] [PubMed]
  34. Popov, A. N. & Bourenkov, G. P. (2003). Acta Cryst. D59, 1145–1153. [DOI] [PubMed]
  35. Ravelli, R. B. G. & McSweeney, S. (2000). Structure, 8, 315–328. [DOI] [PubMed]
  36. Ravelli, R. B. G., Theveneau, P., McSweeney, S. & Caffrey, M. (2002). J. Synchrotron Rad. 9, 355–360. [DOI] [PubMed]
  37. Read, R. J. (1986). Acta Cryst. A42, 140–149.
  38. Shimizu, N., Hirata, K., Hasegawa, K., Ueno, G. & Yamamoto, M. (2007). J. Synchrotron Rad. 14, 4–10. [DOI] [PubMed]
  39. Soltis, S. M., Cohen, A. E., Deacon, A., Eriksson, T., Gonzalez, A., McPhillips, S., Chui, H., Dunten, P., Hollenbeck, M., Mathews, I., Miller, M., Moorhead, Phizackerley, R. P., Smith, C., Song, J., van dem Bedem, H., Ellis, P., Kuhn, P., McPhillips, T., Sauter, N., Sharp, K., Tsyba, I. & Wolf, G. (2008). Acta Cryst. D64, 1210–1221. [DOI] [PMC free article] [PubMed]
  40. Song, J., Mathew, D., Jacob, S. A., Corbett, L., Moorhead, P. & Soltis, S. M. (2007). J. Synchrotron Rad. 14, 191–195. [DOI] [PubMed]
  41. Teplyakov, A., Oliva, G. & Polikarpov, I. (1998). Acta Cryst. D54, 610–614. [DOI] [PubMed]
  42. Weik, M., Bergès, J., Raves, M. L., Gros, P., McSweeney, S., Silman, I., Sussman, J. L., Houée-Levin, C. & Ravelli, R. B. G. (2002). J. Synchrotron Rad. 9, 342–346. [DOI] [PubMed]
  43. Weik, M., Ravelli, R. B. G., Kryger, G., McSweeney, S., Raves, M. L., Harel, M., Gros, P., Silman, I., Kroon, J. & Sussman, J. L. (2000). Proc. Natl. Acad. Sci. USA. 97, 623–628. [DOI] [PMC free article] [PubMed]
  44. Weiss, M. S. (2001). J. Appl. Cryst. 34, 130–135.
  45. Weiss, M. S., Panjikar, S., Mueller-Dieckmann, C. & Tucker, P. A. (2005). J. Synchrotron Rad. 12, 304–309. [DOI] [PubMed]
  46. Yano, J., Kern, J., Irrgang, K.-D., Latimer, M. J., Bergmann, U., Glatzel, P., Pushkar, Y., Biesiadka, J., Loll, B., Sauer, K., Messinger, J., Zouni, A. & Yachandra, V. K. (2005). Proc. Natl Acad. Sci. USA, 102, 12047–12052. [DOI] [PMC free article] [PubMed]

Articles from Journal of Synchrotron Radiation are provided here courtesy of International Union of Crystallography

RESOURCES