A Theoretical Investigation of the Ni(II)-Catalyzed Hydrovinylation of Styrene

Abstract

We report a detailed and full computational investigation on the hydrovinylation reaction of styrene with the Ni(II)-phospholane catalytic system, which was originally presumed to proceed through a cationic mechanism involving a nickel hydride intermediate. The following general features emerge from this study on a specific catalyst complex that was found to give quantitative yield and moderate selectivity: (a) the activation barrier for the initiation (18.8 kcal/mol) is higher than that for the reaction due to a low-lying square-planar pentenyl chelate intermediate originating from a Ni(II)-allyl catalyst precursor. Consequently there is an induction period for the catalysis; (b) the exit of product from the catalyst is via a β-H-transfer step instead of the usual β-H elimination pathway, which has a very high activation energy due to a trans effect of the phospholane ligand; (c) the turnover-limiting and enantio- determining transition state is also the β-H-transfer; (d) because of the absence of a hydride intermediate, the unwanted isomerization of the product is prevented; (e) since the enantio-discrimination is decided at the H-transfer stage itself, the configuration of the product in a catalytic cycle influences the enantioselectivity in the subsequent cycle; (f) the trans effect of the sole strong ligand in the d⁸ square-planar Ni(II), the stability of the η³-benzyl intermediate, and the availability of three coordination sites enable regioselective hydrovinylation over the possible oligomerization/polymerization of the olefin substrates and linear hydrovinylation. This work has also confirmed the previously recognized role of the hemilabile group at various stages in the mechanism.

Introduction

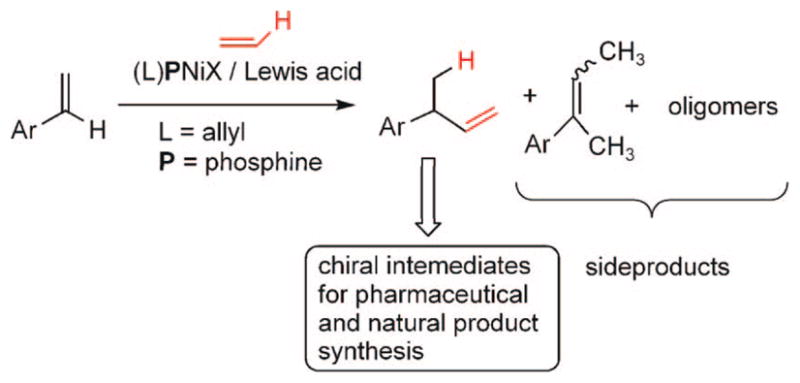
Among the Ni(II)-catalyzed olefin dimerization reactions, the hydrovinylation reaction, viz., the addition of a vinyl group and a hydrogen across a double bond (Scheme 1), has attracted the most attention.¹ Since the branched product is chiral, a regio-and stereoselective version of this reaction could provide easy access to a variety of olefin-derived products including carboxylic acid derivatives. For example, the hydrovinylation of vinylarene derivatives that leads to 3-arylbutenes could be used for the synthesis of widely used anti-inflammatory 2-arylpropionic acids such as ibuprofen and naproxen. Even though the hydrovinylation reaction has had a long history dating back to 1965, until recently no catalyst system gave satisfactory yield and selectivity to be of practical value. The use of high pressures of ethylene and metal components incompatible with sensitive organic groups were also major limitations of many of the initially reported procedures. In addition, isomerization of the primary products and oligomerization of the vinylarene and ethylene were other detractions of this powerful reaction (Scheme 1).

Scheme 1.

Hydrovinylation of Vinylarenes

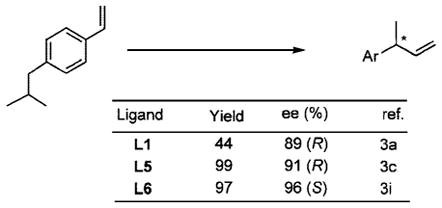
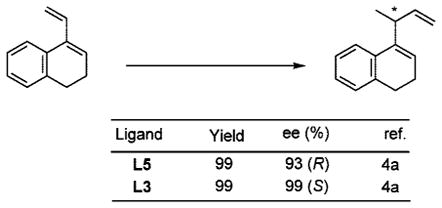
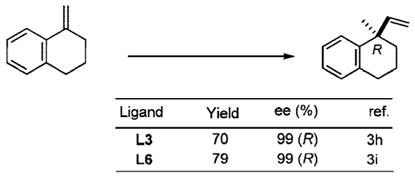
Since our initial disclosure of new protocols for this reaction (Scheme 2),² its scope has been considerably broadened. Application of old (Figure 1: L1, L2, L3) and new (L4, L5, L6) ligands has enabled successful asymmetric hydrovinylation of vinyl arenes,³ 1,3-dienes,^3i,4 and strained bicyclic olefins such as norbornene.^3f,5 Several examples are illustrated in eqs 1–3.

Scheme 2.

Asymmetric Hydrovinylation Using Hemilabile Ligands

Figure 1.

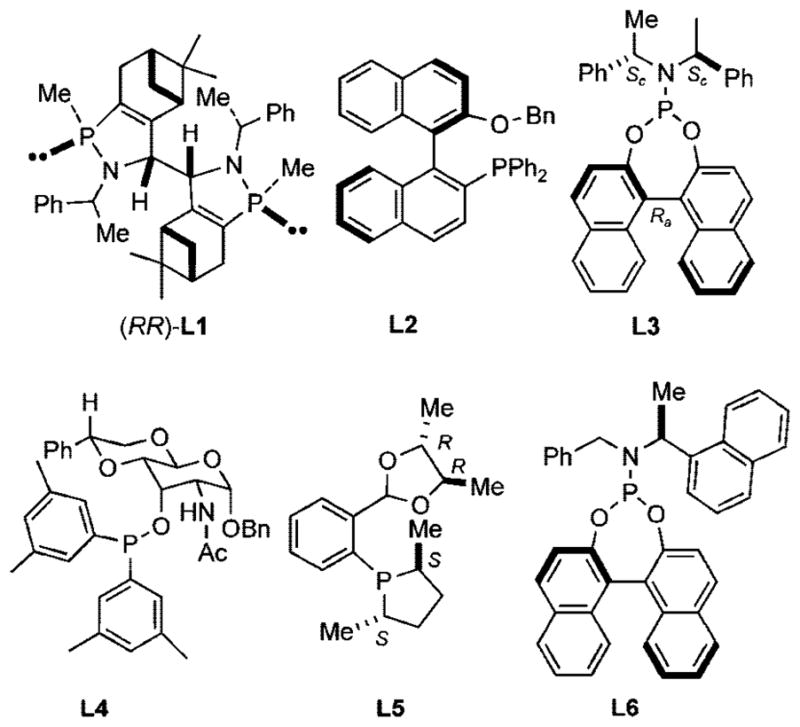
Assorted ligands used for asymmetric hydrovinylation.

(1)

(2)

(3)

Mechanism of Ni-Catalyzed Hydrovinylation of Vinylarenes

Even though much of the early studies of hydrovinylation of styrene are characterized by a lack of any selectivity, many of them provide significant mechanistic insights into the reaction. For example, kinetic and solvent effect studies of hydrovinylation with NiX₂/AlEt₃/BF₃ • OEt₂/P(OPh)₃ ^6a–c provided some early indications of the [Ni–H]⁺ coordination to a styrene and subsequent addition. The deactivating effect of a solvent was found to increase in the order CH₂Cl₂, PhF, PhCl, PhMe, PhNO₂, Et₂O, consistent with the inhibitory effect of a coordinating Lewis base. Electron-withdrawing substituents on styrene retard the reaction rate. Studies of D-distribution in the product when the hydrovinylation was carried out with D₂C=CD₂ provided further evidence for the involvement of a cationic nickel hydride intermediate.^6c Even though a catalytically active L_n[Ni–H]⁺ has not been isolated, its generation and inter-⁷ and intramolecular⁸ additions have been documented. Since these early studies, Brookhart and DiRenzo⁹ have provided more details of their mechanistic study of closely related Pd-catalyzed co-dimerization of styrene and ethylene.

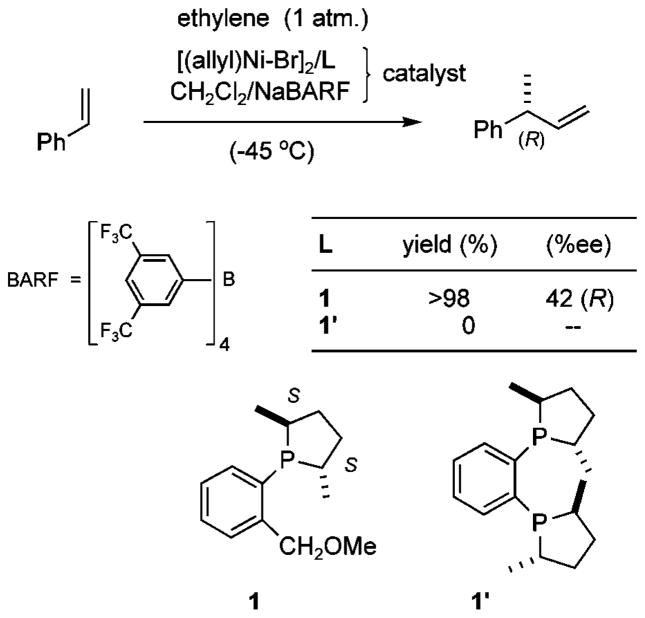
Mechanistically one of the most significant early observations that we made^3b was the total inability of chelating phosphines to effect the reaction under our standard protocol. One such example is shown in Scheme 2. The chelating bisphosphine 1′ gave no trace of coupling products, whereas ligand 1, carrying one chelating phosphorus and a hemilabile –OMe group, gave a quantitative yield of the product in ~42% ee at −45 °C using 0.014 equiv of the precatalyst under 1 atm of ethylene. All ligands that have yielded useful levels of asymmetric induction in the hydrovinylation reaction share this common structural feature.³ In this connection, we also recognized^3b a strong synergy between a hemilabile ligand and a highly dissociating counterion {e.g., [3,5-(CF₃)₂C₆H₃]₄B, Scheme 2}. In the absence of a hemilabile ligand, a coordinating counterion such as triflate (CF₃SO₃ ⁻) is essential for the success of the reaction.

In this computational probe, we explore the reaction depicted in Scheme 2, which uses the ligand 1. The reaction under these conditions was chosen for detailed study because it represents a minimalist catalyst system that gives significant enantioselectivity, yet small enough to be amenable to extensive ab initio study. A study of this reaction, we hope, would allow the delineation of the basic mechanism and at the same time revealing the possible origin of the stereoselectivity.

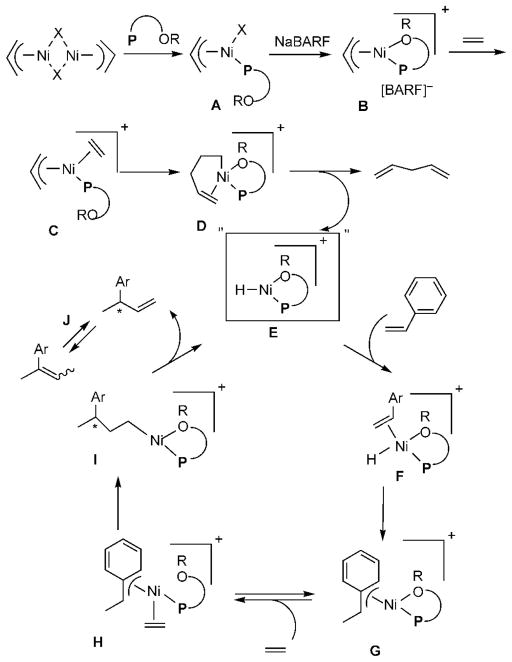
At the outset of the synthetic studies we relied on a “working model” for the mechanism of the reaction as shown in Scheme 3. In this model, the functional equivalent of a catalyst is represented by E, shown within quotations inside a square box. This representation is meant to emphasize the point that this cationic metal hydride intermediate, associated with a noncoordinating counteranion and a phosphine, is highly speculative. The active catalyst precursor B is produced from a reaction of allylnickel bromide dimer and ligand 1 with one hemilabile donor atom, followed by abstraction of the bromide by Na-BARF. Several crystal structures of complexes related to Ni-allyl compounds A and B are known with phosphines, Cy₃P [X = MeAlCl₃],^10a P(menthyl)(Me)(Bu^t) [X = Cl],^10b P(menthyl)₂(Me) [X = Me].^10c and [o-MeOC(O)-C₆H₄]-PPh₂.^10d The crucial metal hydride E is formed by (a) ligand substitution of the hemilabile group of B by ethylene to form C and (b) insertion of ethylene into the allyl–Ni bond followed by (c) a β-hydride elimination. Addition of the metal hydride to the vinylarene would lead to the benzyl complex G, which is shown as a 16-electron η³-structure. Ligand substitution with ethylene leads to H. At higher concentrations of ethylene and styrene this species could serve as a catalyst resting state. Strong evidence for such a situation has been provided by Brookhart and Direnzo⁹ in mechanistically related [(allyl)Pd(Cy₃P)]⁺-[BARF]⁻ mediated dimerization of styrene. Insertion of ethylene followed by β-hydride elimination from I regenerates the metal hydride catalyst E and the product, 3-aryl-1-butene. Enantioselectivity in the reaction could arise from diastereoselective addition of metal hydride to styrene (E → G) when the ligand is chiral and nonracemic. A number of anecdotal observations reported in the literature and some made during our studies can be accommodated by this mechanism.

Scheme 3.

Proposed Mechanism of Hydrovinylation of Styrene

1. Diminished reactivity of electron-deficient vinylarenes might arise from low rate of metal hydride addition (E →G).

2. Deactivating effects of the coordinating solvents.

3. The observed isomerization of the initially formed 3-aryl-1-butene to 2-aryl-2-butene with some catalytic systems could be mediated by the metal hydride via sequential addition–elimination reactions.

4. Total inhibition of the reaction by chelating phosphines. In this work, we will examine each step in the mechanism (or alternatives if the step was found to be energetically unfavorable) to reveal the exact nature of the transition states and intermediates, and estimate the activation barriers for critical steps. We will also attempt to determine the origin of asymmetric induction in the reaction.

Details of the Computational Methods

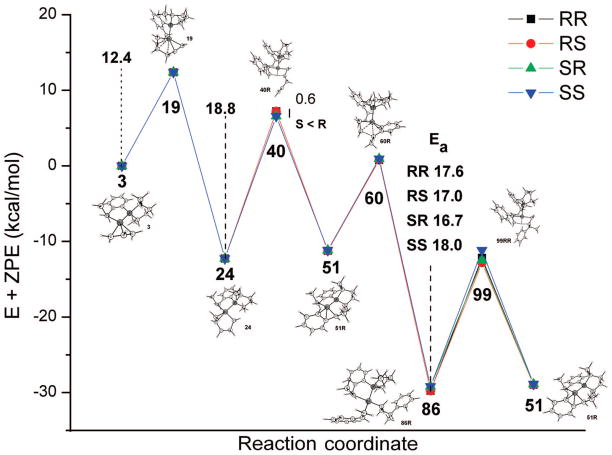
The problem at hand is computationally very demanding, and unless otherwise mentioned, we are forced to restrict the calculations to the B3LYP/6-31G* level, available in the Gaussian package.¹¹ This is quite a reasonable level¹² and has been used previously by Leitner et al. to examine the last stages of asymmetric hydrovinylation catalyzed by Ni(II)-phosphoramidite complexes.¹³ All reported energies are in kcal/mol and include zero-point energy (ZPE) at the optimized level. We employed the following strategy for the exploration of the reaction paths to track the vast potential energy surface: a detailed conformational search has been made only for the crucial transition states and their previous lowest energy intermediates so as to get exact activation energies for all the important steps. For all other “connecting” transition states (and intermediates) involved in the reaction path, either at least one conformer was located whose energy lies in between the above identified lowest intermediate and transition state, or some obvious low-lying (mainly rotational) transition states/intermediates were ignored. We shall illustrate this using Figure 2, which summarizes the results (vide infra). All points in Figure 2 representing key intermediates and transition states and the structures shown represent the lowest conformers of these species in the reaction.¹⁴ The reaction path connecting two points, one minimum (intermediate) and one maximum (transition state), was confirmed to lie in between them.

Figure 2.

Summary of the reaction. The structures shown are for one series; other structures can be found in the article.

To find out which two intermediates are connected by a transition state, we applied a frequency following method. This was done by first obtaining the geometries by a very small displacement of the imaginary vibrational mode of the transition state in either directions, and then both were optimized by calculating the force constants at all optimization steps.

To avoid cluttering in the schemes depicting reaction paths, two types of arrows are used to connect an intermediate to a transition state (and vice versa). A “single” arrow means the two neighboring species are directly connected, while a “double” arrow means either another conformer of the intermediate connects to the transition state or some steps that are already described are involved, or some of the trivial steps are skipped in the drawing. The equilibrium arrows in the schemes have the usual connotation, so do square brackets that envelop the transition state structures. The additional # symbol signifies the highest transition state in the reaction steps under consideration. The images of all structures shown in the article were generated using ChemCraft software.

Results and Discussion

Generation of the Active Catalyst

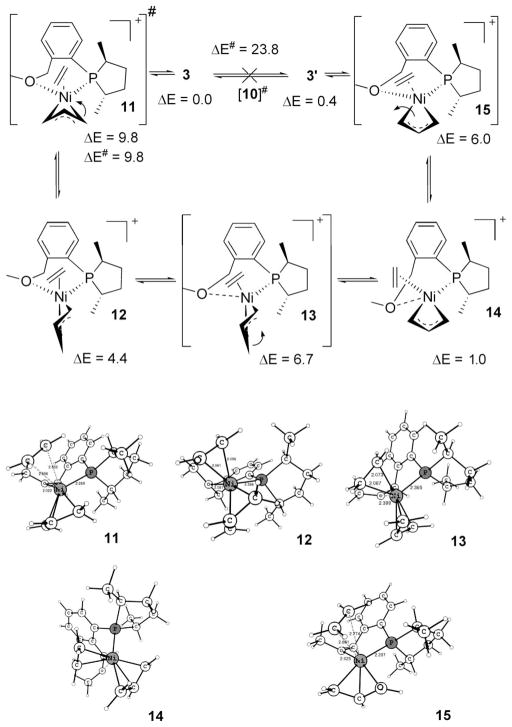
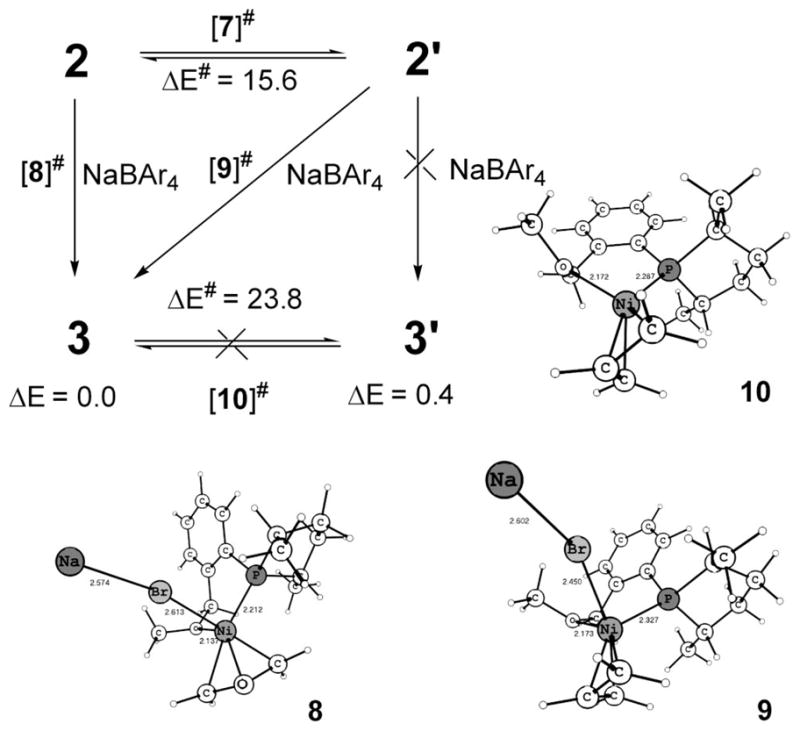
Scheme 4 shows the generation of active catalyst precursors from [(allyl)Ni-Br]₂ and ligand 1. The experiments reveal^3b that there is only one diastereomer (either 3 or 3′) present before the start of the hydrovinylation reaction, and we attempted to identify which of these could be present, because it is the first chiral organometallic intermediate in the catalytic process and thus has the potential to affect the eventual stereochemical outcome of the reaction. The difference in energy between 3 and 3′ is only 0.4 kcal/mol (in favor of 3), which is low enough for both to be observed if there is an equilibration between them after they have been generated. To refine the relative energies, we did the calculation at the B3LYP/6-311++G** level, where the result was further validated (0.5 kcal/mol). The activation energy for their interconversion is 23.8 kcal/mol, which is large and rules out a rapid equilibrium causing the single peak observed in the ³¹P NMR at room temperature and below. That means formation of one of these diastereomers (either 3 or 3′) is favored over the other. Below this, diastereomer 3 is located; we use the available experimental NMR results for the corroboration of our arguments.

Scheme 4.

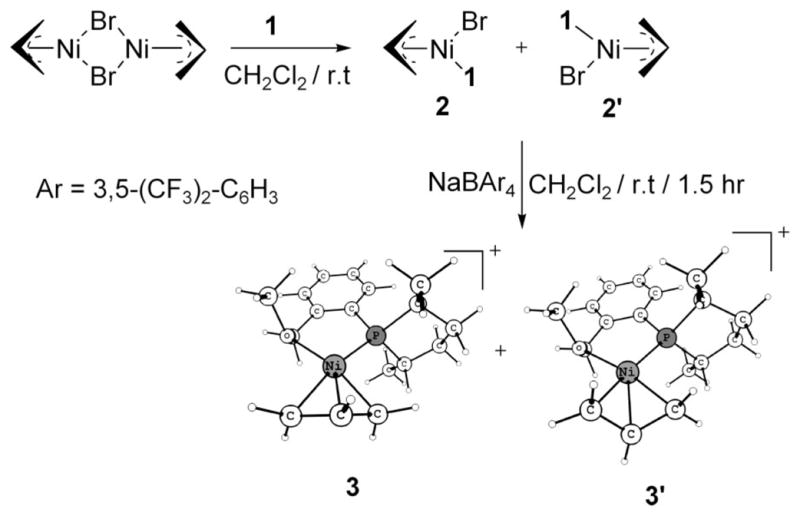
Generation of Precatalysts (2, 2′; 3, 3′)

Effect of an Extra Ligand on the Equilibration of the Square-Planar Diastereomers 2 and 2′

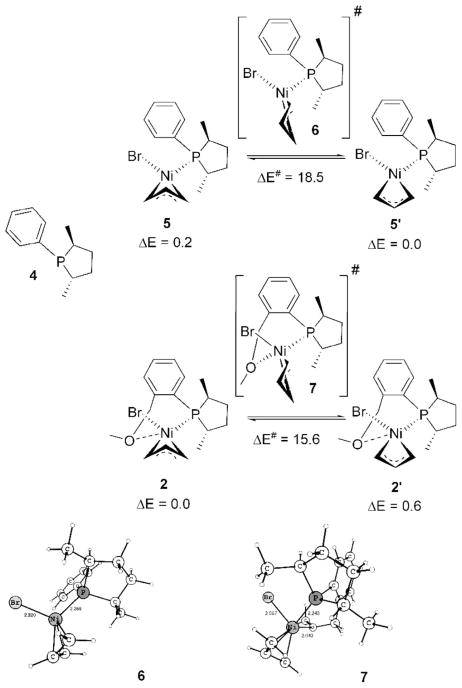
The starting nickel salt, [(allyl)Ni-Br]₂, is expected to yield two diastereomers, 2 and 2′ (Scheme 4), upon reaction with ligand 1. The ³¹P NMR shows a single peak at room temperature, but reveals the presence of another diastereomer at lower temperatures, 3:1 at −20 °C and 4:1 at −80 °C.^3b Insight into this isomerization reaction can be gleaned by looking at a closely related system containing the ligand 4, without the extra ligating –OMe group, and the corresponding square-planar complexes 5 and 5′ (Scheme 5). These complexes are found in a ratio of approximately 1:1 at temperatures between 27 and −70 °C. We find that the extra (hemilabile) ligating group in 1 affects not only the rate of interconversion between 2 and 2′ but also the equilibrium constant (Scheme 5). Ligand 4, without any such group, makes both diastereomers virtually iso-energetic (ΔE = 0.2 kcal/mol, corresponds to 1.4:1.0 at 300 K), so even if there is an equilibrium between 5 and 5′, they appear in an approximate ratio of 1:1.^3b The activation energy, 18.5 kcal/mol, is low enough, but a slow interconversion at room temperature occurs. At lower temperatures, the interconversion is more difficult, and hence the same ratio at room temperature prevails. In contrast, ligand 1 does distinguish the diastereomers energetically (ΔE = 0.6 kcal/mol, corresponding to 2.7:1.0 at 300 K) because of the fifth coordination via oxygen and to the exo/endo effect of the η³-allyl for a d⁸ square-planar complex.¹⁵ Endo (2′) (O endo to the central C–H bond of η³-allyl) is higher in energy compared to exo (2) because both O and the central C compete for the same orbitals of Ni. The extra ligand also makes interconversion between 2 and 2′ faster by allowing the otherwise tetrahedral transition state 6 to change to a pseudo-square-planar (to be exact, square pyramidal allowing for the weak O/Br coordinations) transition state 7, a preferred geometry for a d⁸ electronic configuration. The square plane of 7 involves P, O, and η³-allyl, as shown in Scheme 5, and Br occupies the axial position if we consider it as a square pyramid. Thus the extra ligand lowers the barrier to 15.0 kcal/mol. So the single peak at room temperature^3b must correspond to coalescence. The lower barrier allows it to readjust the equilibrium ratio at lower temperatures, unlike with ligand 4.

Scheme 5.

Energetics of Interconversion between the Diastereomers of 2 and 5: Effect of Hemilabile Coordination

Formation of 3 and 3′ by Bromide Abstraction. Why Only One Diastereomer?

Despite the presence of both diastereomers (2 and 2′), and the possibility of interconversion between them, we found that the feasible path for Br abstraction precludes 3′ from being formed, so the sole diastereomer present initially is 3. This is because the expulsion of Br assisted by Na⁺ has the lowest energy in an endo route. Thus both initial diastereomers 2 and 2′ can give only 3 via the respective endo transition states 8 and 9 (Scheme 6). The orientation of the allyl unit with respect to the exiting Br is the principal difference between these two transition states. The dihedral angle Br–Ni–C² _allyl–H is −33° in 8 (transition state from 2) and 54° in 9 (transition state from 2′). Upon coordination of Na with Br, the Ni–Br bond is weakened. Now the NaBr is able to exit via a turnstile rotation^16a of η³-allyl, as shown in Scheme 6. Achieving transition state 8 is easier than transition state 9 since the latter has to undergo considerably more rotation with respect to 2′ to reach the endo arrangement. The energy difference between 8 and 9 is 5.9 kcal/mol. Since a reasonable estimation of the activation energy is difficult because of the charge separation between the intermediate and transition state, it is not certain whether 9, which is higher than 8, is actually involved. We conclude that if the barrier for 9 is less than 15.0 kcal/mol, the activation energy for the conversion of 2′ to 2, transition state 9 is involved in the formation of 3; otherwise 3 is obtained through transition state 8 even from 2′ (via 2). As pointed out before, the diastereomer 3′ is only 0.4 kcal/mol higher than 3, but its generation from 3 is also prohibited because it involves a barrier (10) of 23.8 kcal/mol. (It may be noted that transition state 10 is remarkably higher than analogous, but neutral tetrahedral transition state 6.) Thus we conclude that 3 is the active catalyst precursor present before the addition of substrates, ethene and styrene.

Scheme 6.

Formation of Sole Active Catalyst Precursor 3 from 2 and 2′

Interconversion of Diastereomers 3 and 3′ in the Presence of Ethene, an Extra Ligand

Since in the presence of an extra ligand allyl interconversion is easier in neutral 2 and 2′ (Scheme 5), we examined whether an added olefin makes interconversion of cationic 3 and 3′ feasible and hence nullify any possible consequences of the absence of the diastereomer 3′ initially. As anticipated, we found that ethene lowers the barrier for interconversion between 3 and 3′ via a turnstile rotation route, 15 (Scheme 7). The barrier for interconversion is only 9.8 kcal/mol (at 0 K). Even if we consider the additional entropy disadvantage of ethene association, it is still low enough for their interconversion at −45 °C, where the reaction was conducted. The catalyst precursor 3 can incorporate the ethene via transition state 11, which involves the allyl ligand rotating counterclockwise to reach the intermediate 12, which may be considered a square pyramid with P at the axial position. Continued allylic rotation at intermediate 12 leads to 14 via transition state 13. Note that now oxygen is endo to η³-allylic central C–H (dihedral angle O–Ni–C² _allyl–H = 14° in 14) and hence that the bond is weakened. The intermediate 14 is nothing but ethene incorporated in 3′ by the replacement of hemilabile O; that is, ethene ejection from 14 will give 3′.

Scheme 7.

Interconversion between 3 and 3′ via a Turnstile Rotation with the Help of Ethene

Although the coordinating ability of O is weak (S1, Scheme S1, Supporting Information), compared to styrene (S3, Scheme S1), for the cationic square-planar Ni(II) complex, in this particular ligand system that inherent advantage of styrene has been lost possibly to steric effects, so only 3 and to a lesser extent 3′ are present at the beginning of the hydrovinylation reaction. The lowest among the olefin complexes, the ethene complex (S6, Scheme S2), is only 0.4 kcal/mol lower than 3 despite having an additional (weak) ligation by O in the cationic complex. Considering the entropy effect it can be concluded that none of the olefin complexes have high concentrations in comparison with 3 (or 3′).

Mechanism of Hydrovinylation

Initiation

Since at least two coordination sites on a Ni(II) complex are required for the reaction, and our precursor 3 has only one vacant site in the form of a hemilabile ligation, the first requirement is to enable at least one more site. As outlined in the mechanism, a C–C coupling with the η³-allyl will do just that. One conceptual problem with the C–C bond formation via insertion of ethylene into the allyl–Ni bond (see mechanism, Scheme 3: C → D) is that it leads to a three-coordinated cationic intermediate and consequent large activation barrier, a disadvantage for the reaction at low (−45 to −77 °C) temperatures. So it is important to investigate how the catalytic system takes care of this problem. An alternate path that begins with η¹–η³ slippage of the allyl unit followed by ligand substitution of the alkene (Scheme 8) could not be located because of the strong preference of the allyl unit to remain in the η³ mode when two coordination sites are available in a d⁸ square-planar complex.

Scheme 8.

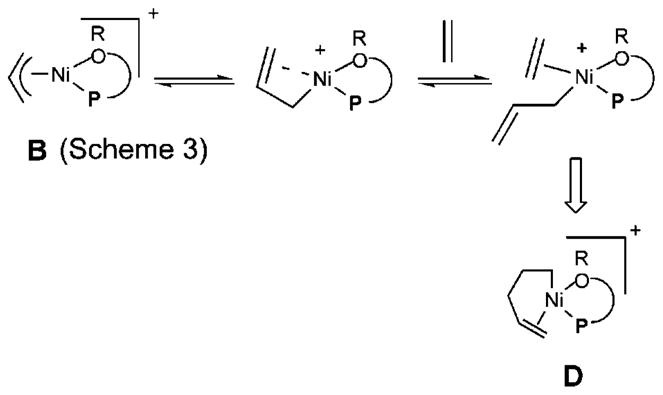
Generation of the Active Catalyst: (I) An Unlikely High-Energy Dissociative Initiation Path

Role of the Hemilabile Group

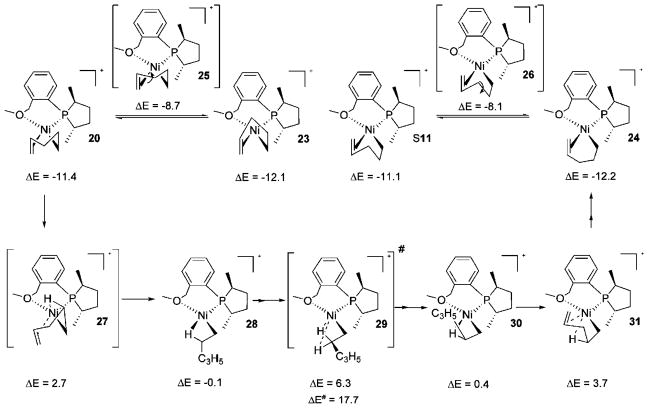
The labile ligand has been found to have an important role for the C–C bond forming transition state from the allyl-ethene complex (Scheme 9). The labile group’s involvement allows Ni(II) to have a four-coordinated intermediate, and therefore the total activation energy is only 12.4 kcal/mol. The lowest path is shown in Scheme 9. Catalytic precursor 3 incorporates ethene to become 16. The C–C coupling ensues via 17, 18, and 19 to rest at 20. The square-planar intermediate 20 is very low in energy, thanks to C–C bond formation, and represents one of the conformers for the lowest intermediate in the initiation path. Note that 17, 18, and 19 (Scheme 9) are very close in the potential energy surface and represent virtually the same species, so the unique C–C agostic complex 18 does not deserve much attention.¹⁷ For an alternative path having fewer steps from the precursor 3, the activation barrier is just 0.3 kcal/mol higher (see S10, Scheme S3, ΔE^# = 12.7 vs ΔE^# = 12.4 for 19 in Scheme 9). None of the attempts to identify a viable transition state for a C–C bond formation from model complexes (with ligand PH₃) having no hemilabile group were successful, further emphasizing the disadvantage of a transition state leading to a three-coordinated intermediate. The involvement of the hemilabile group as the fifth coordination in 16–19 for lowering the C–C coupling barrier has experimental precedence.¹⁸ We consider that the lack of reaction^3b with ligand 4 under identical conditions depicted in Scheme 2 could be attributed to this effect, although decomposition of the catalyst is observed due to lack of coordination (only three-coordinate) during its preparation; thus its presence in the reaction medium is doubtful.

Scheme 9.

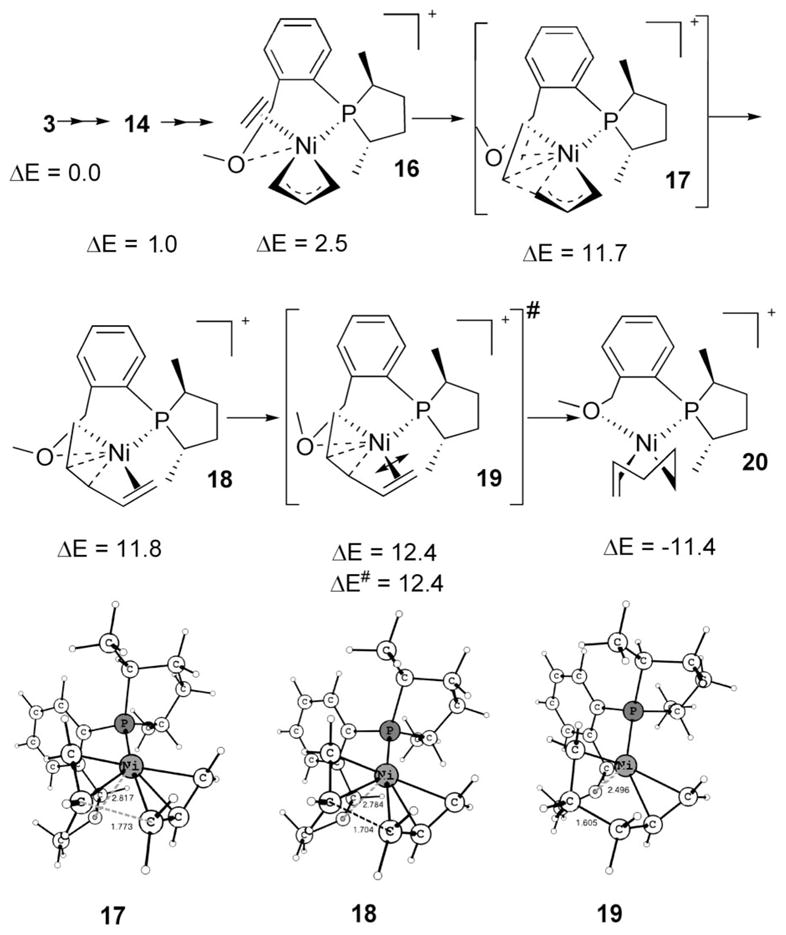
Generation of the Active Catalyst: (II) The Lowest Initiation Path

Next we understood why styrene, the other olefin present in the solution and relatively more abundant, cannot be involved in initiation. Styrene, in fact, is inherently more advantageous for the C–C bond formation because of its delocalization, as has been confirmed by model studies (Scheme S4). However, with the actual ligand, possibly due to steric effects between the phospholane Me with Ph of styrene, the corresponding transition state is higher in energy (21, Scheme 10) and the activation energy increases by 3.3 kcal/mol, making it kinetically noncompetitive. Note that no trace of C–C coupling products at the methylene carbon of styrene has been observed. The other styrene route, via 22, is difficult, as expected mainly due to conjugative disadvantage. Unlike 22, the coordinately unsaturated Ni can derive additional stabilization from being at the benzylic position in 21.

Scheme 10.

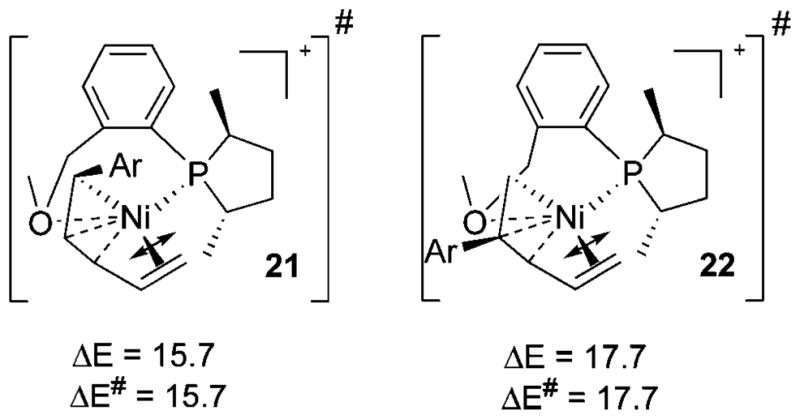
Lowest C–C Coupling Transition States with Styrene for Initiation

Catalyst Resting State in the Initiation Stages

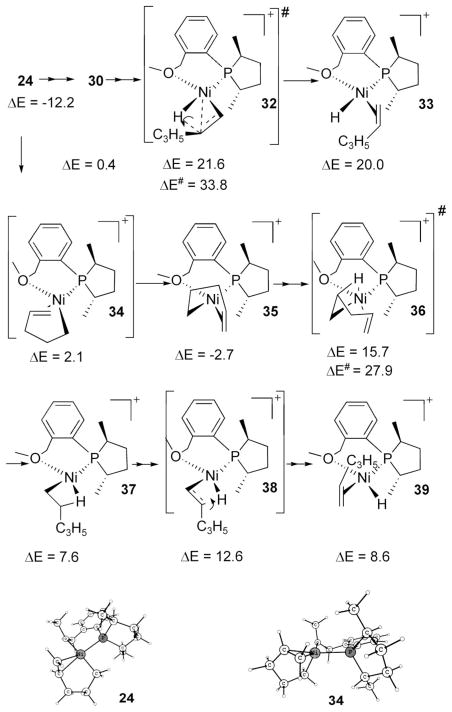
The energetically most accessible intermediate, 20, has three other isomers, as shown in Scheme 11. All four isomers (20, 23, S11, and 24) are close in energy, and 24 is the lowest; it could easily be obtained from S11, which is the direct outcome of the path involving 3 having fewer steps (vide supra, Scheme S3). Transition state 26 is a simple C–C flipping in the pentenyl chelate and hence has a small barrier, as is the case for transition state 25, which gives 23 starting from 20. The lowest intermediate, 24, can also be arrived at from 20 through the transition state 29 with an activation energy of 17.7 kcal/mol. This requires many steps, as represented in Scheme 11. An agostic C–H • • • Ni (cf. 28) needs to be invoked first, which is accomplished by the transition state 27. Subsequently through transition state 29 another intermediate with an agostic interaction, 30, is formed. Now the steps repeat in a reverse sense via the transition state 31 to yield the square-planar pentenyl chelate 24, with the olefin trans to phosphorus. Although 17.7 kcal/mol is the highest barrier of the reaction up to this point, it is lower than the pentadiene’s exit transition state (see below); thus we conclude that 24 is the resting state of the catalyst during initiation.

Scheme 11.

Generation of the Active Catalyst: (III) Reaction Path to the Lowest Intermediate during Initiation

A Surprise. The Expected β-Hydride Elimination Has an Unacceptably High Barrier

The usual β-H elimination, assumed to be the route for the exit of pentadiene (D → E in Scheme 3), has been found to have a high barrier of 33.8 kcal/mol (Scheme 12). This is most possibly due to the trans effect. Hydride does not favor being positioned trans to the sole strong ligand P, but this path demands such an arrangement. Note that the hydride 33 and the transition state to this species, 32, are prohibitively high in energy. That is, the weak stabilization of the metal–hydride bond by no means compensates the breaking of the C–H bond and losing a strong cis P–Ni–alkyl arrangement.

Scheme 12.

Energetics of the β-Hydride Elimination Pathway

To circumvent these disadvantages, an alternative path was explored where the hydride can be brought to a position cis to the phosphorus. This route begins by a pseudo-trigonal-pyramid transition state, 34, to reach the square-planar complex 35, where the alkyl group is positioned trans to the phosphorus.¹⁹ A look at the relative energies of square-planar structures 24 (−12.2 kcal/mol) and 35 (−2.7 kcal/mol) shows the effect of the trans effect. The difference of 9.5 kcal/mol clearly reveals that in the square-planar geometry the metal–alkyl bond prefers to be cis and the olefin trans to the phosphorus vis-à-vis the opposite arrangement, in which the olefin is cis to the phosphorus. β-Hydride elimination has to proceed through the intermediate 35. In the transition state (36) leading to β-hydride elimination there is an alkyl group trans to P (destabilizing) and the stabilizing cis olefin has been separated from the metal, thus effectively creating a vacant site at the cis position. So this transition state corresponds to a large barrier of 27.9 kcal/mol in creating a relatively stable agostic complex, 37. As anticipated, the C–H bond breaking transition state 38 to form the cis hydride 39 is considerably lower than the corresponding transition state 32, formation of which would appear to be more straightforward from the resting state 24. The large difference between the energies of the two hydrides 39 and 33 is yet another manifestation of the trans effect. Thus this alternate path decreased the barrier of β-hydride elimination of pentadiene from 33.8 kcal/mol (24 30 → 32 → 33) to 27.9 kcal/mol (24 → 35 → 36 → 39). However, both processes are still large for a reasonable reaction rate at −45 °C. So we are forced to explore alternate paths for this key step in the generation of the active catalyst. This is described in the next section.²⁰

A Possible β-H Transfer?

Since all viable intermediates (20, 23, 24, or S11) have three coordination sites (except the site occupied by the phospholane ligand in the square-planar d⁸ complex) usable for reaction, we explored how they can be utilized in avoiding energetically costly positioning of the hydride or alkyl group trans to P. Can alternate paths be found that decrease the barrier for 1,4-pentadiene’s exit? We conceived that a transfer²¹ of the β-H to another olefin positioned at the vicinal position to P (cis) bypasses the problem of having an alkyl/hydride intermediate formed trans to P. The lowest H-transfer transition state for the exit of 1,4-pentadiene is shown in Scheme 13.

Scheme 13.

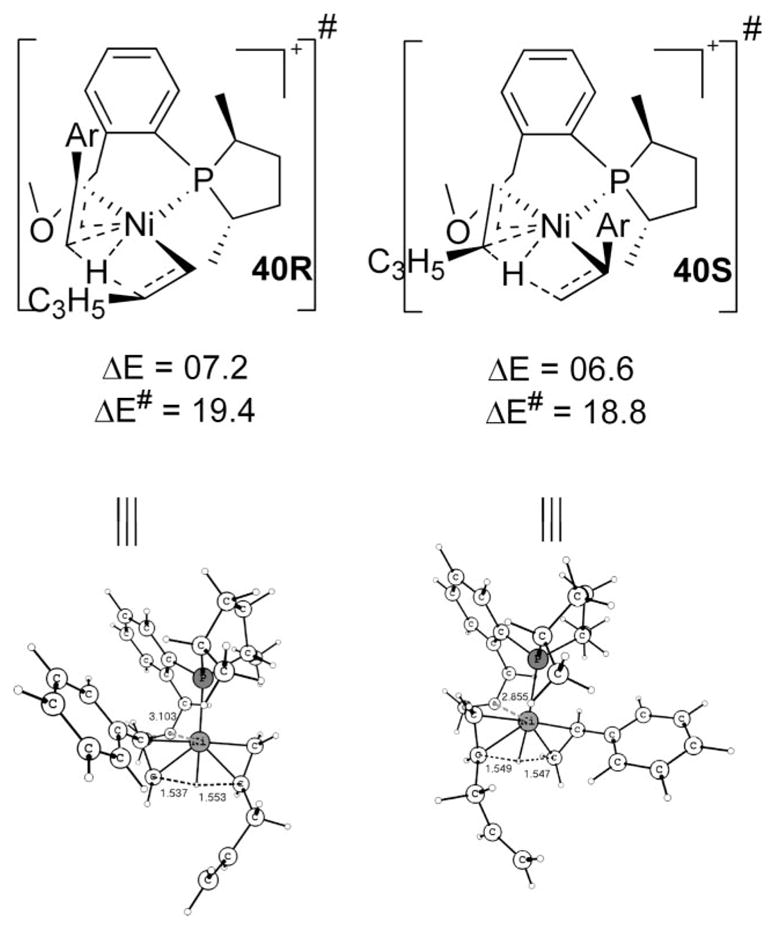
The Lowest Transition States for the Exit of Pentadiene

In Scheme 13, the putative β-hydride resulting from the expulsion of pentadiene is transferred directly to the styrene. It must be remembered that even in the “free metal hydride” path (D → E → F → G in Scheme 3) the hydrogen needs to be added to styrene for the hydrovinylation to proceed; thus transition state 40 in fact decreases the number of required steps in comparison to the “free” hydride path. Note that in this scheme the incipient η¹-benzyl is being formed at a position cis to the P, a favorable situation. Further, there is no genuine Ni–H bond. Both of these bonding situations enable decreasing of the barrier. Since a new chiral center is created, we have two diastereomeric possibilities. The energy of the transition state 40S is 18.8 kcal/mol, and it is 19.4 kcal/mol for the transition state 40R. Since no alternate lower route for the pentadiene’s exit could be located, and the barrier 18.8 kcal/mol is the highest among all steps in the initiation, transition state 40 corresponds to the rate-determining (turnover-limiting) step during the initiation stage. Although a model study (Scheme S5) also suggests that styrene has an inherent advantage to accept the transferred H, because of the possibility of steric repulsion in the actual case, we examined how ethene fares. The corresponding ethene transition states in the real system are slightly lower, but for the hydrovinylation to carry on, another H-transfer to styrene needs to ensue. These energies, though small (activation barriers 19.1 and 19.8 kcal/mol for S and R, respectively; see Scheme S6), are still higher than for the formation of 40R and 40S. It is assumed that two such discontinuous high-energy transition states would not be preferred over a single transition state. Besides, the concentration of ethene is lesser than styrene in the successful reaction conditions (cf. Scheme 2). Similar is the situation for the H-transfer to styrene with the alternate regioselectivity, where the second H-transfer has a barrier of 20.5 and 20.9 kcal/mol, respectively, for S and R (Scheme S6). The lowering in energy of 40 with respect to the above-described second H-transfer has been ascribed to the C–H---π hydrogen bonding possibility with the pentenyl double bond and styrene’s tail C–H.²²

Since styrene is involved at this stage and the H-transfer decides the enantioselectivity, we will comment on it. As displayed in Scheme 13, 40S is preferred slightly over 40R, which means during initiation there is an advantage for the S isomer (benzyl-Ni complex), but since the amount of active catalyst precursor 3 is only about 1 mol %, this outcome has little bearing on the final enantioselectivity of the reaction. The slight disadvantage of 40R is likely to be steric in origin, even though we cannot exactly pinpoint the particular groups in the complexes due to the fact that the ligand system is very flexible.

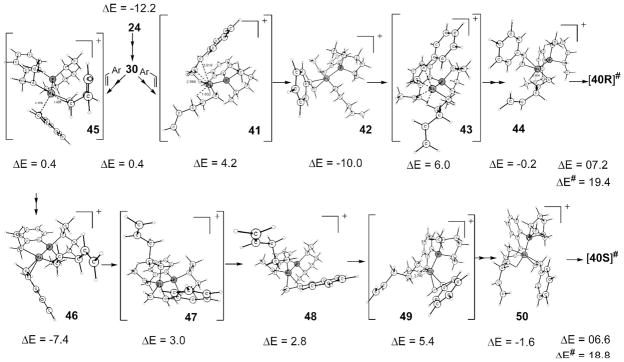
Scheme 14 depicts the details of the transformations that lead to 40 from the resting state 24. Approach to the transition state 40R from 24 is quite straightforward as shown. A direct substitution at 24 is not possible due to steric effects that prevent styrene π-electrons to make a close approach to the metal required for a concerted path. But 40R can be reached readily as follows: styrene can be incorporated into 30 (see Scheme 11), an intermediate with an agostic Ni • • • H bond alluded to earlier via transition state 41. Even though the agostic H in 30 removes some of the potential steric problems mentioned above, styrene replaces agostic H rather than O in a concerted fashion to give 42, because the trans agostic H is weaker than cis O and because there are fewer steric problems (farther from the rest of the ligand) associated with its replacement. Now a turnstile rotation (43) involving agostic H, styrene, and the hemilabile O results in 44, the penultimate intermediate for the transition state 40R.

Scheme 14.

Reaction Path to Reach 40 from 24

Reaching the corresponding 40S requires many more steps since the phospholane ligand is not able to rotate easily along the P–Ni bond when the coordination sites are occupied. But 40S can be attained as follows: unlike 41, styrene replaces the agostic H of30 in the required S fashion from the bottom (45) to reach the square-planar 46. Note that these square-planar styrene complexes are not as favored as the chelate pentenyl 24 (ΔE = −12.2 vs −7.4 and −10.0). Now a pseudo-trigonal-pyramid transition state, 47, similar to the previously described transition state 34, brings the system to 48. In contrast to 34, 47 fails to yield a square-planar structure directly because, instead of the restricted chelate in 34, two separate species are involved here, and so there are other intermediates possible before the square-planar intermediate. Intermediate 48 may be considered, at least for book keeping purposes, as a square pyramid with the P, styrene, agostic H, and O defining the square plane. The penultimate intermediate of the H-transfer transition state, 50, can be arrived at via 49, which may be regarded as the axial alkyl of the square-pyramid 48 replacing the hemilabile O at the cis position. It is clear from the energies in Scheme 14 that a flexible hemilabile group is required not only for providing the third active site for the H-transfer but to arrive at the transition states 40. A more rigid group would have rendered some of the transition states more energetic, and thus difficult to access.

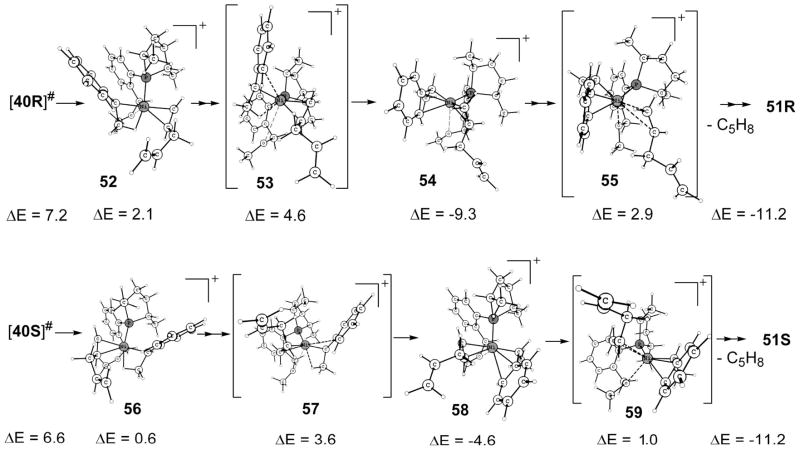
The next lowest intermediate after the above crucial H-transfer transition state is η³-benzylic 51 (Scheme 15). The intermediacy of η³-benzylic species has been assumed from exclusive regioselectivity (Ni placed at the benzylic position), which will be described in the next section. The η³-benzylic intermediate 51 can be reached as shown in Scheme 16. For 51R, first the transition state 53 takes the immediate intermediate from 40R, viz., agostic 52, to η³-benzylic 54 with pentadiene still attached in the cis position. The η³-benzyl 54, like η³-allyl, further undergoes a turnstile-type rotation, 55, effecting the pentadiene’s exit and O’s coordination to reach 51R. An analogous pathway from 40S leads to η³-benzylic 51S. The immediate intermediate of the H-transfer transition state, 56, changes to η³-benzylic 58 via transition state 57, a transition state from η¹-benzyl agostic to true η³-benzylic. Pentadiene exits from 58 by η³-benzyl rotation (59).

Scheme 15.

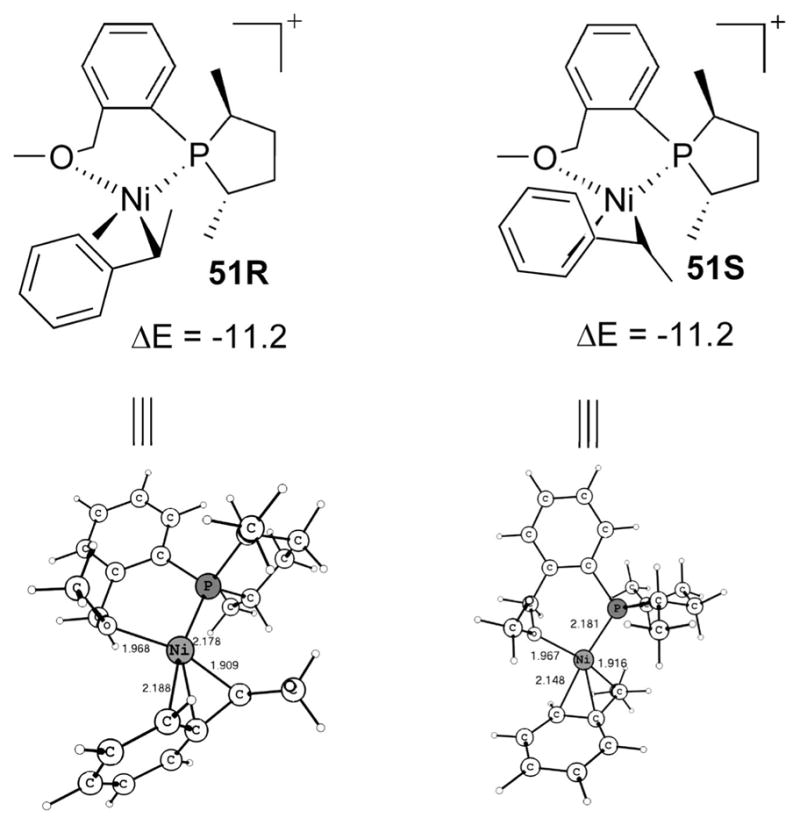
η³-Benzylic Intermediates

Scheme 16.

Reaction Path to η³-Benzylic Intermediates

Note that, although the η³-benzylic is not as strong as η³-allyl and is replaceable readily by an olefin, any olefin substitution has been found to be higher in energy due to steric effects from cis η¹-benzyl. So 51 is the lowest intermediate before any C–C coupling but is not the resting state since the lowest intermediate in the catalytic cycle comes only after the C–C bond formation thanks to the energy lowering achievable by a new C–C bond (Figure 2, vide infra). It may be emphasized that there is no clear-cut demarcation possible from initiation to actual reaction, as the real reaction starting at the point of styrene incorporation though the initiation was formally completed only at the exit of 1,4-pentadiene.

Propagation of Catalytic Cycle

Carbon–Carbon Bond Formation via the η³-Intermediate

The stage is set for the key carbon–carbon bond formation of the hydrovinylation reaction. Transition states 60R and 60S shown in Scheme 17 are the lowest for the C–C coupling. Thanks to the ability of phenyl to adopt multiple (η⁴ and η⁶) ligations, the barrier is only around 12 kcal/mol from the η³-benzyl intermediates. This situation is somewhat similar to the C–C coupling process in the initiation, where the hemilabile “O” helped the coordination problem; here the phenyl group itself can accommodate the needed changes. In fact reaching 60 involves a slightly higher barrier (Scheme 18), which still is much lower than the previous H-transfer; thus once 40 is crossed, it is effectively a downhill move and thus the small difference in energy for 60R and 60S also has no role in affecting the enantioselectivity of the overall reaction.

Scheme 17.

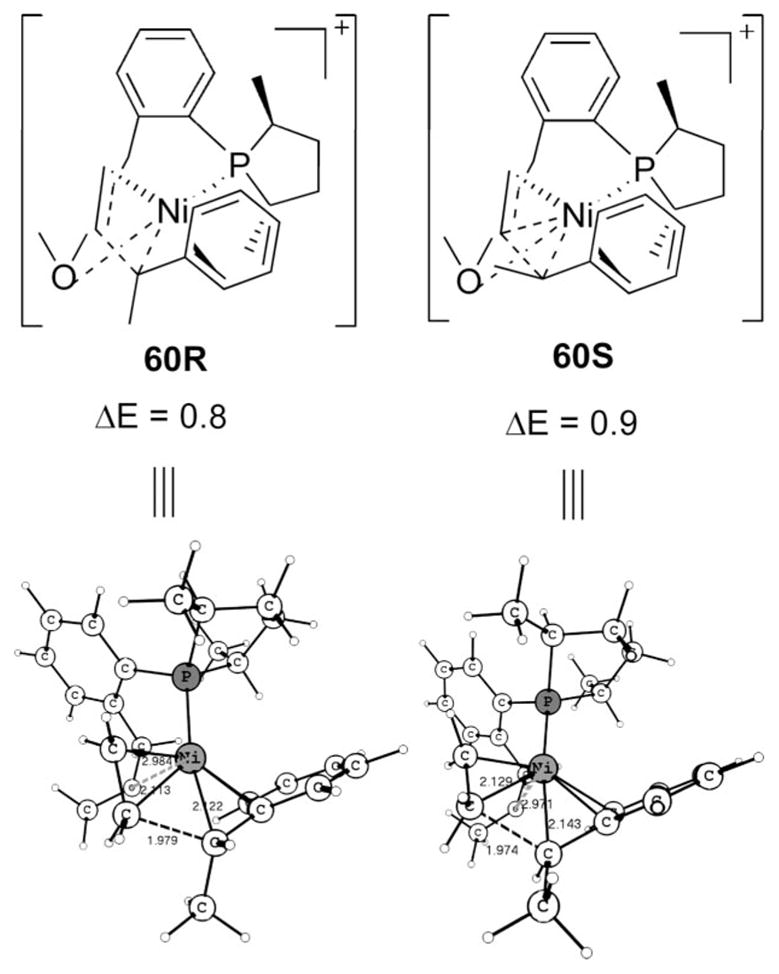
Transition States for C–C Bond Formation

Scheme 18.

Reaction Path Leading to C–C Bond Formation

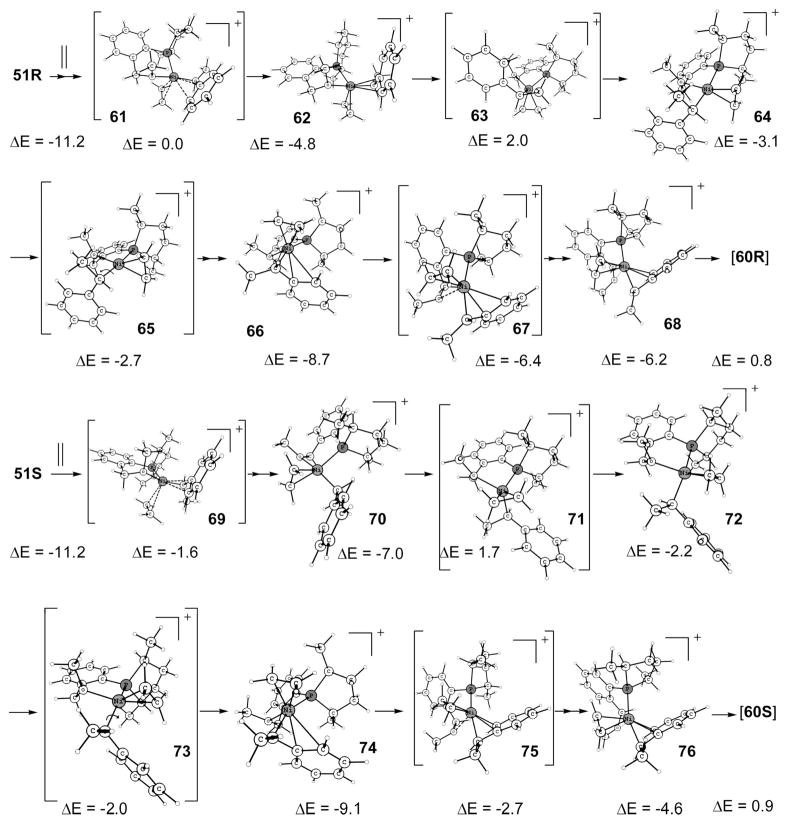
A look at the structures 51 and 60 makes it clear that many steps are needed to attain the C–C bond forming transition state. The first required step is to change the η³-benzylic orientation so that the sigma-bonded C, which undergoes reaction, is positioned trans to the phosphorus. Such a cis–trans conversion is difficult by the default tetrahedral transition states, which have barriers of 21.2 and 22.8 kcal/mol, respectively, for R and S (Scheme S7). We already know that a flexible olefin and alkyl together lowers the barrier for cis–trans interconversion (cf. 34 vs 10).¹⁹ In this case also, such a route involving ethene has been located. The trigonal-pyramid transition states 63 and 71, respectively, for R and S will accomplish this (Scheme 18). The resemblance of 63 and 71 to 34 rather than to 13 is another exemplification of the differences of η³-benzyl and η³-allyl ligands, the former being part of an aromatic system, where the π coordination is weak.

The η³-benzylic 51R can incorporate ethene as in 61 to give 62, which may be considered as a square pyramid with ethene in axial position. It may be noted again that unlike η³-allyl, η³-benzyl easily undergoes a synchronous transition for the reason described above. Intermediate 62 then goes through the trigonal-pyramid transition state 63 to reach 64, which is an almost perfect square-planar complex. Now ethene has to move into the left cis position from the right position now occupied to reach the lowest C–C coupling transition state conformation (60R). This is possible to accomplish by ethene first getting ejected out and then substituting hemilabile O in the next step. Since the ethene needs to be replaced from the cis position, the barrier is high, and higher than 63, so we searched for a route where ethene does not separate from the complex. In this path the square-planar 64 changes to square-pyramid 66, which is similar to 62 but with ethene in the opposite axial position. Now this axial ethene replaces the cis O via 67 to attain 68, the penultimate intermediate of 60R.

The intermediate 51S analogously incorporates ethene to become a square-pyramid intermediate and is changed to square-planar 70 for the trigonal-pyramid transition state 71, the highest transition state in this path. The immediate square-planar intermediate 72 passes through a rotational transition state 73 to arrive at the square-pyramid intermediate 74 (analogous to 66), which then removes the hemilabile O to yield 76, the intermediate before for C–C coupling.

Note that, as mentioned earlier, the transition states 63 and 71 are slightly higher than the C–C coupling, but both are lower than the previous H-transfer transition states; therefore we did not attempt any additional search for further lowering of this route, which anyhow appears to be unlikely. So in Figure 2 the C–C bond forming transition state is shown, and the peak labeled 60 represents the minimum barrier for the coupling.

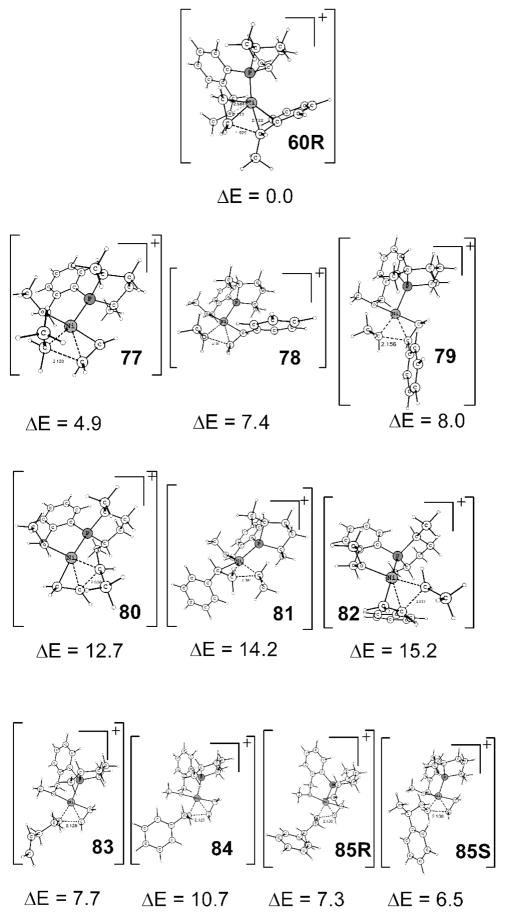
Regioselectivity

The absence of the formation of linear product and oligomerization/polymerization may now be understood. Scheme 19 shows transition states for the C–C coupling process (77–82) for ethyl with ethene and styrene—the substrates of the title reaction—in comparison with 60R. We chose ethyl as a representative of any possible alkyls that may be generated under the reaction conditions. Whether with styrene or ethene, or whether from cis or trans, the transition states 77–82 are all at least 4.9 kcal/mol higher than C–C bond forming transition state 60R for the hydrovinylation reaction. So, kinetically, they are simply not competitive. The reasons for the disadvantages of all other C–C bond forming transition states other than that involved in a η³-benzylic species can easily be attributed to the trans effect and loss of coordination. Note that 80, 81, and 82 are way too high in energy, as the incipient sigma metal–carbon bond is trans to phosphorus. For 77, 78, and 79 the only agostic H at trans position in the intermediate after the transition state is no match for an η⁶ (or other polydentate) bonding possible with 60.

Scheme 19.

Trans and Vacant Coordination Effect for C–C Bond Formation

For the mechanism to be rigorous, one has to consider whether 77–79 could be species present under the reaction conditions. Then the barriers for 78 and 79 are only 1.6 and 2.2 kcal/mol higher than the H-transfer transition state for the exit of pentadiene, 40S, and 77 is 0.9 kcal/mol lower than 40S. As a matter of fact, ethyl can form via an H-transfer from the pentadiene, which is 1.1 kcal/mol lower than 40S (vide supra). So a question may arise as to why 77–79 were not observed, since ideally a difference of about 3 kcal/mol excludes only a competitive path. We consider some of the reasons that the results in Scheme 19 will suffice to conclude that no other C–C coupling paths are competitive and to account for the fact that experimentally no other C–C coupling reaction is observed. (a) Computational limitation: comparisons of different kinds of transition states are less accurate than the same kinds of transition states, so the systematic error may be lowering the energies of transition states shown in Scheme 19 with respect to H-transfer transition states. (b) The assumptions involved in the transition state theory: the concept of a rate-determining step (in the case of a catalytic cycle, turnover-limiting step) is less valid when there are transition states of comparable energy. For 77–79 we already have the H-transfer transition state of comparable energy that is to be passed before the C–C coupling. Also there could be other comparable or higher transition states to achieve the path that leads to these C–C couplings. (c) The concentration of ethene is less in the solution; so practically, 77, which involves two ethenes, is more difficult than the above data suggest. Note that with pentenyl, 83, a transition state to be considered before the pentadiene’s exit, the barrier for C–C coupling increased by another 2.8 kcal/mol. Transition states 78 and 79 indicate that styrene is less likely to undergo C–C coupling due to steric effects, so with pentenyl they all make it more than 3 kcal/mol higher than 40S. Similar to 83, the linear hydrovinylation transition state 84 is 4.9 kcal/mol higher than 40S and hence not at all competitive. Transition states 85R and 85S are relevant after the hydrovinylation C–C coupling. They too are higher than the exit of hydrovinylation product (see below) transition states: 85R by 3.2 kcal/mol relative to 99RS, and 85S by 2.0 kcal/mol relative to 99SR. We conclude here that the trans effect and vacant coordination problem control the regioselectivity; so the exclusive outcome in the reaction, thanks to our custom-made catalyst, is hydrovinylation. It must be remembered that Ni(II) is versatile in C–C coupling ability and different ligand systems lead to different regioselectivity. So unlike oligomerization²³ and polymerization,²⁴ hydrovinylation requires a hemilabile group and a strong trans-directing ligand so that we have the correct requirements of an easy exit of product by a β-H transfer (using three coordination sites) than any C–C coupling, except the one involving an η³-allyl or η³-benzyl (again using three coordination sites).

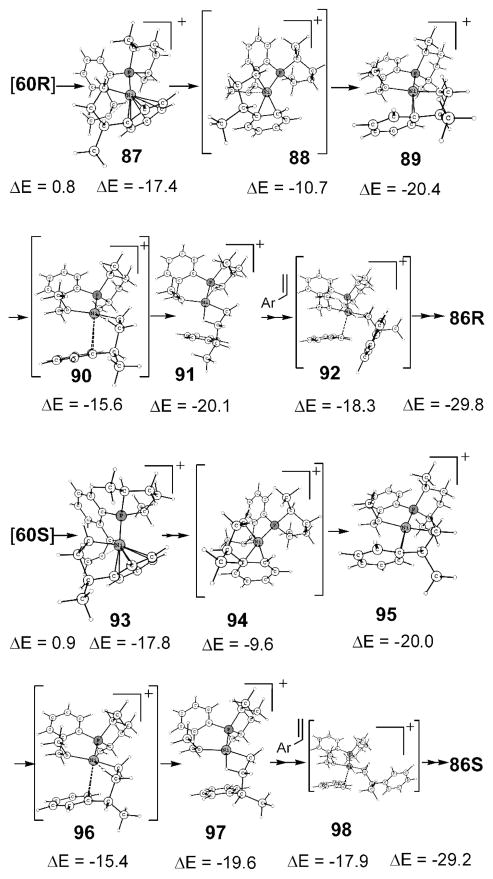
Exit of Product from Catalyst

Structures 86R and 86S in Scheme 20 represent the lowest intermediates after the C–C coupling, and the activation barrier for the exit of product should be measured from there. These intermediates can be reached as shown in Scheme 21. The immediate intermediates after the C–C bond formation are 87 (for R) and 93 (for S), which as described earlier may be considered as η⁶ or η⁴, effectively occupying the available two coordination sites in a square-planar complex.

Scheme 20.

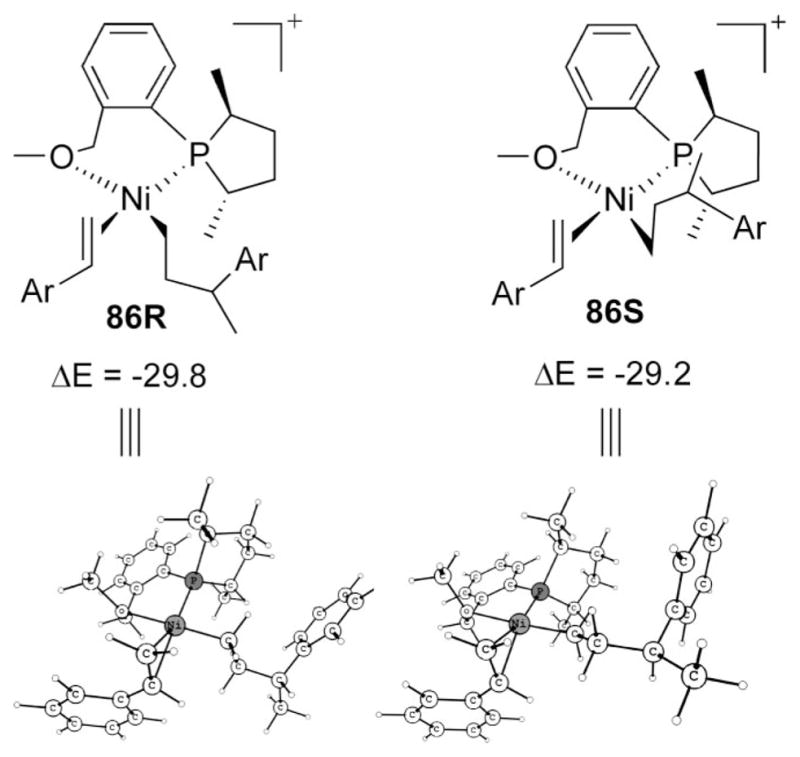
Lowest Intermediate before the Exit of Product

Scheme 21.

Path Leading to the Lowest Intermediates

Intermediate 87 from 60R (and correspondingly 93 from 60S) is readily convertible to η² structures, still maintaining tetra-coordination via transition state 88 (and 94). Unlike a strong olefin ligation in analogous 24, η²-coordination of phenyl is weak, and consequently the lowering of 89 (and 95) is less than the changes in 24, the resting state during initiation. Styrene or ethylene coordination more resembles 24. We found styrene has a slight edge over ethene, and so 86 is the lowest intermediate. Intermediate 89 can easily support agostic stabilizations via transition state 90. The same is true with 95 and 96. Styrene incorporations in agostic 91 and 97, respectively, for R and S isomers, lead to the lowest intermediates before the product’s exit. Intermediate 86 is in fact the lowest state in the catalytic cycle, and thus we assign this to be the global resting state of the catalyst.

Enantioselectivity

As expected from the forgoing discussion, the exit of product through a β-hydride route is prohibited. The barriers now are 32.6 and 31.3 kcal/mol for the direct path for R and S (Scheme S8). For the alternate β-hydride path the corresponding barriers are 23.0 and 22.8 kcal/mol (Scheme S8). The lowering of energy in this path compared to 36 in the initiation step is due to the ease of ethene to interact with cationic Ni(II) than the chelate olefin, which is not as flexible and so not positioned well. (Because η²-phenyl is a very weak ligand, ethene intermediacy is required to lower the energy to the present value in this cis-hydride path.)

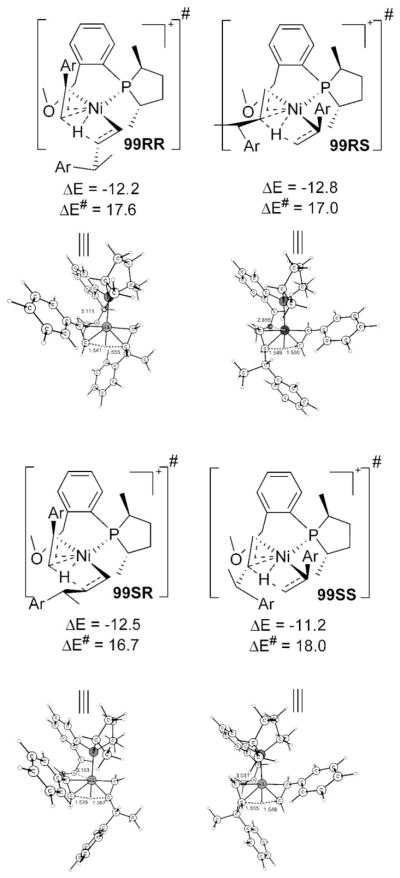
The rate-determining β-H transfer transition states for the exit of product are shown in Scheme 22. The barrier here is lesser than that during the initiation, partially due to the fact that the intermediate 86 is not as low with respect to 99 as the chelate 24 is with respect to 40 (cf. Scheme 13) and may be partially due to the improved C–H---π interaction with phenyl over pentenyl. It is to be noted that the energy of 99SS is the highest despite that styrene is positioned in the right cis coordination site, which is less congested. The reason is that, to maintain the hydrogen bond, the group has to orient as pictured and causes extra steric congestion with –O-Me at the bottom. Again, as in initiation, ethene intermediacy necessitates a second H-transfer transition state, which is higher in energy and more so than initiation thanks to a better hydrogen bond with Ph in 99 than is possible with pentenyl. Contrast the respective barriers displayed in Scheme 22 with ethene intermediacy barriers: 99RR 19.6, 99RS 18.9, 99SR 19.0, and 99SS 18.3 kcal/mol (cf. Scheme S6).

Scheme 22.

β-H Transfer from Product to Styrene

Since an intermediate with R configuration in the early stages of catalyst generation prefers to give the S product in the next C–C coupling stage, and vice versa (see Scheme 22), an estimation of the enantioselectivity is not straightforward. A detailed analytical derivation for the enantioselectivity based on the computational results on the barrier is beyond the scope of the present study. But it can be surmised that formation of R is easier than S because the resting state 86S is higher than 86R and because 96SS is unfavorable. Or to put in a less rigorous way, the average activation barrier leading to product R (17.2 kcal/mol) is lower than that of S (17.5 kcal/mol). So we conclude that the computation, despite its limitations, faithfully reproduces the experimental trend for enantioselectivity thanks to the protocols used in the calculation, which compares similar transition states along the reaction coordinates, thereby eliminating many of the errors. Since the enantioselectivity is determined by steric effects in a composite way due to the flexibility of the ligand system, even a simple modification in the ligand could alter the energies of various transition states in this complex reaction, and this has been experimentally validated.^2,3 It is premature to suggest suitable candidates for better enantioselectivity without doing adequate calculations on the new reaction path for each of the proposed ligands.

The path leading to transition states 99 and the formation of η³-benzylic 51 from the transition states are similar to the corresponding path involving the pentenyl intermediates described in Schemes 14 and 16, respectively. These paths are given in the Supporting Information as Schemes S9 to S12.

Summary and Conclusion

Figure 2 summarizes the reaction profile. Square-planar η³-allyl complex 3, the sole diastereomer of the active catalyst present before the addition of olefins, reacts with ethene via transition state 19 to yield the square-planar 24, which is the resting state during initiation. Pentadiene’s exit from 24 involves the rate-determining H-transfer transition state 40, which leads to η³-benzylic 51. The originally proposed β-hydride elimination requires prohibitively high energy, and we suggest that this is not feasible along the reaction coordinate. The activation barrier for the new initiation is 18.8 kcal/mol. The hydrovinylation reaction continues by the incorporation of ethylene at η³-benzylic 51 and a subsequent low-barrier C–C coupling (60). Unlike 60, any other C–C coupling has a much higher barrier due to the trans effect of the ligand and a resultant vacant coordination that explains the regioselectivity. The next lowest intermediate (the resting state), 86, is attained by the incorporation of styrene. Exit of the product requires H-transfer transition state 99, and this is the rate- and enantio-determining step for the reaction. The barrier of 16.7 kcal/mol is lower than that of initiation, and considering the effect of entropy excluded in the initiation barrier, computation suggests a definite induction period for the catalysis. The possible isomerization of product, a recurrent problem in metal hydride reaction paths and often observed with hydrovinylation reactions catalyzed by other metals such as Pd(II), is prevented because soon after the H-transfer transition state 99 it is a downhill process (cf. 99 → 51 → 60 → 86). In other words, once the β-H of the product is transferred to styrene, there is no recovery for that hydrogen to transfer back to the product. Another interesting aspect of this reaction is that the configuration of the product present in one cycle affects the enantioselectivity in the next cycle, and so the enantiomeric excess of the product varies as the reaction progress.

An examination of the originally proposed mechanism (Scheme 3) reveals that most of the major conjectures remain in tact, the main difference being how the β-hydrogen from the η¹-Ni complex-carrying product (I, Scheme 3) is transferred to a new product. There is little support for the formation of a free-standing [L_nNi–H]⁺ (E, Scheme 3). A concerted mechanism in which the H-transfer from I takes place directly to the prochiral faces of the styrene appears to be the path of least activation energy. However, this introduces a new complication in the mechanism in that the penultimate intermediate before ejection of the product has three chiral entities involved (e.g., 86), two from the substrate and one from the ligand. The initiation involves the formation of two diastereomeric complexes (51R and 51S) even before the prochiral faces of the substrate of the formal catalytic cycle are encountered, and these complexes are necessarily parts of a productive catalytic cycle, not a simple metal hydride (E, Scheme 3) as was initially assumed in the working model.

To accommodate these findings, we modify the original proposal as shown in Scheme 23.

Scheme 23.

Modified Mechanism of Hydrovinylation of Vinylarenes

In conclusion, we hope that the present study fulfills several gaps in our understanding of the hydrovinylation reaction. We expect this study to help with further mechanistic studies directed at improving the substrate scope, efficiency, and selectivity of this important reaction. Such studies are in progress.