Is Iterative Reconstruction Ready for MDCT?

INTRODUCTION

Although the very first computed tomographic scanners used the iterative algebraic reconstruction technique, the filtered back-projection (FBP) method soon became the gold standard for computed tomographic reconstruction. Image quality has dramatically improved over the past 30 years thanks to advances in x-ray tubes, detector technologies, and overall system design and integration, as well as refinements to image reconstruction algorithms. Typical effective dose values range from 5 to 7 mSv for chest computed tomography (CT) and from 8 to 12 mSv for abdominal and pelvic CT, compared with 0.02 to 0.2 mSv for chest x-ray, making CT a comparatively high-dose modality.

Nearly 68.7 million CT procedures were performed in the United States in 2007 [1]. The number of CT procedures has been increasing dramatically in the United States, by nearly 10% annually, since the commercial introduction of multirow detector CT scanners. Because of this significant increase in the use of CT, there is concern about radiation exposure to the population. Methods to reduce radiation dose and at the same time retain comparable image quality are being actively pursued both in academia and in the industry. In the past decade, thanks to increasing computational power, statistical iterative reconstruction (IR) has become a hot research topic in CT, with a focus on noise suppression, artifact reduction, and dual-energy or energy-sensitive imaging. Some of these efforts are now under translation from bench to bedside.

ITERATIVE RECONSTRUCTION TECHNIQUES

Similar to the FBP algorithm widely used in MDCT, IR is a method to reconstruct 2-D and 3-D images from measured projections of an object. Unlike the FBP algorithm, which is based on the theoretical inversion of the Radon transform, IR starts with an initial guess of the object and iteratively improves on it by comparing the synthesized projection from the object estimate with the acquired projection data and making an incremental change to the previous guess. The method has been applied routinely in emission tomography modalities such as single-photon emission CT (SPECT) and positron emission tomography (PET). In x-ray CT, this method is not currently used in commercial scanners, largely because of its high computational cost. For a comparison, if the computational cost of FBP is measured as 1, the cost of IR to generate an image with similar quality can be measured on a scale of 100 to 1,000 [2].

However, there are undeniable advantages of IR methods compared with FBP. In emission modalities such as SPECT and PET, IR techniques, together with accurate modeling of image-degrading factors, such as tissue attenuation, scatter, and partial volume effects, have been demonstrated to improve both image quality and quantitative accuracy [3]. It is reasonable to assume that similar benefits are available for MDCT. The hypothesis of the advocates of IR for x-ray CT is that by using a realistic data acquisition model incorporating the various image-degrading factors, IR for MDCT can achieve superior image quality to its analytical counterparts, such as FBP, and at a similar or even lower radiation dose level.

A natural question is how IR makes this possible. Two frequently used image-quality indices are image noise and resolution. Good image quality demands lower image noise and better image resolution. Reconstructed image noise is affected by many factors; the two most relevant here are radiation dose and image-processing methods, such as the reconstruction algorithms. The higher the radiation dose, the lower the image noise if all other factors remain the same. The FBP algorithm implicitly regards the acquired projection data as noise free, which is a good approximation at high radiation dose levels, when the statistical fluctuation of the x-ray photon noise is negligible. As the radiation dose gets lower, the acquired raw data depart from the noise-free assumption, and the reconstructed images exhibit the streaking artifacts commonly seen in low-dose images. Statistically based IR methods, on the other hand, can model the uncertainty in raw projection data and incorporate such statistical considerations in the IR algorithm, so that the final reconstructed images are more robust to data noise and therefore fewer streaking artifacts [5]. The reconstructed image resolution is also influenced by many factors, most obviously the data sampling pattern, such as the slice thickness and the number of projection views. More importantly, the image resolution depends on the finite size of the detector cell, the focalspot size of the x-ray tube, and image-processing methods. Analytical FBP algorithms assume that the acquired data are the ideal line integrals of rays that connect the point focal spot at one end and the point detector cell at the other. In fact, the acquired projection data are more realistically modeled as a strip integral connecting the finite-sized focal spot and the finite-sized detector element. In an IR method, it is possible to approximate this strip integral by subdividing the finite size of the focal spot and the detector into a number of sublets, and the total strip integral is the sum of all the partial contributions from the sublets. This accurate image acquisition model can be built into the formulation of an IR method, and the final reconstructed images can better delineate the object details and achieve better resolution. Recent advances in statistical IR promise to achieve dramatic improvements in image quality, as illustrated in Figure 1.

Fig 1.

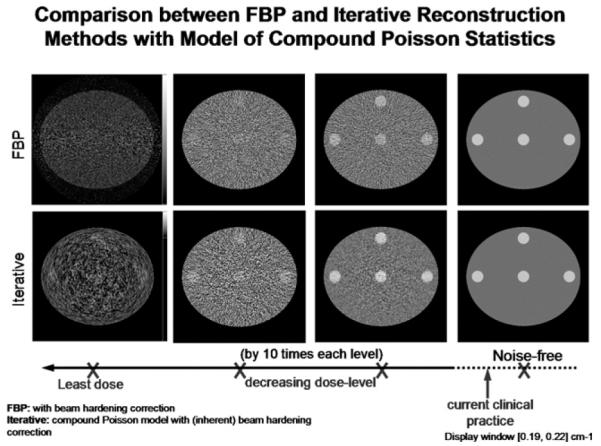
A simulation study comparing reconstructed images at different radiation dose levels. (Top row) Conventional FBP reconstruction; (bottom row) statistical IR [4]. The images in the fourth column are from noise-free projection data. The dose increases by 10 times each from the first to the third column. The advantage of statistical IR methods over FBP methods is demonstrated at lower radiation dose levels (images in the 1st-3rd column). The clinical dose level is shown schematically on the horizontal dose axis.

Image noise and image resolution are two conflicting factors of image quality. Lower image noise can be obtained at the expense of poorer image resolution, and vice versa. If one wants to declare that a particular reconstruction method is superior to another, it is meaningful only to compare the reconstructed image noise at a fixed resolution, or to compare the image resolution at the same reconstructed noise level. Therefore, the hypothesis of the IR advocates is more precisely read as “IR for MDCT can achieve a superior noise resolution trade-off than its analytical counterparts, such as FBP.”

In studies to optimize IR for CT imaging and comparing its performance with FBP algorithms, IR demonstrated more than 6-fold lower noise compared with the best resolution FBP algorithm while improving spatial resolution, by 10% in the axial plane (the x-y plane) and 40% in the longitudinal direction (the z-axis) [5]. Compared with a standard FBP algorithm, IR achieved 50% lower noise and 90% higher resolution in the axial direction and 40% higher resolution in the longitudinal direction [5]. It is expected that the full implementation of IR will revolutionize CT imaging, achieving lower than ever x-ray doses and better than ever image quality.

PRACTICAL CONCERNS

Several factors have prevented statistical IR from being deployed on CT products so far. The first is the high computational cost, about 2 to 3 orders of magnitude larger than that of FBP. To increase the computational speed, researchers have looked into using the Cell processor engine (STI, Austin, Texas), commodity graphics processing units, or custom-built field programmable gate arrays to hard-code the computational extensive part in an IR method. Significant increases in speed have been reported in published works. It is expected that the first product realizations can produce reconstructed images on the order of tens of seconds per reconstructed slice.

The second factor is the robustness of iterative algorithms across different protocols and applications. Currently, some parameter tuning may be needed for the practical use of an iterative method in a specific application. The best imaging performance is sometimes sensitive to the particular choice of parameters.

The third factor is the potentially new look of statistically reconstructed images. Because images are reconstructed in a statistically optimal fashion, their noise and artifact characteristics can be rather different from those obtained using the FBP algorithm. Radiologists are used to FBP image appearance and the associated various image-quality trade-offs. Consequently, statistical reconstruction may give an impression of somewhat reduced diagnostic value in certain cases.

CONCLUSIONS

In perspective, IR offers distinct advantages relative to analytic reconstruction in important cases in which data are incomplete, inconsistent, and rather noisy. Even in cases in which analytic reconstruction performs well, there is no fundamental reason why IR would perform any worse. It provides an opportunity to further lower the scanning techniques, yielding lower radiation doses during CT examinations. Scanner manufacturers are currently developing various IR methods for image reconstruction, and it is only a matter of time before IR becomes widely available on commercial CT scanners. Hence, we predict that the fast development in computing methods and hardware will lead to a paradigm shift from analytic to statistical reconstruction, or at least a fusion of analytic and iterative approaches. In spite of the high computational cost and the time needed for radiologists to adapt to this new technology, the increasing concern for radiation dose in CT will certainly enhance the adoption of this technology more rapidly.