Abstract
Supraspinatus tendon tears are complex yet common. We have shown that the supraspinatus and infraspinatus tendons interact, indicated by parallel changes in strain in the supraspinatus and infraspinatus with increasing size of supraspinatus tear, load applied to the supraspinatus, and changes in glenohumeral rotation but not abduction angle, suggesting disruption in the interaction between the two tendons with increase in abduction angle. While considering these factors individually is valuable, the contribution of each factor in the context of all others on strain in the supraspinatus, or on the interaction between the two tendons is unknown and has important implications in the management of rotator cuff tears. In this study, regression models using least-square estimation with backward and forward elimination were used to predict strains in the infraspinatus and supraspinatus from joint position, supraspinatus load, and supraspinatus tear size or repair. Interestingly, despite previous findings showing that supraspinatus tear size significantly affects infraspinatus strain, tear size was not a significant predictor of infraspinatus strain, emphasizing the importance of other factors evaluated such as joint position and shoulder loading in management of cuff tears and postoperative care. A better understanding of the loading environment in rotator cuff tendons necessitates multifactorial complex models.
Keywords: Rotator cuff, Glenohumeral abduction, Glenohumeral rotation, Principal strain
INTRODUCTION
Supraspinatus tendon tears are a common and not well understood soft tissue injury.6–9 The high incidence of rotator cuff tears has motivated evaluation of the likelihood of tear propagation, which would influence surgical intervention. To address this problem, strain was used to measure the load-bearing capacity in the torn supraspinatus tendon.4,12 However, the inhomogeneity of the supraspinatus tendon and the complex loading environment of the rotator cuff confound the predictability of rotator cuff tear propagation.
Because of its high incidence of injury, several studies have investigated the effect of a supraspinatus tendon tear on the remaining intact portion of the tendon to understand changes in its loading environment due to a tear.4,12 Strain, indicative of the load-bearing response of the remaining intact portion of the tendon, was calculated in order to infer the risk of tear propagation. However, despite the importance of this data, assessing the likelihood of tear propagation is further complicated by the complex loading environment and the tissue architecture of the rotator cuff. For instance, the interaction between the humeral head and the torn supraspinatus tendon has been shown to decrease the effect of a supraspinatus tendon tear on tendon strain at certain joint positions.4 Therefore, other rotator cuff structures may impact the likelihood of supraspinatus tear propagation and reciprocally be impacted by the existence of a supraspinatus tendon tear.
Our previous findings indicate that the supraspinatus and infraspinatus tendons mechanically interact such that conditions that result in increased strains in the supraspinatus tendon also result in increased strain in the infraspinatus tendon.1–3 More specifically, such interaction existed with increase in supraspinatus tendon full-thickness3 and partial-thickness tear size,1 two different repair techniques, increase in supraspinatus tendon load,1,3 and change in joint rotation angle. We have also shown that the mechanical interaction between the two tendons is interrupted with increase in joint abduction angle. While considering these factors individually is valuable, the contribution of each factor in the context of all others on strain in the supraspinatus, or on the interaction between the two tendons is unknown and has important implications in the management of rotator cuff tears.
Regression models provide statistical quantification of the relationship between a response (dependent) variable and predictor (independent) variable(s). Such model(s) allow simultaneous evaluation of the relationship between a dependent variable and several independent variables. Development of a multiple regression model to predict the effect of supraspinatus tendon load, tear size, and joint position on strain in the supraspinatus and infraspinatus tendons would have significant clinical implications, since it would demonstrate the level of contribution of each factor in the context of all other factors. Using the developed model(s), clinical management of supraspinatus tendon tears can be efficiently and optimally focused to target the factors that have the most impact on strain in the supraspinatus and infraspinatus tendon. Additionally, the developed regression model(s) also allows extrapolation to predict the effect of conditions that have not been experimentally evaluated resulting in more guiding data than can be practically collected experimentally. Therefore, the objective of this study was to develop multivariate regression models of infraspinatus and supraspinatus tendon strain as a function of supraspinatus tendon load, tear type or repair technique, and rotator cuff joint position. We hypothesize that (H1) supraspinatus tendon tear type, load, repair technique, and joint position will all be significant predictors of strain in the infraspinatus tendon; and that (H2) supraspinatus tendon tear type, load, repair technique, and joint position will all be significant predictors of strain in the supraspinatus tendon.
MATERIALS AND METHODS
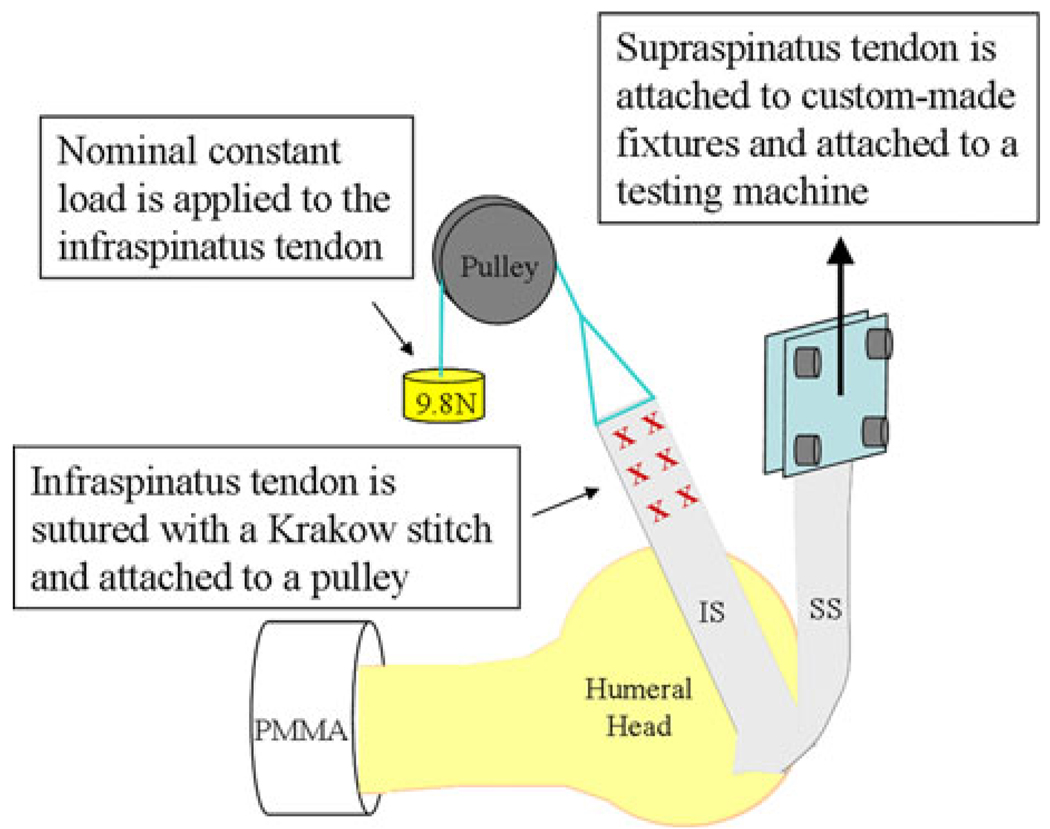
All experimental methods were previously described in detail.1–3 Briefly, 10 healthy, fresh-frozen cadaveric shoulders (average age 48.7 ± 15.1 years) were carefully dissected free of soft tissue, retaining only the proximal humerus, supraspinatus, and infraspinatus tendons. The proximal end of the infraspinatus tendon was sutured using a Krakow stitch to allow application of a load. Prior to mechanical testing, the specimens were maintained in a physiologic bath of phosphate-buffered saline (PBS). The experimental setup is shown in Fig. 1.
FIGURE 1.
Schematic representation of experimental setup.
The bursal side of both the supraspinatus and the infraspinatus tendons was air-brushed with black paint to create a fine speckled texture for subsequent texture correlation strain analysis using Vic2D (Version 4.4.1, Correlated Solutions Inc., Columbia, SC) as previously described.1–3
The specimen was mounted in poly-methyl methacrylate (PMMA) in custom grips that allowed for repeatable and controlled changes in glenohumeral abduction and rotation.1,2 The supraspinatus tendon was attached to a testing machine (5543, Instron, Norwood, MA) to allow for controlled loading and the infraspinatus tendon was attached to a pulley system with a nominal, constant load of 9.8 N.1–3
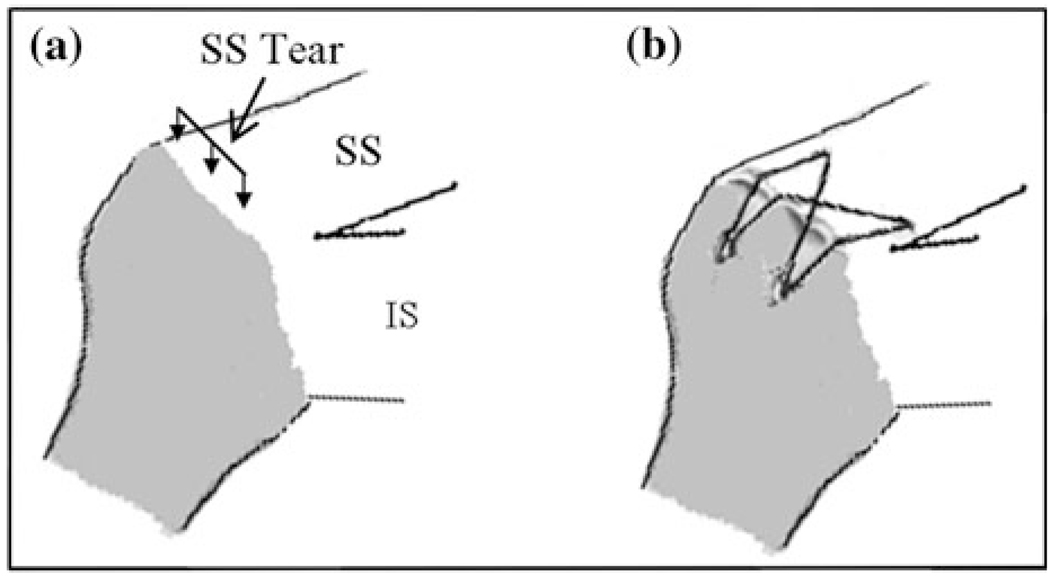
Supraspinatus tendon loading protocol, previously described, consisted of preconditioning followed by a constant ramp to 90 N at a strain rate of 0.1% per second of the length of the tendon.1–3 Loading protocol was applied for the intact, 33%, 66%, and 100% bursal-side partial thickness tears through the anterior 66% of the width of the supraspinatus tendon and for two supraspinatus repairs (modified Mason-Allen with transosseous bone fixation or 4-suture-bridge suture-anchor as often used in arthroscopic repair; Fig. 2). Each supraspinatus tear and repair were evaluated at each of the following joint positions: (1) neutral rotation with 0°, 30°, and 60° abduction2; and (2) 0° abduction with 0°, 30° internal, and external rotation1. These joint positions were evaluated because they provided a good sampling of the interaction between the supraspinatus and infraspinatus tendons as their respective relationships to the humeral head was altered. Both tendons were generously moistened with PBS after each completion of the loading protocol.
FIGURE 2.
Schematic representation of (a) 4-suture-bridge suture-anchor as often used in arthroscopic repair, and (b) supraspinatus tendon tears. Bursal-side partial thickness tears through the anterior 66% of the width of the supraspinatus tendon were surgically introduced through the 0% (intact), 33%, 66%, or 100% of the thickness of the tendon.
As previously described, digital images were taken of the insertion site of both the supraspinatus and the infraspinatus tendons at 1 s intervals during the loading ramp phase of the mechanical testing protocol.1–3 For each supraspinatus tendon tear level and joint position, images at 5, 30, 60, and 90 N of supraspinatus tendon loads were chosen for evaluation for the infraspinatus and supraspinatus tendons. Similarly, for transosseous and arthroscopic supraspinatus tendon repairs, images at 5, 30, 60, and 90 N of supraspinatus tendon loads were chosen for evaluation at each joint position for the infraspinatus tendon only. Local strains in the repaired supraspinatus tendon could not be evaluated due to tendon buckling at the repair site.
A digital grid of nodes was then fitted to the insertion site of the infraspinatus and the consistently intact posterior 1/3 of the supraspinatus tendons as previously described.3 Displacements of the nodes between the 5 N load and each of the 30, 60, and 90 N loads were determined from which two-dimensional Lagrangian finite strain tensor (εxx, εyy, and εxy) and principal strain components were calculated.1,2 Average maximum and minimum principal strains were determined for the regions of interest in both tendons, thereby completely and simply depicting the loading environment by absorbing the shear strain component into the orthogonal tensile (maximum principal strain) and compressive (minimum principal strain) components through a coordinate rotation.
Using the collected strain data, the following multiple regression equation was used.
| (1) |
where i = 1, 2 represents average maximum and minimum principal strain, respectively; j = 1, 2 represents supraspinatus and infraspinatus tendons, respectively.
Cij represents constant, β1ij, β2ij β3ij, and β4ij are the regression coefficients calculated from each of the regression models. Abduction angle and rotation angle are represented by Abd_angle (0°, 30°, or 60°) and Rot_angle (internal rotation: −30°, and external rotation: 30°), respectively. Load was inputted in Newtons, and tear size was inputted on a scale of 1–100. Equation (1) produces four different regression models (four models from two tendons and two mechanical parameters: maximum and minimum principal strain). In addition, the following multiple regression equation was used:
| (2) |
Equation (2) produces two different regression models (for the infraspinatus tendon and two mechanical parameters: maximum and minimum principal strain).
Summary statistics of all variables were examined and described by mean, median, standard deviation, minimum and maximum to ensure that assumptions necessary for linear regression analysis were met. For each experimental condition, average maximum and minimum strain value of all 10 specimens was calculated each tendon, yielding a total of 60 y-values inputted into regression model 1, and 30 y-values inputted into regression model 2. Standard deviation for each data point was calculated and used for model assessment as will be discussed below. Multiple linear regression models were used to quantify the relationship between the dependent variables (principal strain) and the predictor variables (supraspinatus load, tear size or repair technique, joint rotation, and joint abduction). Regression models utilizing least-square estimation with backward and forward elimination were used to predict strain values.10 In this method, a simple linear regression model is first fit for each of the potential independent variables. For each simple linear regression model, partial F statistic (F*) is calculated to determine whether or not the slope is zero. An independent variable with the largest F* is identified and compared to a predetermined value of F to enter. If F* exceeds F then the variable is added to the regression model, and the analysis is repeated for the additional independent variables. If F* does not exceed F to enter, stepwise analysis terminates. After each independent variable is added, the analysis is repeated for all the independent variables with revised model. F* is calculated for the previously included variables, and compared to a predetermined value of F to remove. If F* falls below the predetermined value of F, the variable is removed from the model. Tolerance level was set at 0.01, preventing entry of highly correlated independent variables in the model. Based on the degrees of freedom, F to enter and to be removed were, respectively, set to 4 and 3.9, corresponding to a significance level of 0.05 for a single test. Significance was set at p ≤ 0.05 and a trend at p ≤ 0.1.
Additionally, Durbin Watson (DW) statistic was calculated to identify the existence of correlation between independent variables included in the model. For Eq. (1) (n = 60), based on established guidelines for interpretation of DW statistic,11 a DW value lower than 1.55 indicated correlation between the independent variables. Similarly, for Eq. (2), a DW value lower than 1.35 indicated correlation between the independent variables.11
The robustness of the model was evaluated by randomly selecting and removing 3 of 60 data points (for the supraspinatus tendon tear cases) or 2 of 30 data points (for the supraspinatus tendon repair cases) at a time and recalculating the regression coefficients for a total number of five trials. This number of data points was removed at a time because regression coefficients calculated without this number of data points did not differ from those calculated including these data points. The model was then used to predict the removed data points, and the results were compared with the actual values as a way to assess model stability. The prediction was considered accurate if the predicted value was within 1 standard deviation of the actual value.
RESULTS
In general, glenohumeral abduction angle and supraspinatus tendon load consistently correlated with both, supraspinatus and infraspinatus tendon strain. Results shown in Tables 1 and 2 will be discussed in detail below. Shown R2 (coefficient of determination) values represent the contribution of the set of independent variables in describing the variability in the dependent variable. The significance of the overall model fit is indicated by the p values.
TABLE 1.
Significant coefficient (β) results using multiple regression analysis for strain in the infraspinatus and supraspinatus tendon with supraspinatus partial-thickness tear.
| Dependent variable | Model P | Model R2 | Glenohumeral abduction angle (β) |
Joint rotation angle (β) |
SS load (β) |
SS partial-thickness tear size (β) |
|---|---|---|---|---|---|---|
| Average maximum principal strain in IS | 0.001 | 0.68 | −0.05 | 0.03 | 0.019 | – |
| Average minimum principal strain in IS | 0.001 | 0.66 | 0.05 | – | 0.02 | – |
| Average maximum principal strain in SS | 0.001 | 0.35 | 0.04 | – | 0.06 | – |
| Average minimum principal strain in SS | 0.001 | 0.72 | 0.06 | −0.05 | −0.05 | −0.01 |
P = model significance; R2 = correlation coefficient of model.
SS Supraspinatus tendon; IS Infraspinatus tendon.
TABLE 2.
Significant coefficient results using multiple regression analysis for strain in the infraspinatus tendon with supraspinatus repair.
| Dependent variable | Model P | Model R2 | Glenohumeral abduction angle (β) |
Joint rotation angle (β) |
SS load (β) |
SS repair technique (β) |
|---|---|---|---|---|---|---|
| Average maximum principal strain in IS | 0.001 | 0.85 | −0.04 | 0.03 | 0.02 | 0.47 |
| Average minimum principal strain in IS | 0.001 | 0.77 | 0.03 | – | −0.01 | – |
P = model significance, R2 = correlation coefficient of model.
SS Supraspinatus tendon; IS infraspinatus tendon.
Correlations Between the Independent Variables Including Supraspinatus Tendon Tear, and Infraspinatus Tendon Strain
Glenohumeral abduction angle, joint rotation and supraspinatus tendon load were all significant predictors of average maximum principal strain in the infraspinatus tendon. DW statistic of 2.15 was calculated, indicating no correlation between the independent variables included in the model. Similarly, glenohumeral abduction angle, and supraspinatus tendon load were predictors of average minimum principal strain in the infraspinatus. A calculated DW statistic of 1.84 indicates no correlation between the independent variables. Results are shown in Table 1.
Correlations Between the Independent Variables Including Supraspinatus Tendon Tear, and Supraspinatus Tendon Strain
Glenohumeral abduction angle and supraspinatus tendon load were significant predictors of average maximum principal strain in the supraspinatus tendon. A model R2 of 0.35 implies that the dependent variable is not completely modeled by the significant independent variables. A calculated DW statistic of 0.73 indicates correlation between the independent variables. Glenohumeral abduction angle, joint rotation, supraspinatus tendon load, and partial-thickness tear size were significant predictors of average minimum principal strain in the infraspinatus tendon. R2 of 0.72 for this model indicates that the dependent variable is well modeled by the significant independent variables. A calculated DW statistic of 1.11 indicates some correlation between the independent variables. Results are shown in Table 1.
Correlations Between the Independent Variables Including Supraspinatus Tendon Repair, and Infraspinatus Tendon Strain
Glenohumeral abduction angle, joint rotation, and supraspinatus tendon load and repair were significant predictors of average maximum principal strain in the infraspinatus tendon. DW statistic of 1.27 was calculated, indicating some correlation between the independent variables in this model. Similarly, glenohumeral abduction angle, and supraspinatus tendon load were predictors of average minimum principal strain in the infraspinatus tendon. A calculated DW statistic of 1.2 indicates some correlation between the independent variables. Results are shown in Table 2.
Results shown in Tables 1 and 2 can be represented in equation form where the dependent variable values are equal to the significant independent predictors multiplied by their individual coefficient. Note that based on model 1, four-fitted independent equations were produced. Equations (3) and (4) represent principal strain in the infraspinatus tendon with supraspinatus tears, and Eqs. (5) and (6) represent principal strain in the supraspinatus tendon. Based on model 2, two fitted independent equations were produced. Equations (7) and (8) represent principal strain in the infraspinatus tendon with supraspinatus tendon repair. The fitted equations developed using models 1 and 2 are:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Model Assessment
Infraspinatus Tendon Strain with Supraspinatus Tendon Tear
Random removal of three data points at a time from the data set and re-calculating the regression coefficients did not alter the regression coefficients calculated from the overall model. Results ensure that removing this number of data points for model assessment was acceptable. Regression coefficients from all five trials are shown in Table 3.
TABLE 3.
Significant coefficient (β-values) results using multiple regression analysis for strain in the infraspinatus and supraspinatus tendons with supraspinatus tear for the overall model and five validation trials.
| Associated β values for maximum principal strain |
Associated β values for minimum principal strain |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Constant | Abd | Rot | SS Load | SS Tear | Constant | Abd | Rot | SS Load | SS Tear | |
| Infraspinatus tendon | ||||||||||
| Overall model | 1.90 | −0.05 | 0.03 | 0.02 | −1.88 | 0.05 | 0.02 | |||
| Avg of five trials | 1.90 ± 0.06 | −0.05 ± 0.00 | 0.03 ± 0.00 | 0.02 ± 0.00 | −1.86 + 0.07 | 0.05 ± 0.00 | −0.02 ± 0.00 | |||
| Supraspinatus tendon | ||||||||||
| Overall model | 2.98 | 0.04 | – | 0.06 | – | −1.9 | 0.06 | −0.05 | −0.05 | −0.01 |
| Avg of five trials | 2.85 ± 0.10 | 0.04 ± 0.01 | – | 0.06 ± 0.00 | 0.00 ± 0.01 | −2.21 ± 0.27 | 0.06 ± 0.00 | −0.05 + 0.00 | −0.05 + 0.00 | −0.00 + 0.01 |
Abd Glenohumeral abduction angle; Rot Joint rotation angle; SS Tear SS partial-thickness tear size.
For both average maximum and minimum principal strain, the developed regression model accurately predicted strains. The actual and predicted average maximum and minimum principal strain values from all five evaluation trials are shown in Table 4. Predicted values generally fell within 1 standard deviation of the actual value, supporting the stability and robustness of the model. However, predicted strain did not accurately mirror actual strain for small strain values near 0%.
TABLE 4.
Actual and predicted maximum and minimum principal strain values in the infraspinatus tendon for a supraspinatus tendon tear.
| Actual maximum principal strain |
Predicted maximum principal strain |
Actual minimum principal strain |
Predicted minimum principal strain |
|
|---|---|---|---|---|
| Trial 1 | 1.43 | 1.70* | −1.82 | −2.39* |
| 4.26 | 4.46* | −3.20 | −3.41* | |
| 0.17 | −0.76*** | −0.27 | 0.61*** | |
| Trial 2 | 3.50 | 2.43* | −3.50 | −2.32* |
| 4.60 | 4.41* | −2.38 | −3.34* | |
| 0.32 | −0.09*** | −0.36 | 0.11*** | |
| Trial 3 | 3.47 | 3.89* | −2.94 | −2.88* |
| 0.44 | 0.95** | −0.25 | −0.93*** | |
| 0.38 | 0.53* | −0.44 | −0.42* | |
| Trial 4 | 2.19 | 2.48* | −2.63 | −2.34* |
| 1.73 | 3.02** | −2.22 | −2.91* | |
| 0.95 | 2.15** | −0.53 | −0.87** | |
| Trial 5 | 2.29 | 3.35* | −1.84 | −2.42* |
| 2.09 | 2.87* | −2.38 | −3.44* | |
| 0.73 | 1.52** | −0.40 | −1.46*** |
The predicted value is within 1 standard deviation from the actual value;
the predicted values is within 2 standard deviations from the actual values;
the predicted value is not a good prediction of the actual value.
Supraspinatus Tendon Strain with Supraspinatus Tendon Tear
Random removal of three data points at a time from the data set and re-calculating the regression coefficients did not significantly alter the regression coefficient for abduction, rotation, and load. The correlation coefficient for tear ranged between 0 and 0.02 (for maximum principal strain) and 0 and 20.01 (for minimum principal strain) through the five trials. The high (but significant) p-values associated with tear (p ~ 0.05) suggests that supraspinatus tendon tear size may be a weak predictor of supraspinatus tendon strain. The regression coefficients from all five trials are shown in Table 3.
In the supraspinatus tendon, the developed regression model accurately predicted strains within 1 standard deviation of actual strain values for 80% and 93% of all the conditions for maximum and minimum principal strain, respectively. Actual and predicted maximum and minimum principal strain values from all five evaluation trials are shown in Table 5. Since this fit for maximum principal strain in the supraspinatus tendon is associated with a low R2, it is likely that the inclusion of additional factors would improve the fit to the data.
TABLE 5.
Actual and predicted maximum and minimum principal strain values in the supraspinatus tendon for a supraspinatus tendon tear.
| Actual maximum principal strain |
Predicted maximum principal strain |
Actual minimum principal strain |
Predicted minimum principal strain |
|
|---|---|---|---|---|
| Trial 1 | 5.58 | 4.62* | −3.08 | −2.58* |
| 5.30 | 6.33* | −4.26 | −5.61* | |
| 7.01 | 8.04* | −7.48 | −7.23* | |
| Trial 2 | 3.58 | 4.63* | −2.49 | −4.06* |
| 4.07 | 7.51** | −1.89 | −4.03** | |
| 3.33 | 9.28*** | −4.07 | −5.65* | |
| Trial 3 | 5.14 | 4.58* | −4.29 | −5.15* |
| 7.23 | 6.22* | −7.63 | −6.71* | |
| 8.59 | 7.88* | −10.27 | −8.27* | |
| Trial 4 | 2.10 | 6.03*** | −1.86 | −2.51* |
| 9.18 | 7.41* | −3.42 | −1.69* | |
| 13.33 | 9.87* | −3.71 | −4.04* | |
| Trial 5 | 5.94 | 4.52* | −4.18 | −5.40* |
| 7.29 | 6.17* | −7.49 | −5.58* | |
| 9.02 | 7.82* | −5.52 | −5.76* |
The predicted value is within 1 standard deviation from the actual value;
the predicted values is within 2 standard deviations from the actual values; and
the predicted value is not a good prediction of the actual value.
Infraspinatus Tendon Strain with Supraspinatus Tendon Repair
Random removal of two data points at a time from the data set and re-calculating the regression coefficients did not alter the values of the regression coefficients calculated from the overall model. Results support removing this number of data points for model assessment. The regression coefficients from all five trials are shown in Table 6.
TABLE 6.
Significant coefficient (β-values) results using multiple regression analysis for strain in the infraspinatus tendon with supraspinatus repair for the overall model and each of the five validation trials.
| Associated β values for maximum principal strain |
Associated β values for minimum principal strain |
|||||||
|---|---|---|---|---|---|---|---|---|
| Constant | Abd | Rot | Load | Repair | Constant | Abd | Load | |
| Infraspinatus tendon | ||||||||
| Overall model | 0.60 | −0.04 | 0.03 | 0.02 | 0.47 | −1.17 | 0.03 | −0.01 |
| Avg. of five trials | 0.59 ± 0.12 | −0.04 ± 0.00 | 0.03 ± 0.00 | 0.02 ± 0.00 | 0.49 ± 0.05 | −1.17 ± 0.05 | 0.03 ± 0.00 | −0.01 ± 0.00 |
Abd Glenohumeral abduction angle; Rot joint rotation angle; SS Tear SS partial-thickness tear size.
For both maximum and minimum principal strain, results showed that the developed regression model accurately predicted strains. The actual and predicted maximum and minimum principal strain values from all five evaluation trials are shown in Table 7. Generally, predicted values fell within 1 standard deviation of the actual value, supporting that the model very accurately predicted the removed conditions. As was found with the supraspinatus tendon tear model, for supraspinatus tendon repair, the predicted strain in the infraspinatus tendon did not accurately mirror actual strain for small actual strain values near 0%.
TABLE 7.
Actual and predicted maximum and minimum principal strain values in the infraspinatus tendon for a supraspinatus tendon repair.
| Actual maximum principal strain |
Predicted maximum principal strain |
Actual minimum principal strain |
Predicted minimum principal strain |
|
|---|---|---|---|---|
| Trial 1 | 2.93 | 2.48* | −2.68 | −1.96* |
| 0.47 | 0.98** | −0.28 | −0.67** | |
| Trial 2 | 1.62 | 1.77* | −2.35 | −2.46* |
| 0.25 | −0.81*** | −0.23 | 0.43*** | |
| Trial 3 | 1.79 | 2.1* | −1.77 | −1.57* |
| 0.73 | 1.55** | −0.44 | −1.09** | |
| Trial 4 | 1.44 | 1.31* | −1.92 | −1.99* |
| 4.52 | 3.61* | −1.96 | −2.41* | |
| Trial 5 | 2.39 | 2.92* | −1.13 | −1.64* |
| 0.57 | 0.31* | −0.52 | −0.05** |
The predicted value is within 1 standard deviation from the actual value;
the predicted values is within 2 standard deviations from the actual values; and
the predicted value is not a good prediction of the actual value.
DISCUSSION
In this study, multiple regression analysis was used to simultaneously evaluate the effect of glenohumeral joint position, supraspinatus tendon load, tear and repair on both, supraspinatus and infraspinatus tendon strain. This approach demonstrates the contribution of each independent variable in the context of the remaining variables, more appropriately mimicking the complex in vivo environment where multiple factors simultaneously coexist.
All independent variables evaluated were expected to be significant predictors of supraspinatus and infraspinatus tendon strain. Interestingly, supraspinatus tendon load and glenohumeral abduction angle were consistently significant predictors of strain. Previously, we have shown that glenohumeral abduction angle significantly impacts supraspinatus tendon strain,5 where higher strain in the supraspinatus tendon were associated with abduction angles that minimized contact between the supraspinatus tendon and the humeral head. Unexpectedly, infraspinatus tendon strain dropped to negligible amounts with increase in abduction angle indicating a disruption in the interaction between the two with increase in abduction angle. The significance of abduction angle as predictor of both principal strain components in the supraspinatus tendon even in the context of all other factors evaluated, emphasizes the importance of joint position in management of rotator cuff tears and postoperative care. This finding is further supported by the effect of rotation angle since it was a significant predictor of average maximum principal strain in the infraspinatus tendon (for both supraspinatus tendon tear and repair) and average minimum principal strain in the supraspinatus tendon (for supraspinatus tendon tear).
Previously, we have shown that introduction of supraspinatus tendon tear resulted in increase in supraspinatus and infraspinatus tendon strain.1,3 However, in the context of all other factors evaluated, supraspinatus tendon tear size was a significant predictor of minimum principal strain in the supraspinatus tendon but of neither strain component in the infraspinatus tendon. Findings imply that the commonly encountered propagation of supraspinatus tendon tears into large tears that also encompass the infraspinatus tendon is likely driven by loading and joint position, and can possibly be mitigated by controlling these factors. These results combined with findings that supraspinatus tendon load was a significant predictor of supraspinatus and infraspinatus tendon strain implies that tear propagation can be minimized and the success of repair can be improved through modulating shoulder loading and constraining shoulder motion to 30° abduction and neutral rotation (the angle at which strain in both tendons is minimized).
Surprisingly, the model developed for maximum principal strain (Eq. 5) in the supraspinatus tendon had a coefficient of determination, R2, value of only 0.35. While abduction angle and load were found to be significant predictors in this model, the low R2 indicates that a very small portion of the variability in strain is attributable to these independent factors. It is likely that the inclusion of factors not considered in this model would result in an improvement in this R2 value. Such additional factors could include other types of supraspinatus tendon tears (vary through the thickness), simulated flexion and extension, and interaction terms between the evaluated dependent factors, or other factors introduced from dynamic joint motion.
Correlations between the independent variables were evaluated using DW statistic. While for the most part no correlation was found, in the cases where a correlation between the independent variables was found, the effect of individual factors cannot be separated out. However, since this correlation is not an experimental artifact, but rather the result of the complex environment experienced by the tendon, manual removal of any factor was not conducted. In addition, the regression analysis manages such correlations by removing strongly correlated variables in the backward elimination step, leaving only the strongest predictor variables in the model. However, it should be noted that correlations between independent variables potentially allows one variable to mask the contribution of another.
The use of cadaveric human shoulders introduces a range of degeneration between subjects. However, since the same subjects were used for each independent variable evaluated, the variability in the data due to different levels of degeneration is unlikely to have biased inclusion or exclusion of any parameter into the regression model. Additionally, the regression model in this study describes the contribution of several independent factors on the mechanical interactions between the supraspinatus and infraspinatus tendons without accounting for in vivo factors such as tissue degeneration and remodeling. While this is noted as a limitation, it is unlikely to have an impact on our findings in a chronic tear case (unaccompanied by repair or healing), but can have an impact in an acute tear or repair case where tissue repair and remodeling can introduce additional complexity to the model.
Results presented in this study suggest that several factors combine to predict strains in the supraspinatus and infraspinatus tendons. While a significant effect on tendon strain was found in association with the independent variables examined, a regression model evaluating their simultaneous effect showed different contributions of each parameter. Results emphasize the importance of joint position and loading on management of tendon tears and repairs. The low R2 associated with maximum principal strain in the torn supraspinatus tendon requires further evaluation to determine the necessary additional factors to improve the model fit. For the remaining five correlation strain regression models, the conducted evaluation experiments verify that the models developed can be used to predict strain values for untested conditions that fall within the range of the conditions evaluated. Results from this study suggest that a better understanding of the loading environment in rotator cuff tendons necessitates a multifactorial complex model.
ACKNOWLEDGMENTS
This study was supported by a grant from the NIH/NIAMS (AR050176) and the NIH/NIAMS supported Penn Center for Musculoskeletal Disorders (AR050950). We thank Arthrex for providing the suture anchors.
REFERENCES
- 1.Andarawis-Puri N, Kuntz AF, Kim S-Y, Soslowsky LJ. Effect of anterior supraspinatus tendon partial-thickness tears on infraspinatus tendon strain through a range of joint rotation angles. J. Shoulder Elbow Surg. 2009 doi: 10.1016/j.jse.2009.10.003. in print, PMID: 20080051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Andarawis-Puri N, Kuntz AF, Ramsey ML, Soslowsky LJ. Effect of glenohumeral abduction angle on the mechanical interaction between the supraspinatus and infraspinatus tendons for the intact, partial-thickness torn and repaired supraspinatus tendon conditions. J. Orthop. Res. 2009 doi: 10.1002/jor.21068. in print, PMID: 20058264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Andarawis-Puri N, Ricchetti ET, Soslowsky LJ. Interaction between the supraspinatus and infraspinatus tendons: effect of anterior supraspinatus tendon full-thickness tears on infraspinatus tendon strain. Am. J. Sports Med. 2009;37(9):1831–1839. doi: 10.1177/0363546509334222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bey MJ, Ramsey ML, Soslowsky LJ. Intratendinous strain fields of the supraspinatus tendon: effect of a surgically created articular-surface rotator cuff tear. J. Shoulder Elbow Surg. 2002;11(6):562–569. doi: 10.1067/mse.2002.126767. [DOI] [PubMed] [Google Scholar]
- 5.Bey MJ, Song HK, Wehrli FW, Soslowsky LJ. Intratendinous strain fields of the intact supraspinatus tendon: the effect of glenohumeral joint position and tendon region. J. Orthop. Res. 2002;20(4):869–874. doi: 10.1016/S0736-0266(01)00177-2. [DOI] [PubMed] [Google Scholar]
- 6.Breazeale NM, Craig EV. Partial-thickness rotator cuff tears. Pathogenesis and treatment. Orthop. Clin. North Am. 1997;28(2):145–155. doi: 10.1016/s0030-5898(05)70275-3. [DOI] [PubMed] [Google Scholar]
- 7.Fukuda H. Partial-thickness rotator cuff tears: a modern view on Codman’s classic. J. Shoulder Elbow Surg. 2000;9(2):163–168. [PubMed] [Google Scholar]
- 8.Fukuda H, Hamada K, Nakajima T, Tomonaga A. Pathology and pathogenesis of the intratendinous tearing of the rotator cuff viewed from en bloc histologic sections. Clin. Orthop. Relat. Res. 1994;304:60–67. [PubMed] [Google Scholar]
- 9.Fukuda H, Hamada K, Yamanaka K. Pathology and pathogenesis of bursal-side rotator cuff tears viewed from en bloc histologic sections. Clin. Orthop. Relat. Res. 1990;254:75–80. [PubMed] [Google Scholar]
- 10.Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. Applied Linear Statistical Models. 4th edn. New York, NY: Irwin; 1996. Building the regression model I: selection of predictor variables; pp. 327–355. [Google Scholar]
- 11.Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. Applied Linear Statistical Models. 4th edn. New York, NY: Irwin; 1996. Table B.7 Durbin Watson test bounds; p. 1349. [Google Scholar]
- 12.Reilly P, Amis AA, Wallace AL, Emery RJ. Supraspinatus tears: propagation and strain alteration. J. Shoulder Elbow Surg. 2003;12(2):134–138. doi: 10.1067/mse.2003.7. [DOI] [PubMed] [Google Scholar]