Revealing protein oligomerization and densities in situ using spatial intensity distribution analysis

Abstract

Measuring protein interactions is key to understanding cell signaling mechanisms, but quantitative analysis of these interactions in situ has remained a major challenge. Here, we present spatial intensity distribution analysis (SpIDA), an analysis technique for image data obtained using standard fluorescence microscopy. SpIDA directly measures fluorescent macromolecule densities and oligomerization states sampled within single images. The method is based on fitting intensity histograms calculated from images to obtain density maps of fluorescent molecules and their quantal brightness. Because spatial distributions are acquired by imaging, SpIDA can be applied to the analysis of images of chemically fixed tissue as well as live cells. However, the technique does not rely on spatial correlations, freeing it from biases caused by subcellular compartmentalization and heterogeneity within tissue samples. Analysis of computer-based simulations and immunocytochemically stained GABA_B receptors in spinal cord samples shows that the approach yields accurate measurements over a broader range of densities than established procedures. SpIDA is applicable to sampling within small areas (6 μm²) and reveals the presence of monomers and dimers with single-dye labeling. Finally, using GFP-tagged receptor subunits, we show that SpIDA can resolve dynamic changes in receptor oligomerization in live cells. The advantages and greater versatility of SpIDA over current techniques open the door to quantificative studies of protein interactions in native tissue using standard fluorescence microscopy.

Cell-signaling mechanisms are regulated by protein–protein interactions and their trafficking to different cellular compartments. Our ability to unravel the complex molecular mechanisms of cell function, thus, relies critically on the development of quantitative techniques that can measure the density of proteins in different cellular compartments along with their oligomerization state and interactions (1). To date, such quantification has remained a daunting challenge when it comes to in situ (animal intact tissue) studies. Several optical methods have been developed in recent years based on fluorescence fluctuation spectroscopy (2–6) and resonance energy transfer (RET) (7, 8), but they each have a number of constraints that limit their use for in situ analysis. For example, densities and oligomerization states can be measured using a photon-counting histogram (PCH) (3), fluorescence intensity distribution analysis (FIDA) (4), or fluorescence correlation spectroscopy (FCS) (9) by analyzing temporal fluorescence intensity fluctuations in time excited from a stationary laser beam focal volume. For such time-dependent approaches, molecules must undergo diffusion or flow to be detected, and hence, the methods cannot be applied to fixed tissue samples. Image correlation spectroscopy (ICS), an extension of FCS to the spatial domain, can overcome some of those limitations (6). However, with ICS, samples with spatial fluorescence intensity discontinuities introduce artifacts in the spatial correlation functions that result in systematic errors in the measurements (10). Approaches based on RET have proven to be powerful, because they directly reveal protein interactions within a 10-nm-length scale. However, lack of suitable fluorescent probes for in situ measurements make RET mainly amenable to studies in expression systems (7), and furthermore, RET does not provide information on protein densities or multimeric organization beyond dimers, because multiple experimental steps must be used to vary the donor to acceptor ratio. Alternative immunocytochemical analyses at the ultrastructural level can quickly become impractical when performed on large tissue areas and may introduce processing steps that limit their use for detection of certain antigens.

We introduce spatial intensity distribution analysis (SpIDA), which is based on spatial histogram analysis of fluorescence intensities from images that can accurately extract information on protein densities and aggregation states and is not significantly perturbed by the inhomogeneities inherently present in real tissue samples. The approach allows for dynamic measurements of receptor oligomeric states, densities, and cellular/tissue localization. A unique advantage of SpIDA is that it is applicable to single images, and therefore, it can be applied to measure protein interactions and distributions in situ in fixed tissue samples using fluorescent antibody labeling. However, the technique remains compatible with live cell analysis using fluorescent protein expression systems.

Theory

The SpIDA technique is based on fitting super Poissonian distributions to intensity histograms calculated from confocal laser scanning microscopy (CLSM) images of cells to measure numbers of fluorescent molecules and their quantal brightness. It is inspired by the temporal PCH approach (3), but it is applied to the spatial domain, enabling measurements on single images collected on microscopes with analog detectors. The intensity histogram simply reports the numbers of pixels for each intensity calculated from an imaged region of interest (ROI). The pixel intensity in a CLSM image is the integrated fluorescence from within the beam focal volume at a given position. Histogram-fitting functions are then calculated by computing the fluorescence intensity of all possible configurations of n particles in the beam focal volume. Then, the values obtained for each of these possible particle configurations are weighted by their probability considering a Poisson distribution of particles in space analogous to what is done in PCH (3).

Let I(r) be the illumination intensity profile of the excitation laser and ε be the quantal brightness of a single fluorescent particle. In a noise-free situation, the probability of observing an intensity of light k (assumed proportional to the number of photons emitted) by one particle of brightness ε is given by (Eq. 1)

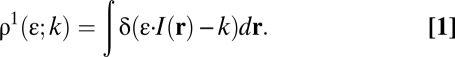For two particles, ρ² is the convolution of the average configuration for one particle (Eq. 2),

and recursively for n particles (Eq. 3),

The final histogram can be calculated by weighting each density configuration with its proper probability assuming a Poisson distribution. The fitting function becomes (Eq. 4)

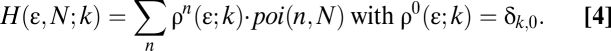H is then normalized over all of the intensity values so that the integral over k is unity. With the normalized functions, the two fitting parameters in Eq. 4 are the fluorescent particle density (N particles per laser beam-effective focal volume) and the quantal brightness (ε intensity units in iu per unit of pixel integration time).

Usually, the fluorescence intensity is measured using analog photomultiplier tubes (PMTs) on CLSMs, and the number of collected photoelectrons is a function of the polarization voltage in contrast to PCH, where the ε has units of photon counts per second. PMTs broaden the signal variance, but this broadening can be characterized and corrected for in the analysis, as shown below.

Given an image time series, SpIDA can determine the aggregation state of the fluorescent particles in time and space. The first step is to measure the monomeric quantal brightness ε₀. Then, for a mixture of monomers and dimers, fitting the data with a one-population model (Eq. 4) will yield an intermediate value of ε between ε₀ and 2ε₀, indicating that a higher-order model must to be used.

We refer to a population with ε = 2ε₀ as the dimer population. In contrast to RET techniques, SpIDA does not give insights on the distance between the fluorophores labeling a dimer, and therefore, particles separated by 5 or 50 nm are treated the same way provided that the interparticle distance is constant and within the point-spread function (PSF) spatial resolution. Thus, SpIDA cannot reveal direct protein–protein interactions. However, unlike RET-based techniques, where nonspecific RET occurs at densities >1,000 particles/μm³ and where measurable signals require very close proximity of donor and acceptor (8), SpIDA can detect protein associations over distances >10 nm and can differentiate between monomers and oligomers at high densities of randomly distributed particles [e.g., >10,000 particles/μm³ or an average distance of <30 nm, assuming sufficient signal to noise ratio (S/N)].

A population of true dimers can be differentiated from a population of single monomers of two times the density by the difference in the intensity fluctuations. Even if the mean intensities for those two cases are equal, the histograms will be different, and SpIDA will differentiate them.

Two Population Image Histograms

Two populations can be either spatially segregated, which leads to visible edge boundaries, or spatially mixed. When two populations are spatially segregated, the histogram of the image is the sum of the two independent histograms for each population (Eq. 5),

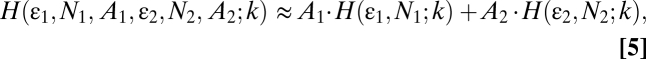where A_i, N_i, and ε_i are the parameters of Eq. 4 for the ith population. The two sides of Eq. 5 are not strictly equal because of the contribution of the edge boundary between the two populations. Indeed, this edge introduces a distortion in the distribution. However, because the technique does not rely on correlations, this error decreases as the ratio of the edge length to total area decreases with larger ROI sampling. In contrast, for correlation-based methods such as ICS and FCS, the distortions introduced when analyzing populations segregated in space and time cannot be compensated for by increasing the ROI.

When the populations are mixed within the same region in space, the total histogram becomes the convolution of the two individual distributions (Eq. 6):

Eq. 6 can be used when there is a mixture of more than one oligomerization state or when significant autofluorescence occurs, which is often the case with tissue samples.

Results

Validation of SpIDA Using Simulated Data.

Single oligomeric state population.

To establish the sensitivity and detection limits of SpIDA for images containing a single oligomeric state population (i.e., single ε), computer-simulated datasets of multiple images with known densities, N_o, and brightness values, ε_o, and their histograms were generated and fit to single-population distributions (Eq. 4 and Fig. 1A).

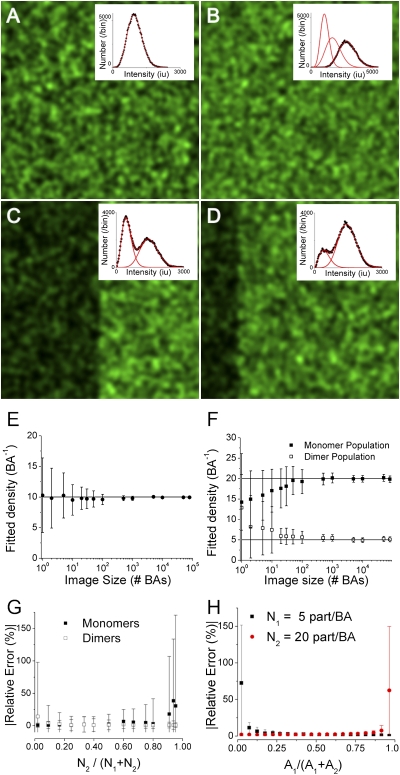
Fig. 1.

Validation of SpIDA using computer simulated data. A–D show simulated images. (A) A single-point emitter population, with N_o = 10 particles/BA and ε_o = 100 iu; the fit to Eq. 4 yielded N_SpIDA = 9.6 particles/BA and ε_SpIDA = 104 iu. (B) Two intermixed populations made of monomers and dimers. N_oM and N_oD = 10 particles/BA, with ε_o = 100 iu. The fitted distribution to Eq. 6 (convolution of two independent populations) yielded N_M-SpIDA = 9.6 with ε_M-SpIDA = 102 iu and N_D-SpIDA = 10.2 particles/BA with ε_D-SpIDA = 198 iu. (C) Two monomeric (ε_o = 100 iu) populations segregated within equal area regions (left and right), with N_oL = 5 and N_oR = 15 particles/BA. The fit to Eq. 5 returned N_L-SpIDA = 5.3 particles/BA with ε_L-SpIDA = 93 iu and N_R-SpIDA = 14.5 particles/BA with ε_R-SpIDA = 102 iu. (D) Two monomeric populations segregated within two regions (left and right) that differ in area by a factor of four (100 and 400 BA, respectively). N_oL = 5 and N_oR = 15 particles/BA. The histogram fit to Eq. 5 returned N_L-SpIDA = 4.5 with ε_L-SpIDA = 109 iu and N_R-SpIDA = 14.3 particles/BA with ε_R-SpIDA = 103 iu. (E and F) Accuracy of SpIDA for one- and two-population images as a function of sample size (number of BAs). (G) Accuracy of SpIDA applied to images of monomer/dimer mixtures while varying the fraction of dimers. Fixed image size of 1,000 BAs was chosen for these simulations. The monomer density was fixed at 50 monomers/BA, whereas the dimer density varied from 1 to 1,000 dimers/BA. (H) Accuracy of SpIDA applied to segregated population images. The total image size was fixed to 1,000 BA. Each data point was obtained as the mean from analysis of 100 separate simulated images, and the error bars represent the SDs.

We first determined the minimum ROI necessary to obtain accurate and precise estimates of N_o and ε_o. The density estimates and their deviations obtained with SpIDA were plotted as a function of ROI in units of laser beam areas (BAs) for simulated images containing on average 10 monomeric particles per BA. For any sample size, the technique provided accurate estimates (Fig. 1E). A precision of >80% was obtained if at least 50 BAs were sampled. In practice, an image region of 128 × 128 pixels was needed to obtain a statistical sampling error of 20% for a real image obtained using a Gaussian beam with an e⁻² radius of 10 pixels (Fig. 1E).

To establish the dynamic range of the technique, we then conducted simulations for densities ranging from 1 to 10,000 particles per BA. The technique yielded accurate measurements over the entire range of simulated densities. Thus, SpIDA is not biased by high-density conditions assuming detection above noise background. For a typical sampling condition using a diffraction limited-beam focus with a radius of 200 nm, 1,000 particles/BA represents >10,000 particles/μm², which is well beyond typical protein densities found in native cells.

Two oligomeric state populations.

To determine the accuracy and precision of SpIDA to measure values from heterogeneous oligomer populations, we simulated images with two species of different ε (ε₁ and ε ₂), each with variable densities (N₁ and N₂). We simulated either spatially segregated or intermingled (mixed) populations (Fig. 1 B–D). SpIDA yielded unbiased values with <10% error for sample sizes >50 BAs (Fig. 1 E and F) and <5% error for 500 BAs. When distinct populations were unevenly represented within a sample, we obtained accurate measurements for both populations when the dimer density fraction was within the range of 0.1–0.85 (Fig. 1G). Finally, for distributions segregated in space, SpIDA yielded unbiased measured values (<10% error) for populations occupying >8% of the sample region (Fig. 1H).

Potential Sources of Error.

Effect of sample heterogeneity.

Heterogeneities occur in biological tissue, where cells can contain microdomains and protein clusters as well as gradients across subcellular compartments, and these have the potential for biasing measurements. In the case of clustering or microcompartments (e.g., fine neuronal dendrites), a mask can be used to select areas with distinct intensities in the image. Using this approach, SpIDA can be applied to measure accurately different densities of particles inside vs. outside the masked area (Fig. S1 A–I). For gradients, by modifying the sample area to cover a smaller fraction of the gradient, it was possible to minimize estimation bias to <5% (Fig. S1J). In practice, this corresponds to adapting the sample area to a region where the gradient is not visible by eye (Fig. S1H). Biases caused by spatial heterogeneities in distributions can, therefore, be minimized by adjusting the sampling strategy to the features of the image, which represents a significant advantage of SpIDA over correlation-based techniques like ICS. This is because SpIDA does not calculate correlation functions, making it compatible with a mask-based sampling strategy (Fig. S1 K–P has illustrations of distortions in the correlation function). Thus, SpIDA can be applied more robustly to analyze images that contain significant heterogeneity because of cell morphology or boundaries of fluorescence labeling in ramified cells (e.g., neurons), which is often the case with immunolabeling in tissue sections.

Impact of detector properties, signal strength, and noise.

SpIDA is based on the assumption that the measured intensity is linearly proportional to the photon counts. We, thus, first confirmed that the response of our PMT was linear over the range of intensity used in our experiments (0–2,000 iu) (Fig. S2A). To properly model the measurement in a real experiment, we must include the noise characteristics of the light detector in the fitting function. For this, we empirically determined the inherent noise over the entire output range of the PMT for our system (Fig. S2B). The SpIDA histograms incorporating this detector noise for one or two populations can be obtained assuming a Gaussian noise function at all intensities (Eq. 7):

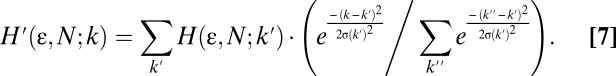Replacing each value in the histogram with a normalized Gaussian centered at the intensity k′ with variance σ²(k′) corrects the final histograms for PMT noise. Plots of histograms generated by Eq. 4 (without noise) and Eq. 7 (with noise) for the same ε and N show that the data are best fit with Eq. 7 (Fig. S2 C and D). Similar noise properties can be measured for other types of detectors, making SpIDA compatible with CCD-based systems such as total internal reflection fluorescence (TIRF).

Impact of signal strength.

We performed additional simulations to assess the accuracy of SpIDA as a function of ε. Given the noise characteristics of our PMT (Fig. S2B), the minimal ε needed to obtain accurate estimates with the analysis was 6 iu (Fig. S2E). Thus, to ensure negligible bias resulting from low ε, in each experiment, PMT parameters and laser power were set to achieve an equivalent ε > 20 iu/pixel dwell time while remaining in the linear regime.

Impact of autofluorescence.

To investigate how autofluorescence affects the accuracy of SpIDA, we simulated images containing background signal. Applying SpIDA under these conditions but assuming a single-population model yielded values with >95% accuracy for S/N > 4 (Fig. S2F). Empirical measurements of S/N achieved with our labeling approaches ranged from 10 to >50 (Fig. S3). Therefore, the impact of autofluorescence was considered negligible in these studies.

Effects of distributions in ε.

The ε-value reflects the response of a single fluorescent molecule (e.g., GFP) or a group of fluorescent moieties attached to a single probe (e.g., labeled antibodies). In the case of labeled antibodies, the total number of fluorophores per antibody can vary, thus yielding a greater SD for ε. However, the S/N may improve by increasing the number of fluorophores per antibody. To examine the impact of a distribution in ε, we simulated probes having dye labels that followed a Poisson distribution (11) with mean μ for the number of dyes per probe, and we generated images with varying density from 1 to 100 particles/BA. Under such conditions, applying SpIDA without correcting for the distribution of ε yields underestimated densities relative to the set values (Fig. S2G). However, for μ > 6, the error on the fits is <15%. Furthermore, the estimates are always linearly related to density, which means that ε is constant at all densities for a given labeled probe. Thus, although a correction for the distribution could be incorporated into SpIDA (Eq. 4), it is not necessary when using the same probe across samples.

Measurement of Oligomerization States in Tissue Samples.

We then sought to test whether, under experimental conditions, SpIDA was able to reveal receptor oligomerization. To verify the applicability of the technique for different combinations of oligomeric states, we used a system where we could control the subunit labeling for monomers and dimers. For this, we analyzed the densities and aggregation states of a G protein-coupled receptor (GPCR), the GABA_B receptor, and a known heterodimer (12) with a B₂ subunit that seems linked to trafficking of the receptor, whereas its B₁ subunit contains the agonist binding site (13). By labeling with antibodies specific for each of the two subunits alone or in combination, we tested whether SpIDA measures the expected oligomerization state. We applied SpIDA to sets of immunocytochemically labeled sections of rat spinal cords, one with only B₁ labeled, another with only B₂ labeled, and the third with labeling of both subunits. Each time, the analysis was performed on the same subregion of the dorsal horn of the spinal cord (Fig. 2A). Thus, only the combination of subunits labeled varied between the samples.

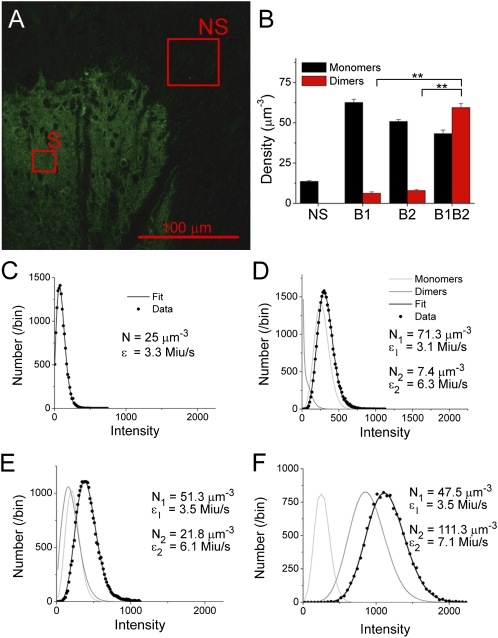
Fig. 2.

Detecting receptor oligomerization by immunocytochemistry in native tissue by SpIDA. (A) CLSM image of a spinal dorsal horn section in which only the GABA_B1 subunits were detected by immunofluorescence. The pixel size is 0.058 μm. ROIs of analyzed regions with nonspecific (primary with secondary; NS) and specific labeling (S) are also shown; six regions per section were analyzed. C–F show examples of histograms fitted for the four types of samples analyzed with their corresponding fits and the best-fit values. (B) Results of SpIDA applied to the section incubated with anti-GABA_B1 only, anti-GABA_B2 only, and a mixture of the two antibodies. A total of 125 regions was analyzed for the nonspecific labeling taken from the three types of samples from five rats; 66 regions were analyzed for B1, 79 regions were analyzed for B2, and 60 regions were analyzed for both subunits combined. Error bars = SEM. **P < 0.01. (C–F) Examples of intensity distributions and fits of data from (C) a region where the labeled protein is not present (i.e., NS background), (D and E) samples where only one type of primary antibody was used to label the proteins (anti-B1 and anti-B2, respectively), and (F) a sample in which both types of primary antibodies were applied (labeling the GABA_B heterodimer).

To obtain a measure of monomeric ε, we applied SpIDA to regions where the tissue was exposed to a secondary fluorescent antibody in absence of the primary antibody. Under these conditions, the signal reflects a nonspecific and assumed monomeric distribution of the secondary antibody. The analysis revealed an ε of 3.2 ± 0.2 Miu/s (n = 11 samples from three rats). We also conducted similar analysis after performing a complete immunostaining, with primary and secondary antibodies, in a region of the tissue section where there was only nonspecific labeling (no receptor expression). In this region, the signal reflects a nonspecific and assumed monomeric distribution of primary antibody, which is detected by the secondary antibody (Fig. 2A). The ε measured was 3.3 ± 0.7 Miu/s (n = 20 samples from five rats) (Fig. 2C), which is the same as the value obtained with secondary antibody alone within error (P > 0.5). This result indicated a ratio of 1:1 for secondary to primary antibody binding, and the ε value obtained for these controls served as the reference for monomers to be used for subsequent analysis.

SpIDA was then applied to the labeled samples using a two-population model, including the known monomeric ε. For samples in which only one of two subunits was labeled, the analysis revealed mostly monomers (Fig. 2 B, D, and E). In contrast, when labeling both subunits through the two types of primary antibodies and revealing them with the same secondary antibody, SpIDA detected a significant proportion of dimers (Fig. 2 B and F). Furthermore, the dimer to monomer ratio increased when the two subunits were labeled together, such that the estimated total number of proteins (273 ± 12 per μm³; from 60 regions taken from five rats) was comparable with the sum of proteins detected with each antibody separately [127 ± 4 per μm³ for B1 (66 regions) and 113 ± 4 per μm³ for B2 (79 regions) for a sum of 240 ± 8 per μm³; P > 0.1], confirming the consistency of the analysis. Complementary ultrastructural immunolabeling confirmed that the spatial distribution of the receptors was well-approximated by a Poisson distribution (Fig. S4A).

These results indicate that the method is able to provide accurate information on protein density and oligomerization in fixed tissue sections using antibody labeling.

Measurement of Dynamic Changes in Oligomerization States in Live Cells.

To test the applicability of SpIDA to detect dynamic dimerization of membrane receptors in live cells, we studied the epidermal growth factor receptor (EGFR) labeled with GFP that is expressed in Chinese hamster ovary (CHO-k1) cells (Fig. 3A). It is well-accepted that EGFRs exist mainly as monomers in the absence of EGF, but on ligand binding, the receptors homodimerize (14, 15).

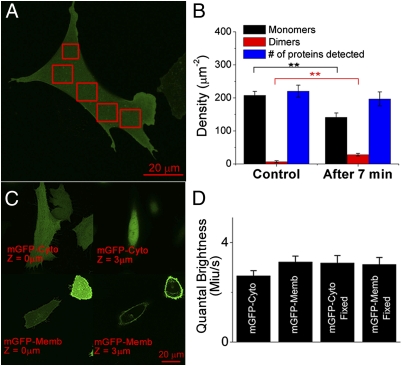
Fig. 3.

Detecting receptor oligomerization in live cells by SpIDA. (A) Image of CHO-k1 cells expressing EGFR-GFP before treatment with EGF. Boxes indicate the ROIs that were analyzed. (B) Shift in the distribution of monomers to dimers after the addition of EGF (20 nM; the experiment was performed at room temperature). The error bars represent the SE taken from five measurements. **P < 0.01 between monomers and dimers for the two cases. No significant difference (P > 0.1) was found for the total number of proteins measured. (C) Images of CHO-k1 cells expressing cytoplasmic mGFPs (mGFP-Cyto) and membrane-targeted mGFP (mGFP-Memb). Two images of the same cell are shown for the two different sample types at two heights in the z stack (0 and 3 μm). (D) Histogram representing the values of the best-fit ε on cells expressing mGFP on the membrane (2D) and cells expressing mGFP in the cytosol (3D). The experiments were performed on both living and fixed cells. For each bar, a minimum N = 20 was sampled. Error bars = SEM. Image size = 1,024 × 1,024 pixels. Pixel size = 0.092 μm. Step size in the z stack = 0.5 μm.

CHO-k1 cells expressing the EGFR-GFP were serum-starved for 16 h to ensure a dominant distribution of monomeric EGFR on the membrane surface. This cell line was found to express 600,000 receptors/cell (16). With this cell line, SpIDA recovered a density of EGFR on the membrane of 220 ± 18 per μm². In contrast, for another cell line with 100,000 receptors/cell, SpIDA recovered a density of 32 ± 9 EGFR per μm² of membrane (n = 15 cells). This corresponds to a ratio of 6.9 ± 2.5, consistent with the ratio of EGFRs expressed by the two cell lines (16). Cell images were obtained before activation with 20 nM EGF and 7 min poststimulation at room temperature (Fig. 3B). Although no clear change was apparent by eye, SpIDA resolved the relative contributions from the monomers and an emerging homodimer population (Fig. 3B). There was no change in the total proteins detected, indicating that changes in monomer density were not resulting from receptor internalization. Detection of dimers was confirmed with Förster resonance energy transfer (FRET) measurements in Swift et al. (17). EGF-induced dimerization occurred even in the absence of clustering and internalization (14, 17). The results show that SpIDA can resolve dynamic changes in receptor oligomerization within living cells, showing the power of the technique and its applicability to fluorescent protein expression systems. Furthermore, because SpIDA yields values from single images, it can be applied to series with few images, minimizing photobleaching and phototoxicity problems. Further validation of the quantitative nature of SpIDA is presented in Swift et al. (17); receptor binding dose-response curves using dimerization as an index of receptor activation from which conventional biochemical parameters such as EC₅₀ and maximum activation values were calculated are shown to match those obtained from conventional binding assays.

Effect of 2D vs. 3D sampling.

It has been argued for FCS and PCH measurements that, because 2D and 3D samples have different random particle distributions, the analysis yields different ε-values if one does not apply a correction factor, termed the γ-factor (18) (Fig. 3 C and D). In contrast to temporal techniques, we do not think that this correction for 2D bias is required with spatial techniques, because cell surfaces are highly uneven and the scan is unlikely to be perfectly perpendicular to the membrane. Thus, the membrane position will significantly vary in z within the PSF, because it is rastered across the cell surface, generating spatial variations in 3D. To test our assumption, we compared ε obtained from analysis of cells transfected with cytoplasmic vs. membrane-anchored monomeric GFPs (mGFP) (19). SpIDA yielded the same ε in both cases (Fig. 3D). This was also true for samples with up to 10-fold differences in expression levels, confirming that a γ-factor correction is not necessary for SpIDA measurements on cell membranes.

Effect of photobleaching.

If photobleaching of monomeric fluorophores occurs as a random stepwise loss of fluorescence (20), SpIDA should report a decrease in density, but values of ε should be unaffected. To test this, we imaged mGFP-expressing cells or immobilized Alexa488 on coverslips during repeated scans (Fig. S5 A and D). As expected, SpIDA yielded constant ε and decreasing N (Fig. S5 C–F).

Discussion

Resolving Oligomerization in Native Tissue.

Although SpIDA allows detection of interacting molecules below the optical resolution limit, it does not imply direct protein interactions (i.e., the interactions may occur through intermediary proteins in a multimolecular complex. RET methods can reveal direct protein–protein interactions but would fail to detect interactions at distances >10 nm. SpIDA offers several advantages over previous methods. Because measurements do not require protein dynamics, SpIDA can be used to analyze single images and hence, fixed tissue samples. The fact that SpIDA was applicable to conventional immunocytochemical analysis opens the door to direct studies of protein oligomerization in native tissue, which is difficult with existing analytical techniques. SpIDA is also more versatile and more general than ultrastructural approaches. Conversely, other fluorescence-based methods of analysis of receptor oligomerization in subcellular compartments mostly rely on genetic engineering approaches and expression systems or protein overexpression in native tissue. These approaches have limitations, including altered functionality of engineered proteins and imperfect modeling of native conditions by expression systems (1).

SpIDA vs. RET.

SpIDA and RET provide complementary information on oligomerization. Direct comparisons of the two techniques are presented in ref. 17. SpIDA, nevertheless, presents several advantages. First, in addition to providing direct information on protein densities, it can detect oligomerization using a single fluorophore and can be used to measure homooligomerization. Second, SpIDA is not biased and limited by an increase in protein expression levels as are RET approaches. The latter requires a calibration to take into account spontaneous collisional RET events at high densities (8). Third, a negative result in an RET experiment is not necessarily interpretable in the absence of a positive control, showing that specific RET can be achieved with the molecular constructs used, and furthermore, changes in probe dipoles orientation because of conformation changes can yield changes in RET efficiency, which can be erroneously interpreted as dimerization. Fourth, SpIDA can be used to resolve mixtures of oligomerization states within a single subcellular compartment, which is nearly impossible to do with RET. Finally, in addition to being applicable to conventional immunocytochemical approaches, SpIDA relies on conventional image acquisition techniques such as confocal microscopy that are widely used in the life sciences; it, therefore, does not require more specialized acquisition systems, such as photon counters, lifetime measurement systems, or hardware correlators.

Homo-FRET or energy migration and anisotropy measurements have the advantage, compared with two-color FRET, of being able to detect interactions using a single fluorophore. They are not amenable, however, to use with fluorescent antibody labeling and are subject to the same limitations as those exposed above for two-color FRET.

Spatial vs. Temporal Analysis Approaches.

SpIDA relies on spatial sampling, and therefore, it provides information on density and oligomerization states within multiple subcellular compartments in parallel. This has advantages for dynamic studies of trafficking and molecular interactions in live cells. Currently, PCH and FCS rely on sampling single or a few points at a time, and therefore, they are not easily amenable to parallelization. Furthermore, they are difficult to apply to the analysis of moving cellular compartments (e.g., migrating cells or growing neurites) when these occur on time scales comparable with that needed to obtain a time trace. A more recent technique based on fluctuation moment analysis [numbers and brightness (N&B) analysis] of pixels across a temporal stack of images has been developed to extract density and quantal brightness values (21). However, as with PCH and FCS, N&B relies on repeated sampling in time, and therefore, it too is not suitable for fixed samples; all of these temporal methods are sensitive to photobleaching. Although ICS, raster image correlation spectroscopy (RICS) (5), and other techniques (22) also allow parallel measurements in multiple compartments, they remain highly limited for tissue studies, because unlike SpIDA, they are strongly perturbed by inhomogeneous particle distributions. More importantly, those techniques only provide average information on oligomer mixtures (6) and thus, do not yield information on monomer to dimer ratios as achieved with SpIDA.

A comparison summary between SpIDA and other fluorescent techniques is presented in Table S1.

Immunocytochemical vs. GFP Labeling.

In principle, SpIDA is applicable to samples prepared using any of the standard fluorescence labeling methods. However, the fact that it can be applied to samples prepared by standard immunocytochemistry offers the advantage that the quanta of fluorescence—the labeled secondary antibodies—can be built from clusters of fluorophores, yielding a stronger, possibly more stable signal that is less susceptible to unwanted photophysics, such as blinking or stepwise bleaching events. In a paired submission (17), we show an example of application of SpIDA to monitor receptor activation and transactivation in situ.

Materials and Methods

A summary of experimental techniques is given here, and full methods are presented in SI Materials and Methods. All of the simulated images were generated and analyzed by means of custom-designed software (A.G. Godin; SpIDA routines can be downloaded from: www.neurophotonics.ca/tools/software.html) and are described in SI Materials and Methods.

Cell Cultures.

Stably transfected CHO-k1 cells containing EGFR tagged with GFP (EGFR-GFP; gift from the Dr. Jovin Laboratory, Max Planck Institute for Biophysical Chemistry, Göttingen, Germany) were prepared and maintained as described in SI Materials and Methods. To avoid dimerization of EGFPs, we used the monomeric A207K-mutant (mGFP) (19). Cells were transfected with membrane-delimited (farnesylated) mGFP or regular mGFP, which distributes in the cytoplasm, using Lipofectamine 2000 (Invitrogen) as described by the manufacturer.

Animals.

All protocols were performed in accordance with the guidelines from the Canadian Council on Animal Care. Adult (250 g) male Sprague–Dawley rats (Charles River) were anesthetized with Equithesin (6.5 mg chloral hydrate, 3 mg Na-pentobarbital in a volume of 0.3 mL i.p. per 100 g body weight) and perfused transcardially with perfusion buffer followed by 4% paraformaldehyde in 0.1 M phosphate buffer (PB), pH 7.4, for 30 min as described in detail elsewhere (23). Spinal cords were collected, postfixed for 2 h in the same fixative, and cryoprotected overnight in 30% sucrose in 0.1 M PB. The L4–L6 spinal cord segments were sectioned at 35 μm on a sledge-freezing microtome (SM2000R; Leica).

Immunocytochemistry.

Sections were pretreated for 1 h with 4% normal goat serum (NGS) in phosphate buffer saline with 0.2% Triton (PBS+T) and then incubated overnight at 4 °C in affinity-purified rabbit anti-GABA_B1 (B17) and/or anti-GABA_B2 (B232) antibodies kindly provided by R. Shigemoto Okazaki National Research Institutes, Okazaki, Japan (24) diluted 1:200 (3.3 μg·mL⁻¹) or 1:1,000 (0.25 μg·mL⁻¹), respectively, in PBS+T with 4% NGS. After incubation, all sections were washed in PBS+T (four times for 5 min each) and incubated in different wells for 2 h in a goat anti-rabbit IgG antibody conjugated to Alexa488 at room temperature.

Imaging and Analysis.

All of the images were obtained with an Olympus FV300-IX71 (Olympus America) CLSM with a 60× plan-apochromatic apomorphine (Apo) oil immersion objective (numerical aperture = 1.4). An optimal setting of the laser power and PMT voltage was chosen to minimize pixel saturation and photobleaching. The CLSM settings were kept constant for a given sample type and its controls (laser power, filters, dichroic mirrors, polarization voltage, and scan speed) so that valid comparisons could be made between measurements from different images. Acquisition parameters were always set within the linear range of the detector, which was determined by calibration.