Can we track holes?

Abstract

The evidence is mixed as to whether the visual system treats objects and holes differently. We used a multiple object tracking task to test the hypothesis that figural objects are easier to track than holes. Observers tracked four of eight items (holes or objects). We used an adaptive algorithm to estimate the speed allowing 75% tracking accuracy. In Experiments 1–5, the distinction between holes and figures was accomplished by pictorial cues, while red-cyan anaglyphs were used to provide the illusion of depth in Experiment 6. We variously used Gaussian pixel noise, photographic scenes, or synthetic textures as backgrounds. Tracking was more difficult when a complex background was visible, as opposed to a blank background. Tracking was easier when disks carried fixed, unique markings. When these factors were controlled for, tracking holes was no more difficult than tracking figures, suggesting that they are equivalent stimuli for tracking purposes.

1. Introduction

The Belgian painter Rene Magritte is known for a gentle form of surrealism in which the normal grammar of scenes is subtly disrupted. For example, in L’Homme et la Nuit (1964), the central figure is a man-shaped hole through which a peaceful evening scene is visible. In Le Printemps (1965) et Le Retour (1940), we see a nest with eggs at the bottom of the frame, on a flat surface, while the main figure in the sky above is a bird-shaped hole through which can be seen a different sky or a forest scene, respectively. The key element which makes these paintings surrealistic is that a hole is presented as the central object of our attention. While there are many holes in our everyday experience, such as doorways and windows, we typically don’t attend to these apertures per se, but the objects which are visible through them. Can we attend to a hole as an “object” in and of itself (outside of a surrealist painting)?

The perception of holes has interested vision researchers ever since Chen’s (1982) influential suggestion that the visual system is sensitive to topological properties (for a review, see Pomerantz, 2003). In some cases, holes seem to be treated as perceptual objects in their own right. In a shape memory task, for example, Palmer, Davis, Nelson, and Rock (2008) argued that holes were perceived as easily as figures, and encoded in memory as simply an object with a “missing matter” tag. In visual search, Bertamini and Lawson (2006) demonstrated that there was no search asymmetry between holes and figures; that is, searching for a figure among holes is no more efficient than searching for a hole among figures. Furthermore these searches were inefficient¹, suggesting that the distinction is not coded preattentively.

In other circumstances, holes seem to be treated quite differently. Hulleman and Humphreys (2005) found that search for a C among Os was substantially less efficient when the stimuli were holes than when they were figures (whether defined by motion or contrast or both). Bertamini and Croucher (2003) found that it was easier to judge the relative position of vertexes when a shape was presented as a figure as opposed to a hole. Both of these results can be explained by assuming that the shape of a hole is only perceived indirectly, because its contour is actually owned by the surround (Bertamini, 2006; Bertamini & Croucher, 2003).

While the Bertamini and Lawson (2006) study suggests that it is just as easy to deploy attention to a hole as to a figure, an interesting experiment from Albrecht, List, and Robertson (2008) suggests that attention is really deployed to the surface visible through the hole. They used the Egly, Driver, and Rafal (1994) paradigm, in which the observer is presented with two parallel rectangles. One end of one rectangle is cued. “Space-based attention” effects manifest as an RT advantages for targets appearing at this cued location relative to targets appearing at the uncued end of the same rectangle, while “object -based” effects are demonstrated when RTs for targets appearing on the same rectangle are faster than RTs appearing the same distance from the cue but on the other rectangle. Albrecht et al. found the standard space-based effects in all conditions. More interesting were the object-based effects. When the rectangles were figures, they replicated the classic Egly et al. results. When the rectangles were holes, however, the storywas more complicated. When a single surface was visible through both holes, no object-based effects were observed. When the background object was bisected so that each hole was a window onto a different surface, however, object-based effects returned, suggesting that attention was directed to the surface visible through the hole rather than to the hole itself (or its contour).

Our contribution is to apply the multiple object tracking (MOT, Pylyshyn & Storm, 1988) paradigm to the problem. It is by now well-established that observers can track several moving objects among identical moving distractors (for reviews, see Cavanagh & Alvarez, 2005; Scholl, 2009). Scholl and his colleagues have demonstrated that asking what sort of entities are trackable provides important information about how the visual system parses the world (Scholl & Pylyshyn, 1999; Scholl, Pylyshyn, & Feldman, 2001; VanMarle & Scholl, 2003). For example, consider two independently moving squares, one of which is a target. If we add a line between the two squares, without quite touching them, tracking is unimpeded. If we let the line physically touch the contours of the squares to form a dumbbell shape, tracking becomes more difficult. If we draw a “rubber band” outline around the dumbbell so that the two squares are just the undifferentiated ands of a single, deforming parallelogram, then it becomes nearly impossible to keep track of which end is which (Scholl et al., 2001).

Before continuing, we should be more precise about what such experiments can tell us about how the visual system parses the world. While Scholl et al. (2001) proposed MOT as a method for determining what counts as an “object”, it is probably better to think of trackable items as “proto-objects” (Pylyshyn, 2001) rather than objects per se. The distinction is subtle but important. The term “object” comes with a lot of baggage, both in terms of perceptual theory and everyday experience. Objects are like pornography: we know them when we see them (Stewart, cited in Gewirtz, 1996), yet different researchers tend to define what actually constitutes an object in different ways. A proto-object, on the other hand, is a theoretical construct that sits somewhere between the raw sensory input and conscious perception, and can therefore have well-defined properties without offending anyone’s natural sense of what an object should be. Proto-objects structure the visual input into bundles of features, without fully specifying the relationship between those features. In turn, these bundles then serve as tokens to which attention can be deployed, which facilitates more complex processing (Rensink & Enns, 1995; Wolfe & Bennett, 1997).

The assumption underlying this study is that the units of tracking are proto-objects. Furthermore, if a target and a distractor are included in the same proto-object, tracking will be impaired. Therefore, MOT experiments may engender a better understanding of how how the basic units of attention are parsed by the visual system.

Here we report a series of experiments comparing observers’ ability to track holes to their ability to track figures. For our purposes, a hole is defined as a shape that can be interpreted as an aperture through a surface, whereas a figure is a surface in its own right. More precisely, in Experiment 1, the holes were perfectly transparent circular apertures through surfaces of intermediate transparency, while the figures were disks of intermediate transparency (see Figure 1). In the remaining experiments, the holes were transparent circular apertures through opaque surfaces, while the figures were opaque disks (see Figures 3 and 6).

Figure 1.

Stimuli for Experiments 1 and 2. The top row illustrates the hole conditions, and the bottom row the figure conditions. Columns illustrate conditions of decreasing transparency, from left to right: 75%, 50%, and 25%

Figure 3.

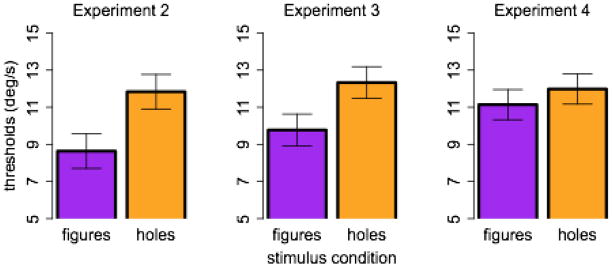
Stimuli for Experiments 2–4. Top row shows example stimuli from Experiment 2, middle row example stimuli from Experiment 3, and bottom row example stimuli from Experiment 4. In all rows, hole stimuli are on the left, and figure stimuli on the right.

Figure 6.

Data from Experiment 5. Threshold speed in °/s is plotted for the figure (purple) and hole (orange) conditions.

What should we expect to happen when observers try to track holes? If we follow the Albrecht et al. (2008) results, we might expect that cueing a hole as a target would actually cue the surface visible through the aperture, in which case it would be very difficult to track, since all of the targets and all of the distractors would be the same surface, which would be like tracking the rubber band stimuli from Scholl et al. (2001). Alternatively, we might imagine that the visual system attempts to track the contours of the hole rather than the hole itself. Again, however, this should be problematic, since the contour belongs to the surround, which is the front plane: the same surface for all stimuli. Thus, on the basis of the existing literature, we predicted that that holes would be more difficult to track, compared to stimuli that are more obviously figural.

To anticipate our results, we did not find any difference between tracking holes and figures in Experiment 1, which featured Gaussian pixel noise backgrounds. In Experiments 2 and 3, we switched to photographic scenes. Here we obtained an advantage for tracking holes. However, when we removed the semantic content of the scenes by replacing them with statistically similar textures in Experiment 4, there was again no difference. In Experiment 5 we presented both figures and holes against blank backgrounds. Here we obtained a significant figure advantage, but only in the case where figures were fixed samples from the background, and each object was therefore unique. Tracking performance was equivalent for identical figures and holes (both unique and identical). In Experiment 6, we added stereo disparity cues to reinforce the difference between holes and figures, but again found no difference in tracking performance. Taken together, these experiments disconfirm our prediction: holes are tracked just as easily as figures, suggesting that the visual system treats the two equally for purposes of tracking.

2. Experiment 1: Transparent foregrounds and noise texture backgrounds

In this experiment, the stimuli comprised blue filters of varying transparency superimposed over a background of Gaussian pixel noise. There were two stimulus conditions (hole vs. figure) and three transparency conditions (25%, 50%, and 75%). In the hole condition, the blue filter (at one of the three transparency levels) filled the display, and the tracking stimuli were disks of 100% transparency. In the figure condition, the tracking stimuli were disks of one of the three transparency levels (see Figure 1). Note that the two types of stimuli are identical in terms of contrast and changes in contrast across the contour, the difference is whether the contour is assigned to the moving disk or the surrounding surface.

One of our goals in designing the experiment was to ensure that the task difficulty would be neither too easy nor too difficult for all observers. We therefore used an adaptive algorithm (QUEST, King-Smith, Grigsby, Vingrys, Benes, & Supowit, 1994; Watson & Pelli, 1983) to control the speed, and measured the speed threshold yielding 75% accuracy.

2.1. Method

2.1.1. Observers

We recruited eleven observers (ages 21–55, mean 34.9, sd = 14.0, five females) from the volunteer observer panel of the Brigham and Women’s Hospital Visual Attention Laboratory. Each observer passed Dr. Ishihara’s Tests for Color -Blindness and had 20/25 corrected vision or better. All observers gave informed consent before participating, and were compensated for their time at a rate of $10/hour.

2.1.2. Apparatus and stimuli

Stimulus presentation was controlled by Macintosh G4 computers running Mac OS 10.5. Experiments were written in Matlab 7.5 (The Mathworks) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997), version 3. Stimuli were presented on 20” CRT monitors (SuperScan Mc801 Raster Ops or Mitsubishi Diamond Pro 91TXM) with resolution set to 1280 × 960 pixels, and an 85 Hz refresh rate. Observers were placed so that their eyes were 57.4 cm from the monitor. At this viewing distance, 1 cm subtends 1 degree of visual angle (°).

The background was a 288 × 216 random dot texture, with the gray value of each dot randomly sampled from a gaussian distribution with a mean of 128. This texture was then magnified and presented as an 1152 × 864 pixel (36° × 27°) rectangle, centered within the monitor, so that each dot occupied a 4×4 pixel square. A different random texture was used on each trial. In the hole condition, a transparent blue filter was superimposed over the background. The alpha value of the filter was varied so that the transparency was 75%, 50%, or 25%. Eight circular masks, 2 degrees visual angle (°) in diameter, were placed at pseudorandom locations at least 100 pixels (3.1°) apart. These masks were 100% transparent (see top row of Figure 1). In the figure condition, thebackground was completely visible, and the eight masks were instead filter disks of 75%, 50%, or 25% transparency (see bottom row of Figure 1). Note: we will refer to both holes and filters as disks.

2.1.3. Procedure

Each block comprised five practice trials and fifty experimental trials. Stimulus condition (hole vs figure) and transparency were varied in separate blocks. Since there were 720 possible orders, order of conditions was generated randomly for each observer.

Each trial began with the disks presented stationary on the screen for one second. Four target disks were then highlighted in green for two seconds. The highlighting then disappeared and the disks moved for a tracking duration selected from a uniform distribution between 3 and 6 s (quantized by the refresh rate of the monitor). At the end of the trial, the disks stopped moving, and observers were asked to click on each of the targets. Once they had clicked on all of the disks, their correct selections were highlighted in green and incorrect selections in red. The experiment was self-paced, taking roughly 45 minutes per observer.

Disks were initially assigned to move in random directions. They bounced off the boundaries of a 25° square region centered on the background texture, and off of each other. In the practice block, the speed was set to 7.5°/s. In the experimental block, speed was controlled by the QUEST algorithm. QUEST is a maximum likelihood technique for measuring psychophysical thresholds (Watson & Pelli, 1983). The results from all prior trials are used to estimate the likely threshold value, and this estimated threshold value is then used to select the stimulus intensity on the next trial. The final threshold estimate used all fifty experimental trials.

QUEST was given an initial threshold estimate of 15°/s, a standard deviation estimate of 9°/s, a beta estimate of 3.5, and told to find the 75% threshold. Speeds above 30°/s were not allowed. Note that QUEST was originally designed for contrast sensitivity, and thus expects that high stimulus intensity will yield better performance. Since increasing speed reduces MOT performance, QUEST was actually provided with 1/speed as input, and we inverted the resulting threshold. For purposes of the QUEST computations, a trial was considered “correct” only if the observer correctly reported all four targets: even a single error led to the trial being classified as “incorrect”.

2.1.4. Data analysis

Thresholds were analyzed with a 3 (transparency: .25, .50, .75) × 2 (stimulus: figures vs. holes) within-subjects analysis of variance (ANOVA). Analyses were conducted in R 2.12.0 using the “ez” package (Lawrence, 2010). We report generalized eta-squared (hereafter η²) as a measure of effect size (Bakeman, 2005).

2.2. Results and Discussion

One observer (male) was excluded for disproportionately low speed thresholds. The mean threshold speeds for the remaining ten observers are shown in Figure 2 as a function of transparency. Performance declined as transparency increased (F(2, 18) = 4.64, p = .02, η² = 025), which is not surprising as contrast declines with increasing transparency (see Figure 1). However, there were no differences between holes and figures (F(1, 9) = 0.05, p = .83, η² = .00007), nor did stimulus condition interact with transparency (F(2, 18) = 0.24, p = .79, η² = .001).

Figure 2.

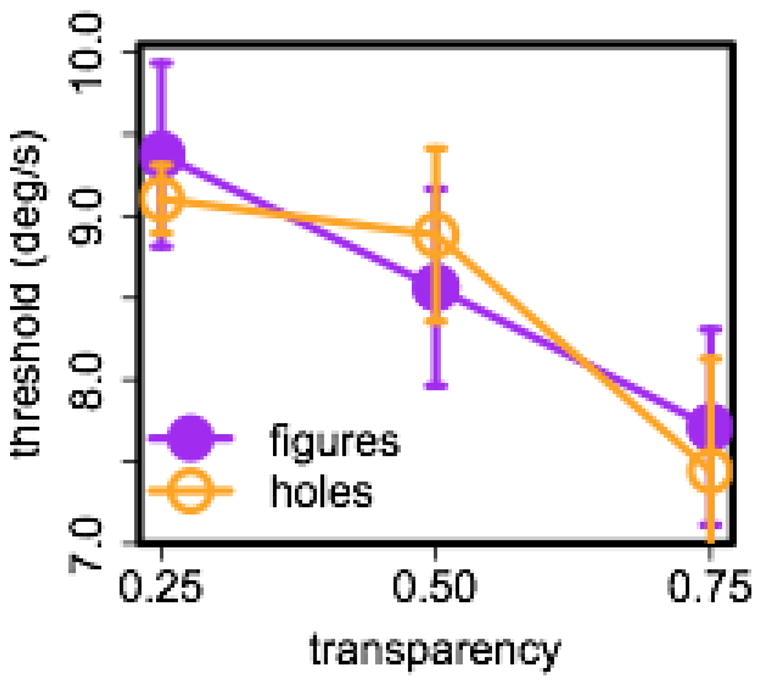
Performance in Experiment 1 as a function of stimulus condition and transparency. 75% threshold speed in degrees visual angle (°) per second is plotted against transparency (α). Filled (purple) symbols represent stimulus conditions where observers tracked figures, open (orange) symbols conditions where observers tracked holes. Error bars here and in subsequent figures denote the Cousineau- Morey within-subjects standard error of the mean (Cousineau, 2005; Morey, 2008).

It may be, however, that these were not the ideal stimuli to investigate tracking of holes. If the grain of the Gaussian texture was too fine, then observers may have perceived the holes as high contrast disks on a low contrast background. In fact, if tracking holes is indeed difficult, observers might have deliberately blurred their vision in order to induce this percept and turn the holes into objects. None of our observers reported anything along these lines, but we thought it prudent to test tracking with opaque surfaces and less homogenous backgrounds in the following experiments.

3. Experiments 2 - 4: Complex scenes

In this series of experiments, we replaced the Gaussian pixel noise textures with photographic scenes or synthetic textures coerced to statistically resemble them. In the hole conditions, the stimuli were transparent circular masks through a colored opaque surface placed on top of the image (Figure 3, left column). In the figure conditions the stimuli were opaque colored disks (Figure 3, right columns).

In these experiments, the word “background” can be used to refer to either the scene or synthetic texture that is revealed through the holes and surrounds the figures, or to the area that is not the moving disks. To avoid confusion, we will use the term “back layer” to refer to the former sense of background, and leave “background” to refer to the latter sense. So in the top row of Figure 3, a scene is the back layer for both images, but on the left the background is a uniform brown and on the right it is a kitchen scene.

3.1. Method

3.1.1. Observers

As before, observers were recruited from the volunteer observer panel of the Brigham and Women’s Hospital Visual Attention Laboratory. There were twelve observers for Experiment 2 (ages 21–48, mean 29.7, sd = 8.5, 5 females), ten for Experiment 3 (ages 18–51, mean 26.1, sd = 9.2, 9 females), and twelve for Experiment 4 (ages 19–44, mean 28.1, sd = 7.2, 8 females).

3.1.2. Stimuli

The stimuli are illustrated in Figure 3, with Experiment 2 in the top row, Experiment 3 in the middle row, and Experiment 4 in the bottom row. The hole conditions are illustrated in the left-hand column, and the figure conditions are illustrated in the right-hand column. For the back layer, Experiments 2 and 3 used a set of 135 indoor scenes downloaded from the MIT Computational Visual Cognition Laboratory. The scenes were 1024 × 768 pixels, and enlarged to fill the monitor. For Experiment 4, we generated a set of synthetic textures coerced to match these scenes on a set of statistical properties (Portilla & Simoncelli, 2000). The holes and figures were created as described in Experiment 1, with two exceptions. First, transparency was always set to 0, so that the holes were apertures through an opaque surface and the figures were opaque disks. Second, the color of the foreground (surface or disks) was determined by the average RGB vector for the image. In Experiment 2, we simply averaged the RGB values of the image for that trial, whereas in Experiments 3 and 4, we set each channel of the foreground to 0 if the mean value of the back layer was 128 or above, and to 255 if the mean value was below 128.

3.1.3. Procedure

The procedure was the same as in Experiment 1, except that there were only two conditions, tracking holes and tracking figures. The order was counterbalanced across observers. Each experiment took approximately 30 minutes to complete.

3.2. Results and Discussion

The thresholds from Experiment 2 are shown in the left panel of Figure 4. Holes were easier to track than figures, (F(1, 11) = 11.80, p = .006, η² = .249). This was an unexpected outcome. We considered two possible explanations. First, it is clear that the figures do not seem to be as salient with respect to the background than the holes (see top row, Figure 3), even though the contrast at the edges must be equivalent, on average. Second, while observers could probably tell us something about the scene in the hole condition, the scene is more readily available in the figure condition, and this may distract observers from the tracking task. We dealt with the first possibility in Experiment 3 and the second possibility in Experiment 4.

Figure 4.

Data from Experiments 2–4. Threshold speed in °/s is plotted for the figure (purple) and hole (orange) conditions. Experiment 2 is shown in the left-hand panel, Experiment 3 in the middle panel, and Experiment 4 in the right-hand panel.

In Experiment 3, we simply changed the method of computing the foreground color in order to ensure a larger color contrast between foreground and background (as described in the Method section above; compare top and middle rows of Figure 3). We hypothesized that this manipulation would eliminate (or reverse) the advantage for tracking holes. This hypothesis was disconfirmed (middle panel of Figure 4). Performance improved slightly in this experiment (but not significantly, according to an ANOVA comparing the two experiments ). However, holes were again easier to track than figures, (F(1, 9) = 8.89, p = .015, η² = .118).

In Experiment 4 we addressed the back layer rather than the foreground. This experiment was identical to Experiment 3, except that instead of indoor scenes we used the Portilla and Simnocelli (2000) algorithm to generate synthetic textures which matched those scenes on a set of image statistics. The exact statistical properties of the texture are less important for our purposes than the fact that they have structure at various scales, yet have no semantic content to distract the observer.

This manipulation substantially reduced the difference between holes and figures. The threshold speeds (right panel of Figure 4) were statistically indistinguishable (F(1, 9) = 1.07, p = .33, η² = 016), though the trend was in the same direction as in the previous two experiments. With meaningless texture back layers, the holes and figures were tracked at the same speeds. Thus, it seems that the semantically rich and interesting backgrounds were distracting observers while they were tracking the figures in previous experiments.

Of course, the meaningless textures might still be more interesting than the blank backgrounds used in the hole conditions. It is possible that figures are actually easier to track, but the textures distract observers just enough to reduce performance to the level of the hole condition. In the next experiment, we tested both holes and figures on blank backgrounds.

4. Experiment 5: Unique vs. identical items

In this experiment, both holes and figures were disk-shaped sections of the synthetic texture back layer, presented against a blank background. The holes were holes because the patch of back layer they display changes systematically as the hole moves across the texture. The figures were static: the same patch of back layer was simply moved across the screen. The two conditions were thus identical during the target designation phase; the difference only became apparent when the disks moved. In the response phase, all disks were replaced with identical opaque disks in the mean RGB color of the back layer image.

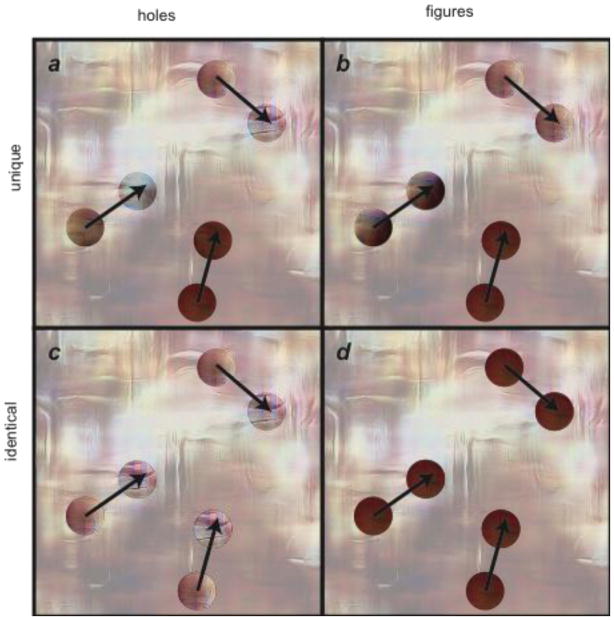
A potential problem introduced by these stimuli is that, since the figures were taken from separate patches of the back layer, they were unique. In any given frame, the hole stimuli were also unique, but these figure stimuli retain the same appearance across the entire tracking interval. It has been shown that unique items make tracking easier (Horowitz et al., 2007; Makovski & Jiang, 2009). This might create a misleading advantage for the figure condition. Therefore, we independently manipulated whether stimuli were figures or holes, and whether they were identical to one another or unique. In all four conditions, the stimuli were disk-shaped patches of the back layer texture. In the unique conditions (Figure 5a, b), the patches on the first frame were sampled from portion of the texture lying behind each stimulus on that frame. In the identical conditions (Figure 5c, d), one patch was chosen at random (equally likely to be a target patch or distractor patch) on the first frame and cloned for all of the stimuli. In the figure conditions (Figure 5b, d), the patch did not change as the stimuli moved, while in the hole conditions (Figure 5a, c), the patches changed smoothly. The unique hole condition thus replicated the hole conditions we have used previously, where each stimulus reflected the texture directly underneath it on every frame. In the identical hole condition, however, all of the stimuli reflected the texture directly underneath one of the stimuli. These stimuli might not be easily interpretable as holes, since the motion of the image seen through the hole was decoupled from the motion of the hole itself (except for one master item).

Figure 5.

Cartoons of stimuli used in Experiment 5. In each panel, we superimpose two frames each with three disks. The arrows indicate each disk’s direction of motion from the first frame to the second. In the actual stimulus, the background would be a uniform white, but here we show a low contrast version of the back layer in order to illustrate the relationship between the disks and the back layer. Panel A depicts the unique hole stimuli. Each disk reveals the texture lying behind it in the back layer atany given time. Panel B depicts the uniquefigure stimuli. The texture of each disk is drawn from the corresponding patch of the back layer on the very first frame, and then the texture is fixed for the rest of the trial. Panel C depicts the identical hole stimuli. One randomly selected master disk (in this case, the uppermost one) reveals the texture lying behind it in the back layer, and all of the other disks are copies of it. Panel D depicts the identical figure stimuli. The initial texture of one randomly selected master disk (in this case the lowermost one) is used for all disks throughout the trial.

The four conditions were counterbalanced via a latin square design.

4.1. Observers

We recruited sixteen observers (ages 18–51, mean 24.8, sd = 8.2, 14 females) from the volunteer observer panel of the Brigham and Women’s Hospital Visual Attention Laboratory.

4.2. Results and Discussion

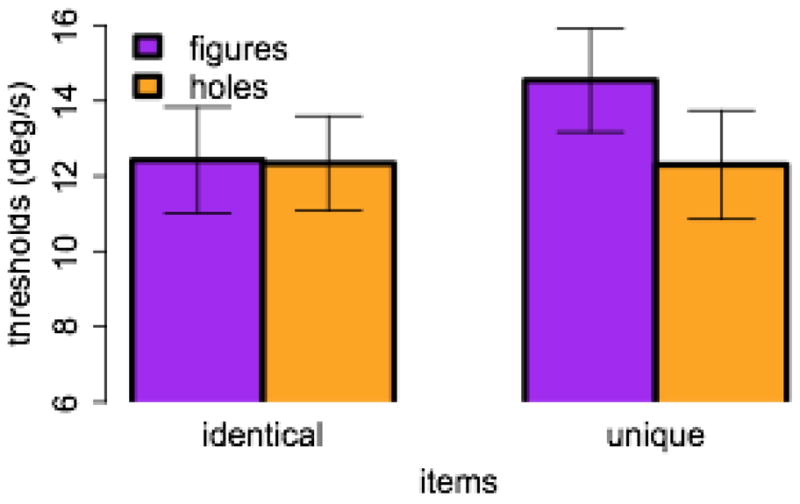
We analyzed the results with a 2 (figures vs. holes) × 2 (unique vs. identical) ANOVA. There was a marginal advantage for unique items (F(1, 15) = 3.8, p = .07, η² = .017), and an advantage for figures over holes (F(1, 15) = 12.3, p = .003, η² = .021). However, Figure 6 makes it clear that both of these effects are driven by the unique figures condition, which yielded better performance than all of the other conditions, which were roughly comparable to one another, producing a significant interaction (F(1, 15) = 4.6, p = .05, η² = .018).

When we eliminated the unique item benefit, figures and holes were tracked at the same speeds. It is interesting that the visual content of the holes did not seem to affect tracking performance. It does not appear to matter whether the pattern inside the contour changes or not, or even whether the pattern of change is consistent with a moving hole or not (cf. St Clair, Huff, & Seiffert, 2010).

5. Experiment 6: Stereo disparity cues

In all of the preceding experiments, hole or figure status was defined solely by 2D pictorial cues. Holes were holes because the pattern inside the aperture changed in a way consistent with a moving hole revealing the background. However, it’s possible that the visual system interpreted the holes as disks with a changing pattern on them, as might result from a rolling marble, for example. Therefore, in Experiment 6 we added stereo disparity cues to reinforce the hole vs. figure interpretation.

The displays are cartooned in Figure 7. We used red-cyan anaglyphs to present stimuli in three depth planes. In the back plane we presented a background texture, which was either a gaussian pixel noise field (as in Experiment 1) or a synthetic texture (as in Experiments 4 and 5). In the middle, neutral disparity plane, we presented a gray square with a white grid. The disks were confined to the region bounded by this square. In the figure conditions, the disks were presented in the plane in front of the square. In the hole conditions, the disks were presented in the back plane, and thus seemed to be holes in the gray square through which the background texture could be seen.

Figure 7.

Stimuli for Experiment 6. Left panel shows gaussian pixel noise stimuli in the figure condition. The noise texture is in the back plane (uncrossed disparity), the gray gridded rectangle at neutral disparity, and the disks in the front plane (crossed disparity). Each disk has the identical pixel texture. The right panel shows the synthetic texture stimuli in the hole condition. The synthetic texture is in the back plane (uncrossed disparity), the gray gridded rectangle at neutral disparity, and the disks in the back plane (uncrossed disparity). Note that drop shadows are for illustration purposes only; depth was conveyed entirely by disparity.

The figure and hole conditions replicated the identical figure and unique hole conditions, respectively, from Experiment 5. We made the disks in the figure conditions identical by taking one patch of the background texture and cloning it for all eight items. In the hole conditions, the texture inside the moving disks changed to reflect the background texture.

5.1. Observers

We recruited twelve observers (ages 18–54, mean 31.25, sd = 13.07, 9 females) from the volunteer observer panel of the Brigham and Women’s Hospital Visual Attention Laboratory. We tested observers for stereoblindness before the experiment. One participant (not included in the statistics) was excluded for stereoblindness.

5.2. Results and Discussion

Adding stereo cues did not change the results. Overall, tracking performance was better in this experiment relative to previous experiments (note the y-axis scale). A 2 (figures vs. holes) × 2 (gaussian noise vs. synthetic texture) ANOVA obtained no significant effects. Specifically, the effect of figures vs. holes was F(1, 11) = 0.19, p = .668, η² = .0007, and the interaction with the background texture was F(1, 11) = 0.009, p = .928, η² = .00004.

6. General Discussion

Taken together, these experiments showed no evidence for a deficit in tracking holes compared to figures. We conclude that holes are trackable items. Based on the account we sketched in the Introduction, this is an unexpected result. According to Bertamini (2006), the contour of a hole belongs to its surround, whereas according to Albrecht et al. (2008), cueing a hole actually cues the surface behind the hole. Thus, the existing literature suggests that in our displays, target and distractor holes would be associated with the same surface, either the front layer (foreground) in the case of tracking contours, or the back layer in the case of tracking the apertures themselves. Following the logic of Scholl et al.’s “target merging” experiments (Scholl et al., 2001), it should be more difficult to track targets that are linked with distractors in this fashion. We will discuss the implications of this finding in Section 6.3, below, but first we deal with two ancillary findings.

6.1. Background effects

Our observers found it more difficult to track objects that moved against a complex background, compared to objects that moved against a blank background (Experiments 2–4). This does not seem to be a purely visual effect. For one, the events at the disk boundaries were precisely equated in these experiments, since the disks moving against complex backgrounds were blank, while the disks moving against blank backgrounds were sampled from the same complex back layers that provided the complex backgrounds. For another, the interference was substantially reduced when we changed from interpretable scene back layers to abstract synthetic textures coerced to be statistically similar to the scenes. The most straightforward explanation is that observers were simply distracted by the scenes and diverted attention from the tracking task, perhaps because they anticipated a surprise memory test, or perhaps simply because they found the images intrinsically interesting.

6.2. Unique target effects

Experiment 5 replicated the unique target advantage: the finding that targets are easier to track if they are visually distinct from one another and from the distractors (Horowitz et al., 2007; Makovski & Jiang, 2009). When we originally reported the unique target advantage, we hypothesized that unique targets improve performance by helping observers to recover lost targets. If an observer is tracking a red, green, and yellow target, for example, and loses the yellow target, she can search for yellow among the untracked objects. When an identical twin distractor accompanies each target the unique target advantage is neutralized (Horowitz et al., 2007). Similarly, the unique target advantage is reduced when stimuli are defined by conjunctions of features (which are difficult to search for), as opposed to single features (Makovski & Jiang, 2009).

Experiment 5 provides additional support for this “search and recovery” hypothesis. Note that in both of the unique item conditions, the disks are unique on every frame of the motion sequence. However, only the unique figure condition shows a unique target advantage; performance in the unique hole condition was indistinguishable from the two identical conditions. Similarly, the unique hole conditions produced similar performance to the identical figure conditions in Experiment 6. This finding suggests that the unique identity must be stable over time in order to produce a unique target advantage. This is consistent with the search and recovery hypothesis: by the time the observer notices which target is missing, its features have drifted from the last known state, and thus the missing target becomes difficult or impossible to recover unless it is found immediately.

Another interpretation is that the visual content of the holes is simply not bound to the “proto-object” that encompasses the hole, and thus the holes are treated as visually identical “empty” contours. This is also consistent with the search and recovery hypothesis.

6.3. Implications for proto-objects and attention

What does it mean that holes were tracked as easily as figures? In the Introduction, we put forth two assumptions. First, we assumed that MOT can tell us what the visual system treats as a proto-object. Items which can be separately attended can be tracked, and the visual system cannot independently track multiple spatial features of a single object (Scholl et al., 2001). Second, we assumed that the contour of a hole belongs to its surround (Bertamini, 2006; Bertamini & Croucher, 2003).

Given these two assumptions, from our finding that holes can be tracked it follows that a proto-object does not require a visible bounding contour; a “shapeless bundle”, to borrow a phrase from Wolfe and Bennett (1997). At first glance, this would seem to contradict the substantial body of evidence showing that contour ownership is indeed represented within proto-objects (Khurana, 1998; Rensink & Enns, 1998). However, those experiments tell us about the internal structure of proto-objects. If a square overlaps a disk (as in Rensink & Enns, 1998), the contour between them belongs to the square. But our results speak to the boundary of the proto-object itself: the bundle containing the square and disk. These bundles need not have a visible contour of their own. Attention can be directed to a region which lacks an image-based boundary. This is not to say that the region does not have a boundary at all. As Bertamini and Hulleman (2006) point out, surfaces seen through holes may have amodal boundaries which extend beyond the contour of the hole. While these amodal boundaries, perceived under focused attention, pertain to the back surfaces, they may reflect preattentively generated boundaries for the corresponding proto-objects.

This hypothesis can neatly explain the Bertamini and Lawson (2006) search results: both holes and figures exist as proto-objects to which attention can be directed, so one can search as efficiently through an array of holes looking for the figure as through an array of figures looking for the hole. Directing attention to the proto-object then resolves contour ownership, allowing the figure/hole decision to be made. If a hole is cued, however, as in the Albrecht et al. (2008) experiments, attention is directed to the proto-object, which is then resolved such that attentional facilitation is imputed to the surface visible through the aperture. Contextual factors may then determine whether a single surface or multiple surfaces are inferred (Bertamini & Hulleman, 2006).

Evidence in support of this hypothesis comes from work on color-from-motion (CFM, V. J. Chen & Cicerone, 2002a; V. J. Chen & Cicerone, 2002b), apparent motion is created from a field of stationary dots by changing the color assignments of the dots in a manner consistent with a moving object. Critically, there is no visible edge or border. Thus, it is possible to have a motion token which lacks an image-based contour.

Our assumption that the visual system cannot independently track multiple spatial features of a single object is based on the target merging experiments of Scholl et al. (2001). One key difference between our experiments and those of Scholl et al. is that they required observers to divide attention between multiple objects, and track one spatial feature of each object, whereas our study (in the hole tracking conditions) could be interpreted as asking observers to simply track a subset of features of one object. Logically, it may be possible to track multiple spatial features of a single object, as long as attention is not divided across multiple objects. In this case, we could relax our first assumption.

Thus, a second interpretation of our data is to assume that it is the item with the contour that is being tracked. That is, observers are not tracking four separate objects. Rather, they are tracking four parts of the front surface. This interpretation has two novel implications: first, just as both concave and convex regions can be searched with equal ease (Bertamini & Lawson, 2006), so can they be tracked with equal ease; second, that multiple spatial features of a single object (e.g., the front surface) can be tracked independently.

A third interpretation can be derived if we instead abandon the assumption that the contour belongs to the surround. Our experiments differ from those in most previous studies on the perception of holes and on proto-objects in that our stimuli were in motion. Motion information is a powerful cue, which may override the usual assumptions made by the visual system with static scenes. For example, Caplovitz and Tse (2006) argue that the usual rules for assigning contour ownership can be overridden by the presence of trackable features. In the case of their bar-and-ellipse illusion, the percept of an elliptical aperture rotating in front of a rigid cross is dominated by the percept of a nonrigidly deforming cross, because the ends of the cross are the only trackable features. The moving contours at the ends of the crossbars get assigned to the cross itself, overruling the rigidity constraint. It may be that rules governing the construction of proto-objects are different in dynamic scenes, such that moving holes do own their contours. Against this interpretation is the only previous experiment that we are aware of with moving holes, the final experiment in Bertamini and Hulleman (2006), which provided phenomenological evidence to support the hypothesis that holes do not own their contours. Since both studies report observers’ impressions of a single object under full focal attention, it is difficult to determine which set of rules applies when the visual system is parsing the visual scene under conditions of diffuse attention.

7. Conclusions

Can we attend to holes as objects? We found that, all other things being equal, holes are as easy to track as figures, which suggests to us that the answer is yes. There are several ways to interpret this finding. Under the assumptions we laid out in the Introduction, our more precise answer is that holes are proto-objects. Thus, we can attend to the bird-shaped hole in the sky of LeRetour, even if it takes us a little longer to identify it as a bird.

Figure 8.

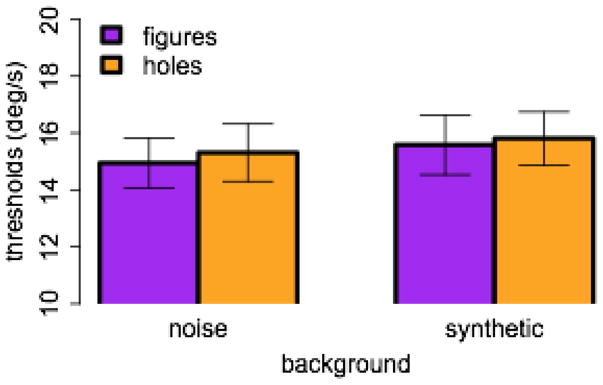
Data from Experiment 6. Threshold speed in °/s is plotted for the figure (purple) and hole (orange) conditions, with gaussian noise texture backgrounds on the left and Portilla-Simoncelli synthetic texture backgrounds on the right.