A mathematical model for foreign body reactions in 2D

Abstract

The foreign body reactions are commonly referred to the network of immune and inflammatory reactions of human or animals to foreign objects placed in tissues. They are basic biological processes, and are also highly relevant to bioengineering applications in implants, as fibrotic tissue formations surrounding medical implants have been found to substantially reduce the effectiveness of devices. Despite of intensive research on determining the mechanisms governing such complex responses, few mechanistic mathematical models have been developed to study such foreign body reactions. This study focuses on a kinetics-based predictive tool in order to analyze outcomes of multiple interactive complex reactions of various cells/proteins and biochemical processes and to understand transient behavior during the entire period (up to several months). A computational model in two spatial dimensions is constructed to investigate the time dynamics as well as spatial variation of foreign body reaction kinetics. The simulation results have been consistent with experimental data and the model can facilitate quantitative insights for study of foreign body reaction process in general.

1 Introduction

The process of foreign body inflammatory reactions to implants involves complex interactions of many types of cells and proteins and occurs as a sequential cascade of parallel and overlapping chemical processes (Dee et al 2002 [1]). During a short but complex initiation period of surface mediated reactions mainly involving implant-mediated fibrin clot formation and then acute inflammatory responses, various tissue growth factors are released (Anderson 1994 [2], Tang and Eaton 1995 [3]). In response to the gradient field of tissue growth factors released in the implant domain, fibroblasts migrate towards the implant from the surrounding tissues and/or proliferate within the fibrinogen absorbed on implant surface. The fibroblasts consequently synthesize chains of amino acids called procollagens, a process that is activated by growth factors, including in particular type-β transforming growth factor (TGFβ) (McDonald 1988 [4], Appling et al. 1989 [5]). The procollagens then get converted into their respective collagens by enzymes (Goldberg 1977 [6]). Inactive (latent forms of) TGFβ isoforms are also secreted by many cells (Martin et al. 1992 [7]; Streuli et al. 1993 [8]) and they have a considerably longer half-life than their active forms (Roberts and Sporn 1990 [9]). The implant site contains enzymes that activate latent growth factors and also initiate the stabilization of collagen precursors (Miller and Gay 1992 [10]). Similar to other collagen formation such as dermal wound healing, collagenase is synthesized and secreted by fibroblasts as a zymogen (Stricklin et al. 1978 [11]), but collagen degradation cannot occur until the zymogen is activated. These basic reactions were considered in similar modeling study of wound healing (Dale et al. 1996 [12]) and their corresponding key features of kinetics were incorporated in our modeling. Recently, Schugart et al 2008 successfully incorporated modeling of more biophysical features such as angiogenesis and oxygen level into wound healing process [13, 14], and the modeling and simulations of these systems have attracted a substantial mathematical interest.

Inflammatory cells and associated products influence greatly on fibrotic tissue formation. Among all inflammatory cells, macrophages are found to reside in the wound and to exert long term tissue reactions [15]. Macrophages clean foreign and debris material; they send chemotactic signals to other cell types that will participate in wound healing and finally they play roles in remodeling of Extracellular Matrix (EMC) [16]. They are classified into 3 phenotypes according to their roles in the process. Classically activated macrophages designate the effector macrophages that are produced during cell-mediated immune responses. Two signals, interferon-γ (IFNγ) and tumor-necrosis factor-α (TNF-α), resulted in a macrophage population that have enhanced microbicidal or tumoricidal capacity and secret high levels of pro-inflammatory cytokines and mediators. On the other hand, the clearance of apoptotic inflammatory cells, including polymorphonuclear cells (PMNs) by macrophages during inflammation can lead to an inhibition of inflammation, owing in part to the production of transforming growth factor-β (TGFβ) [17]. Wound-healing macrophages can develop in response to innate or adaptive signals through interleukin-4 (IL-4). IL-4 stimulates arginase activity in macrophages, allowing them to convert arginine to ornithine, a precursor of polyamines and collagen, thereby contributing to productions of Extracellular Matrix [18]. Regulatory macrophages can also arise during the later stages of adaptive immune responses, the primary role of which dampen the immune response and limit inflammation through production of interleukin-10 (IL-10) [19]. Although all three types are observed experimentally in general wound healing process, the phagocytes biomaterial interactions are known to be similar (Tang 1997 [20]).

Using the quantitative predictive tool, our goal was to investigate all possible pathways of foreign body reaction networks and consider impacts of various tissue growth factors, enzyme and how their migrations redistribute at a limited speed through diffusion. Further, because of a significant precursor of collagens is the formation of fibrin layers that provides the domain for growth factors activations in implant process, an important component of our modeling paper is to test numerically various hypotheses on reactions on plasma or chemically coated bio-materials surface (Tang et al 1998 [21]). Our numerical result indicated trends for these variations, serving as a plausible clue for developing new experiment hypotheses.

We describe our mathematical model that matches with experimental data in Section 2, and numerical methods in Section 3. In Section 4, we illustrate the transient dynamics of foreign body reaction dynamics in pure temporal behavior and in 2+1 spatial/temporal dimensions and several numerical experiments that are related to implant coating. The summary and discussion are in Section 5.

Section 2 Mathematical Modeling

Our model is based on collagen kinetics framework developed by Dale et al in 1996 [12] for temporal dynamics and Dale et al in 1997 [22] for temporal-spatial dynamics, that were proposed as models for normal adult and foetal wound healing. Then we include new kinetics of foreign body reaction by macrophages. The new dynamics is in a different parametric range and they present different characters. The difference is primarily due to the fact the foreign body reactions in implantation are deep sub-dermal phenomena, but the normal wound healings are primarily based on dermal wound experimental data.

2.1 Chemical Kinetics Equations

We briefly state the modeling considerations for the variables involved, listed in Table 1:

Table 1.

Variables in foreign body reactions (after scaling so they are dimensionless).

f(x, y,t)	Fibroblast density
β1(x, y,t)	Total TGFβ isoform 1 and isoform 2 density
β3(x, y,t)	TGFβ isoform 3 density
l1(x, y,t)	Total Latent TGFβ isoform 1 and isoform 2 density
l3(x, y,t)	Latent TGFβ isoform 3 density
e1(x, y,t), e2(x, y,t), e3(x, y,t)	Generic enzymes type 1, 2, 3 densities
p1(x, y,t), p3(x, y,t)	Procollagens (latent form of collagens) I and III densities
c1(x, y,t), c3(x, y,t)	Collagens I and III densities
z1(x, y,t), z3(x, y,t)	Zymogens (latent forms of collagenases) I and III densities
s1(x, y,t), s3(x, y,t)	Collagenases I and III densities
l(x, y,t)	Macrophage cell density

Fibroblast density f(x, y,t) represents the main cell type in implant domain. We ignore directional effects of fibroblast cells and assume that cell migration is through diffusion. Under transforming growth factor TGFβ (total isoform 1 and isoform 2 density β₁(x, y,t), isoform 3 density β₃(x, y,t)), the cell population can be approximated by a chemically enhanced logistic growth, along with a natural decay:

$$\frac{\partial f}{\partial t}=D_1{\nabla }^{2}f+(A_1+A_2{\beta }_1+A_3{\beta }_3)f\left(1-\frac{f}{k_1}\right)-A_{4}f.$$ (2.1)

The fibroblasts are stimulated via autocrine regulation (Roberts & Sporn 1990 [9]) to secrete the corresponding latent TGFβ l₁(x, y,t) and l₃(x, y,t) with a limiting production rate when l₁(x, y,t) and l₃(x, y,t) saturate (Wakefield 1988 [23]). Latent TGFβ also undergoes an autocrine mechanism, whereby TGFβ induces self-secretion. The concentration of latent growth factor is also decreased because of activations into respective active forms of TGFβ by specific enzymes [9]. Fibroblast proliferation and collagen synthesis are up-regulated by TGFβ, but by their active rather than latent forms (Krummel et al. 1988 [24]). We assume all forms of TGFβ have constant diffusion coefficients. They are modeled by equations:

$$\frac{\partial l_1}{\partial t}=D_2{\nabla }^2{l}_1+\frac{A_5{fl}_1}{1+A_6{l}_3+A_7{l}_1}-A_8{l}_1-A_{16}{e}_1{l}_1,$$ (2.2)

$$\frac{\partial l_3}{\partial t}=D_3{\nabla }^2{l}_3+\frac{A_9{fl}_3}{1+A_{10}{l}_3}-A_{11}{l}_3-A_{17}{e}_1{l}_3,$$ (2.3)

$$\frac{\partial {\beta }_1}{\partial t}=D_4{\nabla }^2{\beta }_1+A_{12}{e}_1{l}_1-A_{13}{\beta }_1,$$ (2.4)

$$\frac{\partial {\beta }_3}{\partial t}=D_5{\nabla }^2{\beta }_3+A_{14}{e}_1{l}_3-A_{15}{\beta }_3.$$ (2.5)

During early stages of foreign body implantation, monocytes and macrophages release a range of enzymes, which activate growth factors, procollagens and zymogens (Sinclair and Ryan 1994 [25]). We use the law of mass action to model the activation of latent TGFβ 1 and 3, latent collagen I and III and latent collagenases I and III, by e₁, e₂ and e₃ respectively:

$$\frac{{de}_1}{dt}=-e_1(A_{16}{l}_1+A_{17}{l}_3),$$ (2.6)

$$\frac{{de}_2}{dt}=-e_2(A_{18}{p}_1+A_{19}{p}_3)+B_{36}l,$$ (2.7)

$$\frac{{de}_3}{dt}=-e_3(A_{40}{z}_1+A_{41}{z}_3).$$ (2.8)

Procollagen is synthesized by fibroblasts, in response to injury (McDonald 1988 [4]). Further experiments showed up-regulation of procollagen synthesis by active TGFβ (Appling et al. 1989 [5]) hence the inclusion of a linear function of active TGFβ 1 and 3. We use the law of mass action to model activations of latent collagens 1 and 3 as well as degradations because of collagenases. Activations of collagenases follow similar mass-action laws under specific enzyme e₃:

$$\frac{{dp}_1}{dt}=(A_{20}+A_{21}{\beta }_1+A_{22}{\beta }_3)f-A_{23}{p}_1-A_{18}{e}_2{p}_1,$$ (2.9)

$$\frac{{dp}_3}{dt}=(A_{24}+A_{25}{\beta }_1+A_{26}{\beta }_3)f-A_{27}{p}_3-A_{19}{e}_2{p}_3,$$ (2.10)

$$\frac{{dc}_1}{dt}=A_{28}{p}_1{e}_2-A_{29}{s}_1{c}_1,$$ (2.11)

$$\frac{{dc}_3}{dt}=A_{30}{p}_3{e}_2-A_{31}{s}_3{c}_3,$$ (2.12)

$$\frac{{dz}_1}{dt}=\frac{A_{32}}{1+A_{33}{\beta }_1+A_{34}{\beta }_3}{fc}_1-A_{35}{z}_1-A_{40}{e}_3{z}_1+B_{37}l,$$ (2.13)

$$\frac{{dz}_3}{dt}=\frac{A_{36}}{1+A_{37}{\beta }_1+A_{38}{\beta }_3}{fc}_3-A_{39}{z}_3-A_{41}{e}_3{z}_3+B_{38}l,$$ (2.14)

$$\frac{{ds}_1}{dt}=A_{42}{z}_1{e}_3-A_{43}{s}_1,$$ (2.15)

$$\frac{{ds}_3}{dt}=A_{44}{z}_3{e}_3-A_{45}{s}_3.$$ (2.16)

Macrophage has been playing multiple roles in foreign body reactions. Our model differes from early collagen model, primarily because we incorporated feautres: (a) macrophages produce procollagens specific enzymes at a near saturated level and (b) macrophage regulate collagen growth through productions of zymogens. These changes led to substantial new quantitative behavior changes in the model.

The activation and prolifiration of macrophage are through upregulation of growth factors TGFβs [26], but the prudction does reach a limiting value once TGFβs reaches saturation. The macrophage cell’s programmed death normally occurs after several weeks to a month. Here we assume a life span of 30 day (as a typical case). Thus,

$$\frac{dl}{dt}=D_6{\nabla }^{2}l+B_{39}(e_1{l}_1+e_1{l}_3)l\frac{(N_n+N_e)}{N_n+l}-B_{40}l-B_{41}{\sigma }_0(t-30)l.$$ (2.17)

2.2 Model Reduction and Modification

We first consider a reduced system with the following assumptions:

1. The system has no spatial inhomogeniaty and therefore no diffusion. So, it becomes a pure temporal model with D₁ = D₂ = D₃ = D₄ = D₅ = D₆ = 0.

2. The activation of latent TGFβ 1 and 3, and type I and type III collagens and collagenases reaches equilibrium within a relatively short period of time. We assume that the equations (2.4), (2.5), (2.9), (2.10), (2.13) and (2.14) are at equilibrium.

The system is reduced to 11 equations of Ordinary Differential Equations (ODEs) (see Appendix 1 for detail of derivations):

$$\frac{df}{dt}=(A_1+B_2{e}_1{l}_1+B_3{e}_1{l}_3)f\left(1-\frac{f}{k_1}\right)-A_{4}f,$$ (2.18)

$$\frac{{dl}_1}{dt}=\frac{A_5{fl}_1}{1+A_6{l}_3+A_7{l}_1}-A_8{l}_1-A_{16}{e}_1{l}_1,$$ (2.19)

$$\frac{{dl}_3}{dt}=\frac{A_9{fl}_3}{1+A_{10}{l}_3}-A_{11}{l}_3-A_{17}{e}_1{l}_3,$$ (2.20)

$$\frac{{de}_1}{dt}=-e_1(A_{16}{l}_1+A_{17}{l}_3),$$ (2.21)

$$\frac{{de}_2}{dt}=-e_{2}f\left(\frac{B_{14}+B_{16}{e}_1{l}_1+B_{17}{e}_1{l}_3}{A_{23}+A_{18}{e}_2}+\frac{B_{15}+B_{19}{e}_1{l}_1+B_{20}{e}_1{l}_3}{A_{27}+A_{19}{e}_2}\right)+B_{36}l,$$ (2.22)

$$\frac{{de}_3}{dt}=-\frac{e_3}{\lambda }\left(\frac{B_{34}{fc}_1}{(1+B_{27}{e}_1{l}_1+B_{28}{e}_1{l}_3)(A_{35}+A_{40}{e}_3)}+\frac{B_{35}{fc}_3}{(1+B_{31}{e}_1{l}_1+B_{32}{e}_1{l}_3)(A_{39}+A_{41}{e}_3)}\right),$$ (2.23)

$$\frac{{dc}_1}{dt}=\lambda \left((B_{22}+A_{28}{C}_3{e}_1{l}_1+A_{28}{C}_2{e}_1{l}_3)f\left(\frac{1000e_2}{A_{27}+1000e_2}\right)-A_{29}{s}_1{c}_1\right),$$ (2.24)

$$\frac{{dc}_3}{dt}=\lambda \left((B_{24}+A_{30}{C}_3{e}_1{l}_1+A_{30}{C}_4{e}_1{l}_3)f\left(\frac{1000e_2}{A_{27}+1000e_2}\right)-A_{31}{s}_3{c}_3\right),$$ (2.25)

$$\frac{{ds}_1}{dt}=\frac{B_{26}{fc}_1{e}_3}{\lambda (1+B_{27}{e}_1{l}_1+B_{28}{e}_1{l}_3)(A_{35}+A_{40}{e}_3)}-A_{43}{s}_1+B_{37}l,$$ (2.26)

$$\frac{{ds}_3}{dt}=\frac{B_{30}{fc}_3{e}_3}{\lambda (1+B_{31}{e}_1{l}_1+B_{32}{e}_1{l}_3)(A_{39}+A_{41}{e}_3)}-A_{45}{s}_3+B_{38}l,$$ (2.27)

$$\frac{dl}{dt}=B_{39}(e_1{l}_1+e_1{l}_3)l\frac{(N_n+N_e)}{N_n+l}-B_{40}l-B_{41}{\sigma }_0(t-30)l.$$ (2.28)

We then proceed to find out the parameters that can be categorized into three groups.

The parameter group number 1 consists of well-established parameters from experiments, and all of them are taken from existing literature. We refer to [12, 26] for details and their related original references. These parameters are not expected to change substantially during different settings of experiments. They are:

$$\begin{array}{l}{A}_1=0.72222,B_2=\frac{A_2{A}_{12}}{A_{13}}=0.5,B_3=\frac{A_3{A}_{14}}{A_{15}}=0.5,A_5=100,A_9=100,A_{16}=0.1,\\ A_{17}=0.1,A_{18}=10,A_{19}=10,B_{14}=A_{18}{A}_{20}=3,\\ B_{15}=A_{19}{A}_{24}=3,B_{16}=\frac{A_{18}{A}_{21}{A}_{12}}{A_{13}}=1.5,B_{17}=\frac{A_{18}{A}_{22}{A}_{14}}{A_{15}}=3.5,A_{23}=1,\\ B_{19}=\frac{A_{25}{A}_{19}{A}_{12}}{A_{13}}=1.5,B_{20}=\frac{A_{26}{A}_{19}{A}_{14}}{A_{15}}=2,B_{22}=A_{28}{A}_{20}=5.4,A_{29}=1,A_{31}=1,\\ B_{26}=A_{32}{A}_{42}=1.5,B_{27}=\frac{A_{33}{A}_{12}}{A_{13}}=1,A_{35}=10,B_{30}=A_{36}{A}_{44}=4.5,B_{31}=\frac{A_{37}{A}_{12}}{A_{13}}=3,\\ B_{32}=\frac{A_{38}{A}_{14}}{A_{15}}=1,A_{39}=10,A_{40}=10,A_{41}=10,B_{34}=A_{40}{A}_{32}=50,B_{35}=A_{41}{A}_{36}=50,\\ A_{43}=1,A_{45}=1,k_1=3.5,C_1=\frac{A_{21}{A}_{12}}{A_{13}}=\frac{1.5}{A_{18}},C_2=\frac{A_{22}{A}_{14}}{A_{28}}=\frac{3.5}{A_{18}},\\ C_3=\frac{A_{30}{A}_{25}{A}_{12}}{A_{13}}=\frac{1.5}{A_{19}},C_4=\frac{A_{26}{A}_{14}}{A_{15}}=\frac{2}{A_{19}},B_{36}=0.005,B_{39}=0.5,\\ N_n=0,N_e=20,B_{40}=0.001,B_{41}=8,\end{array}$$

The group number 2 of parameters contains implantation experimental specific constants.

For implantation process, one unique character is that the activation rate from latent collagens to collagens can easily saturate, while there is an abundant amount of e₂. In equations (2.24–2.25) for collagens, we use two steps:

1. Approximate $\frac{1000e_2}{A_{27}+1000e_2}$ by $\frac{1}{1+10e_2}$ so e₂ does not reach collagen reaction saturation level too quickly. We run the replaced system to find out the most fitting curves among the group of parameters in group number 3 below to establish our base parameters for the model.

2. In final simulation, we resume $\frac{1000e_2}{A_{27}+1000e_2}$ with A₂₇ = 1 for our purpose. The level 1000 is arbitrarily imposed to ensure the factor being close to 1 as soon as e₂> 0.01. The purpose of these extra steps is to achieve a better approximation for initial 4 or 5 days of reaction kinetics.

The parameters B₃₇ and B₃₈ are taken to be the smallest possible values to minimize the effect of macrophage on collagenases within the extent of this paper. We plan to further explore its variations in kinetics in a separate paper. Here, B₃₇= 10⁻⁸, B₃₈= 10⁻⁸.

The scaling parameter λ = 0.07 is a scale factor that makes the numerically computed values of collagens 1 and 3 to be at same order of magnitute as experimental data. While our computational result reflects the trend and quantative features very well in a relative scale level. We have not seen a direct transformation between experimental data and our calculated values. There are a number of factors involved. Typically collagens are measured by count in a specific surface area under microscope (surface density), and our model calculates volume density, the distribution in vertical level is not uniform. More accurate collagen measures derive from measures of hydroxyproline (a constituent of collagen type I, but the scaling factors are not explicitly given also.

The group number 3 of parameters or “selected group” is achieved by numerical simulations to match the experimental data. We pick this group of parameters to fit experiments, because they are subject to change during human development. For example, Dale et al¹² has shown the difference of this group of values for adult and foetal dermal healing processes.

Based on an experimental data set from Liping Tang’s lab (shown in Table 2, details of experimental setup will be given in a separate paper), we found that the following choice of parameter values: A₆= 7.5, A₇ = 0.1, A₈= 15, A₁₀= 0.45, A₁₁= 15, B₂₄= A₃₀A₂₄= 67.5, B₂₈= A₃₄A₁₄= 202.5, gives a smallest residual for error for calculated and measurement collagen data. We note for the comparison purpose, the effect of macrophage was not included.

Table 2.

Experiment data of collagen deposit in a PET membrane.

Collagen deposition on PET 20 um membrane (unit, ug/cm2)
	#1	#2	#3	#4	#5
4 days	1.5	1.12	0.847	0.957	0.957
7 days	19.63	19.12	20.29	25.8	27.43
14 days	149.96	74.73	89.54	128.82	110.76
21 days	106.32	115.52	140.52	132.94	115.89
28 days	148.32	134.92	179.93	111.8	148.34

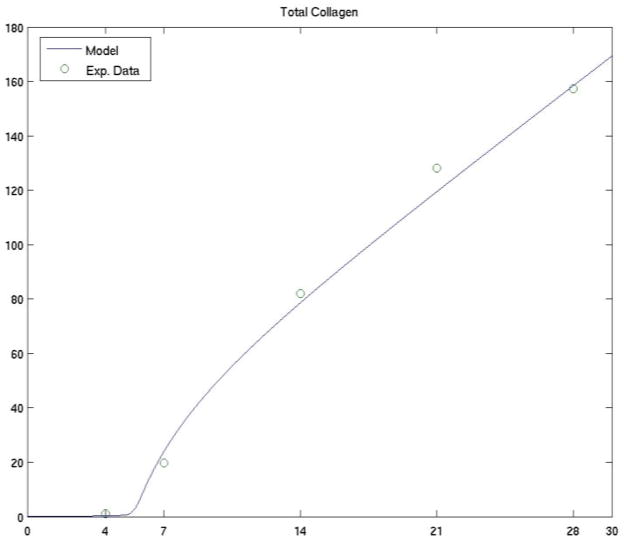
We demonstrate in Figure 1a the comparison of the two data sets for the set of parameters given above. These preliminary results were obtained by the authors in [27].

Figure 1.

Figure 1a. The comparison of collagen of experimental data (the average value of samples during a 28-day period, unit: up/cm²) with a simulated data from the mathematical model.

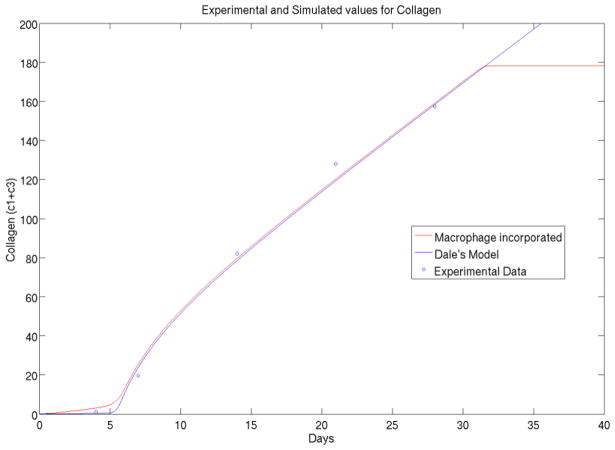
Figure 1b. The original Dale model (blue) has asymptotic collagen variable goes to increase linearly as time increases. The proposed foreign body reaction model incorporated macrophage cell using physiological principal and Mass-action law, and improved model (red) is shown to have realistic behavior.

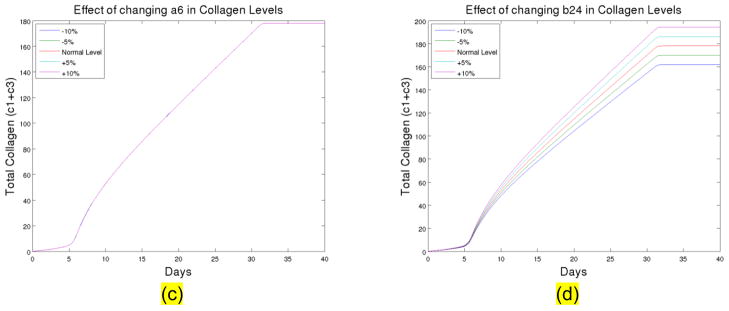
Figure 1. (c) The total collagen level for up to 40 days at different levels of A₆. (d) The total collagen level for up to 40 days at different levels of B₂₄. The normal level is the parameter used in current model.

2.3 Role of Macrophage in Foreign Body Dynamics

As discussed in 2.1, our important modification to the original Dale model is to incorporate the feature of macrophage kinetics in the reactions. From physiological point of view, macrophage and subsequent foreign body reaction giant cells (i.e. fused macrophage cells) are the main driving force behind the cascades of immunological responses, as we discussed in introduction. From quantitative point view, these two models also have a clear distinction. Differing to wound healing where collagen or scare formation complete within several days of time, the foreign body reactions is a rather slow developing process upto several months but ingredients may react in several time scales (days, weeks to months). In kinetics, they present topologically different dynamical features such as steady state and oscillations.

We observe in Figure 1b that using the same set of parameter values, Dale model will have its asymptotical behavior going to infinity linearly in collagen variable, which contracts with experimental measurements and common sense. While Dale model was successful in modeling wound healing, it cannot be applied directly to foreign body reaction problem because of its unboundedness. Thus, there is an essential need for modeling of macrophage and incorporating into the foreign body reactions model.

Macrophage has its self-programmed death, which can be modeled in either time threshold or macrophage value theshould. Here we use time threshold because experimental data suggests in this way. The marcophage ceases activity after a certain active period. There are other changes in physiological nature, we plan to discuss those issues further in a separate paper towards readers in biological fields.

Because of the difficulties in obtaining systematic in-vivo data of the collagen growth, due to large variation and fluctuations of animal experiments. We use other land marks such as the activiation times and the sequence of activations of elements as a way to measure the validility of our model. For example, experimental observations indicated that typically fibroblast activates first, and then collagens activate and proliferate around 4–8 days after implatation, and our model has shown the transition charactics rather well.

2.4 Sensitivity of System Parameters

To know if the model is robust enough to various measurement errors and external noises, we further tested the sensitivity of the system with respect to the chosen paramters. We found that the system is not sensitve to most of the parameters including: A₆, A₇, A₈, A₁₀, A₁₁, and B₂₈, we show a typical simulation of A₆ with respect to 10% variation up and down in Figure 1(c). However the system is sensitive to B₂₄ (the ground level activation rate for collagen III), the variation of B₂₄ can lead to a large discrepancy of collagen amounts. We illustrate in Fig. 1c–d sensitivity analysis of parameters A₆ and B₂₄.

Section 3. Numerical Methods

We now discuss numerical solutions for the model we proposed. For purpose of this research, we did not give rigorous proof for existence or uniqueness of partial differential equations (PDEs) solutions, but simply assume that is true. We also assume that the numerical procedure is stable and numerical solutions converge to true solution when the time step and mesh size go to zero, but we did take extra precaution to ensure numerical stability. We, on the other hand, conducted an exhaustive set of standard tests aiming at a thorough validation of the numerical scheme and estimates of truncation errors. These tests included halving the time and spatial increments in both coordinate directions, doubling the magnitude of outer boundary for fixed inner one, checking the affect of diffusion upon the diffusionless (1D) numerical solution, in particular the influence of its magnitude on the long-time asymptotics of solutions. At last we repeated a dozen of fully diffusionless cases (1D) computed by 4^th order Runge-Kutta method using XPPAUT [28] and compared them with our calculation using the full model. The results with the same parameters and the same initial conditions turned out indistinguishable within the order of round-off error. The specific values of computation detail can be found in Appendix 2.

3.1 Governing Equations

We consider the foreign body reactions is 2-dimsional space. The physical setting is as follows.

• G₀={(r, θ), 0 ≤ r ≤ 1,0 ≤ θ < 2π} is the location of implant,

• G₁= {(r, θ), 8 ≤ r < ∞, 0 ≤ θ < 2π} is the normal surrounding tissue, and the region in between

• G = {(r, θ), 1≤ r ≤ 8, 0 ≤ θ < 2π} is the physical implant domain where foreign body reactions take place. The domain G serves as our computational domain.

We now describe the full model in 2 spatial desminsion. The governing equations with diffision are:

$$\frac{\partial f}{\partial t}=D_1{\nabla }^{2}f+(A_1+B_2{e}_1{l}_1+B_3{e}_1{l}_3)f\left(1-\frac{f}{k_1}\right)-A_{4}f,$$ (3.1)

$$\frac{\partial l_1}{\partial t}=D_2{\nabla }^2{l}_1+\frac{A_5{fl}_1}{1+A_6{l}_3+A_7{l}_1}-A_8{l}_1-A_{16}{e}_1{l}_1,$$ (3.2)

$$\frac{\partial l_3}{\partial t}=D_3{\nabla }^2{l}_3+\frac{A_9{fl}_3}{1+A_{10}{l}_3}-A_{11}{l}_3-A_{17}{e}_1{l}_3,$$ (3.3)

$$\frac{\partial e_1}{\partial t}=-e_1(A_{16}{l}_1+A_{17}{l}_3),$$ (3.4)

$$\frac{\partial e_2}{\partial t}=-e_{2}f\left[\frac{B_{14}+e_1(B_{16}{l}_1+B_{17}{l}_3)}{A_{23}+A_{18}{e}_3}+\frac{B_{15}+e_1(B_{19}{l}_1+B_{20}{l}_3)}{A_{27}+A_{19}{e}_3}\right]+B_{36}·l,$$ (3.5)

$$\frac{\partial e_3}{\partial t}=-e_{3}f\left[\frac{B_{34}{c}_1}{(1+e_1(A_{23}{l}_1+A_{18}{l}_3))(A_{35}+A_{40}{e}_3)}+\frac{B_{35}{c}_3}{(1+e_1(B_{19}{l}_1+B_{20}{l}_3))(A_{39}+A_{41}{e}_3)}\right],$$ (3.6)

$$\frac{\partial c_1}{\partial t}=\frac{B_{22}+A_{28}{e}_1(l_1+C_1{l}_3)}{A_{27}+A_{29}{e}_2}{fe}_2-A_{29}{s}_1{c}_1,$$ (3.7)

$$\frac{\partial c_3}{\partial t}=\frac{B_{24}+A_{30}{e}_1(l_1+C_4{l}_3)}{A_{27}+A_{19}{e}_2}{fe}_2-A_{31}{s}_3{c}_3,$$ (3.8)

$$\frac{\partial s_1}{\partial t}=\frac{B_{26}}{(1+e_1(B_{27}{l}_1+B_{28}{l}_3))(A_{35}+A_{40}{e}_3)}{fc}_1{e}_3-A_{43}{s}_1+B_{37}·l,$$ (3.9)

$$\frac{\partial s_3}{\partial t}=\frac{B_{30}}{(1+e_1(B_{31}{l}_1+B_{32}{l}_3))(A_{39}+A_{41}{e}_3)}{fc}_3{e}_3-A_{45}{s}_3+B_{38}·l,$$ (3.10)

$$\frac{\partial l}{\partial t}=B_{36}{e}_{1}l(l_1+l_3)\frac{N_n+N_e}{N_n+l}-[B_{40}+B_{41}{\sigma }_0(t-30)]l,$$ (3.11)

where we assume all the functions are defined and smooth in a central circular annulus G = {(r, θ),1 ≤ r ≤ 8, 0 ≤ θ < 2π}, σ₀ stands for Heaviside function and ${\nabla }^2=\frac{{\partial }^2}{{\partial }^{2}r}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\theta }^2}$ is Laplacian in polar coordinates.

Let us assume a symmetry on axis θ = 0,π for all solutions. Then we can restrict our considerations on domain G′ = {(r,θ),1 ≤ r ≤ 8, 0 ≤ θ ≤ π}. We note that the assumption of symmetry is only for simplicity of computations and visualization, but not for a physical reason. We tested a few cases in full domain, and observed that dynamic behavior did not change in a full annulus region when initial values are symmetric. The authors plan to simulate in full domain for problems where symmetry is not realistic.

3.2 Initial and Boundary Conditions

In general, the system consists of 3 parabolic (diffusion) (2+1)D equations and 8 diffusionless ODEs and one has to pose mixed problem. The symmetry is assumed on axis θ = 0, π, requiring Neumann conditions to be taken on all functions there.

For other boundaries, the possible initial and boundary conditions are taken as follows.

• ---Motile fibroblast f:

  $$f(r,\theta ){|}_{t=0}=0.1,{\frac{\partial f}{\partial r}|}_{r=1}=0,{f|}_{r=8}=1.$$
• ---Latent TGFβ l₁:

  $$l_1(r,\theta ){|}_{t=0}=0.1,{\frac{\partial l_1}{\partial r}|}_{r=1}=0,l_1{|}_{r=8}=1.$$
• ---Latent TGFβ l₃:

  $$l_3(r,\theta ){|}_{t=0}=0.1,{\frac{\partial l_3}{\partial r}|}_{r=1}=0,l_3{|}_{r=8}=1.$$
• ---Generic Enzyme e₁:

  $$e_1(r,\theta ){|}_{t=0}=0.1,{\frac{\partial e_1}{\partial r}|}_{r=1}={\frac{\partial e_1}{\partial r}|}_{r=8}=0.$$
• ---Generic Enzyme e₂:

  $$e_2(r,\theta ){|}_{t=0}=0.1,{\frac{\partial e_2}{\partial r}|}_{r=1}={\frac{\partial e_2}{\partial r}|}_{r=8}=0.$$
• ---Generic Enzyme e₃:

  $$e_3(r,\theta ){|}_{t=0}=0.1,{\frac{\partial e_3}{\partial r}|}_{r=1}={\frac{\partial e_3}{\partial r}|}_{r=8}=0.$$
• ---Collagen c₁:

  $$c_1(r,\theta ){|}_{t=0}=0.01,{\frac{\partial c_1}{\partial r}|}_{r=1}={\frac{\partial c_1}{\partial r}|}_{r=8}=0.$$
• ---Collagen c₃:

  $$c_3(r,\theta ){|}_{t=0}=0.01,{\frac{\partial c_3}{\partial r}|}_{r=1}={\frac{\partial c_3}{\partial r}|}_{r=8}=0.$$
• ---Collagenase s₁:

  $$s_1(r,\theta ){|}_{t=0}=0,{\frac{\partial s_1}{\partial r}|}_{r=1}={\frac{\partial s_1}{\partial r}|}_{r=8}=0.$$
• ---Collagenase s₃:

  $$s_3(r,\theta ){|}_{t=0}=0.01,{\frac{\partial s_3}{\partial r}|}_{r=1}={\frac{\partial s_3}{\partial r}|}_{r=8}=0.$$
• ---Macrophage l:

  $$l(r,\theta ){|}_{t=0}=0.01,{\frac{\partial l}{\partial r}|}_{r=1}={\frac{\partial l}{\partial r}|}_{r=8}=0.$$

3.3 Splitting Method

The system in question is inextricably coupled nonlinear, containing both PDEs and ODEs. This property requires to combine splitting method (ADI) for PDEs and implicit method for ODEs in one. Having in mind the latter, we use the method of stabilizing correction (see [29]) for whole system and only the second split equation for PDEs part. In this way the solution on each time step can be obtained by using of special modification of Thomas’ algorithm (see [30] and [31]) for multidiagonal band matrices in polar coordinates. So,

$$\frac{U^{n+1/2}-U^n}{\tau /2}=F(U^{n+1/2}){\mathrm{\Lambda }}_r{U}^{n+1/2}+{\mathrm{\Lambda }}_{\theta }{U}^n,$$ (3.12)

$$\frac{U^{n+1}-U^{n+1/2}}{\tau /2}={\mathrm{\Lambda }}_{\theta }(U^{n+1}-U^n)$$ (3.13)

where U = (f, l₁, l₃, e₁, e₂, e₃, c₁, c₃, s₁, s₃, l)^T, Λ_r is a linear operator containing the derivatives with respect to r as well as the algebraic terms, Λ_θ is a linear differential operator with respect to θ, F(U) is a functional matrix. Let us note that the θ-derivatives are not present in ODE’s part of system (3.1–3.11) and in this way one has Uⁿ⁺¹≡U^n+1/2 for discrete approximations of equations (3.4–3.11) at each time stage.

3.4 Finite Difference Method

We use a finite difference method for solving the above split system. The equation (3.12) approximates fully the original system of differential equations but it is nonlinear and its direct treatment is by itself a very difficult task. On the other hand, using Crank-Nicolson-like scheme, we can employ internal iterations to achieve implicit approximation of the nonlinear terms, i.e., we use its linearized implementation [32]:

$$\frac{U^{n+1/2,k+1}-U^n}{\tau /2}=F(U^{n+1/2,k}){\mathrm{\Lambda }}_r{U}^{n+1/2,k+1}+{\mathrm{\Lambda }}_{\theta }{U}^n.$$ (3.14)

The linearized scheme (3.14) has sparse twenty-three-diagonal banded matrix, while the linear scheme (3.13) has seven-diagonal banded matrix and it is accomplished only for the functions with nontrivial diffusion, i.e., for f(r,θ), l₁(r,θ), and l₃(r,θ). The above compound manner of treatment allows immediatelly to expand or to decrease the original differential system adding or removing the reached an equilibrium equations as well as involving uniform or discontinuous (jumped) initial conditions.

3.5 General Sequence of Algorithm

At each time stage n we use the function values as an initial approximation U^n+1/2,0 = Uⁿ and conduct the internal iterations (repeating the calculations for the same time step (n+1/2) with increasing value of the superscript k) until convergence, i.e., when the following criterion is satisfied

$$\underset{i,j}{max}\left|\frac{U^{n+1/2,k+1}-U^{n+1/2,k}}{U^{n+1/2,k+1}}\right|<\epsilon \text{for}\epsilon ={10}^{-8}.$$

We selected the time step τ such that no more than five-six internal iterations were required to reach the precision of 10⁻⁸. After the internal iterations converge, one gets the solution of the nonlinear scheme by setting U^n+1/2≡U^n+1/2,k+1. We mention here that for physically reasonable time increments τ and having in mind the general durability of modeled evolution the technics of internal iterations is a small price to pay to have fully implicit and nonlinear scheme.

Section 4. Specific Numerical Examples of Collagen Growth

4.1 Temporal Dynamics

We now show a few numerical experiments of the foreign body reactions.

1) General temporal kinetics

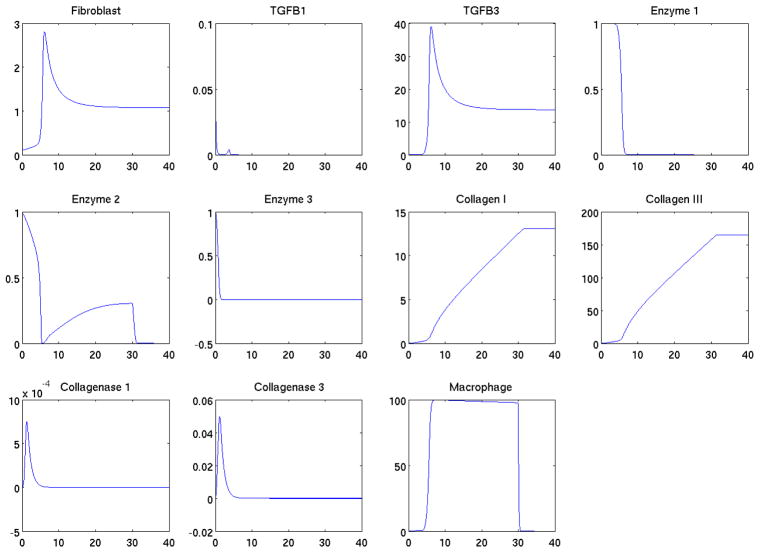
Using the parameter set we estimated in Section 2, and assuming the system is homogeneous in space, the governing system is a system of 11 ODEs. Based on initial values set at Section 3.2, we solved the system numerically to obtain the temporal behavior. All variables in the system were calculated and the time courses of each variable were depicted in Figure 2. The transient behavior indicated the early jump and fall of fibroblast and TGFβ, the collagen growth presented a slow rising curve. The timings of the kinetics were consistent with experimental observations.

Figure 2.

The simulated kinetics dynamics of various variables representing collagens, collagenases, TGFβs etc during first 40 days.

In experiments 2)–7), we investigated foreign body reactions under different initial conditions. The purpose was to understand how initial ingredient levels and their variations can modify the kinetics in all variables, particularly in collagen levels.

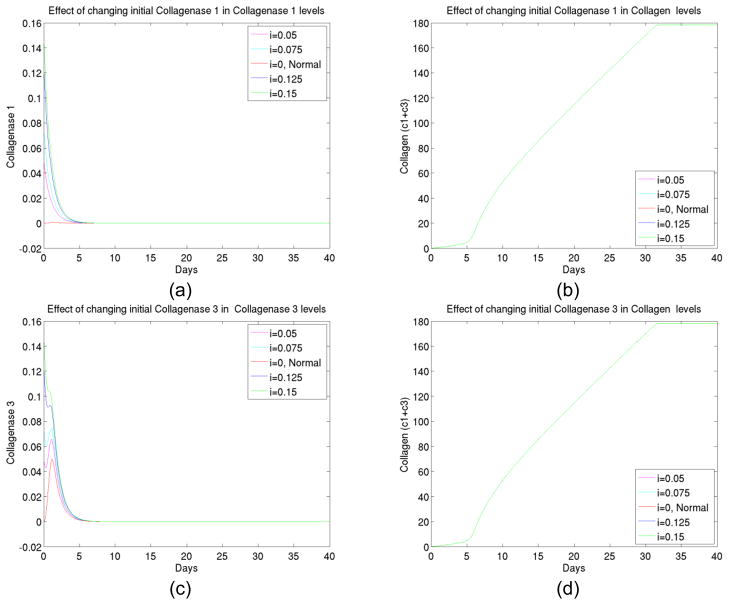
2) The effect of initial collagenases changes

The idea of the experiment was to see if an initial variation of collagenases (by coating implant or injecting surrounding tissues with collagenases) would alter the collagen deposit level at the end. We increased the initial collagenase I and III to several values, and studied the kinetics using the model. As shown in Figure 3, the numerical simulations gave a negative answer to such a variation.

Figure 3.

(a) The transient behavior of collagenase I up to 40 days at different initial levels of collagenase I, (b) The total collagen level for up to 40 days at different initial levels of collagenase I, (c) The transient behavior of collagenase III up to 40 days at different initial levels of collagenase III, (d) The total collagen level for up to 40 days at different initial levels of collagenase III.

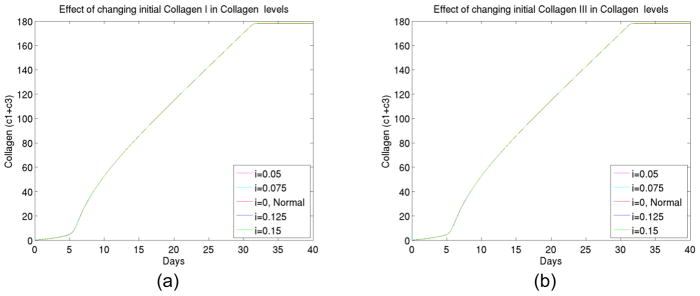
3) The effect of initial collagen changes

We also found (shown in Figure 4) that initial deposit of collagen changes had few impact on the kinetics as well as final collagen deposit layers. The result was also expected biologically. Collagen growth accelerated at late stages of foreign body reactions and variations in initial collagen level therefore had minor impact on early stages of development that controls the kinetics.

Figure 4.

(a) The total collagen level for up to 40 days at different initial levels of collagen I, (b) The total collagen level for up to 40 days at different initial levels of collagen III.

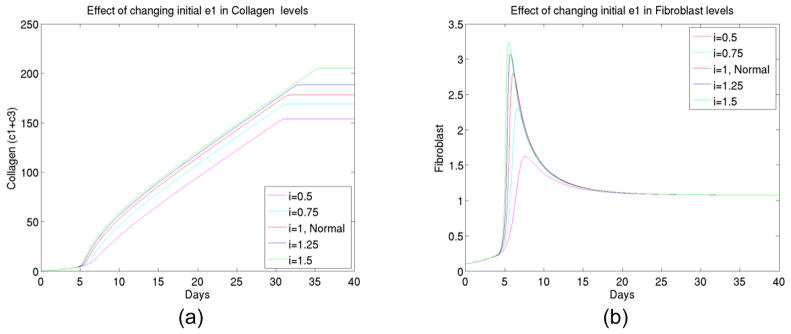
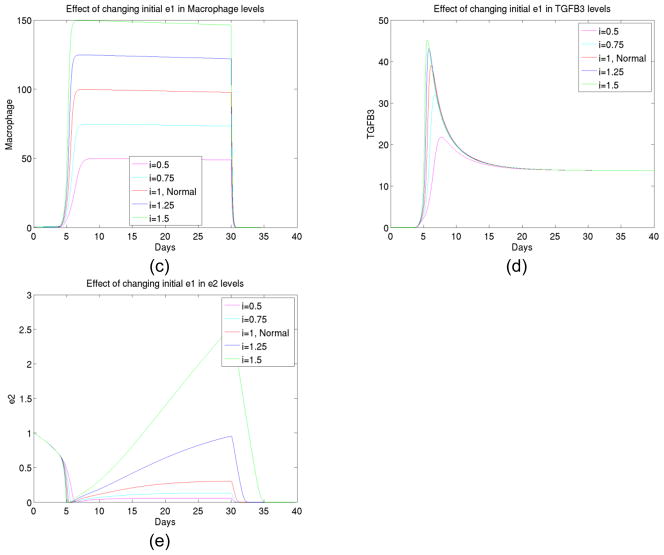
4) The effect of initial enzyme 1 changes

As we continued our numerical experiments to see what can be significant factors in the foreign body reaction process, we observed (shown in Figure 5) that specific enzyme type 1 (which converts latent TGFβ to active TGFβ) played an important role in kinetics. It promoted both TGFβ and fibroblast activations and as well as enzyme type 2. In combination of the facts below (see experiment 7) that latent TGFβ amounts were not significant factors, we believe there is always abundance of latent TGFβ available but the availability of active TGFβ is a key in a reaction pathway.

Figure 5.

(a) The total collagen level for up to 40 days at different initial levels of enzyme type 1, (b) The transient behavior of fibroblast up to 40 days at different initial levels of enzyme type 1, (c) The macrophage concentration for up to 40 days at different initial levels of enzyme type 1, (d) The TGFβ concentration for up to 40 days at different initial levels of enzyme type 1, (e) The enzyme type 2 concentration for up to 40 days at different initial levels of enzyme type 1.

5) Other enzymes are not as significant

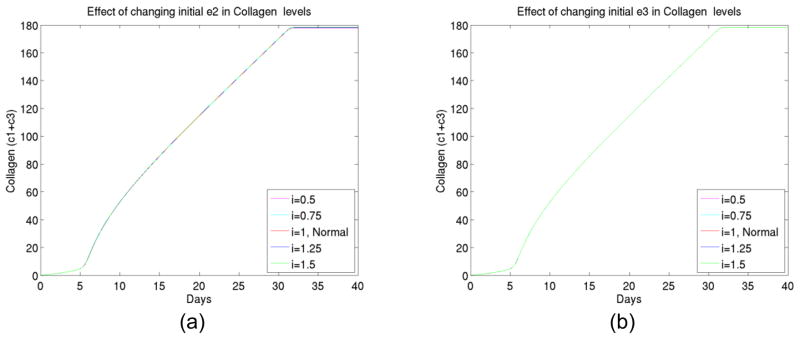
We proceeded to test the initial level changes at specific enzyme type 2 and specific enzyme type 3, and found (shown in Figure 6) the level changes would not cause significant changes in collagen growth.

Figure 6.

(a) The total collagen level for up to 40 days at different initial levels of enzyme type 2, (b) The total collagen level for up to 40 days at different initial levels of enzyme type 3.

6) The effect of initial fibroblast changes

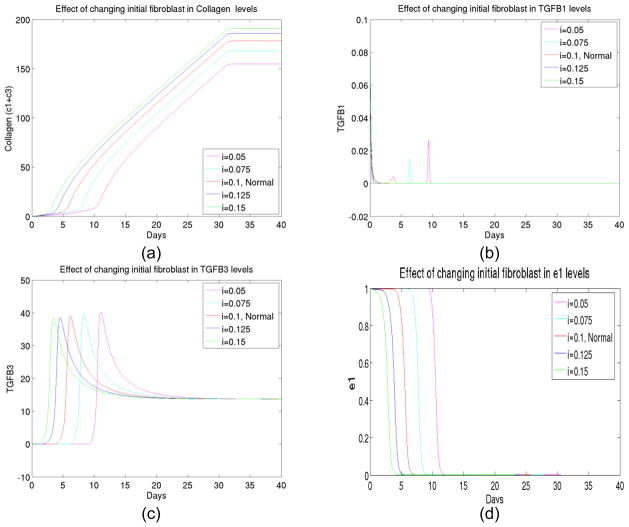
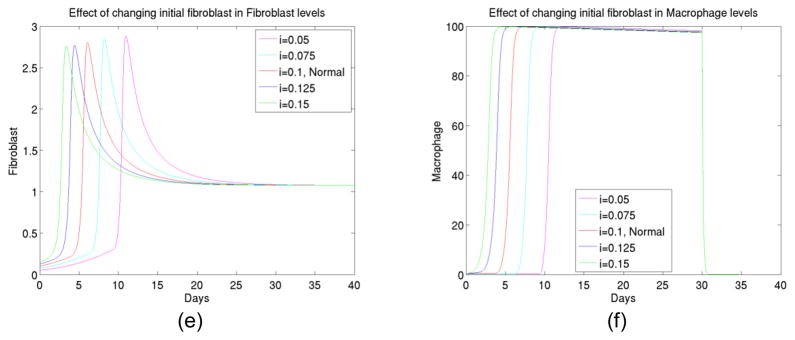
Next we tested the effect of initial level change in fibroblast. As expected from biological reasons, fibroblast was a controlling factor in the foreign body reactions process. We observed (See Figure 7) that not only the initial fibroblast changes significantly altered levels of collagen deposit, they also changed the timing of activations of various elements such as TGFβ and macrophage. Therefore suppression of fibroblast might be crucial in deduction of collagen encapsulations.

Figure 7.

(a) The total collagen level for up to 40 days at different initial levels of fibroblast, (b) The transient behavior of TGFβ I concentration up to 40 days at different initial levels of fibroblast, (c) The transient behavior of TGFβ III concentration up to 40 days at different initial levels of fibroblast, (d) The transient behavior of enzyme type 1 concentration up to 40 days at different initial levels of fibroblast, (e) The transient behavior of enzyme type 3 concentration up to 40 days at different initial levels of fibroblast, (f) The transient behavior of macrophage concentration up to 40 days at different initial levels of fibroblast.

7) The effect of latent growth factor TGFβ changes

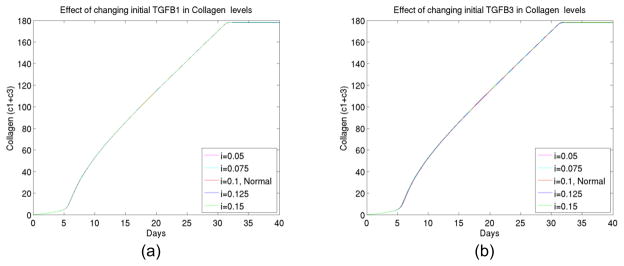
Finally we experimented changes of initial TGFβ. As shown in Figure 8, the latent level did not change the kinetics as much. Since active TGFβs were significant, the conversions to active TGFβs were important to over al kinetics. To reduce collagen deposit, controlling specific enzyme 1 (hence reducing the conversion rate of latent to active TGFβs) can serve as another plausible approach. This will also be explored further.

Figure 8.

(a) The total collagen level for up to 40 days at different initial levels of latent growth factor TGFβ I, (b) The total collagen level for up to 40 days at different initial levels of latent growth factor TGFβ III.

4.2 Spatial Kinetics

Now we start to present simulated collagen growth near an implant in 2 spatial dimensions. The purpose of these simulations was two-fold. One was to understand how the migration of cell will influence the foreign reaction kinetics. The second reason was to understand if inhomogeneous spatial patterns will alter the results of kinetics.

1) Symmetric spatial patterns at 0,5,15,35 days

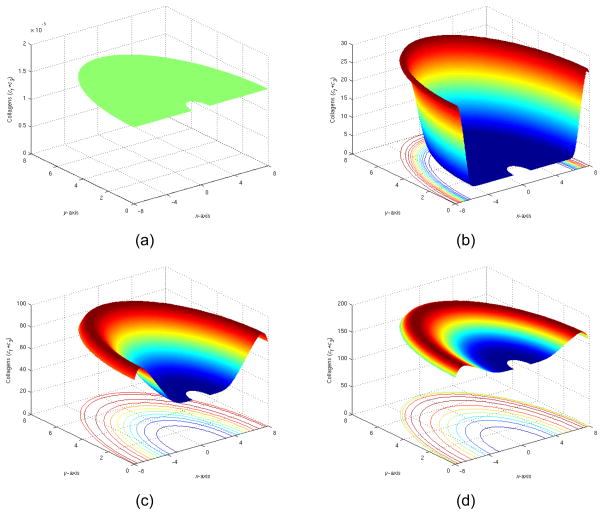
We had our first experiment with symmetric initial conditions as described in Section 3.2. We observed (shown in Figure 9) that after 35 days, the collagen level gradually approached a flat level at around 180. This was consistent with pure temporal kinetics simulations. The implant domain was gradually filled with collagen through both activation and migration of cells. We also observed the collagen peak did travel inward at a finite speed.

Figure 9.

(a) The total collagen level at t=0, (b) The total collagen level at t=5 days, (c) The total collagen level at t=15 days, (d) The total collagen level at t=35 days.

We had then experimented with implant that was partially coated with various active ingredients of foreign body reactions. The overall purpose of experiments 2)–4) was to study the effect of spatially inhomogeneous patterns due to coating of implant.

2) Implant partially coated with fibroblast

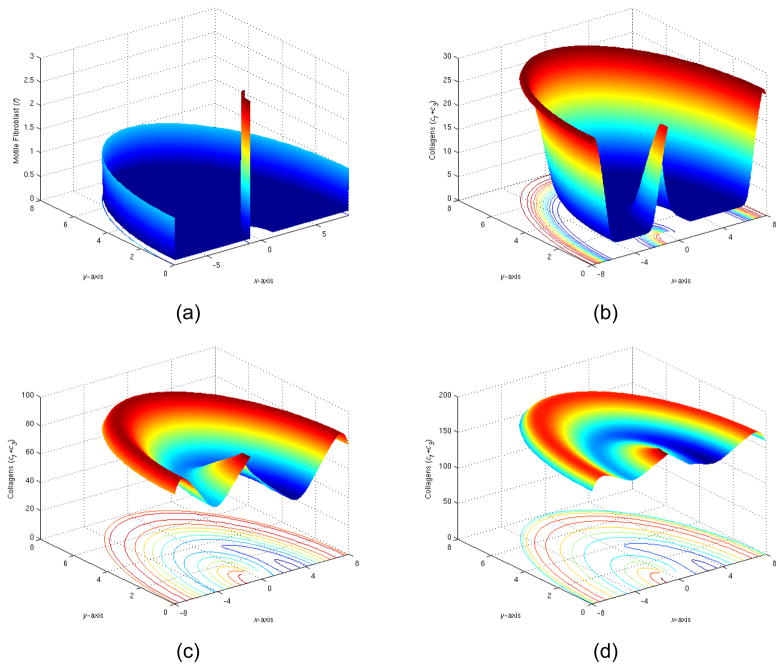
We first experimented with adding a thin layer of fibroblast to left half of the circle on implant surface and leaving right half circle intact.

We observed that the added layer of fibroblast did have lasting impacts in changing the spatial pattern of collagen as well as other ingredients of reactions, as demonstrated in Figure 10. The final collagen level also altered with this coating modestly. We further observed that the migration has limited impact in spread the spatial difference. The overall kinetics changes were mainly due to activation.

Figure 10.

(a) The initial distribution of fibroblast (t=0), (b) The total collagen level at t=5 days, (c) The total collagen level at t=15 days, (d) The total collagen level at t=35 days.

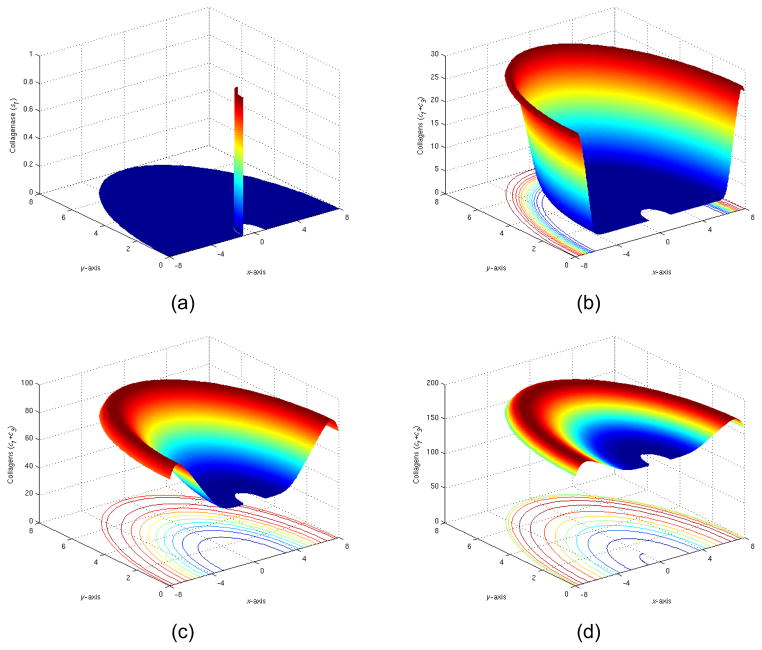
3) Implant partially coated with collagenases

Next we experimented by adding a layer of collagenases on one side of the implant and have other half uncoated. As expected, collagenases played rather passive roles in kinetics model, and no significant changes had been observed. The behavior shown in Figure 11 closely resembled the same behavior as the symmetric solutions (in Figure 9).

Figure 11.

(a) The initial distribution of collagenase I (t=0), (b) The total collagen level at t=5 days, (c) The total collagen level at t=15 days, (d) The total collagen level at t=35 days.

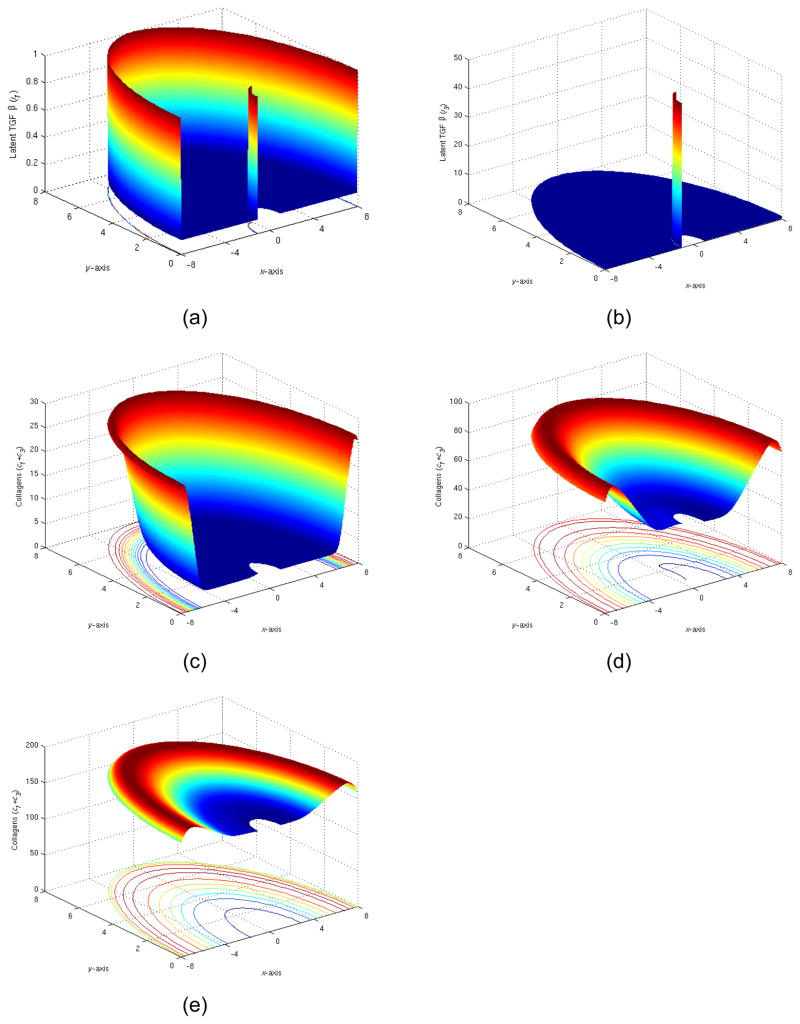
4) Implant partially coated with latent TGFβs

In our final numerical experiment shown in Figure 12, we tested the coating implant with a layer of TGFβ. Namely the initial distribution was imposed as: l₁=0.1 inside G, l₁=1 on the normal tissue boundary and l₁=1 on the left half of implant; l₃=0.1 inside G, l₃=1 on the normal tissue boundary and l₃=50 on the left half of implant, and other conditions elsewhere remained unchanged from the conditions in Section 3.2.

Figure 12.

(a) The initial distribution of latent TGFβ I (t=0), (b) The initial distribution of latent TGFβ III (t=0), (c) The total collagen level at t=5 days, (d) The total collagen level at t=15 days, (e) The total collagen level at t=35 days.

Even though we did not observe spectacular spatial variation. The mathematical computation had been extremely unstable. It showed the two variables had been rather singular for the system and their corresponding computational matrix. Extremely small time steps (1/100 of usual time step) had been taken for providing a stable computation of this experiment.

Section 5. Summary and Discussion

The proposed mathematical model has shown its capability to predict some fine features of foreign body reaction process. We have calibrated both temporal and spatial dynamics in the correct order of magnitude. It also confirmed main characters of collagen growth observed in laboratory experiments by a series of numerical simulations.

The main advances reported in this paper are 1) establishing a mechanism-based mathematical model of foreign body reactions that are consistent with experimental data; 2) incorporating important feature of macrophage kinetics; and 3) extensive temporal and 2D spatial simulations that provided quantitative insight for bioengineering application such as reducing collagen deposit on bio-implants.

In technical level, we found that values of enzyme type 1 (e₁) and fibroblast (f) were very significant to foreign body reactions kinetics, but other variables did not change the kinetics as much. We plan to continue to explore different variations patters to observe the full spectrum of changes in kinetics. We have concluded also a parameter sensitivity analysis for the full system and the result will be presented in an incoming paper, which will explore the physiological features by modeling method and address to readers in biological fields.

Another observation from 2-D process was that the implant coating had useful but limited effects in manipulating the overall kinetics of foreign body reactions, their limited roles were mostly restricted within initial activation period, and transient behavior.

Appendix 1

We assume that (2.4), (2.5), (2.9), (2.10), (2.13) and (2.14) are at equilibrium. This implies:

• - A₁₂e₁l₁ − A₁₃β₁ = 0 or

  $$\frac{A_{12}{e}_1{l}_1}{A_{13}}={\beta }_1,$$
• - A₁₄e₁l₃ − A₁₅β₃ = 0 or

  $$\frac{A_{14}{e}_1{l}_3}{A_{15}}={\beta }_3,$$
• - (A₂₀ + A₂₁β₁ + A₂₂β₃)f − A₂₃p₁ − A₁₈e₂p₁ = 0 or

  $$\frac{(A_{20}+A_{21}{\beta }_1+A_{22}{\beta }_3)f}{A_{23}+A_{18}{e}_2}=p_1,$$
• - (A₂₄ + A₂₅β₁ + A₂₆β₃)f − A₂₇p₃ − A₁₉e₂p₃ = 0 or

  $$\frac{(A_{24}+A_{25}{\beta }_1+A_{26}{\beta }_3)f}{A_{27}+A_{19}{e}_2}=p_3,$$
• - $\frac{A_{32}}{1+A_{33}{\beta }_1+A_{34}{\beta }_3}{fc}_1-A_{35}{z}_1-A_{40}{e}_3{z}_1=0$ or

  $$\frac{\frac{A_{32}}{1+A_{33}{\beta }_1+A_{34}{\beta }_3}{fc}_1}{A_{35}+A_{40}{e}_3}=z_1,$$
• - $\frac{A_{36}}{1+A_{37}{\beta }_1+A_{38}{\beta }_3}{fc}_3-A_{39}{z}_3-A_{41}{e}_3{z}_3=0$ or

  $$\frac{\frac{A_{36}}{1+A_{37}{\beta }_1+A_{38}{\beta }_3}{fc}_3}{A_{39}+A_{41}{e}_3}=z_3.$$

After replacing the previous values of β₁,β₃, p₁, p₃, z₁, and z₃ we obtain the reduced system (2.18)–(2.28). Here we used B_i or C_i for the coefficients to indicate that do not correpond exactly to those in the system (2.1)–(2.16), rather they represent dimensionless parameters, normalized by the unwounded levels or aggreations of parameters.

Appendix 2

For the functions with diffusion (the first three in the system (3.1–3.3)) the difference equations in the splitting scheme (3.12) look like:

$$\left[D_1\left(\frac{1}{h_r^2}-\frac{1}{2r_i{h}_r}\right)\right]f_{i-1,j}^{n+1/2}-2[\frac{1}{\tau }+\frac{D_1}{h_r^2}+(A_1+B_2{e}_{1ij}{l}_{1ij}+B_3{e}_{1ij}{l}_{3ij})\left(1-\frac{f^{n+1/2}}{k}\right)-A_4)]f_{i,j}^{n+1/2}+D_1\left(\frac{1}{h_r^2}+\frac{1}{2r_i{h}_r}\right)f_{i+1,j}^{n+1/2}=-\frac{2}{\tau }{D}_1{f}_{ij}^n-\frac{2}{\tau }\frac{f_{i,j-1}^n-2f_{ij}^n+f_{i,j+1}^n}{h_{\theta }^2},$$ (A1)

$$\frac{D_1}{r_i^2{h}_{\theta }^2}{f}_{i,j-1}^{n+1}-2\left(\frac{D_1}{h_{\theta }^2{r}_i^2}+\frac{1}{\tau }\right)f_{ij}^{n+1}+\frac{D_1}{r_i^2{h}_{\theta }^2}{f}_{i,j+1}^{n+1}=-\frac{2}{\tau }{f}_{ij}^{n+1/2}+\frac{D_1}{r_i^2}\frac{f_{i,j+1}^n-2f_{ij}^n+f_{i,j-1}^n}{h_{\theta }^2},$$ (A2)

$$\left[D_2\left(\frac{1}{h_r^2}-\frac{1}{2r_i{h}_r}\right)\right]l_{1i-1,j}^{n+1/2}-2\left[\frac{1}{\tau }+\frac{D_2}{h_r^2}+(A_5\frac{f_{ij}^{n+1/2}}{1+A_6{l}_{3ij}^{k+1/2}}+A_7{l}_{1ij}-A_8-A_{16}{l}_{1ij})\right]l_{1i,j}^{n+1/2}+D_2\left(\frac{1}{h_r^2}+\frac{1}{2r_i{h}_r}\right)l_{1i+1,j}^{n+1/2}=-\frac{2}{\tau }{D}_2{l}_1{ij}^n-\frac{2}{\tau }\frac{l_{1i,j-1}^n-2l_{1ij}^n+l_{1i,j+1}^n}{h_{\theta }^2},$$ (A3)

$$\frac{D_2}{r_i^2{h}_{\theta }^2}{l}_{1i,j-1}^{n+1}-2\left(\frac{D_2}{h_{\theta }^2{r}_i^2}+\frac{1}{\tau }\right)l_{1ij}^{n+1}+\frac{D_2}{r_i^2{h}_{\theta }^2}{l}_{1i,j+1}^{n+1}=-\frac{2}{\tau }{l}_{1ij}^{n+1/2}+\frac{D_2}{r_i^2}\frac{1_{i,j+1}^n-2l_{1ij}^n+l_{1i,j-1}^n}{h_{\theta }^2},$$ (A4)

$$\begin{array}{l}\left[D_3\left(\frac{1}{h_r^2}-\frac{1}{2r_i{h}_r}\right)\right]l_{3i-1,j}^{n+1/2}-2\left[\frac{1}{\tau }+\frac{D_3}{h_r^2}+(A_9\frac{f_{ij}^{n+1/2}}{1+A_{10}{l}_{3ij}^{k+1/2}}-A_{11}-A_{17}{l}_{1ij})\right]l_{3i,j}^{n+1/2}\\ +D_3\left(\frac{1}{h_r^2}+\frac{1}{2r_i{h}_r}\right)l_{3i+1,j}^{n+1/2}=-\frac{2}{\tau }{D}_3{l}_3{ij}^n-\frac{2}{\tau }\frac{l_{3i,j-1}^n-2l_{3ij}^n+l_{3i,j+1}^n}{h_{\theta }^2},\end{array}$$ (A5)

$$\frac{D_3}{r_i^2{h}_{\theta }^2}{l}_{3i,j-1}^{n+1}-2\left(\frac{D_3}{h_{\theta }^2{r}_i^2}+\frac{1}{\tau }\right)l_{3ij}^{n+1}+\frac{D_3}{r_i^2{h}_{\theta }^2}{l}_{3i,j+1}^{n+1}=-\frac{2}{\tau }{l}_{3ij}^{n+1/2}+\frac{D_3}{r_i^2}\frac{l_{3i,j+1}^n-2l_{3ij}^n+l_{3i,j-1}^n}{h_{\theta }^2},$$ (A6)

for i = 2, M−1, j = 2, N−1 with respective difference approximations of the boundary conditions on radial and transverse directions for i = 1, M and j = 1, N. We introduce uniform grid r_i = 1+(i−1)h_r, θ_j = (j−1)h_θ with spatial steps h_r= 7/(M−1) and h_θ =π/(N−1), M and N are numbers of nodes in both coordinate directions, τ is a time step.

For the rest of functions, the diffusion terms are not present and two difference splitting equations (3.12)–(3.13) can be reduced to only one difference equation for each function with full time step

$$\left(\frac{1}{\tau }+A_{16}{l}_{1i,j}^{n+1/2}+A_{17}{l}_{3ij}^{n+1/2}\right)e_{1ij}^{n+1}=\frac{1}{\tau }{e}_{1ij}^n,$$ (A7)

$$\left\{\frac{1}{\tau }+f_{ij}^{n+1/2}\left[\frac{B_{14}+e_{1ij}^{n+1/2}(B_{16}{l}_{1ij}^{n+1/2}+B_{17}{l}_{3ij}^{n+1/2})}{A_{23}+A_{18}{e}_{2ij}^{n+1/2}}+\frac{B_{15}+e_{1ij}^{n+1/2}(B_{19}{l}_{1i,j}^{n+1/2}+B_{20}{l}_{3i,j}^{n+1/2})}{A_{27}+A_{19}{e}_{2i,j}^{n+1/2}}\right]\right\}{e}_{2ij}^{n+1}-B_{36}{l}_{ij}^{n+1}=\frac{1}{\tau }{e}_{2ij}^n,$$ (A8)

$$\{\frac{1}{\tau }+f_{ij}^{n+1/2}[\frac{B_{34}{c}_{1ij}^{n+1/2}}{(1+e_{1ij}^{n+1/2}(B_{27}{l}_{1ij}^{n+1/2}+B_{28}{l}_{3ij}^{n+1/2}))(A_{35}+A_{40}{l}_{3ij}^{n+1/2})}+\frac{B_{35}{c}_{3i,j}^{n+1/2}}{(1+e_{1ij}^{n+1/2}(B_{31}{l}_{1ij}^{n+1/2}+B_{32}{l}_{3i,j}^{n+1/2}))(A_{39}+A_{41}{e}_{3i,j}^{n+1/2})}\left]\right\}{e}_{3ij}^{n+1}=\frac{1}{\tau }{e}_{3ij}^n,$$ (A9)

$$-f_{ij}^{n+1/2}\left[\frac{B_{22}+A_{28}{e}_{1ij}^{n+1/2}(C_1{l}_{1i,j}^{n+1/2}+C_2{l}_{3ij}^{n+1/2})}{A_{27}+A_{19}{e}_{2ij}^{n+1/2}}\right]e_{2ij}^{n+1}+\left(\frac{1}{\tau }+A_{29}{s}_{1ij}^{n+1/2}\right)c_{1ij}^{n+1}=\frac{1}{\tau }{c}_{1ij}^n,$$ (A10)

$$-f_{ij}^{n+1/2}\left[\frac{B_{24}+A_{30}{e}_{1ij}^{n+1/2}(C_3{l}_{1i,j}^{n+1/2}+C_4{l}_{3ij}^{n+1/2})}{A_{27}+A_{19}{e}_{2ij}^{n+1/2}}\right]e_{2ij}^{n+1}+\left(\frac{1}{\tau }+A_{31}{s}_{3ij}^{n+1/2}\right)c_{3ij}^{n+1}=\frac{1}{\tau }{c}_{3ij}^n,$$ (A11)

$$-B_{26}\frac{c_{1ij}^{n+1/2}{e}_{3ij}^{n+1/2}}{[1+e_{1ij}^{n+1/2}(B_{27}{l}_{1ij}+B_{28}{l}_{3ij})](A_{35}+A_{40}{e}_{3ij}^{n+1/2})}{f}_{ij}^{n+1}+\left(\frac{1}{\tau }+A_{43}\right)s_{1ij}^{n+1}-B_{37}{l}_{ij}^{n+1}=\frac{1}{\tau }{s}_{1ij}^n,$$ (A12)

$$-B_{30}\frac{c_{3ij}^{n+1/2}{e}_{3ij}^{n+1/2}}{[1+e_{1ij}^{n+1/2}(B_{31}{l}_{1ij}+B_{32}{l}_{3ij})](A_{39}+A_{41}{e}_{3ij}^{n+1/2})}{f}_{ij}^{n+1}+\left(\frac{1}{\tau }+A_{45}\right)s_{3ij}^{n+1}-B_{38}{l}_{ij}^{n+1}=\frac{1}{\tau }{s}_{3ij}^n,$$ (A13)

$$\left[\frac{1}{\tau }-B_{36}{e}_{1ij}(l_{1ij}^{n+1/2}+l_{3ij}^{n+1/2})\frac{N_n+N_e}{N_n+l_{ij}^{n+1/2}}+B_{40}+B_{41}{\sigma }_0(t_q-30)\right]l_{ij}^{n+1}=\frac{1}{\tau }{l}_{ij}^n$$ (A14)

with t_q = (q−1)τ for q = 1,2,3…

In our computations we used time increments τ∈[0.001, 0.01], a grid with dimensions 204 × 110 (M=204, N=110) and a difference scheme of second-order of approximation with respect to all spatial and temporal variables, i.e., $O(h_r^2+h_{\theta }^2+{\tau }^2)$. The calculations were executed on 8-core workstation platform. One 40-day (long-time) simulation for given initial conditions did not exceed at the rate of 2.5–3 hours.