(Mathematical) Necessary conditions for the selection of gradient vectors in DTI

Abstract

A set of necessary conditions for the choice of diffusion gradient vectors to make the linear equations nonsingular for the estimation of the diffusion matrix are given in a coordinate free manner. The conditions assert that the initial step in the design of a DTI experiment with six or more acquisitions must be to select six valid diffusion gradients first and then add new ones.

1. Introduction

One way of estimating the diffusion matrix from DTI experiments is to solve a set of linear equations. The number of the measurements and thus the number of the equations is generally chosen to be over determined to alleviate the effects of noise. First pointed out by Papadakis et al. [1] and later used by different researchers [2-4] the linear algebraic technique can be described as follows. To estimate d = [d₁, d₂, d₃, d₄, d₅, d₆]^T, six entries of the diffusion matrix corresponding to

$$D=\left[\begin{array}{ccc}\hfill d_1\hfill & \hfill d_4\hfill & \hfill d_6\hfill \\ \hfill d_4\hfill & \hfill d_2\hfill & \hfill d_5\hfill \\ \hfill d_6\hfill & \hfill d_5\hfill & \hfill d_3\hfill \end{array}\right]$$

one has to solve one of the following equations depending on the number of acquisitions denoted by $\widehat{m}$:

$$b{V}_{g}d=\widehat{p}\text{or}$$ (1)

$$b{V}_g^{\mathrm{T}}{V}_{g}d=V_g^{\mathrm{T}}\widehat{p}.$$ (2)

The scalar factor b is ${\delta }^2(\Delta -\frac{1}{3}\delta )$, where γ is the gyromagnetic ratio, δ is the length of and Δ is the time between the rectangular diffusion gradient pulses in the pulsed gradient spin echo (PGSE) experiment. The result of the experiment is kept in a vector $\widehat{p}=-{\gamma }^{-2}{[\ln \left(\frac{{\widehat{S}}_1}{S_0}\right)\cdots \ln \left(\frac{{\widehat{S}}_{\widehat{m}}}{S_0}\right)]}^{\mathrm{T}}$, where ${\widehat{S}}_i$ is the measurement corresponding to the ith diffusion gradient and S₀ is the reference image. Define a nonlinear function w that maps the diffusion gradient vector g_i = [g_ix g_iy g_iz] in ${\mathbb{R}}^3$, to a vector in ${\mathbb{R}}^6$

$$w\left(g_i\right)=\left[g_{ix}^2{g}_{iy}^2{g}_{iz}^{2}2g_{ix}{g}_{iy}2g_{iy}{g}_{iz}2g_{ix}{g}_{iz}\right],$$

then V_g is the $\widehat{m}\times 6$ matrix

$$V_g=\left[\begin{array}{c}\hfill w\left(g_1\right)\hfill \\ \hfill ⋮\hfill \\ \hfill w\left(g_m\right)\hfill \end{array}\right]=\left[\begin{array}{cccccc}\hfill g_{1x}^2\hfill & \hfill g_{1y}^2\hfill & \hfill g_{1z}^2\hfill & \hfill 2g_{1x}{g}_{1y}\hfill & \hfill 2g_{1y}{g}_{1z}\hfill & \hfill 2g_{1x}{g}_{1z}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill g_{\widehat{m}x}^2\hfill & \hfill g_{\widehat{m}y}^2\hfill & \hfill g_{\widehat{m}z}^2\hfill & \hfill 2g_{\widehat{m}x}{g}_{\widehat{m}y}\hfill & \hfill 2g_{\widehat{m}y}{g}_{\widehat{m}z}\hfill & \hfill 2g_{\widehat{m}x}{g}_{\widehat{m}z}\hfill \end{array}\right].$$ (3)

If the number of acquisitions is equal to six, d (thus D) is estimated by using Eq. (1), otherwise if the number of acquisitions is larger than six, $\widehat{m}>6$, the expression of Eq. (2) is used. It is a standard fact from linear algebra [5] that in either case V_g must be full rank for the equations to have a unique solution. When $\widehat{m}=6$, V_g is a (6 × 6) square matrix and the rank condition is equivalent to the invertibility of V_g. In the case $\widehat{m}>6$ the rank condition guarantees the invertibility of the Gram matrix $V_g^{\mathrm{T}}{V}_g$.

Note that in Eq. (3) there is no restriction on the norm of gradient vectors, they might or might not be unit vectors.

2. Necessary conditions for gradient vectors

By definition (Eq. (3)) V_g is a $\widehat{m}\times 6$ matrix. The previous section shows that in the case $\widehat{m}>6$ the Gram matrix of Eq. (2) will be invertible if and only if V_g has a 6 × 6 submatrix which is invertible. This problem is equivalent to first choosing six gradient vectors g = {g₁, … ,g₆} such that the corresponding matrix V_g will be full rank. There has to be six gradient vectors guaranteeing the rank condition on V_g regardless of the number of aquisitions, $\widehat{m}\ge 6$.

It is stated without proof in [1,6-11] that for the equations to have a unique solution “the only requirement is that the six gradient vectors not all lie in the same plane and no two gradient vectors are collinear.”¹ The statement is in fact only a necessary condition and is not complete. To see this note that neither any pair of the six gradient vectors given below are pointing to the same direction nor all six of them belong to the same two dimensional subspace and yet when V_g is calculated by Eq. (3)

$$\left[\begin{array}{c}\hfill g_1\hfill \\ \hfill g_2\hfill \\ \hfill g_3\hfill \\ \hfill g_4\hfill \\ \hfill g_5\hfill \\ \hfill g_6\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \frac{1}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right];V_g=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 2\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill \frac{1}{4}\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -2\hfill \end{array}\right]$$ (4)

its determinant |V_g| = 0, i.e., V_g is not full rank.

As a preliminary to the problem in ${\mathbb{R}}^3$ take a look at the problem in ${\mathbb{R}}^6$. The gradients and the corresponding matrix V_g are

$$\left[\begin{array}{c}\hfill g_1\hfill \\ \hfill g_2\hfill \\ \hfill g_3\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill g_{1x}\hfill & \hfill g_{1y}\hfill \\ \hfill g_{2x}\hfill & \hfill g_{2y}\hfill \\ \hfill g_{3x}\hfill & \hfill g_{3y}\hfill \end{array}\right],V_g=\left[\begin{array}{ccc}\hfill g_{1x}^2\hfill & \hfill g_{1y}^2\hfill & \hfill 2g_{1x}{g}_{1y}\hfill \\ \hfill g_{2x}^2\hfill & \hfill g_{2y}^2\hfill & \hfill 2g_{2x}{g}_{2y}\hfill \\ \hfill g_{3x}^2\hfill & \hfill g_{3y}^2\hfill & \hfill 2g_{3x}{g}_{3y}\hfill \end{array}\right].$$

A straightforward calculation shows that the determinant of V_g is given by the product of the determinants of the pairs of gradient direction vectors:

$$\mathrm{Det}\left(V_g\right)=2\mid \begin{array}{cc}\hfill g_{1x}\hfill & \hfill g_{1y}\hfill \\ \hfill g_{2x}\hfill & \hfill g_{2y}\hfill \end{array}\mid \mid \begin{array}{cc}\hfill g_{1x}\hfill & \hfill g_{1y}\hfill \\ \hfill g_{3x}\hfill & \hfill g_{3y}\hfill \end{array}\mid \mid \begin{array}{cc}\hfill g_{2x}\hfill & \hfill g_{2y}\hfill \\ \hfill g_{3x}\hfill & \hfill g_{3y}\hfill \end{array}\mid .$$ (5)

The necessary and sufficient condition for nonsingularity in ${\mathbb{R}}^2$ is clear:

V_g is nonsingular if and only if no pair of gradient vectors are pointing to the same direction.

In ${\mathbb{R}}^3$, there is unfortunately no clear formula like Eq. (5) to describe the determinant of V_g that relates it to the diffusion gradients. The formula for the determinant can be obtained by direct calculation. For this remember that the number of three element subsets of

$$\{1,\dots ,6\}\text{is}\left(\begin{array}{c}\hfill 6\hfill \\ \hfill 3\hfill \end{array}\right)=20.\text{Let}{\Gamma }_r=\{i,j,k\}\subset \{1,\dots ,6\}$$

denote rth of these subsets with ordered elements i.e., i < j < k. Denote the complement of Γ_r by {l,m,n} = {1, … ,6}/{i,j,k}. Define

$$\alpha (i,j,k)=\mid \begin{array}{ccc}\hfill g_{ix}\hfill & \hfill g_{iy}\hfill & \hfill g_{iz}\hfill \\ \hfill g_{jx}\hfill & \hfill g_{jy}\hfill & \hfill g_{jz}\hfill \\ \hfill g_{kx}\hfill & \hfill g_{ky}\hfill & \hfill g_{kz}\hfill \end{array}\mid$$

then the determinant is

$$\mathrm{Det}\left(V_g\right)=\sum _{r=1}^{20}{(-1)}^{(i+j+k+1)}\alpha \left({\Gamma }_r\right)\times \mid \begin{array}{cc}\hfill g_{lx}\hfill & \hfill g_{ly}\hfill \\ \hfill g_{mx}\hfill & \hfill g_{my}\hfill \end{array}\mid \mid \begin{array}{cc}\hfill g_{lx}\hfill & \hfill g_{ly}\hfill \\ \hfill g_{nx}\hfill & \hfill g_{ny}\hfill \end{array}\mid \mid \begin{array}{cc}\hfill g_{mx}\hfill & \hfill g_{my}\hfill \\ \hfill g_{nx}\hfill & \hfill g_{ny}\hfill \end{array}\mid g_{iz}{g}_{jz}{g}_{kz}.$$

It follows immediately from the formula that “a necessary condition for nonsingularity is that there exists at least one triplet of linearly independent gradient vectors.” Otherwise α(Γ_r) = 0 for all r ∈ {1, … ,20} which implies Det(V_g) = 0. This is equivalent to say that not all six gradient vectors belong to the same two-dimensional subspace. This condition will be absorbed in (NC3) described below.

It is clear from the definition of V_g that if there exists $a\in \mathbb{R}$ such that for i ≠ j, g_i = ag_j then w(g_i) = a²w(g_j) and V_g will be singular. The first necessary condition for the nonsingularity of V_g is therefore:

(NC1) No two gradient vectors should point to the same direction.

Without loss of generality let g₄,g₅,g₆ be linearly dependent without violating (NC1). This implies that there exists a₁, a₂ ≠ 0 such that g₆ = a₁g₄ + a₂g₅.

A direct calculation shows

$$\mathrm{Det}\left(V_g\right)=-8a_1{a}_2\alpha (1,2,3)\alpha (1,4,5)\alpha (2,4,5)\alpha (3,4,5).$$ (6)

One of the conditions this equation brings up is that g₁,g₂,g₃ should be linearly independent: (see Fig. 1)

Fig. 1.

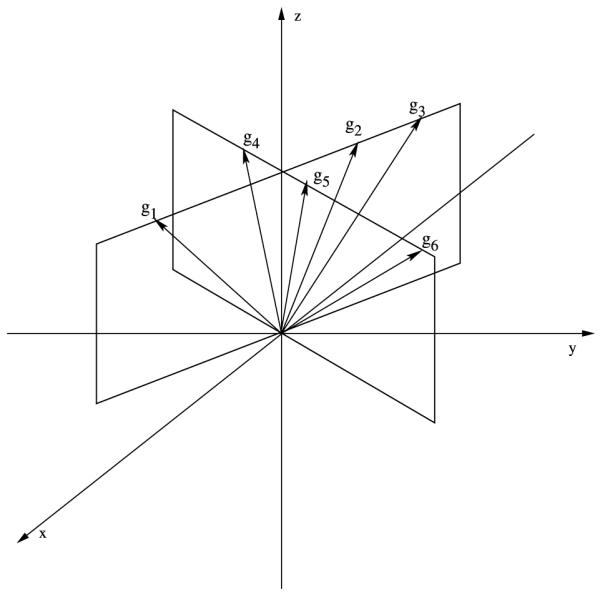
An example violating (NC2), g₁,g₂,g₃ are linearly dependent as well as g₄,g₅,g₆.

(NC2) If there is a triplet of vectors belonging to a two dimensional subspace that conform to (NC1), the remaining triplet should be linearly independent.

In addition Eq. (6) indicates that none of the vectors g₁,g₂,g₃ should belong to the two-dimensional subspace spanned by g₄,g₅. To investigate this assume that four of the gradient vectors belong to the same two-dimensional subspace and are (NC1), say g₃,g₄,g₅,g₆. This means that there exists a₁₁,a₁₂,a₂₁,a₂₂ ≠ 0 such that Det[a_ij] ≠ 0 with g₅ = a₁₁g₃ + a₁₂g₄ and g₆ = a₂₁g₃ + a₂₂g₄. A straightforward calculation shows that

$$a_{21}{a}_{22}(w\left(g_5\right)-a_{11}w\left(g_3\right)-a_{12}w\left(g_4\right))=a_{11}{a}_{12}(w\left(g_6\right)-q_{21}w\left(g_3\right)-a_{22}w\left(g_4\right)).$$

The rows of V_g corresponding to those directions are linearly dependent. Therefore:

(NC3) No four gradient vectors should belong to the same two dimensional subspace.

Notice that all of the conditions above are described in a coordinate free manner, since being an element of a subspace and linear independence are in fact properties that are independent of coordinate frame. This important fact provides the possibility of constructing different valid gradient sets starting from one set by means of nonsingular linear transformations.

It is crucial to note that the conditions are only necessary and are not necessary and sufficient.

3. Conclusion

In any DTI experiment where the diffusion matrix is to be estimated completely (i.e., all six elements), the initial step must be to choose six diffusion gradients that will make the corresponding V_g invertible. This skeleton gradients guarantee that the addition of more diffusion gradients or more acquisitions to the experiment will be safe. The earlier condition given in [6] that requires not all of the gradients to be in the same subspace, is not complete. Interested reader is encouraged to do the calculations for the following set of gradients with unit norm to see that although the number of acquisitions is larger than six and that not all of the gradients are in the same two-dimensional subspace, still the system of linear equations Eq. (2) does not posses a unique solution:

$$\left[\begin{array}{c}\hfill g_1\hfill \\ \hfill g_2\hfill \\ \hfill g_3\hfill \\ \hfill g_4\hfill \\ \hfill g_5\hfill \\ \hfill g_6\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill \frac{1}{\sqrt{2}}\hfill & \hfill \frac{1}{\sqrt{2}}\hfill & \hfill 0\hfill \\ \hfill \frac{-1}{\sqrt{2}}\hfill & \hfill \frac{1}{\sqrt{2}}\hfill & \hfill 0\hfill \\ \hfill \frac{1}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill \frac{1}{\sqrt{2}}\hfill \end{array}\right],\left[\begin{array}{c}\hfill g_7\hfill \\ \hfill g_8\hfill \\ \hfill g_9\hfill \\ \hfill g_{10}\hfill \\ \hfill g_{11}\hfill \\ \hfill g_{12}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill \frac{-1}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill \frac{1}{\sqrt{2}}\hfill \\ \hfill \frac{1}{2}\hfill & \hfill 0\hfill & \hfill \frac{\sqrt{3}}{2}\hfill \\ \hfill \frac{-1}{2}\hfill & \hfill 0\hfill & \hfill \frac{\sqrt{3}}{2}\hfill \\ \hfill \frac{1}{2}\hfill & \hfill \frac{\sqrt{3}}{2}\hfill & \hfill 0\hfill \\ \hfill \frac{-1}{2}\hfill & \hfill \frac{\sqrt{3}}{2}\hfill & \hfill 0\hfill \\ \hfill \frac{\sqrt{3}}{2}\hfill & \hfill \frac{-1}{2}\hfill & \hfill 0\hfill \end{array}\right].$$ (7)

Moreover, there is no six element subset of these gradients which makes the corresponding square V_g invertible.