Quantitative variation in autocrine signaling and pathway crosstalk in the Caenorhabditis vulva network

Abstract

Background

Biological networks experience quantitative change in response to environmental and evolutionary variation. Computational modeling allows exploration of network parameter space, corresponding to such variations. The intercellular signaling network underlying Caenorhabditis vulva development specifies three fates in a row of six precursor cells, yielding a quasi-invariant 3°-3°-2°-1°-2°-3° cell fate pattern. Two seemingly conflicting verbal models of vulval precursor cell fate specification have been proposed: sequential induction by the EGF-MAP kinase and Notch pathways, or morphogen-based induction by the former.

Results

To study the mechanistic and evolutionary system properties of this network, we combine experimental studies with computational modeling, using a model that keeps the network architecture constant but varies parameters. We first show that the Delta autocrine loop can play an essential role in 2° fate specification. With this autocrine loop, the same network topology can be quantitatively tuned to use in the six-cell row morphogen-based or sequential patterning mechanisms, which may act singly, cooperatively or redundantly. Moreover, different quantitative tunings of this same network can explain vulval patterning observed experimentally in C. elegans, C. briggsae, C. remanei and C. brenneri. We experimentally validate model predictions, such as interspecific differences in isolated vulva precursor cell behavior and in spatial regulation of Notch activity.

Conclusions

Our study illustrates how quantitative variation in the same network comprises developmental patterning modes that were considered qualitatively distinct and also accounts for evolution among closely related species.

INTRODUCTION

Genetic and cellular analysis of biological systems has yielded a molecular understanding of regulatory interactions in networks. This information now allows the construction of computational models to explore the dynamics and range of behaviors that a system can produce. Especially, modeling is a powerful tool to understand how a common network is modified quantitatively in different environments or in evolution. The molecular network properties that underlie system-level behavior are shaped by environmental, stochastic and genetic variation during evolution, yet the network output may be robust to perturbations and the normal final phenotype persists [1]. In a computational model, this robustness corresponds to a large region of parameter space that leads to an equivalent system output [2–5]. We here explore the possibility that such phenotypically neutral (sensu Wagner, 2005) regions may include qualitatively distinct modes of developmental patterning.

Caenorhabditis vulva patterning is an attractive model for computational modeling because the molecular signaling network is well understood, yet two seemingly conflicting mechanisms of cell fate patterning have been proposed (see next paragraph). The vulva is the egg-laying and copulatory organ of Caenorhabditis, specified from a row of six vulval precursor cells, P(3–8).p (Fig 1A). All six cells are competent to adopt vulval fates, but only three normally do so, due to inductive signaling from the anchor cell (AC), a uterine cell close to P6.p. P6.p adopts the inner vulval fate (1°) and P5.p and P7.p, outer vulval fates (2°). The other cells normally adopt non-vulval fates (3°), but can replace P(5–7).p [6]. Formation of the normal P(3–8).p fate pattern (3°3°2°1°2°3°) is buffered against some level of environmental and genetic variation [7–10] and relies upon two major signaling pathways, EGF-Ras-MAP kinase (MAPK) and Delta-Notch (Fig 1A). These pathways interact through three intra- and inter-cellular crosstalks: 1) activation of Delta transcription downstream of MAPK; 2) activation of Notch degradation downstream of MAPK; and 3) inhibition of MAPK activity by Notch. The latter two are intracellular cross-inhibitions between MAPK and Notch pathways, which we abbreviate M ⊣ N and N ⊣ M, respectively.

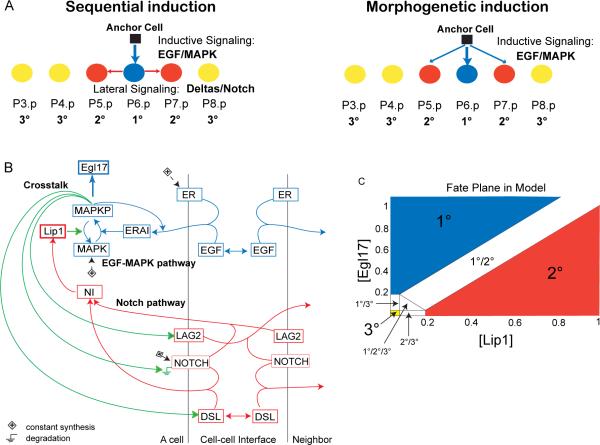
Figure 1. Vulval induction network in C. elegans.

(A) Two verbal models of fate specification in the row of six vulval precursor cells in C. elegans: 1° (blue), 2° (red) and 3° (yellow) fates. (B) Schematic diagram summarizing interactions in the model between EGF (blue) and Notch (red) pathways, and their crosstalk (green). All cells have the same network wiring. Boxes are gene products. ER: EGFR, ERAI: activated EGFR or Ras pathway, MAPKP: phosphorylated MAP kinase, Egl17: 1° cell fate effector, DSL: diffusible Delta, LAG2: membrane-bound Delta, NOTCH: Notch receptor, NI: Notch intracellular domain, Lip1: 2° cell fate effector and MAP kinase phosphatase. The Ground symbols indicate degradation, and (+) constant synthesis. Simple arrows indicate transformation (MAPK to MAPKP and conversely), binding (ligands to receptors) or activation of the downstream node, according to equations in Supplemental Procedures. Double arrows indicate diffusion. (C) Fate plane in the model showing the criteria used to assign cell fates, according to concentrations of Lip1 and Egl17, which are 2° and 1° fate effectors, respectively. Cell fates at the boundaries correspond to (experimentally observed; [11]) intermediate fates. See also Figure S1 and Table S1.

Two verbal “models” have been proposed to describe vulva patterning mechanisms: i) the morphogen or graded model [11] and ii) the sequential induction model [12, 13] (Fig 1A). In both cases, patterning depends on EGF secretion by the anchor cell. In the morphogen model, EGF forms a gradient that triggers different MAPK pathway activity levels and thereby distinct Pn.p fates as a function of distance to the EGF source. The main evidence for this model comes from the graded response of an isolated Pn.p cell to EGF doses [11, 14]. In the sequential model, EGF's main role is to trigger the MAPK pathway in P6.p, which in turn expresses Deltas, thus activating in P5.p and P7.p Notch signaling and 2° fate specification. The main support for the sequential model comes from: (a) observations that cells require Notch signaling to adopt a 2° fate [15, 16] and (b) genetic mosaics for egfr where an EGFR loss in cells adjacent to a 1°-fated cell does not prevent them from adopting a 2° fate [12, 13].

The apparent conflict between these models arises because an isolated cell lacks neighbors to activate Notch. Sternberg and Horvitz (1989) proposed that 2° fate adoption could rely on autocrine secretion mediated by LIN-12/Notch, whose molecular identity was then unknown (the so-called “spaghetti model”, last figure in [16]). This autocrine loop was later omitted from network descriptions both for simplicity and because the transmembrane nature of known Deltas seemed to preclude autocrine action [17]. However, a role for diffusible Notch ligands was recently uncovered in several contexts [18, 19], including C. elegans vulva patterning [20].

Here, to study the mechanistic and evolutionary system properties of this signaling network, we construct a model that keeps the network architecture constant but varies parameters, such as biochemical reaction rates, over a wide range. This approach has been used on various systems [4, 21], including a simpler version of the C. elegans vulva network [22, 23]. Our model combined with experiments reveals the role of secreted Deltas in isolated 2° fate specification. We show that for different parameter tunings, the same network can use morphogen-based or sequential induction, or both, which correspond to distinct network dynamics. We further show that vulval patterning in different Caenorhabditis species [24] can be explained as quantitative tunings of the same network. We experimentally validate model predictions, such as isolated precursor cell behavior and the expression of pathway-specific markers in different species. Our study thus demonstrates how cryptic quantitative variation in the same network can give rise to distinct modes of developmental cell fate patterning and account for evolution among closely related species.

RESULTS

The computational model reproduces the wild-type cell fate pattern over a wide range of parameter values

We constructed a computational model based on ordinary differential equations that includes known interactions within and between the EGF and Notch pathways in a row of six identical Vulva Precursor Cells (VPCs) (Fig 1B and Supplementary Methods). The model network reconstitutes the known topology of the real network, but long pathways were abbreviated for simplicity. We thus distinguish the model nodes (called DSL, LAG2, Egl17, Lip1, etc.) from actual genes and gene products (DSL-1 and other diffusible Deltas, LAG-2 and APX-1, EGL-17, LIP-1, etc.).

In the model, EGF (LIN-3 in the worm) binds its receptor ER (LET-23) and activates it to the ERAI form. The Ras cascade is summarized by a single step where ERAI phosphorylates MAPK (MAP kinase MPK-1). Such activation steps are characterized by an affinity k and a cooperativity or Hill coefficient u, treated as parameters. MAPKP (phosphorylated MAPK) activates degradation of Notch (LIN-12) and synthesis of two Delta forms: a secreted Delta called DSL (any secreted LIN-12 ligand, such as DSL-1) and a trans-membrane form called LAG2 (LAG-2 and APX-1). The Delta ligands bind to Notch, activating it to a NI form (intracellular active LIN-12), which activates Lip1 synthesis. Lip1 stands for any cross-inhibitory interaction of LIN-12 to the MAPK pathway, such as the LIP-1 MAPK phosphatase. All cells contain the same network. A simulated AC releases EGF onto P6.p, EGF diffuses, and our model predicts the resulting normalized concentrations of the nodes through time. The model assigns cell fates based on the levels of fate effectors Egl17 and Lip1 (Fig 1C), named after egl-17 and lip-1, transcriptional targets of the EGF and Notch pathways [25, 26] and markers for 1° and 2° cell fate specification, respectively.

To test whether our model could reproduce the wild-type cell fate pattern (3°3°2°1°2°3°), we performed a Monte-Carlo search in which values for each parameter were independently drawn from a random distribution over a wide range. For each random parameter set, EGF production started at time 0, and 400 min of development were simulated; then we catalogued fate patterns that were stable between 300 and 400 min; note that the solutions did not have to reach steady-state (Table S1). Of 9,014,000 parameter sets, 667,000 (7.4%) reproduced the wild-type pattern, which was the most frequent non-trivial pattern, with different cell fates. We refer to these as wild-type solutions and used these parameter sets as the basis for further analysis.

Isolated 2° cell specification at intermediate EGF levels is explained by a DSL-NOTCH autocrine loop

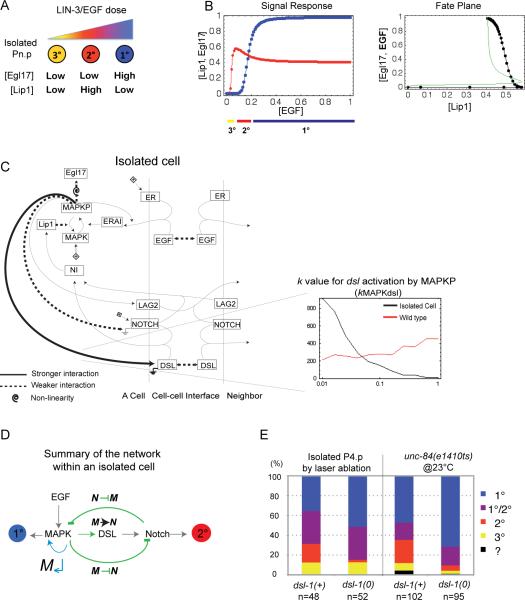
Katz et al. [11] reported that an isolated VPC could adopt a 2° fate at intermediate EGF levels without lateral signaling from neighbors (Fig 2A). We simulated an isolated VPC with exposure to increasing EGF levels, using the parameter sets that produced wild-type patterning in the six cells. Of these, we found that 1.9% could stabilize a 2° fate for some intermediate EGF dose, with a sharp transition between 3°, 2° and 1° fates at increasing EGF levels (e.g. Fig 2B). Compared to other wild-type solutions, those that could stabilize a 2° fate in isolated cells tended to express high DSL levels (Fig 2C histogram) and present high cooperativity of Egl17 activation by MAPKP and low intracellular cross-inhibition between pathways (N ⊣ M and M ⊣ N) (Figs 2C–D, S3A). Our model indeed required that 2° fate specification of an isolated cell was based on a DSL-Notch autocrine loop.

Figure 2. Role of DSL-1 autocrine signaling in the response of an isolated cell to EGF.

(A) Cartoon depicting the response of an isolated cell to EGF doses, based on experimental evidence, obtained either by varying their distance from the EGF source [14] or using a tunable promoter driving EGF synthesis [11]. (B) Signal response curve in an isolated simulated cell showing the concentrations at 300 min of Lip1 (red) and Egl17 (blue) for increasing EGF doses. The cell fate trajectory is shown below. (C) Network diagram indicating the strength of the interactions characteristic of solutions that can stabilize an isolated cell in any of the three cell fates, without intermediate fates (summarizing Table S4 and Fig S3). Thick solid lines indicate stronger interactions, and thin dotted lines weaker interactions compared to wild-type solutions, as defined by the parameter values for the corresponding step: a low k value is expressed as a strong interaction. A spiral indicates high cooperativity. An example of parameter distribution histogram is displayed on the bottom right, plotting the binned number of solutions where k_MAPKdsl has the corresponding parameter value on the x axis. (D) Vulval induction network summary showing the feedback and crosstalk (green) of the MAPK and the Notch pathways within a cell. M↵: MAPK pathway positive feedback loop; M → N: MAPK-mediated activation of DSL production; M ⊣N: MAPK-mediated inhibition of Notch; N ⊣M: Notch-mediated inhibition of MAPK. (E) Experimental proportions of fates adopted by an isolated cell in wild-type and dsl-1(0) worms in the C. elegans N2 background (Table S2). In the laser ablation, all competent Pn.p cells except P4.p were killed. In unc-84 mutant animals with defective Pn.p formation, only animals with a single Pn.p cell were scored. We separated the cases where the two daughters adopted 2° and 1° fates, respectively, as such 2° fates are not isolated from a 1° fate. The 2° fate proportion differs significantly between the dsl-1(+) and dsl-1(0) groups: p=0.006 in the laser ablation and p<0.001 in the unc-84 experiment See also Figure S2 and Table S2.

To experimentally test the role of diffusible Notch ligands in isolated 2° fate specification, we ablated with a laser all VPCs but P4.p before induction (early L2 stage). In wild-type dsl-1(+) worms, the isolated P4.p adopted a 2° fate in 9/48 animals (Fig 2E, Table S2A). In dsl-1(0) worms, we observed a strong decrease in 2° fate frequency (1/52 animal; Fisher's exact test, p=0.006), with a corresponding 1° fate increase. We observed a similar effect using the unc-84 mutation as “genetic” ablation of all but one Pn.p [14] (p<0.001; Fig 2E, Table S2B). Thus, the fraction of 2° fates adopted by an isolated cell strongly decreased in the absence of DSL-1, suggesting that autocrine Notch activation plays an important role in isolated 2° cell specification. A similar result was observed in the osm-11 mutant, where the gene coding another diffusible Notch ligand is mutated, while the 2° fate frequency decrease corresponded to a 3° fate increase (Fig S2A). Thus, modeling and experiment both support the idea that isolated cells can attain a 2° fate through autocrine Notch signaling.

The vulval patterning network can use morphogen-based and/or sequential mechanisms of induction

In the six-cell row, neither molecular pathway can function alone, but their combination may be used in two distinct manners to specify 2° fates. We wished to determine whether the morphogen-based and sequential mechanisms (Fig 3A) are mutually exclusive and whether their respective use is associated with qualitative differences in network dynamics.

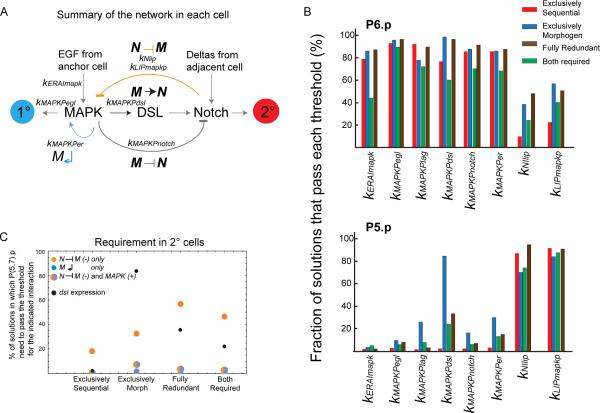
Figure 3. Sequential and morphogen-based inductions are found for different parameter sets of the model.

(A) Tests for morphogen-based versus sequential induction in the model. The simplified intercellular network characteristic of each patterning mechanism is shown on the right, with the color code from Fig 1. (B) Robustness of the vulval induction network to parameter variation. Graph showing the fraction of solutions (y-axes) that produced a stable wild-type pattern after 10-fold variation in the specified parameter (x-axes) (n=300 solutions from each mode). High values (close to 1) indicate insensitivity to the 10-fold parameter change. (C) Network diagrams indicating the interaction strength characteristic of the patterning mode, as defined by parameter values for the corresponding step: for example, a low k value is expressed as a strong interaction. These networks summarize the results of the Kolmogorov-Smirnov test comparing parameter distributions of wild-type solutions against solutions from each mode (Table S4 and Fig S3A). Two parallel bars on an arrow indicate low cooperativity. (D) Schematic representation of model parameter space in two dimensions. The parameter sets that produce the wild-type pattern, each patterning mode, “C. elegans” (AC ablation and egf overexpression criteria only) and “C. elegans N2” are schematically represented as a fraction of space (other species sets are omitted for simplicity). See also Figure S3 and Tables S3, S4.

We used three simulated perturbations that distinguish requirements for the two mechanisms (Fig 3A): (1) Restricting egfr expression to P6.p mimics egfr mosaics [12, 13]; (2) eliminating EGF diffusion prevents EGF from functioning as a morphogen; (3) eliminating LAG2 expression and DSL diffusion between cells abolishes lateral signaling, i.e. both lateral induction of the 2° fate and lateral inhibition of the EGF pathway and 1° fate (Table S3). The loss of wild-type patterning in the first two perturbations indicates that patterning requires morphogen-based induction, while a loss upon the third perturbation indicates that patterning relies on sequential signaling (Fig 3A).

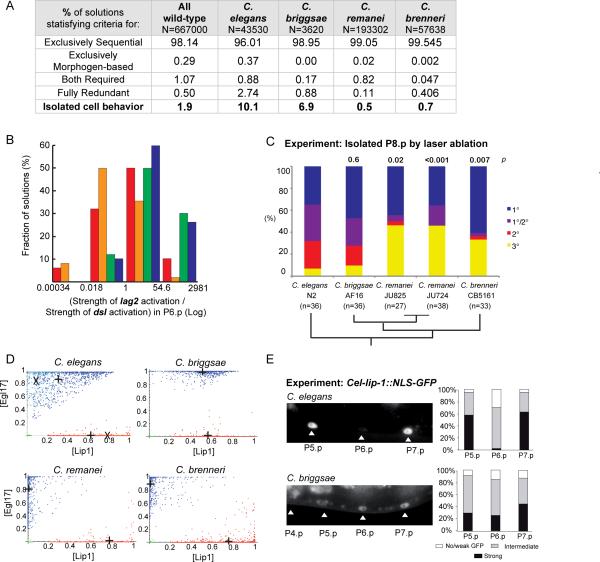
Based on these tests, we defined four patterning modes; 98.1% of the solutions used an exclusively sequential mode of induction, 0.3% used an exclusively morphogen mode, 1.1% required both mechanisms, and for 0.5% both mechanisms were fully redundant (Fig 3A). Thus, with the same network topology, the morphogen-based and sequential mechanisms are not mutually exclusive and may operate redundantly; the sequential mechanism is predominant in terms of proportion of parameter sets.

To test the robustness of solutions to parameter variation, we measured for each parameter the frequency of parameter sets for which correct patterning persisted over a 10-fold parameter variation. Solutions relying on sequential induction were on average much more robust to perturbations than those relying on morphogen-based induction, consistent with the higher fraction of solutions relying on the former (Fig 3B). Overall, patterning was most sensitive to large changes in EGF synthesis, EGFR half-life, and ease of activation of MAPK and lip1 synthesis. In addition, solutions relying on morphogen-based induction were more sensitive to EGF and DSL dosage or activity changes.

To explore mechanistic differences between patterning modes, we identified the most significant differences between parameter distributions for a specific mode versus all wild-type solutions (Figs 3C, S3A, Table S4). Morphogen-based induction required a stronger DSL-Notch autocrine loop, manifest as a requirement for higher dsl transcription and more localized DSL profiles (low diffusion, rapid degradation). In exclusively morphogen solutions, reciprocal inhibitions between Notch and MAPK pathways were weak, as in solutions that stabilized an isolated 2° cell (Fig 2C). Indeed, morphogen-based solutions reproduced the isolated cell behavior more frequently than sequential solutions (Fig S3B). Solutions that relied on morphogen induction usually had lower EGF pathway cooperativity, resulting in graded MAPK activation. Indeed, while in the other modes the EGF gradient between P6.p and P5.p was highly amplified at the level of MAPKP or downstream events, the amplification remained weak in exclusively morphogen solutions (Fig S4A).

Vulval patterning involves extensive feedback and crosstalk within and between EGF and Notch pathways (Fig 4A). We assessed for each patterning mode: i) activation over half-maximal level of subpathways in 1° and 2° cells (Fig 4B) and ii) requirement for intracellular crosstalks in 2° cells (Fig 4C).

Figure 4. Variation in activation and requirement for different network components in the different patterning modes.

(A) Vulval induction network scheme showing the interactions between MAPK and Notch pathways within a cell, with external input from adjacent cells in the six-cell row. (B) Percentage of solutions of each patterning mode for which a given event occurs in P6.p (upper panel) or P5.p (lower panel). An event is defined as occurring when a given protein concentration reaches the threshold for a specified interaction (k_Ab denotes the concentration in factor “A” where downstream factor “b” is half-activated, see Supplement). n=500 solutions from each mode. (C) Percentage of solutions belonging to each patterning mode in which P(5,7).p need to pass the indicated threshold to become 2°: Lip1 threshold to activate N ⊣ M (yellow), MAPKP threshold to activate M↵ (blue), both of them (not necessarily at the same time) (yellow-blue dot), MAPKP threshold for dsl expression (black). See also Figure S4 and Table S5.

Fig 4B shows for key model parameters the proportion of solutions for which a given event occurs in P6.p or P5.p - an event being defined as occurring when the upstream protein concentration reaches the threshold for a specified interaction. In solutions that rely on sequential induction only, MAPK activity is typically above thresholds for downstream events in P6.p and below in P5.p, whereas events downstream of Notch show the converse pattern (Fig 4B). In solutions with morphogen-based induction, the distinction is not as sharp; DSL synthesis is often activated in P5.p and Notch to MAPK inhibition in P6.p. Solutions where both modes are required show low activation of events in P6.p compared to the other modes.

In Fig 4C, we measured the fraction of parameter sets where the MAPK positive feedback (M↵) and MAPK inhibition by Notch (N ⊣ M) not only occurred but were required to be at least half-maximal at some timepoint in P5.p and P7.p for them to become 2°. Strikingly, the lateral inhibition threshold was often crossed in 2° cells (k_LIPmapkp high in Fig 4B) yet dispensible (low in Fig 4C). In the modes where morphogen induction operates, the requirement for higher dsl transcription downstream of MAPKP was balanced by N ⊣ M, which was more likely to be required than in the exclusively sequential mode. In addition, upon removal of this N ⊣ M crosstalk, cell fate patterns varied significantly between patterning modes (Table S5). The type and extent of crosstalk between EGF and Notch pathways thus strongly vary with the patterning mode.

Evolutionary differences among species are captured through quantitative variation in the model

The vulval cell fate pattern is conserved across Caenorhabditis species, which likely share the same regulatory interactions and pathways, as shown for C. briggsae [24]. Among these species, the relative contributions of lateral and inductive pathways differ, as determined by their responses to two perturbations. First, anchor cell (AC) ablations at the early-mid L3 stage revealed different fate patterns. In all species, early ablations produced an all-3° pattern and late ablations did not perturb wild-type patterning. However, at intermediate ablation timepoints, the predominant pattern for P(5–7).p differed: 2°-2°-2° in C. briggsae, 2°-3°-2° for C. remanei and no intermediate pattern in C. brenneri; C. elegans displayed a mix of P6.p cell fates that was classified as 2°-1°/2°-2° [24]. Second, EGF overexpression in the AC produced in C. briggsae a 2°-1°-1°-1°-2° pattern for P(4–8).p [24]. Performing here a similar experiment in C. elegans, we found that in contrast to C. briggsae, P4.p and P8.p could be induced at EGF concentrations where P5.p and P7.p still adopted a 2° fate (Table S6, summarized in Fig 5A).

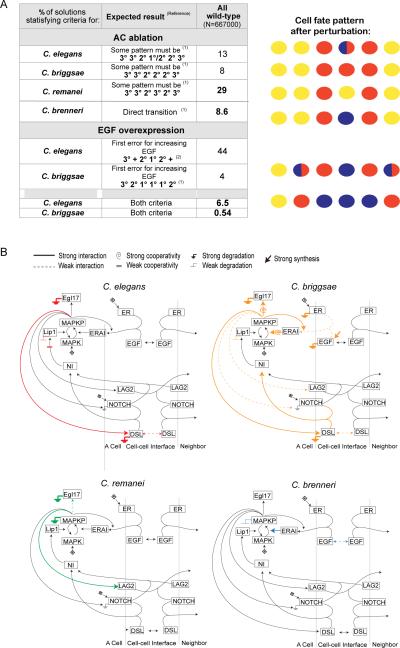
Figure 5. Localization of Caenorhabditis species in parameter space.

(A) Anchor cell ablation and EGF overexpression criteria used to identify the species sets within the parameter space of all wild-type solutions, after experiments in [14] and Table S6. Numbers indicate the percentage of wild-type solutions that produce the expected pattern. + signs indicate any fate different from 3°, whereas 1°/2° indicates the intermediate fate shown in Fig 1C. A schematic drawing of cell fates after perturbation is shown on the right (color code as in Fig 1). (B) Network diagrams indicating the strength of the interactions characteristic of Caenorhabditis species. These networks summarize the Kolmogorov-Smirnov tests comparing parameter distributions of each species set against wild-type solutions (Table S7A, Fig S5). See Figure 1 legend and the legend above the figure panel for explanations. See also Figure S5 and Tables S6–S7.

Could these differences among species be explained by quantitative variation in the same network? To address this, we simulated AC ablation and EGF/LIN-3 overexpression by eliminating EGF production at various times and by overexpressing egf, respectively. Then we categorized the wild-type parameter sets according to the species behavior that they reproduced: 6.5% for C. elegans, 0.54% for C. briggsae, 8.6% for C. brenneri and 29% for C. remanei (Fig 5A). The remaining solutions did not capture experimentally observed responses to perturbation in any of these species, for example with a 3°1°3° fate for P(5–7).p.

We then analyzed these sets of solutions for systematic differences in parameter distributions (Figs 5B, S5A, Table S7). We describe these differences for each species.

C. elegans

A tendency for slow DSL diffusion and long Lip1 activity is observed and needed to reproduce the 2°-1/2°-2° pattern after AC ablation (as in C. briggsae solutions below), in association with weak cooperativities for MAPK, Egl17 and Lip1 activation (Figs 5B, S5A). The egf overexpression pattern does not produce any strong constraint by itself (not shown).

C. briggsae

The C. briggsae solutions were the least frequent and correspondingly most constrained. The intermediate fate pattern after AC ablation is 3°-3°-2°-2°-2°-3°, which corresponds to solutions that favor the 2° cell fate, with a combination of highly active ligands and persistent Notch signaling, including: strong DSL synthesis, slow diffusion and fast degradation of DSL, fast Notch-DSL binding, low Notch degradation downstream of MAPKP and persistent Lip1 activity. We also noted a tendency for switch-like (high cooperativity) Egl17 activation and fast Egl17 degradation, which prevents 1° fate acquisition by P6.p at low EGF (Figs 5B, S5A, Table S7A).

Autocrine DSL signaling was required but never sufficient for 2° fate specification after AC ablation in C. briggsae-like solutions: restricting DSL action to the producing cell abolished proper patterning after AC ablation (n=200 solutions). The 2° cells needed some Notch ligand from neighbors, in the form of either DSL or more often LAG2 (Fig S6A).

Reproducing the C. briggsae 3°-2°-1-°1°-1°-2° pattern after EGF overexpression required strong EGF synthesis, fast degradation of EGF and EGFR, and a slow binding rate. The C. briggsae-like solutions presented a relatively flat EGF gradient (Fig S4B), which did not translate into a flat MAPK activity gradient, because of two mechanistic features of the MAPK pathway: i) strong intrinsic non-linearity and ii) strong positive feedback (Figs 5B, S5A).

C. remanei

The 3°-3°-2°-3°-2°-3° pattern observed after AC ablation is due to P6.p inducing the 2° fate of its neighbors while still adopting a 3° fate [24]. This suggests that the minimum inductive signal needed for the 1° fate must exceed that necessary to upregulate lateral induction. Indeed, we found that a high threshold for 1° specification was achieved in the C. remanei set through generally weak MAPKP activation of Egl17 combined with high MAPK and Egl17 degradation rates. A low threshold for lateral signaling was achieved by MAPKP strongly activating LAG2 production (Figs 5B, S5A). Consequently, temporal dynamics were affected: the 2° fate was more often specified before the 1° fate compared to other species sets (not shown).

C. brenneri

The direct transition from the all-3° to wild-type pattern in AC ablations implies that the 1° fate in P6.p and the 2° fate in P(5,7).p remain induced in the same individuals. This direct transition had the following requirements (Figs 5B, S5A): i) a long MAPK half-life, allowing activated MAPKP to persist after AC ablation, ii) a low EGF diffusion and iii) a low threshold for MAPK phosphorylation by the EGF pathway, allowing early MAPK activation.

Experimental tests of hypotheses provided by the model

The species sets differed in the proportion of solutions that relied on each patterning mode (Fig 6A), and in their respective expression level of membrane-bound (LAG2) and diffusible (DSL) Deltas: most C. brenneri and C. remanei-like solutions expressed more LAG2 than DSL, opposite to the C. elegans and C. briggsae sets (Fig 6B). Given the role for DSL autocrine signaling in isolated 2° fate specification (Fig 2), we reasoned that as a consequence of activity differences between the two Notch ligand forms, we may see differences among species upon experimental Pn.p cell isolation. Indeed, our model predicts that the species sets will also vary in their ability to stabilize an isolated 2° cell (Fig 6A, last row). The C. elegans set showed the highest proportion of solutions that produced an isolated 2° fate (10.1%), and the C. remanei set the lowest (0.5%). To test this prediction, we isolated P8.p by ablating all other vulval precursors in two C. remanei wild isolates (the AC was kept intact). We found a significantly lower proportion of 2° fates compared to C. elegans, similar to the C. elegans dsl-1 mutant (Fig 6C). This feature was fully unexpected since the C. remanei set requirement was to produce a 3°-3°-2°-3°-2°-3° pattern, i.e. 2° fates without adjacent 1° fate. C. briggsae and C. brenneri also displayed high and low proportions of isolated 2° fate (Fig 6C). These experimental findings match the modeling predictions (Fig 6A), and not the phylogenetic relationships among species [27]. These results suggest evolutionary variation in autocrine versus paracrine Notch signaling among Caenorhabditis species.

Figure 6. Prediction and experimental confirmation of interspecific variation in the propensity for isolated 2° fates (A–C) and in Notch pathway activation in P6.p (D–E).

(A) Percentage of solutions of each species set that belong to each of the four patterning modes. Caenorhabditis species solutions differed in their capacity to stabilize an isolated 2° cell at intermediate EGF doses (p<0.001, d.f.=3, G test of independence after Williams correction=11726.1). (B) Histograms showing the distributions of the ratio between the strength (flux value) of lag2 activation over the strength of dsl activation by MAPKP in P6.p (n=500 solutions from each species). The median value is 0.5 for C. briggsae (orange), 1.7 for C. elegans (red), 12.5 for C. brenneri (blue) and 27.0 for C. remanei (green). (C) Experimental proportions of fates adopted by an isolated P8.p cell in different species. p s of isolated 2° cells compared to C. elegans are noted above the bars. Phylogenetic relationships [27] are indicated below. (D) Fate plane distributions of P6.p (blue) and P5.p (red) in the Caenorhabditis species solutions (n=1000 solutions for each). Crosses indicate the average cell position. In the C. elegans graph, the paler dots and “X” correspond to “C. elegans N2”. (E) Experimental test of the prediction in (D). On the left, representative fluorescence micrographs show Cel-lip-1∷GFP expression in Pn.p nuclei in C. briggsae AF16 (mfIs29 transgene) and C. elegans N2 (zhIs4 transgene) backgrounds. The same pattern was observed with an independent C. briggsae transgenic line (mfIs30 transgene, obtained from another injected animal). Histograms on the right show semi-quantitative measurements of Cel-lip-1 reporters. Data for C. elegans are from [10], placed on a semi-quantitative scale for comparison with C. briggsae. Differences between P(5–7).p are not (or marginally) significant in C. briggsae, but highly significant in C. elegans. χ² tests: p=0.054 in C. briggsae (n=78), p=3.10⁻⁸ in C. elegans (n=40). See also Figure S6 and Table S8.

Another model prediction was that the species differed in characteristic network dynamics, including Notch pathway activation in P6.p (Fig S4B, S5, S6B) and thus its average position in the fate plane (Fig 6D). Especially, the high Lip1 half-lives allow persistent Notch signaling after AC ablation in C. briggsae solutions, and the average Lip1 level in P6.p is high (Fig 6D). This result was unexpected, but consistent with the previously hard to interpret description of Cel-lip-1 reporter expression in C. briggsae, where P6.p expressed similar levels of lip-1∷GFP as P5.p and P7.p (Fig 6E) [24].

The model reproduces the C. elegans N2 behavior and transitions between Caenorhabditis species

The C. elegans wild-type reference strain is called N2. We challenged our model to reproduce the results of well-established perturbations that were performed in this genetic background. We could obtain parameter sets (n=583) that reproduced all perturbations in Table S7B. To distinguish these solutions from the C. elegans set (above), we call the narrower set “C. elegans N2”. Note that for “C. elegans N2” solutions we enforced the EGFR mosaic wild-type pattern, which implicitly requires sequential induction.

Comparison of the parameter distribution in the “C. elegans N2” set with all wild-type solutions (Fig S5B, Table S7A) showed that the C. elegans N2 behavior required low EGF synthesis and rapid binding to EGFR. One “C. elegans N2” requirement is that the double mutant of a hypomorph lowering EGFR level (let-23(sy1)) and a silent mutation in a MAPK pathway inhibitor (gap-1) displays a Multivulva phenotype [28]. Our results support the verbal model proposed by Hajnal et al., who suggested that this counterintuitive synthetic phenotype was due to lower EGF binding in the egfr hypomorph, resulting in excess induction in gap-1 mutants [28] (Fig S6B).

By experimentally manipulating signaling pathway activities (at levels that did not modify the final pattern), we could modify P6.p fate in the AC ablation paradigm and thus mimic interspecific variations [24]. We reproduced these experiments computationally by simulating the same pertubations using the C. elegans N2 solutions. Specifically, C. elegans experimentally adopted a C. briggsae-like pattern with a lin-45/Raf hypomorphic mutation that decreased MAPK pathway activity [24]. This mutation was simulated in the model by increasing the MAPK phosphorylation threshold, which resulted in 2% (n=583) C. elegans N2 solutions switching to the C. briggsae ablation pattern. Mutations in sel-10, coding for a negative Notch regulator, made C. elegans adopt a C. remanei-like pattern [24], which was simulated by increasing Notch half-life, resulting in 7% “C. elegans N2” solutions acquiring the C. remanei ablation pattern. Finally, the C. elegans to C. brenneri transformation was simulated by increasing EGFR half-life, which mimicked the reduction-of-function mutation in ark-1, coding for a negative EGFR regulator. This resulted in 17% C. elegans N2 solutions switching to the C. brenneri ablation pattern. Thus, we could reproduce the experimental transformation of C. elegans N2 into the other species' behavior, i.e. cryptic variation among species.

DISCUSSION

Known interactions explain the isolated cell behavior and evolution in the Caenorhabditis genus

C. elegans vulval patterning has been previously modeled with diverse goals and methods [22, 23, 29–34]. A previous quantitative model based on differential equations included more simplified pathways and less feedback [22, 23] and could not reproduce the results of several experiments, such as an isolated 2° fate, and the C. elegans and C. briggsae AC ablation phenotypes. All added features of our model correspond to experimentally demonstrated molecular interactions: diffusible Delta-like ligands, positive feedback loop in MAPK pathway, pathway cooperativity (e.g. MAPK pathway with its kinase cascade). We feel that our model provides for our purposes an optimal balance between mechanistic detail and abstraction, retaining all topological features such as feedback loops and crosstalk. We explored parameter space randomly rather than expanding around one parameter set as in [23], allowing for unbiased sampling of space. We chose a different fate plane, which, while the exact boundaries are arbitrary, appears qualitatively justified by observations in C. briggsae, where P6.p adopts a 1° fate with high levels of both egl-17 and lip-1 expression (Fig 6D,E). We explicitly allowed intermediate cell fates, such as 1/2°. Finally, we interpreted the C. elegans AC ablation results of [24] as a 2°-1/2°-2° pattern, differently from the 3°-1°-3° pattern assumed in [23]. Altogether, our model is more comprehensive than previous ones, and our analyses explored evolutionary and mechanistic differences that previous models could or did not address.

First, our model allows an isolated 2° fate at intermediate EGF doses through autocrine Delta signaling and we experimentally confirmed this feature (Fig 2). The residual 2° fate in dsl-1(0) mutants may result from other diffusible Deltas [20] and/or secreted DOS-domain proteins such as OSM-11 [19] (Fig S2A). While we cannot exclude that another pathway further contributes to 2° specification [35], an autocrine loop is a simple and viable way to explain this phenomenon.

Second, our model allowed to rigorously explore the requirement and cooperation of two general patterning mechanisms that previously relied on verbal models: morphogen-based patterning and sequential induction [12, 13] (Fig 3A, Table S3). All combinations of requirement and sufficiency of each mechanism could be found within the same network parameter space, where sequential induction largely predominates (Fig 3D). Strict reliance on the morphogen gradient is unlikely, as such solutions are not highly robust to parameter variation. Yet natural variation may include these parameter space regions where both mechanisms act redundantly or cooperatively. Indeed, in C. elegans, some patterning errors occur in egfr mosaic analyses, suggesting that direct 2° fate activation by EGF plays a patterning role [12, 13]. Importantly, we showed that the two patterning mechanisms are not contradictory and may co-occur when the known molecular network is considered.

Third, lateral Notch signaling may differentially operate upon quantitative change in two different manners, i.e. lateral induction of the 2° fate and lateral inhibition of the MAPK pathway (Table S5).

Fourth, our model explains and reproduces the cell fate pattern upon AC ablation in C. briggsae, with three adjacent 2° fates (Fig 5A).

Biological significance of parameter variation: environmental and evolutionary variation

We showed that vulva patterning was generally robust to variation in most parameters. For a given genotype, variation in model parameters biologically corresponds to environmental change acting on each reaction. The environment affects biochemical reactions directly (e.g. temperature), or indirectly through regulatory pathways. Many developmental systems like vulval patterning produce outputs that are robust to environmental variation, a feature that is generally under stabilizing selection [8, 36].

Does morphogen-based induction increase robutsness to parameter variation when used redundantly with sequential induction? Robustness to parameter variation is generally not increased in solutions that use both mechanisms redundantly compared to those relying on sequential induction only (Fig 3B). Parameter variation in our model does not however reconstitute all sources of stochastic or environmental variation in the system, for example cellular events such as AC positioning [8] or the time of contact between P6.p and its neighbors. Late contact between VPCs could explain the need for diffusible Deltas and the morphogen-based mode. Indeed, Pn.p cells are born away from each other, progressively grow and contact each other in the late L2 stage, while fate patterning occurs: the autocrine Delta loop would help correct fate patterning in case of late contact between P6.p and its neighbors. Such perturbations could be explored by extensions of our model.

Like environmental variation, genetic variation may correspond to parameter space exploration, with selection maintaining a constant final pattern [8, 36]. Because of robustness to parameter variation, evolution in parameter space may occur without change in the resulting fate pattern. Such cryptic evolution may result from neutral drift or selective drive, acting directly or pleiotropically on the system [10, 24, 37]. Parameter sets attributed to each species correspond to those compatible with experimental data and do not imply that the actual species covers all of those. In addition, each parameter covers a wide range of molecular players, possibly including Wnt signaling or the SynMuv pathway [6], which may be interpreted in the model as a change in EGF-MAPK pathway sensitivity. Parameter values are indeed difficult to determine experimentally. Here we could use qualitative or semi-quantitative experimental data, such as fate patterns upon perturbation (Figs 2, 5), as input to the model to identify parameter space regions reproducing key system behaviors. The quantitative model can explain all present data in Caenorhabditis species, which suggests that network evolution since their common ancestor could have operated via quantitative change.

Experimental tests of quantitative change in Caenorhabditis species

The quantitative variation found in the model in turn provided several hypotheses that were experimentally verified. These hypotheses stem from the large proportion of possible solutions for one species displaying the tested behavior. We chose to test the model predictions that were the least trivial and most relevant to the system dynamics, considering the relationship of the model nodes to real molecular species. Specifically, we tested two main axes of evolution in the Caenorhabditis genus: i. the relative involvement of diffusible versus transmembrane Deltas and ii. the temporal dynamics of Notch pathway effectors.

First, most solutions in C. remanei and C. brenneri displayed a low activity of diffusible compared to trans-membrane Deltas and did not produce isolated 2° fates (Fig 6). We confirmed this prediction experimentally (Fig 6C). The C. remanei input criterion upon AC ablation was a 3°-3°-2°-3°-2°-3° pattern, thus the low frequency of isolated 2° fates was not trivial. This result is consistent with evolutionary variation in autocrine signaling.

Second, most C. briggsae solutions express a high level of Lip1 (2° fate effector) in P6.p (Fig 6D,E). Observations of the Notch pathway transcriptional reporter Cel-lip-1∷GFP in C. briggsae matched this prediction, and also justified our fate plane with 1° and 2° fate domains including relatively high levels of the other fate effector.

In summary, our combined computational and experimental analyses of the Caenorhabditis vulval signaling network opened novel insights into mechanistic and evolutionary variation of this model network and provided testable hypotheses. From a mechanistic viewpoint, analyzing system behavior in equivalent or “neutral” regions uncovered distinct yet potentially co-occurring operational mechanisms. A key mechanistic feature that was predicted computationally and confirmed experimentally was the role of diffusible Notch ligands. From an evolutionary viewpoint, we could assign distinct parameter space regions to different species and thus quantify cryptic evolution within this conserved network.

EXPERIMENTAL PROCEDURES

Model of the vulval induction network

Our model simulated a row of six Vulva Precursor Cells (VPCs) with an anchor cell (AC) that releases EGF onto P6.p. Each VPC possessed the network shown in Fig 1B, which was translated into a system of ordinary differential equations that describe the time evolution of protein concentrations, following standard mass-action biochemical kinetics with a pseudo-steady state assumption [4, 38]. EGF protein synthesis was initiated at the start of the simulation. EGF and DSL diffusions were simulated by allowing transfer between adjacent cells. The system was solved numerically, and cell fates determined according to Egl17 and Lip1 levels from 300 to 400 min of simulated development. Fig 1C represents the cell fate boundaries following the “fate plane” introduced by [22]. The mathematical formulation of the model is described in the Supplement.

Laser cell ablations and fluorescent reporters

See Supplemental Information.