Construction of patient specific atlases from locally most similar anatomical pieces

Abstract

Radiotherapy planning requires accurate delineations of the critical structures. To avoid manual contouring, atlas-based segmentation can be used to get automatic delineations. However, the results strongly depend on the chosen atlas, especially for the head and neck region where the anatomical variability is high. To address this problem, atlases adapted to the patient’s anatomy may allow for a better registration, and already showed an improvement in segmentation accuracy. However, building such atlases requires the definition of a criterion to select among a database the images that are the most similar to the patient. Moreover, the inter-expert variability of manual contouring may be high, and therefore bias the segmentation if selecting only one image for each region. To tackle these issues, we present an original method to design a piecewise most similar atlas. Given a query image, we propose an efficient criterion to select for each anatomical region the K most similar images among a database by considering local volume variations possibly induced by the tumor. Then, we present a new approach to combine the K images selected for each region into a piecewise most similar template. Our results obtained with 105 CT images of the head and neck show that our method reduces the over-segmentation seen with an average atlas while being robust to inter-expert manual segmentation variability.

1. Introduction

The purpose of radiotherapy planning is to optimize the dose received by the tumor while controlling the dose on the surrounding Organs At Risk (OARs). This requires the accurate delineation of the Clinical Target Volume (CTV) and the OARs. In clinical routine, this task is often performed manually, which is tedious and prone to inter-expert variability. To ease this task, atlas-based segmentation may be used to get automatic delineations, and showed satisfying results for the brain [1] and promising results for the head and neck region [2].

In the head and neck, the anatomical variability among patients is high, mainly due to corpulence and neck flexion. Previous studies showed that an average atlas has difficulties to cope with this high variability, and may result in over-segmentation for some structures [2]. Utilizing an atlas that is specifically adapted to the anatomy of the patient to delineate may help to improve the registration quality, and therefore the accuracy of the segmentation. To this end, one solution is to compute population-specific atlases, for example by clustering the database into homogeneous sub-groups [3] and computing an average atlas for each sub-group. To be even more specific to the patient (and not only to a given population), other approaches [4, 5] have been developed to consider each manually delineated image of a database as a potential atlas, and to select the most appropriate one for each new query image to segment. By extension, and to enhance robustness, it has been proposed to select several of the most appropriate images, register them independently to the patient and combine the segmentation results [6]. All these approaches bring up two questions: how to select the most appropriate images for a given patient and how to fuse them.

The selection criterion must be able to account for the anatomical variability in the database (various corpulence, neck flexion, various tumor size and grade), and it must be fast enough to be used in clinical routine. Selection criteria based on meta-information (e.g. age [6]) have been used, but they are not suitable when dealing with anatomical variability independent of simple meta-information. Therefore, criteria based on intensities [6, 4] have been proposed. However, our database is composed of pathological images, which may corrupt intensity based criteria. Commowik et al. proposed to estimate the amount of deformation needed to warp each image onto the patient image, using the average atlas to reduce computation time [5]. This criterion is computationally interesting but it still requires inverting and composing many deformation fields. Our first contribution is to propose an efficient selection criterion based on the degree of contraction and dilation of the structures. This criterion is well-suited for our case as it may account for the local volume variations caused by the tumor.

Regardless of the nature of the selection criterion, it may be applied globally on the images [6, 5], or locally in order to cope with the local changes of each region [7–10, 4]. Because of the high anatomical variability and as our database is composed of pathological images, a local selection seems more appropriate to consider the local impact of the tumor on the surrounding anatomical structures.

Once the most appropriate images have been selected for each region of interest, the fusion step has to be performed. In [9], a framework was proposed to build a piecewise most similar atlas from a set of images selected on predefined regions. This showed an improvement in segmentation accuracy with respect to an average atlas. However, it was restricted to the selection of a single image for each region, which makes it more sensitive to the selection step (e.g. outliers may exist in the selection process). Moreover, it may also be sensitive to the relatively high inter-expert variability in the head and neck region. Our second contribution is then to provide a framework to combine K_l selected images for each region R_l into one template for segmentation, taking into account the relative values of the selection criterion to weight each selected image accordingly.

We illustrate the capacities of our framework with 105 CT images of the head and neck region, showing its ability to reduce the over-segmentation seen with an average atlas while being less sensitive to inter-expert segmentation variability than a piecewise atlas computed using only one image per region.

2. Method

We present a new method to design an atlas locally adapted to the patient P to delineate on predefined regions. We assume that a database of N manually delineated images {I_j}_j∈[1…N] is available. Moreover, we suppose that an average atlas M has been built from this database. The average atlas construction provides for each image I_j a transformation warping it on M. We denote by T_Ij←M the non-linear part of the transformation allowing to resample I_j on M, and J_Ij←M the corresponding image of the Jacobian determinant values.

2.1. Efficient Local Selection of the Most Similar Images through Volume Variation Estimation

We wish to select among the images {I_j}_j∈[1…N] the ones that are the most similar to the query patient P on predefined regions {R_l}_l∈[1…L]. The regions R_l are defined once and for all on the average atlas M. Typically, one may define them as a dilation of the anatomical structures of interest. For a given region R_l in M, we define our criterion as a comparison of the average degree of contraction/dilation when deforming I_j on M and when deforming P on M. To do this, we first average on R_l the logarithms of the determinants of the Jacobian matrices for each non-linear deformation T_Ij←M, as described below:

$${\overline{J}}_{R_l}(I_j\leftarrow M)=\frac{1}{\text{card}(R_l)}\sum _{x\in R_l}log(J_{I_j\leftarrow M}(x))$$ (1)

In the same way, after registering M and P, we can estimate J̄_Rl (P ← M) from T_P←M. Then, the images {I_j}_j∈[1…N] can be ranked from the most similar to the least similar to the patient P on R_l according to the distance d_Rl (I_j, P) = ||J̄_Rl (P ← M) − J̄_Rl (I_j ← M)||. This criterion is well-suited for the local selection of the most similar images. Our images indeed present tumors of various sizes and grades that can induce local volume variations of the CTV and of the surrounding OARs. Moreover, it is very efficient as the J̄_Rl (I_j ← M) are pre-computed. It only requires performing one non-linear registration between P and M and computing J̄_Rl (P ← M). By comparison, other methods either require multiple registrations [3, 4] or many inversions and compositions of deformation fields [5].

2.2. Construction of a Piecewise Most Similar Atlas Incorporating Selection Weights

For each region R_l, the K_l images of the database having the lowest distances d_Rl (I_j, P) are selected to build the piecewise most similar atlas and are denoted {Ĩ_l,n}_n∈[1…Kl]. Further, we associate each image Ĩ_l,n with a selection weight α_l,n, based on d_Rl (Ĩ_l,n, P), that reflects its relative degree of similarity to P on R_l. To compute α_l,n, we used the Gaussian kernel, i.e. α_l,n = G_μ,σ(d_Rl (Ĩ_l,n, P)), as it allows us to discriminate distances that are very large. The Gaussian can be centered either on zero, or on the minimum distance found for the region R_l (we chose the second solution). As to the standard deviation σ, it controls the rejection of images with a large distance and was computed from the whole distribution of distances on R_l. The weights are then normalized for each region, so that for each l, ${\sum }_{n=1}^{K_l}{\overline{\alpha }}_{l,n}=1$. In addition, we also consider spatial weights to allow a smooth transition when interpolating between the regions R_l in the construction of the piecewise atlas. The spatial weight of the region R_l at location x is defined as w_l(x) = 1/(1+βdist(x,R_l)) where dist(x,R_l) refers to the minimal distance to R_l at location x. It is then normalized so that ${\sum }_{l=1}^L{\overline{w}}_l(x)=1$.

Construction of the Piecewise Most Similar Image

The construction process may be seen as a classical atlas construction [11] where the images have varying weights depending on the spatial location of each voxel (w̄_l(x)) and on the selection distances (ᾱ_l,n). We iterate over the following steps (M̃₀ = M):

1. Register the images Ĩ_l,n on the current reference M̃_k. This step provides affine transformations A_Ĩl,n←M̃k and non-linear transformations T_Ĩl,n←M̃k

2. Compute the new average image M_k+1 by interpolating the intensities of the warped Ĩ_l,n using the two sets of weights w̄_l,k(x) and ᾱ_l,n

3. Compute an average diffeomorphism T̄_k from the T_Ĩl,n←M̃k and the weights

4. Apply ${\overline{T}}_k^{-1}$ to M_k+1 to get the new reference ${\stackrel{\sim }{M}}_{k+1}=M_{k+1}\circ {\overline{T}}_k^{-1}$

5. Update the regions of interest by applying ${\overline{T}}_k^{-1}$ to R_l,k: $R_{l,k+1}=R_{l,k}\circ {\overline{T}}_k^{-1}$, and update the spatial weights w̄_l,k+1(x) accordingly

This process is similar to [9]. However, it is much more general as it allows the combination of several images for each region R_l. This is achieved by the following equations for steps 2 and 3. First, the intensities are interpolated by:

$$M_{k+1}(x)=\sum _{l=1}^L\left[{\overline{w}}_{l,k}(x)\left(\sum _{n=1}^{K_l}{\overline{\alpha }}_{l,n}\left({\stackrel{\sim }{I}}_{l,n}\circ A_{{\stackrel{\sim }{I}}_{l,n}\leftarrow {\stackrel{\sim }{M}}_k}\circ T_{{\stackrel{\sim }{I}}_{l,n}\leftarrow {\stackrel{\sim }{M}}_k}\right)(x)\right)\right]$$ (2)

The inner term (sum over n) computes a weighted average of the selected images for a region R_l, while the outer term uses the spatial weights to combine the contributions from each region R_l. Similarly, in step 3, we compute an average polydiffeomorphism T̄_k using the Log-Euclidean framework [12] ¹. This framework ensures to remain on the manifold of diffeomorphisms and leads to an autonomous Ordinary Differential Equation that can be easily integrated: $\stackrel{.}{x}={\sum }_{l=1}^L\left[{\overline{w}}_{l,k}(x)\left({\sum }_{n=1}^{K_l}{\overline{\alpha }}_{l,n}log\left(T_{{\stackrel{\sim }{I}}_{l,n}\leftarrow {\stackrel{\sim }{M}}_k}\right)(x)\right)\right]$.

Construction of the Associated Segmentation

After building the piece-wise most similar template, we need to compute its associated segmentation from the delineations of the selected images. The images of our database have been delineated for a clinical purpose, and some contours are missing for some structures. To deal with this difficulty, we chose to define one region R_l for each anatomical structure in the construction of the template image.

The construction of the associated segmentation is then achieved in two steps. First, we compute a probability map for each structure independently using the selected manual segmentations and the selection weights ᾱ_l,n. Then, we assign each voxel of the template image to the structure that has the highest probability.

3. Evaluation

We evaluated the proposed framework with N = 105 CT images of the head and neck region. On these images, the CTVs and OARs were manually delineated following the guidelines in [13]. The structures involved are the lymph node levels II, III and IV (CTVs), the parotids, the spinal cord, and the brainstem (OARs). We performed a Leave-One-Out analysis, each patient being successively excluded from the database and delineated with each of the three following atlases built from the N − 1 remaining images: (1) AVE: average atlas built as in [2], (2) PW_1: piecewise most similar atlas built with K_l = 1 image for each region, and (3) PW_10: piecewise most similar atlas built with K_l = 10 images for each region. As registration algorithm, we used the framework described in [2].

3.1. Qualitative Results

Fig. 1 shows the three different atlases (b,c,d) computed for a given patient (a) whose neck flexion is above average. The spinal cord contours show that the average atlas (b) and the piecewise atlas PW_1 (c) both have a relatively low neck flexion, whereas the neck flexion of PW_10 (d) looks much more similar to the patient’s one (see arrows). When registering head and neck images, a different neck flexion between the atlas and the patient is a common issue, often leading to registration errors and low segmentation accuracy. Therefore, our method’s ability to provide a correct neck flexion may increase segmentation quality.

Fig. 1. Illustration of the atlases used for a given patient.

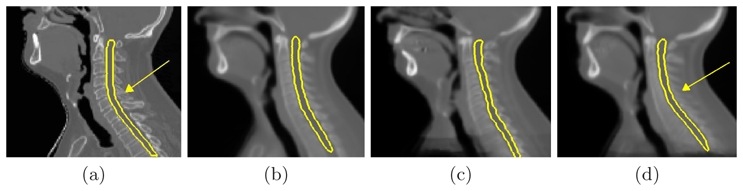
For the given patient (a), comparison between the average atlas (AVE) (b), the piecewise most similar atlases PW_1 (c) and PW_10 (d). The atlases shown were affinely registered on the patient.

Fig. 2 illustrates some qualitative segmentation results on the parotids and on the lymph nodes levels III-IV using the three atlases. Compared to the manual contours (a), the automatic contours provided by the average atlas (AVE) (b) are too large, which was already observed in [2]. As mentioned in [9], PW_1 (image (c)) allows to reduce the over-segmentation. However, it was built from only one image for each region, and it is therefore likely to be biased by the inter-expert variability of delineation. The two small arrows on image (c) show the influence of local specificities of the selected segmentations on each region. Moreover, by construction, PW_1 segmentations can present some discontinuities. For instance, the large arrow on image (c) shows some non-connected lymph node levels III and IV, which is anatomically inconsistent. The automatic contours obtained with PW_10 (image (d)) are much less dependent on the inter-expert variability as 10 segmentations were fused for each structure. Moreover, the obtained contours are closer to the manual contours than both contours from AVE (b) and PW_1 (c), which results in shorter correction time for the clinician.

Fig. 2. Qualitative segmentation results of each method.

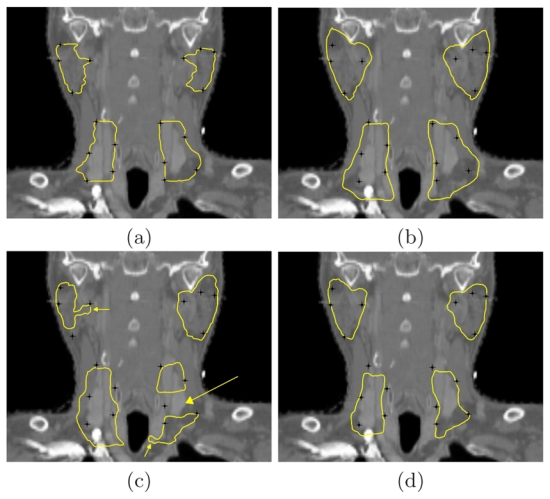
(a) Manual contours. Automatic contours with AVE (b), with PW_1 (c) and with PW_10 (d). Black landmarks attached to the manual contours are also shown to draw the comparison.

3.2. Quantitative Results

We now compare the performance of the three atlases AVE, PW_1 and PW_10 in terms of segmentation accuracy. To this end, sensitivity and specificity were averaged for each structure over all the Leave-One-Out tests. The results are presented in Fig. 3. First, as observed in [9], PW_1 shows an improvement of the specificity with respect to AVE, which is related to the reduction of the over-segmentation. However, this improvement is achieved at the expense of the sensitivity. With PW_10, the specificity is even higher than with PW_1 and the decrease in sensitivity is lower. For all structures, we also performed paired t-tests on the Dice values for each pair of methods. Whereas PW_1 has significantly lower Dice than AVE and PW_10 (P < 0.05), the differences between AVE and PW_10 are statistically not significant (P > 0.05), illustrating that the overall overlap is similar while PW_10 significantly reduces the over-segmentation. Therefore PW_10 combines the advantages of both PW_1 (avoiding over-segmentation) and AVE (avoiding errors due to inter-expert variability).

Fig. 3. Quantitative segmentation results.

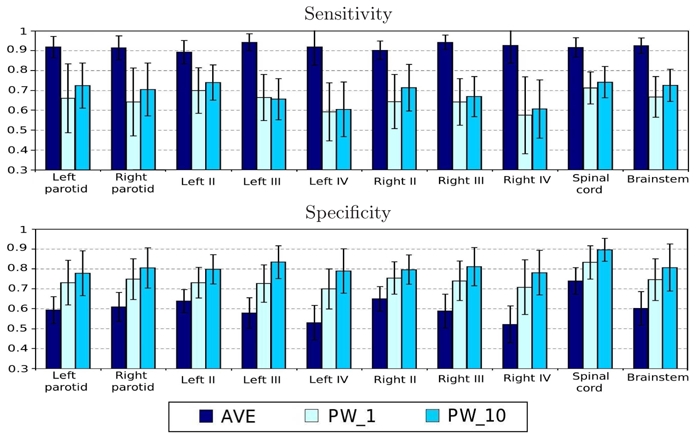
Average sensitivities and specificities for atlas-based segmentation using the atlases AVE, PW_1, and PW_10.

4. Conclusion

We presented a new approach to build a piecewise most similar atlas to the patient. We first introduced an efficient criterion to select among a database the images that are the most similar to the patient for each region. This criterion is well adapted to model the impact of the tumor on the CTVs and the OARs as it is based on the local degree of contraction/dilation. Then, we presented a novel approach to build from the selected images a piecewise atlas and its associated segmentation. We applied our algorithm with 105 CT images of the head and neck region. The proposed approach was compared to other atlas-based approaches (single average atlas and piecewise most similar atlas built from a single image per region). We showed that our approach combines the advantages of both techniques. It indeed enables reducing the over-segmentation observed with the average atlas, and it is less dependent on the inter-expert segmentation variability than the piecewise atlas built from a single image per region.

The number K_l of images selected for each region plays an important role, as well as the standard deviation σ of the Gaussian in the selection weights. Here we used arbitrarily K_l = 10 mainly for computational reasons, but we will study the influence of these two parameters to find out the optimal solution between the average atlas (K_l = N, infinite σ) and the method proposed in [9] (K_l = 1). Future work will also include a separate evaluation of the selection criterion and the piecewise atlas construction method. Finally, we will assess our framework on different groups of patients, e.g. on corpulent patients or patients with high neck flexion for which the average atlas provides low segmentation accuracy.