Fast Analysis of Molecular Dynamics Trajectories with Graphics Processing Units—Radial Distribution Function Histogramming

Abstract

The calculation of radial distribution functions (RDFs) from molecular dynamics trajectory data is a common and computationally expensive analysis task. The rate limiting step in the calculation of the RDF is building a histogram of the distance between atom pairs in each trajectory frame. Here we present an implementation of this histogramming scheme for multiple graphics processing units (GPUs). The algorithm features a tiling scheme to maximize the reuse of data at the fastest levels of the GPU’s memory hierarchy and dynamic load balancing to allow high performance on heterogeneous configurations of GPUs. Several versions of the RDF algorithm are presented, utilizing the specific hardware features found on different generations of GPUs. We take advantage of larger shared memory and atomic memory operations available on state-of-the-art GPUs to accelerate the code significantly. The use of atomic memory operations allows the fast, limited-capacity on-chip memory to be used much more efficiently, resulting in a fivefold increase in performance compared to the version of the algorithm without atomic operations. The ultimate version of the algorithm running in parallel on four NVIDIA GeForce GTX 480 (Fermi) GPUs was found to be 92 times faster than a multithreaded implementation running on an Intel Xeon 5550 CPU. On this multi-GPU hardware, the RDF between two selections of 1,000,000 atoms each can be calculated in 26.9 seconds per frame. The multi-GPU RDF algorithms described here are implemented in VMD, a widely used and freely available software package for molecular dynamics visualization and analysis.

1. Introduction

The increase in available computing power in recent years has been a boon for computational chemists wishing to simulate larger systems over longer timescales, but the ability to create massive quantities of molecular dynamics trajectory data also creates difficulties. Without advanced data analysis software, computationally expensive analysis tasks can become a bottleneck in the discovery process. One such task is the calculation of the radial distribution function (RDF).

The RDF is an important measure of the structure of condensed matter for several reasons. Radial distribution functions can be determined both experimentally and from simulation, allowing direct comparison. In addition, all thermodynamic quantities can be derived from an RDF under the assumption of a pair-wise additive potential energy function [1, 2]. The RDF has long been applied as a descriptor of the structure of liquids such as water [3, 4, 5, 6], and though they can be very computationally expensive to calculate, RDFs derived from large-scale molecular dynamics (MD) simulations have been useful in a wide range of applications. For example, Kadau and coworkers investigated shock wave induced phase transitions in metals using radial distribution functions calculated from simulations of systems with 8 million atoms [7]. Radial distribution functions calculated from systems of several hundred thousand to one million atoms have also been useful in studies of radiation damage in nuclear waste [8] and long-range order in self-assembled alkanethiol monolayers [9]. The RDF is also widely used in astrophysics, where stars replace atoms and the function is typically known as the two-point correlation function [10].

Massive molecular dynamics simulations like those cited above were once unusual, but now are becoming common. The extreme computational expense of data analysis of this type requires that we bring to bear computers as powerful as those used to run production simulations. Sometimes it is surprising which hardware offers the greatest performance to scientists, though. The introduction of the Beowulf cluster marked an important change in high performance computing [11]. Unlike previous high performance computers which were based on expensive, proprietary hardware, Beowulf clusters utilized inexpensive personal computers and commodity server hardware in large quantities to perform scientific tasks. Beowulf clusters soon became the standard in high performance computing because commodity hardware provided more computation per dollar spent than did the more expensive proprietary alternatives.

Recently the computer game market has driven the development of graphics processing units (GPUs) which provide much faster floating point performance than a typical CPU at a comparable price. As such they have been receiving a great deal of attention from scientists wishing to accelerate their applications [12]. Making use of massively parallel processors and high bandwidth memory systems, GPUs have already been applied to accelerate a wide variety of methods in computational chemistry and biomolecular simulation [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34]. The first generation of large scale heterogeneous clusters based on highly parallel commodity processors are already online—e.g. Los Alamos National Laboratory’s Roadrunner [35], the National Center for Supercomputer Applications’ Lincoln [36], and Texas Advanced Computing Center’s Longhorn [37]—and three GPU-based clusters are now among the ten fastest supercomputers in the world, with the top place currently held by a GPU-based cluster [38]. With additional large-scale GPU-based clusters planned [39], it appears that technology developed for the gaming market will increase the capability of available scientific computing resources dramatically.

One of the most attractive features of GPUs, however, is that they are already present in a typical desktop workstation where they accelerate visualization software. As such, it is natural to employ them not only to speed up large scale simulations, but also time consuming data analysis tasks which a scientist would typically perform on their local desktop machine. By executing such tasks on GPUs one accelerates the discovery process; data analysis that used to require a cluster can be run on a desktop, and time consuming tasks formerly run only in batch mode can be performed interactively.

One example of a visualization and analysis software package for molecular dynamics (MD) data which has begun to take advantage of GPU acceleration is VMD [40]. Specifically, a fast implementation of electrostatic and nonbonded force calculations is used to place ions and calculate time averaged potentials from MD trajectories [28, 41].

In this work we have implemented the calculation of the RDF from molecular dynamics trajectory data on NVIDIA GPUs into VMD using the CUDA parallel programming architecture [42]. The computation time of the task, inherent data parallelism, and opportunity for data reuse make RDF calculation a perfect target for GPU acceleration. However, the calculation of an RDF requires histogramming, which can be difficult to parallelize. In section 2 of this paper we define the RDF histogramming problem, describe the difficulties encountered in developing a parallel implementation, and present our GPU-accelerated solution. In section 3 we present the results of our optimization and benchmarks that analyze the performance of our implementation on several generations of NVIDIA GPU hardware. In section 4 we draw conclusions from our work.

2. Methods

The radial distribution function calculation contains several component algorithm steps. All of the steps can be formulated as data-parallel algorithms, but the histogramming operations are more difficult to adapt to the massively parallel architecture of GPUs, and are therefore the main focus of the discussion. Below we introduce the mathematical basis for computing radial distribution functions and describe how this relates to a naive serial implementation. We then describe high performance data-parallel algorithms for the histogram computation component of RDF calculation on multi-core CPUs and GPUs and the attributes that affect their performance.

2.1. RDF math and serial histogramming

The radial distribution function, g(r), is defined,

$$g(r)=\underset{dr\to 0}{lim}\frac{p(r)}{4\pi (N_{\mathit{pairs}}/V)r^{2}dr}$$ (1)

where r is the distance between a pair of particles, p(r) is the average number of atom pairs found at a distance between r and r +dr, V is the total volume of the system, and N_pairs is the number of unique pairs of atoms where one atom is from each of two sets (selections), sel₁ and sel₂. The definition of N_pair is given for two special cases by the following equations; the cases where sel₁ = sel₂ and where there are no atoms shared between sel₁ and sel₂ are given in 2 and 3 respectively.

$$N_{\mathit{pair}}=N_1(N_1-1)$$ (2)

$$N_{\mathit{pair}}=N_1{N}_2$$ (3)

where N₁ and N₂ are the number of atoms in sel₁ and sel₂ respectively. Note that the denominator of 1 is equal to p(r) of an ideal gas.

In general the average, p(r), is calculated over a thermodynamic ensemble. In the context of MD simulations, a finite number of frames are chosen from one or more trajectories which sample the thermodynamic ensemble of interest. Thus, this average takes the form

$$p(r)=\frac{1}{N_{\mathit{frame}}}\sum _i^{N_{\mathit{frame}}}\sum _{j\in se{l}_1}\sum _{k\in se{l}_2;k\ne j}\delta (r-r_{\mathit{ijk}})$$ (4)

where N_frame is the number of frames, r_ijk is the distance between atom j and atom k for frame i, and δ is the Dirac delta function. Given that only finite sampling is possible, the continuous function p(r) is replaced with a histogram on a grid:

$$p(r)=\frac{1}{N_{\mathit{frame}}}\sum _i^{N_{\mathit{frame}}}\sum _{j\in se{l}_1}\sum _{k\in se{l}_2;k\ne j}\sum _{\text{all}\kappa }{d}_{\kappa }(r;r_{\mathit{ijk}})$$ (5)

where κ indexes the bins of the histogram and

$$d_{\kappa }(r_{\mathit{ijk}})=\{\begin{array}{ll}1/\mathrm{\Delta }r\hfill & \text{if}{r}_{\kappa }\le r\le r_{\kappa }+\mathrm{\Delta }r\text{and}{r}_{\kappa }\le r_{\mathit{ijk}}\le r_{\kappa }+\mathrm{\Delta }r\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (6)

where Δr is the width of the bins and r_κ is the minimum distance associated with each bin, given by

$$r_{\kappa }=r_0+\kappa \mathrm{\Delta }r$$ (7)

where r₀ is the lower bound of the histogram. The summation over κ in 5 can be thought of as a coarse-grained delta function.

Note that the calculation of the distance, r_ijk, is complicated by the use of periodic boundary conditions. Assuming that the upper bound of our histogram is less than or equal to half of the width of the periodic box, the value of r_ijk is actually the distance between atom j and the closest periodic image of atom k. The process of identifying this distance is simplified by re-imaging all atoms into a single unit cell. The magnitudes of the x component of the shortest vector connecting atom j to a periodic image atom k, |x_ijk| can then be identified:

$$\mid x_{\mathit{ijk}}\mid =\{\begin{array}{ll}\mid x_k-x_j\mid \hfill & \text{if}\mid x_k-x_j\mid \le a/2\hfill \\ a-\mid x_k-x_j\mid \hfill & \text{otherwise}\hfill \end{array}$$ (8)

Where x_j and x_k are x components of the coordinates of atoms j and k and a is the length of the periodic box in the x direction. The magnitudes of the y and z components of the minimum displacement vector are easily generalized from 8, and together these three magnitudes allow the calculation of the minimum distance:

$$r_{\mathit{ijk}}=\sqrt{{\mid x_{\mathit{ijk}}\mid }^2+{\mid y_{\mathit{ijk}}\mid }^2+{\mid z_{\mathit{ijk}}\mid }^2}$$ (9)

The summation in 5 is the computationally expensive portion of the radial distribution function calculation, as it requires looping over all selected pairs of atoms in all frames. A naive, serial implementation would be based on three nested loops; at each iteration the distance between a pair of atoms is calculated and the appropriate histogram bin is incremented (updated).

Note that it is possible to significantly improve on the performance of a naive, serial implementation without resorting to parallel histogramming. In the RDFSOL module implemented in CHARMM [43], for example, a cutoff and spatial decomposition are employed to reduce the total cost of the calculations. This approach takes advantage of the fact that most liquids become unstructured beyond some distance, and thus there is not need to calculate the distances between blocks of atoms that are more than a user defined cutoff distance away from one another. Though we have not employed this strategy in the current work, we intend to implement this strategy in conjunction with GPU-acceleration in the future, taking advantage of spatial decomposition techniques previously developed for fast GPU-accelerated electrostatics calculations in VMD [41].

2.2. Parallel RDF histogramming

Many of the difficulties which must be overcome in a parallel RDF implementation arise in implementations for both multi-core CPUs and GPUs. As described above, a serial RDF implementation involves two main calculations, the computation of atom pair distances, and the insertion of the computed pair distances into a histogram by incrementing the appropriate histogram bin counter for each pair distance. The pair distance computation is inherently parallelizable since each combination of atom pairs can be considered independently and atomic coordinates may be treated as read-only data that can be shared or replicated among cooperating processors as needed.

The main complication in parallelizing RDF calculation arises in the histogram update step. In a serial implementation, the histogram bins are usually updated with a simple fetch-increment-store approach, where the counters associated with each histogram bin are directly incremented as pair distances are processed. Although this approach is trivial to implement for a serial implementation, the scattered memory updates present problems for parallel implementations due to the potential for counter update conflicts. In general, such scatter operations are often converted into either some form of data-parallel atomic increment or scatter-add operation, or gather operations wherein histogram bins gather their counts by reading the same input values but only incrementing their local counter as appropriate.

Since a single histogram results from the entire RDF computation, a parallel implementation may take one of three main approaches. The first approach consists of updating a single histogram instance in parallel, through close coordination between processing units or by updating histogram bin counters with special scatter-add or other atomic update hardware instructions [44, 45, 46]. The second approach, privatization, consists of maintaining multiple independent histogram instances, each updated by a single processing unit, followed by a parallel reduction of independent histograms into a single resulting histogram. A third approach uses a hybrid of the first two approaches, wherein tightly-coupled groups of processing units update a shared histogram, with many such groups independently updating their own histograms followed by a global parallel reduction for the final resulting histogram. Of these variations, the specific approach or hybrid that yields the best performance depends greatly on the number of processing units performing the parallel RDF calculation, the availability and performance of hardware instructions for scatter-add or atomic increment operations, and the speed and capacity of fast on-chip memory or caches to hold histogram instances.

2.3. CPU parallel RDF histogramming

Before discussing the GPU implementation of the RDF, it is instructive to consider the details of the reference implementation for multi-core CPUs. Most modern CPUs provide some form of SIMD instruction set extensions for acceleration of data-parallel workloads associated with interactive graphics and multimedia applications. For example, recent x86 CPUs support MMX and SSE instructions that operate on four-element vectors of 32-bit integers and single-precision floating point data. Although these instructions can be effectively employed to improve the performance of the atom pair distance portion of the RDF computation, they currently do not provide the necessary hardware instructions needed for parallel histogram updates [45, 46].

Given the limited applicability of the x86 CPU SIMD instructions for accelerating the histogram update, the main remaining opportunity for parallelism then comes from the use of multithreading on multi-core processors, and from approaches based on distributed memory message passing on HPC clusters. Since state-of-the-art CPUs contain a modest number of cores, an efficient multithreaded RDF implementation can be created by maintaining independent (privatized) histogram instances associated with each CPU worker thread and gathering the independent histogram results into a final histogram at the end of the calculation. In such an implementation the atom coordinates can be treated as read-only data and shared among all of the threads, promoting efficient use of CPU caches. In a distributed memory cluster scenario, a similar strategy may be used, but with atomic coordinate data being replicated as-needed among nodes in the cluster. Individual cluster nodes may employ multi-core CPUs using the multithreaded approach above for intra-node CPU cores, performing a second level parallel reduction or gather operation to compute the final histogram from the independent histogram instances computed locally on each node.

2.4. GPU parallel RDF histogramming

There are a number of competing issues involved in achieving the best performance for GPU-accelerated RDF calculations. Depending on the parameters of the RDF calculation, the hardware capabilities of the target GPU devices, and the number of devices to be used, one may employ one of a number of strategies for decomposing the problem and balancing the workload across the available GPUs. Below we describe the trade-offs involved, and the solutions we employ in each case.

2.4.1. GPU RDF parallel decomposition strategies

The key to achieving maximum performance on the GPU is to decompose the problem into thousands or millions of independent threads in such a way as to make efficient use of the GPU’s many multiprocessors. A CUDA kernel is executed by a large number of threads. These threads are grouped into user defined thread blocks which share a fast, on-chip memory space known as shared memory. Though each thread in the block accesses the same shared memory, a full block of threads does not run concurrently; instead, blocks are divided into warps, each of which contains 32 threads that run concurrently.

The GPU is composed of several multiprocessors. Each multiprocessor can process one or two instructions for one warp at a time. However, each multiprocessor is occupied by several warps simultaneously. A single warp will run until it reaches a point where an access to the slow, off-chip global device memory is required. At this point the data is requested from device memory and the multiprocessor switches to process another warp while the data is retrieved. The multiprocessor is idle only if all warps assigned to it are waiting for data from device memory at the same time. Thus, reducing the number of accesses to device memory reduces the probability that a multiprocessor is idle waiting on memory accesses, and therefore increases performance.

In the case of our RDF algorithm (the performance-critical portion of which is represented in Fig. 1), this is achieved by maximizing the reuse of data in fast, on-chip memory. Our strategy is similar in spirit to the cache- [47, 48, 49] and register-level [50] tiling schemes employed in the optimization of other algorithms that benefit from data reuse, such as matrix-matrix multiplication.

Figure 1.

This pseudocode describes the performance-critical portion of the RDF code. The code of the various GPU kernels is shaded light blue. The remaining code is executed by the CPU. The chosen loop structure and distribution of the data to different portions of memory allows maximum reuse of data between accesses to device memory.

Before considering the algorithm itself we describe how atom coordinates and histogram bin counters are divided into tiles, and which GPU memory system they are stored in. The distribution of sel₁, sel₂, and histogram data is illustrated in Fig. 2. To calculate each histogram point (an element of the summation in 5) we need access to the Cartesian coordinates of one atom from sel₁ and one from sel₂. We use two different tiers of the GPU memory hierarchy to minimize the cost of loading this data from device memory. We choose to store sel₁ in constant memory. Constant memory is a segment of device memory which is associated with a fast, read-only on-chip cache. Reading from constant memory is as fast as from registers so long as the requested data is in cache and all threads in the warp access the same address. Constant memory is limited, so we must divide the coordinate data of sel₁ into tiles of N_const atoms which approximately fill it (N_const ≈ 5,000 for the standard 64 kB of constant memory) and operate on these tiles one at a time. By accessing sel₁ contiguously we make optimal use of the cache and therefore must read from device memory only once per cache line. Because constant memory is read-only from the point of view of the compute kernel, control must be returned to the CPU to reload constant memory after each tile is processed. The most recent Fermi generation of NVIDIA GPUs provide an L1 cache for both read and write accesses to global memory. The Fermi L1 cache could in principle be used in a manner similar to our use of constant memory above, but without the need for the host to load individual tiles. This approach could be advantageous in cases where the host CPU is otherwise occupied or constant memory is needed for another purpose such as storage of spatial decomposition lookup tables [41].

Figure 2.

This illustration depicts the way our implementation of RDF histogramming makes use of the memory hierarchy of the GPU to store geometric (sel₁ and sel₂) and histogram data. Main memory (off-GPU) is shaded red. Constant memory and the constant cache are shaded dark and light green respectively. Global and shared memory are shaded dark and light blue respectively. The number of atoms or histogram bins stored at each level of memory is marked on each piece of memory.

We handle sel₂ differently, but the goal is the same—to minimize accesses to slow off-chip device memory. Before building the histograms, sel₂ is loaded in its entirety into global memory, the slow device memory space which on all but the most recent GPU devices is not associated with a cache. Rather than relying on a cache, the atoms in sel₂ are divided into tiles which are loaded into fast on-chip shared memory. Data in a shared memory can be accessed close to the speed of registers so long as there are no bank conflicts. Shared memory bank conflicts are trivially avoided in our implementation. Each tile contains N_block atoms, where N_block is a parameter defining the number of threads in a thread block. For each such tile the algorithm will loop over all N_const elements in the current tile of sel₁. Thus, N_constN_block atom pairs can be processed after only a single load operation from global memory for sel₂.

A second, higher, level of tiling is also used for sel₂. This second tiling scheme is not intended to improve performance, but instead to avoid integer overflow of histogram bins when a large number of atoms (over 60,000 in the current implementation) are present. These larger tiles are termed overflow tiles in Fig. 1. The size of the overflow tiles is selected such that a bin will not overflow even if all atom pairs in the selection fall into the same bin. It is important to note that these overflow tiles do not reflect a separate location in memory, but are reflected in the loop structure of the code. The possibility of a histogram bin overflow is eliminated by processing only a single overflow tile at a time.

Because histogram data is accessed at each iteration it is also advantageous to store it in fast on-chip memory. Thus each histogram bin is stored in shared memory as a 32-bit unsigned integer. The limited shared memory capacity and large number of processor cores make it impossible for each thread to maintain its own instance of the histogram, as was described above for the parallel CPU implementation. Instead, a hybrid approach is employed where groups of threads cooperatively operate on shared histogram instances, and the histogram instances produced by different groups are summed at the end of the calculation to produce the final result. In addition, it is only possible to store a segment of N_bin histogram bins in shared memory at one time. If a histogram larger than N_bin is requested by the user, multiple passes over all atom pairs are done to build the histogram N_bin at a time, using a gather approach.

One must take note that each multiprocessor has only a small amount of shared memory, and therefore the number of thread blocks occupying each multiprocessor depends inversely on the shared memory requirement of each thread block. To achieve optimal performance, a delicate balance must be reached between data reuse and the efficient use of limited resources. As such, below we will describe how we empirically optimized the various parameters defining the memory usage of our algorithm.

Having described the partitioning of the data to different levels of the GPU memory hierarchy, it is now possible to describe how the algorithm is structured. For each tile of sel₁ the RDF computation proceeds as follows (Fig. 1): The atom coordinate data for the current tile is loaded into constant memory and a grid of N_grid thread blocks are launched. Each thread block loops over a set of tiles of sel₂, such that each tile is assigned to one and only one thread block. At each iteration the coordinates of the atoms in sel₂ are loaded into shared memory. Each thread is assigned its own atom from the tile in shared memory, and it then loops over all atoms in constant memory, calculating distances and updating the histogram as necessary. By looping over all atoms in sel₁ contiguously, we minimize cache misses and therefore must read from device memory only once per cache line.

The RDF histogramming kernel described above scales as O(N₁ * N₂), making it the most computationally costly portion of the RDF calculation (See Supplementary Table 1 for details). However, we have written GPU kernels to perform several required pre- and post-processing tasks to ensure maximum performance. Specifically, we initialize the values of all histogram bins to zero, re-image all atomic coordinates into a single unit cell, and sum the many histogram instances into the final histogram in parallel on the GPU, ensuring that these computationally inexpensive tasks do not become the performance determining step in extreme cases.

2.4.2. Multi-GPU decomposition and load balancing

The GPU algorithm described above can be extended to enable concurrent execution on multiple GPUs by assigning combinations of tiles from sel₁ and histogram regions to different GPUs. A straight forward decomposition across multiple GPUs using only tiles from sel₁ frequently results in an insufficient number of independent work units to effectively utilize and load balance multiple GPUs. By decomposing over both tiles of sel₁ and histogram regions, a much larger number of work units are available for scheduling. This is particularly helpful in the case where the pool of available GPUs contain devices with significantly different performance characteristics. Since each GPU independently computes its own partial histogram, the final histogram is produced by summing the contributions from each of the independently computed histograms at the end of the computation.

One of the challenges that arises with the use of multiple GPUs in parallel is additional overhead associated with per-host-thread CUDA context creation and GPU device binding. When a host CPU thread first creates a CUDA context and binds to a specific GPU device, a small 0.1 second delay occurs when binding the host thread to the device. There is also a potentially much more significant delay—approaching one second—that can occur when the GPU hardware is brought fully online, particularly in the case of cluster nodes where no windowing system or other processes are keeping the GPU in a “ready” state. These delays are cumulative per-GPU, and are most noticeable on multi-GPU systems that do not have a windowing system running. In the case of a four-GPU system with no windowing system running, the time to create a group of four new host threads and attach them to their respective GPUs can take between 3 and 7 seconds depending on whether the GPU kernel drivers are fully loaded and the GPUs are in a ready state or not. Subsequent calculations launching new host threads incur less delay, but the overhead can still be as high as 2–3 seconds each time a newly created group of host threads attaches to the GPUs.

The potential for significant multi-GPU initialization delays on certain hardware configurations has had a significant impact on the design of the multi-GPU algorithm. Overhead can be eliminated for all multi-GPU calculations by creating a persistent pool of host CPU worker threads that remain attached to their respective GPUs for the entire program run. When host CPU worker threads become idle, they are put to sleep using an efficient barrier synchronization primitive based on condition variables provided by the POSIX threads programming interface. Waking the pool of CPU worker threads sleeping on the barrier synchronization primitive and causing them to begin execution of a new calculation takes less than 10 microseconds, many orders of magnitude faster than creating a fresh group of host threads and having them attach to their respective GPUs. The CUDA GPU management framework implemented in VMD creates a persistent pool of CPU worker threads and attaches them to their respective GPUs when the program starts. This pool of worker threads is retained and reused repeatedly until the program exits. Each execution of the multi-GPU RDF algorithm wakes the thread pool and launches a new calculation, avoiding all of the overheads associated with initializing and binding to GPU devices. As soon as the RDF calculation is complete, the CPU worker threads sleep on the synchronization barrier until they are awoken again, thereby minimizing idle processor load and idle CPU and GPU power consumption.

2.4.3. GPU parallel histogram updating techniques

The histogram update (the summation of each histogram point into the histogram) must be implemented carefully. With hundreds of threads simultaneously calculating histogram points, there is no guarantee that multiple threads will not attempt to increment the same histogram bin at the same time. Precautions need to be taken to ensure that these collisions do not result in incorrect results. In addition, the update must be implemented efficiently because it is usually performed by every thread for every iteration.

We have implemented the histogram update in two different ways: a general implementation that runs on any CUDA-capable GPU hardware, and an implementation that takes advantage of atomic operations to shared memory which are available only on CUDA devices of compute capability 1.2 (cc1.2) and above.

We will first describe the general implementation, which is based on the method for simulating atomic updates developed by Shams and Kennedy [51]. Example histogram codes using this algorithm are available in the CUDA SDK [42]. In this implementation, each warp is associated with its own copy of the histogram in shared memory. By doing so we ensure that any two threads that attempt to increment the same bin at the same time are in the same warp, and therefore are executing the update concurrently.

Absent the availability of an atomic addition operation, we must mimic the functionality of this hardware feature to prevent data loss. To this end, a thread incrementing a histogram bin does so in the following steps:

1. The value of the histogram bin is loaded into a register which is local to that thread.

2. The register is incremented.

3. A tag, which is unique to each thread of the warp, is written to the most significant bits of the register.

4. The thread writes the value of the register, including the tag, back to the histogram bin in shared memory from which it came. If multiple threads attempt to write to the same bin at the same time only a single thread will succeed.

5. Each thread reads the value of the histogram bin again. If the value of the histogram bin matches the value of the register then the update was successful and the thread is done with the update. If not, the thread returns to step 1 and tries again.

In this way the code loops until all threads have successfully updated the histogram bin.

The compute capability 1.2 implementation is much simpler. In CUDA devices of capability 1.2 and higher an atomic add instruction is available. This instruction adds directly to shared memory in an atomic fashion, thus eliminating the need for the complicated update scheme described above. In addition, it allows us to reduce our total shared memory usage by creating a single copy of the histogram in shared memory per thread block, rather than per warp as is required by the general scheme.

2.5. Performance analysis and parameter optimization

Below we present an analysis of the performance of the RDF histogramming code as a function of the problem size (sel₁, sel₂, and N_hist). In all cases an equilibrated water box containing 4,741,632 water molecules is used as the test case. Smaller test cases are created by selecting a subset of these water molecules. These selections are chosen such that the molecules are physically near one another to ensure that the measured performance corresponds to that of a dense system. The reported times correspond to the entire RDF histogramming procedure, including the initial transfer of data to the GPU from main memory and the retrieval of the final result from the GPU to main memory.

The tiling scheme involves four parameters which can be tuned to achieve optimum performance–N_block, N_bin, N_const, and N_grid–all of which are described above. A number of four-dimensional scans over a wide range of possible values for these parameters were performed in order to identify optimal parameter sets for a variety of hardware configurations and problem sizes. In addition, we have analyzed the performance of the code as a function of these tiling parameters. The full range of these scans is described in the supplementary information.

A number of hardware configurations were employed in our testing:

1. Two NVIDIA Tesla GPU processors (S1070) on a single node of NCSA’s Lincoln GPU-accelerated cluster [36]. Compiled with CUDA 3.0. (Hereafter this configuration is referred to as “2×Tesla”.)

2. A heterogeneous configuration of five NVIDIA Tesla processors (4 from a single S1070 + 1 C1060) and a GTX 285. Compiled with CUDA 3.0. (Hereafter this configuration is referred to as “5×Tesla + GTX 285” or “6×G200”.)

3. Four NVIDIA C2050 (Fermi) GPU processors. Compiled with CUDA 3.0. (Hereafter this configuration is referred to as “4×C2050”.)

4. Four NVIDIA GTX480 (Fermi) GPU processors. Compiled with CUDA 3.0. (Hereafter this configuration is referred to as “4×GTX480”.)

We will hereafter use the term Tesla to refer to a single C1060 card or a single processor of a S1070, since their technical specifications are equivalent. All other processors will be referred to by their model number or by the more general designations G200 for Tesla and GTX 285 cards and G400 for the C2050 and GTX480.

3. Results and Discussion

Below we provide a discussion of performance results scanning over a wide range of tiling parameters, and the variation in performance according to problem size and algorithm on several GPU hardware generations. Finally, we present performance results for multiple-GPU calculations, and analyze the effectiveness of our dynamic load balancing technique on multiple GPU hardware generations.

3.1. Tiling parameter optimization and analysis

Four tiling parameter sets were developed to provide optimal performance under different conditions. These conditions are presented in Tab. 1. The tiling parameter sets themselves are presented in Tab. 2. Three sets (cc1.0_8192, cc1.2_8192_a, and cc1.2_1024_a) were optimized on the 2×Tesla hardware configuration for use with G200 and older generations of GPUs, while the remaining was optimized on the 4×C2050 machine for use with G400 series GPUs. The optimization of these sets were performed with different histogram sizes (either 8,192 or 1,024 bins) and taking advantage of different hardware features (size of shared memory, atomic operations). The abbreviations of the parameter sets indicate the compute capability required to provide the features used in their optimization (ccx.y) followed by the number of histogram bins for which these parameters are optimal. The _a suffix is appended if atomic memory operations where used.

Table 1.

The conditions for which the four tiling parameter sets were optimized are shown below. One general parameter set was optimized which is capable of running on any NVIDIA GPU hardware (cc1.0_8192). Two sets were optimized for compute capability 1.2 hardware, taking advantage of atomic memory operations (Atom. Op.). These parameter sets differ in that their performance was optimized for different numbers of histogram bins (N_hist). Finally, a parameter set was optimized for compute capability 2.0 hardware, taking advantage of both atomic memory operations and a larger shared memory (Sh. Mem.) space.

Set	Nhist	Atom. Op.	Sh. Mem.
cc1.0_8192	8192	No	16 kB
cc1.2_8192_a	8192	Yes	16 kB
cc1.2_1024_a	1024	Yes	16 kB
cc2.0_8192_a	8192	Yes	48 kB

Table 2.

These tiling parameter sets were found to provide optimum performance under the conditions described in Tab. 1. Also presented is the amount of shared memory used per block (Mem./B.) for each set.

Set	Nblock	Nbin	Nconst	Ngrid	Mem./B.
cc1.0_8192	32	1024	5440	256	4.38 kB
cc1.2_8192_a	320	3072	5440	256	15.75 kB
cc1.2_1024_a	256	1024	5440	512	7.00 kB
cc2.0_8192_a	896	8192	5440	256	42.50 kB

The dependence of the performance of the code on N_block and N_bin is shown in Fig. 3. Fig. 3a and b show the performance over a range of values of N_block (keeping all other parameters constant at their optimized values). As described above, the size of the thread block is defined by N_block; in addition the amount of shared memory allocated to store histogram and atom coordinate data is related to N_block. Remember that for the general (non-atomic) histogramming algorithm, which is employed in cc1.0_8192 but not the other three sets, one instance of the histogram must be stored in shared memory for every warp in the thread block. Thus for cc1.0_8192 the amount of shared memory required per block scales dramatically with the increase in N_block. In fact, there is not enough shared memory to run with N_block > 96. The optimum balance between data reuse and efficient use of shared memory occurs at N_block = 32, with N_block = 96 providing similar performance.

Figure 3.

Performance as a function of tiling parameters. Selections of 1,000,000 atoms were processed on the cc2.0 hardware, while a 200,000 atom test case was used in the other two cases. All tiling parameters besides the dependent variable are kept constant at their optimized values. Red, purple, and cyan lines represent the behavior around the cc2.0_8192_a, cc1.2_8192_a, and cc1.0_8192 parameter sets respectively. This data was recorded on the machine on which these parameters were optimized. a–b) The performance as a function of N_block. When atomic operations are used the performance benefits greatly from increasing N_block. c–d) The performance as a function of N_bin. In the cases where atomic operations are used performance increases linearly with N_bin because increasing N_bin decreases the number of passes the code must make over all atom pairs. In both scans it can be seen that the need to store more instances of the histogram data in shared memory in the absence of atomic operations severely limits performance.

The situation is different when atomic operations are used, as in cc1.2_8192_a, because only a single instance of the histogram need be stored in shared memory for the entire thread block. Thus, the scaling of the required shared memory with N_block is much less severe. As such, the best performance is achieved at a much larger value of N_block, 320, above which there is not enough shared memory to accommodate both the histogram and a tile of coordinate data. Notice that the each block requires 15.75 kB of shared memory in this case, which is nearly the full 16 kB available.

Compute capability 2.0 GPUs differ from the previous generation in a number of ways. Of particular interest for our application is that a cc2.0 GPU has three times more shared memory available per multiprocessor than does a cc1.2 GPU. Given the the monotonic increase in performance with N_block seen above for cc1.2_8192_a, it is not surprising to see that the cc2.0 optimized parameter sets make use of more shared memory than their cc1.2 counterparts. In fact, optimum performance is reached at N_block = 896, a number too large to be used with the limited shared memory of cc1.2 hardware. This improves performance on cc2.0 hardware by 31 percent compared to N_block = 320, the optimum value on cc1.2 hardware. It should be noted that N_block is limited to 1,024 not by the size of shared memory but instead by the hard limit of 1,024 threads per block enforced by the CUDA cc2.0 standard.

Plots of the performance as a function of N_bin are shown in Fig. 3c and d. The size of the histogram segment stored in shared memory is defined by N_bin. If N_bin is less than N_hist then multiple passes through the atom pairs are required to calculate the full histogram, and the cost of the calculation increases proportional to the number of passes. However, a large value of N_bin results in a greater shared memory requirement, which can in turn decrease occupation and degrade performance. In the case without atomic operations (cc1.0_8192) the optimal balance is achieved at a relatively low value of 1,024, though performance does not decrease dramatically at larger values. For cc1.2_8192_a, where atomic operations are used, a larger value of 3,072 is optimal. This is the largest value for which the there is enough shared memory to store the histogram. A much larger value of 8,192 is found to be optimal for cc2.0 hardware. This yields a factor of 2.35 improvement in performance compared to the cc1.2 optimized value (3,072) run on cc2.0 hardware.

Values of N_const and N_grid which give optimum performance are given in Tab. 2, but in all cases the performance is relatively insensitive to the choice of these parameters in the range we investigated (see supplementary information). Unlike N_block and N_bin, the amount of shared memory required per block does not depend on the choice of N_const and N_grid, nor does the number of accesses to global memory. As such, it is not surprising that their effect on the performance is small compared to N_block and N_bin.

The analysis presented here underlines the importance of the efficient use of shared memory in achieving good performance on the GPU, and that reoptimization of shared memory usage is a key strategy for porting applications to the new G400 series GPUs.

3.2. Performance benchmarks

The performance of the RDF histogramming code as a function of the number of atoms in sel₁ and sel₂ on a variety of hardware configurations is shown in Fig. 4. When not otherwise noted the optimal parameter sets for the 8,192 bin histogram were used (cc1.2_8192_a on G200 or cc2.0_8192_a on G400). For comparison we also present the performance of the multithreaded CPU implementation of RDF histogramming from VMD. The CPU data was collect on a single Intel X5550 quadcore CPU running at 2.67 GHz. Eight threads were launched to take advantage of the CPU’s hyperthreading feature.

Figure 4.

The performance of the RDF histogramming code as a function of the number of atoms in sel₁ and sel₂. A variety of hardware was tested: Orange, red, purple, and blue lines show the performance of the 4×GTX480, 4×C2050, 6×G200, and 2×Tesla machines, respectively, with optimal tiling parameters. The cyan line shows the performance of the 2×Tesla machine without the benefit of atomic memory operations. For comparison, the gray line indicates the performance of the highly optimized multithreaded implementation of RDF histogramming in VMD, running 8 threads on a single quadcore Intel Xeon X5550 processor at 2.67 GHz with hyperthreading enabled. In the 4×GTX480 case, the performance is a factor of 92 faster than the CPU for large selections.

Five GPU results are presented. The four hardware configurations described above with their optimal parameter set (cc1.2_8192_a in the case of the G200 hardware and cc2.0_8192_a for the G400) are presented, as are results for the 2×Tesla hardware configuration without the benefit of atomic operations (using parameter set cc1.0_8192).

All four GPU configurations are significantly faster than the CPU. Eighty percent of peak performance is achieved on all four configurations for selections of 200,000 or more atoms. Note that many of the plotted system sizes were chosen to not be multiples of N_block or N_const to demonstrate that the this implementation handles the edges of the problem gracefully. The fastest Tesla configuration (6×G200) produces RDFs at a rate of 16.34 billion atom pairs per second (hereafter abbreviated bapps) for the largest test problem (4,741,632 atoms). This is a factor of 39 faster than the fastest performance recorded on the CPU (0.42 bapps). The 2×Tesla configuration runs at 5.91 bapps, a factor of fourteen faster than the fastest CPU performance.

As discussed above, the absence of atomic operations results in the inefficient use of shared memory which in turn leads to relatively poor performance. Still, when the 2×Tesla configuration is run without atomic operations the maximum performance is 1.04 bapps, twofold better performance than the CPU. However, this is a factor of 5.7 slower than the same hardware configuration when atomic operations are used.

At 38.47 bapps, the 4×GTX480 hardware configuration provided the fastest results we observed, with the 4×C2050 hardware just slightly slower at 29.62 bapps. The peak performance result for the GTX480 hardware is 92 times faster than the CPU result and more than double the speed of the 6×G200 configuration.

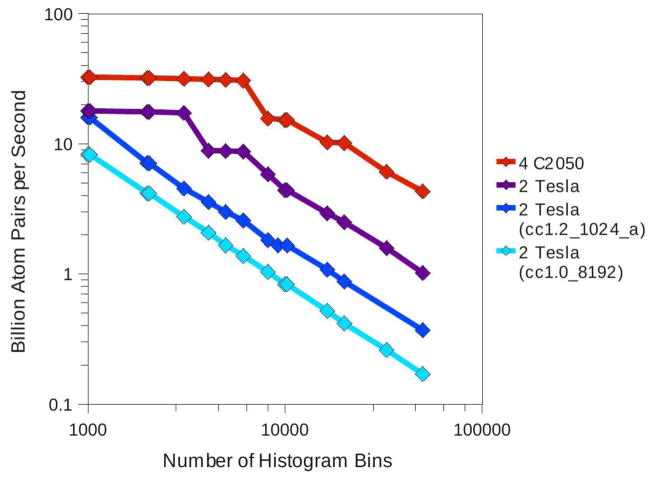
The performance of the various hardware configurations as a function of N_hist (the length of the desired histogram) is shown in Fig. 5. Note that the performance degrades most slowly for the 4×C2050 configuration where the largest amount of shared memory is allocated to histogram storage, and therefore the smallest number of passes over all coordinate data are required. In fact the performance degrades by only a factor of 7.5 over the range 1000–50000 bins compared to 17.6 for the 2×Tesla configuration with the use of atomic memory operations. The performance decreases by a factor of 48.7 over this range in the case where the least shared memory is applied to store histogram data: the 2×Tesla case where no atomic operation are used.

Figure 5.

The performance of the RDF histogramming code as a function of the number of histogram bins requested by the user. Performance of the 4×C2050 and 2×Tesla machines with optimal tiling parameters are shown in red and purple respectively. Performance of the 2×Tesla machine using the cc1.2_1024_a and cc1.0_8192 tiling parameters are shown in blue and cyan respectively. Selections of 1,000,000 atoms were processed in all cases. The performance decreases with increasing histogram length in all cases. The rate of the decrease is inversely proportional to the value of N_bin, with performance of the 4×C2050 machine declining the most slowly.

The cc1.2_1024_a parameter set, which was optimized for smaller histograms, was also tested in this context. As seen in Fig. 5, the performance is comparable to cc1.2_8192_a for the small histograms for which it was optimized. However the performance degrades very quickly with an increasing number of histogram bins. Despite the fact that a 8192-bin histogram is larger than is needed for most applications (histograms with hundreds of bins are typical), there seems to be little benefit to optimizing the tiling parameters for a smaller number of bins. As cc1.2_1024_a produces performance which is effectively equivalent to cc1.2_8192_a in the best case and much worse in other cases, we concluded that the parameter sets optimized for longer histograms are suitable for all histogram lengths.

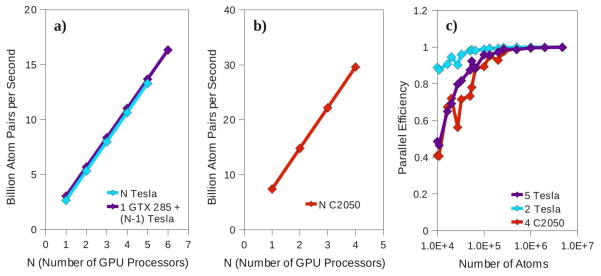
The scaling of performance with respect to the number of GPUs employed is shown in Fig. 6. Fig. 6a shows the scaling on the 6×G200 machine, measured for the full 4,741,632 atom system. Nearly perfect linear scaling with the number of processors is observed when between 1 and 5 Tesla processors are employed.

Figure 6.

a–b) The performance of the RDF histogramming code as a function of the number of GPU processors employed. In all calculations the full 4,741,632 atom test case was run. a) The performance of various combinations of processors on the 6×G200 machine. Homogeneous combinations of Tesla processors are shown in cyan while those configurations containing a single, faster GTX 285 processor are shown in purple. Note that nearly perfect linear scaling is achieved in both cases. The GTX 285 performance is 37 bapps faster than that of a Tesla. Dynamic load balancing allows this performance gain to persist even when the GTX 285 is run in parallel with five Tesla processors. b) The performance on the 4×C2050 system is shown in red. Again, nearly perfect linear scaling is observed. c) The parallel efficiency as a function of the selection size for five Tesla GPUs of the 6×G200 machine (purple), 2×Tesla GPUs of the same machine (cyan), and the 4×C2050 machine (red). Greater than 90 percent efficiency is achieved for selection of 100,000 atoms in the five Tesla case, 16,000 atoms in the 2×Tesla case, and 130,000 in the 4×C2050 case.

To test the dynamic load balancing feature of our code we used a set of heterogeneous GPU configurations incorporating a single GTX 285 GPU with between zero and five Tesla processors. Note that a single GTX 285 outperforms a single Tesla processor by 37 bapps. This increase in performance is maintained as additional Tesla processors are employed in parallel with the GTX 285. In fact, for up to 5 GPUs total, performance is increased by between 37 and 38 bapps when a single Tesla is replaced by the GTX 285.

The parallel scaling on the 4×C2050 machine operating on the full 4,741,632 atom system is shown in Fig. 6b. Again, nearly perfect linear scaling is observed.

The parallel efficiency as a function of system size can be seen in Fig. 6c. Three cases are shown: running on all five Tesla GPUs of the 6×G200 machine, running on only two Tesla GPUs of the same machine, and running on the entire 4×C2050 machine. When only two Teslas are employed, greater than 90 percent parallel efficiency is achieved down to the 16,000 atom system. In the 5×Tesla and 4×C2050 cases peak performance is approached more slowly, with 90 percent parallel efficiency surpassed at approximately 100,000 and 130,000 atoms, respectively.

4. Conclusions

The large quantity of molecular dynamics data which can be produced on today’s supercomputers demands that data analysis be performed using optimized software on high-performance machines as well. In this paper we have presented an implementation of radial distribution function histogramming for multiple NVIDIA GPUs. The high performance of this code compared to existing CPU implementations will accelerate the discovery process by allowing scientists to perform previously cumbersome data analysis tasks in seconds.

This implementation runs on multiple GPUs via a threading scheme with dynamic load balancing. Near perfect parallel efficiency is observed for both homogeneous and heterogeneous multi-GPU configurations.

Two different histogramming schemes were employed in our implementations: one that takes advantage of atomic memory operations, which are available only on NVIDIA GPUs of compute capability 1.2 or higher, and one which is compatible with all CUDA-capable GPUs. The scheme based on atomic operations allows a more efficient distribution of shared memory than does the more general scheme, leading to a factor of 5.7 speedup.

A tiling scheme is employed to maximize the reuse of data in the fast shared memory of the GPU. The parameters of this tiling scheme are optimized empirically for both NVIDIA G200 (Tesla) and G400 (Fermi) GPUs. The threefold larger shared memory space of the G400 generation of GPUs allows for a significant performance increase when compared with G200. When running on four GTX480 GPUs in parallel we are able to achieve performance a factor of 92 better than can be achieved by a highly optimized multithreaded implementation running on four cores of an Intel X5550 CPU. The comparison of the performance of G400 to G200 and the analysis of the relationship between the tiling parameters and performance suggest that the hardware parameter limiting the performance of this histogramming algorithm is the size of the shared memory space.