Divergent Shear Thinning and Shear Thickening Behavior of Supramolecular Polymer Networks in Semidilute Entangled Polymer Solutions

Abstract

The steady shear behavior of metallo-supramolecular polymer networks formed by bis-Pd(II) cross-linkers and semidilute entangled solutions of poly(4-vinylpyridine) (PVP) in dimethyl sulfoxide (DMSO) or N,N-dimethyl formamide (DMF) is reported. The steady shear behavior of the networks depends on the dissociation rate and association rate of the cross-linkers, the concentration of cross-linkers, and the concentration of the polymer solution. The divergent steady shear behavior—shear thinning versus shear thickening—of samples with identical structure but different cross-linker dynamics (J. Phys. Chem. Lett. 2010, 1, 1683-1686) is further explored in this paper. The divergent steady shear behavior for networks with different cross-linkers is connected to a competition between different time scales: the average time that a cross-linker remains open (τ₁) and the local relaxation time of a segment of polymer chain (τ_segment). When τ₁ is larger than τ_segment, shear thickening is observed. When τ₁ is smaller than τ_segment, only shear thinning is observed.

Introduction

The rich rheological behavior of associative polymers fuels their use in a wide range of applications, including rheology modifiers for paintings, cosmetics, pharmaceutics and coatings.^1,2 Their non-Newtonian rheological behavior, e.g., shear thickening and/or shear thinning, is often at the foundation of their utility, and extensive experimental and theoretical effort has been devoted to understanding the molecular origin of shear thickening or shear thinning.^3–7

The majority of these investigations have been performed in the semidilute unentangled regime.^8–11 While a comprehensive molecular picture remains elusive, the theories associated with shear thickening and shear thinning in this concentration regime are typically united in that they are interpreted through the time scale of a single dynamic process — the dissociation of the transient, associative cross-linkers.^3–14 The situation is more complicated as the concentration of the associative polymer solution increases into the semidilute entangled regime.^15,16 For example, English et al. reported an associative polymer solution for which shear thickening at intermediate shear rate was observed below the overlap concentration, while shear thinning was observed above the overlap concentration.¹⁵ They concluded that in the semidilute entangled regime, both topological entanglements of the polymers and the kinetics of cross-linking contributed to the rheological properties. In their work,¹⁵ however, the reversible associations were driven by hydrophobic association, and the structure and distribution of the hydrophobic aggregates could, in principle, vary with concentration, creating some ambiguity as to the contributions of non-dissociative dynamics in the entangled solutions.

Our group has previously demonstrated a useful method for probing the contributions of molecular reversibility to the rheological properties of polymers.^17–20 The method takes advantage of steric effects at the N-alkyl positions of N,C,N-pincer Pd(II) and Pt(II) complexes, through which the dissociation rate of the cross-linkers can be changed by orders of magnitude independently of the association constant.¹⁷ This methodology allows us to differentiate the influence of cross-linker kinetics from that of other dynamic processes (e.g., disentanglement of polymer chains) or structural contributions (e.g., changes in entanglement structure and/or spacing) on the rheological behavior of the supramolecular polymer networks.

We recently reported the nonlinear rheological properties of metallo-supramolecular networks formed by the reversible cross-linking of semidilute unentangled solutions of poly(4-vinylpyridine) (PVP).²⁰ In these unentangled networks, shear thickening at intermediate shear rate is observed above a critical shear rate under steady shear, and that critical shear rate is experimentally correlated with the dissociation rate of the cross-linkers. Because the relaxation time of the samples increases with the applied shear stress during shear thickening, the primary mechanism of shear thickening was ascribed to the shear-induced transformation of intrachain cross-linking to interchain cross-linking, rather than nonlinear high tension along polymer chains that are stretched beyond the Gaussian range.²⁰

When the concentration of PVP increases to the semidilute entangled regime, however, the picture is more complex. For two networks with identical cross-linker density, shear thinning is observed for the network formed with the faster cross-linkers (dissociation rate k_d ~ 1450 s⁻¹), while shear thickening at intermediate shear rate is observed for the network formed with the relatively slower cross-linkers (k_d ~ 17 s⁻¹).²¹ To the best of our knowledge, this behavior deviates not only quantitatively, but qualitatively, from all reported models for nonlinear rheology of associative polymer networks. Here we investigate the steady shear behavior of these semidilute entangled polymer networks in greater detail, mapping out a “structure-property phase space” for the steady shear behavior and exploring the relationships between the rate of cross-link dissociation and association, and the dynamics of polymer chain in the entangled polymer networks. The additional structure-activity relationships further support a mechanism, not previously uncovered, for nonlinear steady shear behavior that involves competition between dissociation/re-association of the cross-linkers and dynamics of polymer chain segments in semidilute entangled PVP solutions.

Experimental Section

Materials

The bis-Pd(II) cross-linkers [2,3,5,6-tetrakis{(dimethylamino)methy}phenylene-1,4-bis(palladiumtrifluoromethane-sulfonate)] (1a) and [2,3,5,6-tetrakis{(diethylamino)methy}phenylene-1,4-bis(palladiumtrifluoromethane-sulfonate)] (1b) were synthesized as reported elsewhere.²² The binding thermodynamics and exchange kinetics of the metal–pyridine interactions have been characterized previously.¹⁸ The equilibrium association constants (K_eq) and dissociation rate constants (k_d) for 1a•pyridine in DMSO at 25 °C are 29 M⁻¹ and 1450 s⁻¹, respectively. K_eq and k_d for 1b•pyridine in DMSO at 25 °C are 33 M⁻¹ and 17 s⁻¹, respectively.¹⁸ Dimethyl sulfoxide (DMSO), N, N-dimethyl formamide (DMF), and poly(4-vinylpyridine) (PVP) with M_w of ~ 60,000 as reported from producer, were used as received from Aldrich. The M_n and M_w of above PVP from Aldrich have been reported to be 22,000 and 64,300 (M_w/M_n is 2.92), respectively, in the literature.²³ Rough estimates of the Kuhn length and related parameters are provided in pages S27 – S30 of the Supporting Information.

Sample Preparation

Samples were prepared by mixing PVP solutions with cross-linker solutions. Two different solvents, DMSO and DMF, were used. Details of sample preparation can be found in a previous paper.²⁰ The concentration of cross-linkers in the samples varied from 1% to 5% (ratio of Pd atoms to N atoms in the pyridine units of the PVP), all of which are above the critical concentration to form a gel (shown previously to be approximately 0.8 % for ~ 0.10 g/mL PVP/DMSO solutions).²⁴ The concentration of PVP in the samples varies from ~0.08 (semidilute unentangled regime) to ~0.27 g/mL (semidilute entangled regime). Details regarding the concentration regimes of the PVP/DMSO solutions and PVP/DMF solutions are provided in the supporting material. The critical concentration of entanglement of PVP/DMSO solution is ~ 0.155 g/mL at 25 °C, while it is ~ 0.148 g/mL at 50 °C. The critical concentration of entanglement of PVP/DMF solution is ~ 0.147 g/mL at 25 °C while it is ~ 0.145 g/mL at 0 °C (Figure S1 and S2 in supporting material). The average number of entanglements per polymer chain varies from 1 to 3 in ~ 0.16 g/mL to ~ 0.27 g/mL PVP solution (see Table S1 in supporting material). Concentrations are often denoted with a “~” to reflect the slight variation between samples made with cross-linker 1a vs. 1b; see Supporting Information for details.

Rheological Measurements

Rheological data were obtained by using an AR G2 rheometer (TA Instruments) with cone-plate geometry (diameter of 20 mm, cone angle of 2°, truncation height of 49 μm) and concentric cylinder geometry (the concentric cylinder geometry was used only to characterize the concentration regimes of pure PVP/DMSO and PVP/DMF solutions without cross-linkers). A solvent trap was used with the cone-plate geometry to minimize the evaporation of solvent from the samples. Strain sweep experiments were performed at a frequency of 10 rad/s (unless otherwise noted) to determine the region of linear response. Oscillatory frequency sweeps from 0.1 to 500 rad/s were carried out with appropriate strain within the linear region. Steady shear measurements were performed over a range of shear rates between 10⁻³ and 10³ s⁻¹, although higher shear rates were occasionally employed for samples with low viscosity. Parallel superposition of oscillation onto steady-shear flow was carried out at various applied stresses to explore the mechanism of the local shear thinning and/or shear thickening in semidilute entangled solutions. A detailed introduction to the parallel superposition of oscillation onto steady-shear flow technique can be found in an earlier report by Tam et al.²⁵ Experiments were carried out at 25 °C unless otherwise noted.

Results

Linear Oscillatory Frequency Sweep in the Semidilute Entangled Regime

Before examining the nonlinear rheological properties of the networks, we begin by presenting the rheological properties of the network in the linear regime. In Figure 1, the linear oscillatory frequency sweep of ~ 0.27 g/mL PVP/DMSO with 2% 1 is shown as an example. Although both topological entanglements between polymer chain and dissociation of cross-linkers are expected to contribute to the network relaxation, the dynamic mechanical moduli can still be superposed by the scaled frequency (oscillatory frequency divided by cross-linker dissociation rate, ω/k_d). This behavior, shown in Figure 1, is consistent with our earlier observations ²⁰ and Leibler et al.’s theory regarding the dynamics of reversible networks.²⁶

Figure 1.

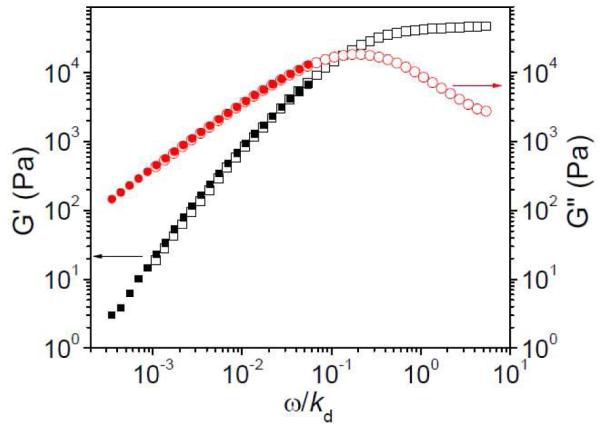
Storage (G’) and loss (G”) moduli versus scaled frequency (ω/k_d) for ~0.27 g/mL PVP/DMSO solution with 2% 1a or 2% 1b. Filled symbols represent cross-linker 1a and unfilled symbols represent cross-linker 1b. T = 25 °C. The unit for frequency (ω) here is Hz. For 1a, k_d = 1450 s⁻¹, and for 1b, k_d = 17 s⁻¹.

Steady Shear Results

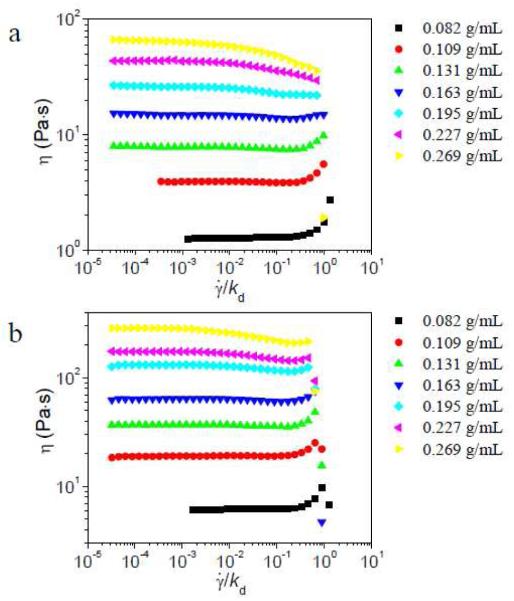
We begin by considering networks in which the concentration of cross-linker (relative to pyridine) is held constant at 2 %, but the concentration of PVP in the network is varied. The steady shear results for these networks are shown in Figure 2. At lower concentrations of the network in the semidilute unentangled regime ([PVP] < ~ 0.155 g/mL), as previously reported²⁰ and shown again here for comparison, shear thickening at intermediate shear rate is observed for both 1a•PVP and 1b•PVP. At ~ 0.16 g/mL PVP concentration (just above the critical concentration for entanglement, 0.155 g/mL),¹⁹ modest shear thickening at intermediate shear rate is still observed for samples with either 1a or 1b. With the further increase of PVP concentration, however, both the absolute behavior of the 1a•PVP networks, as well as the relative steady shear behavior of 1a•PVP vs. 1b•PVP, change. Once the PVP concentration is decidedly in the semidilute entangled regime (~ 0.23 g/mL and ~ 0.27 g/mL), samples with 2% 1a show shear thinning, while samples with 1b show shear thickening at intermediate shear rate.

Figure 2.

Steady shear viscosity (η) versus scaled shear rate ($\stackrel{.}{\gamma }∕k_{\mathrm{d}}$) for different concentrations of PVP/DMSO solution with 2% of 1a (a) or 2% 1b (b) at 25 °C.²¹ k_d of 1a is 1450 s⁻¹, and k_d of 1b is 17 s⁻¹ here. Reproduced from J. Phys. Chem. Lett. 2010, 1, 1683-1686, with permission (Copyright © 2010 American Chemical Society).

The steady shear behavior of ~ 0.27 g/mL PVP/DMSO with 2% 1 is shown in greater detail in Figure 3. The steady shear viscosity of 1b•PVP exhibits four flow regimes with increasing shear rate, which are, respectively, Newtonian (Regime A), local shear thinning (Regime B, comprising points with a negative slope in viscosity with respect to shear rate), local shear thickening (Regime C, positive slope in viscosity with respect to shear rate) and dramatic shear thinning (Regime D). A curve for steady shear results of 1a•PVP network is also divided into the four flow regimes according to the same value of scaled shear rate ($\stackrel{.}{\gamma }∕k_{\mathrm{d}}$) with 1b•PVP network.²⁰ The dramatic shear thinning in Regime D is attributed to network fracture and/or the subsequent ejection of sample from the rheometer geometry,²⁰ and it is not explored further here. In Regimes A and B, the viscosities of the two samples are in inverse proportion to the relative dissociation rates of the 1a and 1b cross-linkers.^18,20 This is consistent with the expectation that the two samples have similar network structure in these two flow regimes, even though Regime B is non-Newtonian. At the start of Regime C, the Weissenberg number (the product of the shear rate and relaxation time of the network) is estimated to be 0.81 (1.93 s⁻¹ × 0.42 s, sample with 2% 1b) from the data in Figure 1. As discussed previously in our examination of rheological behavior in the semidilute unentangled regime,²⁰ this corresponds to the onset of polymer chain orientation. In the entangled solutions, it also corresponds to the onset of divergent behavior between the two networks; shear thinning is observed in this flow regime for 1a•PVP, while shear thickening is observed in this flow regime for 1b•PVP. For simplicity, we will use “shear thinning” and “shear thickening” to describe the divergent behavior of the two networks in Regime C, the characteristics of which are the emphasis of this paper.

Figure 3.

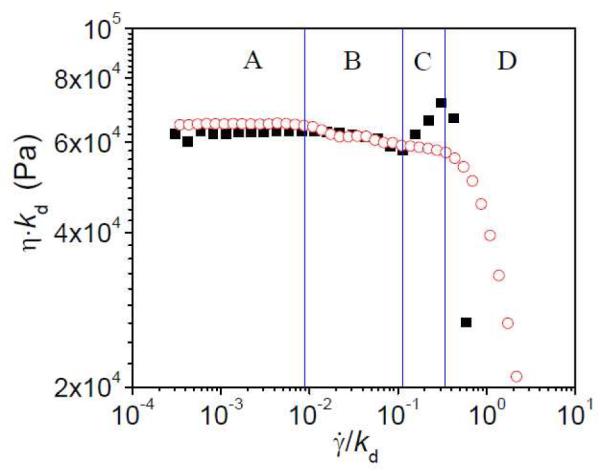
Scaled steady shear viscosity (η·k_d) versus scaled shear rate ($\stackrel{.}{\gamma }∕k_{\mathrm{d}}$) for ~0.27 g/mL PVP/DMSO solutions with 2% 1a or 2% 1b at 25 °C. Open circles represent networks formed with cross-linker 1a, and filled squares represent networks formed with cross-linker 1b. For 1a, k_d = 1450 s⁻¹, and for 1b, k_d = 17 s⁻¹.

The measurements shown for 2 % cross-linker concentration are repeated for samples with 1%, 3%, 4% and 5% of 1 at different PVP/DMSO concentrations (Figures S3–S6 in supporting material). The remaining observed steady shear behaviors could be qualitatively classified into one of four categories shown schematically in Scheme 1, depending on the relative contributions from rate-dependent shear thinning and shear thickening. As shown in Scheme 1, type I behavior denotes a sample that transitions from Newtonian to shear-thickening behavior above a critical shear rate. Type II behavior also exhibits net shear thickening (maximum viscosity is larger than the zero shear viscosity), but there is a period of local shear thinning between the Newtonian and local shear thickening regimes. Type III behavior is similar to type II, but magnitude of the local shear thickening is not sufficient to overcome that of the local shear thinning, and so there is no net shear thickening at any shear rate. Finally, type IV behavior goes from Newtonian to shear thinning only, with no discernable region of local shear thickening.

Scheme 1.

Schematic curves of viscosity versus shear rate corresponding to four different classifications of steady shear behavior. Note that these classifications are qualitative only.

A notable feature of the classifications in Scheme 1 is that the phenomenologically opposite behaviors of pure shear thickening and shear thinning (types I and IV) might reasonably be viewed as simply two extremes from the same continuum of behavior. Although the classification scheme itself is, a priori, arbitrary, the experimental results discussed below lend some credence to its validity (or, at least, its utility). The steady shear classification type is shown as a function of both the cross-linker concentration and the concentration of the PVP/DMSO solution in Figure 4. In Figure 4, four different steady shear behaviors (Type I–IV in Scheme 1) are observed for samples with 1a while only three types of steady shear behaviors (Type I–III in Scheme 1) are observed for samples with 1b in the experimental range. The steady shear behavior of the samples varies smoothly (Type I borders type II, etc.), with the change of concentration of cross-linkers and concentration of PVP/DMSO solution, supporting the validity of the classification in Scheme 1. In Figure 4, the types of steady shear behavior for samples with 1a or 1b are the same below or just above the critical concentration of entanglement (~ 0.155 g/mL) whereas apparent differences are observed in Figure 4a and Figure 4b with the further increase of PVP concentration. Both the concentration of cross-linkers and concentration of PVP/DMSO solution are expected to affect the fraction of interchain cross-linkers (elastically active chains),²⁰ and we next explore the relationship between the steady shear behavior shown in Figure 4 and the fraction of elastically active chains.

Figure 4.

Steady shear behavior type (see Scheme 1) as a function of the concentration of cross-linkers and the concentration of PVP in DMSO. (a) Samples with cross-linker 1a; (b) Samples with cross-linker 1b. T = 25 °C. Dashed line across the chart indicates the critical concentration of entanglement (~ 0.155 g/mL).

Influence of Fraction of Elastically Active Chains on Steady Shear Behavior

According to the affine network model or the phantom network model used in the unentangled polymer network and Edward’s tube or related models used to describe the entangled polymer networks, the plateau modulus depends on the number density of elastically active chains (or number of entanglements).²⁷ For simplicity, the affine network model was used previously to calculate the apparent number density of elastically active chains (ν) in semidilute unentangled solutions,²⁰ and we make use of it again here. From the frequency sweep data for samples with cross-linker 1b (Figures S7–S11 in supporting material), the plateau moduli (G₀) are obtained, and the apparent number density of elastically active chains (ν) are then calculated by the following equation ²⁷

$$\nu =G_0∕k_{\mathrm{B}}T$$ (1)

where k_B is Boltzmann’s constant, and T is the temperature. In the entangled regime, elastically active chains can result from either cross-linking or topological entanglement, and so ν is the sum of the number of interchain bound cross-linkers and entanglement knots between polymer chains. The maximum theoretical number of cross-linkers per unit volume (ν₀) in the samples is simply calculated from the concentration of cross-linkers 1a or 1b. We refer to the ratio of apparent to theoretical active chains, ν/ν₀, as the fraction of elastically active chains. It is apparent that the value of ν/ν₀ for some samples can be larger than 1 when topological entanglements between polymer chains contribute to the elastic modulus. ²⁸

Because the accessible range of frequencies is limited, it is impossible to get the G₀ of samples with cross-linkers 1a directly, but we assume it is the same as for networks formed by 1b. This assumption is consistent with the similar association constant of the complexes, our previous reports on similar systems,¹⁸ and the scaling behavior observed in Figure 1. As shown in Figure 1, only the frequency (ω) is scaled by k_d of 1a or 1b to give the collapsed master curves. The storage (G’) and loss (G”) moduli of samples with 1a or 1b are not scaled, but are the same for a given value of scaled frequency (ω/k_d).

In Figure 5, the fraction of elastically active chains (ν/ν₀) is shown as a function of PVP concentration for samples with different concentrations of 1b. As expected, ν/ν₀ increases with PVP/DMSO concentration, reflecting the higher probability of forming interchain bound cross-linkers at higher PVP concentration,¹¹ and/or topological entanglements between polymer chains contribute to the elastic modulus of samples in the semidilute entangled regime.²⁸ Interestingly, not only the absolute number of active cross-linkers, but ν/ν₀ also increases with concentration of cross-linkers, a point not discussed further in this paper. A comparison of Figure 5 with Figure 4b shows that the three different steady shear behaviors of samples with 1b can be related to the value of ν/ν₀, largely independently of the PVP/DMSO concentration or concentration of cross-linkers. When ν/ν₀ is smaller than ~ 0.6, only Type I (Scheme 1) steady shear behavior is observed. For samples with a value of ν/ν₀ between ~0.6 and ~1, Type II (Scheme 1) steady shear behavior is observed. When ν/ν₀ is larger than ~1, Type III (Scheme 1) steady shear behavior is observed. Two dashed lines in Figure 5 separate these three regions of steady shear behavior. These results imply that the fraction of elastically active chains, are a primary determinant of the steady shear behavior of 1b•PVP networks.¹¹

Figure 5.

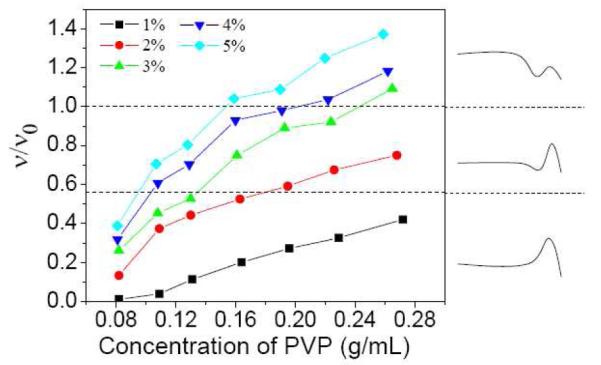
Fraction of elastically active chains (ν/ν₀) versus PVP concentration in DMSO for samples with different concentration of 1b. Dashed lines are used to connect the ν/ν₀ with the steady shear behavior in Figure 4b. Types of steady shear behavior (see Scheme 1) are shown to the right of the graph for convenience. T = 25 °C.

The situation, however, is more complicated for networks formed from 1a (Figure 6). Up to just around the critical entanglement concentration (~ 0.16 g/mL), the type of steady shear behavior of 1a•PVP network can be related to the value of ν/ν₀, in the same way as 1b•PVP network. For samples in which the concentration of PVP/DMSO solution is above ~0.19 g/mL, however, the steady shear behavior of the 1a•PVP network does not depend on ν/ν₀. Rather, it is correlated instead with the concentration of the PVP solution. When the PVP concentration is ~0.19 g/mL, samples show Type III (Scheme 1) steady shear behavior. When the PVP concentration is ~ 0.23 g/mL or 0.27 g/mL, the networks show Type IV (Scheme 1) steady shear behavior. The fact that the steady shear behavior of samples in the semidilute entanglement regime depends on the concentration of PVP suggests that physical entanglement of polymer chains have an important influence on the steady shear behavior of 1a•PVP networks.

Figure 6.

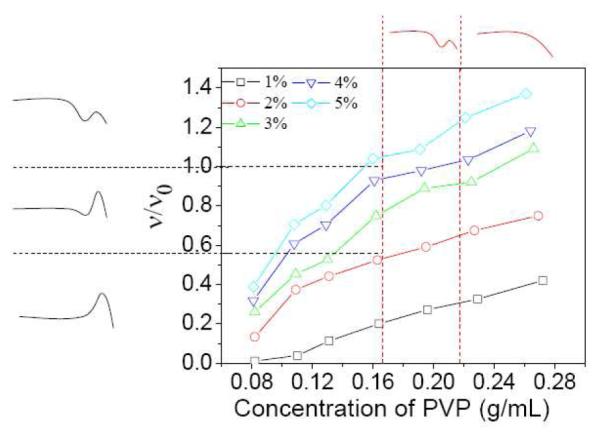
Fraction of elastically active chains (ν/ν₀) versus PVP concentration in DMSO for samples with different concentration of 1a. Black dashed lines are used to connect the ν/ν₀ with the steady shear behavior in Figure 4a. Red dashed lines are used to connect the PVP concentration with the steady shear behavior in Figure 4a. Types of steady shear behavior (see Scheme 1) are shown on the perimeter of the graph for convenience. T = 25 °C.

Changing the Dissociation Rate of Cross-linkers by Changing Temperature

Fine-tuning of the dissociation rate is accomplished by changing the temperature. As we reported before, the k_d of 1a and 1b in DMSO at 50 °C is ~ 5400 s⁻¹ and ~ 90 s⁻¹, respectively.²⁰ As the activation energies (E_a) for cross-link dissociation are 42 kJ/mol and 53 kJ/mol for 1a and 1b, respectively,²⁰ the k_d of 1a and 1b at 0 °C is calculated to be ~ 300 s⁻¹ and ~ 2.4 s⁻¹, respectively, using following equation ²⁹

$$\ln \frac{k_2}{k_1}=\frac{E_a}{R}\left(\frac{T_2-T_1}{T_1{T}_2}\right)$$ (2)

in which R is the gas constant, and k₁ and k₂ are the dissociation rates at temperatures T₁ and T₂, respectively. Because DMSO freezes at 18 °C, the experiments at 0 °C were performed in DMF. This substitution is reasonable. The dynamic mechanical moduli and relaxation times of the networks in DMSO and DMF are nearly identical (Figure S14 in supporting materials). In addition, the same divergent steady shear behavior (shear thickening at intermediate shear rate in semidilute entangled 1b•PVP network vs. shear thinning in semidilute entangled 1a•PVP network) is observed in DMF, and the nonlinear response starts at almost the same shear rate as in DMSO (Figure S15 in supporting materials). We therefore conclude that both the structure of 1•PVP network and k_d of 1 are effectively the same in DMSO and DMF.

At the same time, frequency sweep results for samples with 1b in ~ 0.27 g/mL PVP solution at different temperature (Figure S16 in supporting materials) show that the storage (G’) and loss (G”) moduli of samples are the same for a given value of frequency scaled by the temperature-dependent dissociation rate (ω/k_d). We therefore infer that the topological structure (number of active cross-linkers) of the samples is similar for temperatures from 0 °C to 50 °C.²⁰

The steady shear behavior of samples with 2% 1 at 50 °C is shown in Figure 7. When the concentration of PVP/DMSO range from ~ 0.16 to ~ 0.27 g/mL, samples with 2% 1a all show shear thinning while samples with 2% 1b all show shear thickening at intermediate shear rate. These data are qualitatively similar to those found at 25 °C. Also as observed at 25 °C, samples with 1a and 1b in the semidilute unentangled regime both show shear thickening at 50 °C.

Figure 7.

Steady shear viscosity (η) versus scaled shear rate ($\stackrel{.}{\gamma }∕k_{\mathrm{d}}$) for different concentrations of PVP/DMSO solution with 2% of 1a (a) or 2% 1b (b) at 50 °C. Scaling is based on k_d = 5400 s⁻¹ for 1a and 90 s⁻¹ for 1b.

The steady shear behavior of samples with 2% 1a in different concentrations of PVP/DMF solution at 25 °C and 0 °C is shown in Figure 8. The 1b•PVP network in PVP/DMF solution shows similar shear thickening at 0 °C that is similar to that observed at 25 °C (Figure S17, supporting materials). In Figure 8, at 25 °C, the steady shear behavior of samples with 2% 1a in different concentrations of PVP/DMF solution (Figure 8a) is similar to samples with 2% 1a in PVP/DMSO solution (Figure 2a). But at 0 °C, the behavior changes. Samples with 2% 1a at all concentrations of PVP show shear thickening at intermediate shear rate; the behavior is similar to that of 1b•PVP network in PVP/DMSO solution (Figure 4b). The 1a•PVP network at 0 °C is not, however, identical to the 1b•PVP network at 25 °C; as the concentration of 1a is increased above 2% in ~ 0.27 g/mL PVP/DMF solution at 0 °C, shear thickening at intermediate shear rate is no longer observed, as shown in Figure 9. This is contrary to the results of 1b•PVP network in PVP/DMSO solution in Figure 4b, where shear thickening at intermediate shear rate is observed for samples with 1% to 5% of 1b. The reasons for this difference in behavior are discussed below.

Figure 8.

Steady shear viscosity (η) versus scaled shear rate ($\stackrel{.}{\gamma }∕k_{\mathrm{d}}$) for different concentration of PVP/DMF solution with 2% of 1a at different temperatures. (a) 25 °C; (b) 0 °C. Scaling is based on k_d = 1450 s⁻¹ for 1a at 25 °C and 300 s⁻¹ for 1a at 0 °C.

Figure 9.

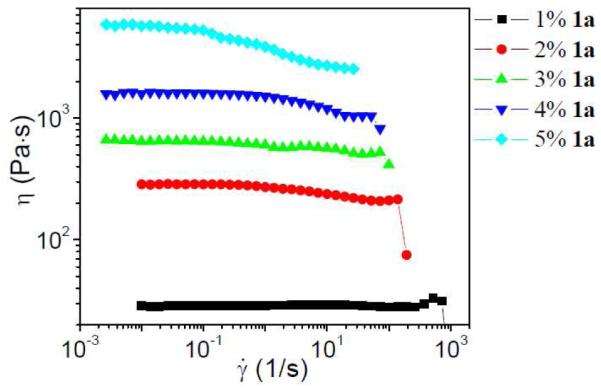
Steady shear viscosity (η) versus shear rate ($\stackrel{.}{\gamma }$) for −0.27 g/mL PVP/DMF solution with different concentrations of 1a at 0 °C.

Discussion

Mechanism Underlying Local Shear Thinning

The influence of shear stress on the local shear thinning (e.g., Regime B in Figure 3) is gained from studies involving parallel superposition of oscillation onto steady-shear flow.²⁵ This technique allows us to investigate how applied shear stress (before the fracture of the network) affects the relaxation behavior of the network. This method has proven to be very useful previously in describing the balance between the disentanglement of polymer chains and the association of hydrophobic groups under steady shear.¹⁵

The effects of the superposition of a steady deformation on dynamic mechanical moduli are shown in Figure 10 for ~ 0.27 g/mL PVP/DMSO solution with 2 % 1a or 2% 1b. In Figure 10, the applied shear stress (~ 8000 Pa) is at the end point of Regime B in Figure 3. The superposed shear has an apparent influence on the slope of the storage moduli (G’) at low frequency; the slope of storage moduli increases from G’ ~ ω^1.6 in the absence of shear stress to G’ ~ ω² at 8000 Pa of applied shear stress. Change in the slope of the loss modulus at low frequency is not so apparent; G” ~ ω¹ both with and without applied shear stress. Similar parallel superposition of oscillation onto steady-shear flow was also performed for a sample with 5% 1a in ~ 0.11 g/mL PVP solution (i.e., in the semidilute unentangled regime), and a similar increase of the scaling law of G’ versus frequency at low frequency is also observed in the local shear thinning regime (Figure S18, supporting materials). This phenomenon has been referred to as a “truncation” of the relaxation spectrum, i.e., longer time modes of relaxation are lost as a consequence of the superposed shear. ¹⁵

Figure 10.

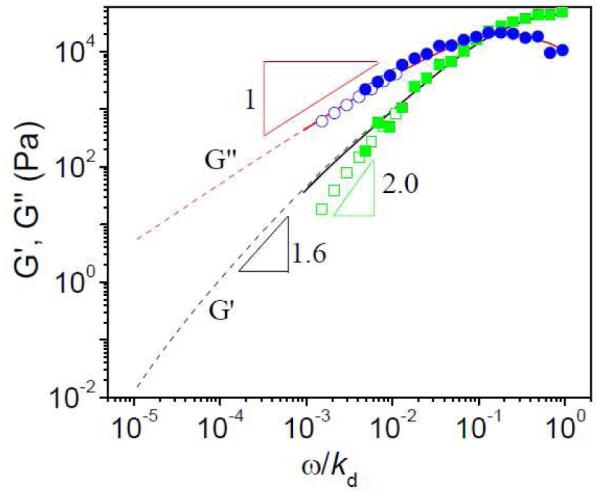
Storage (G’) and loss (G”) moduli versus scaled frequency (ω/k_d) for ~0.27 g/mL PVP/DMSO solution with 2% of 1a or 2% 1b under parallel superposition of oscillation onto steady-shear flow. Dashed lines and straight lines represent samples with cross-linker 1a and 1b respectively without superposed shear stress; Open symbol and filled symbols represent samples with cross-linker 1a and 1b respectively under superposed shear stress (~8000 Pa). T=25 °C. The unit for frequency (ω) here is Hz. Scaling is based on k_d = 1450 s⁻¹ for 1a and 17 s⁻¹ for 1b.

As noted previously, the relaxation modes in these samples are more complex than the single apparent relaxation time obtained by the crossover of G’ and G”.²⁰ The distance between cross-linkers in the samples is not uniform, and there are different relaxation modes in the samples. A possible physical picture for the local shear thinning is depicted below. On the microscopic scale, the number of cross-linkers on each polymer chain is not the same; polymer chains with more cross-linkers have longer relaxation time. Under shear, the polymer chains with more cross-linkers deform first and induce the partial breakage of the original network structure, and some of the cross-linkers are transferred to other chains with shorter relaxation time. The final distribution of cross-linkers on each polymer chain is more homogenous, and the relaxation mode of the samples is close to a single-element Maxwell model (G’ ~ ω² and G” ~ ω¹).¹⁸

Mechanisms Underlying Shear Thickening in the Semidilute Entangled Regime

How shear stress influences the structure of the network during Regime C in Figure 3 was also explored by the parallel superposition of oscillation onto steady-shear flow.²⁵ Our data are shown in Figure 11. The applied shear stress of ~8,000 Pa corresponds to the starting point of Regime C (Figure 3), while the applied shear stress of ~16,000 Pa lies in the shear thickening region prior to the shear thickening maximum point (~22,000 Pa) of samples with 2% 1b. The divergent shear thinning/thickening behavior of the 1a•PVP vs. 1b•PVP networks is reflected in the parallel superposition experiments: as the shear stress increases from 8000 Pa to 16000 Pa, G’ and G” of samples with 2% 1b both increase, while G’ and G” of samples with 2% 1a decrease or stay roughly constant, respectively.

Figure 11.

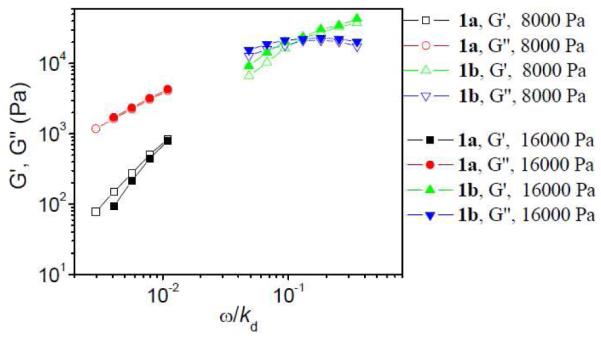
Storage (G’) and loss (G”) moduli versus scaled frequency (ω/k_d) for ~0.27 g/mL PVP/DMSO solution with 2% of 1a or 2% 1b under superposed shear stress (8000 Pa and 16000 Pa). T=25 °C. The unit for frequency (ω) here is Hz. k_d of 1a is 1450 s⁻¹, and k_d of 1b is 17 s⁻¹ here.

In Figure 11, the relaxation time (τ) of samples with 2% 1b increases slightly from ~ 0.52 s to ~ 0.55 s with increasing of shear stress from 8,000 Pa to 16,000 Pa. This is connected with the small degree of shear thickening (maximum viscosity vs. zero-shear viscosity), as shown in Figure 2b.²⁰ Samples with 1% 1b, however, have a larger degree of shear thickening at intermediate shear rate (Figure S3b in supporting material) than the samples with 2% 1b. In Figure 12, τ of samples with 1% 1b in semidilute entangled PVP/DMSO solution versus applied shear stress imposed during oscillation measurements are shown. To be sure that the network is not broken during the experiments, the maximum applied shear stress used is less than the critical shear stress at the shear thickening maximum point. Comparison with the steady shear data (Figure S3b in supporting material) shows that τ increases in the shear thickening regime. Similar behavior has been observed for samples in the semidilute unentangled regime,²⁰ and the results in Figure 12 support that shear thickening in the semidilute entangled PVP/DMSO solution has the same mechanism as in the semidilute unentangled regime: the shear induced conversion of intrachain cross-linkers to interchain cross-linkers.²⁰

Figure 12.

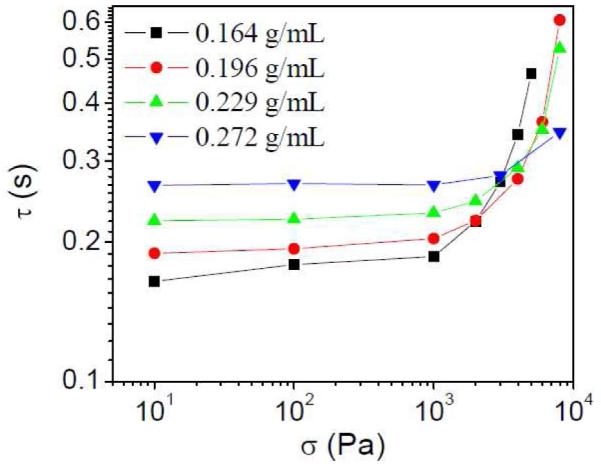
Plot of relaxation time (τ) of samples with 1% 1b in different concentration of PVP/DMSO solution versus applied shear stress (σ) imposed during parallel superposition of oscillation onto steady-shear flow. T=25 °C.

Possible Mechanisms Underlying Divergent Shear Thinning versus Shear Thickening Behavior

In considering the origins of the divergent shear thinning vs. shear thickening in Regime C in Figure 3, we first rule out contributions from two mechanisms that have been invoked to explain shear thinning and/or shear thickening in related systems. The first is the influence of shear stress on the dissociation of the coordinative cross-links. In Regalado et al’s work,¹⁶ shear thinning in the semidilute entangled regime is tentatively attributed to the change of lifetime in active cross-linkers that are coupled to the shear flow. In other words, shear thinning may be caused by an increase in the dissociation rate under applied stress.³⁰ Such effects are possible contributors to the observed shear thinning here. Force-accelerated dissociation of similar Pd(II)-pyridine complexes has been observed by single-molecular force spectroscopy,^{31, 32} and (presumably much larger) shear forces during sonication have been used to activate latent mechanocatalysts.³³ The force induced increase in dissociation, however, is expected to be very similar for cross-linkers 1a and 1b because of the similarity in the mechanisms of pyridine displacement.³¹ The influence of stress on dissociation rate, therefore, cannot explain the divergent steady shear behavior for samples with 1a and 1b in semidilute entangled PVP solutions, which occur under similar applied shear stress.

Second, Tripathi et al. reported that for C₁₆H₃₃ end-capped urethane-coupled poly(oxyethylene) with molecular weights (M_w) of 65.3 kDa, shear thickening is observed at a concentration of 20 kg/m³ while only shear thinning is observed at a concentration of 40 kg/m³.¹¹ The authors reasoned that at high concentrations the distance between neighboring micelles is small, and so there exist large numbers of active bridging chains. The flow induced generation of active bridging chains, responsible for shear thickening at low concentrations, is therefore minimal, and only shear thinning is observed in concentrated samples.¹¹ Although the shear thickening observed in 1b•PVP is attributed to the formation of new active cross-linkers, however, the fraction of elastically active chains for samples with identical concentration of 1a and 1b in the fixed PVP concentration is the same (Figure 5 and Figure 6). The absence of shear thickening in 1a•PVP, therefore, is not due to a difference in its nascent structure, but instead to a difference in its dynamics.²¹

Coupling of Cross-linker Kinetics and Polymer Chain Dynamics

The divergent steady shear behavior is only observed in the semidilute entangled regime, suggesting the influence of chain entanglement, so the nonlinear steady shear behavior in the semidilute entangled regime implies that the contribution from different time scales is that between the kinetics of cross-linkers and the dynamics of polymer chains in the semidilute entangled solution.

We discuss the kinetics of cross-linker dissociation and reassociation and the dynamics of polymer chain segments in terms of their respective time scales. The lifetime (τ₀ = 1/k_d) of a cross-linker is the average time that the cross-linker spends in the closed state.³⁴ The average time of cross-linkers remain in the open state (τ₁, τ₁ is termed as free-time of a cross-linker in later discussion) is calculated by

$${\tau }_1=1∕\left(k_{\mathrm{a}}•C_{\mathrm{N}}\right)$$ (3)

where k_a is the association rate constant for cross-linker formation, and C_N is the concentration of pyridine monomer. In Leibler et al. work,²⁶ the average time of a cross-linker remains in the open state (τ₁) is given by:

$${\tau }_1={\tau }_0(1-p)∕p$$ (4)

where p is the fraction of closed cross-linkers. As shown in our previous calculations regarding the fraction of closed cross-linkers (p),²⁰ equation 3 can be obtained from equation 4.

In equation 3, the association rate constant k_a is not measured directly, but is calculated from the reported equilibrium constant for pyridine association, K_eq = k_a/k_d, which is ~ 30 M⁻¹, as k_d of cross-linkers are known.²² We acknowledge that this is an approximate value, and does not account for steric or electronic contributions from tethering the pyridine to the PVP backbone.²¹ Nonetheless, pyridine coordination has proven to be a useful model for pincer coordination to PVP, and the true value probably does not deviate substantially from that of the model system.¹⁸ The concentration of pyridine monomer (C_N) in equation 3 is calculated from the concentration of PVP solution. We should note that the true value of the free-time of a cross-linker (τ₁) in the network depends on the local concentration of pyridine monomer [C_N(local)] rather than the overall concentration of pyridine monomer (C_N) in the PVP solution. However, because C_N(local) can not be determined experimentally, the whole concentration of pyridine monomer (C_N) in the PVP solution is used to calculate τ₁. As the concentration of pyridine monomer (C_N) ranges from 1.5 to 2.6 M in ~0.16 to ~0.27 g/mL PVP solution, we use the average value of C_N = 2 M to obtain τ₁= τ₀/60.

In order to characterize the intrinsic dynamics of the polymer chains, the disentanglement times (τ_d) of pure semidilute entangled PVP/DMSO (or PVP/DMF) solutions were determined in the absence of cross-linker, by identifying the shear rate at the onset of shear thinning at different concentrations (Figure S19 and Figure S20, supporting materials). Shear thinning occurs in semidilute entangled solutions as polymer chains disentangle under conditions in which when the Weissenberg number is larger than 1, giving τ_d.^35,36 The Rouse relaxation time of a chain of length equal to one tube segment [τ_e(ϕ)] as a function of concentration is then calculated from the value of τ_d (see Supporting Information).^{27, 37} Relative to the uncertainties discussed above, the resulting τ_e(ϕ) does not change substantially from ~ 0.16 to ~0.27 g/mL (Figure S21, Supporting Information), and so ${\stackrel{‒}{\tau }}_e$ — an average value of τ_e(ϕ) for PVP concentrations of from ~ 0.16 to ~ 0.27 g/mL — is used to represent the dynamics of the polymer chains in PVP/DMSO (or PVP/DMF) at different temperature. This does not mean, however, that the concentration of PVP does not affect the critical polymer dynamics, simply that attempts to assign a precise value to τ_e(ϕ) are unwarranted. We will return to the influence of concentration on τ_e(ϕ) later.

For samples with from 1% to 5% of 1a or 1b in 0.16 - 0.27 g/mL PVP/DMSO or PVP/DMF solution at different temperatures, the average distance between two cross-linkers (r) along the polymer chain is smaller than the tube diameter (a)²⁷ in the semidilute entangled regime, and most r are larger than the correlation length (ξ)²⁷ in the semidilute entangled regime (Supporting Information). For this reason, a discussion in terms of ${\stackrel{‒}{\tau }}_e$ is more appropriate than τ_d.²⁷ Though the dynamics of free polymer chain segments in the cross-linked networks should differ from the dynamics of polymer chains in pure PVP solution,²⁶ ${\stackrel{‒}{\tau }}_e$ provides a useful metric for discussing the critical competition between dynamic timescales.

A quantitative comparison of the different time scales in various samples is provided in Figures S22-S25, and results in the semidilute entangled regime are summarized in Table 1. As discussed previously, the mechanism of shear thickening involves shear induced conversion of intrachain cross-linking to interchain cross-linking.²⁰ The microscopic physical picture is that the intrachain cross-linkers break first, then the polymer chain is oriented and reorganized under shear, and finally the cross-linkers recombine between two different chains. The average time from cross-linker dissociation to recombination is given by τ₁. For the polymer chain, the local orientation and reorganization of a polymer chain segment is connected to its ability to diffuse within the remainder of an intact network, and the time scale of this diffusion, dubbed here τ_segment, is roughly estimated by the value of ${\stackrel{‒}{\tau }}_e$ described above. Table 1 shows that the critical competition occurs not between polymer segment relaxation and cross-linker dissociation; dissociation is always much slower than segmental motion. Rather, the important balance is between polymer segment relaxation and re-association of the cross-linker. Comparing the results in Table 1 with the steady shear behavior of samples in ~0.27 g/mL PVP solution (the influence of concentration of PVP on steady shear behavior will be discussed below), shear thickening is observed for values of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ that are much greater than ~4.2, and mixed behavior (shear thinning or shear thickening, depending on cross-linker concentration) is observed for samples with values of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ around ~4.2, and only shear thinning is observed for values of values of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ that are less than ~4.2. We note that ${\stackrel{‒}{\tau }}_e$ might underestimate τ_segment, because τ_segment is the time scale of local motions in the network, while ${\stackrel{‒}{\tau }}_e$ is extrapolated from the shear thinning data in pure semidilute entangled PVP solution without cross-linkers. Considering the approximations necessary in our calculations of τ₁ and ${\stackrel{‒}{\tau }}_e$, we regard ${\tau }_1∕{\stackrel{‒}{\tau }}_e\sim 1$ to correspond to conditions under which τ₁/τ_segment ~ 1.

Table 1.

Value of ${\tau }_0∕{\stackrel{‒}{\tau }}_e$ and ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ for samples with 1%~5% of cross-linker 1a or 1b in 0.16~0.27 g/mL PVP/DMSO or PVP/DMF solution at different temperatures. τ₀ is the lifetime of intact cross-linkers, and τ₁ is the free-time of partially dissociated cross-linkers. ${\stackrel{‒}{\tau }}_e$ is the average value of the relaxation time of an entanglement strand [τ_e(ϕ)] in ~ 0.16 to ~ 0.27 g/mL PVP/DMSO (or PVP/DMF) solution at different temperatures. Bold values indicate samples for which shear thickening is observed in ~0.27 g/mL PVP solution with 1%~5% cross-linkers, whereas unbolded values indicate samples for which shear thinning is observed in ~0.27 g/mL PVP solution with 1%~5% cross-linkers, and the italicized entry corresponds to shear thinning or shear thickening behavior in ~0.27 g/mL PVP solution, depending on cross-linker concentration

		Conditions
Ratio of time scales	Cross-linker	PVP/DMSO 25 °C	PVP/DMSO 50 °C	PVP/DMF 25 °C	PVP/DMF 0 °C
${\tau }_0∕{\stackrel{‒}{\tau }}_e$	1a	26	30	90	250
	1b	2300	1800	7600	32000
${\tau }_1∕{\stackrel{‒}{\tau }}_e$	1a	0.4	0.5	1.5	4.2
	1b	38	30	130	530

The value of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ is based on average values, and it is not the only parameter that determines the steady shear behavior of the networks: the concentration of polymer also plays a role. For the 1a•PVP networks, for example, the value of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ is smaller than 4.2 in semidilute entangled PVP/DMSO solution at 25 °C and 50 °C and in semidilute entangled PVP/DMF solution at 25 °C. For semidilute entangled PVP/DMSO solution at 50 °C, no shear thickening is observed in ~0.16 to ~0.27 g/mL PVP/DMSO solution, and this is consistent with the value of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ that is smaller than ~ 4.2. Shear thickening is observed, however, in ~0.16 to ~0.19 g/mL PVP/DMSO solutions at 25 °C (Figure 4a), and in ~0.16 g/mL PVP/DMF solutions at 25 °C (Figure 8a). Only the samples with PVP concentration decidedly in the semidilute entangled regime (~0.23 g/mL and ~0.27 g/mL) exhibit purely shear thinning behavior (Figure 4a). We note here that the critical concentration for entanglement (see Figure S1 and Figure S2 in supporting material) is determined by a semiempirical method,^38,39 and it is possible that the ~0.16 g/mL PVP/DMSO solutions at 25 °C may still be in the semidilute unentangled regime, as the inferred critical concentration for entanglement is 0.155 g/mL. The samples with 1a in ~0.19 g/mL PVP/DMSO solutions at 25 °C, however, exhibit steady shear behavior that is quite different from that of samples in the semidilute unentangled regime (Figure 4a), and so we believe that the ~0.19 g/mL PVP/DMSO solutions at 25 °C are definitely in the semidilute entangled regime. As shear thickening is still observed in these samples (but not at higher PVP concentration), a value of ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ is not the full criterion for steady shear behavior in these samples. The concentration of PVP solution in the semidilute entangled regime, or microscopically, the number of entanglements per polymer chain, also influences the steady shear behavior.

The number of topological entanglements per polymer chain increases with concentration, and varies for our samples from 1 to 3 for concentrations of PVP from ~0.16 g/mL to ~0.27 g/mL (Table S1 in supporting material). In Figure 13a, we depict the original 1•PVP network in which the number of entanglements per polymer chain is only one, close to that in the ~0.16 and ~0.19 g/mL PVP solutions. In Figure 13b, we depict a situation in which the number of entanglements per polymer chain is two, close to that in the ~0.23 and ~0.27 g/mL PVP solutions. In Figure 13a/b, the total number of cross-linkers and the number of intrachain cross-linkers are fixed. In Figure 13a, as most of the intrachain cross-linkers are not constrained by the single entanglement point of the polymer chain, the local disentanglement and/or chain slippage of the polymer strand is not always necessary for the transfer of intrachain cross-linkers to interchain cross-linkers. In Figure 13a, the dynamics of a segment of PVP chain with one intrachain cross-linker are best described in this case by a relaxation time (τ_segment) that is smaller than ${\stackrel{‒}{\tau }}_e$, so the recombination time (τ₁) of dissociated cross-linkers are larger than τ_segment, and so the polymer segment can be oriented under shear, permitting the transfer of intrachain cross-linking to interchain cross-linking and resulting in shear thickening. This differential effect is particular to the local polymer segment dynamics in a way that is not captured in the analysis based on the ratio ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ in Table 1. This situation can be extrapolated to the semidilute unentangled regime, for which τ_segment is far smaller than τ₁ for both cross-linkers 1a and 1b, and for which shear thickening is observed in all samples.²⁰ In Figure 13b, with the increase of PVP concentration above ~0.23 g/mL, the larger number of entanglements per polymer chain bracket and constrain intrachain cross-linkers, so that local disentanglement and/or chain slippage of the polymer strand is needed for orientation, and the ratio ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ in Table 1 can described the steady shear behavior in ~0.23 and ~0.27 g/mL PVP solutions.

Figure 13.

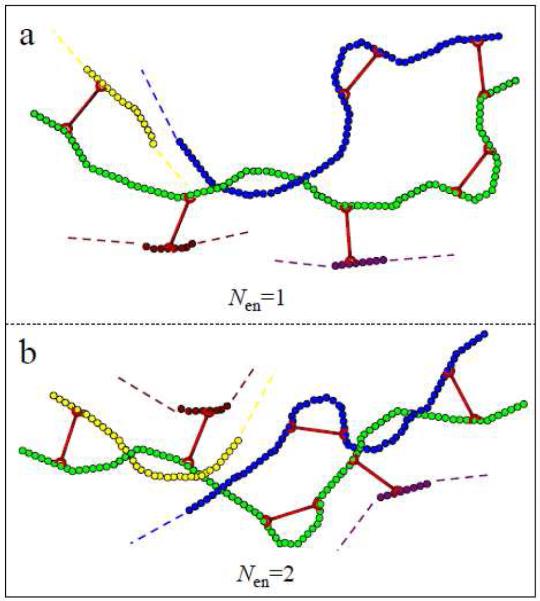
Schematic picture of the original 1•PVP network with different average number of entanglements (N_en) per polymer chain (green). (a) N_en is one; (b) N_en is two.

The local effects of cross-linker density are similarly not fully accounted for in the simplest model. We now return to samples with 1% and 2% of 1a in ~0.27 g/mL PVP/DMF at 0 °C, for which shear thickening is observed (Figure 9), and for which ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ of around 4.2 placing it at the extreme of samples for which that is true (Table 1). As the concentration of 1a increases to 3% or greater, the shear thickening disappears. On the contrary, for 1b•PVP network in ~0.27 g/mL PVP/DMSO solution at 25 °C (Figure 4b), shear thickening at intermediate shear rate is observed for samples with 1% to 5% of 1b, as ${\tau }_1∕{\stackrel{‒}{\tau }}_e$ is larger than ~ 4.2 (Table 1). As the concentration of cross-linkers is increased, the number of cross-linkers in an entangled strand of polymer chain increases. When the intrachain cross-linkers open, other nearby cross-linkers remain closed, and local segmental orientation is retarded (i.e., τ_segment increases). The effect of multiple physical cross-linkers on chain relaxation has been discussed previously, most notably by Leibler et al.,²⁶ who have noted the importance of considering the dynamic interplay of multiple interactions (albeit in a different context). In ~0.27 g/mL PVP/DMF with 1a at 0 °C, we suggest that the increasing concentration of cross-linkers above 3% forces τ_segment to be greater than τ₁ and precludes the reorientation necessary for shear thickening. As with the effect of concentration of cross-linkers, the effect of additional cross-linking is only significant in situations where τ_segment is close to τ₁ (here, when ${\tau }_1∕{\stackrel{‒}{\tau }}_e\sim 4$).

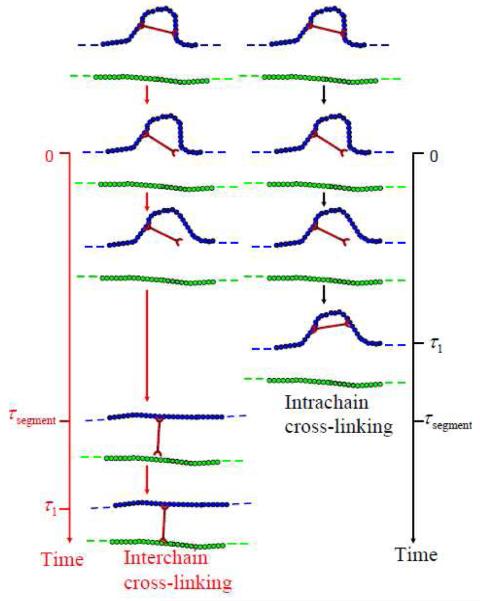
We therefore propose that the microscopic physical significance of the competition between τ₁ and τ_segment is captured in Figure 14. In Figure 14, the original local 1•PVP network has an intrachain cross-linker in a segment of polymer chain with relaxation τ_segment, and we assume the cross-linkers are closed in the original network. The cross-linkers will open during shear deformation (at time 0 in Figure 14). When τ₁ is smaller than τ_segment (right side of Figure 14), the segment of polymer chain does not have enough time to slip or disentangle altogether before the cross-linker recombines after time τ₁. In this case, the lack of reorganization does not permit cross-linkers to form interchain cross-linkers, instead remaining intrachain cross-linkers, which are not elastically active. As a result, no shear thickening is observed.¹⁹ When τ₁ is larger than τ_segment (left side of Figure 14), the polymer chain segment disentangles and/or slips along the entanglement and orients under shear after time τ_segment, and recombination after time τ₁ results in the transfer from intrachain to interchain cross-linkers. Because the total number of elastically active chain increases, shear thickening results.²⁰ The scheme shown in Figure 14 is obviouslyi meant to capture average ensemble behavior only, and the actual occurrence of the individual processes will, in practice, be dictated by the probabilities associated with the kinetics.

Figure 14.

Schematic picture about the deformation of original local 1•PVP network has an intrachain cross-linkers in a segment of polymer chain with relaxation τ_segment. Left side, τ₁ is larger than τ_segment (τ₁ > τ_segment); Right side, τ₁ is smaller than τ_segment (τ₁ < τ_segment).

Conclusions

We have described the rich steady shear behavior of metallo-supramolecular networks formed by bis-Pd(II) cross-linkers in semidilute entangled PVP solution. The mechanism behind the divergent steady shear behavior—shear thinning versus shear thickening at intermediate shear rate—for samples with different cross-linker dynamics is explored. Empirical “phase diagrams” for steady shear behavior indicate that shear thinning and shear thickening are simply different endpoints on a continuum of shear response, and they point to the importance of chain entanglements and the number of inactive (“intrachain”) cross-linkers in the zero-shear state, the latter of which serve as latent cross-linkers that are activated as stress-bearing sites upon shear-induced network reorganization. A competition between cross-linker recombination and polymer segment orientation is implicated as the determinant of the divergent behavior observed as a function of cross-linker dynamics. Two time scales—the average time that a cross-linker remains open (τ₁) and the local relaxation time of a polymer chain segment (τ_segment) — are used to compare the time scale of cross-linker recombination and polymer segment orientation, respectively. When τ₁ is larger than τ_segment (τ₁ > τ_segment), shear thickening is observed. When τ₁ is smaller than τ_segment (τ₁ < τ_segment), no shear thickening is observed. The criteria also apply for the steady shear behavior of samples in the semidilute unentangled regime.