Abstract
The objectives of this study were to estimate the genetic parameters for milk yield unadjusted and adjusted for days in milk and, subsequently, to assess the influence of adjusting for days in milk on sire rank. Complete lactations from 90 or 150 days of lactation to 270 or 350 days in milk were considered in these analyses. Milk yield was adjusted for days in milk by multiplicative correction factors, or by including lactation length as a covariable in the model. Milk yields adjusted by different procedures were considered as different traits. Heritability estimates varied from 0.17 to 0.28. Genetic correlation estimates between milk yields unadjusted and adjusted for days in milk were greater than 0.82. Adjusting for days in milk affected the parameter estimates. Multiplicative correction factors produced the highest heritability estimates. More reliable breeding value estimates can be expected by including short length lactation records in the analyses and adjusting the milk yields for days in milk, regardless of the method used for the adjustment. High selection intensity coupled to the inclusion of short length lactations and adjustment with multiplicative factors can change the sire rank..
Keywords: genetic correlations, heritability, lactation length, milk production, rank correlations
Introduction
When estimating genetic parameters, the influence of environmental effects on milk yield is generally accounted for by using previously calculated correction factors or by including these effects directly in the model. These procedures decrease environmental variation and allow more reliable comparisons among animals raised in different environments (Miller, 1973). According to Bhat and Batro (1978), a large portion of the variability in milk yield in milking buffaloes is explained by lactation length.
Buffalo lactation lasts around 250 days (Tonhati et al., 2004), but shorter lactations are common. The criteria for deciding when to discard or include a short lactation in breeding value estimations are still unclear. The lack of information on the reasons or circumstances leading to the interruption of lactation is the major obstacle in including short lactation length records in genetic evaluations (Bajwa et al., 2002).
Several studies have shown that 5–6 test days are required to extend the lactation period during genetic evaluations in dairy cattle (Keown and Van Vleck, 1971; Wilmink, 1987; Pander et al., 1992; Pander and Hill, 1993; Ribas et al., 1994). For genetic evaluations in milking buffaloes, the I.C.A.R. (2007) recommends the inclusion of lactations with = 150 days in milk.
Various procedures have been used to adjust milk yield for days in milk. Bajwa et al. (2002) stated that short lactation length records can be dealt with in three ways: 1) by deleting them from the analysis, 2) by using them regardless of the lactation length, and 3) by adjusting them for days in milk and including this effect in the model. Madalena et al. (1992), Khan et al. (2000) and Bajwa et al. (2002) used linear regression in their analyses, with Khan et al. (2000) and Bajwa et al. (2002) combining the average daily milk yield and the last test day milk yield. In contrast, Melo et al. (2000) used quadratic logarithmic functions in their study. In Brazil, Tonhati et al. (2004) developed multiplicative correction factors for different classes of days in milk when working with milking buffaloes.
Madalena et al. (1992) found that deleting short lactation length records from the analyses or adjusting them for days in milk tended to reduce the additive genetic variance estimates of milk yield in crossbreed dairy cattle in Brazil. The authors attributed this reduction to the high correlation between lactation length and milk production. However, more recently, Khan et al. (2000) and Bajwa et al. (2002), who studied buffaloes and dairy cattle, respectively, indicated an increase in heritability estimates when total milk yield was adjusted for days in milk.
In Brazil, the genetic evaluation for milking buffaloes is based on total milk yield, truncated at 305 days, with lactation length records < 120 days being discarded. There is no consensus on whether or not to adjust buffalo milk yield for days in milk, or how to best correct for this effect. Consequently, there is an urgent need to develop alternative models that can be applied to genetic evaluation programs for milking buffaloes in Brazil.
The objectives of this study were to estimate the genetic parameters for unadjusted and adjusted milk yield by using multiplicative correction factors or including lactation length as a covariable in the model, and to examine the influence of adjusting for days in milk on sire rank.
Material and Methods
Buffalo milk yields were obtained from the monthly test day records of a database maintained by the Departamento de Zootecnia at FCAV, UNESP, Jaboticabal. The data were from 12 herds in the State of São Paulo and were recorded from 1987 to 2004. All animals were from the Murrah breed raised on pastures, with feed supplementation during the dry season (April to September). The data consisted of 4,408 complete lactation records from 1,879 buffaloes with an overall mean (± SE) of 1,617 ± 14.4 kg per lactation.
Complete lactations from 90 or 150 days of lactation to 270 or 350 days of lactation were considered in the analyses. Lactation lengths > 270 or 305 days were truncated at these points. Records of abnormal lactations or records for cows older than 144 months at calving were excluded. Total milk yields were adjusted for days in milk by multiplicative correction factors (for 270 or 305 days) developed by Tonhati et al. (2004) or by including lactation length as a covariable in the model (linear effect).
The following traits were studied: 1) milk yield unadjusted for days in milk, considering complete lactations from 150 to 270 (UM150_270), 150 to 305 (UM150_305), 90 to 270 (UM90_270) and 90 to 305 (UM90_305) days in milk, 2) milk yield adjusted for days in milk using multiplicative correction factors, considering complete lactation from 150 to 270 (FM150_270), 150 to 305 (FM150_305), 90 to 270 (FM90_270) and 90 to 305 (FM90_305) days in milk, and 3) milk yield adjusted for days in milk including this effect as a covariable in the model, considering complete lactations from 150 to 270 (CM150_270), 150 to 305 (CM150_305), 90 to 270 (CM90_270) and 90 to 305 (CM90_305) days in milk. Table 1 provides descriptive statistics of the traits studied.
Table 1.
Number of animals (na) and lactations (nl), mean (kg), standard deviation (SD), variation coefficient (CV%) and minimum (Min) and maximum (Max) values for each trait.
| Trait1 | na | nl | Mean | SD | CV% | Min | Max |
|---|---|---|---|---|---|---|---|
| UM150_270 | 1,799 | 4,204 | 1,636 | 637 | 38.9 | 110 | 4,475 |
| FM150_270 | 1,798 | 4,205 | 1,767 | 628 | 35.5 | 110 | 4,475 |
| UM90_270 | 1,891 | 4,449 | 1,592 | 654 | 41.8 | 110 | 4,475 |
| FM90_270 | 1,888 | 4,442 | 1,780 | 642 | 36.1 | 110 | 4,650 |
| UM150_305 | 1,800 | 4,208 | 1,664 | 659 | 39.6 | 110 | 4659 |
| FM150_305 | 1,798 | 4,201 | 1,973 | 689 | 34.9 | 123 | 5,052 |
| UM90_305 | 1,891 | 4,450 | 1,619 | 676 | 41.7 | 110 | 4,659 |
| FM90_305 | 1,879 | 4,408 | 1,981 | 691 | 34.9 | 319 | 5,502 |
FM150_270 and UM150_270: adjusted and unadjusted milk production for 270 days in milk for lactations from 150 to 270 days; FM90_270 and UM90_270: adjusted and unadjusted milk production for 270 days in milk for lactations from 90 to 270 days; FM150_305 and UM150_305: adjusted and unadjusted milk production for 305 days in milk for lactations from 150 to 305 days; FM90_305 and UM90_305: adjusted and unadjusted milk production for 305 days in milk for lactations from 90 to 305 days.
Heritabilities, genetic correlations and breeding values were estimated for each trait. The model adopted, represented in matrix notation, was:
where y is a vector of observed traits, X is the incidence matrix of fixed effects, β is a vector of fixed effects, Z is the incidence matrix of additive genetic random effects, a is a vector of additive genetic random effects, W is the incidence matrix of permanent environmental random effect, c is a vector of permanent environmental random effects, and e is a vector of random error effects. The assumptions about expectation and variances for multi-trait analyses were: E[y] = Xb, Var(a) = A ⊗ Sa, Var(c) = I ⊗ Sc and Var(e) = I ⊗ Se, where Sa is the additive genetic effect covariance matrix, Sc, is the permanent environmental effect covariance matrix, Se is the residual covariance matrix, A is the relationship matrix between animals, I is the identity matrix, and ⊗ is the Kroenecker product between matrices.
The model of analysis included the fixed effects of a contemporary group (CG) and the covariable ‘cow’s age at calving’ (linear and quadratic effects). The covariable (linear and quadratic effects) ‘days in milk’ was included in the model for CM150_270, CM150_305, CM90_270 and CM90_305. The CG was defined as cows that calved in the same herd, year and season (season 1 = from April to September, and season 2 = from October to March). CGs with less than five lactations and cows with a milk yield 3.0 standard deviations above or below the CG average were deleted from the analyses.
Variance and covariance components were estimated by the restricted maximum likelihood method (REML), using Wombat (Meyer, 2007). There were 11,749 animals and 261 sires in the relationship matrix.
The sire breeding values were predicted for each trait by one-trait analysis. Only sires (n = 130) with progeny in the data were considered. Spearman correlations between the breeding values of sires and the percentage of common sires chosen for mating for milk yield unadjusted and adjusted for days in milk were calculated based on two selection intensities (5% and 10%) for the chosen sires.
Results and Discussion
Eighty-six percent, 70% and 11% of complete lactations had a length equal to or lower than 305, 270 and 150 days, respectively. The heritability and variance estimates for each trait are shown in Table 2. Permanent environmental, residual and phenotypic variances decreased when milk yield was adjusted for days in milk, independently of the method used, i.e. this adjustment decreased environmental variation, as expected. The highest additive genetic variances were obtained with multiplicative correction factors and the lowest when ‘days in milk’ was included as a covariable in the model. This probably occurred because including ‘days in milk’ as a covariable in the model adjusted the milk yield records for the average lactation length of the population. However, when milk yield was adjusted by multiplicative correction factors, the milk yield for 270 or 305 days in milk was affected and resulted in an increase in the average milk yield of the population.
Table 2.
Estimates of additive genetic variance (
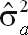 ), permanent environmental variance (
), permanent environmental variance (
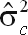 ), residual (
), residual (
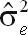 ) and phenotypic (
) and phenotypic (
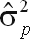 ) variances and heritability (
) variances and heritability (
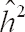 ) obtained by one-trait analyses.
) obtained by one-trait analyses.
| Trait1 | 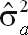 |
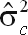 |
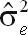 |
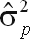 |
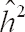 ± SE ± SE
|
|---|---|---|---|---|---|
| UM150_270 | 39,042 | 50,041 | 108,973 | 198,057 | 0.20 ± 0.04 |
| CM150_270 | 36,128 | 38,321 | 80,182 | 154,631 | 0.23 ± 0.04 |
| FM150_270 | 45,640 | 41,761 | 94,851 | 182,252 | 0.25 ± 0.04 |
| UM90_270 | 38,656 | 55,827 | 123,105 | 217,589 | 0.18 ± 0.04 |
| CM90_270 | 34,748 | 36,829 | 79,572 | 151,148 | 0.23 ± 0.04 |
| FM90_270 | 54,485 | 41,501 | 98,408 | 194,395 | 0.28 ± 0.04 |
| UM150_305 | 43,039 | 54,172 | 122,830 | 220,039 | 0.20 ± 0.04 |
| CM150_305 | 37,470 | 39,762 | 80,195 | 157,427 | 0.24 ± 0.04 |
| FM150_305 | 54,595 | 49,019 | 112,484 | 216,097 | 0.25 ± 0.04 |
| UM90_305 | 40,906 | 60,968 | 137,820 | 239,693 | 0.17 ± 0.04 |
| CM90_305 | 35,278 | 38,696 | 79,226 | 153,200 | 0.23 ± 0.04 |
| FM90_305 | 56,598 | 44,984 | 109,766 | 211,348 | 0.27 ± 0.04 |
Unadjusted milk yield for lactations from 150 to 270 (UM150_270), 150 to 305 (UM150_305), 90 to 270 (UM90_270) and 90 to 305 (UM90_305) days in milk; Adjusted milk yield for days in milk using multiplicative correction factors for lactations from 150 to 270 (FM150_270), 150 and 305 (FM150_305), 90 and 270 (FM90_270) and 90 to 305 (FM90_305) days in milk; Adjusted milk yield for days in milk including days in milk in the model for lactations from 150 to 270 (CM150_270), 150 to 305 (CM150_305), 90 to 270 (CM90_270) and 90 to 305 (CM90_305) days in milk. SE – standard error.
The heritability estimates for milk yield adjusted for days in milk were generally higher than the unadjusted values (Table 2). These results were similar to those reported by Khan et al. (2000) and Bajwa et al. (2002) in buffaloes and Melo et al. (2000) in dairy cattle. However, Madalena et al. (1992) observed a decrease in genetic variability when milk yield was adjusted for days in milk.
The highest heritability estimates were obtained when the records were adjusted by multiplicative correction factors, probably as a consequence of the larger additive genetic variance estimates. Bajwa et al. (2002) also observed differences in milk yield heritability estimates when adjusted for days in milk by linear regression or by a method combining the average daily milk yield and the last test day milk yield.
The differences between heritability estimates for unadjusted and adjusted milk yields were higher when short lactation length records (from 90 days) were included in the analyses (Table 2). The heritability estimates reported by Melo et al. (2000) for milk yield in dairy cows were similar to those described here when they used projected lactations from 91, 151, 211 and 240 days to 305 days in milk.
For nonadjusted records, the inclusion of lactations shorter than 150 days lead to a slight decrease in the genetic variance estimates. This finding differed from Madalena et al. (1992) who reported an increase in genetic variability when short lactation length records (< 120 days) were included in the analyses without adjusting the records for days in milk. These authors worked with crossbred populations and did not exclude any lactations, regardless of their length. Bajwa et al. (2002) stated that the major obstacle to the inclusion of short lactation length records in genetic evaluations was the lack of information about the reasons or circumstances for the interruption of lactation, i.e., whether the interruption had an environmental or genetic origin.
The heritability estimates obtained here for milk yield unadjusted and adjusted for days in milk were low to moderate. Our results agree with those described of Kuralkar and Raheja (1997) in India who used milk yields adjusted for 305 days, and Tonhati et al. (2004) in Brazil who used milk yields unadjusted and adjusted for 305 days; these two studies reported heritability estimates of 0.22 and 0.14–0.19, respectively, in milking buffaloes. In contrast, Rosati and Van Vleck (2002) in Italy and Khan et al. (2000) in Pakistan reported lower heritability estimates for milk yield (0.14 and 0.09–0.12, respectively) than those observed here.
The genetic correlation estimates between adjusted and unadjusted milk yields were greater than 0.82, regardless of the method used to adjust milk yield for days in milk or lactation length. Melo et al. (2000) also reported high genetic correlations (close to 1.0) between extended and unextended milk yields for 305 days in Holstein cows.
Table 3 provides a statistical summary of the breeding value estimates for the traits studied in this work. Breeding value estimates were higher when milk yield was adjusted for days in milk. This finding suggests that genetic variability increased when milk yield was adjusted for days in milk, in agreement with the higher heritability estimates obtained for adjusted milk yield (Table 2). The highest mean breeding value estimate was obtained for FM90_270, which agreed with the highest heritability estimate obtained for this trait.
Table 3.
Mean, median, standard deviation (SD), skewness, kurtosis, minimum and maximum values of breeding value estimates for the studied traits.
| Trait1 | Mean | Median | SD | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| UM150_270 | 34.1 | 25.7 | 148.1 | –460.6 | 520.8 | 0.53 | 2.19 |
| CM150_270 | 38.9 | 27.2 | 154.7 | –547.5 | 532.3 | 0.29 | 2.70 |
| FM150_270 | 37.0 | 24.5 | 173.8 | –678.4 | 612.9 | 0.04 | 3.13 |
| UM90_270 | 36.5 | 31.6 | 138.2 | –256.9 | 545.7 | 0.79 | 1.51 |
| CM90_270 | 39.7 | 27.0 | 153.0 | –525.5 | 523.9 | 0.20 | 2.08 |
| FM90_270 | 42.8 | 33.9 | 200.8 | –1,010.9 | 598.9 | –0.82 | 6.10 |
| UM150_305 | 33.7 | 20.9 | 151.8 | –444.6 | 519.6 | 0.59 | 1.81 |
| CM150_305 | 35.2 | 26.0 | 155.3 | –543.9 | 534.5 | 0.21 | 2.49 |
| FM150_305 | 39.4 | 29.6 | 188.0 | –735.9 | 618.2 | –0.09 | 2.96 |
| UM90_305 | 36.7 | 27.1 | 139.1 | –245.2 | 538.6 | 0.82 | 1.39 |
| CM90_305 | 37.5 | 23.6 | 152.2 | –513.0 | 494.7 | 0.14 | 1.90 |
| FM90_305 | 37.3 | 31.9 | 197.8 | –981.6 | 575.3 | –0.86 | 5.56 |
Unadjusted milk yield for lactations from 150 to 270 (UM150_270), 150 to 305 (UM150_305), 90 to 270 (UM90_270) and 90 to 305 (UM90_305) days in milk; Adjusted milk yield for days in milk using multiplicative correction factors for lactate lactations from 150 to 270 (FM150_270), 150 and 305 (FM150_305), 90 and 270 (FM90_270) and 90 to 305 (FM90_305) days in milk; Adjusted milk yield for days in milk including days in milk in the model for lactations from 150 to 270 (CM150_270), 150 to 305 (CM150_305), 90 to 270 (CM90_270) and 90 to 305 (CM90_305) days in milk.
Table 4 provides a statistical summary of the accuracy of the breeding value estimates for the traits examined in this study. The accuracy of the breeding value estimates was greater when milk yield was adjusted for days in milk since higher heritability estimates were obtained for adjusted milk yields compared to unadjusted yields. The differences between the accuracy estimates for unadjusted and adjusted milk yields were greater when short length lactation records (from 90 days) were included in the analyses.
Table 4.
Mean, median, standard deviation (SD), skewness, kurtosis, minimum and maximum values of breeding value estimates for the studied traits.
| Trait1 | Mean | Median | SD | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| UM150_270 | 0.60 | 0.61 | 0.19 | 0.22 | 0.93 | –0.27 | –0.79 |
| CM150_270 | 0.62 | 0.64 | 0.18 | 0.24 | 0.94 | –0.31 | –0.76 |
| FM150_270 | 0.63 | 0.65 | 0.18 | 0.25 | 0.94 | –0.34 | –0.74 |
| UM90_270 | 0.59 | 0.61 | 0.19 | 0.21 | 0.93 | –0.27 | –0.76 |
| CM90_270 | 0.63 | 0.65 | 0.18 | 0.24 | 0.94 | –0.34 | –0.69 |
| FM90_270 | 0.66 | 0.67 | 0.19 | 0.26 | 0.95 | –0.41 | –0.62 |
| UM150_305 | 0.60 | 0.61 | 0.19 | 0.22 | 0.93 | –0.27 | –0.79 |
| CM150_305 | 0.62 | 0.64 | 0.18 | 0.24 | 0.94 | –0.32 | –0.76 |
| FM150_305 | 0.63 | 0.65 | 0.18 | 0.25 | 0.94 | –0.34 | –0.74 |
| UM90_305 | 0.59 | 0.61 | 0.19 | 0.20 | 0.92 | –0.26 | –0.76 |
| CM90_305 | 0.63 | 0.65 | 0.18 | 0.24 | 0.94 | –0.34 | –0.70 |
| FM90_305 | 0.65 | 0.67 | 0.18 | 0.26 | 0.95 | –0.39 | –0.63 |
Unadjusted milk yield for lactations from 150 to 270 (UM150_270), 150 to 305 (UM150_305), 90 to 270 (UM90_270) and 90 to 305 (UM90_305) days in milk; Adjusted milk yield for days in milk using multiplicative correction factors for lactations from 150 to 270 (FM150_270), 150 and 305 (FM150_305), 90 and 270 (FM90_270) and 90 to 305 (FM90_305) days in milk; Adjusted milk yield for days in milk including days in milk in the model for lactations from 150 to 270 (CM150_270), 150 to 305 (CM150_305), 90 to 270 (CM90_270) and 90 to 305 (CM90_305) days in milk.
The use of multiplicative factors to adjust milk yield resulted in more reliable breeding value estimates than those obtained for milk yields adjusted by including ‘days in milk’ as a covariable in the model. The accuracy of breeding value estimates were almost the same for lactation records from 90 or 150 days in milk. The inclusion of short length lactation records was desirable since this resulted in almost equal or more reliable breeding value estimates for milk yield. Although the inclusion of short length lactation records decreased the heritability estimates, more animals and lactation records were considered in the analyses and this increased the accuracy of the breeding value estimates.
For lactation records longer than 150 days, most of the sires would be the same if 5% of the sires were selected, regardless of whether adjustment was made by multiplicative factors or by including days in milk as a covariable in the model (Table 5). In general, the percentage of sires selected for unadjusted milk yield that would also be selected for adjusted milk yield decreased when short length lactation records were included in the analyses. The inclusion of short length lactation records decreased the rank correlations between breeding value estimates for unadjusted and adjusted milk yields, particularly when multiplicative correction factors were applied. High selection intensity would change the profile of chosen sires, particularly for short lactations (90 days) and after adjustment by multiplicative factors.
Table 5.
Rank correlations (r), percentage, and number of sires (in parentheses) selected for adjusted milk yield for days in milk. The values were calculated using different selection intensities based on the predicted breeding values for unadjusted milk production.
| Trait1 | Selection intensity | |||
|---|---|---|---|---|
| 5% (6) 2 | r | 10% (13) | r | |
| FM150_270 | 100% (6) | 0.89 | 85% (11) | 0.95 |
| CM150_270 | 100% (6) | 0.77 | 85% (11) | 0.80 |
| FM90_270 | 66% (4) | 0.40 | 69% (9) | 0.67 |
| CM90_270 | 83% (5) | 0.70 | 69% (9) | 0.73 |
| FM150_305 | 100% (6) | 0.89 | 77% (10) | 0.86 |
| CM150_305 | 100% (6) | 0.77 | 85% (11) | 0.90 |
| FM90_305 | 83% (5) | 0.30 | 62% (8) | 0.64 |
| CM90_305 | 83% (5) | 0.70 | 62% (9) | 0.73 |
Adjusted milk yield for days in milk using multiplicative correction factors for lactations from 150 to 270 (FM150_270), 150 and 305 (FM150_305), 90 and 270 (FM90_270) and 90 to 305 (FM90_305) days in milk; Adjusted milk yield for days in milk including days in milk in the model for lactations from 150 to 270 (CM150_270), 150 to 305 (CM150_305), 90 to 270 (CM90_270) and 90 to 305 (CM90_305) days in milk.
Percentage and number (between parentheses) of chosen sires for higher unadjusted milk yield based on two selection intensities (total of sires with progeny in the data: 130).
In conclusion, adjusting for days in milk affected the parameter estimates. Milk yield must be adjusted for days in milk in order to decrease environmental variances and increase heritability estimates. Multiplicative correction factors produced the highest heritability estimates. More reliable breeding value estimates can be obtained by including short length lactation records in the analyses and adjusting milk yield for days in milk, regardless of the adjustment procedure used. With high selection intensity, changes in the sire rank and in the sires chosen can be expected if the records are adjusted by multiplicative factors and short length lactations are included in the data set.
The results of this study should help to improve the genetic assessment of Brazilian milking buffaloes through the use of procedures to adjust or correct the data for environmental effects.
Acknowledgments
This study was supported by the Committee for Postgraduate Courses in Higher Education (CAPES), the State of São Paulo Research Foundation (FAPESP) and the National Council of Technological and Scientific Development (CNPq).
Footnotes
Associate Editor: Pedro Franklin Barbosa
References
- Bajwa IR, Khan MS, Ahmad Z, Gondal KZ. Genetic parameters of lactation milk yield as affected by lactation length adjustment procedures. Proceedings of 7th World Congress on Genetics Applied to Livestock Production, Montpellier, Communication 01–56.2002. [Google Scholar]
- Bhat PN, Batro BN. Effect of various non-genetic factors on milk yield and lactation length in Indian buffaloes. Indian J Anim Sci. 1978;31:321–325. [Google Scholar]
- Keown JF, Van Vleck LD. Selection on test-day fat percentage and milk production. J Dairy Sci. 1971;54:199–203. [Google Scholar]
- Khan MS, Chaudhry HZ, Raza SH. Impact of lactation length adjustment procedures on accuracy and heritability of adjusted milk yield in buffaloes. J Dairy Sci. 2000;83:223. [Google Scholar]
- Kuralkar SV, Raheja KL. Relationships among early performance, lifetime production and reproduction traits in Murrah buffaloes. Indian J Anim Sci. 1997;67:798–801. [Google Scholar]
- Madalena FE, Lemos AM, Teodoro RL. Consequences of removing the variation in lactation length on the evaluation of dairy cattle breeds and crosses. Braz J Genet. 1992;15:585–593. [Google Scholar]
- Melo CMR, Oliveira AIG, Martinez ML, Verneque RS, Gonçalves TM, Freitas RTF. Sires genetic evaluations using complete or partial projected lactation records. 1: Genetic parameters estimates. Braz J Anim Sci. 2000;292:1060–1066. [Google Scholar]
- Meyer K. WOMBAT – A tool for mixed model analyses in quantitative genetics by restricted maximum likelihood (REML) J Zhejiang Univ Sci B. 2007;8:815–821. doi: 10.1631/jzus.2007.B0815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller P. A recent study of age adjustment. J Dairy Sci. 1973;56:952–959. [Google Scholar]
- Pander BL, Hill WG, Thompson R. Genetic parameters of test day records of British Holstein-Friesian heifers. Anim Prod. 1992;55:11–21. [Google Scholar]
- Pander BL, Hill WG. Genetic evaluation of lactation yield from test day records on incomplete lactation. Livest Prod Sci. 1993;37:23–26. [Google Scholar]
- Ribas M, Perez B, Guzman G. Monthly test-day yields and the extension of lactations in Cuba. Cuban J Agric Sci. 1994;28:125–139. [Google Scholar]
- Rosati A, Van Vleck LD. Estimation of genetic parameters for milk, fat, protein and mozzarella cheese production for the Italian river buffalo Bubalus bubalis population. Livest Prod Sci. 2002;74:185–190. [Google Scholar]
- Tonhati H, Muñoz MFC, Duarte JMC, Reichert RH, Oliveira JA, Lima ALF. Estimates of correction factors for lactation length and genetic parameters for milk yield in buffaloes. Arq Bras Med Vet Zootec. 2004;56:251–257. [Google Scholar]
- Wilmink JBM. Efficiency of selection for different cumulative milk, fat, and protein yields in first lactation. Livest Prod Sci. 1987;17:211–224. [Google Scholar]
Internet Resources
- International Committee for Animal Recording (I.C.A.R) http://www.icar.org (March, 2007).


