THE ROLE OF INERTIAL CAVITATION IN ACOUSTIC DROPLET VAPORIZATION

Abstract

The vaporization of a superheated droplet emulsion into gas bubbles using ultrasound – termed acoustic droplet vaporization (ADV) – has potential therapeutic applications in embolotherapy and drug delivery. The optimization of ADV for therapeutic applications can be enhanced by understanding the physical mechanisms underlying ADV, which are currently not clearly elucidated. Acoustic cavitation is one possible mechanism. This paper investigates the relationship between the ADV and inertial cavitation (IC) thresholds (measured as peak rarefactional pressures) by studying parameters that are known to influence the IC threshold. These parameters include bulk fluid properties such as gas saturation, temperature, viscosity, and surface tension; droplet parameters such as degree of superheat, surfactant type, and size; and acoustic properties such as pulse repetition frequency and pulse width. In all cases the ADV threshold occurred at a lower rarefactional pressure than the IC threshold indicating that the phase-transition occurs before IC events. The viscosity and temperature of the bulk fluid are shown to influence both thresholds directly and inversely, respectively. An inverse trend is observed between threshold and diameter for droplets in the 1 to 2.5 μ range. Based on a choice of experimental parameters, it is possible to achieve ADV with or without IC.

I. INTRODUCTION

Emulsions containing micron and nanometer-sized perfluorocarbon (PFC) droplets are being studied in diagnostic and therapeutic applications of ultrasound (US). For example, the use of PFC nanodroplets has been explored in US molecular imaging and the targeted delivery of therapeutic agents [1]–[4]. Another research area is acoustic droplet vaporization (ADV), where a superheated, micron-sized liquid droplet - stabilized by a surfactant shell – is phase-transitioned into a gas bubble using US. The superheated liquid is a straight-chain PFC, which belongs to a class of compounds that are inert, hydrophobic, lipophobic, and biocompatible [5]. The therapeutic potentials of ADV were described by Apfel [6] and Kripfgans et al. [7] in applications such as embolotherapy and drug delivery. Additional applications of ADV include its use in phase aberration correction [8],[9].

Micron-sized PFC droplets can be systemically administered - either intra-arterially or intravenously - and greater than 95% (by number) of the droplets are small enough to pass through capillaries without producing obstructions [10]. Upon ADV, the generated bubbles grow to typically five to six times that of the original droplet diameter [7]. Therefore, upon vaporization, the bubbles can become lodged within capillaries, thus selectively occluding blood flow to targeted tissues or organs. The use of ADV in occlusion therapy has been successfully demonstrated in vivo in canine [8] and lepus [11] models to reduce cerebral and renal perfusion, respectively. The in vitro ADV of nanometer-sized PFC droplets has also been demonstrated [12].

The physical mechanisms involved in ADV are not clearly understood. The optimization of ADV for therapeutic applications can be potentially enhanced by elucidating the mechanisms involved in the ADV process. One proposed mechanism is acoustic cavitation, which can be defined as the creation, growth, and/or collapse of a bubble or cavity within a fluid when the fluid is exposed to an acoustic pressure field [13]. It has been found that the tensile strength of a liquid is much lower than the theoretical tensile strength due to the presence of cavitation nuclei within the fluid [14]. Two general types of cavitation exist – stable and inertial [15] - although there has been considerable debate about the terminology used. Stable cavitation is the oscillation, both linear or non-linear, of a bubble about an equilibrium size. The oscillation can continue for many cycles of acoustic pressure. Inertial cavitation (IC) occurs when the bubble diameter grows to at least twice its original diameter, generally during a single cycle of acoustic pressure [13]. The bubble then collapses violently, driven by the inertia of the fluid, potentially fragmenting into many smaller bubbles. Such cavitation can occur repetitively and even within a single bubble. The bioeffects of IC, which stem from the generated high temperatures, pressures, and velocities (i.e. shock wave and liquid jet formation), include cellular erosion or lysis, molecular degradation, and the formation of free radicals [15],[16]. In the case of embolotherapy, the minimization of these bioeffects may be important to prevent the extravasation of blood components, which could reduce the efficacy of ADV-induced embolotherapy. Alternatively, these bioeffects could enhance drug delivery via sonoporation, as highlighted in a recent review [17].

The cavitation process is started by nucleation, either within the fluid itself due to thermal motion, termed homogeneous, or at a boundary between the fluid and another surface, termed heterogeneous. In most practical situations, heterogeneous nucleation is more common since homogeneous nucleation tends to require higher rarefactional pressures. However, the body contains few, if any, cavitation nuclei that can be activated by diagnostic US pulses [18], and the probability of homogenous nucleation within the body using diagnostic US is expected to be rare [19]. Therefore, the introduction of materials within the body, such as microbubbles or droplets, may serve as cavitation nuclei depending on the rarefactional pressure levels of applied diagnostic or therapeutic US. Hence the mechanical index (MI) is used as a metric to determine the susceptibility of IC with diagnostic US scanners.

The nucleation of ADV can occur in three regions: within the droplet core (i.e. PFC phase); adjacent to the surfactant shell (either inside or outside of the droplet); and external to the droplet within the bulk fluid phase. Previous work demonstrated that the ADV threshold at 1.44 MHz decreased when US contrast agent was present with the droplets [20]. In this case, it was surmised that the microbubbles acted as cavitation nuclei external to the droplet. Counter to this however, micrographs, taken using a high-speed camera, of single droplets undergoing ADV indicate that the nucleation location is within the imaged cross section of the droplet, when using transducers in the 3 to 10 MHz range with microsecond pulse lengths [21].

A previous study measured the in vitro, IC threshold of micron-sized PFC droplets as a function of droplet composition and US parameters [22]. This study investigates the relationship between ADV and IC, specifically the necessity of IC for ADV to occur, and adds insight into the location of ADV nucleation. The threshold pressures required to induce ADV and IC are simultaneously determined in an in vitro setup. The materials and methods, including ADV and IC threshold determination, utilized in this study are described in Section II. Parameters that are known to influence both thresholds – bulk fluid properties such as gas saturation, temperature, viscosity, and surface tension; droplet parameters such as degree of superheat, surfactant type, and size; and acoustic properties such as pulse repetition frequency and pulse width – are investigated with the intent of determining experimental conditions that yield ADV without IC and ADV with IC. These results are presented and discussed in Section III, with a focus on connecting the experimental results with possible mechanisms involved in ADV. Section IV describes conclusions concerning the ADV mechanism that are supported by the results in Section III as well as discussing similarities between the observed trends for the ADV and IC thresholds.

II. MATERIALS AND METHODS

A. PFC Droplets

Albumin droplets were prepared according to a method established by Kripfgans et al [7]. Briefly, 750 μL of 4 mg per mL bovine albumin (A3803, Sigma-Aldrich, St. Louis, MO) in normal saline (0.9% w/v, Hospira Inc., Lake Forest, IL) was added to a 2 mL glass vial (Cat. No. 223693, Shamrock Glass, Seaford, DE). Liquid PFC – either perfluoro-n-pentane (L16969, Alfa Aesar, Ward Hill, MA), perfluoro-n-hexane (1100-2-07, SynQuest Labs Inc., Alachua, FL), or perfluoro-n-octane (L16840, Alfa Aesar) – was added gravimetrically to a final PFC volume fraction of 25%. Table I lists the different PFC core materials that were tested. The vial was sealed with a rubber stopper (Cat. No. 224100-094, Shamrock Glass) and metal cap (Cat. No. 224177-01, Shamrock Glass). The vial was then shaken for 45 seconds at 4550 cycles per minute using an amalgamator (VialMix, Lantheus Medical Imaging, Billerica, MA).

Table I.

Boiling points of PFCs used to make emulsions and average droplet diameters, including standard deviations of the means, of the resulting emulsions one day after their formulation so that Ostwald ripening has not significantly occurred. The average number density, including the standard deviation of the mean, is listed for the undiluted emulsions.

Name	Formula	CAS #	Abbreviation	Tboil (°C)	Mean diameter (μm)	Mean number density (×109, number per mL)
Perfluoro-n-pentane	C5F12	678-26-2	PFP	29	2.09+0.02	4.28±0.05
Perfluoro-n-hexane	C6F14	355-42-0	PFH	56	2.20±0.06	3.51±0.20
Perfluoro-n-octane	C8F18	307-34-6	PFO	100	2.63±0.04	4.20±0.30

Lipid droplets were made in a similar manner using 750 μL of a lipid blend rather than albumin. The blend consisted of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC, 5 mg per mL)(850355, Avanti Polar Lipids, Alabaster, AL) and 1,2-dipalmitoyl-sn-glycero-3-phosphate monosodium salt (DPPA, 0.2 mg per mL)(830855, Avanti Polar Lipids) dissolved in propylene glycol (15872-0010, Acros Organics, Morris Plains, NJ), which was heated to 50°C. The resulting solution was then diluted with an equal volume of an 8:1 volumetric ratio of normal saline to glycerol (G9012, Sigma Aldrich) to produce the final lipid blend. PFC was then added gravimetrically and the vial sealed and shaken in the same manner as the albumin droplets.

The shaken vials were refrigerated (5°C) overnight prior to use. A droplet pre-dilution, used for sizing and flow tube experiments, was made by diluting 1 vial of droplets to 10 mL with normal saline that had been filtered with a syringe filter (0.22 μm, Millex GV, Millipore Co., Bedford, MA). A Coulter Counter (Multisizer III, Beckman Coulter Inc., Fullerton, CA) with a 50 μm aperture was used to determine the number and size of the resulting droplet solutions.

B. Experimental Setup

All experiments were conducted in a tank (40 × 60 × 27 cm) containing degassed, deionized water heated to 37°C (Ex 7, ThermoNESLAB, Newington, NH), unless otherwise noted. A calibrated 3.5 MHz single-element transducer (1.9 cm diameter × 3.81 cm focal length, A381S, Panametrics, Olympus NDT Inc., Waltham, MA) was focused at the center of dialysis tubing (14.6 mm diameter, Spectra/Por, Spectrum Laboratories Inc., Laguna Hills, CA), which was used as a flow tube. A droplet solution, containing approximately 9×10⁴ droplets per milliliter, was prepared by adding 100 μL of the droplet pre-dilution to 500 mL of degassed, deionized water heated to the same temperature as the tank water, unless otherwise noted. The same number density of droplets was used for all trials. By comparison, the droplet concentration used for the lepus studies [11], assuming an average rabbit weight of 2.5 kg and a cardiac output of 250 mL per minute [23], was 6.4×10⁵ droplets per mL. The droplet solution was pumped (Masterflex pump and speed controller, Cole-Parmer, Chicago, IL) at 2 cm·s⁻¹ (average linear speed in flow tube) against gravity in a recirculated manner from a 500 mL stirred flask. The single-element transducer was used to generate ADV while cross-sectional B-mode cineloops were simultaneously collected downstream using a 10 MHz linear array (L9, GE Healthcare, Milwaukee, WI). Note that the imaging array is purposefully located downstream of the single-element transducer so that the imaging acoustics cannot impact the vaporization acoustics. A schematic of the setup is displayed in Fig. 1.

Fig. 1.

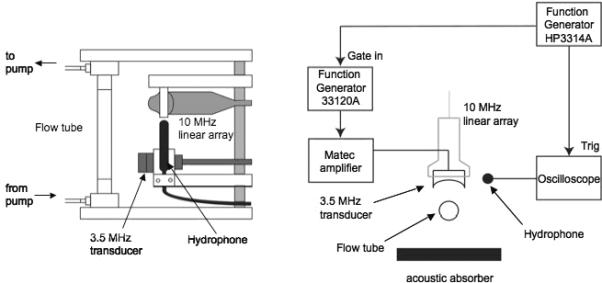
Side (left) and top (right) views of the in vitro setup used for measuring ADV and IC in flow. A 3.5 MHz single element transducer vaporized the flowing droplets while a 10 MHz linear array recorded cineloops; IC noise was simultaneously detected using the hydrophone.

Acoustic pulses sent to the single-element transducer were achieved using a master function generator (33120A, Agilent Technologies, Palo Alto, CA) gated by a secondary function generator (3314A, Agilent Technologies). The gated output signal was sent to a power amplifier (60 dB, Model 350, Matec, Northborough, MA). IC noise was passively detected using an omnidirectional hydrophone (ITC-1089D, International Transducer Co., Santa Barbara, CA) and radiofrequency (RF) segments (n = 100, 10 MHz sampling) were digitized using an oscilloscope (9314L, LeCroy, Chestnut Ridge, NY), which was triggered with each transmitted acoustic pulse. A passive acoustic detector was used to detect IC since it has been demonstrated that an active detector can affect the cavitation process [24], especially considering the nature of this experiment where droplet vaporization is triggered acoustically. The gas content of both the tank water and the recirculated fluid was measured using a blood-gas analyzer (ABL5, Radiometer, Westlake, OH). All ADV and IC measurements were taken while the fluid was being recirculated since it was confirmed, using the Coulter Counter, that only a small fraction of the droplets were vaporized over the course of each run due the relatively short on-time of the single-element transducer. The flow tube and pump tubing were thoroughly flushed with degassed, deionized water between runs to eliminate carryover of any residual droplets or bubbles. A new droplet solution was prepared for each run. Each run consisted of cycling through a range of acoustic pressures from the single-element transducer for the combination of parameters being interrogated for that particular run. By analyzing the range of pressures tested, it was possible to determine the ADV and IC thresholds (see next section).

C. ADV and IC Data Analysis

The recorded B-mode images were analyzed for an increase in echogenicity due to the presence of stable bubbles. The mean echo power (MEP) was computed, as seen in (1), using Matlab (The MathWorks, Inc., Natick, MA) from the decompressed amplitude data from the collected cineloops, where the compression algorithm used in the US system was reversed.

$$\text{MEP}\left(\mathrm{m}\right)=\frac{1}{\mathrm{MN}}\sum _{\mathrm{i}=1}^{\mathrm{M}}\sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{A}}^2(\mathrm{i},\mathrm{j})$$ (1)

Similar to the mean echo amplitude (MEA) [7], MEP is the sum of the squared amplitude (A) at pixel (i,j) for frame number (m) that has dimensions M by N.

As seen in Fig. 2, a circular region of interest, consisting of the entire interior of the flow tube cross section, was used for the MEP calculations. Each cineloop (17 Hz frame rate, MI = 0.2) was 10 seconds in duration, with 3 seconds captured with the single-element transducer off. As seen in Fig. 2, each cineloop consisted of four regions. A differential MEP value, (2), was used in this work so that any increases in baseline echogenicity due to the interference pattern from the single-element transducer was accounted for.

$$\Delta \text{MEP}={\text{MEP}}_4-{\text{MEP}}_2$$ (2)

MEP₂ and MEP₄ are the mean MEP values of regions 2 and 4, respectively. MEP₂ includes the interference from the single-element transducer, but does not contain ADV-generated bubbles due to the spatial separation between the single-element transducer and the imaging array. It was confirmed, using polystyrene spheres (1–50 μm or 381 μm, Duke Scientific, Palo Alto, CA) as IC nuclei, without droplets, that any bubbles produced by IC (detected by the hydrophone as described next) in the bulk fluid, but not associated with ADV, were not detected by the imaging array due to their collapse, fragmentation and/or dissolution. The bubble dissolution model [25] in a static fluid predicts that an air bubble would have to be at least 8 μm in diameter for the bubble to persist long enough to travel from its generation location (the focus of the single-element transducer) to the imaging plane of the linear array. Since only gas bubbles produced by ADV are stable or large enough, versus bubbles produced by the IC of the bulk fluid, MEP is a direct measure of bubbles produced by ADV.

Fig. 2.

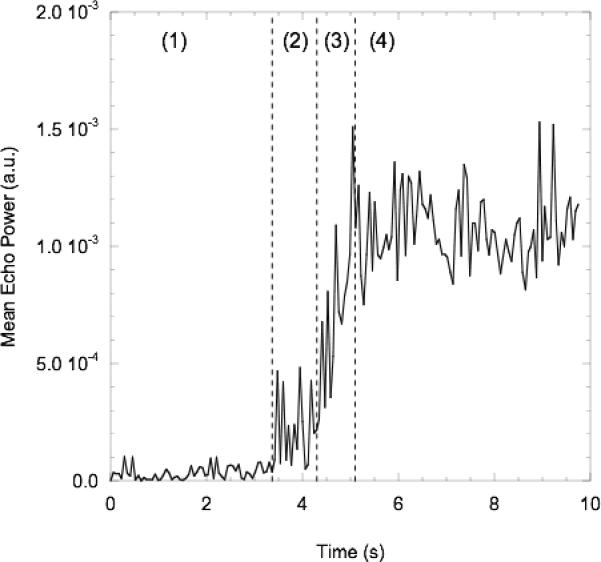
Left: MEP as a function of time for four different regions: US off (region 1); US on but no bubbles in linear array field of view (FOV) (region 2); US on and initial wave of bubbles appear in the linear array FOV, prior to achieving a steady state (region 3); US on with a steady state number of bubbles in linear array FOV (region 4). Right: B-mode frames (compressed intensity scale) of a flow tube in region 1 (top) and region 4 (bottom). The exterior boundary of the region of interest used to calculate the MEP is denoted as a white, dashed circle.

The presence of IC in the RF segments was determined relative to a baseline of degassed water, where it was observed that no IC occurred. Fig. 3 displays example RF and spectral data for a segment with and without IC. The integrated Fourier transform (IFT) in the range 5 to 60 kHz was used to differentiate segments with and without IC. The criterion for a segment containing IC, at a given acoustic pressure (P), is given in (3) where IFT_cav,P is the IFT of a segment containing IC at acoustic pressure P, IFTdegas, P is the IFT of the degassed water at acoustic pressure P, and σ is the standard deviation.

$${\text{IFT}}_{\text{cav,P}}\ge \text{mean}\left({\text{IFT}}_{\text{degas,P}}\right)+9\cdot \sigma \left({\text{IFT}}_{\text{degas,P}}\right)$$ (3)

Nine standard deviations were empirically chosen as a threshold to distinguish an IC event from the increase in acoustic backscatter due to the presence of droplets alone. As seen in Fig. 4, the calculated IC threshold is directly correlated with the number of standard deviations used to determine the threshold. However, from three to nine standard deviations the threshold increases only slightly. The 0.6 MPa increase in the IC threshold as the number of standard deviations is increased from one to nine is smaller than the difference between the ADV and IC thresholds (see Section III). Therefore, nine standard deviations minimizes the probability of falsely predicting IC at lower rarefactional pressures and reduces the variability of the calculated IC threshold while maintaining sensitivity to correctly detecting IC events. The RF data was processed using Matlab. Each IC data point consists of the average of three runs with 100 RF lines collected for each run.

Fig. 3.

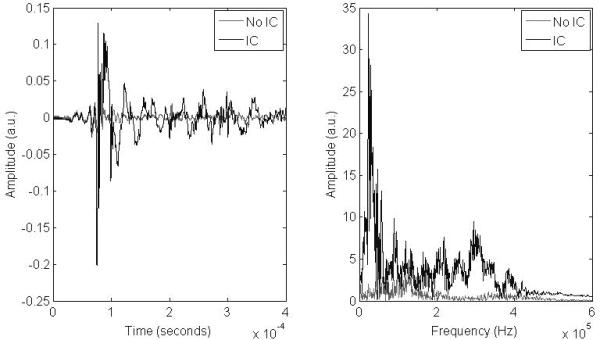
Left: RF data of a segment with and without IC. Right: Fourier transforms of RF data from left, showing the large spectral differences between a segment with and without IC. The following conditions were used: degassed water at 37°C with albumin-coated PFP droplets, 83 Hz PRF, 13 cycles, and 6.2 MPa.

Fig. 4.

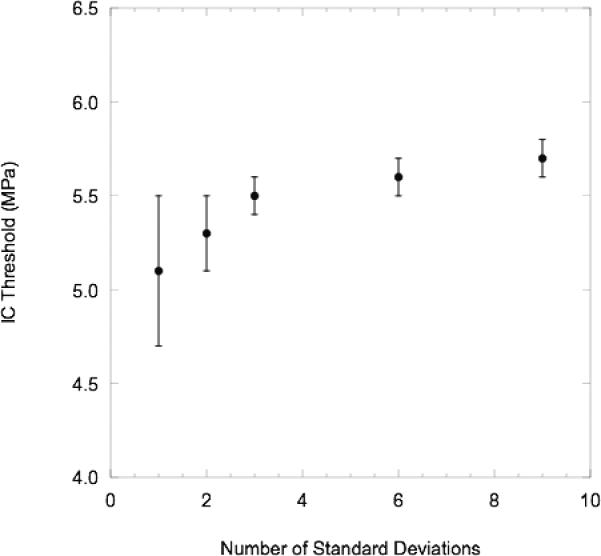
The effect of varying the number of standard deviations - σ(IFT_degas,P) – on the calculated peak rarefactional pressure IC threshold. Refer to Equation 3 for the criterion used to determine the presence of IC in an RF segment. The average (n=3) IC thresholds, plotted with the respective standard deviations, are from the following experimental conditions: degassed water at 37°C with albumin-coated PFP droplets, 83 Hz PRF, and 13 cycles.

D. ADV and IC Threshold Determination

Fig. 5 displays an example of the normalized MEP and the percent of segments containing IC, which is the ratio of segments containing an IC event (defined according to the previous criterion) to the total number of collected segments, versus the peak rarefactional pressure for a given experimental condition. The raw MEP data was normalized, vertically shifted by 10⁻⁴ and scaled by 10⁵, to facilitate display in Fig. 5. Two methods have been previously used to determine the ADV threshold. In the first method [7], the ADV threshold was the peak rarefactional pressure at the intersection of two line segments fit to the flat baseline portion and the upward sloping portion of the ADV data (peak rarefactional pressure versus MEA). In the second method [20], the slope between adjacent points in the ADV data was calculated. The threshold was defined as the pressure at which this slope exceeded a certain criterion. This work uses a refined version of the previously used slope method [20]. The data in each curve was fit to a sigmoid (4), where m₁ is the maximum y-value, m₂ is the minimum y-value, m₃ is the x-value at the midpoint of y, and m₄ is the slope at the y-midpoint.

$$\mathrm{y}={\mathrm{m}}_1+\frac{{\mathrm{m}}_2-{\mathrm{m}}_1}{1+{\left(\frac{\mathrm{x}}{{\mathrm{m}}_3}\right)}^{{\mathrm{m}}_4}}$$ (4)

The ADV and IC thresholds were defined as the pressures where the slope of the sigmoidal curve fit exceeded a predefined value (10⁻⁴ for raw MEP and 1 for IC). The predefined values were determined by observing the values of the derivative at the pressure threshold as determined by the two line intersection approach for a small subset of data. The predefined value was then applied to all of the data sets. The sigmoid derivative method was used in general because it is not as susceptible to variance in the experimental data. The locations of the derivative thresholds for both the ADV and IC curves are denoted in Fig. 5 by asterisks.

Fig. 5.

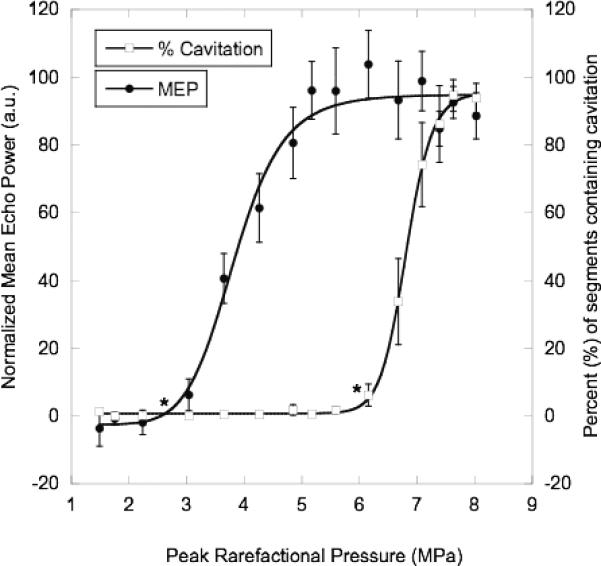
Mean (n=6) normalized MEP and IC data plotted along with the respective sigmoidal curve fits and standard deviation at each data point. The raw MEP data was normalized – vertically shifted by 10⁻⁴ and scaled by 10⁵ – to facilate display on this plot. The threshold for each curve is denoted by an asterisk (*). The following conditions were used: degassed water at 37°C with albumin-coated PFP droplets, 83 Hz PRF, and 13 cycles.

III. RESULTS AND DISCUSSION

A. Bulk Fluid Parameters

Table II displays the ADV and IC thresholds for albumin-coated perfluoro-n-pentane (PFP) droplets in different bulk fluids used. The thresholds in heparinized whole blood, water, and water-glycerol mixtures were measured to determine the impact of gas saturation, viscosity, and surface tension. Heparin (Elkins-Sinn Inc., Cherry Hill, NJ) was added to whole, canine blood (8 units per mL blood) to prevent coagulation; the blood was used within 2 hours of withdrawal. The ADV threshold is lower than the IC threshold for the presented cases (p < 0.001). In the case of gas saturation, both the ADV (p = 0.7) and the IC (p = 0.4) thresholds were not statistically different for the degassed and gas saturated conditions. Additionally, the presence of droplets caused the IC threshold to decrease for the degassed water condition while the IC threshold was not statistically different (p = 0.1) in the gas saturated water condition. Increasing the gas saturation of a highly filtered bulk fluid, containing polystyrene spheres as nuclei, is known to decrease the IC threshold for heterogeneous nucleation [26]. The rate at which a bubble dissolves increases as the dissolved gas concentration of the bulk fluid decreases; the dissolved gas concentration is also known to affect the nucleation threshold [26]. This lack of gas saturation dependence on the IC threshold may be explained with three relevant scenarios. First, the wettability of the albumin surface, adjacent to the bulk fluid, may be so high that there are few hydrophobic crevices with gas nuclei present. Second, there are still enough gas nuclei on the droplet exterior, even in the degassed fluid, to be above the critical concentration of nuclei necessary for IC. Third, IC occurs only when gas bubbles are present, presumably created via ADV. Therefore, since the ADV threshold did not display a dependence on gas saturation, then neither would the IC threshold. The ADV finding are consistent with results found by Kripfgans, who noted no difference in the ADV threshold in degassed or gas saturated fluids [27]. This result goes towards rejecting the hypothesis that heterogeneous nucleation causes the IC measured in this experimental setup.

Table II.

The effect of bulk fluid gas saturation, surface tension, and viscosity on the mean (n = 5) ADV and IC thresholds. All fluids were heated to 37°C and contained albumin-coated, PFP droplets at a concentration of 9×10⁴ droplets per mL. The IC threshold of gas-saturated water without droplets, tested under the same conditions, was 5.6±0.2 MPa while no IC was observed for degassed water without droplets.

Fluid	Gas Saturation (mmHg O2)	Density (g/mL)	Surface Tension (mN/m)	Viscosity (mPa·s)	Rarefactional ADV Threshold (MPa)	Rarefactional IC Threshold (MPa)
Water	60	0.995	72	0.7	2.7±0.2	5.7±0.4
Water	170	0.995	72	0.7	2.8±0.1	6.0±0.3
Whole Blood	141	1.059	48	5.0	3.6±0.3	7.1±0.1
Glycerol (60 wt%)	60	1.146	66.9	5.2	3.3±0.1	> 8.0
Glycerol (80 wt%)	60	1.199	65.7	24.7	3.8±0.2	> 8.0

In the tested cases, an increase in both the ADV and IC thresholds was observed in whole, heparanized canine blood as well as aqueous solutions of glycerol. The relationship between the IC threshold and fluid properties such as surface tension and viscosity has been derived by Holland and Apfel, assuming preexisting bubbles, where it was found that the IC threshold should increase with the viscosity [28]. Our data is qualitatively consistent with this as the IC threshold increased with increasing bulk fluid viscosity. Concerning surface tension, an experimental study by Holland and Apfel - which measured the IC cavitation threshold of polystyrene spheres in water or an ethylene glycol solution - noted a lower IC threshold in the ethylene glycol solution, which was attributed to the reduction in surface tension [29]. For submicron-sized nuclei, the effects of decreasing surface tension dominate, even in the case of increasing viscosity [28]. Given that the viscosity trend and not the surface tension trend was observed, it is likely that the IC nuclei for this experiment were not submicron in size, suggesting that the bubbles generated by ADV were the IC nuclei.

The ADV results in whole blood are consistent with previous findings [7]. No IC was observed in the glycerol solutions with PFP droplets for the tested pressures. Church proposes a higher IC threshold in blood due to the extra damping associated with the higher blood viscosity [30]. It is hypothesized that the bulk fluids of higher viscosity retard the expansion of the ADV nucleus, possibly even causing a recondensation of the vaporized nucleus at lower acoustic pressures. Therefore larger rarefactional pressures are required to overcome this effect.

B. Droplet Parameters

Apfel patented the use of superheated immiscible droplets in medical applications and experimentally showed that the vaporization threshold of such droplets can be controlled using chemical ad-mixtures [6]. Droplets composed of a highly superheated dispersed phase, relative to normal body temperature, could be vaporized with less energy than droplets with a lower degree of superheat. An example of this was published by Kawabata et al., in which the ADV threshold of a PFC emulsion was adjusted by varying the ratio of PFP to 2H,3H-perfluoropentane [12]; the latter component has a boiling point of 53.5°C. Table I lists the different PFC core materials that were tested in our experiments as a function of degree of superheat. The bulk fluid temperature was adjusted and it was assumed, due to the small size of the droplets, that the droplets equilibrated to the bulk fluid temperature before they were circulated to the focus of the vaporization transducer. The increase in droplet diameter from PFP to PFH to PFO is attributed to the increase in viscosity across the homologous PFC series, since increasing the viscosity of an emulsion phase causes an increase in particle size [31]. Unless otherwise stated, the droplets used in the experiments had a mean diameter as listed in Table I.

The behaviors of the ADV and IC thresholds as a function of superheat are displayed in Fig. 6. All tested cases reveal an ADV threshold that is lower than the IC threshold (p < 0.01 for both PFP and PFH droplets). For both thresholds, an inversely proportional trend exists when the droplets are not superheated. In the case of PFH droplets, the 95% confidence interval (CI) of the slope through the IC data, when the droplets are not superheated is [−0.07, −0.02] with the squared correlation coefficient (r²) equal to 0.99, thus indicating a non-zero slope. Once the droplets become superheated, the ADV threshold remains relatively constant (95% CI of the slope of the PFP data is [−0.03, 0.01]) and so does the IC threshold (95% CI of the slope of the PFP data is [−0.07, 0.01]). No ADV or IC was observed for PFP, PFH, or PFO droplets at 19°C, 25°C, and 63°C below their respective boiling points. An IC threshold was observed for PFP and PFH droplets at 11°C and 19°C, respectively, below boiling though no corresponding ADV was recorded. It is likely that both ADV and IC occurred in these cases, but the resulting bubbles of PFP or PFH gas either condensed or dissolved into the surrounding bulk fluid before reaching the linear array. Therefore using the setup seen in Fig. 1, there are three regions of activity for droplets that are not superheated: no ADV or IC detected, IC without detected ADV, and both ADV and IC detected. However, if the experimental setup allowed for the imaging of bubbles generated at the focus of the vaporization transducer, there are likely only two regions of activity – no ADV or IC and both ADV and IC. The functional dependence of IC on the degree of superheat, at least below the droplet boiling point, suggests that the event leading to IC is internal to the droplet. If the ADV or IC nucleus were external to the droplet, then the probability of an IC event external to the droplet should be relatively constant regardless of whether the droplet is or is not superheated.

Fig. 6.

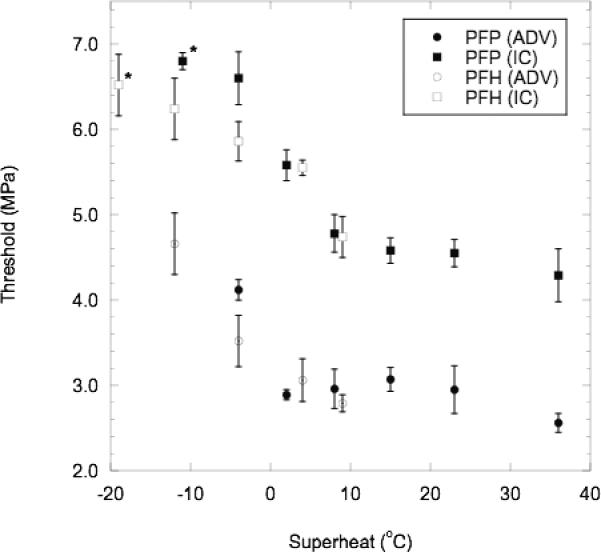
Mean (n=5) ADV and IC thresholds, plotted with standard deviations, for PFP and PFH droplets as function of degree of superheat. The points denoted with asterisks (*) are cases where IC was measured 11°C or 19°C below the boiling point of PFP or PFH, respectively – though no corresponding increase in MEP was recorded. The following conditions were used: degassed water with albumin-coated droplets, 83 Hz PRF, and 13 cycles.

Fig. 7 displays the relationship between the ADV and IC thresholds and the mean droplet diameter. Different droplet diameters were obtained by either centrifuging the droplets or by allowing the droplets to grow in diameter due to Ostwald ripening [5]. The ADV threshold is inversely proportional to the mean droplet diameter below 2.5 μm (95% CI of the slope is [−.99, −0.73], r² = 0.86); the ADV threshold then appears to plateau for droplets larger than 2.5 μm. The IC threshold is statistically constant for the size range tested (95% CI of the slope is [−0.45, 0.13]), and occurring at a higher rarefactional pressure than the ADV threshold (p < 0.001). It is important to note that the droplet distributions are not monodispersed in size, and thus the effect of a polydisperse distribution must be considered, such as the preferential vaporization of larger droplets for each distribution. A similar trend, as observed in Fig. 7, was obtained by plotting the ADV threshold versus d_10% or d_25%, defined respectively as the droplet diameter at which 10% or 25% of the droplets, by number, are larger than that diameter. Extrapolating based on the inverse relationship below 2.5 μm, it becomes apparent that submicron-sized droplets can be phase-transitioned below the corresponding IC threshold. Particle size is known to affect the IC threshold, with smaller diameter polystyrene spheres yielding higher IC thresholds than larger diameter polystyrene spheres [24]. The statistically similar IC threshold for the size range of droplets tested indicates that that despite an almost sixteen fold increase in the droplet surface area, the IC threshold does not decrease as the average droplet diameter increases. This suggests that the IC nucleation process involved in ADV is dissimilar to the nucleation process of IC of polystyrene spheres. It is speculated that IC nuclei are generated from the presence of gas pockets on the surface of the spheres, due to the hydrophobicity and surface roughness on the sphere. Considering the favorable wettability properties of albumin and lipid shells in the bulk fluid, as well as the high fluidity of the PFC in the dispersed phase, it may be likely that the presence of gas pockets, compared to polystyrene spheres, is minimal.

Fig. 7.

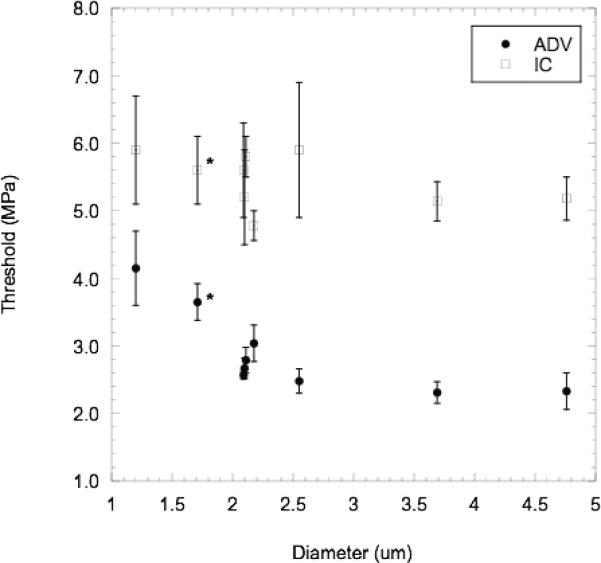
Mean (n=3) ADV thresholds and IC thresholds, plotted with standard deviations, for albumin-coated PFP droplets of various mean diameters. The points denoted with an asterisk (*) are lipid-coated droplets, whereas the other points are albumin-coated droplets. The following conditions were used: degassed water at 37°C, 83 Hz PRF, and 13 cycles.

Based on an approximate five-fold expansion of a droplet as it is vaporized into a gas bubble [7], a 1 μm and 10 μm droplet would yield a 5 μm and 50 μm bubble, respectively. Using an analytical model [28] the minimum acoustic rarefactional pressures required to produce IC in the aforementioned bubbles sizes, using a 3.5 MHz insonation frequency, are 3.77 MPa and 39.2 MPa, respectively. This is based on a collapse temperature of 5000 K and the surface tension, viscosity, and density of water as input parameters to the model; additionally, the heat capacity ratio of PFP at 37°C was determined to be 1.044 using the Universal Functional Activity Coefficient (UNIFAC) method in Aspen Plus software (Aspen Technology Inc., Cambridge, MA). For a micron-sized or larger bubble, the viscous and inertial effects of the surrounding fluid cause the IC threshold to increase as the diameter of the bubble (IC nucleus) increases. This range of computed values supports the hypothesis that gas bubbles generated by ADV can undergo IC due the application of US from the single-element transducer.

Fig. 7 also displays the effect of the shell material – albumin versus lipid – that is seemingly negligible relative to the mean diameter. For gaseous contrast agents, lipid shells, which are on average 1 to 2 nm thick, are more stable and inhibit diffusion due to their greater flexibility than albumin shells, which are on average 10 to 15 nm thick and more rigid [32]. If this is the case, then the smaller diffusion coefficients of liquid PFCs relative to gaseous PFCs coupled with the mechanistic differences between ADV and contrast agent destruction may render the effects of the shell negligible except for Ostwald ripening. This further indicates that the nucleation mechanism does not occur at the shell of the droplet.

C. Acoustic Parameters

The effects of the pulse repetition frequency (PRF) on the ADV and IC thresholds are shown in Fig. 8. In all cases, the ADV threshold is lower than the IC threshold (p < 0.001). Additionally, an inverse trend is observed for both thresholds below 25 Hz while the thresholds are statistically constant above 25 Hz (95% CI of the slopes of ADV and IC data are [−6.3×10⁻⁵, 3.0×10⁻⁴] and [−6.7×10⁻⁴, 4.8×10⁻⁴], respectively). The ADV and IC data above and below 25 Hz form two distinct populations with respective p-values of <0.03 and <0.02. The decrease in both thresholds, clearly seen from 10 to 100 Hz PRF, relates to the number of times a fluid volume passing the single element transducer is exposed to an acoustic pulse. The time needed for a new fluid volume to traverse the −6 dB beam width, based on the average flow speed within the tube, is 40 ms (or 25 Hz). Therefore, at PRF values less than 25 Hz each fluid volume is exposed to only a single pulse whereas above 25 Hz PRF each fluid volume is exposed to multiple pulses. The slowest and fastest particle velocities within the tube were estimated by calculating the rate at which the MEP increased and decreased from vaporized droplets for a specific US on-time (i.e. a bolus of ADV generated bubbles). The velocities were calculated from the known distance between the single-element transducer and the time delay between the single-element transducer on-time and the passage of bubbles in the linear array FOV; the single-element transducer on-time was also subtracted from the delay in the decreasing MEP. The time delays were calculated based on an MEP threshold, which was at least three-times the average MEP of the initial or final baselines (i.e. no bubbles present). Therefore, the behavior of the MEP was similar to Fig. 2, except that the MEP later decreased to the baseline value since the single-element transducer was turned off while the linear array was still recording. The slowest and fastest velocities were 1.2 cm·s⁻¹ and 4.3 cm·s⁻¹, corresponding to transit times of 67 and 19 ms, or fluid volume refresh rates of 15 and 53 Hz, respectively. Therefore, referring back to Fig. 8 and when considering the range of velocities in the flow tube, it becomes evident that when a fluid volume is exposed to multiple exposures of US, both the ADV and IC thresholds decrease relative to when a fluid volume is exposed to only a single pulse.

Fig. 8.

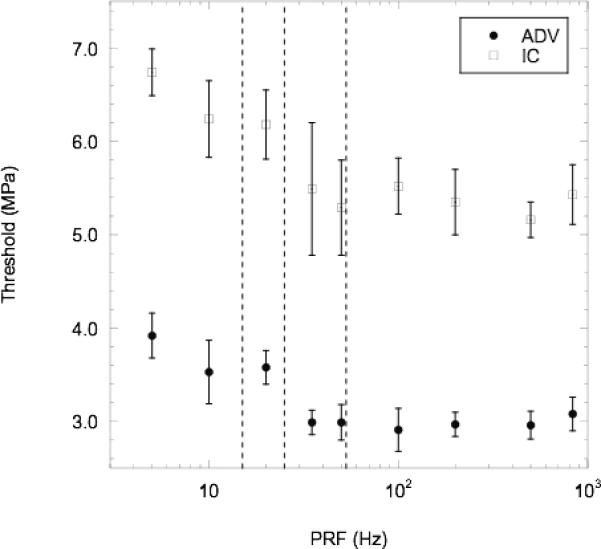
Mean (n=5) ADV and IC threshold, plotted with standard deviations, for various PRFs. The following conditions were used: degassed water at 37°C and 13 cycles. By comparison, the rate at which a new volume of fluid crossed the −6 dB beam width of the single-element transducer, based on the average flow velocity, was 25 Hz (middle dotted line). Therefore, PRFs less than 25 Hz exposed each fluid volume to only a single acoustic pulse from the single element transducer. The left and right dotted lines display the slowest and fastest rates, respectively, at which a fluid volume passes the single-element US beam width, based on the experimental data.

The effect of pulse width on the ADV and IC thresholds is displayed in Fig. 9. Two different PRFs – 10 Hz and 83 Hz – were chosen as cases where each flow volume was exposed to a single exposure versus multiple exposures, respectively. In both cases, for a given PRF, the ADV threshold was statistically constant (95% CI of the slopes for 10 Hz and 83 Hz are [−;0.003, 0.004] and [−0.006, 0.013], respectively) over the range of pulse widths tested, which is consistent with results by Lo et al. where the ADV threshold was relatively constant for microsecond pulse lengths [20]. Additionally, the IC threshold decreased as the pulse width increased, which could imply that longer pulse widths increase the probability of interacting with a bubble that can undergo IC, perhaps as a bubble begins to dissolve or fragment.

Fig. 9.

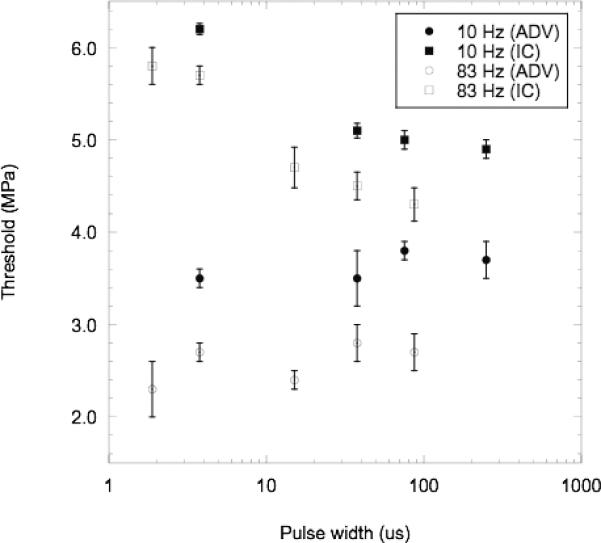
Mean (n=3) ADV thresholds and IC threshold (right), plotted with standard deviations, for various pulse widths at two different PRFs (10 Hz and 83 Hz). The following conditions were used: degassed water at 37°C and albumin-coated PFP droplets.

IV. CONCLUSIONS

The elucidation of the physical mechanisms involved in ADV can allow for the optimization of ADV in therapeutic applications such as embolotherapy and drug delivery. Since acoustic cavitation is one possible mechanism for ADV, it is important to understand the role of IC due to its bioeffects. As discussed previously, the minimization or maximization of IC, depending on the application, may be integral to the success of therapeutic ADV.

Table III is a summary of the presented results from Fig. 6 through 9. Based on these results, it is possible to relate the observed trends of the ADV and IC thresholds to physical mechanism of ADV. The possibilities are that IC helps initiate ADV, ADV helps initiate IC (possibly by providing a bubble), or the two events are totally uncorrelated. The correlation between ADV and IC varies for the tested parameters. For the case of PRF, ADV and IC are highly correlated with an r² of 0.94, which for nine data points yields less than a 0.1% probability, the percentage probability [33] (Prob_N), that the data points are actually uncorrelated. For droplet superheat, the r² values are 0.74 and 0.76 for PFP and PFH droplets, respectively; based on the number of data points, the Prob_N values are less than 5.6% and 20%, respectively. Alternatively, the ADV and IC thresholds are more uncorrelated in the cases of droplet diameter (r² = 0.12) and pulse width (r² = 0.39 for 10 Hz and r² = 0.21 for 83 Hz) where the Prob_N values are less than 43%, 40%, and 50%, respectively. Given that ADV and IC are correlated for some of the tested parameters, the next most important fact is that the ADV threshold is always less than the IC threshold. Thus an IC event is not necessary to cause vaporization, though it has been shown that IC nuclei, specifically US contrast agent, external to the droplet can lower the ADV threshold, which is beneficial in certain situations [20]. Instead it appears that ADV occurs and (possibly) provides a bubble that can then go through IC. The distinct nature of ADV and IC is also supported by examining the frequency dependence of ADV and IC. It was previously shown that the ADV threshold decreased as frequency increased [8], which is opposite of the theoretical behavior of the IC threshold [34] and the experimental results from Giesecke and Hynynen [22] for micron-sized PFC droplets. This may imply that the role of IC in ADV may change for lower frequencies since as the frequency decreases and the IC threshold in the host medium approaches the ADV threshold, IC could then be the dominant mechanism for triggering ADV.

Table III.

Summary of the effects of the various bulk fluid, droplet, and acoustic properties on the ADV and IC thresholds. Refer to Table II and Figs. 6–9 for each parameter and its corresponding ADV/IC data.

Properties	Parameter	ADV Threshold	IC Threshold
Bulk Fluid	Gas saturation	No effect	No effect
	Viscosity	Direct	Direct
Droplet	PFC superheat	Inverse (below boiling point) No effect (above boiling point)	Inverse (below boiling point) No effect (above boiling point)
	Diameter	Inverse (1–2.5 μm)	No effect
		No effect (2.5 – 5 μm)
	Shell	No effect	No effect
Acoustic	PRF	No effect (multiple US exposures)	No effect (multiple US exposures)
	Pulse width	No effect	Inverse

Knowing that ADV and IC are related, the next point of interest is to determine where the nucleation for ADV and IC occur. Since the IC threshold remained constant when the gas saturation of the bulk fluid was changed, as well as when the droplet diameter increased, it is likely that the nucleus for IC is not external to the droplet and may be the ADV bubble itself. This is supported by the IC threshold correlation with viscosity and not surface tension, which indicated that the IC nuclei were likely greater than one micron. However, high-speed photography would be needed to definitively verify this. Additionally, both thresholds are dependent on the degree of superheat of the dispersed phase, thereby suggesting that the nucleus of ADV or IC is within the droplet. This is further supported by the fact that the droplet shell material did not affect the ADV threshold. Interestingly, the viscosity of the bulk fluid – which is known to affect the IC threshold – also influenced the ADV threshold. It is possible that a viscous fluid retards the initial expansion of the gas bubble generated by ADV, even causing recondensation of the gas nucleus at lower rarefactional pressures due to increasing pressure within the collapsing gas nucleus. Overall, the IC threshold occurred at a higher rarefactional pressure than the ADV threshold. Therefore it is possible to operate with a given set of experimental parameters and achieve either ADV with IC or ADV without IC. The results suggest that the ADV nucleus is internal to the droplet and within the PFC phase while the IC nucleus may be the bubble generated by ADV.

Additional studies will be needed to further understand the initiation mechanism for ADV. This work can assist future in vivo studies by the selection of a droplet formulation and acoustic parameters that can be vaporized with or without IC, depending on the intended therapeutic application.