Application of a fast proton dose calculation algorithm to a thorax geometry

Abstract

Treatment planning in proton therapy requires the calculation of absorbed dose distributions on beam shaping components and the patient anatomy. Analytical pencil-beam dose algorithms commonly used are not always accurate enough. The Monte Carlo approach is more accurate but extremely computationally intensive. The Fast Dose Calculator, a track-repeating algorithm, has been proposed as an alternative fast and accurate dose calculation. In this work FDC is applied to a proton therapy patient thoracic anatomy.

1. Introduction

For some tumors proton therapy may reduce the risk of normal-tissue complications such as radiogenic second cancers. Such an advantage has led to a proliferation of proton cancer therapy centers worldwide. As of 2009, there are 30 operational hadron-therapy centers worldwide and 22 others are in various stages of construction or planning. Because of the sharp lateral and distal falloff of proton dose distributions, dosimetric and spatial accuracy in treatment planning is essential. Usually, commercial treatment plans calculate dose distributions with analytical pencil-beam dose algorithms (Schaffner et al., 1999), which do not always provide accurate results (Ciangaru et al., 2005). Analytical algorithms’ inaccuracies are most important in inhomogeneous media like the thoracic and head-and-neck anatomic sites. The Monte Carlo method provides superior accuracy (Titt et al., 2008; Koch et al., 2008), however it is very computationally intense. Hence its utilization for clinical treatment planning is challenging. The Fast Dose Calculator (FDC), a track-repeating algorithm (Yepes et al., 2009a,b), has been shown to provide accurate and fast dose calculations. FDC reproduces Monte Carlo dose calculations within 2%, while reducing computational times by more than two orders of magnitude. The objective of this study was to test the feasibility of applying FDC to the highly heterogeneous anatomy of the human thorax. Dose calculation improvements for that anatomic site might have an important impact in the accuracy of proton therapy treatment plans. The human thorax is a particularly challenging geometry due to the large inhomogeneities: high density areas, like bone, are contiguous to very low density media, like the lungs.

2. Methods

An irradiated patient, a range compensator and a collimating aperture were simulated in GEANT4 (Agostinelli et al., 2003; Allison et al., 2006) and FDC. The irradiated patient was represented as a voxelized phantom based on the CT images of the thoracic region of a typical patient who had previously been treated for lung cancer at The University of Texas M. D. Anderson Cancer Center. The phantom contained 6,064,305 voxels, each having dimensions of 1 × 1 × 2.5 mm³. Each voxel was assigned a material composition and density that corresponded to the Hounsfield unit value in the CT scan for that voxel, following the approach described elsewhere (Newhauser et al., 2008).

The field-defining collimating aperture (i.e., tumor-shaped block) and range compensator were also modeled. Only one of the fields utilized to treat the patient was implemented in the study. Moreover a 10 cm radius circular field with 140 MeV fixed energy was utilized for simplicity. The FDC algorithm and the computational facilities were described in previous studies (Yepes et al., 2009a,b). For the current study a DICOM interface was implemented in FDC, which allows the program to read the patient anatomy data and field definition directly from the files generated by the clinical treatment planning system.

3. Results

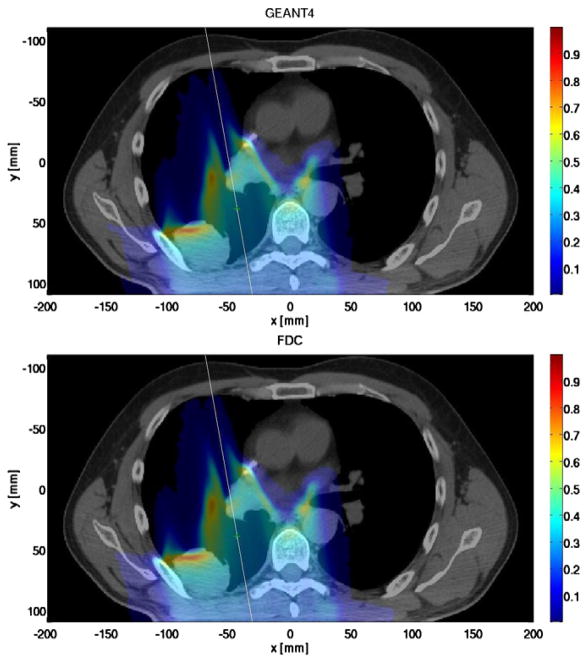
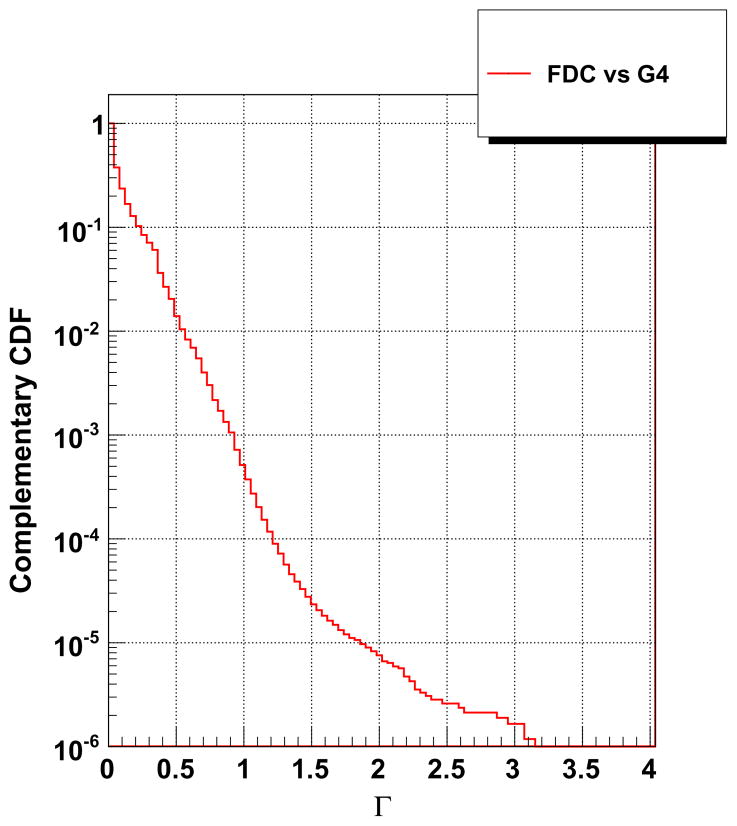
Fig. 1 shows the dose distribution through the axial plane (z = −17.5 mm) for both GEANT4 and FDC. Good agreement was observed between the doses calculated by each code. A more comprehensive comparison was obtained by calculating the Γ index of FDC relative to GEANT4 for each voxel (Low et al., 1998). A Γ value below unity is considered satisfactory. The Γ index results are presented in Fig. 2, as the complimentary cumulative distribution function such, that the ordinate represents the probability that Γ will be greater than the value of the abscissa. Less than 0.1% of the voxels had Γ values larger than unity. Thus, the dose distribution from FDC is in good agreement with the reference dose distribution from GEANT4. The time to process one history was 2.9 s and 0.9 ms for GEANT4 and FDC, respectively.

Fig. 1.

Dose distribution in a plane parallel to the circular mono-energetic 140 MeV proton field calculated with GEANT4 (top) and FDC (bottom) for a patient being treated for lung cancer.

Fig. 2.

The complementary cumulative distribution function of the Γ index for FDC using GEANT4 as reference for the phantom representing a patient being treated for lung cancer.

4. Conclusions

The dosimetric accuracy of FDC was tested in a particularly challenging anatomic geometry: the thorax. The acceptable level of agreement previously achieved for more homogeneous regions like the pelvis has been preserved. FDC shows gains up to a factor of one thousand with respect to GEANT4 for the patient phantom used in the study.