Validity of microsphere depositions for regional myocardial flows

Abstract

Due to the particulate nature of microspheres, their deposition in small-tissue regions may not be strictly flow dependent. To evaluate the importance of rheological and geometric factors and random error, their deposition densities in small regions of rabbit hearts were examined in comparison with those of a new “molecular microsphere,” 2-iododesmethylimipramine (IDMI), whose high lipid solubility allows it to be delivered into tissue in proportion to flow, and whose binding in tissue prevents rapid washout. ¹⁴¹Ce- and ¹⁰³Ru-labeled 16.5-µm spheres in one syringe and [¹²⁵I]- and [¹³¹I]DMI in another syringe were injected simultaneously into the left atrium of open-chest rabbits, while obtaining reference blood samples from the femoral artery. Hearts were removed 1 min after injection, cut into ~100 pieces averaging 54 mg, and the regional deposition densities calculated for each tracer from the isotopic counts. Correlations between the differently labeled microspheres were r > 0.95 and for the two IDMIs were >0.98. Scatter plots of sphere densities vs. IDMI densities showed that differences between microspheres and IDMI had substantial scatter, 0.87 < r < 0.96 and were not random. Microsphere depositions tended to be lower than IDMI depositions at low flows and higher at high flows. The tendency for spheres to be deposited preferentially in high-flow regions may be explained by a bias at bifurcations toward entering the branch with higher flow and secondarily toward entering those branches that are straighter. We conclude that microspheres are generally adequate for estimating regional flows but suffer systematic error when the regions of interest are supplied via arteries of diameters only a few times those of the microspheres.

Microspheres have in the past been considered to provide the “gold standard” for estimation of regional intramyocardial flows, principally because they are nearly 100% extracted during transorgan passage, and capillary beds in series are not found normally in the heart. Although there is little question that microspheres are good indicators of whole body or organ-to-organ distribution of flow, there has been some doubt that they provide an adequate measure of the heterogeneity of flows in small regions of the heart. Yipintsoi et al. (31) observed a tendency for 25- and 35-µm spheres to be delivered preferentially to subendocardial myocardium. From the theory of Fung (11) and Yen and Fung (29), and the hydraulic experiments of Chien et al. (8), one might expect greater deposition of microspheres in high-flow regions and less deposition in low-flow regions because at branch points spherical particles have a bias toward entering the higher-flow branch. This can explain the observations of Yipintsoi et al. (31), who found in dogs in which subendocardial flows were higher than subepicardial, that 25- and 35-µm spheres had disproportionately high subendocardial depositions compared with 15- and 10-µm microspheres. Also, inertial effects would tend to keep a microsphere moving along the straightest path, which might be toward the endocardium, since the feeding arteries are on the epicardial surface.

The particulate nature of microspheres results in both statistical and physiological problems. To obtain a reasonably accurate measure of regional deposition, Buckberg et al. (7) estimated that a minimum of 400 spheres/piece was needed to achieve a standard deviation <10%, although we in this study and Nose et al. (23) have experimental evidence that fewer are needed.

The physiological problem in using large numbers of spheres is their potential to obstruct flow. Large-sized spheres (25–50 µm) produce patchy ischemia (10), but small, less obstructing spheres (≤9 µm) can escape into the venous outflow (9), as do the rather heterogeneous albumin macroaggregates (25). Careful disaggregation of medium-sized microspheres (10–16 µm), using Tween 80 and sonification, as described by Heymann et al. (14), minimizes obstruction due to aggregation and maximizes their entry into capillaries in the rabbit ear (13) and the rabbit heart (2) where they cause very little problem. The required parsimony in numbers of injected spheres means that statistical error remains substantial. A fairly common practice of using relatively large pieces of myocardium, of the order of 1 g (e.g., 22) is a compromise providing more spheres per piece, but results in an underestimate of the true heterogeneity of flows since such large pieces are not internally uniform. In any case, although apparently satisfactory for measuring the distribution of cardiac output, microspheres have not yet been proven to provide an adequate measure of the heterogeneity of flows within the heart.

Preliminary studies (20, 21) on 2-iododesmethylimipramine (IDMI), a new gamma-emitting tracer, indicate that it is a good marker of regional flows in rabbit hearts. This molecular microsphere technique for the estimation of local flow provides for the first time an approach that is not subject to artifacts due to rheological or geometric effects on the delivery of particles into the microvasculature. Even if no artifacts were involved, the best information that microsphere deposition could provide would presumably be a measure of erythrocyte (particulate) flow that might differ from plasma or whole blood flows. In contrast, IDMI can be expected to be delivered to the tissue in proportion to local whole blood flow because it is carried by both plasma and erythrocytes (21). In organs where its extraction is complete, its deposition should provide an accurate measure of the local flow.

The purpose of this study is to provide an evaluation of the magnitude of errors in the microsphere method and to show whether the errors are random or systematic. The results show small random and systematic differences between microsphere distributions and the distributions of a marker soluble in blood. These errors are subtle and are not so large as to invalidate the microsphere method generally. The broad heterogeneity of flows indicated by the microsphere technique for rabbit ventricular myocardium is validated by the use of the molecular microsphere, IDMI.

METHODS

General Protocol

Experiments were performed in seven New Zealand White rabbits anesthetized with pentobarbital sodium (30 mg/kg). Following tracheal cannulation, both femoral arteries were cannulated using PE-90 tubing for the recording of arterial pressure and for blood sampling. The chest was opened via a midsternal incision, and a 10-cm length of PE-160 tubing for the injection of tracers was introduced 1.5 cm into the left atrium through the lumen of a large needle puncturing the tip of the left atrial appendage and held in place using a clamp at the site of entry. The outside portion of the tubing was then cut off to 2.5 cm and attached to a three-way stopcock for injection. Four different radioactive tracers (2 different microspheres mixed together in 1 syringe and 2 differently labeled IDMIs in another syringe) were injected precisely simultaneously via the two inflow ports to the stopcock, through the tubing, and into the left atrium, while obtaining a “reference organ” sample from one femoral artery to provide a measure of the cardiac output and absolute coronary blood flow. The tracers were injected over ~3–4 s, and the timing was recorded on photokymographic paper. All injections covered more than one cardiac cycle. After ~50 s, the sampling was stopped and the heart quickly removed, rinsed in physiological saline to remove superficial blood (most of that in the blood vessels), and frozen by immersion in liquid nitrogen. The hearts were sectioned in accordance with a standard scheme similar to that used for baboons (17). The left ventricle was divided into four rings from apex to base, each ring into eight sections, and each section into two or three slices from endo- to epicardium, for a total ≤96 pieces. The right ventricle was divided into four half rings from apex to base, and each ring into four sections for a total of ≤16 pieces. The pieces were identified so that three-dimensional reconstructions of the flow profiles might be made. The atria were not included in this study. Radioactivity in each piece was assayed with a high-resolution NaI detector and a multichannel analyzer system, providing 1,024-channel spectra for analysis with a Data General MV/10000 computer. A standard matrix inversion approach (16) was used to calculate the radioactivity due to each of the four isotopes and to background.

Tracer Methods

IDMI

The soluble deposition marker, IDMI, was synthesized as described by Little et al. (21). (Its noniodinated parent compound is the tricyclic antidepressant and α₂-adrenergic antagonist desipramine.) The molecular weight of [¹³¹I]DMI is 396; it is highly lipid soluble and only slightly soluble in water. [¹²⁵I]DMI and [¹³¹I]-DMI were prepared to provide specific activities of 12 and 8.4 Ci/mmole, respectively. The injection solutions contained ~20 µCi [¹³¹I]DMI (half-life = 8.06 days, γ peak energy 364 keV) and 7 µCi [¹²⁵I]DMI (half-life = 60.2 days, γ peak energy 35 keV). The radiochemical purity of IDMI was measured by high-performance liquid chromatography before each use and was always >98.5%.

Microspheres

The microsphere-injection solution contained ~13 µCi ¹⁴¹Ce-labeled spheres (half-life = 32.5 days, γ peak energy = 145 keV; ~8.72 × 10⁴ spheres/µCi) and 16 µCi ¹⁰³Ru-labeled spheres (half-life = 39.6 days, γ peak energy 497 keV; ~8.81 × 10⁴ spheres/µCi). The microspheres, from New England Nuclear (Cambridge, MA), were 16.5 ± 0.3 µm in diameter with specific gravities of 1.4 g/ml.

Injection technique

Microspheres were injected from a 1-ml tuberculin syringe and the IDMIs from a 1-ml glass syringe. (IDMI dissolves slowly into the rubber plungers of disposable tuberculin syringes.) Injections of the microspheres and IDMI were made simultaneously from the two syringes through a three-way stopcock (dead volume = 0.15 ml) into the left atrial cannula (dead volume = 0.04 ml). Different syringes were used because in a preliminary experiment we found that IDMI dissolves into polystyrene microspheres when in contact for several minutes.

Calibration of dose, q₀

Prior to injection each dose syringe was placed in a “high activity counting system” composed of an immobile receptacle 38 cm from a 3 × 3 in. NaI (Harshaw) probe. The syringes were oriented so that the axis of each syringe was perpendicular to, but centered on, the axis of the probe. The γ-ray spectrum from each syringe was acquired with a 1,024-channel multichannel analyzer (Tracor Northern Econ 700) and recorded on digital magnetic tape (Wangco model 8B). After injection, the residual activity in the syringes, stopcock, and atrial cannula was measured using the same system and the doses calculated from the difference between the initial and final activities.

Spectra for pure samples of each tracer in individual syringes were also recorded. These pure samples were then distributed into test tubes for later counting with the heart tissue and blood samples.

Sample counting

Each piece of tissue was placed in the bottom of a test tube. The radioactivity in each sample was measured in a 3 (diam) × 3 in. (deep) NaI well crystal (Harshaw) equipped with an automatic sample changer (Baird Atomic model 708). The γ-ray spectra, obtained over a 5-min counting period, were recorded using the previously described multichannel analyzer and digital recording unit. All sample spectra were corrected for background counts and the individual tracer activity was determined using a Gaussian elimination algorithm to invert the spillover coefficient matrix (16). This matrix inversion technique was used rather than spectrum stripping because it avoids the propagation of error inherent to the method of successive subtractions. In addition, it has the advantage of accounting for spillover by any nuclide into energy windows both above and below its own, which spectrum stripping does not permit. Finally, all activities of samples and doses were decay corrected to a common time point.

Sample activity was correlated to the activity in the injected dose using conversion factors calculated from the activities of the pure tracer samples counted in both counting systems.

Estimation of Blood Flows

Cardiac output and total cardiac flow

The cardiac output (CO; ml·min⁻¹) was calculated from the flow (F_ref; ml·min⁻¹) into the reference femoral sample syringes (averaging 7.61 ml·min⁻¹), the activity (q_ref; counts per minute), of the “reference organ” sample (collected over 50 s), and the injected dose, q₀ (counts per minute)

$$\text{CO}={\mathrm{F}}_{\text{ref}}·{\mathrm{q}}_0/{\mathrm{q}}_{\text{ref}}$$

Arterial dilution curves obtained from a second femoral artery showed <1% recirculation of IDMI, indicating high extraction and retention in body tissues. Myocardial total blood flow (F_H; ml/min) was calculated from the total amount of each tracer deposited in the ventricles, q_H; (counts per minute)

$${\mathrm{F}}_{\mathrm{H}}={\mathrm{F}}_{\text{ref}}·{\mathrm{q}}_{\mathrm{H}}/{\mathrm{q}}_{\text{ref}}$$

The average flow per gram of myocardium $({\mathrm{F}}_{\mathrm{H}}^{\prime })$ is F_H/M, where M is the mass (g) of both ventricles. (In this study we use F′ to denote flow per unit mass; F for flow in ml/min; and f, subscripted i or j, to denote regional flow per unit mass relative to the mean flow. Subscript j denotes individual pieces; i denotes classed groupings.)

Computation of local tracer deposition densities, flows, and their distributions

We calculate the local relative deposition densities for each piece of tissue from the concentration of a tracer in that piece divided by the mean concentration of that tracer over the entire ventricular myocardium. The organ was cut into a total of J pieces, whose total mass M is ${\displaystyle {\sum }_{j=1}^J{m}_j}$. Considering C_j, to be the activity in counts per minute in the jth piece of mass m_j, we calculate d_j, the local concentration in this piece relative to the mean concentration in the organ

$${\mathrm{d}}_j=\frac{{\mathrm{C}}_j/{\mathrm{m}}_j}{{\displaystyle \sum _{j=1}^J{\mathrm{C}}_j/\mathrm{M}}}$$ (1)

These values of d_j provide the raw data for the comparisons of microsphere deposition to IDMI deposition in each piece, as in Fig. 1. Because of the strong evidence that IDMI is delivered to and retained in the tissue in proportion to local flow, we make the overt assumption that the local IDMI depositions define the flow. Thus the local flow per unit mass of tissue relative to the mean flow for the organ is

$${\mathrm{f}}_j={\mathrm{d}}_j\text{for IDMI}$$ (2)

This is used in the scatter plots and for evaluating the correlation. The absolute flow per unit mass in each sample, ${\mathrm{F}}_j^{\prime }(\text{ml}·{\mathrm{g}}^{-1}·{\text{min}}^{-1})$, is

$${\mathrm{F}}_j^{\prime }={\mathrm{f}}_j·{\mathrm{F}}_{\mathrm{H}}(\text{ml}·{\text{min}}^{-1})/\mathrm{M}$$ (3)

FIG. 1.

Intraexperiment paired controls defining methodological error. A: linear scatter plot of [¹²⁵I]DMI vs. [¹³¹I]-DMI deposition densities d_j(¹³¹IDMI) in ventricular myocardium of 1 rabbit; r = 0.993; percent differences averaged 2.1 ± 1.6% (mean ± SD, n = 102). B: linear scatter plot of ¹⁴¹Ce-labeled microspheres d_j(¹⁴¹Ce) vs. ¹⁰³Ru-labeled microspheres deposition densities d_j(¹⁰³Ru) in same animal. For 102 pieces r = 0.976; percent differences averaged 6.4 ± 5.1%. Thus methodological error for microsphere deposition is about 3 times that for IDMI.

To calculate w(d), the probability density function (or frequency function) of relative regional deposition densities (in the case of the microsphere concentrations) or of relative regional flows (in accordance with our confidence in IDMI as a valid marker), the individual values of d_j are grouped into classes centered on d_i and of width Δd_i. (We use Δd_i, = 0.1, i.e., classes of width = 10% of the mean and denote the total number of classes as N.) Formally, w_i is the fraction of the organ per unit of d_i that falls into the Ith class, with class half-width 0.05

$$w_i=\frac{\begin{array}{c}\sum [{\mathrm{m}}_j\text{ for all }{\mathrm{d}}_j\text{ such that }\hfill \\ ({\mathrm{d}}_i-0.05)<{\mathrm{d}}_j<({\mathrm{d}}_i+0.05)]\hfill \end{array}}{\mathrm{\Delta }{\mathrm{d}}_i·{\displaystyle \sum _j{\mathrm{m}}_j}}$$ (4)

This gives the density function, w_i(d_i), in its finite class width histogram representation. Given a very large number of observations or very narrow class widths, the area under the curve w(d) is unity, and the deposition density or mean relative flow is also unity. Because the mean of the d_js in each class is not necessarily at the defined center of the class, the relationships are imperfect but in practice showed <1% in error

$$\text{area}={\displaystyle \sum _{i=1}^N{w}_i\mathrm{\Delta }{\mathrm{d}}_i\simeq 1.0}$$ (5)

$$\text{mean}\overline{\mathrm{d}}={\displaystyle \sum _{i=1}^N{\mathrm{d}}_i{w}_i\mathrm{\Delta }{\mathrm{d}}_i\simeq 1.0}$$ (6)

The spread of the distribution is calculated from the standard deviation, the square root of the variance

$$\text{standard deviation},\text{SD}={\left[{\displaystyle \sum _{i=1}^N{w}_i{({\mathrm{d}}_i-1.0)}^2\mathrm{\Delta }{\mathrm{d}}_i}\right]}^{½}$$ (7)

$$\text{relative dispersion},\text{RD}=\text{SD}/\overline{d}=\text{SD}$$ (8)

Testing of the hypothesis

The statistical test is to ascertain whether or not the pairs of d_js for the microspheres and the pairs of f_js for the IDMIs are more closely associated than are the microspheres to the IDMI. Using two IDMI’s and two microspheres simultaneously reduces the complexity of the statistics; a sign test sufficed for most evaluations. Linear regressions were based on the equal weighting of assumed random error in X and Y and so minimized the lengths of perpendiculars from the points to the line.

RESULTS

Mean Flows

In Table 1 are shown data on the mean flows in the heart in seven anesthetized open-chest rabbits. The heart weight was 0.18 ± 0.01% (means ± SD, n = 7) of body weight. The left ventricle (LV) comprised 70 ± 2% of the total heart weight, the right ventricle (RV) 20 ± 3%, and the atria 10 ± 3%. Atrial flows were not examined in this study, since there was some chance of artifact due to contamination of the atrial wall. The absence of atrial data should not detract from the interpretability of this study, since their mass is small and the flow per gram lower than in the ventricles (17). Cardiac outputs averaged 37 ± 21 ml·min⁻¹·kg⁻¹, and the total ventricular coronary flows averaged 0.64 ± 0.34 ml·g⁻¹·min⁻¹. The LV flow was higher, 0.68 ± 0.37 ml·g⁻¹·min⁻¹, and it received 83 ± 2% of the coronary flow. The relative flow per gram to the LV, ${\mathrm{F}}_{\text{LV}}^{\prime }/{\mathrm{F}}_{\mathrm{H}}^{\prime }$, averaged 1.06 ± 0.02, whereas for the RV the relative flow per gram was 25% less, 0.79 ± 0.06. There was less variation in these relative flows than in the absolute flows, consistent with what was observed earlier by King et al. (17) in baboons and consistent with a stability of relative regional flows in the heart. Just prior to the injections of IDMI and microspheres, the arterial pressures were 73 ± 33 Torr, heart rate was 198 ± 46 beats/min, and the stroke volume was 0.59 ± 0.24 ml.

TABLE 1.

Myocardial blood flows in rabbits

Animal No.	Body Wt, kg	Heart Wt,		Fraction of Heart Wt, %			Cardiac Output		Coronary Flow, ml·min−1·g−1	Regional Flows, ml·g−1·min−1		Fraction of Coronary Flow,%		Relative Flow
		g	% Body wt	LV	RV	A	ml/min	ml·min−1 ·kg−1		${\mathrm{F}}_{\text{LV}}^{\prime }$	${\mathrm{F}}_{\text{RV}}^{\prime }$	LV	RV	$\frac{{\mathrm{F}}_{\text{LV}}^{\prime }}{{\mathrm{F}}_H^{\prime }}$	$\frac{{\mathrm{F}}_{\text{RV}}^{\prime }}{{\mathrm{F}}_H^{\prime }}$
071185*	3.60	5.92	(0.16)	72	16	12	89.9	(25.0)	0.33	0.34	0.23	87	13	1.06	0.72
181185	3.95	6.75	(0.17)	69	17	14	22.6	(5.7)	0.16	0.17	0.14	83	17	1.03	0.89
121285	3.50	6.93	(0.20)	71	21	8	214.4	(61.3)	0.99	1.05	0.79	81	19	1.06	0.80
191285	3.55	6.45	(0.18)	73	19	8	71.8	(20.2)	0.40	0.42	0.32	83	17	1.05	0.80
090186	3.60	6.02	(0.17)	67	23	10	166.7	(46.3)	0.78	0.83	0.62	80	20	1.07	0.79
160186-1	2.60	4.69	(0.18)	69	24	7	159.3	(61.3)	1.02	1.12	0.72	82	18	1.10	0.71
160186-2	3.05	5.13	(0.17)	70	18	12	119.7	(39.2)	0.79	0.81	0.67	83	17	1.03	0.85
n	7	7	(7)	7	7	7	7	(7)	7	7	7	7	7	7	7
Means	3.41	5.98	(0.18)	70	20	10	120.6	(37.0)	0.64	0.68	0.50	83	17	1.06	0.79
±SD	±0.44	±0.83	(±0.01)	±2	±3	±3	±65.0	(±21.1)	±0.34	±0.37	±0.26	±2	±2	±0.02	±0.06

Atria were not included in flow calculations. All flow values derived from mean of 2 simultaneously injected IDMIs, expect as noted. Cardiac output is per kilogram body weight; myocardial flows, F′, are per gram myocardium, LV, left ventricle; RV, right ventricle; A, atrium; ${\mathrm{F}}_{\text{LV}}^{\prime }$ and ${\mathrm{F}}_{\text{RV}}^{\prime }$, average left and right ventricular blood flow, respectively; ${\mathrm{F}}_H^{\prime }$, average myocardial blood flow.

^*Only one IDMI tracer was used in this experiment.

The ventricles were cut into 99 pieces on the average; the average piece weight was 54 ± 27 mg (n = 691) with a range from 14 to 213 mg. The RV was less finely sliced than the LV.

In three animals (071185, 181185, 191285) the cardiac output, coronary flow, and blood pressure were low. Although these animals were not in a normal physiological state, their myocardial tracer distributions did not differ from those of the healthier animals. All animals were considered as valid vehicles for the test of the differences between IDMI and microspheres, for the test should be independent of both blood pressure and the absolute flow levels. The wide variability in conditions is an advantage in establishing the conclusions of the study.

Scatter Due to Methodology

The simultaneous injection of two types of microspheres and two differently labeled IDMIs provides separate methodological controls on the microsphere and IDMI depositions. The results for one experiment are shown in Fig. 1. Figure 1A shows the scatter plot of [¹²⁵I]DMI vs. [¹³¹I]DMI, the reference for the microspheres. The data are summarized in Table 2. There is less scatter with IDMI than with microspheres; the correlation coefficient for the two IDMIs shown here is 0.993 and for six hearts averaged 0.992 ± 0.005. (In 1 heart only 1 IDMI was injected.) The differences between the pairs of IDMI observations in each piece of tissue showed no particular trend toward greater or lesser differences in high- or low-flow regions. Calculated as the absolute value of the percent difference between the two observations of IDMI densities in one piece divided by their mean, the average difference for this heart was 2.1 ± 1.6% (n = 102) and for 6 hearts was 3.4 ± 5.2% (n = 611). This random error averaged about half of that seen with microspheres.

Table 2.

Heterogineity of depositions and flows

Animal No.	Linear Regression					Relative Dispersions of Flow Distributions, %
	IDMI r	Sphere r	Sphere vs. IDMI			IDMI	Microsphere
			slope	y-Intercept	r
071185		0.995	1.68	−0.56	0.940	28.8	41.8
181185	0.998	0.978	1.01	−0.01	0.871	39.5	40.0
121285	0.990	0.982	1.02	0.00	0.938	42.8	45.0
191285	0.995	0.982	1.16	−0.15	0.951	45.8	50.1
090186	0.994	0.951	1.18	−0.18	0.928	24.8	27.3
160186-1	0.993	0.976	1.61	−0.65	0.892	26.1	40.0
160186-2	0.984	0.969	1.32	−0.33	0.876	19.9	26.7
n	6	7	7	7	7	7	7
Means ± SD	0.992±0.005	0.976±0.014	1.28±0.27	−0.27±0.26	0.914±0.033	33±10	39±9

IDMI, iododesmethylimipramine. r, correlation coefficient.

Figure 1B shows the scatter plot of ¹⁴¹Ce vs. ¹⁰³Ru microspheres. There is an approximately linear relationship between the two microspheres over the entire range of flows. The slope of the best fitting regression line (assuming random error equally in both ordinate and abscissal values) was 0.95 ± 0.004. The correlation coefficient between the two sphere types was 0.976. The correlation coefficients between the two microspheres averaged 0.976 ± 0.014 for the seven animals, thus the example portrayed in Fig. 7 is representative. The differences in deposition densities between the two spheres averaged 6.4 ± 5.1% in this heart comprised of 102 ventricular pieces. For all seven hearts the differences averaged 6.5 ± 6.2% (n = 691). The percentage differences were also examined to determine whether or not there was more error in low- vs. high-flow ranges. The differences in microsphere depositions for the those pairs with deposition densities of <70% of the mean averaged 9.5 ± 9.9% (n = 127). With densities between 70 and 130% of the mean, the differences were 6.1 ± 5.0% (n = 399). For those pairs with average depositions >130% of the mean, the differences averaged 5.1 ± 4.4% (n = 159). So with microspheres we saw considerable variation at all flow ranges and significant random error at low flows.

Sources of error in depositions

In the heart illustrated in Fig. 1, there were on average ~695 ¹⁰³Ru- and ~520 ¹⁴¹Ce-labeled spheres deposited in each piece, or a range of 160–1,390 spheres of each type per piece over the observed range of d_j. For the seven hearts the average number was 348/piece (range 128–582) for ¹⁴¹Ce spheres and 450/piece (range 88–777) for ¹⁰³Ru spheres. The percent differences of the previous paragraph were considerably smaller than would have been predicted by the calculations of Buckberg et al. (7) in agreement with the analysis of Nose et al. (23).

Since all four isotopes were counted simultaneously in each piece of tissue with no chemical or other separation, we must question whether counting statistics and count separation techniques are the sole sources of error in the IDMI measurements. Since the specific activity of the IDMI in these experiments ranged from 5.8 to 13.6 Ci/mmole and the average total number of µCi injected was 27, the number of labeled molecules in the average piece was 4.9 × 10¹¹. Because this number is extremely high compared with the ~1,000 particles required to bring the error down to the 5% level (7), the variance cannot be ascribed to delivery of too few molecules to each piece. Although raw counting statistics of the data in Fig. 1 would suggest an error of not more than 1.0% for flows as low as 40% of the mean, a more realistic evaluation of the error should account for both variation in count rate and in the substantial spillover from counts due to other tracers in the same piece. The error for each tracer was approximated by the square root of each of the diagonal elements of the covariance matrix, computed as (A^TA)⁻¹, where A is the matrix of counting efficiencies in the four energy windows chosen for these tracers, times the total counting error. The error for the ¹³¹I was ~0.40% and for ¹²⁵I was 0.41%. The expected error of differences then between [¹²⁵I]DMI and [¹³¹I]DMI would be the square root of the sum of the squares of these errors, namely 0.57%, a value that is only slightly more than the observed error of the differences, 0.43%. The distinction between 0.57 and 0.43% is not statistically significant and leaves little room for error due to differences in delivery of the two molecules. These results are similar to those observed by King and Bassingthwaighte (17) and by Baer et al. (1).

With pieces sized from 20 to 100 mg, equivalent to ~20–100 microvascular units with over 3,000 capillaries each (3), hematocrit differences in the entering arterioles are possible, but since IDMI travels in both erythrocytes and plasma, errors due to local hematocrit changes should be small, as shown mathematically in the APPENDIX by Little et al. (21). There is no chemical difference between the two IDMIs, and variations in hematocrit entering different regions should not produce scatter.

Assessment of Microsphere Method by Comparison With IDMI Depositions

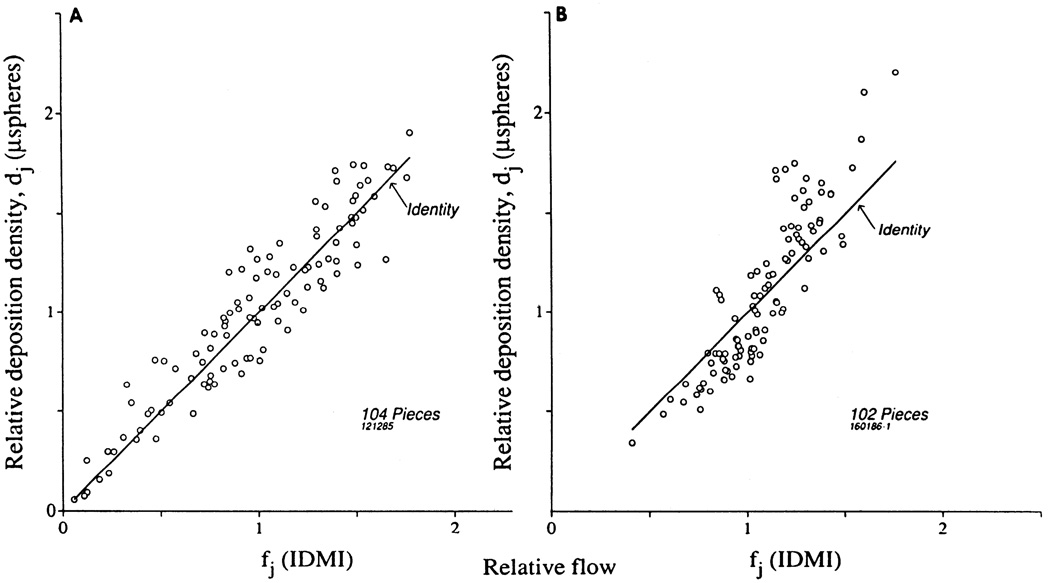
In Fig. 2 are shown the deposition densities for microspheres versus those for IDMI in two different hearts. The average of the deposition densities for the two differently labeled spheres was used to provide the best estimate of the microsphere deposition density. This was plotted against the average deposition density for the two IDMIs in the same piece. In both hearts there is substantial scatter around the line of identity, more than for either IDMI or microspheres themselves. Figure 2A shows the result with lowest sloped regression line. The data of Fig. 2B have a higher than average slope.

FIG. 2.

Microsphere deposition densities (d_j) vs. IDMI deposition densities (f_j), which are assumed equivalent to relative regional flow. Each d_j is average of 2 observations in each piece, as is each f_j. A: rabbit 1, mean ventricular flow $({\mathrm{F}}_{\mathrm{H}}^{\prime })=0.99\text{ml}·{\mathrm{g}}^{-1}·{\text{min}}^{-1};$ r = 0.938. B: rabbit 2, ${\mathrm{F}}_{\mathrm{H}}^{\prime }=1.02\text{ml}·{\mathrm{g}}^{-1}·{\text{min}}^{-1};$ r = 0.892. Regressions given in Table 2.

From the IDMI-to-IDMI percent differences (absolute values), averaging 3.4%, and the sphere-to-sphere percent differences, averaging 6.5%, one would anticipate IDMI-to-sphere differences of ~(3.4² + 6.5²)½ = 7.3%. However, the observed percentage differences between microspheres and IDMI deposition densities in these two hearts were 15.8 and 15.6% and for all hearts averaged 13.2 ± 3.5% (n = 7); therefore the difference is greater than can be attributed to random methodological variation. The differences between microspheres and IDMI are reproducible in that they are consistently larger than those between the pair of deposited microspheres or the pair of IDMIs is each piece of tissue, indicating systematic, nonrandom differences between the microspheres and the IDMI depositions.

The data from all seven animals are plotted in Fig. 3, the mean of the two microsphere depositions in each piece vs. the mean of the two IDMI depositions in the same piece (as in Fig. 2). The scatter on this plot is not discernibly different from the individual plots shown in Fig. 2; the correlation coefficient was 0.90 for the aggregate plot as compared with 0.91 ± 0.03 for the seven individual animals. The percentage differences between the microspheres and the IDMI averaged 13.4 ± 12.5% (n = 691) and were greater in low-flow regions and less in high-flow regions. The average absolute value of the difference between the two microspheres’ deposition densities in a given piece was 0.061 ± 0.054 (n = 691); the corresponding value for the two IDMIs was 0.029 ± 0.026 (n = 611). The absolute values of the differences in flow, |d_j (microspheres) − d_j(IDMI)|, averaged 0.128 ± 0.117 (n = 691). These differences were greater in high-flow regions and less in low-flow regions.

FIG. 3.

Microsphere deposition densities d_j vs. IDMI deposition densities f_j in ventricular myocardium of 8 open-chest rabbits. Each ordinate value represents mean of 2 deposition densities of microspheres in a given piece; abscissa values represent mean of two IDMI deposition densities. Best fitting regression line was d_j (spheres) = −0.067 + 1.087 f_j; r = 0.900, n = 691.

The conclusion from comparing the observations of Figs. 2 and 3 with those of the control data in Fig. 1 is that the delivery of microspheres to small regions of the myocardium was not governed by flow alone. The factors that lead to the observed systematic differences include geometric hindrance at entrances to vessels, biases in accord with flow proportionality at equivalent binary branch points, more complicated biases at multiple branchings, and possibly some relationship to local hematocrit variations, though these are anticipated to be small. The next question to be answered is whether or not these disturbances in microsphere deposition are so severe as to make microsphere deposition densities poor measures of the heterogeneity of regional flows in the heart.

Distributions of Deposition Densities and Flows from Microspheres and IDMI

Probability density functions for IDMI deposition densities and for microsphere deposition densities for one heart are shown in Fig. 4. The two IDMI density distributions (left panel) are seen to be quite similar, as anticipated from the small differences shown in Fig. 1. The differences between the two microsphere distributions (Fig. 4B) are somewhat greater than for the IDMIs, as expected, but both distributions have the same general form and are similar to those of the IDMIs.

FIG. 4.

Distributions of relative deposition densities d_i for 2 different IDMIs (A) and 2 different microspheres (B) in ventricular myocardium of 1 open-chest rabbit. Mean for each distribution is, by definition, 1. For clarity of presentation, the histograms are represented by polygons joining midpoints of classes. Standard deviations of distributions for IDMIs were 0.247 and 0.241 and for microspheres were 0.288 and 0.278.

The aggregate of the average IDMI distributions for the seven animals is shown in Fig. 5 as a histogram rather than as a polygon joining midpoints as in Fig. 4. The standard deviations for the observations in each class are shown. Such composite distributions for several animals must inevitably be broader than for the average individual distribution. The composite microsphere distributions for the seven animals are shown in Fig. 6 in the same fashion as were the IDMIs in Fig. 5. To allow comparison, the distribution of IDMI depositions from Fig. 5 is overlaid as a dashed polygon connecting the midpoints of each class.

FIG. 5.

Distribution of relative flows (from IDMI) in ventricular myocardium of 7 open-chest rabbits. Data are classed within intervals of 0.1 (10% of mean); w_i represents fractions of organ per unit mean flow having flows in specified class. Bars are standard deviations for n = 7. Values for each animal were calculated from mean of 2 IDMIs in each piece. Heterogeneity of flows is indicated by relative dispersion (standard deviation/mean) of 32% for distribution.

FIG. 6.

Distribution of relative deposition densities of microspheres in ventricular myocardium of 7 open-chest rabbits. Bars are standard deviations for each class of width Δd = 0.1 (n = 7 hearts), where values in each individual heart were taken from average of 2 microspheres in each piece. Dotted line gives mean IDMI distribution for comparison and is the same as that in Fig. 5. Relative dispersion of distribution is 45%.

It can be seen that the IDMI distribution is narrower than that of the microspheres (RD of 32 vs. 38%). It is also somewhat more symmetric (skewness of 0.03 vs. 0.27) and more highly peaked (kurtosis of 3.3 vs. 3.0), but the differences between the microsphere and IDMI distributions are not great.

Does methodological error contribute to the breadth of the sphere distributions? Because random errors averaged 6.4%, even though dividing the heart into small pieces tends to magnify error in the microsphere distributions, it may be safely said that microsphere distributions do not greatly exaggerate the observable heterogeneity of regional flows, if indeed they exaggerate it at all. As argued by King et al. (17), dividing the heart more finely will produce a more heterogeneous distribution of depositions of both IDMI and microspheres. Since both distributions must broaden with finer dividing, it cannot be said that microspheres are actually exaggerating the estimates of flow heterogeneity in these hearts, but it may be said that the IDMI distributions can slightly underestimate the true flow heterogeneity.

Patterns of Deposition

The identification of all individual pieces allowed reconstruction of the information with respect to location in the ventricles. Although limited by having only three pieces from endocardium to epicardium in the left ventricle, the profiles of deposition densities showed no consistent patterns, apex to base, endo- to epicardium, septum to free wall, or any particular high-flow or low-flow regions. This result is consistent with the findings in baboon hearts (17) but differs mildly from those of Prinzen (24) in dog hearts, which suggested somewhat higher microsphere deposition in the basal portion of the septum. Differences in microsphere deposition compared with IDMI showed no regional influences, apex to base or endo- to epicardium, although differences did relate to local flow. Thus microspheres and IDMI show close proportionality in all regions.

DISCUSSION

The main result of this study is to demonstrate that although there is less methological error in estimating regional myocardial blood flow with IDMI than with microspheres, microsphere deposition densities are, after all, not a bad measure of regional flows, even in these relatively small rabbit hearts. This is reassuring for users of microspheres and can be said to validate, with minor provisos, methodology that is being used widely. This is not to say that microsphere methods are error free, especially for smaller pieces of organs in small animals, but that in general, the technique works very well. This is particularly true for interorgan distributions, where it is likely that microspheres will continue to play an important role: molecular microspheres are not ready to replace them. At this stage no “molecular microsphere” has been identified that has been proven to be completely extracted in all organs and therefore provide a measure of whole body distributions of flows. Microspheres are imperfect at this as well, for their extraction is incomplete and their retention diminished with time (9). Nevertheless their extraction is high, seemingly always >90%, and their retention is prolonged, the losses of 15-µm microspheres being slower than that of IDMI over long times in blood-perfused organs. [But note that 9-µm microspheres may actually be lost more rapidly than DMI at early times, as suggested by comparing the data of Consigny et al. (9) with those of Little and Bassingthwaighte (20).]

Errors in IDMI distribution due to local variation in hematocrit should be small for two reasons. One is that there will be effects of hematocrit only if the feed hematocrit into different regions is different, something that is unlikely to occur among pieces as large as 50–100 mg. The second reason is that, although the IDMI red cell-to-plasma partition coefficient in most species is >1.0, even with the value of λ = 2.5 in rabbits (21) there is little bias toward regions with higher branch hematocrits. As outlined in the APPENDIX of Little et al. (21), a 40% change in hematocrit at a binary branch with equal flows to each would be reflected only by a 16% error in estimation of regional blood flow from IDMI deposition.

The data affirm the hypothesized systematic error in microsphere distributions, and demonstrate the theory of Fung and the experimental observations on tubes in vitro of Yen and Fung (29) and Chien et al. (8). The data from their artificial systems suggest that microspheres should preferentially enter a branch with higher flow than an otherwise equivalent branch. This is due to the fact that the pressure drop across the sphere at the branch point will be greater in the direction of the higher flowing stream and so bias it into that stream. To be sure, the vascular network is not made up of binary branching arteriolar trees with cylindrical symmetry and equal branch angles but is rather a more complex network with multiple branching and often with multitudinous sets of irregular branches within very short distances. The theory applies best to the branchings in tubes of diameters not much larger than those of the microspheres and has reduced applicability in large arterioles. The arterioles supplying regions of the size studied here, which contain roughly 160,000 capillaries and perhaps 20–100 terminal arterioles, are probably closer to 100 µm in diameter than to microsphere size (15–20 µM). Thus, even though the hypothesis probably cannot be examined with great acuity by these data, the data of Fig. 3 suggest the applicability of their theory and in vitro observations.

However, the biases are not very large for 15-µm diameter microspheres and have an insignificant effect on the estimates of flow distributions. The data of Yipintsoi et al. (31) and of Utley et al. (28) suggest that these biases in the distribution of microspheres should be larger for larger spheres. Both groups showed that subendocardial-to-subepicardial ratios of deposition densities were larger for larger spheres, this being quite marked for 35-µm spheres in the studies of Yipintsoi et al. (31). Yipintsoi et al. (31) interpreted their data on 35-vs. 15-µm spheres to support the thesis that biases were due to flow, and not demonstrably to geometry of the vasculature. The rationale for a geometric effect on microsphere distributions, as opposed to a flow effect, is that the subendocardial region is fed by straight vessels penetrating epicardium toward endocardium, and along which microspheres may be more likely to travel straight rather than taking the side branch. The rabbit heart’s thin-walled left ventricle is suitable for cutting only three slices of tissue from endocardium to epicardium. Thus the geometric question cannot be examined with any precision in rabbits. Accordingly we note that of those left ventricular pieces with deposition densities 20% or more above the mean, 34% were endocardial, 30% mid-wall, and 36% epicardial, which is to say that these data are totally inconclusive.

The results also affirm that the heterogeneity of regional flows in the ventricular myocardium is indeed broad despite the fact that the heart outwardly appears to function uniformly. In the four animals (121285, 090186, 160186-1, 160186-2) in the closest to normal physiological state (despite the thorax being open), the relative dispersions measured by IDMI were from 20 to 43%. These are in line with the observations of King et al. (17) showing relative despersions of 30% around the mean flow in hearts of awake baboons. We infer therefore that errors in the microsphere technique do not explain the spread. In fact, going back to earlier estimates of the heterogeneity, these distributions of flows are similar to those found by Bassingthwaighte, Dobbs, and Yipintsoi (3) and Yipintsoi et al. (31) in blood-perfused dog hearts, and by Hoffman and Buckberg (15), Rivas et al. (26), and Marcus et al. (22) in anesthetized dogs. Data from the washout of diffusible indicators gave similar results (3, 5, 30). We conclude that a broad heterogeneity of myocardial blood flows with relative dispersions of 20–40% are normal.

Accounting for flow heterogeneity is important in estimating rates of transmembrane flux, as shown by Bassingthwaighte and Goresky (4). Various methods of estimating flow variation from dilution curves have been used (27), but one may have greater confidence in analytic methodology in which the deposition data on regional flows has been obtained independently of the dilution curves which are being evaluated (e.g., 19). We therefore recommend using direct measures of flow heterogeneity in conjunction with the multiple indicator-dilution method for estimating parameters of transport and metabolism.