A Nonparametric Riemannian Framework for Processing High Angular Resolution Diffusion Images and its Applications to ODF-based Morphometry

Abstract

High angular resolution diffusion imaging (HARDI) has become an important technique for imaging complex oriented structures in the brain and other anatomical tissues. This has motivated the recent development of several methods for computing the orientation probability density function (PDF) at each voxel. However, much less work has been done on developing techniques for filtering, interpolation, averaging and principal geodesic analysis of orientation PDF fields. In this paper, we present a Riemannian framework for performing such operations. The proposed framework does not require that the orientation PDFs be represented by any fixed parameterization, such as a mixture of von Mises-Fisher distributions or a spherical harmonic expansion. Instead, we use a nonparametric representation of the orientation PDF. We exploit the fact that under the square-root re-parameterization, the space of orientation PDFs forms a Riemannian manifold: the positive orthant of the unit Hilbert sphere. We show that various orientation PDF processing operations, such as filtering, interpolation, averaging and principal geodesic analysis, may be posed as optimization problems on the Hilbert sphere, and can be solved using Riemannian gradient descent. We illustrate these concepts with numerous experiments on synthetic, phantom and real datasets. We show their application to studying left/right brain asymmetries.

1. Introduction

Diffusion weighted magnetic resonance imaging (DW-MRI) is an imaging technique that produces in vivo images of biological tissues by measuring the constrained diffusion of water molecules. DW-MRI exploits the fact that water diffusion is hindered less along fibrous structures because the molecules are less constrained by tissue barriers when they move in that direction. The signal intensity at each position depends on the local microstructure in which the water molecules diffuse, and the strength and direction of the applied magnetic field gradients. Multiple MR scans with varying gradient directions and diffusion weightings are used to estimate the complete diffusion profile of a tissue. As the directions of maximum diffusion indicate the structural anisotropy of the medium, DW-MRI may be used to infer the organization and orientation of tissue components. Many experiments have shown that water diffusion is anisotropic in organized tissues such as the spinal cord, muscles, heart or brain white matter. This has generated great enthusiasm, because DW-MRI is presently the only available approach to non-invasively study the three-dimensional architecture of human fiber pathways, and quantify their physical and geometrical properties.

Several techniques may be used to reconstruct the local orientation of the tissue from DW-MRI. One classical technique, diffusion tensor imaging (DTI) (Basser et al., 1994), characterizes the diffusivity profile by a single oriented 3D Gaussian probability distribution function (PDF). Water diffusion is represented mathematically with a symmetric positive definite (SPD) tensor field D: ℝ³ → SPD(3) ⊂ ℝ^3×3 that measures the extent of diffusion in any direction v ∈ ℝ³ as v^⊤Dv. DTI assumes a relatively simple diffusion model, but it has been successfully applied in regions of the brain and spinal cord with strong white-matter coherence, and has enabled the mapping of anatomical connections in the central nervous system (Basser et al., 2000; Hagmann et al., 2003). However, DTI models the diffusion with a single tensor, so it can only reveal a single dominant fiber orientation within each voxel. When fibers cross or bifurcate at a voxel, which is common in complex brain structures, DTI fails to provide accurate insights into the diffusivity profile or fiber geometry at that voxel.

Recent advances in diffusion MRI address this well-known limitation of DTI. In particular, high angular resolution diffusion imaging (HARDI) (Tuch, 2002) measures diffusion along n uniformly distributed directions on the sphere, and can characterize more complex fiber geometries. Several reconstruction techniques can be used to characterize diffusion based on the HARDI signals. One class is based on higher-order tensors (Barmpoutis et al., 2009; Ghosh et al., 2008), which model diffusivity using higher order polynomials and leverage prior work on DTI which used polynomials of degree two. Another approach reconstructs the orientation distribution function (ODF) from the HARDI measures. The ODF is the angular profile of the diffusion PDF of water molecules. Much current HARDI research focuses on computing the ODF from HARDI signals. One of the earliest methods, Q-ball Imaging (QBI), uses the Funk-Radon transform to estimate ODFs (Tuch, 2004). ODFs have also been approximated using different sets of basis functions such as spherical harmonics (SH) (Özarslan and Mareci, 2003; Descoteaux et al., 2007; Frank, 2002; Hess et al., 2006; Aganj et al., 2010). Such methods are relatively fast to implement because the ODF is computed analytically. Most of these methods model the ODF as a linear combination of basis functions. Consequently, the model parameters may be computed using linear least-squares optimization, rather than using expectation maximization. Besides spherical harmonics, ODFs may be approximated using the Poussin kernel (Rathi et al., 2009), where the optimal linear combination from a large function dictionary is found using matching pursuit. These methods normally do not assume a fixed upper bound on the maximum number of fiber crossings allowed at a voxel.

While many current efforts focus on computing ODFs accurately, much less work has been done on developing methods for processing these high-dimensional datasets, especially across subjects. That is, given a set of ODFs, how does one perform statistical analysis (e.g., principal components analysis), or basic operations such as interpolation, filtering and convolution? For DTI, the geometry of SPD(3) is well-studied and several metrics for comparing tensors have been proposed, including affine-invariant and log-Euclidean metrics (Arsigny et al., 2006; Kindlmann et al., 2007; Lenglet et al., 2006b; Pennec et al., 2006). Based on these metrics, several frameworks for processing tensor fields have been developed and applied to various topics in DTI. These studies have involved tensor estimation (Niethammer et al., 2006; Tschumperle and Deriche, 2003; Wang et al., 2004), processing (Arsigny et al., 2006; Batchelor et al., 2005; Fletcher and Joshi, 2007; Lenglet et al., 2006b; Pennec et al., 2006), segmentation and fiber tractography (Basser et al., 2000; Goh and Vidal, 2008a; Awate et al., 2007; Brun et al., 2004, 2003; Hagmann et al., 2003; Jonasson et al., 2004, 2007, 2005; Lenglet et al., 2006a; Savadjiev et al., 2006; Vemuri et al., 2001; Wang and Vemuri, 2005; Zalesky, 2008; Zhukov et al., 2003; Ziyan et al., 2006) and registration (Cao et al., 2005; Goh and Vidal, 2006; Guimond et al., 2002; Ruiz-Alzola et al., 2002; Zhang et al., 2006), as well as statistical tests such as voxel-based analysis of diffusion tensors (Buchel et al., 2004; Wang et al., 2006; Hua et al., 2008; Jahanshad et al., 2010). This work provided a better understanding of brain connectivity and differences in brain microstructure between populations of subjects. However, despite extensive research on DTI, the question of which metric is more appropriate for analyzing DTI data remains open. (Arsigny et al., 2006; Fletcher and Joshi, 2007; Lenglet et al., 2006b; Pennec et al., 2006) show that the proposed affine-invariant and log-Euclidean metrics avoid the “swelling effect” whereas the Euclidean metric allows swelling to occur. However, (Pasternak et al., 2010) found that the Euclidean metric is consistent with the expected statistical properties of tensor distributions, whereas the affine-invariant metric is not.

For HARDI, several metrics have been proposed for comparing different ODFs have been proposed, but metric selection remains challenging. Existing metrics include the Kullback-Leibler divergence (KLD) (Descoteaux and Deriche, 2009), the Jensen-Shannon divergence (JSD) (Chiang et al., 2008) and the Riemannian distance between a mixture of von Mises-Fisher distributions (McGraw et al., 2006). However, the KLD is difficult to compute for spherical data with high angular resolution and it also has to be symmetrized. Both the symmetrized version of the KLD (SKLD) and of the JSD do not obey the triangle inequality, so they are not proper metrics.

To our knowledge, there are very few existing frameworks for processing HARDI data. McGraw et al. (2006) represent the precomputed ODF with a mixture of von Mises-Fisher distributions whose parameters are computed by expectation-maximization. The authors compute distances and various Riemannian operations between different mixtures of von Mises-Fisher distributions using closed form formulae. However, this framework suffers from two major issues. First, the number of components in the mixture model is arbitrarily chosen. To find the optimal number of components, the difficult question of model selection must be addressed. Second, a nonlinear least-squares technique is used to compute the unknown parameters. This technique may be unstable when the complexity of the tissue increases, due to an increase in the number of parameters to be estimated. Our recent work (Goh et al., 2009b) addresses these issues by using a nonparametric Riemannian framework for HARDI processing. Instead of representing the ODF with a parametric model, we use the fact that, under the square-root re-parametrization, the space of ODFs becomes a convex subset of the unit Hilbert sphere. As such, various Riemannian operations are easily and efficiently computable. This allows one to develop several techniques for processing ODFs, such as filtering, interpolation and principal component analysis. After the publication of our initial conference paper (Goh et al., 2009b), a related framework was published independently in (Cheng et al., 2009). In this work, the authors approximate the square root of the ODF as a linear combination of orthonormal basis functions. Since the coefficients of this expansion live in a finite-dimensional sphere, processing operations can be performed in the space of coefficients with reduced computational complexity.

Paper Contributions and Outline

This paper presents a Riemannian framework for processing ODFs. We operate directly on the precomputed ODF and do not require that the ODF be represented by any parametric model, such as a mixture of von Mises-Fisher distributions. This framework allows us to do population studies - more precisely, ODF-based morphometry - a generalization of voxel-based morphometry. Experimentally, we found that the Riemannian ODF-based morphometry is more sensitive in capturing the variations of the data compared to ODF morphometry based on the Euclidean metric. This paper proceeds as follows. In §2.1 we illustrate the Riemannian structure of the space of ODFs. We exploit the fact that ODFs are PDFs defined on the 2-sphere and that, under the square-root re-parametrization, the space of ODFs forms a Riemannian manifold, namely the unit Hilbert sphere. Therefore, various Riemannian operations such as the exponential map, logarithm map and geodesics are not only available in closed form, but also easily and efficiently computable. §2.2 shows how to calculate the (weighted) mean of an ODF field. §2.3–2.4 show that spatial interpolation and convolution reduce to weighed averaging in the space of ODFs. §2.3 illustrates how to spatially interpolate ODFs on regular and non-regular grids. §2.4 shows how to perform convolution and (isotropic) filtering on an ODF field, followed by anisotropic filtering. §2.5 shows how to calculate the covariance and principal components of an ODF field and generalizes the Hotelling’s T-squared statistic for performing multivariate hypothesis testing on two populations of ODFs. §3 presents experimental results for our processing framework. Experiments are shown for synthetic, phantom, and real HARDI brain data, with illustrative tests of brain asymmetry. §4 is the conclusion.

2. Material and methods

2.1. The Riemannian Manifold of Orientation Distribution Functions

As mentioned previously, HARDI measurements can be used to reconstruct the orientation distribution function (ODF) - the angular profile of the diffusion PDF of water molecules. The ODF is actually a PDF on the 2-sphere and therefore, the manifold structure of the ODFs should be considered. We refer the reader to Appendix A which shows how to convert HARDI signals to ODFs. In this section, we study the Riemannian geometry of the space of PDFs on the 2-sphere ,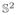

$$\mathcal{P}=\{\mathit{p}:{\mathbb{S}}^2\to {\mathbb{R}}^{+}\mid \forall \mathit{s}\in {\mathbb{S}}^2,\mathit{p}(\mathit{s})\ge 0;{\int }_{\mathit{s}\in {\mathbb{S}}^2}\mathit{p}(\mathit{s})d\mathit{s}=1\},$$

and show that, under the square-root representation, various Riemannian operations can be computed in closed form. To study probability and information theory from a differential geometric point of view, Rao (1945) introduced the Riemannian structure formed by the statistical manifold whose elements are probability density functions. Rao (1945) also showed that the Fisher-Rao metric defined below, determines a Riemannian metric,

$${\langle {\mathit{q}}_j,{\mathit{q}}_k\rangle }_{{\mathit{p}}_i}={\int }_{\mathit{s}\in {\mathbb{S}}^2}{\mathit{q}}_j(\mathit{s}){\mathit{q}}_k(\mathit{s})\frac{1}{{\mathit{p}}_i(\mathit{s})}d\mathit{s},$$ (1)

where q_j, q_k ∈ T_pi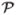 are tangent functions to 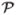at the point p_i. As shown in (Cencov, 1982), this metric is the unique intrinsic metric on the statistical manifold 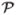, therefore it is invariant to re-parameterizations (essentially coordinate transforms) of the functions. However, this representation is difficult to work with as the geodesic between two elements is hard to compute (Srivastava et al., 2007).

Even though the space is difficult to work with, it is not the only possible representation for PDFs. In this paper, our choice of the parameterization is the square-root representation, used in (Goh et al., 2009b; Cheng et al., 2009; Goh and Vidal, 2008b; Srivastava et al., 2007). The main reason for this choice is that the resulting manifold is a unit sphere in a Hilbert space, and the Fisher-Rao metric is the metric (using the usual inner product between functions). Therefore, the various Riemannian operations such as geodesics, exponential maps, logarithm maps are available in closed form.

The square-root density function is defined as

$$\mathit{\psi }(\mathit{s})=\sqrt{\mathit{p}(\mathit{s})},$$ (2)

where ψ(s) is assumed to be non-negative to ensure uniqueness. The space of such functions is defined as:

$$\mathbf{\Psi }=\{\mathit{\psi }:{\mathbb{S}}^2\to {\mathbb{R}}^{+}\mid \forall \mathit{s}\in {\mathbb{S}}^2,\mathit{\psi }(\mathit{s})\ge 0;{\int }_{\mathit{s}\in {\mathbb{S}}^2}{\mathit{\psi }}^2(\mathit{s})d\mathit{s}=1\}.$$ (3)

From Eqn. (3), the functions ψ lie on the positive orthant of a unit Hilbert sphere, as shown in Fig. 1¹. Making use of the representation in Eqn. (3) and the fact that Riemannian metrics are determined up to a constant scaling factor, we can rewrite Eqn. (1) and obtain the Fisher-Rao metric as the metric

Figure 1.

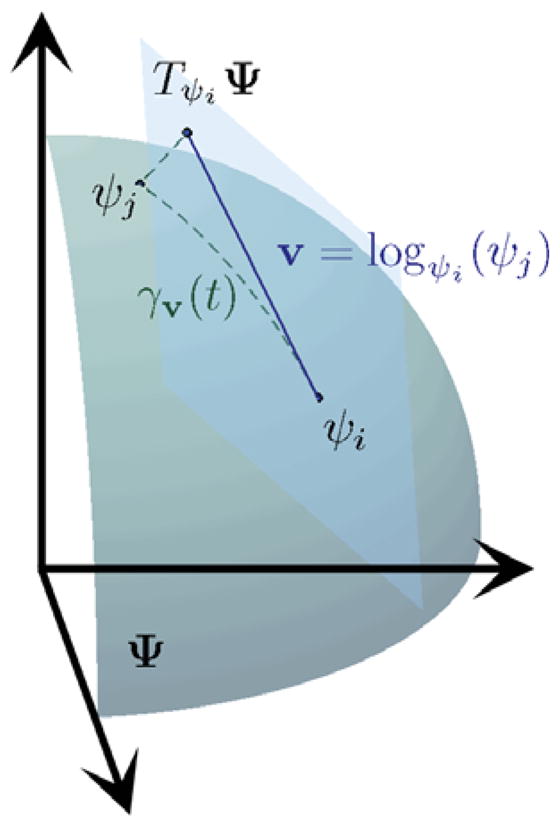
Square root representation of ODFs. The tangent plane at ψ_i, together with the exponential and logarithm maps relating ψ_i and ψ_j, are also shown.

$${\langle {\mathit{\phi }}_j,{\mathit{\phi }}_k\rangle }_{{\mathit{\psi }}_i}={\int }_{\mathit{s}\in {\mathbb{S}}^2}{\mathit{\phi }}_j(\mathit{s}){\mathit{\phi }}_k(\mathit{s})d\mathit{s},$$

where φ_j, φ_k ∈ T_ψiΨ are tangent vectors. The tangent space of Ψ at a point ψ ∈ Ψ, denoted as T_ψΨ, is defined as the span of the tangent vectors for all the possible smooth curves γ, γ (t): ℝ → Ψ, passing through ψ. A curve between ψ_i and ψ_j with minimum length is called a geodesic. The advantage of choosing the square-root density becomes obvious, as many of the Riemannian operations for the unit Hilbert sphere are well-known and computable in closed-form as we show next.

We define the exponential map exp_ψi: T_ψiΨ→ Ψ, which maps each tangent vector tφ∈ T_ψiΨ to the point γ (t) ∈ Ψ obtained by following the geodesic γ (t) (parametrized with arc-length) passing through ψ_i with direction φ for a distance t. For the sphere, the exponential map has the closed-form formula,

$${exp}_{{\mathit{\psi }}_i}(\mathit{\phi })=cos({\left|\right|\mathit{\phi }\left|\right|}_{{\mathit{\psi }}_i}){\mathit{\psi }}_i+sin({\left|\right|\mathit{\phi }\left|\right|}_{{\mathit{\psi }}_i})\frac{\mathit{\phi }}{{\left|\right|\mathit{\phi }\left|\right|}_{{\mathit{\psi }}_i}},$$ (4)

where φ ∈ T_ψiΨ is a tangent vector at ψ_i and

$${\left|\right|\mathit{\phi }\left|\right|}_{{\mathit{\psi }}_i}=\sqrt{{\langle \mathit{\phi },\mathit{\phi }\rangle }_{{\mathit{\psi }}_i}}.$$

By restricting ||φ||_ψi such that the geodesic γ(t) lies in the positive orthant, we ensure that the exponential map is bijective. Note that the range of ||φ||_ψi depends on ψ_i.

Next, we define the set C_ψi ⊂ Ψ as the set of all the points ψ_j = exp_ψi(t₀φ) such that γ = exp_ψi(tφ) is a length-minimizing geodesic for t ∈ [0, t₀]. The boundary of C_ψi is called the cut locus, and, intuitively, it is the set of points for which the distance from ψ_i stops to be a differentiable function of t. The exponential map is therefore invertible for all the points in the interior of C_ψi and we can define the logarithm map log_ψ: C_ψ → T_ψΨ as ${log}_{\mathit{\psi }}={exp}_{\mathit{\psi }}^{-1}$. The logarithm map from ψ_i to ψ_j has the closed-form formula,

$$\overrightarrow{{\mathit{\psi }}_i{\mathit{\psi }}_j}={log}_{{\mathit{\psi }}_i}({\mathit{\psi }}_j)=\frac{{\mathit{\psi }}_j-\langle {\mathit{\psi }}_i,{\mathit{\psi }}_j\rangle {\mathit{\psi }}_i}{\sqrt{1-{\langle {\mathit{\psi }}_i,{\mathit{\psi }}_j\rangle }^2}}{cos}^{-1}\langle {\mathit{\psi }}_i,{\mathit{\psi }}_j\rangle .$$ (5)

Now, we show how to compute the various Riemannian operations in Ψ, to evolve (or “march”) along its geodesic curves. For any two functions ψ_i, ψ_j ∈ Ψ, the geodesic distance between these two points on a unit Hilbert sphere is simply the angle between them,

$$\text{dist}({\mathit{\psi }}_i,{\mathit{\psi }}_j)={\left|\right|{log}_{{\mathit{\psi }}_i}({\mathit{\psi }}_j)\left|\right|}_{{\mathit{\psi }}_i}={cos}^{-1}\langle {\mathit{\psi }}_i,{\mathit{\psi }}_j\rangle ={cos}^{-1}\left({\int }_{\mathit{s}\in {\mathbb{S}}^2}{\mathit{\psi }}_i(\mathit{s}){\mathit{\psi }}_j(\mathit{s})d\mathit{s}\right),$$ (6)

where 〈·, ·〉 is the normal dot product between points in the sphere under the 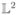metric. For any two points ψ_i, ψ_j ∈ Ψ, the geodesic curve γ from ψ_i to ψ_j is contained in Ψ. Therefore, from the definition of convexity for Riemannian manifolds (Berger, 2003), Ψ forms a convex subset of the unit Hilbert sphere.

2.2. Computing the mean of a set of ODFs

As we show later, many ODF processing operations, such as filtering and convolution, reduce to averaging a set of ODFs. Moreover, the average of a set of ODFs is also important for statistical analysis of group differences. Next, we show how to compute a weighted mean of a set of ODFs.

As defined by Frechet (1948), for a Riemannian manifold, the intrinsic mean ψ̄ of a set of n points ${\{{\mathit{\psi }}_i\}}_{i=1}^n$ is the solution to the following minimization problem

$$\overline{\mathit{\psi }}=\underset{\mathit{\psi }\in \mathbf{\Psi }}{argmin}\frac{1}{n}\sum _{i=1}^n\text{dist}{(\mathit{\psi },{\mathit{\psi }}_i)}^2.$$ (7)

Similarly to Eqn. (7), the weighted Karcher mean is defined as

$$\overline{\mathit{\psi }}=\underset{\mathit{\psi }\in \mathbf{\Psi }}{argmin}\frac{1}{2}\sum _{i=1}^n{w}_i\text{dist}{(\mathit{\psi },{\mathit{\psi }}_i)}^2,$$ (8)

where the weights are chosen such that w_i ≥ 0 and ${\sum }_{i=1}^n{w}_i=1$. Cheng et al. (2009) proved that the weighted Riemannian mean is unique and exists for Ψ. We refer the reader to Appendix B for more details. Notice that when $w_i=\frac{1}{n}$, ψ̄ becomes the intrinsic mean. The gradient of the cost function is given as $\text{grad}\frac{1}{2}{\sum }_{i=1}^n{w}_i\text{dist}{(\mathit{\psi },{\mathit{\psi }}_i)}^2={\sum }_{i=1}^n{w}_i{log}_{\overline{\mathit{\psi }}}({\mathit{\psi }}_i)$. In addition, the (weighted) mean is characterized by $\text{grad}\frac{1}{2}{\sum }_{i=1}^n{w}_i\text{dist}{(\mathit{\psi },{\mathit{\psi }}_i)}^2=\mathbf{0}$, that is, ψ̄ is the unique solution to

$$\sum _{i=1}^n{w}_i{log}_{\overline{\mathit{\psi }}}({\mathit{\psi }}_i)=\mathbf{0}.$$ (9)

Since the exponential and logarithm maps are known (Eqn. (4) and (5)), it is possible to compute ψ̄ using geodesic marching, as detailed in Algorithm 1. Algorithm 1, which iteratively searches for a point ψ̄ which satisfies the condition in Eqn. (9), is equivalent to doing a simple gradient descent, and has a linear rate of convergence. Other algorithms to compute the mean with better convergence rates have also been proposed (Buss and Fillmore, 2001; Absil et al., 2008). In the next section, we show that interpolation and linear convolution of ODF fields reduce to weighted Karcher averaging.

Algorithm 1.

Weighted Karcher Mean

Given data points ψ 1, …, ψn ∈ Ψ, weights w1, …, wn, a predefined threshold ε, and a maximum number of iterations T, Initialize t = 1, ψ̄1 = xi for a random i and φ= 0. While t ≤ T or ||φ||ψ̄ ≥ ε, Compute tangent vector $\mathit{\phi }={\sum }_{i=1}^n{w}_i{log}_{{\overline{\mathit{\psi }}}_t}({\mathit{\psi }}_i)$, Set ψ̄t+1 = expψ̄t (λφ), where λ is the learning rate. Buss and Fillmore(2001) proved that λ = 1 is sufficient for convergence.

Before proceeding further, notice that when computing of the Riemannian weighted mean ψ̄ of continuous PDFs on the sphere is cumbersome, as one needs to compute the dot products between ψ’s and this involves an integral over the 2-sphere 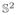. One way to deal with this computational complexity, as proposed by Goh et al. (2009b), is to discretize the PDF and use the square root of histograms. In this case, the Hilbert sphere becomes a finite dimensional sphere and the dot products become summations. The complexity is now a function of the number of bins. Another method, proposed by Cheng et al. (2009), is to approximate the square-root ODF ψ as a linear combination of the first N orthonormal basis functions, i.e., $\mathit{\psi }(\mathit{s})\approx {\sum }_{i=1}^N{c}_i{B}_i(\mathit{s})$, where ${\{B_i(\mathit{s})\}}_{i=1}^{\infty }$ is any orthonormal basis set and {c_i} are the coefficients. Existing literature (Cheng et al., 2009; Descoteaux et al., 2007) propose to used SH basis with orders = 4, 6, 8 with corresponding N = 15, 28, 45 to represent ODFs. The (truncated) spherical harmonics basis is chosen in (Cheng et al., 2009), where the order of the basis is set at a predetermined value of N = 15, and the coefficients are calculated in the least-squares sense. Cheng et al. (2009) noted that since the spherical harmonics functions are orthogonal, in this case, the Hilbert sphere also reduces to a finite-dimensional sphere and the theoretical results of the Riemannian framework, such as the uniqueness of the mean, hold true. Therefore, instead of working with ψ, one can work with {c_i}. The advantage of using such a representation is that it is more efficient and computationally simpler, as the complexity is a function of the number of coefficients considered. Computationally, it may be more efficient to deal with the second alternative, as the number of coefficients is typically smaller than the number of bins. If one works with the discrete histograms and due to the high dimension, the iterative Riemannian operations will require more computational power. However, both approximations incur some errors relative to the continuous domain, and it is not clear which approximation is better. The coefficients would still need to be computed from histograms, so there is also an additional cost of computing the coefficients. It is not clear which method is more efficient or more accurate. In this paper, we choose to work with the discrete square-root of histograms directly.

2.3. Interpolation of ODF Fields

Interpolation is one of the most important operations in image processing. In general, almost any geometric transformation such as translation, rotation, scaling, or warping, requires interpolation of an image or volume. Here we show how to interpolate a given ODF field. As reported in (Chiang et al., 2008), spatial interpolation of ODFs is a new issue.

While trilinear interpolation has been previously used in (Chiang et al., 2008), in this paper, we show how to do spatial interpolation on regular and non-regular grids. We concentrate on linear, bilinear and trilinear interpolation of ODF fields. However, the same analysis can be extended to more sophisticated forms of interpolation such as polynomial interpolation, spline interpolation, radial basis function interpolation and kriging.

We first examine bilinear, trilinear and multi-dimensional interpolation. We assume that we have known data at the m points in an n-dimensional grid. In the standard Euclidean case, multi-dimensional interpolation of a signal ψ at a point x = [x₁, …, x_n] is defined as

$$\mathit{\psi }(\mathit{x})=\sum _{j=1}^m{w}_j(\mathit{x})\mathit{\psi }({\mathit{x}}_j),$$ (10)

where x_j = [(x_j)₁, …, (x_j)_n] are the coordinates of the endpoints, ψ(x_j) are the corresponding signal values and w_j(x) are the interpolation weights. One can show that

$$\mathit{\psi }(\mathit{x})=\underset{\mathit{\psi }\in \mathbf{\Psi }}{argmin}\sum _{j=1}^{2^n}{w}_j(\mathit{x}){\left|\right|\mathit{\psi }({\mathit{x}}_j)-\mathit{\psi }\left|\right|}^2.$$ (11)

Therefore, we can define multi-dimensional interpolation ψ(x) for a Riemannian manifold Ψ as

$$\mathit{\psi }(\mathit{x})=\underset{\mathit{\psi }\in \mathbf{\Psi }}{argmin}\sum _{j=1}^{2^n}{w}_j(\mathit{x})\text{dist}{(\mathit{\psi },\mathit{\psi }({\mathit{x}}_j))}^2.$$

Notice that ψ is the Riemannian weighted mean of {ψ(x_j)}, which can be computed using Algorithm 1.

In the case of a regular grid ${\cup }_{i=1}^n[x_{i,1},x_{i,2}]$, m = 2ⁿ and the weights are simply given by $w_j(\mathit{x})={\prod }_{i=1}^n\left(1-\frac{\mid x_i-{(x_j)}_i\mid }{x_{i,2}-x_{i,1}}\right)$. In the case of a non-regular grid, we can either use simple nearest-neighbor interpolation where $\mathit{\psi }(\mathit{x})=\mathit{\psi }({\mathit{x}}_j^{\ast })$ and ${\mathit{x}}_j^{\ast }$ is the nearest neighbor of x. Alternatively, we can estimate the unknown values via the inverse distance weighting (IDW) method (Shepard, 1968), which is based on the assumption that observations further away should have their contributions diminished according to how far away they are. Specifically, Shepard (1968) defines the interpolation weights as $w_j(\mathit{x})=\frac{K{(\mathit{x},{\mathit{x}}_j)}^{-p}}{{\sum }_{i=1}^{m}K{(\mathit{x},{\mathit{x}}_j)}^{-p}}$, where K is a given metric operator (distance) from x_j to x, and p is a positive real number, called the power parameter. An example of K is K(x, x_j) = dist(x, x_j).

2.4. Convolution and Filtering of ODF Fields

Convolution is used for many image processing tasks such as denoising, smoothing, edge detection, image sharpening and filtering. In this section, we will show how to apply these operations to HARDI data. The motivation for filtering diffusion data is that the signal-to-noise ratio in HARDI data is generally low, especially with the high gradient strengths necessary for imaging and resolving crossing white matter tracts and other regions of complex tissue architecture.

2.4.1. Convolution and Isotropic Filtering

Traditionally, discrete convolution of an image ψ with the filter g is defined as

$$\mathit{\xi }(\mathit{x})=\mathit{\psi }(\mathit{x})\ast \mathbf{g}(\mathit{x})=\sum _{\mathbf{u}}\mathbf{g}(\mathbf{u})\mathit{\psi }(\mathit{x}+\mathbf{u}).$$ (12)

Assuming that Σ_u g(u) = 1, we can rewrite ξ(x) as

$$\mathit{\xi }(\mathit{x})=\underset{\mathit{\xi }}{argmin}\sum _{\mathbf{u}}\mathbf{g}(\mathbf{u}){(\mathit{\xi }-\mathit{\psi }(\mathit{x}+\mathbf{u}))}^2.$$ (13)

For HARDI data, ψ ∈ Ψ and ξ ∈ Ψ, we can define the equivalent minimization problem for convolution as

$$\mathit{\xi }(\mathit{x})=\underset{\mathit{\xi }\in \mathbf{\Psi }}{argmin}\sum _{\mathbf{u}}\mathbf{g}(\mathbf{u})\text{dist}{(\mathit{\xi },\mathit{\psi }(\mathit{x}+\mathbf{u}))}^2.$$ (14)

Again, this is a Riemannian weighted average problem. When g(u) ≥ 0, the optimization problem in Eqn. (14) remains convex and the convergence of Algorithm 1 to the global minimum is again guaranteed. Moreover, the solution ξ(x) is obtained using Algorithm 1. When g(u) < 0, convergence is guaranteed when the Hessian of the function in Eqn. (14) is positive definite.

2.4.2. Anisotropic Filtering

In the case of scalar images, linear filtering can blur and mislocate discontinuities in the data. To that end, nonlinear diffusion filtering techniques have been proposed; these smooth the data while preserving discontinuities, have been proposed (Perona and Malik, 1990; Weickert, 1997; Weickert and Brox, 2002). The idea behind nonlinear diffusion filters in image processing comes from the use of the Gaussian filter in multi-scale image analysis. More precisely, one considers the following linear diffusion equation

$${\delta }_t\mathit{\xi }(\mathit{x},t)=\mathrm{\Delta }\mathit{\xi }(\mathit{x},t)=\nabla ·(\nabla \mathit{\xi }(\mathit{x},t)),$$ (15)

$$\mathit{\xi }(\mathit{x},0)=\mathit{\psi }(\mathit{x}),$$ (16)

where Δξ(x, t) is the Laplacian of ξ(x, t), ψ is the original noisy image and ξ is the filtered image. The solution to this diffusion equation is obtained by convolving ψ with a Gaussian filter $\mathbf{g}(\mathit{x},\sigma )=\frac{1}{2\pi {\sigma }^2}exp(-\frac{{\left|\right|\mathit{x}\left|\right|}^2}{2{\sigma }^2})$. Specifically, $\mathit{\xi }(\mathit{x},t)=g(\mathit{x},\sqrt{2t})\ast \mathit{\psi }(\mathit{x})$.

The main idea behind anisotropic filtering is to use a non-homogeneous diffusivity function c(x, ·) that depends on the data at x. More generally, the following nonlinear diffusion equation is used,

$${\delta }_t\mathit{\xi }(\mathit{x},t)=\nabla ·(c(\mathit{x},t)\nabla \mathit{\xi }(\mathit{x},t)),$$ (17)

$$\mathit{\xi }(\mathit{x},0)=\mathit{\psi }(\mathit{x}),$$ (18)

where c(x, t) is the diffusivity function. When c(x, t) is a decreasing function that depends on the derivative of the image ξ(x, t), it prevents diffusion across the edges, while allowing diffusion along the edge.

When the data lives in d dimensions and if $c(\mathit{x},t)=exp(-\frac{{\left|\right|\nabla \mathit{\xi }(\mathit{x},t)\left|\right|}^2}{{\sigma }^2})$, we obtain the following equation

$${\delta }_t\mathit{\xi }(\mathit{x},t)\propto \sum _{j=1}^{d}exp(-\frac{{\left|\right|{\delta }_j\mathit{\xi }(\mathit{x},t)\left|\right|}^2}{{\sigma }^2}){\delta }_j^2\mathit{\xi }(\mathit{x},t).$$ (19)

In this case, the evolution equation is:

$$\mathit{\xi }(\mathit{x},t+\mathrm{\Delta }t)=\mathit{\xi }(\mathit{x},t)+\mathrm{\Delta }t{\delta }_t\mathit{\xi }(\mathit{x},t).$$ (20)

Now, unlike in the Euclidean case where we make use of the Laplace operator, for a field of ODFs, we will first approximate the Laplace-Beltrami operator on the manifold as the sum of all the second partial derivatives in the spatial coordinates

$$\sum _{i,j}{\delta }_i{\delta }_j\mathit{\xi }(\mathit{x},t),$$

and we will get the following equation

$${\delta }_t\mathit{\xi }(\mathit{x},t)\propto \sum _{i,j}^{d}exp(-\frac{{\left|\right|{\delta }_{ij}\mathit{\xi }(\mathit{x},t)\left|\right|}^2}{{\sigma }^2}){\delta }_{ij}\mathit{\xi }(\mathit{x},t).$$

The evolution equation is again

$$\mathit{\xi }(\mathit{x},t+\mathrm{\Delta }t)=\mathit{\xi }(\mathit{x},t)+\mathrm{\Delta }t{\delta }_t\mathit{\xi }(\mathit{x},t).$$ (21)

Finally, we will show how to approximate the operator δ_iδ_j for a given field of ODFs ξ by using the finite central difference method. To this end, recall that we have the following expressions for the Euclidean derivatives,

$${\delta }_i\mathit{\xi }(\mathit{x})\approx \frac{1}{\epsilon }(\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{2})-\mathit{\xi }(\mathit{x})+\mathit{\xi }(\mathit{x})-\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{2})),$$ (22)

$${\delta }_i^2\mathit{\xi }(\mathit{x})\approx \frac{1}{{\epsilon }^2}(\mathit{\xi }(\mathit{x}+\epsilon {\mathbf{e}}_i)-2\mathit{\xi }(\mathit{x})+\mathit{\xi }(\mathit{x}-\epsilon {\mathbf{e}}_i)),$$ (23)

$${\delta }_i{\delta }_j\mathit{\xi }(\mathit{x})\approx \frac{1}{{\epsilon }^2}(\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}+\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})-\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}-\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})-\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}+\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})+\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}-\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})),$$ (24)

where {e_i} are the orthonormal vectors of the canonical basis for ℝ³ and ε > 0. The derivation of the various approximations of the derivatives of ξ proceeds as in DTI case(Krajsek et al., 2008; Pennec et al., 2006; Castano-Moraga et al., 2007). Therefore, for the first and second order derivatives in Riemannian space ξ, we have the following approximations,

$${\delta }_i\mathit{\xi }(\mathit{x})\approx \frac{1}{\epsilon }(\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{2})}-\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{2})}),$$ (25)

$${\delta }_i^2\mathit{\xi }(\mathit{x})\approx \frac{1}{{\epsilon }^2}(\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}+\epsilon {\mathbf{e}}_i)}+\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}-\epsilon {\mathbf{e}}_i)}),$$ (26)

$${\delta }_i{\delta }_j\mathit{\xi }(\mathit{x})\approx \frac{1}{{\epsilon }^2}(\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}+\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})}-\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}+\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}-\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})}+\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}-\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})}-\overrightarrow{\mathit{\xi }(\mathit{x})\mathit{\xi }(\mathit{x}-\frac{\epsilon {\mathbf{e}}_i}{\sqrt{2}}+\frac{\epsilon {\mathbf{e}}_j}{\sqrt{2}})}).$$ (27)

2.5. Statistics on the Space of ODFs

Here we show how to calculate the covariance and principal components of a set of points lying on Ψ. Once the first and second order statistics for ODFs are defined, we generalize the Hotelling’s T-squared statistic for two populations of ODFs, and extend the commonly used neuroimaging analysis technique known as voxel-based morphometry (Ashburner and Friston, 2000) to what we will call ODF-based morphometry.

2.5.1. Covariance and Principal Geodesic Analysis of ODFs

Principal component analysis (PCA) (Jolliffe, 1986) is the method for finding the optimal subspace that minimizes the sum of squared distances between x_i and its projection π_Φ(x_i) onto the subspace Φ. This is equivalent to maximizing the projected variance along the subspace. Specifically, given a multivariate random variable x ∈ ℝ^D, the d principal components of x are defined as the uncorrelated linear components $y_i={\mathbf{u}}_i^{\top }(\mathit{x}-\mu )\in \mathbb{R}$, u_i ∈ ℝ^D, i = 1, …, d, where μ = E(x), such that the variance of y_i is maximized subject to ${\mathbf{u}}_i^{\top }{\mathbf{u}}_i=1$ and var(y₁) ≥ … ≥ var(y_d). The solution is given as ${\{{\mathbf{u}}_i\}}_{i=1}^d$, which are the d leading eigenvectors of the population covariance matrix E[xx^⊤] and the first d principal components of x are $y_i={\mathbf{u}}_i^{\top }(\mathit{x}-\mu )$.

Now, by the definition of ODFs ∫ p(s)ds = 1, it lies in a hyperplane. While in principle, it may appear as if the original ODF representation is Euclidean, this is actually not the case. The reason is that under the Fisher-Rao metric, the hyperplane is turned into a non-Euclidean manifold. Therefore, while one can work with the hyperplane representation, means cannot be computed as usual, because the Fisher-Rao metric in this space does not coincide with the 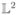metric. The whole point of taking the square-root and working in the Hilbert sphere is that the Fisher-Rao metric becomes the 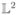metric, hence we know how to compute the Riemannian operations. There may be other valid choices for the metric but the Fisher-Rao metric makes it theoretically and computationally easy to deal with this kind of data.

For a Riemannian manifold, the equivalent task of finding the principal components is to fit an optimal low-dimensional geodesic submanifold Φ to the data. This is known as Principal Geodesic Analysis (PGA), first proposed in (Fletcher et al., 2004) for the analysis of shape spaces, and applied to DTI in (Fletcher and Joshi, 2007; Pennec et al., 2006). PGA attempts to find the geodesic submanifold Φ such that the squared Riemannian distance from the data to that submanifold is minimized. Denoting the geodesic submanifold at the mean ψ̄ by Φ, the projection of a point ψ is defined as

$${\pi }_{\mathbf{\Phi }}(\mathit{\psi })=\underset{\mathit{\phi }\in \mathbf{\Phi }}{argmin}\text{dist}{(\mathit{\phi },\overline{\mathit{\psi }})}^2.$$ (28)

Here, the mean ψ̄ of the data can be found by using the Karcher mean algorithm described in §2.2 (see Algorithm 1). For the space of ODFs, the projection that is solved via a minimization problem is guaranteed to exist and to be unique. This is generally not true for arbitrary manifolds. Unlike in Euclidean space, where one could easily find the projection of each data point onto the subspace, finding the equivalent projection onto the Riemannian submanifold is not an easy problem to solve. Fletcher and Joshi (2007) assume that the projection onto the geodesic submanifold may be approximated linearly onto the tangent space of Φ. That is,

$${log}_{\overline{\mathit{\psi }}}({\pi }_{\mathbf{\Phi }}(\mathit{\psi }))\approx \underset{\mathit{v}\in T_{\overline{\mathit{\psi }}}\mathbf{\Phi }}{argmin}{\left|\right|{log}_{\overline{\mathit{\psi }}}(\mathit{\psi })-\mathit{v}\left|\right|}^2=\sum _{i=1}^k\langle {\mathit{v}}_i,{log}_{\overline{\mathit{\psi }}}(\mathit{\psi })\rangle {\mathit{v}}_i,$$ (29)

where v₁, …, v_k forms an orthonormal basis for T_ψ̄Φ. By making such an assumption, in (Fletcher and Joshi, 2007) the tangent vectors that span the principal geodesic submanifolds at ψ̄ are found by performing an eigendecomposition of the covariance matrix

$$cov(\mathit{\psi })=\frac{1}{n-1}\sum _{i=1}^n\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}{\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}}^{\top }=\frac{1}{n-1}\sum _{i=1}^n{log}_{\overline{\mathit{\psi }}}{\mathit{\psi }}_i{log}_{\overline{\mathit{\psi }}}{{\mathit{\psi }}_i}^{\top }.$$ (30)

Pennec et al. (2006) first note that the covariance matrix for Euclidean vectors is simply given as $\frac{1}{n-1}{\sum }_{i=1}^n\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}{\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}}^{\top }$ and give the equivalent covariance matrix that measures the amount of dispersion in the data with respect to the mean as that defined in Eqn. 30. Once the covariance matrix is defined, we can find the d principal components as before. We refer the reader to Appendix C for how to calculate the infinite-dimensional covariance matrix when φ_i is a continuous function. Now in practice, the ODF is not a continuous PDF; rather it is a histogram over M different gradient directions. We refer the reader to Appendix D for practical issues relating to the discrete representation of the ODFs. Therefore, we can calculate the sample covariance matrix $cov(\mathit{\psi })=\frac{1}{n-1}{\sum }_{i=1}^n{\mathit{\phi }}_i{\mathit{\phi }}_i^{\top }\in {\mathbb{R}}^{M\times M}$ exactly. This algorithm is summarized in Algorithm 2.

Algorithm 2.

Principal Geodesic Analysis

Given data points ψ1, …, ψn ∈ Ψ, Compute intrinsic mean ψ̄ as in Algorithm 1. Calculate the tangent vectors φi = logψ̄(ψi) about ψ̄. Construct the sample covariance matrix $cov(\mathit{\psi })=\frac{1}{n-1}{\sum }_{i=1}^n{\mathit{\phi }}_i{\mathit{\phi }}_i^{\top }$. Perform eigenanalysis of the matrix cov(ψ), with the eigenvectors ${\{{\mathbf{u}}_i\}}_{i=1}^d$ giving the principal directions. ${\{{\mathbf{u}}_i\}}_{i=1}^d$ forms an orthonormal basis for Tψ̄Ψ.

In Euclidean space, it is easy to prove that the problem of minimizing the residual sum of squared distances between the data point and its projection reduces to the problem of maximizing the projected variance along the subspace, but there is no corresponding simple proof for Riemannian manifolds. Fletcher et al. (2004) shows that this tangent space approximation is only valid when the data lie in a small neighborhood. Recent works by Sommer et al. (2010a,b) presents a comparison between the two definitions of PGA in addition to the exact computation of geodesic submanifolds on a wide class of manifolds. In this paper, as in (Fletcher et al., 2004; Fletcher and Joshi, 2007; Pennec et al., 2006), we will use the linear approximation onto the tangent space of Φ.

Finally, as mentioned in §2.2, Cheng et al. (2009) assumes that the square-root ODF ψ can be approximated by a linear combination of the first N orthonormal basis functions, i.e., $\mathit{\psi }(\mathit{s})\approx {\sum }_{i=1}^N{c}_i{B}_i(\mathit{s})$, where ${\{B_i(\mathit{s})\}}_{i=1}^{\infty }$ is any orthonormal basis set and {c_i} are the coefficients. Under such a representation, the computation of PGA becomes significantly more efficient as the sample covariance matrix, rather than being infinite-dimensional, is a N × N matrix instead. However, as mentioned previously, it is not clear which method (ψ versus {c_i}) is more efficient and which method is more accurate. Finally, there is a possibility of missing a PC if the function is not included in the initial set using ${\{c_i\}}_{i=1}^N$.

2.5.2. ODF based Morphometry

Voxel based morphometry (VBM) (Ashburner and Friston, 2000) is a neuroimaging analysis technique to investigate regional differences in brain anatomy. VBM-type methods have made a significant contribution to the understanding of brain changes in several disorders and their relation to clinical measures (Whitwell, 2009). For example, VBM has been used to study a number of different disorders, including neurodegenerative diseases (Whitwell and Jack, 2005), multiple sclerosis (Sepulcre et al., 2006), schizophrenia (Williams, 2008), movement disorders (Whitwell and Josephs, 2007) and epilepsy (Keller and Roberts, 2008). Appendix E gives an overview of VBM for multivariate testing. Voxel-based analysis may be applied to any vector-valued data, using nonparametric permutation tests. Therefore, one could treat an ODF as a Euclidean vector, and apply this technique directly to the original ODFs, or to the SH coefficients (via decomposing the ODF is as a linear function of the SH basis) by using the Euclidean T-squared statistic defined in Eqn. E.1. Such an approach is fast as computation for the Euclidean mean is closed-form. However, treating the ODFs or the SH coefficients of the ODF as Euclidean vectors is not theoretically correct, as it does not respect the geometry of the statistical manifold as the Riemannian distance is not equal to the Euclidean distance. We will next show how to generalize the Hotelling’s T-squared statistic that accounts for the Fisher-Rao metric for PDFs.

We first assume that the ODF volumes of different subjects are already registered to a common template (HARDI registration remains an open research question, beyond the scope of this paper). Here, we obtain the registration of the ODF fields by registering the T2 images as we will show in §3. Having registered the ODF volumes, we next compute the mean and covariance matrices of the ODF-valued data, as described in §2.2 and §2.5.1, respectively. Let ψ₁, …, ψ_nψ and φ₁, …, φ_nφ be the ODFs drawn from two populations and let ψ̄ and φ̄ be the sample means of the two populations computed using Algorithm 1. We generalize the Hotelling’s T-squared statistic and VBM to ODFs using a similar strategy in an analogous fashion to what was developed for DTI in (Lepore et al., 2007; Hua et al., 2008) and we get the following equation for computing the T-squared statistic for ODFs,

$$T^2=\frac{n_{\psi }{n}_{\phi }}{n_{\psi }+n_{\phi }}{\overrightarrow{\overline{\mathit{\psi }}\overline{\mathit{\phi }}}}^{\top }{\mathbf{W}}^{-1}\overrightarrow{\overline{\mathit{\psi }}\overline{\mathit{\phi }}}=\frac{n_{\psi }{n}_{\phi }}{n_{\psi }+n_{\phi }}{log}_{\overline{\mathit{\psi }}}{\overline{\mathit{\phi }}}^{\top }{\mathbf{W}}^{-1}{log}_{\overline{\mathit{\psi }}}\overline{\mathit{\phi }},$$

where

$$\begin{array}{l}\mathbf{W}=\frac{{\sum }_{i=1}^{n_{\psi }}\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}{\overrightarrow{\overline{\mathit{\psi }}{\mathit{\psi }}_i}}^{\top }+{\sum }_{i=1}^{n_{\phi }}\overrightarrow{\overline{\mathit{\phi }}{\mathit{\phi }}_i}{\overrightarrow{\overline{\mathit{\phi }}{\mathit{\phi }}_i}}^{\top }}{n_{\psi }+n_{\phi }-2}\\ =\frac{{\sum }_{i=1}^{n_{\psi }}{log}_{\overline{\mathit{\psi }}}{\mathit{\psi }}_i{log}_{\overline{\mathit{\psi }}}{\mathit{\psi }}_i^{\top }+{\sum }_{i=1}^{n_{\phi }}{log}_{\overline{\mathit{\phi }}}{\mathit{\phi }}_i{log}_{\overline{\mathit{\phi }}}{\mathit{\phi }}_i^{\top }}{n_{\psi }+n_{\phi }-2}.\end{array}$$ (31)

Having formulated the equivalent of the Hotelling’s T-squared test for ODFs, we will perform a statistical group comparison of ODFs using multivariate hypothesis testing via the permutation tests. Alternatively, one could make use of the representation in (Cheng et al., 2009) which decomposes the square-root ODF ψ(s) as a linear function of the SH basis, and calculate the Riemannian T-squared statistic in Eqn. 31 based on the SH coefficients ${\{c_i\}}_{i=1}^N$. As in the case for the mean and PGA, this representation is computationally less intensive than using ψ(s). However, while using continuous ψ(s) guarantees that the T-squared statistic calculated in Eqn. 31 correctly determines whether the population means differ, this may not be true of the equivalent statistic calculated using ${\{c_i\}}_{i=1}^N$, or the discretized square-root ODFs (histograms with M directions), or the SH coefficients of the discretized square-root ODFs. Eqn. 31 is only applicable to the square-root ODFs, or its SH expansion, but not to the ODFs or the SH expansion of the ODFs.

3. Results and Discussion

In this section, we show how our proposed algorithms perform on synthetic data, phantom data, and real human brain HARDI data

3.1. Synthetic Data

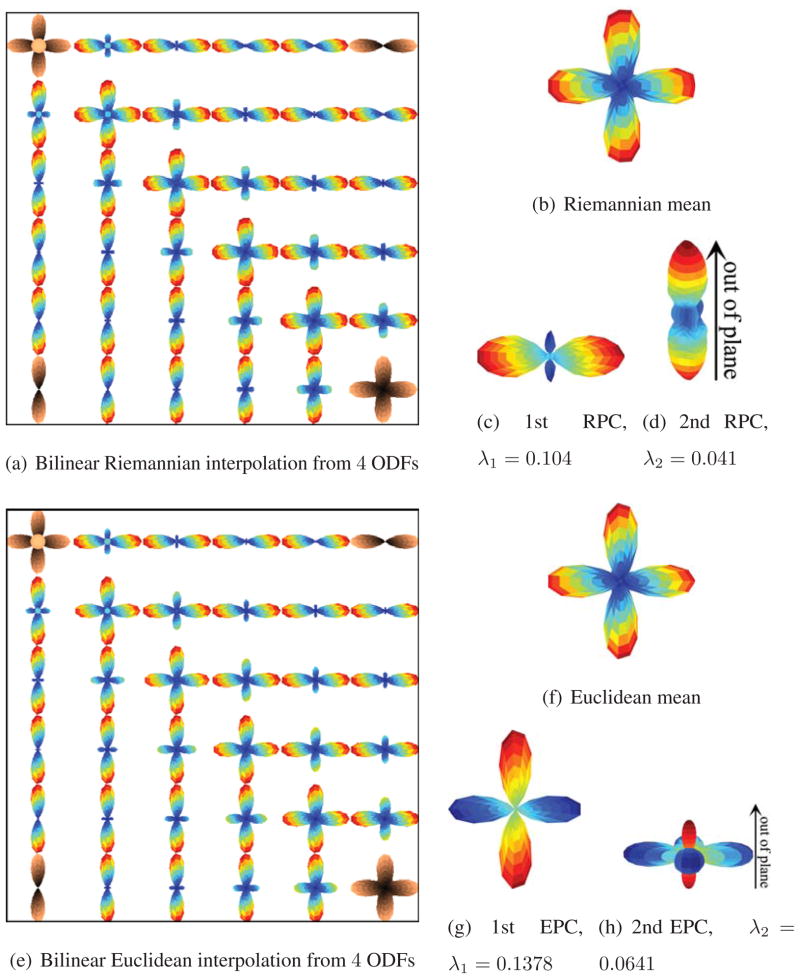
In the first part of this section, we will assume that the ODFs are precomputed and we do not have raw HARDI signals. We first illustrate the various operations previously introduced, such as interpolation, filtering, and computation of the mean and principal components (PC) of the synthetic ODF fields in Fig. 2. Fig. 2(a) shows the bilinear Riemannian interpolation of the four endpoints where the original ODFs are shaded in orange. The top right and bottom left voxels contain ODFs of 1 fiber, the bottom right ODF of 2 fibers and the top left ODF of 3 fibers, with 1 fiber pointing out of the plane. Figs. 2(b)–2(d) show the Riemannian mean and the first two principal components of the ODF field in Fig. 2(a) with eigenvalues 0.104 and 0.041, respectively. The first PC is oriented from left to right, whereas the second PC is oriented going out of the plane. We apply the original PCA to ODFs, based on the Euclidean metric. Fig. 2(e) shows the bilinear Euclidean interpolation. Figs. 2(f)–2(h) show the Euclidean mean and the first two principal components of the ODF field in Fig. 2(e) with eigenvalues 0.1378 and 0.0641, respectively. The Riemannian and Euclidean means are similar, but the principal components computed by the two frameworks are very different. While the Riemannian framework is able to capture primarily, the direction going out of the plane as the second PC, the Euclidean framework does not exhibit the same sensitivity.

Figure 2.

Interpolation and statistical analysis of synthetic ODF fields. Fig. 2(a) shows the bilinear Riemannian interpolation of the four ODFs shaded in orange. Figs. 2(b)–2(d) show the Riemannian mean and the first two principal components. Fig. 2(e) shows the bilinear Euclidean interpolation of the four ODFs shaded in orange. Figs. 2(f)–2(h) show the Euclidean mean and the first two principal components.

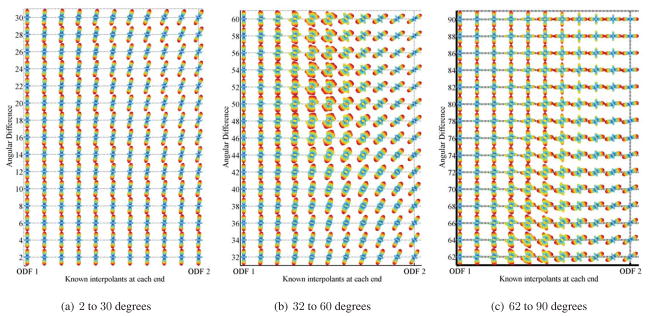
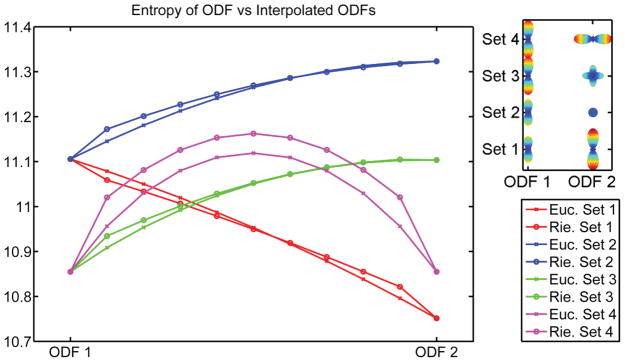
We also examine the interpolation when the rotational discrepancy, in degrees, between two ODFs varies. Essentially, the two ODFs have the same diffusion behavior and are related to each other via a rotation. Figs. 3(a)–3(c) show the results. When the angular difference is around 38 degrees, the interpolated ODFs start to deviate from the diffusion properties of each interpolant. The proposed interpolation scheme allows one to march along the manifold freely and hence does not restrict the interpolated ODFs to be related by a rotation. Since the diffusion properties do not remain the same using our interpolation scheme, the next natural question to ask is whether interpolation for ODFs will result in the so-called swelling effect. For DTI, Euclidean interpolation suffers from the so-called swelling effect, whereas Riemannian interpolation can overcome it. Fig. 4 shows the result of four different sets of interpolation. Set 1 shows interpolation of a single fiber with increased diffusivity in the principal direction, set 2 shows interpolation from a voxel with one fiber to an isotropic voxel, set 3 shows interpolation from a voxel with one fiber to one with two fibers, and finally, set 4 shows interpolation from a voxel with one fiber to another with one fiber rotated 90 degrees. We use the Shannon entropy of the ODF to measure the diffusivity of the ODF. As shown in Fig. 4, both frameworks suffer from the problem of the interpolants having a greater Shannon entropy than the original data points.

Figure 3.

Interpolation between two single-fiber ODFs, whose main orientations are related to each other by a rotation of 2 to 90 degrees. In each row, the first and last ODFs are the known ODFs.

Figure 4.

Study of swelling effects for Riemannian and Euclidean interpolation, using the entropy measure. In each row, the first and last ODFs are known.

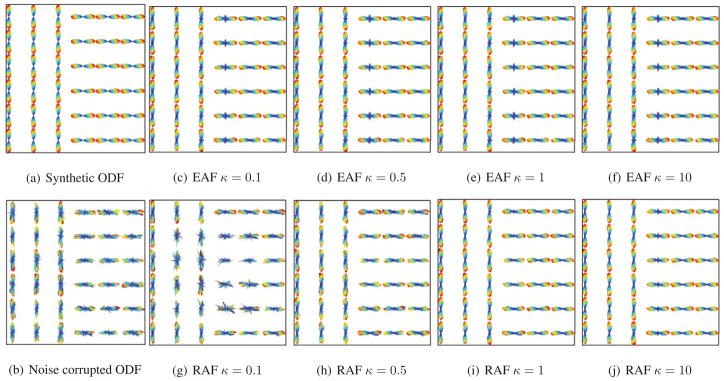
Next, we perform anisotropic filtering (AF) on an ODF field with a sharp discontinuity, as shown in Fig. 5(a). The function $c(x)=exp(-\frac{x^2}{\kappa })$ is used in AF, and 30 iterations are performed. We add noise to this ODF field by applying a random tangent vector to each ODF, as shown in Fig. 5(b). We vary the parameter κ, for κ = 0.1, 0.5, 1, and 10. Figs. 5(c), 5(d), 5(e), and 5(f) show the results of Euclidean Anisotropic Filtering (EAF), where instead of taking into account the Riemannian structure of the ODFs, we simply treat each sampled ODF as a vector in Euclidean space, and perform anisotropic filtering in the classical Euclidean way. Figs. 5(g), 5(h), 5(i), and 5(j) show the results of Riemannian Anisotropic Filtering (RAF). Next, we examine the differences in performance between RAF and EAF over 100 trials for varying κ. For both types of AFs, we measure the amount of error from the ground-truth ODF field using two measures, Riemannian ${\sum }_{\mathit{x}}{\left|\right|{log}_{{\mathit{\psi }}_{\mathit{truth}}(\mathit{x})}({\mathit{\psi }}_{\mathit{filtered}}(\mathit{x}))\left|\right|}_{\mathit{x}}^2$ and Euclidean Σ_x||ψ_truth(x) − ψ_filtered(x)||² dissimilarity. In each trial, we iterate AF 30 times. Table 1 shows the ratio of error for RAF to EAF under the Euclidean and Riemannian measures. RAF gives a smaller error than EAF, except when κ = 0.1, where the error of RAF is larger. This is because the Riemannian distance between two ODFs is always larger than or equal to the Euclidean distance, hence for the same value of κ, the rate of diffusion is faster for EAF than for RAF. This is why for large values of κ, EAF will blur the edges earlier than RAF, whereas for small values of κ, RAF is unable to filter away the noise.

Figure 5.

Euclidean and Riemannian Anisotropic Filtering of synthetic ODF fields, with varying κ.

Table 1.

Mean of (Amount of error after RAF)/(Amount of error after EAF) in 100 trials under two different measures.

κ	0.1	0.5	1	10	100
Euclidean measure	1.197	0.767	0.480	0.468	0.468
Riemannian measure	1.108	0.945	0.801	0.787	0.787

We next evaluate our method’s performance on synthetic data generated using the tensor method in (Descoteaux et al., 2007). Here instead of applying random tangent vectors to the clean ODFs, noise is added to the raw HARDI signals and the ODFs are calculated from the noisy HARDI signals. The HARDI signal S(g) in the direction g, where g is a unit vector, is generated by

$$S(\mathbf{g})=exp(-b{\mathbf{g}}^{\top }\mathbf{Dg}),$$ (32)

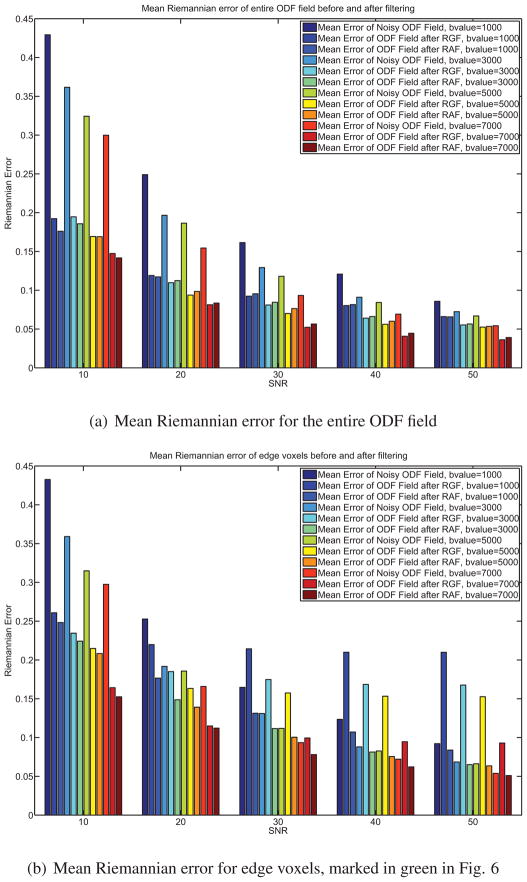
where the b-value is given and D is the diffusion tensor profile. Noisy versions of S(g) are generated by adding complex Gaussian noise with zero mean and standard deviation $\sigma =\frac{1}{\zeta }$, where ζ is the signal-to-noise ratio (SNR). Again, we construct an ODF field with a sharp discontinuity, as shown in Fig. 6(a) using the tensor method. After noise is added to the HARDI signals, we obtain a noisy ODF field and an example is shown in Fig. 6(b). We apply Riemannian Gaussian Filtering (RGF) and RAF to the noisy ODF field and calculate the mean error between the denoised ODF field and the noiseless ODF field. Fig. 6 shows an example when the SNR = 20 and the b-value is 3000 mm/s². The voxels at the edge where the discontinuity occurs are marked in green. Fig. 7 shows the errors before and after applying RGF and RAF for various b-values and SNR ranging from 10 to 50. Fig. 7(a) shows the mean error across the entire ODF field. Notice that when the b-values increase, the errors between the noiseless ODF field and the noisy versions decreases. In addition, Fig. 7(a) shows clearly that both RAF and RGF give ODF fields that are significantly closer to the true ODF. Fig. 7(b) compares the errors in the edge voxels. Notice that the error of RGF is significantly more than the error of the noisy ODF field and the error of RAF. This is because RGF blurs the edge.

Figure 6.

Riemannian Gaussian filtering and anisotropic filtering of a synthetic ODF field at SNR 20 and b-value 3000 mm/s². Both RAF and RGF give ODF fields that are significantly closer to the true ODF. Notice also that RGF blurs the discontinuity.

Figure 7.

Errors before and after filtering of the synthetic ODF field shown in Fig. 6.

3.2. Phantom Data

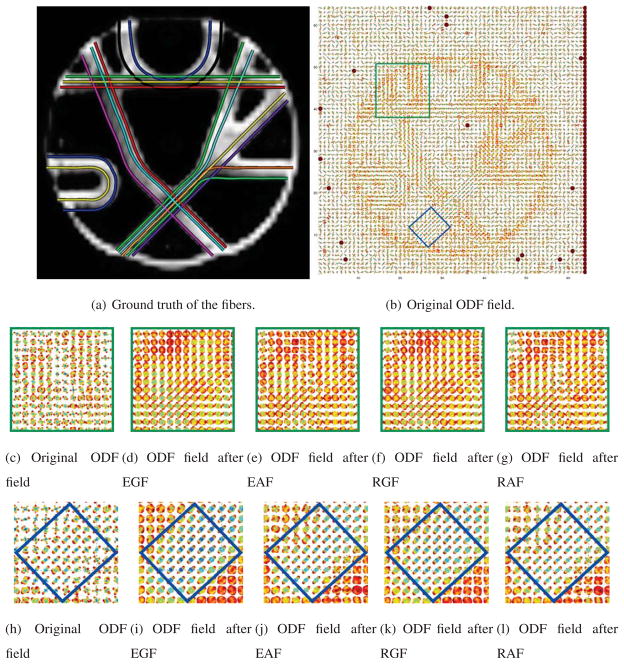
We will now show qualitative results on the biological phantom created from two excised Sprague-Dawley rat spinal cords embedded in 2% agar (Campbell et al., 2005). A diffusion-weighted dataset was acquired using this phantom, with 90 diffusion encoding directions, with b-value of 3000 s/mm² (Campbell et al., 2005). Fig. 8(a) shows the Generalized Fractional Anisotropy (GFA) image for this dataset, which is defined as $\text{GFA}(x)=\frac{\text{std}(\mathit{p}(\mathit{x}))}{\text{rms}(\mathit{p}(\mathit{x}))}$, where std is the standard deviation and rms is the root mean square value of the ODF p(x) at voxel x. Figs. 8(b), 8(e) and 8(h) show three zoomed-in subregions of the ODF field in manually marked areas with different diffusion profiles. Two regions, shown in red and blue, contain a single fiber and one region, shown in green, contains two crossing fibers. Figs. 8(c), 8(f) and 8(i) show the ODF field after applying RGF and Figs. 8(d), 8(g) and 8(j) show the ODF field after applying RAF. While RAF and RGF reduce the noise in the ODF field, RGF tends to mislocate the structure of thin fibers, as shown in the box in red.

Figure 8.

McGill rat phantom data.

Next, we present experiments on a phantom dataset provided at http://www.lnao.fr/spip.php?rubrique79. This MR phantom contains a plethora of crossing, kissing, splitting and bending fiber configurations. Technical details of the phantom construction are provided in (Poupon et al., 2008). Fig. 9(a) shows the ground truth fibers used in the phantom dataset. Diffusion-weighted MR images are obtained using the following imaging parameters. The image size is 64×64×3 with resolution of 3 × 3 × 3 mm. Two repetitions of 65 images are acquired, one image with no diffusion sensitization and N = 64 diffusion weighted images at b = 1500 s/mm², corresponding to the echo times TE = 94 ms.

Figure 9.

Phantom data from Neurospin.

Figs. 9(c) and 9(h) show the reconstructed ODF, Figs. 9(d) and 9(i) show the ODF field after applying Euclidean Gaussian Filtering (EGF), Figs. 9(e) and 9(j) show the ODF field after applying EAF, Figs. 9(f) and 9(k) show the ODF field after applying RGF, and Figs. 9(g) and 9(l) show the ODF field after applying RAF. The effects of filtering are obvious in the region marked in blue, as shown in Figs. 9(k) and 9(l), where the ODFs in the fiber bundle become oriented mostly in the northeast direction. This is correct according to the ground truth given in Fig. 9(a). However, both EGF and RGF merge into a single bundle two fiber bundles that are close to each other - as shown in the region that is marked in green in Figs. 9(j) and 9(k).

3.3. HARDI Human Data

Finally, we apply our Riemannian framework to a real HARDI human brain dataset (from Chiang et al. (2008)). Diffusion-weighted MR images were obtained at 4 Tesla using the following imaging parameters: 55 contiguous slices (2 mm thick), TR/TE= 8250/92.3ms, FOV= 230 × 230 and 1.8 × 1.8 mm² in-plane resolution. A total of 105 images were acquired: 11 with no diffusion sensitization and 94 diffusion-weighted images with b = 1132 s/mm² (Chiang et al., 2008). We apply our Riemannian filtering method to this ODF field, shown in Fig. 10(a). Figs. 10(b) and 10(c) show the results of RGF and RAF, respectively. Figs. 10(d)–10(l) shows the zoomed-in regions of the different ODF fields in manually marked areas of different diffusion. The function c(·) used in RAF is a Gaussian function, and 30 iterations are done. RAF is able to smooth the ODF field sufficiently but still preserves the discontinuities between different bundles. In addition, both RAF and RGF give a GFA map that is significantly cleaner than that of the unfiltered ODF field and the different regions of the brain can be seen more clearly.

Figure 10.

ODF field of a real HARDI brain dataset. The ODFs are superimposed on top of the generalized fractional anisotropy maps.

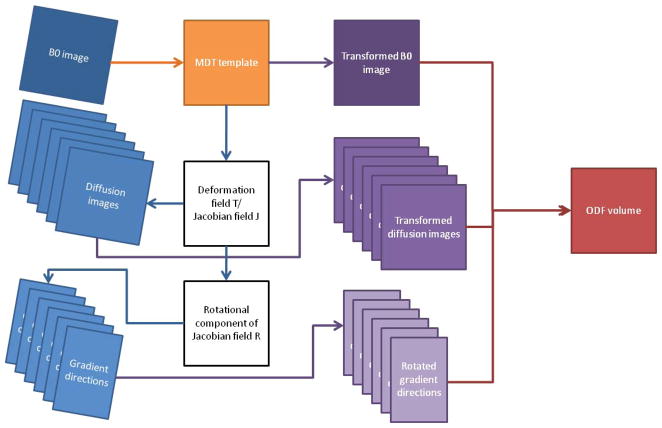
Next, we use our framework to compute multi-subject statistics on ODFs in a database of 40 right-handed healthy young adults, scanned with the imaging parameters given before (Chiang et al., 2009). In order to bring all the ODF volumes of the subjects to the same reference frame, there is a need to register the ODF volume of each subject to a common ODF template. This requires solving the HARDI registration problem, which is an open research question outside the scope of this paper. We circumvent HARDI registration by applying an approximate algorithm, as shown in Fig. 11. First of all, the non-diffusion-weighted images (also called b = 0 images) from all subjects compute a group “average-shape” brain, or minimal deformation template (MDT). The b = 0 images are then nonlinearly registered to this template. Since nonlinear registration is used, the deformation field and the corresponding Jacobian of the transformation for each subject differs depending on the voxel coordinates as well. Therefore, based on this registration, we denote the deformation field T_i,x: ℝ³ → ℝ³ and the corresponding Jacobian field J_i,x: ℝ³ → ℝ^3×3 of each subject, where i = 1,…, N_subjects and x is the voxel coordinates. The deformation field T_i,x of each subject is then applied to the diffusion weighed images of the same subject. We extract the rotational component R_i,x of the Jacobian of the transformation, where J_i,x = R_i,xS_i,x with S_i,x is a shear matrix, and apply it to each gradient direction g̃ _j,x = R_i,xg_j in order to reorient the ODF according to the spatial transformation. Note that since the Jacobian J_i,x of the transformation and the extracted rotational component R_i,x are different at different voxels, and therefore the reorientated gradient is dependent on x.

Figure 11.

Flowchart of steps used to reconstruct the ODF volume of each subject. Each ODF volume is registered to the minimal deformation template (MDT).

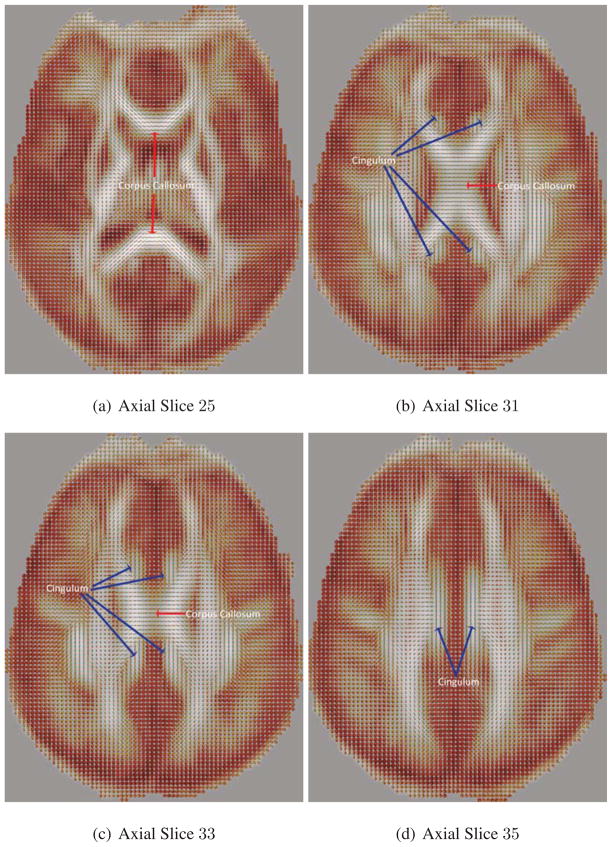
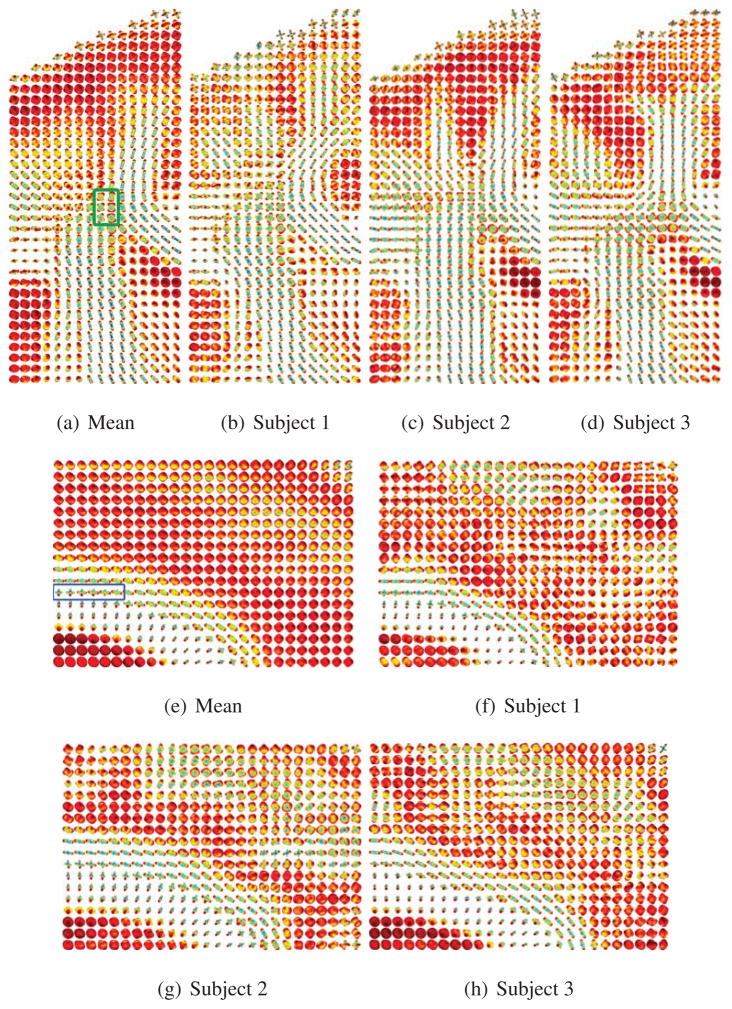
The ODFs are then constructed from the transformed diffusion weighed images at the transformed gradient directions. Fig. 12 shows different axial slices of the calculated mean ODF. Notice that the mean ODF image preserves the features in the corpus callosum, cingulum, and corticospinal tract bundles, in which the directions of the fiber tracts are seen clearly. We also show two different ROIs in Fig. 13. The first ROI shown in Figs. 13(a)–13(d) is the region where the corticospinal tract and the corpus callosum cross and intermix. Notice that in the mean ODF field, we still see the presence of crossing fibers, as shown in green. In the second ROI shown in Figs. 13(e)–13(h), the cingulum and the corpus callosum do not cross each other; however, we expect to see some voxels where there is partial volume averaging of the cingulum and the corpus callosum. Notice that in the mean ODF field, we still see the effect of partial volume averaging, as shown in blue.

Figure 12.

Mean ODF field of a real HARDI brain dataset of 40 subjects. The ODFs are superimposed on top of the GFA maps.

Figure 13.

Comparing the mean ODF to the ODF of individual subjects. Figs. 13(a)–13(d) correspond to the ROI of the cortical spinal tract and corpus callosum. The ROI in green corresponds to the two fiber tracts crossing. Figs. 13(e)–13(h) correspond to the ROI of the cingulum and the corpus callosum. The ROI in blue corresponds to the voxels exhibiting partial volume averaging of the two fiber tracts.

Finally, we show how ODF-based morphometry may be used to study brain asymmetry, as described in §2.5.2. While little is known about white matter connectivity asymmetry (Dubois et al., 2009; Buchel et al., 2004), several recent studies have examined left-right differences from DTI-derived measures in large human populations (N = 374; (Jahanshad et al., 2010)). ODF-based morphometry allows us to extend the study of hemispheric asymmetry to a microscopic scale by examining differences in fiber characteristics across hemispheres rather than just differences in structure shapes and volumes. In order to study brain asymmetry, we reflect each subject’s ODF field with respect to the mid-sagittal plane. We compute voxel-wise maps of significant asymmetries of the differences between the ODFs in the left and right hemispheres, using the Hotelling’s T-squared test to measure differences in the left and right mean ODFs.

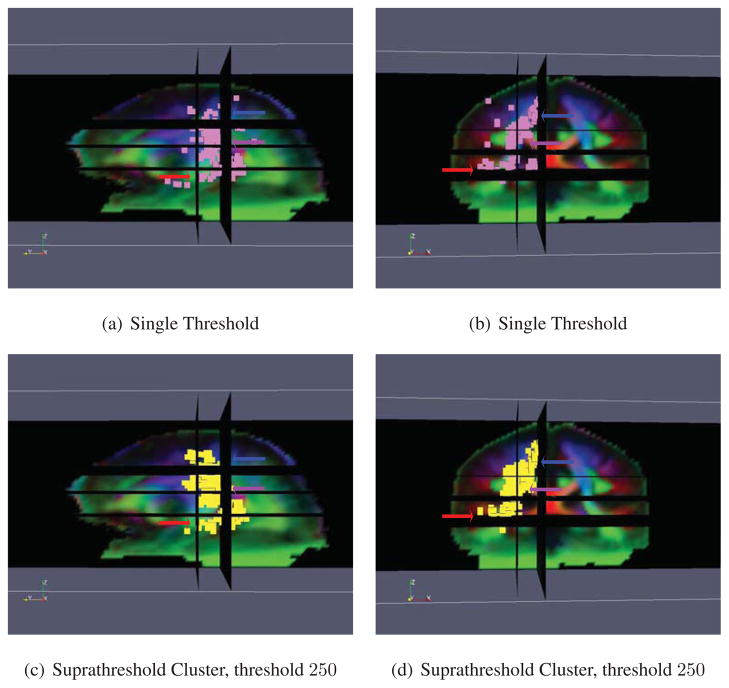
Statistically significant asymmetries (p < 0.05) are shown in Fig. 14. ODF based morphometry reveals a number of white matter microstructural asymmetries. First of all, the planum temporale, a highly lateralized brain structure involved with language processing, is clearly detected. This localization is consistent with the literature, as the language comprehension areas are among the most highly functionally lateralized areas of the brain. Secondly, the posterior limb of the internal capsule and the corticospinal or pyramidal tract are also detected. These areas are major components of the primary sensorimotor pathways. This result agrees well with previous studies reporting the asymmetry of these fiber tracts (Ardekani et al., 2007; Herve et al., 2006; Rademacher et al., 2001; Tensaouti et al., 2009; Westerhausen et al., 2007), further validating this approach. The main regions of the brain that are deemed asymmetric by the two tests are generally in agreement with each other. The suprathreshold cluster test generally gives contiguous regions, at the cost of reduced localizing power since only large regions are detected, but the single threshold approach does not.

Figure 14.

Results of performing the ODF Riemannian statistical test on brain asymmetry. Figs. 14(a) and 14(c) show the sagittal view and Figs. 14(b) and 14(d) the coronal view. The pink voxels in Figs. 14(a) and 14(b) are deemed significant by the single threshold test and the yellow voxels in Figs. 14(c) and 14(d) are deemed significant by the suprathreshold cluster test. The red arrow shows the planum temporale, the purple arrow the internal capsule, and the blue arrow the corticospinal tract.

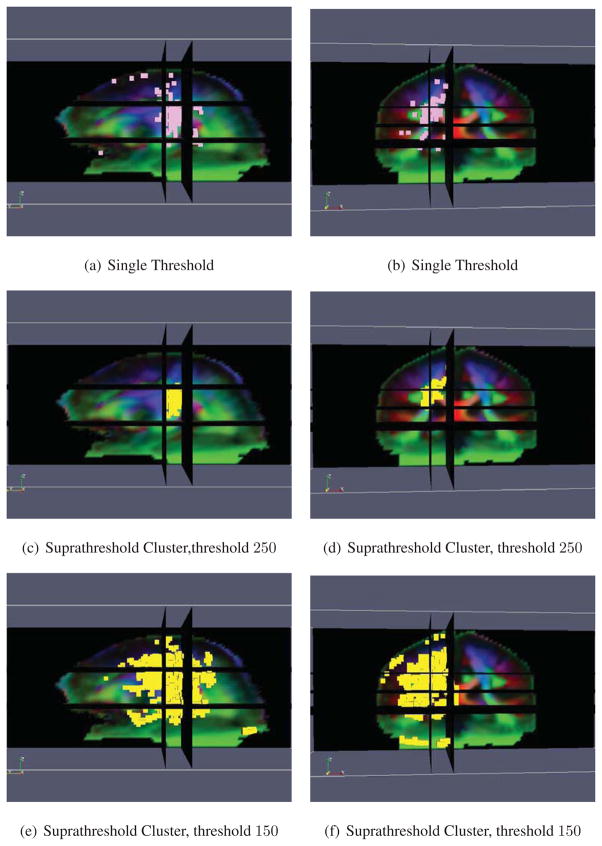
Finally, one can perform morphometry directly on the ODFs by treating them as vectors, as mentioned in §2.5.2. Here, we perform the much simpler Euclidean equivalent and compare the results to those obtained from the Riemannian version. Statistically significant asymmetries (p < 0.05) are found by the Euclidean metric (Fig. 15). From Figs. 15(a)–15(b), we see that the single threshold test does not detect the asymmetric region of the planum temporale. In the suprathreshold cluster test, if we threshold the regions at the same value as in the Riemannian test, we see that the planum temporale is not detected as well, as shown in Figs. 15(c)–15(d). As the two metrics are not equivalent, with the Riemannian distance being greater than or equal to the Euclidean distance, one could lower this threshold to see if similar results can be obtained. The results of the suprathreshold cluster test threshold at a lower value is shown in Figs. 15(e)–15(f). Such a strategy will reduce the localizing power of the test, as almost everywhere is now deemed asymmetric.

Figure 15.

Results of performing the ODF Euclidean statistical test on brain asymmetry. Figs. 15(a), 15(c) and 15(e) show the sagittal view and Figs. 15(b), 15(d) and 15(f) the coronal view. The pink voxels in Figs. 15(a) and 15(b) are deemed significant by the single threshold test and the yellow voxels in Figs. 15(c)–15(f) are deemed significant by the suprathreshold cluster test.

4. Conclusion

We presented a Riemannian framework for processing ODFs. Our approach does not require that the ODF be represented by any specific parametric model. Our framework also offers desirable properties that the other metrics do not have. The various Riemannian operations are in closed form and easily and efficiently computed. Choosing the correct metric for ODFs remains an open question and the question of how we can add in extra constraints into the current framework that respect the appropriate diffusion properties of the ODF field remains unsolved. Results on synthetic, phantom and real data quantify the advantage of working with our proposed framework versus the Euclidean approach. In addition, we also performed ODF-based morphometry to study asymmetries in the microstructure of the brain in a population of healthy subjects. This led to results that are in general agreement with prior reports, further validating our method and showing it is applicable to studies of structural brain asymmetry. Future research will apply the same kind of analysis to study differences between the brains of healthy and diseased subjects to better understand how different disorders affect the brain.

Appendix A. Extracting Orientation from HARDI Signals

In this section, we review what orientation PDFs are and how they can be extracted from HARDI signals. Briefly, DW-MRI measures the molecular water motion in the direction of a given diffusion gradient g. For this purpose, the Stejskal-Tanner imaging sequence (Stejskal and Tanner, 1965) is commonly used. In this case, the MR signal attenuation S(q, &tau;) is related to the diffusion PDF of the net displacement vector R, P(R|&tau;), by

$$\frac{S(\mathit{q},\tau )}{S_0}={\int }_{{\mathbb{R}}^3}\mathbf{P}(\mathbf{R}\mid \tau )e^{-2\pi i{\mathit{q}}^{\top }\mathbf{R}}d\mathbf{R}=\mathcal{F}[\mathbf{P}(\mathbf{R}\mid \tau )],$$ (A.1)

where S₀ is a reference signal acquired with no diffusion gradient, τ is the molecular diffusion time, q = γδg/2π is the displacement reciprocal vector, γ is the gyromagnetic ratio of water protons and δ is the duration of the diffusion gradients.

The signal S(q, τ) is thus expressed as the 3D Fourier transform of the diffusion PDF, also known as the ensemble average propagator (EAP), which is the function we want to reconstruct in DW-MRI. To do this accurately, one could sample the q-space at many gradient directions and then compute the inverse Fourier transform. However, this would be a computationally intensive and would require acquiring too many images. A more efficient scheme is to sample from a single spherical shell (||q||= q₀) and estimate the orientation PDFs. Examples include Q-ball imaging QBI (Tuch, 2004), Persistent Angular Structure (Jansons and Alexander, 2003) and Diffusion Orientation Transform (Özarslan et al., 2006).

While the framework proposed in this paper can be used for any definition of orientation PDFs, in this paper, we use the definition of orientation distribution function (ODF) proposed in (Wedeen et al., 2005; Aganj et al., 2010; Tristan-Vega et al., 2009). The ODF is defined as

$$\mathit{p}(\theta ,\phi )\doteq \mathit{p}(\mathit{r})={\int }_0^{\infty }\mathbf{P}(R\mathit{r})R^{2}dR,$$ (A.2)

where r = R/R and R = R(sin(θ) cos(φ), sin(θ) sin(φ), cos(θ)), where R ≥ 0, θ ∈ [0, π], φ ∈ [0, 2π]. Notice that the ODF is the angular profile of the diffusion PDF of water molecules, so it is actually a PDF on the 2-sphere. Therefore, the manifold structure of the ODFs should be considered as well.

Appendix B. Existence and Uniqueness of the Mean of a Set of Points on the Sphere

Unlike the Euclidean case, in general there is no closed form formula for the intrinsic mean on a Riemannian manifold. Moreover, there is no guarantee that it exists or is unique. The following theorem of Buss and Fillmore (2001) gives the conditions for the existence and uniqueness of the mean of a set of points on the sphere.

Theorem B.1. (Buss and Fillmore, 2001)

Suppose the data points ψ₁,…, ψ_n all lie in a hemisphere with at least one point ψ_i lying in the interior of the hemisphere. Then there exists only one global minimizer to the cost function defined in Eqn. (7).

As a direct consequence of Theorem B.1, Cheng et al. (2009) showed that the mean and the weighted Riemannian mean of a set of points in the space of ODFs is unique and exists for Ψ.

Appendix C. Calculation of Infinite Dimensional Covariance Matrix for Continuous ODFs

In the case of ODFs, each data point φ_i is a continuous function. Therefore, the sample covariance matrix becomes an infinite dimensional operator. Therefore, we need to compute eigenfunctions rather than the eigenvectors. To find the eigenfunctions used in PGA, we will now make use of the kernel trick, commonly used in kernel PCA (Schölkopf and Smola, 2002). More precisely, we seek the non-zero eigenvalues λ and non-zero eigenfunction u of cov(ψ) i.e., cov(ψ)u = λu. Let 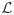: ℝⁿ →ψ be the operator $\mathcal{L}(v)={\sum }_{i=1}^n{\mathit{\psi }}_i{v}_i$. Then cov(ψ) = 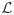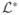, where 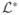: ψ → ℝⁿ is the adjoint operator. Therefore

$$\lambda \mathbf{u}=\mathcal{L}{\mathcal{L}}^{\ast }\mathbf{u}\iff \mathbf{u}=\mathcal{L}({\lambda }^{-1}{\mathcal{L}}^{\ast }\mathbf{u}).$$

Notice that u is always in the span of the operator 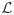. Now if we define v = λ⁻¹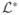u, we see that

$${\mathcal{L}}^{\ast }\mathcal{L}\mathit{v}={\lambda }^{-1}{\mathcal{L}}^{\ast }\mathcal{L}{\mathcal{L}}^{\ast }\mathbf{u}={\mathcal{L}}^{\ast }\mathbf{u}=\lambda \mathit{v}.$$

That is, v is an eigenfunction of 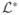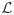with eigenvalue λ. While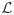 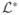is infinite dimensional,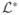 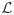is an n × n matrix. Therefore, to compute u, one would first compute v, an eigenvector of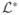 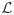, and recover the corresponding u as u = 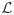v. Finally, if we use the same terminology as in kernel PCA, the kernel matrix 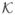∈ ℝ^n×n used here makes use of the Riemannian distance and is

$${\mathcal{K}}_{ij}={\langle {\phi }_i,{\phi }_j\rangle }_{\overline{\psi }}\in \mathbb{R}.$$

In this case, we are using the Fisher-Rao distance to build the kernel matrix and proceeding as in done in kernel PCA. To summarize, we have shown how to calculate the principal components for a set of probability density functions on 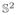. In practice, the ODF is not a continuous PDF; rather it is a histogram over M different gradient directions. Therefore, instead of using the kernel trick, we can calculate the sample covariance matrix $cov(\mathit{\psi })=\frac{1}{n-1}{\sum }_{i=1}^n{\mathit{\phi }}_i{\mathit{\phi }}_i^{\top }\in {\mathbb{R}}^{M\times M}$exactly.

Appendix D. Discrete Representation of ODF in Practice

When ODFs are approximated using different sets of basis functions such as spherical harmonics (SH) (Özarslan and Mareci, 2003; Descoteaux et al., 2007; Frank, 2002; Hess et al., 2006; Aganj et al., 2010), they are continuous functions defined on 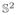. In practice, however, the ODF is sometimes discretized to be a histogram over M different gradient directions. This is precisely the approach that we adopt in this paper. How would one go about selecting the size and the number of bins of the histogram is an important question. So far, existing literature has proposed to sample directions equally spaced on the sphere by the icosahedral tessellation of the unit hemisphere, ranging from the 2nd order with M = 162 directions (Barmpoutis et al., 2009), the 3rd order with M = 642 directions (Leow et al., 2009), to the 4th order with M = 2562 (Zalesky, 2008). In this paper, we choose M = 162 as experimentally, we found that it is a good tradeoff between computational overhead and accuracy. The surface resolution is controlled by the number of bins; when the number of bins is small, the surface is a crude representation of the continuous ODF; when the number of bins is big, the surface is a good representation. Our proposed framework directly works with the histogram. Therefore, when the number of bins is large, the increased surface resolution comes at the expense of increased computational processing cost.

In (J. Cheng and R. Deriche, personal communications, 18 January 2011), the issue of normalization is discussed and we will give a summary here. In theory, if the ODF p(s) is a continuous probability density function defined on 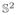, we have ∫_s∈p(s)ds = 1. In the discrete case, we have $1={\int }_{\mathit{s}\in {\mathbb{S}}^2}\mathit{p}(\mathit{s})d\mathit{s}\approx {\sum }_{i=1}^M\mathit{p}({\mathit{s}}_i){\mathrm{\Delta }}_i$ where Δ_i is the surface area at the direction s_i. Note that in the discrete case, ${\sum }_{i=1}^M\mathit{p}({\mathit{s}}_i)\ne 1$. To show this, consider when M equally spaced samples are used, we have $\mathrm{\Delta }={\mathrm{\Delta }}_i=\frac{4\pi }{M}$ and hence ${\sum }_{i=1}^M\mathit{p}({\mathit{s}}_i)=\frac{M}{4\pi }$. Therefore, if the estimated discrete ODF does not satisfy the PDF condition, then it should be normalized by a constant Z as done in (Tuch, 2004) such that $\frac{1}{Z}{\sum }_{i=1}^M\mathit{p}({\mathit{s}}_i)=1$. An alternative method is to do normalization in the continuous case. When spherical harmonics are used to represent the ODF, i.e., $\mathit{p}(\mathit{s})={\sum }_{i=1}^N{d}_i{B}_i(\mathit{s})$, then the ODF should be normalized such that $d_1=\frac{1}{\sqrt{4\pi }}$ in order for ∫_s∈p(s)ds = 1. If the estimation of the ODF is done with solid angle constraints as done in (Aganj et al., 2010; Goh et al., 2009a), then d₁ is automatically normalized to $\frac{1}{\sqrt{4\pi }}$. Cheng et al. (2009) then estimates the coefficients for the square-root samples $\mathit{\psi }(\mathit{s})={\sum }_{i=1}^N{c}_i{B}_i(\mathit{s})$, where ψ²(s) = p(s). In this case, if M equally spaced samples are used, notice that

$$\begin{array}{l}1={\int }_{{\mathbb{S}}^2}\mathit{p}(\mathit{s})d\mathit{s}={\int }_{{\mathbb{S}}^2}\sum _{i=1}^N{c}_i{B}_i(\mathit{s})\sum _{j=1}^N{c}_j{B}_j(\mathit{s})d\mathit{s}\\ \sum _{i,j}{c}_i{c}_j{\int }_{{\mathbb{S}}^2}{B}_i(\mathit{s})B_j(\mathit{s})d\mathit{s}\approx \sum _{i,j}{c}_i{c}_j\sum _{k=1}^M{B}_i({\mathit{s}}_k)B_j({\mathit{s}}_k)\mathrm{\Delta }.\end{array}$$ (D.1)

Since ${\sum }_{k=1}^M{B}_i({\mathit{s}}_k)B_j({\mathit{s}}_k)\mathrm{\Delta }\approx {\int }_{{\mathbb{S}}^2}{B}_i(\mathit{s})B_j(\mathit{s})d\mathit{s}={\delta }_{i,j}$, and hence, $1\approx {\sum }_{i=1}^N{c}_i^2$. Experimentally, ${\sum }_{i=1}^N{c}_i^2$ is always in [0.99, 1.01] if $d_1=\frac{1}{\sqrt{4\pi }}$.

Appendix E. Voxel Based Morphometry for Multivariate Testing

Let x₁,…, x_nx and y₁,…, y_ny be the (Euclidean) feature vectors drawn from two populations, $\overline{\mathbf{x}}=\frac{1}{n_x}{\sum }_{i=1}^{n_x}{\mathbf{x}}_i$ the sample mean of the first population, and $\overline{\mathbf{y}}=\frac{1}{n_y}{\sum }_{i=1}^{n_y}{\mathbf{y}}_i$ the sample mean of the second population. To test the hypothesis that x̄= ȳ, a commonly used statistic is the Hotelling’s T-squared statistic - a generalization of the Student’s t-statistic commonly used in multivariate hypothesis testing. The Hotelling’s T-square statistic is defined as

$$T^2=\frac{n_x{n}_y}{n_x+n_y}{(\overline{\mathbf{x}}-\overline{\mathbf{y}})}^{\top }{\mathbf{W}}^{-1}(\overline{\mathbf{x}}-\overline{\mathbf{y}})=\frac{n_x{n}_y}{n_x+n_y}{\overrightarrow{\overline{\mathbf{y}}\overline{\mathbf{x}}}}^{\top }{\mathbf{W}}^{-1}\overrightarrow{\overline{\mathbf{y}}\overline{\mathbf{x}}},$$ (E.1)

where W is the unbiased pooled covariance matrix estimate defined as

$$\begin{array}{l}\mathbf{W}=\frac{{\sum }_{i=1}^{n_x}({\mathbf{x}}_i-\overline{\mathbf{x}}){({\mathbf{x}}_i-\overline{\mathbf{x}})}^{\top }+{\sum }_{i=1}^{n_y}({\mathbf{y}}_i-\overline{\mathbf{y}}){({\mathbf{y}}_i-\overline{\mathbf{y}})}^{\top }}{n_x+n_y-2}\\ =\frac{{\sum }_{i=1}^{n_x}\overrightarrow{\overline{\mathbf{x}}{\mathbf{x}}_i}{\overrightarrow{\overline{\mathbf{x}}{\mathbf{x}}_i}}^{\top }+{\sum }_{i=1}^{n_y}\overrightarrow{\overline{\mathbf{y}}{\mathbf{y}}_i}{\overrightarrow{\overline{\mathbf{y}}{\mathbf{y}}_i}}^{\top }}{n_x+n_y-2}.\end{array}$$ (E.2)

If x₁,…, x_nx and y₁,…, y_ny are drawn from two independent multivariate normal distributions with the same mean and covariance, one can show that the Hotelling’s T-squared statistic is related to the F-distribution. As we do not assume that the observations come from two multivariate normal distributions, we use nonparametric permutation tests (Nichols and Holmes, 2002; Good, 2004) instead. As all voxels in the volume need to be considered simultaneously, we address the multiple comparisons and give corrected p-values based on two different methods, proposed in (Nichols and Holmes, 2002), that are commonly used for multiple comparisons correction in neuroimaging:

1. the single threshold method, to assess the significance of voxels whose statistical values exceed the critical threshold, whose value is dependent on the fixed significant level; and

2. a suprathreshold cluster test, to assess the significance of clusters of connected voxels that are all above a predetermined threshold.

The reader is referred to (Nichols and Holmes, 2002) for details of the two methods. Note that voxel-based analysis may be applied to any vector-valued data, using the nonparametric permutation tests.