Abstract
In this study, we analyze the processing of low-frequency sounds in the cochlear apex through responses of auditory nerve fibers (ANFs) that innervate the apex. Single tones and irregularly spaced tone complexes were used to evoke ANF responses in Mongolian gerbil. The spike arrival times were analyzed in terms of phase locking, peripheral frequency selectivity, group delays, and the nonlinear effects of sound pressure level (SPL). Phase locking to single tones was similar to that in cat. Vector strength was maximal for stimulus frequencies around 500 Hz, decreased above 1 kHz, and became insignificant above 4 to 5 kHz. We used the responses to tone complexes to determine amplitude and phase curves of ANFs having a characteristic frequency (CF) below 5 kHz. With increasing CF, amplitude curves gradually changed from broadly tuned and asymmetric with a steep low-frequency flank to more sharply tuned and asymmetric with a steep high-frequency flank. Over the same CF range, phase curves gradually changed from a concave-upward shape to a concave-downward shape. Phase curves consisted of two or three approximately straight segments. Group delay was analyzed separately for these segments. Generally, the largest group delay was observed near CF. With increasing SPL, most amplitude curves broadened, sometimes accompanied by a downward shift of best frequency, and group delay changed along the entire range of stimulus frequencies. We observed considerable across-ANF variation in the effects of SPL on both amplitude and phase. Overall, our data suggest that mechanical responses in the apex of the cochlea are considerably nonlinear and that these nonlinearities are of a different character than those known from the base of the cochlea.
Keywords: cochlear mechanics, cochlear apex, phase locking, Meriones unguiculatus
Introduction
Data from direct mechanical measurements have greatly advanced our understanding of auditory processing in the mammalian cochlea. Most of these data were obtained from the base of the cochlea. Mechanical responses in the cochlear base to high-frequency sounds are characterized by high sensitivity, sharp tuning, and strong dynamic compression (reviewed in Robles and Ruggero 2001). Processing of low-frequency sounds in the apex is less well charted. The apex is poorly accessible for direct mechanical measurements, and apical data have thus far been inconclusive concerning both the extent and nature of nonlinearities (Cooper and Rhode 1995, 1996; Hao and Khanna 1996; Rhode and Cooper 1996; Zinn et al. 2000). The interpretation is further hampered by unknown effects of surgical trauma to the cochlea, unavoidable with these methods (Cooper 1997; Khanna and Hao 1999; Zinn et al. 2000). Therefore, less invasive techniques such as recording from the auditory nerve continue to contribute to our knowledge of cochlear mechanics at the apex, even though the relation between auditory nerve fiber (ANF) responses and mechanical vibrations in the cochlea is indirect.
The literature on ANF recordings is vast (reviewed in Ruggero 1992; more recent studies include Recio-Spinoso et al. 2005; Van der Heijden and Joris 2006; Temchin et al. 2008a, b; Palmer and Shackleton 2009; Temchin and Ruggero 2009) and covers many mammalian species. The species tested share a large number of general characteristics, but also differ in their audible range, sensitivity, and sharpness of tuning. The literature on ANF recordings of the Mongolian gerbil (Meriones unguiculatus) includes a detailed inventory of sharpness of tuning at threshold, obtained using frequency-threshold tuning curves (FTCs; Schmiedt 1989; Ohlemiller and Echteler 1990). We have not been able to find comprehensive studies in gerbil ANFs of low-frequency tuning based on phase locking, such as first-order Wiener kernel analysis (reverse correlation) or phase analysis of single-tone responses. Such data are available for other mammalian species (e.g., cat, Carney and Yin 1988; chinchilla, Temchin and Ruggero 2009; guinea pig, Palmer and Shackleton 2009). Also, systematic data on the frequency limits of phase locking in the gerbil auditory nerve are lacking.
In the present study, we analyze the peripheral frequency selectivity in gerbil ANFs using the irregularly spaced tone complexes (zwuis) described in Van der Heijden and Joris (2006). The amplitude and phase curves produced by this technique provide a “filter-like” characterization of neural responses to wideband stimuli. In that respect, the technique is comparable to first-order Wiener-kernel analysis. However, it has the advantage of a better spectral resolution and wider frequency range, extending to frequencies remote from the characteristic frequency (CF). The technique is therefore suitable for studying peripheral frequency selectivity in quantitative detail.
Methods
Animals
Recordings were made from Mongolian gerbils (M. unguiculatus; female; weight ∼60 g; 41 ears). The animals were anesthetized by an initial intraperitoneal injection with a solution of ketamine/xylazine (80 and 12 μg/g body weight, respectively). Anesthesia was maintained by subcutaneous injections of the anesthetics, which kept the paw pinch reflex suppressed. This typically required the injection of 1/3 of the initial dose each hour. The Sokolich approach was used to access the auditory nerve (Sokolich and Smith 1973; Chamberlain 1977). Briefly, the pinna and cartilaginous part of the ear canal were removed, and the inferior posterior mastoid chamber of the ipsilateral bulla was exposed by removing the overlying tissue. The bulla was opened by gently chipping away some bone in a ∼2-mm radius, slightly posterior of the ear canal. This granted a clear view on the basal cochlear turn and the round window antrum. Opening the dorsomedial wall of the round window antrum by means of a small needle provided access to the underlying auditory nerve. The tensor tympani muscle was left intact. The head of the animal was fixed during the experiment using a small metal rod attached to the dorsal part of the skull. Throughout the experiment, body temperature was maintained at 37°C using an electrical heating pad. Since compound action potential thresholds obtained with frequencies of ∼2 kHz and below are not a reliable metric for the state of the cochlea, we used thresholds from the literature as a standard. The experiment was terminated if rate thresholds at CF were more than 20 dB higher than those reported by Ohlemiller and Echteler (1990). All procedures were approved by the Erasmus MC laboratory animal committee.
Stimulus generation and data acquisition
Stimuli were calculated on a personal computer using custom software written in MATLAB (The MathWorks, Natick, MA, USA) and generated from a single 16-bit D/A-channel (PD1; Tucker-Davis Technologies, Alachua, FL, USA) at a sample rate of 16 kHz. The stimuli were fed through a low-pass filter (J85E 7.2 kHz; TTE Inc., Los Angeles, CA, USA), followed by an attenuator (PA4; Tucker-Davis Technologies) and a headphone buffer (HB5; Tucker-Davis Technologies) before being broadcast by a speaker (FRS 7 4 Ω; Visaton, Haan, Germany; or SCL2; Shure, Niles, IL, USA). This speaker was attached to a sound delivery probe sealed to the exposed bony rim of the ear canal with Vaseline. A 1/2-in. condenser microphone (40AG, G.R.A.S., Holte, Denmark), placed inside the probe and connected to a pre-amplifier (2669; Brüel and Kjær, Nærum, Denmark) and a conditioning amplifier (Nexus 2690; Brüel and Kjær), allowed for in situ calibration ∼3 mm from the eardrum. All experiments were carried out in a double-walled sound-attenuating booth on a vibration isolation table (Newport, Irvine, CA, USA).
For intra-axonal recordings, glass micropipettes (1BBL w/fil 1.0 mm; World Precision Instruments, Sarasota, FL, USA) filled with 3 M KCl were used. The electrodes had resistances of 30–80 MΩ (measured in situ). A reference electrode was placed subcutaneously at the edge of the surgical field. Neural signals were fed to a pre-amplifier (Electro 705; World Precision Instruments) and a conditioning amplifier (EG&G PARC 113; AMETEK, Oak Ridge, TN, USA; or SR560; Stanford Research Systems, Sunnyvale, CA, USA) which amplified (100–500×) and filtered (30–10,000 Hz) the signal. Under constant monitoring of the threshold, a custom-built peak detector converted action potentials in the filtered signal to standard rectangular (TTL) pulses. The timing of these pulses was determined by an event timer (ET1; Tucker-Davis Technologies; 1-μs resolution) and stored on computer disc for subsequent analysis.
Stimulus protocol and data analysis
The electrode was advanced through the auditory nerve in 1-μm steps (controller 8200 Inchworm; EXFO, Mississauga, ON, Canada) until a single fiber was found. As a search stimulus, brief tone bursts (70 ms duration, 3 ms rise/fall; duty cycle 0.7) were used. The frequency was varied from 100 Hz to 25 kHz in 1/3-octave steps.
Single-tone stimuli
For each ANF, the same brief tone bursts (70 ms; 3 ms rise/fall; 0.7 duty cycle) were presented 15–20 times over a range of intensities (10–90 dB sound pressure level (SPL)) and frequencies (0.05–0.3 octave steps). The spike rates were used to reconstruct frequency–intensity response areas from which the units’ CF was determined. The spike arrival times, occurring during a window from 10 to 70 ms after the onset of each stimulus, were used in the analysis of phase locking to single tones, which was quantified by the vector strength R (Goldberg and Brown 1969). Statistical significance of R was determined by means of a Rayleigh test (Mardia and Jupp 2000) using a p = 0.001 criterion.
The dependence of maximum vector strength on stimulus frequency was estimated by fitting a polynomial to the highest vector strengths (Fig. 1A, black line). To that end, the data points were binned in non-overlapping bins of a non-uniform bandwidth. For the first bin, starting at 50 Hz, bandwidth was expanded upward until it contained 100 data points. The lower boundary of each consecutive bin started where the previous bin had ended and again the upper frequency limit was found by increasing bandwidth until 100 data points fell within the current bin. The last bin contained the remaining data points (N = 32). A fifth-order polynomial was then fitted to the median of the five highest vector strengths in each bin.
FIG. 1.
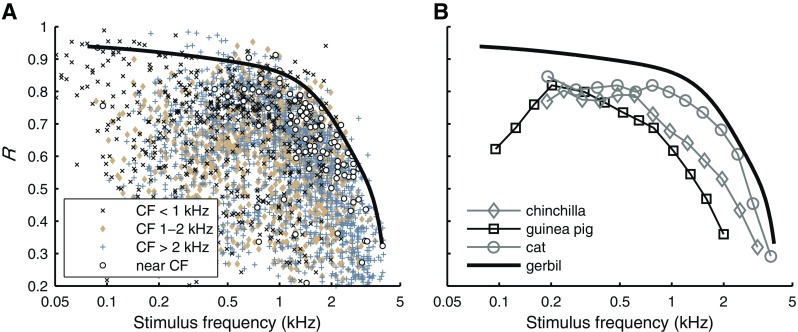
Phase locking to single tones. A Vector strength (R), plotted against stimulus frequency. Different symbols mark different CF subsets as indicated in the legend (N = 4764; 163 ANFs; 10–90 dB SPL). The solid black line is a polynomial fitted to the overall maximal vector strength (see text). The open circles mark maximum vector strength for tones in a 0.25-octave band around CF. B Maximal vector strength for different mammalian species culled from literature. Guinea pig and cat: Weiss and Rose (1988a, Fig. 3: based on Palmer and Russell (1986) and Johnson (1980), respectively). Chinchilla: Temchin and Ruggero (2009, Fig. 7).
Multitone stimuli
Multitone stimuli were used to obtain amplitude and phase curves that represent the effective stimulus at the input of the transduction process. Briefly, each stimulus consisted of multiple, irregularly spaced, frequency components (Victor 1979; Van der Heijden and Joris 2006). Components had equal amplitude and random starting phase. Each multitone stimulus was presented over a single speaker for 60 s. If necessary, multiple 60-s repetitions were combined. If time permitted, responses were obtained using a range of SPLs. See Van der Heijden and Joris (2006) for further details on the generation, analysis, and interpretation of such multitone stimuli.
The analysis of recorded spike trains involved the computation of the vector strength and phase for each of the frequency components of the stimulus. The irregular spacing of frequencies is essential because it ensures that all possible difference and sum frequencies (f1 ± f2), which are present in the response owing to the rectifying character of the transduction, never coincide with any stimulus component. This ensures that the vector strength and phase values computed for a given stimulus frequency results only from that stimulus component and that contamination by second-order components is excluded. A confidence level of p = 0.001 (Rayleigh test) was used as a criterion for significance of phase locking. Due to the low-pass characteristics at the level of the hair cells and their basolateral membrane (Weiss and Rose 1988b), phase locking declines with stimulus frequency. We therefore corrected the amplitude curves by dividing each R value by the corresponding value of the polynomial trend line described above (see also Fig. 1A).
To increase the frequency range of amplitude and phase curves of single ANFs, responses were obtained to multiple tone complexes that partially overlapped in frequency. To combine the separate amplitude curves into a single composite curve, individual curves were aligned by minimizing the sum of squares of their difference in the region of overlap (Van der Heijden and Joris 2006).
As a measure for sharpness of tuning for (composite) amplitude curves, Q 10dB was calculated as the peak frequency divided by the bandwidth 10 dB below the peak. When possible, amplitude curves obtained for different stimulus intensities in a single ANF were aligned on their low-frequency tail (defined as one octave below CF), using the same alignment procedure as described above. From these aligned curves, the growth rate of the normalized amplitude at CF was calculated by fitting a straight line to the stimulus level versus amplitude curve. The growth rate was obtained by converting gain to non-normalized amplitude, i.e., by adding one to the slope of the straight line.
Phase curves represent phase of the response component re rarefaction near the eardrum. Fine structure of phase curves was assessed by increasing each phase by an amount that varied linearly with frequency, corresponding with a positive time shift (see “Results”).
Group delay was calculated by fitting straight lines to phase-frequency curves. Since phase curves were generally poorly described by single straight lines, we calculated separate group delays over four different sections along the phase curves: above CF for frequencies >1.6×CF, near CF for frequencies in a 0.4-octave-wide band around CF, below CF for frequencies between 0.3×CF and 0.6×CF, and well below CF for frequencies <400 Hz. Due to the variation in filter shapes with CF (see “Results”), group delay could not always be calculated at all four sections for a single phase curve.
Results
Responses to single tones
Single tone data were collected with the purpose of determining the limits and degree of phase locking in gerbil ANFs. Responses to 70-ms tones were obtained from 163 ANFs, with CF ranging from 88 Hz to 24.71 kHz, presented at intensities of 10–90 dB SPL. Figure 1A shows vector strength as a function of stimulus frequency. For each ANF, vector strength was determined for a wide range of stimulus frequencies and intensities. Each data point represents a single frequency/intensity combination. Different symbols are used for different ranges of CFs as indicated in the figure. The large spread at each frequency is mainly caused by the inclusion of data obtained with arbitrary SPLs, including low and moderate levels which yield relatively poor phase locking. The solid line is a polynomial fit estimating the upper envelope of the data. The derivation of this curve and its use in the correction of amplitude curves extracted from multitone data are described in “Methods”.
Between 50 Hz and 1 kHz, vector strength was typically below 0.9, with a few outliers as high as 0.99 in the 500-Hz region. Vector strength decreased for stimulus frequencies above 1 kHz and just above 4 kHz it had dropped below 0.2. Notice that the data are not limited to near-CF stimulation; for example, the highest vector strengths were found for stimulus frequencies around 500 Hz, presented to ANFs with CF >2 kHz.
For each ANF, the maximum vector strength found for tones in a 0.25-octave band around CF are indicated in Figure 1A (open circles). These values typically fall below the polynomial fit to the upper envelope of the data (solid line). Only two near-CF data points between 500 Hz and 1 kHz show a vector strength slightly exceeding 0.9. The highest near-CF vector strength (R = 0.94) was found around 100 Hz.
Figure 1B compares the upper limit of vector strength in gerbil to three other mammalian species. Both the guinea pig data (Palmer and Russell 1986) and the chinchilla data (Temchin and Ruggero 2009) were obtained using brief tone bursts covering a wide range of frequencies (i.e., both near-CF and off-CF stimulation). In both studies, the vector strengths from all ANFs and animals were pooled to obtain their maximum for each stimulus frequency, similar to our data from gerbil. In chinchilla, the stimulus level was fixed at 70 dB SPL. The data from cat (Johnson 1980) are different in two ways. Firstly, they were obtained using long tonal stimulation. However, this does not strongly affect vector strength (Joris et al. 1994a). Secondly, stimulation was restricted to near-CF tones. For off-CF stimuli, Joris et al. (1994b) reported vector strengths up to 0.95 for cat ANFs with CF >2 kHz stimulated at 500 Hz. Thus, the restriction to near-CF stimulation in the data of the cat (Johnson 1980) tends to underestimate the overall maximum vector strength in that frequency region, similar to our results in Figure 1A. Taking this tendency into account, phase locking in the gerbil is very similar to that in cat, both in terms of maximum vector strength values and of frequency limit. In a final comparison to phase locking in rat (data not shown), gerbil ANFs also show higher vector strengths for off-CF tones as well as for near-CF tones (Paolini et al. 2001).
Responses to tone complexes
Responses to tone complexes were obtained from 157 ANFs, with CFs ranging from 88 Hz to 5 kHz. Fourier analysis of the response to the tone complexes produced linear estimates of amplitude and phase characteristics of the ANF (see “Methods” and Van der Heijden and Joris 2006). Figure 2 (left panel) shows an example of an amplitude curve from a single ANF, computed from the response to a single tone complex. It represents the relative magnitudes (i.e., the relative vector strength, expressed in decibel) of each of the stimulus components in the response. Since we are mainly interested in cochlear frequency selectivity, we corrected the amplitude curves for the overall decline of phase locking with frequency using the frequency response of the vector strength, derived from population data in Figure 1A (solid line). Note that this correction is small (<4 dB) at frequencies up to 3 kHz; at higher frequencies, the amplitude curves have a very limited dynamic range due to poor phase locking. The corrected amplitude curve (Fig. 2) shows a clear peak near CF, which reflects the peripheral frequency selectivity.
FIG. 2.
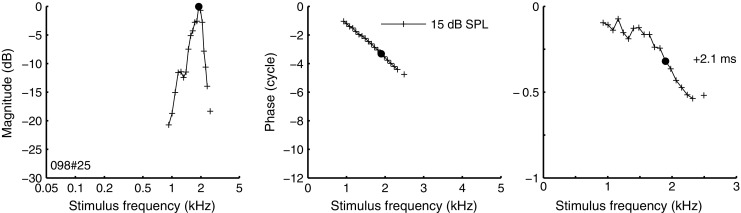
Amplitude curve (left panel) and phase curve (middle panel) for one ANF, obtained from a single response to a multitone stimulus. The magnitude of the amplitude curve, determined by the relative vector strength of each stimulus component, was corrected for the frequency dependence in phase locking (see text), after which its maximum was arbitrarily set to zero. To reveal details in the associated phase curve (middle panel), an overall delay was compensated for by advancing the curve in time by 2.1 ms (right panel). The CF (1.90 kHz), obtained from single tone data, is indicated in each panel (filled circles). The zwuis-stimulus consisted of 20 frequency components (0.93–2.5 kHz), each component at 15 dB SPL. The gap in amplitude and phase curves at 2.41 kHz corresponds to a stimulus component that failed to yield significant phase locking (Rayleigh test, p > 0.001).
The slope of the phase curves, extracted from the multitone responses, reflects overall group delay (∼2.3 ms in the example in Fig. 2, middle panel). This delay combines the contributions from middle-ear transmission, intracochlear propagation, and synaptic and neural transmission. In order to zoom in on the finer details of phase transfer, the curve was advanced in time by 2.1 ms, an amount large enough to compensate most of the overall delay of this ANF response (Fig. 2, right panel; the 2.1-ms compensation is indicated in the graph). The phase compensation revealed deviations from a straight line, i.e., small, frequency-dependent, variations of group delay.
Tuning characteristics at low SPL
For low stimulus intensities (maximally 30 dB above threshold), we observed a gradual, systematic transformation in the amplitude and phase curves with CF. This is illustrated by the examples in Figure 3. Amplitude curves of low-CF ANFs were asymmetric with a steep low-frequency flank and a shallow high-frequency flank (Fig. 3A, left panel). With increasing CF, lower flanks became shallower, while upper flanks became steeper (Fig. 3, left column). Amplitude curves became symmetric (on a logarithmic frequency scale) for CFs near 1 kHz (Fig. 3B). For still higher CFs, the amplitudes became asymmetric again, but now with the lower flanks shallower than the upper flanks (Fig. 3C, D).
FIG. 3.
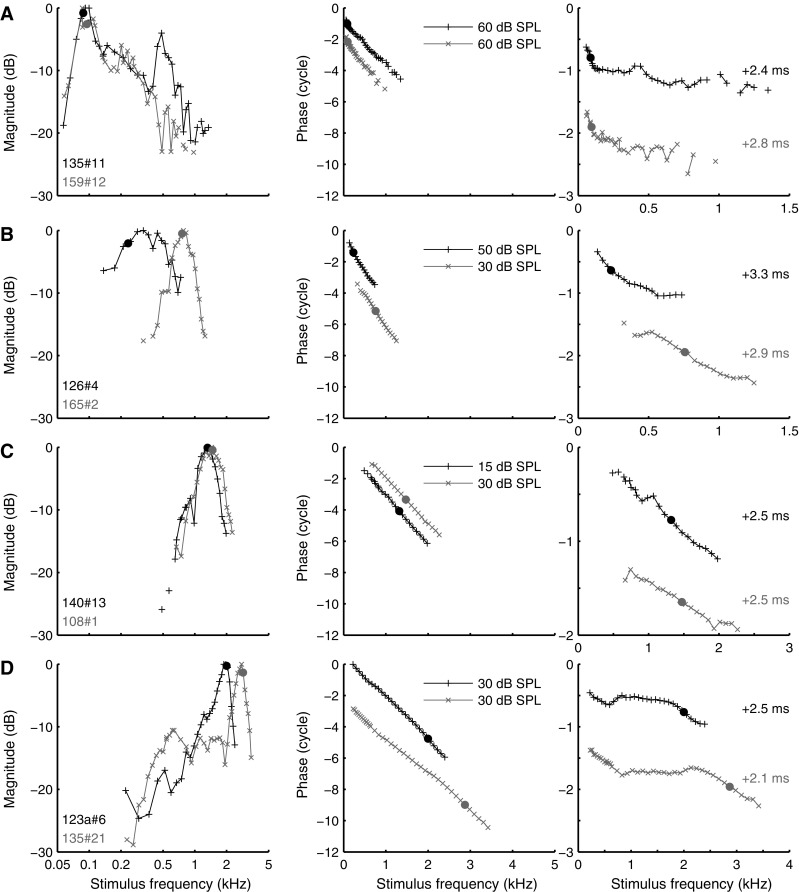
Amplitude curves and phase curves for multiple CFs, obtained at moderate SPLs. Layout of A–D as in Figure 2. Stimulus levels per component and compensatory delays are indicated. A CF 88 Hz (black) and 95 Hz (gray); B CF 234 Hz (black) and 758 Hz (gray); C CF 1.32 kHz (black) and 1.47 kHz (gray); D CF 2.00 kHz (black) and 2.87 kHz (gray).
The corresponding phase curves also show systematic changes with CF. For ANFs with the lowest CF, phase curves were concave from above: they were steepest at the lowest frequencies (including CF) and contain an extended shallow part above CF. With increasing CF, the phase curves became less bent, turning into almost straight lines (Fig. 3C, right panel). For higher CFs, the curves were concave from below with the steepest gradient around CF and a more shallow tail below CF. In addition, many phase curves of higher-CF (>1 kHz) ANFs exhibited a marked upturn (increased group delay) below 1 kHz (Fig. 3D, right panel).
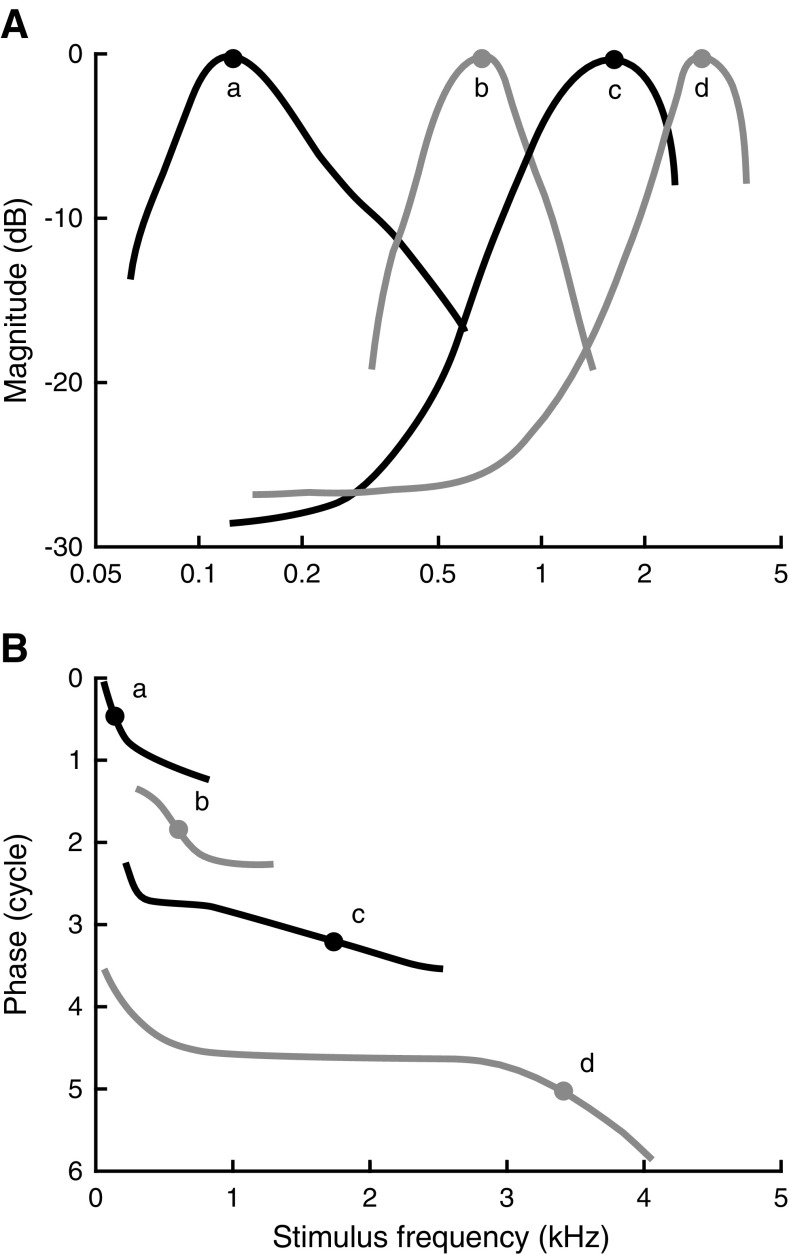
Figure 4 represents a schematic overview of the gradual transformation of the amplitude and phase curves with CF, based on a qualitative analysis of 446 recordings from 157 ANFs. With increasing CF, the amplitude and phase curves (curves marked d in Fig. 4; see also Fig. 3D) start to resemble the characteristics of mechanical responses to single tones measured in the base of the cochlea (Robles and Ruggero 2001).
FIG. 4.
Schematic overview of gradual change of amplitude curves (A) and phase curves (B) with increasing CF. Lowercase letters indicate pairs of amplitude and phase curves. The peaks of the amplitude curves are arbitrarily set to 0 dB. The phase curves are advanced in time by similar amounts as used in Figure 3 and are plotted with an arbitrary vertical offset. Approximate CFs are marked by solid circles.
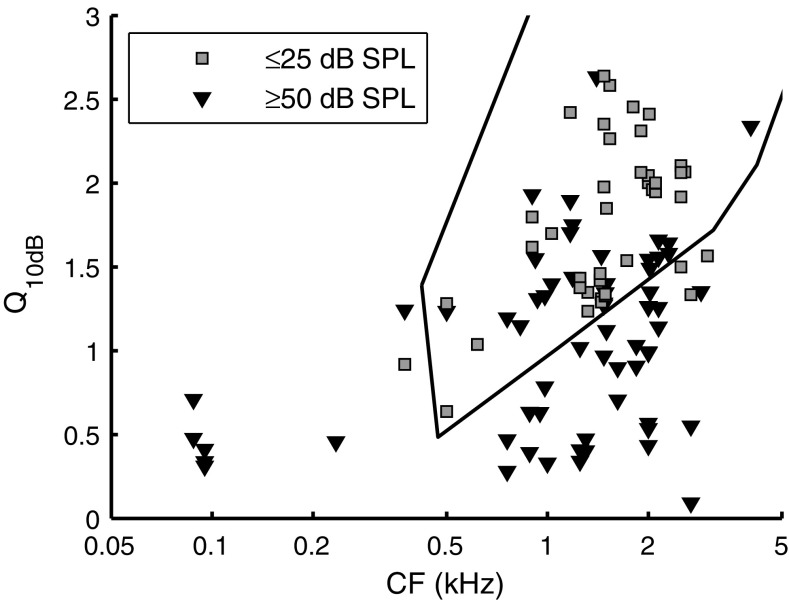
Quality factor
To quantify sharpness of tuning, we computed the quality factor (Q 10dB; peak frequency divided by bandwidth at −10 dB) from the amplitude curves. In Figure 5, Q 10dB is plotted against CF, using different symbols for two non-overlapping ranges of SPL. As expected from the amplitude curves (Figs. 3 and 4), Q 10dB increased with CF. Sound intensity also had a clear effect on Q 10dB: The high-SPL values (Fig. 5, triangles) were systematically lower than the low-SPL values (Fig. 5, squares). A comparison with Q 10dB data from gerbil threshold curves (Fig. 5, solid line; adapted from Ohlemiller and Echteler 1990) revealed a good agreement with our low-SPL Q 10dB values.
FIG. 5.
Tuning sharpness distribution. Q 10dB is plotted as a function of CF for two ranges of SPLs, as indicated in the legend: ≤25 dB SPL (N = 66; 27 ANFs) and ≥50 dB SPL (N = 43; 18 ANFs). Q 10dB values for intermediate SPLs were left out to reduce cluttering of symbols. The solid black line indicates a contour around Q 10dB values obtained from FTCs by Ohlemiller and Echteler (1990).
Near-CF group delays
In most cases, the segment around CF was the steepest part of the phase curve, corresponding to the largest group delay. Consequently, fitting a single straight line to the entire phase curve would underestimate near-CF group delay. We therefore restricted our near-CF group delay estimates to a 0.4-octave-wide band around CF, while pooling data obtained at different SPLs. Near-CF group delay (Fig. 6A, circles) ranged from >10 ms for the lowest CFs (∼100 Hz) down to ∼2 ms for the highest CFs (∼5 kHz). The relation between near-CF group delay and CF was fitted to a power function (Fig. 6A, solid line). The fit describes a lower limit of 2.1 ms for the highest CFs. This is higher than the estimated 1-ms “synaptic delay” for ANFs (Ruggero and Rich 1987), suggesting that for the entire range of CFs covered (<5 kHz), cochlear travel delays of near CF components exceed 1.1 ms. The range of near-CF group delays and their systematic decrease with CF is similar to near-CF group delays reported for squirrel monkey (Anderson et al. 1971), chinchilla (Temchin and Ruggero 2009), guinea pig (Palmer and Russell 1986), and cat (Goldstein et al. 1971), as shown in Figure 6B.
FIG. 6.
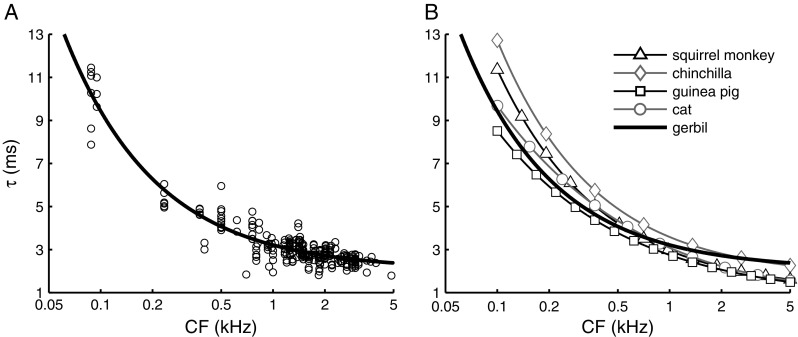
Near-CF group delay τ as function of CF. A Group delay estimated from a 0.4-octave band around CF (N = 257; 88 ANFs). Multiple group delay estimates are often extracted from a single ANF stimulated at multiple sound intensities. The solid line is a power function fitted to the data (τ = a + b∙CFc with a = 2.07±0.11, b = 1.15±0.13, and c = −0.808±0.04). B Comparison of near-CF group delay for different mammalian species. Squirrel monkey (τ = 1 + 1.95∙CF−0.725) is from Anderson et al. (1971), chinchilla (τ = 1.721 + 1.863∙CF−0.771) from Recio-Spinoso et al. (2005), guinea pig (τ = 0.661 + 2.088∙CF−0.575) is adapted from Palmer and Russell (1986, Fig. 8), and cat (τ = 1.25 (1 + (6/CF)2)0.25) from Goldstein et al. (1971). Symbols shown in this panel are not data points but are added to distinguish the curves.
The wide range of stimulus frequencies covered by many phase curves allowed an assessment of group delay for frequencies remote from CF. Motivated by the shapes of phase curves (Fig. 4B), we estimated group delays in three non-CF regions (Fig. 7A–C), which are illustrated in the insets of Figure 7. At very low (<400 Hz) frequencies (Fig. 7A), well-below-CF group delay showed a large variability and little dependence on CF. Large values of group delay in this low-frequency region reflect the upturns in the phase curves mentioned previously (cf. Fig. 3D), which were observed in some, but not all ANFs. Group delays for the frequency region just below CF (∼1.5–0.6 octaves below CF, i.e., 0.3×CF to 0.6×CF) are shown in Figure 7B. These below-CF group delays decreased with CF, but less strongly than the near-CF delays of Figure 6A. Above-CF (>1.6×CF) group delay (Fig. 7C) showed a weak trend to decrease with CF.
FIG. 7.
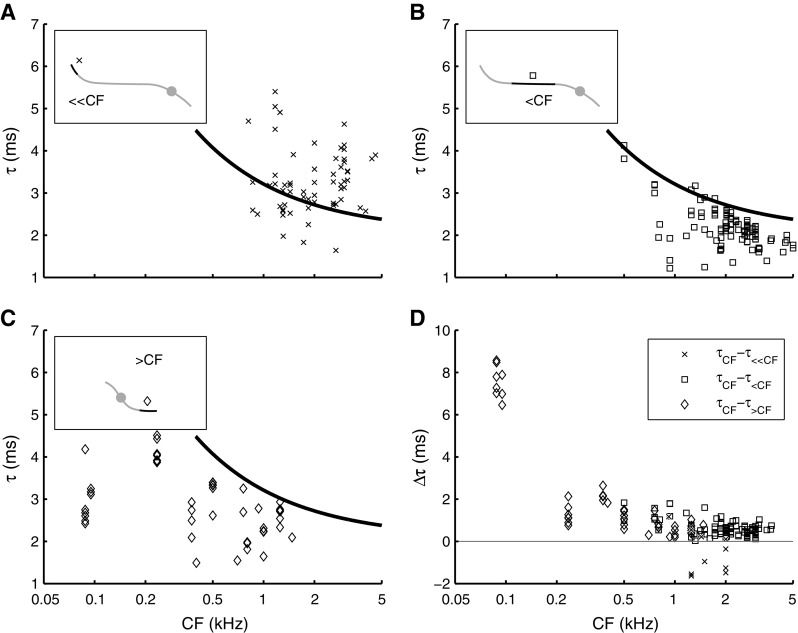
Off-CF group delay τ as function of CF. Insets show schematic phase curves, highlighting the frequency region over which group delays were estimated (see also Fig. 4b). Group delay estimated A in the 100–400-Hz region (≪CF; N = 67; 34 ANFs); B 1.5–0.6 octaves below CF (<CF; N = 132; 54 ANFs); C >0.6 octaves above CF (>CF; N = 46; 16 ANFs). The solid line in A–C is the same power function as described in Figure 6a. D Direct comparison between off-CF group delays (τ ≪CF, τ <CF, and τ >CF) and near-CF group delay (τ CF) evaluated from single phase curves by comparing slope values across frequency. The difference between near-CF group delay and each of the three off-CF group delays, Δτ, is plotted as function of CF. The same symbols as in A–C are used. Associated to A is τ CF − τ ≪CF (N = 10; six ANFs), to B is τ CF − τ <CF (N = 107; 41 ANFs), and to C is τ CF − τ>CF (N = 44; 16 ANFs).
We compared the group delays obtained from the different segments of single phase curves by computing the difference of the near-CF group delay and the various off-CF regions of the same curve, when available. This comparison of steepness across segments provides a quantitative analysis of the deviation of phase curves from straight lines (Fig. 7D). The group delay data of Figures 6 and 7 can be summarized as follows: Most of the variation with CF is observed in the near-CF region, with group delay monotonically decreasing with CF (Fig. 6A). The off-CF regions show little, if any, variation of group delay with CF (Fig. 7A–C). In most ANFs, the largest group delays were obtained for near-CF stimulus frequencies, with the exception of some ANFs with CF of 1 to 2 kHz, for which very low stimulus frequencies yielded the largest group delays (Fig. 7D, X’s).
Effect of SPL on amplitude curves
For 92 ANFs, we obtained responses to tone complexes presented at multiple SPLs. If the auditory periphery were linear, the amplitude curves obtained at different SPLs would have the same shape. The broadening of tuning with SPL (Fig. 5), however, indicates that the shape of amplitude curves is SPL dependent. When considering the effect of SPL on amplitude curves, it is important to realize that each curve only represents the relative amplitudes of the different components. They do not yield any information about the absolute amplitude of the response. Therefore, there is no intrinsic way of comparing amplitude curves across SPLs, so the vertical alignment of the curves is arbitrary (Van der Heijden and Joris 2006).
In contrast, mechanical measurements do yield absolute amplitudes and the variation of tuning with SPL is conveniently visualized by normalizing each amplitude curve by the amplitude of the stimulus. When overlaying these “sensitivity curves” obtained from the base of the cochlea, the linear growth well below CF results in complete overlap in the low-frequency tail, while compressive growth around CF results in a sharp peak at low SPLs that declines with increasing SPL (Rhode 2007).
The similarity of our highest-CF data (Fig. 4, curves marked d) with cochlear mechanical data motivated us to align the multiple amplitude curves at their low-frequency tail. Assuming linear growth for below-CF tones, vertical alignment of low-frequency tails of amplitude curves obtained at different stimulus levels converts them into sensitivity curves (this procedure can be viewed as a “wideband version” of Cooper and Yates’ (1994) method to estimate mechanical compression from single-tone rate-level curves.) Three examples of this alignment procedure are shown in Figure 8 (left column). The curves were aligned by minimizing the squared distance of each low-frequency tail (<CF/2) to the averaged curve. With increasing SPL, the relative response at CF (Fig. 8, filled circles) decreased, indicating compressive growth at CF. A similar alignment procedure could be applied to 44 ANFs (CF between 0.4 and 3 kHz). For each ANF, the growth rate (decibel response growth per decibel stimulus increase) was estimated by fitting a straight line to the magnitude at CF as a function of SPL. The growth rate was obtained by converting gain to non-normalized amplitude, i.e., by adding one to the slope of the straight line. This yielded a median compressive growth rate of 0.66 ± 0.22 dB/dB. The absence of distinct below-CF tails in the response curves of low-CF ANFs largely limited the alignment procedure to ANFs with CF above 800 Hz. An exception is shown in Figure 8C for an ANF with CF = 500 Hz, which yielded a compression of 0.87 dB/dB.
FIG. 8.
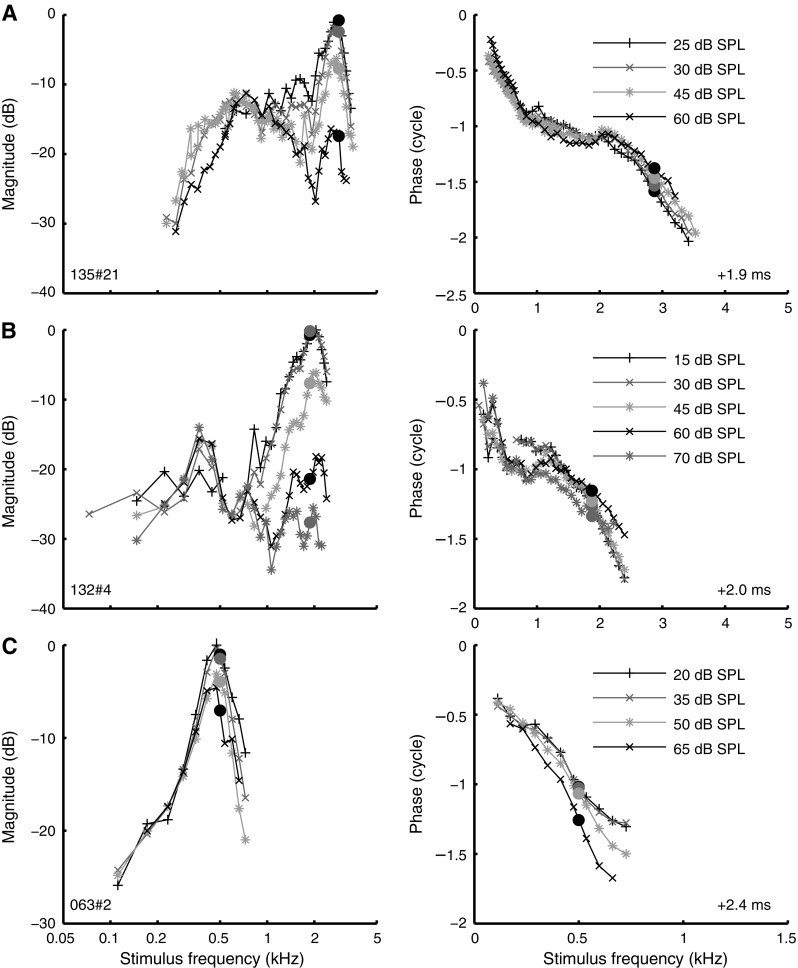
Estimating cochlear mechanical compression from ANF data. Amplitude curves (left column) and phase curves (right column) obtained at different SPLs as indicated in the graph. Amplitude curves were aligned at their low-frequency tail, allowing the assessment of nonlinear growth at CF (see text). Layout of phase data as in Figure 2, right panel. Data of 3 ANFs are shown: A CF 2.87 kHz; B CF 1.88 kHz; C CF 500 Hz.
Many amplitude curves for which low-tail alignment was not feasible did show clear effects of SPL. Some of these effects were systematic: As shown earlier (Fig. 5), peak width broadened with increasing SPL. In other aspects, however, the SPL-induced changes varied considerably across ANFs (Fig. 9). In some ANFs, the broadening of the curves was accompanied by a downward shift to lower frequencies. For other ANFs, the shape of the amplitude curve changed little (Fig. 9E), although sometimes its position also shifted to lower frequencies (Fig. 9D). In other cases, the lower/higher flank became shallower, while the upper/lower flank and best frequency showed little change (Fig. 9A and B, respectively). In three cases, we also observed the occurrence of secondary peaks at higher SPLs (Fig. 9A). Similar secondary peaks were observed in in vivo intracellular recordings of inner hair cells (Chatterjee and Zwislocki 1997, Fig. 4).
FIG. 9.
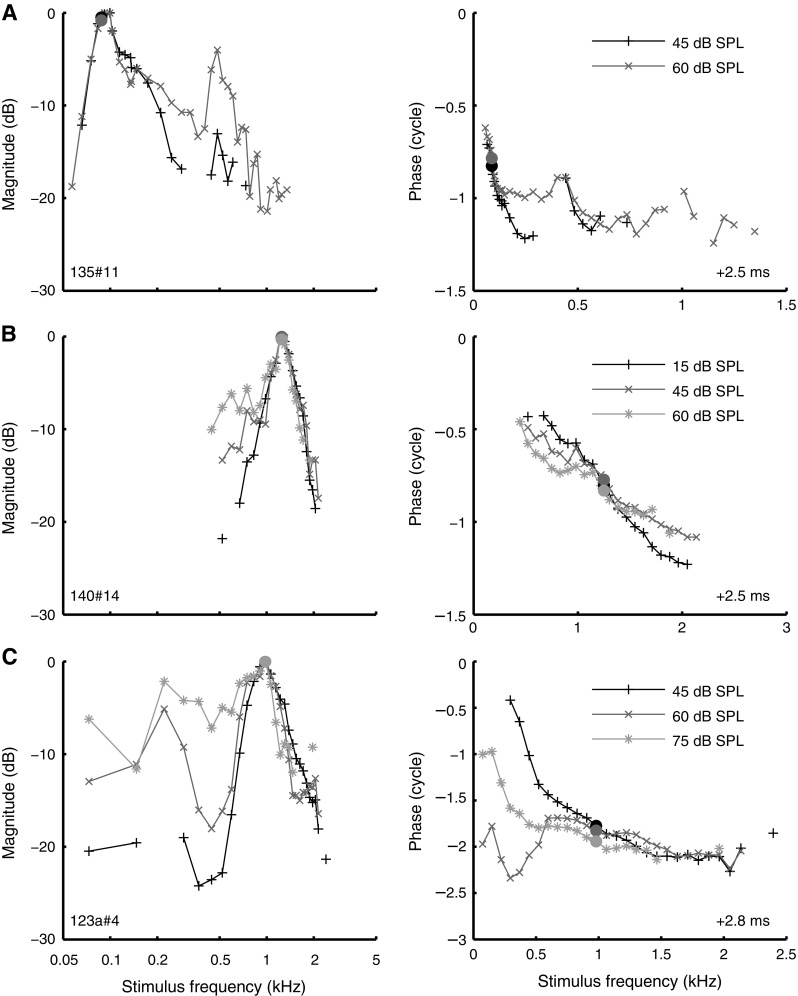
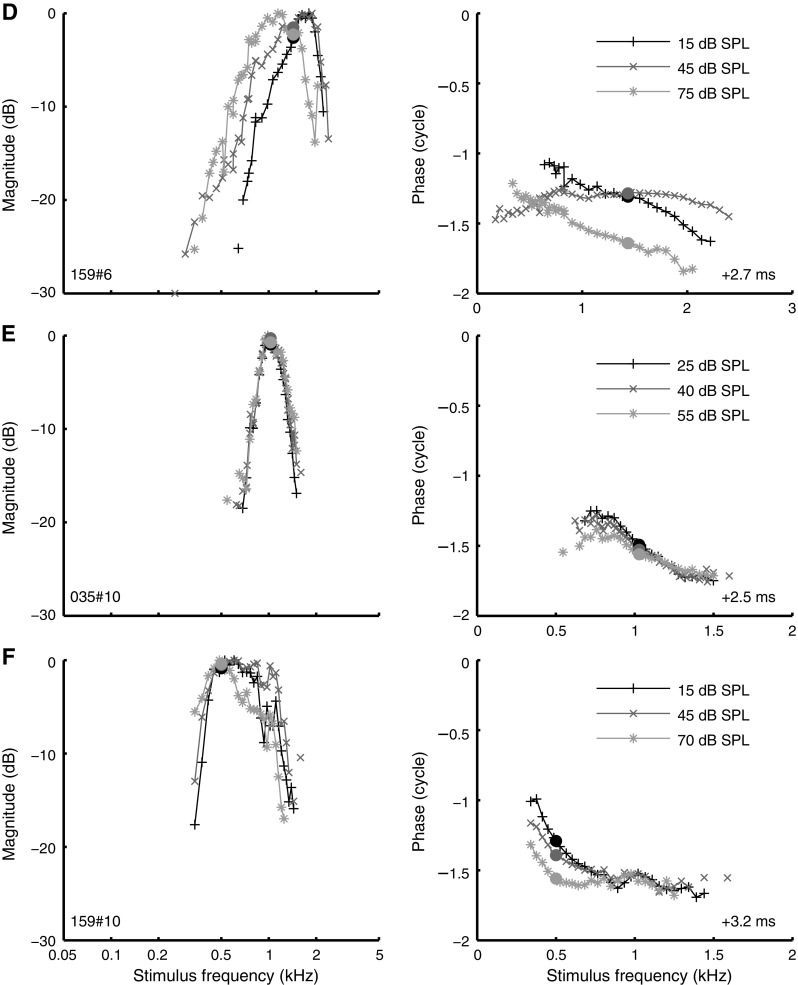
Effect of SPL on the shape of amplitude curves and phase curves. Layout as in Figure 8, but the peak of each amplitude curve was arbitrarily set to zero. A CF 88 Hz; B CF 1.25 kHz; C CF 0.98 kHz; D CF 1.44 kHz; E CF 1.03 kHz; F CF 500 Hz.
Our data did not reveal a systematic relationship between SPL-dependent peak shifts and CF. Some ANFs showed a clear peak shift, while such a shift was completely absent in other ANFs of comparable CF (compare Fig. 9D, E). We have not been able to link the observed variation in SPL-dependent tuning to any systematic experimental factor such as threshold of the ANF, condition of the animal, or time into the experiment. These findings are in contrast to in vivo, intracellular recordings in gerbil of low-CF (500–2,500 Hz) outer hair cells and Hensen cells (Zhang and Zwislocki 1996) and inner hair cells (Chatterjee and Zwislocki 1997), which showed systematic downward peak shifts (as large as two octaves in some cases) of amplitude-versus-frequency curves with increasing SPL. A potential explanation for this discrepancy is the difference in the auditory stimuli used; wideband stimuli tend to linearize the cochlear response compared to single tones (Recio-Spinoso et al. 2009). The comparison between the two types of data is difficult because little is known about the exact relation between transduction potentials in hair cells and ANF responses.
Effect of SPL on phase curves and group delay
The effect of SPL on phase curves was highly variable. The most consistent effect that we observed was a decline in group delay (downward slope of the phase curve) with increasing SPL, but there were exceptions even to that trend (see below). Examples of phase curves obtained at multiple SPLs are shown in Figures 8 and 9 next to the corresponding amplitude curves. As before (Fig. 2), the phase curves were compensated for overall group delay as indicated in the lower-right corner of the graphs. For optimal across-SPL comparison, the same compensation was applied to all curves obtained from the same ANF.
In the examples in Figure 8A, B, phase lag at CF decreased with SPL and the downward slope around CF became shallower. The example in Figure 8C, which showed an amplitude behavior (left column) similar to that of Figure 8A, B, showed an opposite phase behavior, with both phase lag and near-CF group delay increasing with SPL. In Figure 9B, phase at CF is nearly constant across SPL, whereas the curve becomes shallower (decreasing group delay) with increasing SPL. This “pivoting” of the phase curve around CF was previously observed in squirrel monkey ANFs by Anderson et al. (1971). Other examples, however, show pivoting about a frequency different from CF (below CF: Fig. 8C; above CF: Fig. 9F) as previously observed in guinea pig by Palmer and Shackleton (2009) and in one ANF in the squirrel monkey (Anderson et al. 1971). The phase curves of some ANFs showed nonmonotonic effects of SPL (Fig. 9D); in other ANFs, phase was nearly constant over a large range of SPLs (Fig. 9E). A similar variability in phase curves was reported for squirrel monkey (Anderson et al. 1971) and guinea pig (Palmer and Shackleton 2009). In three ANFs, we found phase anomalies (Fig. 9C) reminiscent of those observed in gerbil by Ronken (1986) and in chinchilla by Temchin and Ruggero (2009).
To quantify the effect of SPL on the group delays, we computed the change in group delay per 10-dB increase of stimulus intensity (Δτ 10dB) for each of the segments of the phase curves described earlier (Figs. 6 and 7). The results of this analysis are shown as a function of CF in Figure 10. In most ANFs, near-CF group delay (Fig. 10A, circles) decreased with sound intensity (Δτ 10dB <0). A subset of ANFs (six of 36), however, showed an increase of near-CF group delay with increasing SPL. The effect of SPL on near-CF group delays has been investigated in several mammalian species, using either single tones or first-order Wiener kernels (Anderson et al. 1971; Møller 1977; Carney and Yin 1988; Rhode and Cooper 1997; Recio-Spinoso et al. 2005; Palmer and Shackleton 2009; Temchin and Ruggero 2009). For comparison, Δτ 10dB values estimated from those studies are displayed in Figure 10A (numbered dots). The different studies show comparable ranges of Δτ 10dB values. Interestingly, some studies report increases of group delay with increasing SPL (positive Δτ 10dB values), in contrast with the widespread “textbook view” that group delay around CF always decreases with stimulus intensity.
FIG. 10.
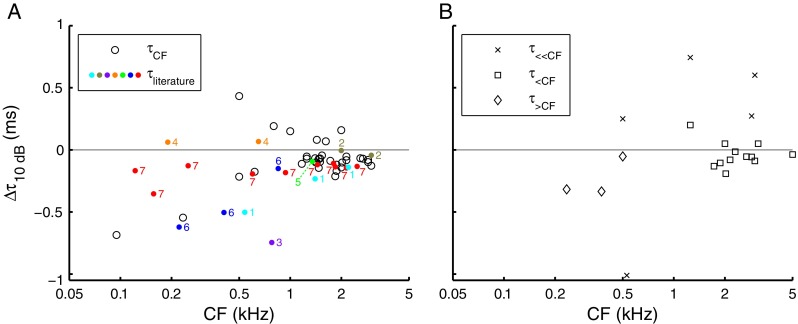
Effect of SPL on group delay. For individual ANFs, the change in group delay per 10-dB increase of SPL, Δτ 10dB, is shown for near-CF group delay (A; τ CF 34 ANFs) and the three types of off-CF group delays illustrated in Figure 7 (B; τ ≪CF five ANFs; τ <CF 12 ANFs; τ >CF three ANFs). Positive values indicate an increase in group delay with increasing SPL. Δτ 10dB was only computed across stimulus conditions differing at least 20 dB. A Near-CF Δτ 10dB values extracted from other ANF studies (black dots), marked by the numbers: 1 Anderson et al. (1971, Figs. 5, 6, and 8), 2 Møller (1977, Fig. 3), 3 Carney and Yin (1988, Fig. 6), 4 Rhode and Cooper (1997, Fig. 3), 5 Recio-Spinoso et al. (2005, Fig. 13), 6 Palmer and Shackleton (2009, Fig. 8), and 7 Temchin and Ruggero (2009, Fig. 15).
As before (cf. Fig. 7), off-CF group delays were split in three sets. Group delay in the 100–400-Hz stimulus range (Fig. 10B, crosses) generally increased with increasing SPL (positive Δτ 10dB), whereas group delay evaluated 1.5–0.6 octaves below CF (Fig. 10B, squares) and >0.6 octaves above CF (Fig. 10B, diamonds) generally decreased with increasing SPL (negative Δτ 10dB). The range of Δτ 10dB values for the latter two regions (Fig. 10B, squares and diamonds) was comparable to that observed in the near-CF region (Fig. 10A, circles).
Discussion
Phase locking to single tones
Single-tone responses of gerbil ANFs showed phase locking up to 4 to 5 kHz (Fig. 1A), a frequency limit comparable to cat and somewhat higher than chinchilla and guinea pig (Fig. 1B). Largest vector strengths (R > 0.9) were found in response to ∼500-Hz tones, primarily in ANFs stimulated in their low-frequency tails. Phase locking to near-CF tones was similar to cat, while maximum off-CF values of vector strength were slightly higher than in cat (Joris et al. 1994b).
Amplitude curves and their dependence on SPL
Frequency selectivity was assessed using amplitude curves derived from multitone responses. Tuning in low-CF gerbil ANFs (Figs. 2, 3, 4, and 5) was less sharp than in cat (Carney and Yin 1988; Van der Heijden and Joris 2006). Low-SPL amplitude curves showed a gradual change of shape with CF (Fig. 4). Similar CF-dependent tuning asymmetries were observed in studies employing single tones, e.g., ANF rate-frequency curves for squirrel monkey (Rose et al. 1971) and chinchilla (Temchin and Ruggero 2009) and FTCs for gerbil (Schmiedt 1989; Ohlemiller and Echteler 1990), cat (Kiang and Moxon 1974), and chinchilla (Temchin et al. 2008a). Similar asymmetries were also found in studies employing first-order Wiener kernels in cat (Carney and Yin 1988) and chinchilla (Recio-Spinoso et al. 2005) and tone complexes in cat (Van der Heijden and Joris 2006). In these studies, tuning was nearly symmetric (on a log-frequency scale) for 0.8 < CF < 1.2 kHz. In the present study, the region of symmetric tuning appeared somewhat larger (∼0.3–1 kHz).
Because the cochlea is highly nonlinear, metrics of frequency tuning depend on the stimulus paradigm. Different paradigms emphasize different aspects. Single tones assess the differential sensitivity to frequency components presented in isolation, whereas wideband stimuli assess the ability to separate out components in the presence of other, simultaneous, components. Cochlear compression typically causes suppression of CF components by off-CF components. This effect may explain why our amplitude curves were broader than FTCs from gerbil ANFs (Fig. 5) and for analogous differences between tuning estimated from Wiener kernels and FTCs in cat (Carney and Yin 1988).
In most ANFs, amplitude curves changed systematically with SPL. The broadening of tuning agrees with Wiener-kernel data in many studies (Møller 1977, 1978; Harrison and Evans 1982; Carney and Yin 1988; Recio-Spinoso et al. 2005). The amplitude curves of many ANFs (particularly for CF >1 kHz) allowed an across-SPL alignment of low-frequency tails (Fig. 8). The resulting estimates of growth at CF (0.66±0.22 dB/dB; N = 44) are similar to estimates of low-CF compression derived from single-tone ANF responses in guinea pig (Cooper and Yates 1994) and less compressive than the 0.1–0.2 dB/dB in first-order Wiener-kernel spectra of basilar membrane responses in chinchilla (Recio-Spinoso et al. 2009, Fig. 5). The lower CF range (<3 versus 9.5 kHz) may well account for the latter difference, consistent with the notion that the degree of nonlinearity increases with CF (Cooper and Yates 1994).
The low-tail alignment was based on the assumption that frequencies well below CF evoke a linear response. This is well documented in the base (e.g., Cooper and Rhode 1997; Ruggero et al. 1997). Unfortunately, a comparably systematic characterization of apical (non)linearity is unavailable, prohibiting the straightforward alignment of amplitude curves from low-CF ANFs. The large variation in SPL effects across individual ANFs further complicates the interpretation of intensity-dependent tuning. Our selection of example curves (Figs. 8 and 9) was guided by the intention to do justice to this variation rather than to suggest a systematic behavior not supported by the data. The variable effects of SPL likely reflect variations in nonlinear response growth in the apex. Both the degree of nonlinearity (steepness of growth) and the frequency range of nonlinear growth at a given cochlear location will affect amplitude curves obtained with wideband stimuli.
Phase curves
Phase curves uncompensated for overall delay appeared approximately linear (Figs. 2 and 3). Their downward slope reflects a group delay that includes cochlear travel and synaptic delay. Compensation for overall delay revealed a fine structure, often comprising multiple segments (Figs. 2, 3, and 4). Previous studies in cat (Pfeiffer and Molnar 1970; Van der Heijden and Joris 2006) and chinchilla (Temchin and Ruggero 2009) reported multisegment phase curves, changing from concave upward for CFs <1 kHz to concave downward for higher CFs. The curves reported here show a similar transition.
We analyzed group delays separately for the different phase-curve segments. Near-CF group delays showed a systematic decrease with CF, similar to group delays reported for other species (Fig. 6B). In most ANFs, phase curves became shallower (smaller group delay) with increasing SPL (Fig. 10), although there were frequent exceptions showing the opposite (Fig. 8C) or nonmonotonic effects (Fig. 9D). Decreasing group delay with increasing SPL was first reported by Anderson et al. (1971) for single-tone responses in the ANF of the squirrel monkey. Their findings are often summarized as “pivoting” of phase curves around CF: When SPL is increased, phase at CF stays constant, and the phase curve “rotates” around this fixed point. Phase pivoting was also reported in single-tone responses of guinea pig ANFs (Palmer and Shackleton 2009) and in noise responses in chinchilla (e.g., Recio-Spinoso et al. 2005) and cat (Carney and Yin 1988). In many of these ANFs, however, the frequency of constant phase deviated from CF.
Irregularities in phase curves and the across-ANF variability of SPL effects are somewhat magnified by the compensation for overall delay from the phase curves, combined with the sharp spectral resolution of the zwuis-method compared to the smeared-out character (caused by temporal windowing) of Wiener-kernel data. The irregularities, however, were stable and reproducible within single ANFs. The deviations from simple pivoting behavior indicate the limited validity of models based on oscillators having a variable damping coefficient. Incidentally, the observation that SPL affects group delay at frequencies remote from CF (Fig. 10B) also contradicts such models (Carney and Yin 1988). Apparently, the nonlinearities in the apical responses are more complicated than an oscillator with variable damping.
Relation to cochlear mechanics
In the range of SPLs of the present study, Hao and Khanna (1996) observed a largely linear behavior of the cochlear apex, whereas three other studies found nonlinear growth of single-tone responses (Cooper and Rhode 1996; Rhode and Cooper 1996; Zinn et al. 2000). These nonlinearities occurred at ∼40–80 dB SPL and were relatively minor compared to nonlinearities at the base. The range of stimulus frequencies evoking nonlinear growth appeared larger in the apex than in the base (Rhode and Cooper 1996). Overall, the phases of single-tone responses in these apical–mechanical studies are compatible with ANF data reported here and elsewhere. For guinea pig (Khanna and Hao 1999) and chinchilla (Rhode and Cooper 1996), phase curves for CF <1 kHz can be approximated by two straight line segments (the steeper one at low frequencies). In contrast to most ANF studies, an increasing group delay with increasing SPL was found in mechanical measurements in the apex (Rhode and Cooper 1996; Zinn et al. 2000) and an in vivo recording in gerbil of a Hensen cell (Zwislocki 1990; Zhang and Zwislocki 1995).
To what extent are the nonlinear effects of SPL in the ANF responses caused by cochlear mechanics? After all, the transduction stage is also nonlinear. However, amplitude curves are largely insensitive to instantaneous nonlinearities of the transduction stage (De Boer 1997; Van der Heijden and Joris 2006), and it is unlikely that the low-pass character of transduction is strongly SPL dependent. We therefore expect amplitude curves to faithfully represent tuning at the level of the bundles of the innervated inner hair cell. This, however, may still differ from mechanical tuning measured at Reissner’s membrane or supporting cells in the apex.
Phase of ANF responses is typically interpreted in terms of mechanical vibrations by simply accounting for a 1-ms “synaptic delay” (Ruggero and Rich 1987), independent of SPL. It is not obvious, however, that the timing of action potentials should be SPL independent. In elementary threshold models of firing, larger amplitudes cause earlier threshold crossings, leading to smaller group delays with increased SPL. At the inner hair cell synapse, processes like vesicle release likely depend on stimulation level too (Keen and Hudspeth 2006; Goutman and Glowatzki 2007). The transduction stage may therefore contribute its own SPL dependencies to the ANF phase. Such nonmechanical contributions are also suggested by our observation that off-CF group delay and near-CF group delay were equally affected by SPL (Fig. 10), whereas cochlear mechanical SPL effects are typically confined to the CF region (Robles and Ruggero 2001). The combination of opposing SPL effects (increasing mechanical delay; decreasing synaptic delay) may explain the apparent contradiction between mechanical data and ANF data and the variable effects of SPL on group delay of the present study (Figs. 8, 9, and 10) and others (e.g., Temchin and Ruggero 2009, Figs. 15 and 16).
Overall, the ANF data presented here and elsewhere indicate that apical mechanics is considerably nonlinear and that apical nonlinearity is qualitatively different from basal nonlinearity. The quantitative interpretation of neural data in terms of cochlear mechanics is hampered by a scarcity of independent data on the character of apical nonlinearity. Apart from additional mechanical measurements, independent insights into apical mechanics may be gained from the study of inherently nonlinear phenomena such as two-tone suppression and distortion products.
Acknowledgments
We thank Dr. Tony Gummer and three anonymous reviewers for helpful comments. This work was supported by NWO grants 818.02.007 (ALW) and 863.08.003 (Veni).
Conflicts of interest
The authors declare that there is no conflict of interest.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Anderson DJ, Rose JE, Hind JE, Brugge JF. Temporal position of discharges in single auditory nerve fibers within the cycle of a sine-wave stimulus: frequency and intensity effects. J Acoust Soc Am. 1971;49:1131–1139. doi: 10.1121/1.1912474. [DOI] [PubMed] [Google Scholar]
- Carney LH, Yin TC. Temporal coding of resonances by low-frequency auditory nerve fibers: single-fiber responses and a population model. J Neurophysiol. 1988;60:1653–1677. doi: 10.1152/jn.1988.60.5.1653. [DOI] [PubMed] [Google Scholar]
- Chamberlain SC. Neuroanatomical aspects of the gerbil inner ear: light microscope observations. J Comp Neurol. 1977;171:193–204. doi: 10.1002/cne.901710205. [DOI] [PubMed] [Google Scholar]
- Chatterjee M, Zwislocki JJ. Cochlear mechanisms of frequency and intensity coding. I. The place code for pitch. Hear Res. 1997;111:65–75. doi: 10.1016/S0378-5955(97)00089-0. [DOI] [PubMed] [Google Scholar]
- Cooper NP. Mid-band sensitivity notches in apical cochlear mechanics. In: Lewis ER, Long GR, Lyon RF, Narins PM, Steele CR, Hecht-Poinar E, editors. Diversity in auditory mechanics. Singapore: World Scientific; 1997. pp. 298–304. [Google Scholar]
- Cooper NP, Yates GK. Nonlinear input-output functions derived from the responses of guinea-pig cochlear nerve fibres: variations with characteristic frequency. Hear Res. 1994;78:221–234. doi: 10.1016/0378-5955(94)90028-0. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Nonlinear mechanics at the apex of the guinea-pig cochlea. Hear Res. 1995;82:225–243. doi: 10.1016/0378-5955(94)00180-X. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Fast travelling waves, slow travelling waves and their interactions in experimental studies of apical cochlear mechanics. Aud Neurosci. 1996;2:289–299. [Google Scholar]
- Cooper NP, Rhode WS. Mechanical responses to two-tone distortion products in the apical and basal turns of the mammalian cochlea. J Neurophysiol. 1997;78:261–270. doi: 10.1152/jn.1997.78.1.261. [DOI] [PubMed] [Google Scholar]
- De Boer E. Connecting frequency selectivity and nonlinearity for models of the cochlea. Aud Neurosci. 1997;3:377–388. [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Goldstein JL, Baer T, Kiang NYS. A theoretical treatment of latency, group delay, and tuning characteristics of auditory-nerve responses to clicks and tones. In: Sachs MB, editor. Physiology of the auditory system. Baltimore: National Educational Consultants; 1971. pp. 133–141. [Google Scholar]
- Goutman JD, Glowatzki E. Time course and calcium dependence of transmitter release at a single ribbon synapse. Proc Natl Acad Sci USA. 2007;104:16341–16346. doi: 10.1073/pnas.0705756104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao LF, Khanna SM. Reissner’s membrane vibrations in the apical turn of a living guinea pig cochlea. Hear Res. 1996;99:176–189. doi: 10.1016/S0378-5955(96)00099-8. [DOI] [PubMed] [Google Scholar]
- Harrison RV, Evans EF. Reverse correlation study of cochlear filtering in normal and pathological guinea pig ears. Hear Res. 1982;6:303–314. doi: 10.1016/0378-5955(82)90062-4. [DOI] [PubMed] [Google Scholar]
- Johnson DH. The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones. J Acoust Soc Am. 1980;68:1115–1122. doi: 10.1121/1.384982. [DOI] [PubMed] [Google Scholar]
- Joris PX, Carney LH, Smith PH, Yin TC. Enhancement of neural synchronization in the anteroventral cochlear nucleus. I. Responses to tones at the characteristic frequency. J Neurophysiol. 1994;71:1022–1036. doi: 10.1152/jn.1994.71.3.1022. [DOI] [PubMed] [Google Scholar]
- Joris PX, Smith PH, Yin TC. Enhancement of neural synchronization in the anteroventral cochlear nucleus. II. Responses in the tuning curve tail. J Neurophysiol. 1994;71:1037–1051. doi: 10.1152/jn.1994.71.3.1037. [DOI] [PubMed] [Google Scholar]
- Keen EC, Hudspeth AJ. Transfer characteristics of the hair cell’s afferent synapse. Proc Natl Acad Sci USA. 2006;103:5537–5542. doi: 10.1073/pnas.0601103103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanna SM, Hao LF. Reticular lamina vibrations in the apical turn of a living guinea pig cochlea. Hear Res. 1999;132:15–33. doi: 10.1016/S0378-5955(99)00027-1. [DOI] [PubMed] [Google Scholar]
- Kiang NY, Moxon EC. Tails of tuning curves of auditory-nerve fibers. J Acoust Soc Am. 1974;55:620–630. doi: 10.1121/1.1914572. [DOI] [PubMed] [Google Scholar]
- Mardia KV, Jupp PE. Directional statistics. Chichester: Wiley; 2000. [Google Scholar]
- Møller AR. Frequency selectivity of single auditory-nerve fibers in response to broadband noise stimuli. J Acoust Soc Am. 1977;62:135–142. doi: 10.1121/1.381495. [DOI] [PubMed] [Google Scholar]
- Møller AR. Frequency selectivity of the peripheral auditory analyzer studied using broad band noise. Acta Physiol Scand. 1978;104:24–32. doi: 10.1111/j.1748-1716.1978.tb06247.x. [DOI] [PubMed] [Google Scholar]
- Ohlemiller KK, Echteler SM. Functional correlates of characteristic frequency in single cochlear nerve fibers of the Mongolian gerbil. J Comp Physiol A. 1990;167:329–338. doi: 10.1007/BF00192568. [DOI] [PubMed] [Google Scholar]
- Palmer AR, Russell IJ. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear Res. 1986;24:1–15. doi: 10.1016/0378-5955(86)90002-X. [DOI] [PubMed] [Google Scholar]
- Palmer A, Shackleton T. Variation in the phase of response to low-frequency pure tones in the guinea pig auditory nerve as functions of stimulus level and frequency. J Assoc Res Otolaryngol. 2009;10:233–250. doi: 10.1007/s10162-008-0151-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paolini AG, FitzGerald JV, Burkitt AN, Clark GM. Temporal processing from the auditory nerve to the medial nucleus of the trapezoid body in the rat. Hear Res. 2001;159:101–116. doi: 10.1016/S0378-5955(01)00327-6. [DOI] [PubMed] [Google Scholar]
- Pfeiffer RR, Molnar CE. Cochlear nerve fiber discharge patterns: relationship to the cochlear microphonic. Science. 1970;167:1614–1616. doi: 10.1126/science.167.3925.1614. [DOI] [PubMed] [Google Scholar]
- Recio-Spinoso A, Temchin AN, van Dijk P, Fan YH, Ruggero MA. Wiener-kernel analysis of responses to noise of chinchilla auditory-nerve fibers. J Neurophysiol. 2005;93:3615–3634. doi: 10.1152/jn.00882.2004. [DOI] [PubMed] [Google Scholar]
- Recio-Spinoso A, Narayan SS, Ruggero MA. Basilar membrane responses to noise at a basal site of the chinchilla cochlea: quasi-linear filtering. J Assoc Res Otolaryngol. 2009;10:471–484. doi: 10.1007/s10162-009-0172-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhode WS. Basilar membrane mechanics in the 6–9 kHz region of sensitive chinchilla cochleae. J Acoust Soc Am. 2007;121:2792–2804. doi: 10.1121/1.2718397. [DOI] [PubMed] [Google Scholar]
- Rhode WS, Cooper NP. Nonlinear mechanics in the apical turn of the chinchilla cochlea in vivo. Aud Neurosci. 1996;3:101–121. [Google Scholar]
- Rhode WS, Cooper NP. Nonlinear mechanisms in the apical turn of the chinchilla cochlea. In: Lewis ER, Long GR, Lyon RF, Narins PM, Steele CR, Hecht-Poinar E, editors. Diversity in auditory mechanics. Singapore: World Scientific; 1997. pp. 318–324. [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronken DA. Anomalous phase relations in threshold-level responses from gerbil auditory nerve fibers. J Acoust Soc Am. 1986;79:417–425. doi: 10.1121/1.393529. [DOI] [PubMed] [Google Scholar]
- Rose JE, Hind JE, Anderson DJ, Brugge JF. Some effects of stimulus intensity on response of auditory nerve fibers in the squirrel monkey. J Neurophysiol. 1971;34:685–699. doi: 10.1152/jn.1971.34.4.685. [DOI] [PubMed] [Google Scholar]
- Ruggero MA. Physiology and coding of sound in the auditory nerve. In: Fay RR, Popper AN, editors. The mammalian auditory pathway: neurophysiology. New York: Springer; 1992. pp. 34–93. [Google Scholar]
- Ruggero MA, Rich NC. Timing of spike initiation in cochlear afferents: dependence on site of innervation. J Neurophysiol. 1987;58:379–403. doi: 10.1152/jn.1987.58.2.379. [DOI] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedt RA. Spontaneous rates, thresholds and tuning of auditory-nerve fibers in the gerbil: comparisons to cat data. Hear Res. 1989;42:23–35. doi: 10.1016/0378-5955(89)90115-9. [DOI] [PubMed] [Google Scholar]
- Sokolich WG, Smith RL. Easy access to the auditory nerve in the Mongolian gerbil. J Acoust Soc Am. 1973;54:283. doi: 10.1121/1.1978024. [DOI] [Google Scholar]
- Temchin AN, Ruggero MA. Phase-locked responses to tones of chinchilla auditory nerve fibers: implications for apical cochlear mechanics. J Assoc Res Otolaryngol. 2009;11:297–318. doi: 10.1007/s10162-009-0197-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory-nerve fibers. I. Dependence on characteristic frequency and relation to the magnitudes of cochlear vibrations. J Neurophysiol. 2008;100:2889–2898. doi: 10.1152/jn.90637.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory nerve fibers. II. Dependence on spontaneous activity and relation to cochlear nonlinearity. J Neurophysiol. 2008;100:2899–2906. doi: 10.1152/jn.90639.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Heijden M, Joris PX. Panoramic measurements of the apex of the cochlea. J Neurosci. 2006;26:11462–11473. doi: 10.1523/JNEUROSCI.1882-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor JD. Nonlinear systems analysis: comparison of white noise and sum of sinusoids in a biological system. Proc Natl Acad Sci USA. 1979;76:996–998. doi: 10.1073/pnas.76.2.996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss TF, Rose C. A comparison of synchronization filters in different auditory receptor organs. Hear Res. 1988;33:175–179. doi: 10.1016/0378-5955(88)90030-5. [DOI] [PubMed] [Google Scholar]
- Weiss TF, Rose C. Stages of degradation of timing information in the cochlea: a comparison of hair-cell and nerve-fiber responses in the alligator lizard. Hear Res. 1988;33:167–174. doi: 10.1016/0378-5955(88)90029-9. [DOI] [PubMed] [Google Scholar]
- Zhang M, Zwislocki JJ. OHC response recruitment and its correlation with loudness recruitment. Hear Res. 1995;85:1–10. doi: 10.1016/0378-5955(95)00026-Z. [DOI] [PubMed] [Google Scholar]
- Zhang M, Zwislocki JJ. Intensity-dependent peak shift in cochlear transfer functions at the cellular level, its elimination by sound exposure, and its possible underlying mechanisms. Hear Res. 1996;96:46–58. doi: 10.1016/0378-5955(96)00029-9. [DOI] [PubMed] [Google Scholar]
- Zinn C, Maier H, Zenner H, Gummer AW. Evidence for active, nonlinear, negative feedback in the vibration response of the apical region of the in-vivo guinea-pig cochlea. Hear Res. 2000;142:159–183. doi: 10.1016/S0378-5955(00)00012-5. [DOI] [PubMed] [Google Scholar]
- Zwislocki JJ. Active cochlear feedback: required structure and response phase. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The mechanics and biophysics of hearing. Berlin: Springer; 1990. pp. 114–120. [Google Scholar]