From Target Selection to the Minimum Acceptable Biological Effect Level for Human Study: Use of Mechanism-based PK/PD Modeling to Design Safe and Efficacious Biologics

Abstract

In this paper, two applications of mechanism-based modeling are presented with their utility from candidate selection to first-in-human dosage selection. The first example is for a monoclonal antibody against a cytomegalovirus glycoprotein complex, which involves an antibody binding model and a viral load model. The model was used as part of a feasibility analysis prior to antibody generation, setting the specifications for the affinity needed to achieve a desired level of clinical efficacy. The second example is a pharmacokinetic–pharmacodynamic model based on a single-dose pharmacology study in cynomolgus monkey using data on pharmacokinetics, receptor occupancy, and the dynamics of target cell depletion and recovery. The model was used to estimate the MABEL, here defined as the minimum acceptable biological effect level against which a dose is selected for a first-in-human study. From these applications, we demonstrate that mechanism-based PK/PD binding models are useful for predicting human response to biologics compounds. Especially, such models have the ability to integrate preclinical and clinical, in vitro and in vivo information and facilitate rational decision making during various stages of drug discovery and translational research.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-011-9256-y) contains supplementary material, which is available to authorized users.

INTRODUCTION

Although perhaps stating the obvious, the process of discovering and developing a new medicine does not start with a drug candidate, but with the selection of an appropriate target for which there is evidence of involvement in a disease pathophysiology. Based on the context of the disease state, a decision must be made as to the modality of the desired therapeutic. One then needs to decide how to tackle said target. Should one go for a new chemical entity, or a biologic such as a monoclonal antibody? Antibodies are naturally generated large molecules that have evolved in animals to fight infections. Monoclonal antibodies, whether they are generated from animals or from in vitro systems, typically have better safety profiles and a higher historical probability of success to be developed and introduced to the market compared with more traditional low molecular weight pharmaceuticals (1). Additionally, much historical data exists about the behavior of monoclonal antibodies in both the presence and absence of various targets. However, even with these advantages, several considerations must be still made. For example, what is the impact of target location, expression level and turnover? What binding affinity should be specified to allow for binding to the desired target and modulation of disease? Does one need several cycles of (expensive) affinity maturation to achieve a picomolar dissociation constant (K_D), or would nanomolar be sufficient?

Calculations can be done in order to provide approximate answers to these questions. Mathematical models can describe the distribution and pharmacokinetics of biological drugs such as monoclonal antibodies (2). They can also describe the tissue distribution, expression level and turnover of interesting targets (3). Biochemical binding reactions can be incorporated to describe the formation of drug–target complexes, whether they occur in the bulk solution (4), or on cell surfaces (5). The models can be anything from simple, one-compartment (single bucket) representations of the body (6), through to more complex but physiologically realistic models with many tissues complete with blood flows, vascular endothelial filtration, and lymphatic drainage (7). While such models can be relatively straightforward to write from a mathematical perspective (for those skilled in the art), significant amounts of information on the likely levels and rates of movement of both biological drug and target around the body are needed to parameterise the model. For biologics such as monoclonal antibodies, these are available from the work done on the pharmacokinetics of many examples, either in the form of simple two-compartment, plasma and lumped tissues (8) or as more extensive physiologic-based pharmacokinetic models (9). Information on the target is often more difficult to find. This can come from basic physiological experiments, conducted either within one’s own institute or gleaned from published literature.

In this paper, we present an example of a feasibility analysis for a monoclonal antibody (mAb) with the ability to bind to human cytomegalovirus (HCMV). As a member of the herpesvirus family of viruses, HCMV has the ability to infect the host for life. While the vast majority of infections are asymptomatic, HCMV is a significant cause of morbidity and mortality in immunocompromised hosts, such as chemically immunosuppressed transplant patients, virally immunosuppressed AIDS patients, and in the developing fetuses of immune naive pregnant women. The use of antibodies for treatment of cytomegalovirus (CMV) infection in a congenital setting has been tested in the clinic (11). Cytotect (Biotest) is a commercially available product comprised of pooled IgG from human donors that is tested for a certain level of anti-glycoprotein B (gB) reactivity. Despite its reported success, Cytotect as a therapy has many drawbacks, including the inherent risks associated with human blood products, the batch to batch variability and the fact that only a small portion of the preparation is actually biologically active. While the majority of IgG found in Cytotect is not directed against CMV, the active portion is directed against the glycoproteins involved in virus entry and fusion. CMV encodes a number of envelope glycoprotein complexes which are needed for infection of various cell types, such as gB, gM/gN, gH/gL/gO, and gH/gL/UL128/Ul130/UL131 (12). A monoclonal antibody targeting functional glycoprotein complexes of CMV is thought to remove the negative aspects of Cytotect and be able to provide therapy in the clinic. A model was developed that described viral dynamics and impact of antibody binding to certain glycoproteins of the virion envelope for inhibiting viral infection. Through dose–response–time simulations, it was used to set the specifications for the level of affinity needed to achieve a desired level of clinical efficacy, prior to initiation of the search for drug candidates.

Once a drug candidate has been produced, the next stage is to check the pharmacokinetics (PK) and pharmacodynamics (PD), assess the candidate for its safety liabilities, and, taking into account any adverse effects that may be observed in toxicology testing, project and decide on a minimum effect level that would be acceptable to be observed in a first-in-human study. Note here that the well-known acronym, MABEL (10), has been rephrased as the minimum acceptable biological effect level. This enables greater focus to be placed on the clinical acceptability of said biological response, whether it is adverse or pharmacologic, in healthy volunteers or patients. The level must therefore be a clinical decision, informed by an integration of available information from experts in the disease area and toxicology, supported by quantitative scientists. To illustrate this process, an example is given of an anti-cell surface target monoclonal antibody which depletes the subset of blood cells carrying the cell-surface target. A pharmacokinetic–pharmacodynamic target binding and cell turnover model described a cynomolgus monkey pharmacology study and enabled the estimation of a level of blood cell subset depletion that was deemed acceptable by the clinical team. This level of depletion was then converted to a dose through simulation.

METHODS

Monoclonal Antibody Targeting Cytomegalovirus Glycoproteins

A mathematical model that took into account in vitro potency and mAb affinity was developed to guide the identification of a candidate likely to satisfy the clinical criteria for therapeutic efficacy.

The in vitro potency was measured in a neutralization experiment as previously described (13). In brief, cells were seeded into 96-well plates at 8,000 cells per well and were incubated overnight at 37°C under 5% CO₂. The next day, antibody was diluted in serum-free media and mixed with or without CMV virus for 1 h at 37°C under 5% CO₂. After the 1-h incubation, the antibody and virus mixture was incubated at 37°C under 5% CO₂ for 3 h followed by an overnight incubation at 37°C under 5% CO₂. Cells were fixed with 4% paraformaldehyde, permeablized with phosphate buffered saline (PBS) containing 0.1% Triton X-100 and washed. Primary antibody was then added to each well consisting of PBS containing 0.2% Gelatin and mouse anti-CMV immediate early antigen (IE) antibody (Millipore). After 1 h incubation, the primary antibody was removed and wells were washed three times with PBS. Each well then received secondary antibody consisting of AlexaFluor goat anti-mouse 594 antibody (Invitrogen) and 4′,6-diamidino-2-phenylindole (Invitrogen) in PBS. After 1 h, the secondary antibody was removed and wells were washed three times with PBS. Plates were then read using a Cellomic ArrayScan®VTI HCS reader. The percent infectivity for each antibody dilution was calculated by dividing the number of CMV IE-positive cells by the number of cells and multiplying by 100. Relative percent infectivity was calculated by dividing the percent infectivity for each antibody by the percent infectivity of the positive control. The concentration of antibody required to neutralize 50% of virus particles (IC₅₀) was determined from a standard curve which was generated by graphing the relative percent infectivity of each virus by the μg/ml of antibody.

The model consisted of standard viral load components similar to those in the viral dynamics models established for HIV or hepatitis C virus (HCV) (14,15) combined with a PK/PD component to describe mAb distribution and binding; binding to the glycoprotein complex was modeled instead of virus as a whole, however. The model schematic is shown in Fig. 1 with the equations below.

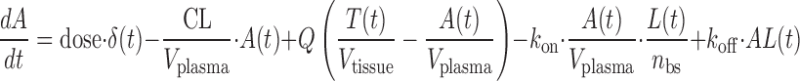1

2

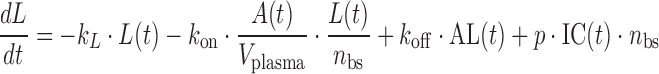3

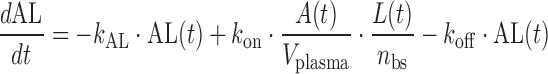4

5

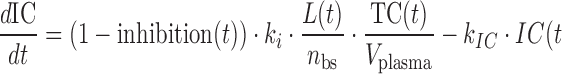6

7

8

where A(t) free antibody amount in plasma [nmol], T(t) free antibody amount in tissue [nmol], δ(t) Dirac delta function describing the injection bolus, Q distribution clearance [L/day], V_plasma plasma volume [L], V_tissue tissue volume [L], k_on [(nM⁻¹ day⁻¹)] and k_off [1/day] rate constants for antibody binding to its target, L(t) free glycoprotein complex in plasma [nmol], AL(t) bound antibody amount in plasma [nmol], TC(t) amount of target uninfected cell in plasma [nmol], IC(t) amount of infected cell in plasma [nmol], k_L death rate of virus [1/day], k_AL death rate of bound antibody [1/day], k_TC death rate of target cell [1/day], k_IC death rate of infected cell [1/day], p production rate of virus from infected cell [1/day], s_TC synthesis rate of target cell [nmol/day], k_i infection rate [copies mL⁻¹ day⁻¹], n_bs number of binding sites of glycoprotein complex on the surface of each virus, occupancy(t) is the glycoprotein complex binding occupancy rate, inhibition(t) inhibition rate of infection. Antibody clearance CL [L/day] was assumed to occur from both plasma and tissue interstitia. Fluid phase endocytosis can occur from both the blood and from the tissue side of vascular endothelia. That fraction of IgG not rescued by the neonatal Fc receptor FcRn is catabolised in lysosomes (16,17).

Fig. 1.

Schematic of viral load model with mAb binding. Cytomegalovirus infects the host cell to become infected cell which produces more viruses. The mAb binds to the virus which prevents the infection. Host cell has proliferation, and all the entities have their own eliminations through certain mechanisms. The mAb distributes in both plasma and peripheral interstitial tissue. Each of the entities is modeled as a compartment. Each of these processes and interactions is described using a system of mathematical equations. Model parameters are based on informed assumptions or are estimated based on literature and internal experimental and clinical data

Antibody PK was assumed to be similar to other IgG1 (molecular weight (MW) of 150 kDa), described with a two-compartment model using a CL of 0.2 L/day, V_plasma 2.5 L, V_tissue 2.6 L, and Q 0.5 L/day (Eqs. 1–2). Antibody binding to glycoprotein complex was modeled with rate constants k_on and k_off (Eqs. 1, 3, and 4), which were used to explore antibody binding affinity requirements. Viral kinetics were modeled as virus (MW 10⁵ kDa) infected uninfected cells (Eq. 5) then becoming infected thereby producing more viruses (Eqs. 3, 6). The effect of antibody binding to glycoprotein complexes was to inhibit the ability of the virus to infect cells; infectivity depends on the proportion of glycoprotein complexes bound (Eqs. 5, 6, 7, and 8). The inhibition function was assumed to be zero when less than 30% of glycoprotein complexes were occupied, unity when more than 90% occupied, with a linear function between the two extremes (Eq. 8).

Immune responses were assumed to be negligible, since the target populations are immunosuppressed transplant patients or at-risk pregnant women. The following additional model assumptions were made: (1) clearance of free and mAb-bound viruses are comparable, such that the dose estimates are conservative; (2) each virus presents 10–1,000 glycoprotein complexes but only show the results with 100 glycoprotein complexes, which is a typical abundance with this virus family (12,18); (3) each infected cell produces 100 viruses, which represents an internal experimental result that 10⁶ infected cells yields 10⁸ pfu (plaque forming unit, approximately 100 pfu/cell) (19); (4) values of half-life estimated from in vitro experiments are 1 day for virus, 4 days for infected cells, and 30 days for normal uninfected cells; (5) mAb molecular and PK properties in human are similar to other IgG antibodies. The infection rate k_i was estimated by matching the data from the in vitro neutralization experiment. The initial number of target cells was estimated by matching the human CMV infection viral load curve from literature (20).

Then dose–response–time simulations were conducted with various binding affinities to investigate the level of affinity and in vitro potency needed to achieve a desired clinical efficacy. The simulations were run with the Berkeley–Madonna software, version 8.0.1 (1997–2000 Robert I Macey and George F Oster).

Mechanistic Modeling for First-in-Human Dose Determination

An antibody compound targeting a blood cell surface receptor was being developed to treat, potentially, a range of diseases. The antibody acted as both a blocker of proliferation and a facilitator of antibody-dependant cellular cytotoxicity (ADCC), resulting in depletion of the targeted blood cell subtype—abbreviated “target cell” in the remainder of the text.

In order to support determination of a safe starting dose and the subsequent dose escalation for the first-in-human study, a mechanistic model for human pharmacokinetics and pharmacodynamics including receptor occupancy (RO) and target blood cell depletion was developed based on monkey and in vitro data. The purpose of the modeling work was to predict the compound’s pharmacological effect in terms of target cell depletion, to support definition of a safe starting dose in human after reconciliation with other pre-clinical findings. The mechanistic model was first developed in cynomolgus monkeys. Namely, the model was built and fitted to describe monkey data from a dose–range finding study (PK, RO, and target blood cell depletion over time). The dose–range finding study included six animals in each of the three single intravenous dose levels (0.02, 0.8, 16 mg/kg). PK samples were taken at 2 and 6 h, then 1, 4, 7, 14, 21 days post-dose, and RO and target blood cell measurements, obtained respectively using immunoassays and FACS, were conducted weekly for 10 weeks. Subsequently, parameters of the monkey model were adapted to the human case using both in vitro measurements and allometry scaling.

The monkey PK/PD model consisted of a set of deterministic ordinary differential equations describing the dynamics of antibody (Eq. 9), free receptor, receptor bound to antibody, and target blood cells (Eq. 10). Antibody monkey PK was described using a two-compartment model thus assuming conventional antibody distribution (first three terms in Eq. 9). In addition, the antibody was allowed to bind to target receptors, with an affinity estimated from a monkey whole blood binding assay (fourth and fifth terms in Eq. 9). The central compartment clearance was estimated through data fitting, with a Michaelis–Menten process introduced to account for an additional saturable elimination process (i.e., accelerated drop in PK below a given concentration) observed in all PK curves around 10 μg/mL (last term in Eq. 9). As a result, the amount of antibody in plasma was described by the differential equation Eq. 9 below.

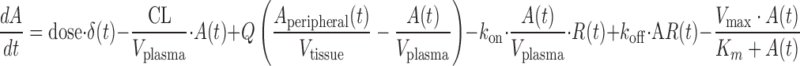9

where A(t) : free antibody amount in plasma [nmol], δ(t): Dirac delta function describing the injection bolus, CL non-specific clearance from the systemic compartment (plasma) [L/day], Q the antibody flow rate between plasma and tissue [L/day], V_plasma and V_tissue volume [L], k_on [nmol⁻¹ day⁻¹] and k_off [day⁻¹] rate constants for antibody binding to its target, R(t) free target amount in plasma [nmol L], AR(t) bound antibody amount in plasma [nmol]. V_max [day⁻¹] and K_m [nmol] are Michaelis–Menten constants.

Target blood cells were assumed to carry a fixed total number of target receptors. In absence of drug, target blood cells were hypothesized to turn over at a constant rate k_out. Accelerated depletion was driven by receptor occupancy according to the equation Eq. 10:

10

where B is the target blood cell number [cells/μL]; k_in, cell production rate [cells.μL⁻¹ day⁻¹]; k_out, cell depletion rate in absence of drug [day⁻¹]; E_max, maximal increase in depletion [unitless]; RO, percentage receptor occupancy directly linked to A(t), R(t) and AR(t); IC₅₀, receptor occupancy at 50% of the maximum increase in depletion. CL, Q, V_plasma, V_tissue, Michaelis–Menten elimination parameters, k_in, k_out, E_max, and IC₅₀ were all estimated by sequential fit to monkey experimental data (pharmacokinetics A(t), then RO through AR(t), finally target cell count B(t)) with the Berkeley–Madonna software.

The same model structure was subsequently used for the human PK/PD model, except that the Michaelis–Menten parameters were removed, i.e., V_max was set to zero. Not including the unidentified saturable mechanism in human (empirically represented by Michaelis–Menten equation in monkey) enabled simulation of a worse-case scenario for target cell depletion; therefore, a more conservative assumption for safety. All other model parameters were adapted to the human case. Specifically, antibody binding affinity to the target (1/K_d) was increased by a factor of 3 (i.e., 92/30) reflecting species cross-reactivity; the in vitro EC₅₀ was 92 pM for target-transfected monkey cells versus 30 pM for target-transfected human cells, measured by FACS titration. Similarly, k_on was assumed to be the same as in the monkey, with k_off decreased by a factor 3 (since K_d = k_off/k_on). For the PD, IC₅₀ from Eq. 10 was increased by a factor of 2 (i.e., 4.7/2.2) reflecting species cross-reactivity; in vitro EC₅₀ for ADCC was 4.7 pM for monkey receptor target on peripheral blood mononuclear cells—PBMC—versus 2.2 pM for human receptor target on PBMC, measured by FACS analysis. All other parameters were adapted to the human case using allometric laws (21–24); each PK or PD parameter was scaled using the ratio of human (BW_Human70 kg) and monkey body weights (BW_Monkey3.5 kg) according to:

11

where, P is the parameter (CL, Q, V_plasma, V_tissue, k_in, k_out, or E_max), and b the unitless allometric exponent. Metabolic elimination and distribution represented in CL and Q were scaled with b equal to 0.8 (24) and 0.75 (21,22) respectively. Volumes and E_max were scaled with b set to 1; the same body density and maximal effect was assumed across species. The rate k_out was scaled with b set to 1, that is, it was assumed that target cell removal in absence of antibody occurred at the same rate in monkeys and human; k_in is directly dependant on k_out and plasma volume, and hence was scaled with b set to the ratio of plasma volumes in both species.

The human model was then used to simulate PK/RO profiles and target blood cell counts following a range of single dose injections in human. The MABEL, first starting dose and dose escalation in human were determined based on these simulations and clinical considerations of the acceptability of a level of target cell depletion at the first dose.

Computer codes for both examples are provided in Supplementary Materials.

RESULTS

Monoclonal Antibody Targeting Cytomegalovirus Glycoproteins

The in vitro neutralization experiment was simulated to determine the infection rate by matching the experimental data. The simulation followed the procedure as follows: (1) 5,000 virions and mAb (with defined concentrations) were mixed for 60 min; (2) 10,000 cells were then added into the mixture for 3 h; (3) cells were then washed by removing the mAb, virus and the binding complex; finally (4) infection was allowed cells to continue for 24 h. At the end of the experiment, infectivity was measured as the percentage infected cells and percentage relative infectivity to the control with no mAb treatment. Negligible host cell proliferation during the experiment was assumed. Experimental data showed that the infectivity with no mAb treatment was 40–50%, compared with that predicted by the model of 45.3% with an infection rate of 1.2 × 10⁻⁶ copies mL⁻¹ day⁻¹.

Human CMV infection was modeled by adding the antibody PK functions, with viral kinetics only represented for the plasma. Other model structure and parameters were exactly the same as those used for modeling in vitro neutralization experiment. Emery et al. (20) reported that patients reached a viral load of 5–7 logs in approximately 1 week. The model specified parameters that enabled the CMV viral load curve of patients to reach 7 logs within 1 week, where the target cell concentration TC₀ was estimated to be 10⁵ cells/mL. Target cell synthesis rate s_TC was model ed as k_TC*TC₀ based on equilibrium assumption on the initial condition.

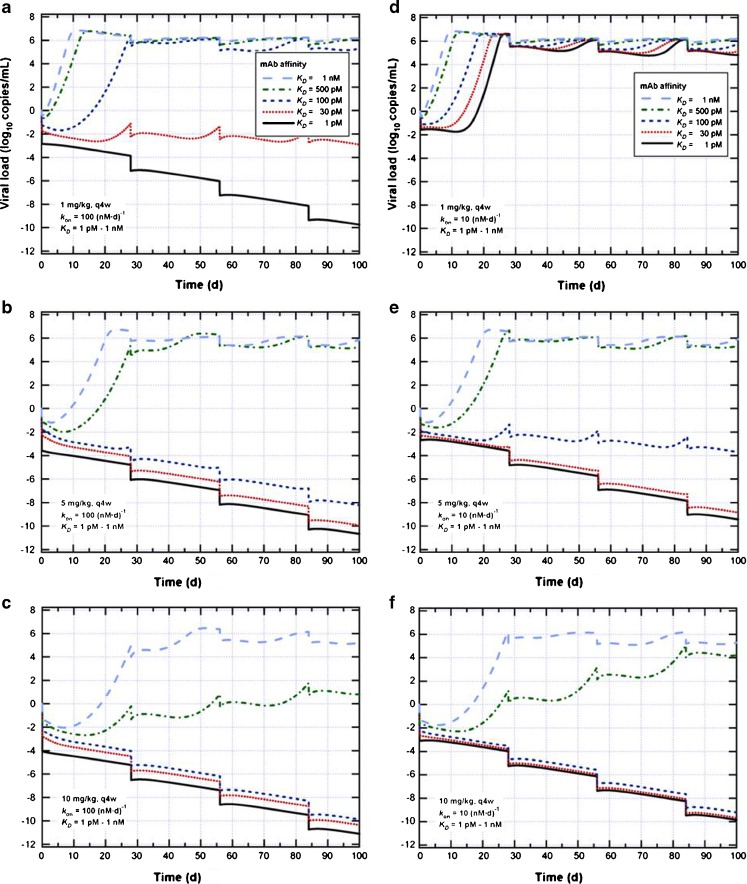
The model was then used to predict the viral load for various mAb affinities, doses, and dosing frequencies (Fig. 2). In cases of prophylactic treatment (assuming zero log10 copies mL⁻¹ viral load pre-treatment, as shown in Fig. 2), treatment initiated at the viral load detection limit (not shown); treatment for symptomatic patients was simulated (not shown). The clinical input was that 5 mg/kg every 4 weeks (q4w) was preferred. A range of parameters was explored, including k_on between 10 and 100 nM⁻¹ d⁻¹, K_D between 1 nM and 1 pM, dose from 1 to 10 mg/kg. For treating transplant patients, the goal of the treatment was to prevent viral load from increasing during the 100-day period of immunosupression immediately following a transplant. For the pre-fixed base case of 5 mg/kg q4w and k_on of 100 nM⁻¹ d⁻¹, an affinity of 100 pM was predicted to be the minimal affinity requirement to suppress infection; otherwise, virus was predicted to increase over time. Decreasing the desired dose to 1 mg/kg raised the required affinity to 30 pM. If k_on were relaxed to 10 nM⁻¹ d⁻¹, a dose ≥5 mg/kg and a minimal affinity of 100 pM was predicted to be required to suppress the infection. Increasing the dose from 5 to 10 mg/kg did not reduce the required affinity.

Fig. 2.

Model simulations of viral load versus time with different settings for q4w dosing. For prophylactic treatment, the viral load is assumed to be 0 log10 copies/mL. The three figures on the left are with k _on = 100 (nM day)⁻¹ and 1 (a), 5 (b), 10 (c) mg/kg, respectively, from top to bottom; the three figures are the right (d, e, and f) are the same except with k _on = 10 (nM day)⁻¹. In each figure, K _D values are simulated as 1 nM, 500, 100, 30 and 1pM.

Since at the early stage of the discovery program, it was difficult to obtain accurate estimates for k_on and K_D values since IC₅₀ values from the in vitro neutralization experiment were usually reported, a wide range of k_on (1–3,000 nM⁻¹ d⁻¹) and K_D (1 pM–1 nM) were simulated and mapped out to corresponding IC₅₀ ranges, as shown in Table I, in order to guide candidate selection. For each k_on and K_D pair, a series of in vitro neutralization experiments were simulated with a range of mAb concentration as input and relative% infectivity as output, such that the corresponding IC₅₀ ranges can be decided. In summary, in order to have an efficacious dose of 5 mg/kg every 4 weeks, the model predicted that the mAb should have an association rate constant k_on of 10 nM⁻¹ d⁻¹ and an equilibrium dissociation constant K_D of 100 pM to ensure viral suppression; for the desired dose to be as low as 1 mg/kg every 4 weeks, more stringent binding parameters were required: k_on 100 nM⁻¹ d⁻¹ and K_D 30 pM. For both of these cases, the model predicted an IC₅₀ of <0.1 μg/mL in the in vitro neutralization assay, which was used to guide candidate selection.

Table I.

Correlating in vitro IC₅₀ with Clinical Outcome

IC50 [μg/mL]	k on [(nM∙d)−1]
		1	10	100	200	1,000	3,000
K D [nM]	0.001	0.1–1.0	0.01–0.1	<0.01	<0.01	<0.01	<0.01
	0.03	0.1–1.0	0.01–0.1	0.01–0.1	<0.01	<0.01	<0.01
	0.1	0.1–1.0	0.01–0.1	0.01–0.1	0.01–0.1	0.01–0.1	0.01–0.1
	0.5	0.1–1.0	0.1–1.0	0.01–0.1	0.01–0.1	0.01–0.1	0.01–0.1
	1	1.0	0.1–1.0	0.1–1.0	0.1–1.0	0.1–1.0	0.1–1.0

The corresponding IC₅₀ ranges with certain combinations of k _on and K _D values

Mechanistic Modeling for First in Human Dose Determination

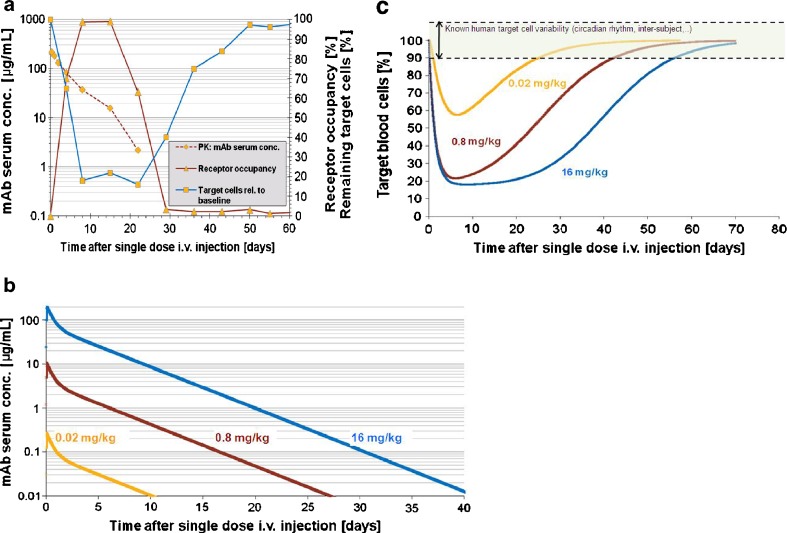
Dose linearity in the initial parts of the antibody pharmacokinetics (high concentrations) was observed in all monkeys from the three dose levels in the dose–range finding study. The PK was not dose linear since an accelerated elimination consistently appeared around 10 μg/mL in monkeys from all dose groups (Fig. 3a). The monkey model predicted a close relationship between PK and receptor occupancy with a target plasma concentration of about 10 μg/mL for maximal occupancy (75–100% occupied receptors). Systemic clearance was estimated by data fitting and corresponded to a 3.5-day half-life. Antibody depletion through target blood cell removal alone could not explain the discontinuity at ∼10 μg/mL in the slope of the PK curve (Fig. 3a). It was therefore concluded that the antibody was also being cleared through another saturable mechanism, for example immunogenicity or endocytosis of the antibody-receptor complex. This process was described in the model by a straightforward Michaelis–Menten elimination of the antibody with a V_max of 0.6 nmol/day and K_m of 3 nM. Michaelis–Menten elimination was chosen since it described a saturable process that became apparent at a fixed concentration (related to K_m) with only two parameters. However, the Michaelis–Menten model was an empirical and not a mechanistic representation of a second target-mediated drug disposition (TMDD) mechanism. Both Michaelis–Menten and cell-binding mechanisms were retained in the model to ensure that due account of both processes was incorporated in the human prediction, even though the cell binding mechanism was not required for PK fitting, only for calculating target binding. Target blood cell counts—defined and measured as cells carrying the target receptor—followed receptor occupancy closely; target blood cells started recovering immediately after receptor occupancy fell below about 75–100%. At the time of initial recovery, antibody concentrations were about 10 μg/mL. Hence, the target plasma concentration for maintenance of maximal target blood cell suppression in cynomolgus monkey was estimated to be about 10 μg/mL.

Fig. 3.

MABEL determination for a mAb binding to blood-based cell surface receptors. a Example of data (from one monkey) used to build the PK/PD monkey model. In Cynomolgus monkeys, depletion of target cells (outlined as percentage of remaining target cells in circulation, relative to baseline; on right axis) is modulated by receptor occupancy (RO,% occupied receptors from all available receptors at the specific time point; on right axis) on target cells. A time delay exists between mAb injection (i.v.) (time = 0) and rise in receptor occupancy (days 0–7) and target cell depletion (days 0–7). Only when mAb serum concentration (PK; left axis, logarithmic scale) falls below a certain level (∼10 μg/mL for this mAb) decrease in RO (days 15–29) is observed followed by remission, i.e., recovery of target cell counts (days 22–50). b Simulation result: human PK dose-response for three single i.v. doses and a half-life hypothesized to be at the lower end (3.5 days). c Simulation result: human target blood cell depletion dose-response for three single i.v. doses. Intensity and duration of the target cell suppression depend on dose. On this figure, MABEL corresponds to a dose <0.02 mg/kg, where suppression of target cells is minimum and transient (always less than <10%, which corresponds to normal target cell variability in human). (Note: Data was blinded in this example, so as to not reveal information on the actual Novartis compound)

Maximal target blood cell suppression (the nadir at high doses) was estimated to be 80% (70–90%) of the initial target blood cell count in monkey. It was assumed to be similar in the human model. The duration from maximal suppression to recovery of >90% initial target blood cells was predicted to be dose independent, approximately 40 days (Fig. 3c).

The target blood cell half-life in the absence of drug was estimated between 5 and 10 days in the monkey. This corresponded to a turnover rate, k_out, of 7–14% per day. This is above the 2% per day turnover rate measured with no drug in a different non-human primate (rhesus macaques) using BrdU labeling (25). One explanation for this discrepancy is the disease-modifying nature of the antibody that changed the blood cell subset population. In particular, a compensatory mechanism of increased associated ligand concentration has been observed in monkey (data not shown). This could explain the increased turnover of target blood cells in monkey necessary to fit the data from the monkey dose–range finding experiment. The human turnover rate was obtained through allometry, and was also larger from the measured turnover rate in non-treated human subjects (26). Although k_in may not be constant in the monkey (given the compensatory changes), assuming no compensation in man is a worse-case scenario predicting more depletion and therefore conservative for dose selection.

Target blood cell depletion over time was predicted for human for a range of single dose levels (three dose levels shown on Fig. 3c). The MABEL was defined as the dose giving 10% target blood cell depletion, corresponding to natural target blood cell variability. The MABEL as defined by target cell depletion was reconciled with other preclinical findings to choose the first in human dose. Dose escalation was also supported by these predictions, so as to optimize information collected on the dose target blood cell depletion response in human.

DISCUSSION

The two examples presented herein demonstrate that the development of mechanism-based PK/PD models and the use of simulation to predict clinical outcome in the early stages of a project provides a firm quantitative basis on which to select lead candidates and design the first in human trials for biologics and chemical drugs alike. Indeed, assessing target feasibility before candidate searching has been initiated can set the binding potency specifications for said candidates and provide a valuable contribution to program strategy—including answering the question as to whether a biological drug is even sensible.

Mathematical modeling of viral dynamics was initially proposed for HIV infection (14) by modeling the interactions between populations of viruses and immune system cells. The model was then adapted for hepatitis B virus and HCV infections (27,28). For the antibody feasibility analysis, a similar model structure was adopted for cytomegalovirus, the model parameters being estimated from existing experimental data or knowledge. However, a major difference in our model was antibody binding to glycoprotein complex was modeled instead of virus as a whole, since the antibody was known to target the specific type of glycoprotein complexes. Beside antibody affinity, the number of targeted glycoprotein complexes turned out to have a major impact on potency (not shown). This is the first application of viral load modeling for cytomegalovirus, especially combined with specific antibody binding model, as far as we are aware at this time.

As has been demonstrated herein, creating a realistic biologically oriented model of a system at the target selection stage is not trivial. Although setting out the equations is relatively straightforward, with a number of compartments representing production, distribution and elimination of the target, complete with binding reactions with other entities, setting realistic parameter values is not. Very often, there is a distinct lack of knowledge of the molar expression levels of target molecules at various sites in the body, or of the production and turnover rates; the suggestion that a target is involved in a disease may only be indirect or circumstantial. Levels of a target may be known only from (relative) gene expression, not the (absolute) protein, with the ratio between one and the other unknown. Yet further, many targets are not expressed only in a disease-related tissue, but in many others, albeit perhaps at lower levels per gram. Yet if the potentially larger mass of these other tissues were to be taken into account, it is perfectly possible for there to be more target in the unaffected non-diseased tissue. The impact of this on the mass–balance disposition of a putative binding agent introduced into the system, i.e., a drug, is rarely considered; yet binding to targets in other tissues may be a primary safety liability and cause of adverse effects. Given some realistic assumptions on protein expression levels and turnover, much can be decided through the creation of a mathematical model, even if it is a gap analysis revealing how little is actually known. The model can then at least indicate, through sensitivity analysis, which information is most critical, and direct appropriate experiments to enable go/no go decisions for a program.

Following on from feasibility analysis, once one has a candidate monoclonal, the importance of the determination of a starting dose for first-in-human studies was thrown into the spotlight after the incident with the anti-CD28 superagonist mAb TGN1412 (10). The impact of assessing pharmacological as well as adverse effects in determining a safe starting dose has been stressed, with several guidelines emerging as a result (29). We have presented herein an example of a PKPD-guided MABEL approach for dose determination in a first in human trial. It differs from the traditional no observable adverse effect level (NOAEL) approach in that it examines the desired pharmacological effects as per guideline, quantifying by predicting the dose-concentration-desired response for human. This is particularly relevant for cellular receptor targets, for which binding by a divalent antibody could trigger intracellular pathways through receptor clustering (e.g., anaphylaxis). The MABEL approach is inherently safer than the NOAEL approach, as it takes the lower of the doses anticipated from toxicology and pharmacology. In the general drug development context, the definition of a minimum acceptable biological effect for the first dose of a new compound in man is of paramount importance for compounds where there are significant unknowns. These prototypical compounds, with uncertainty on the consequences of binding the target, should be assessed more rigorously, quantitating mechanism-related pharmacodynamic endpoints (30). The classical development scheme of Phase I safety and tolerability followed by dose range finding (II) and confirmation (III) is more appropriate for compounds where the foreseen uncertainty is low. Using the integrative in vivo and in vitro PKPD approach should also enable a more precise determination of a safe dose at the start of a dose–response in human, as it identifies further sources of uncertainty in the prediction, such as natural target cell variability, turnover of target cells in human, etc. In this respect, it offers the possibility to define a safe starting dose without subjecting the first human patients or healthy volunteers to an overly extended dose escalation process, especially if emerging data from the first cohorts were to be compared with model predictions and dosing escalation adapted accordingly.

Antibody pharmacokinetics differ from low-molecular weight molecules (2). In this report, a simple two-parameter (V_max, K_M) representation was used to empirically describe a non-linearity in monkey pharmacokinetics below drug concentrations of 10 μg/mL. Non-linearity could not be explained solely by immunogenicity, nor solely by antibody removal through its binding to the target blood cell by ADCC (which is present in the model Eqs. 9 and 10). This non-linearity may stem from a combination of immunogenicity and TMDD, that is, antibody depletion through endocytosis in target cells, and/or compound removal along with the target cell by ADCC (already present in the model).

More complex models for TMDD were not used due lack of resolution in the experimental data (in both time and lack of very low concentration data) with resulting difficulties with parameter identifiability, an issue raised by the Gibianskys in 2009 (31). However, a mechanism by which TMDD parameters varied over time as target blood cell counts varied would perhaps be a closer approximation of the true mechanism of antibody elimination.

Translational mechanism-based PKPD modeling for biologics has more applications than feasibility and determination of a minimum acceptable biological effect level for the first-in-man study. For example, after a drug candidate has successfully entered early clinical trials, longer-term toxicology testing is carried out to assure patient safety for chronic treatment paradigms. To set appropriate doses for these extended toxicology studies, one should continue to take account of the differential ability of the compound to bind its target in the preclinical species and man. With biological drugs which target soluble proteins, there is the opportunity to directly quantify the capture of target by measuring the total concentration of target in the serum or plasma (32). Using a PKPD binding model, due account can be taken of interspecies differences in the binding constant and the production and elimination rates of the target (4,5,32–34). In toxicology testing, greater proportions of target should be captured than in clinical studies, thereby assuring patient safety. Similarly, for biologics targeting cell surface receptors, the nonlinear pharmacokinetics seen with target-mediated drug disposition indicate the whole-body level of target occupancy and enable toxicology doses to be appropriately higher than those being used in clinical studies (32).

CONCLUSION

In conclusion, mechanism-based PKPD binding models are useful for predicting the human response to biological compounds, by integrating in vitro and in vivo information, thus that facilitating rational decision making. This can occur from the earliest stages of drug discovery with a physiology-based feasibility analysis for antibodies binding their targets, through translational research with the determination of the minimum acceptable biological response level for a dose in a first human study. Beyond that, there’s the investigation of differing patient populations, diseases, and dose responses; but that is another story.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.